Introduction

The recent discovery of superconducting kagome metals AV3Sb5 (A = K, Rb or Cs) provides new opportunities for exploring many intriguing physical phenomena1,2. In their normal metallic state, charge-density-wave (CDW) order with a 2 × 2 in-plane supercell appears at \(80-105{{{{{\rm{K}}}}}}\)1,3\(.\) The CDW is thought to be highly unconventional, with evidence for time-reversal-symmetry (TRS) breaking suggested by scanning tunneling microscopy (STM)4, muon-spin relaxation (µSR)5, and Kerr spectroscopy6,7,8 measurements, despite the absence of local spins in these materials9. Moreover, multiple experimental probes have revealed that a nematic electronic phase that breaks rotational symmetry emerges within the CDW state10,11. Superconductivity develops at \(T{{{{{\rm{c}}}}}}\approx 0.9-2.5{{{{{\rm{K}}}}}}\), depending on the alkali-metal element A;2,12 interestingly, in the A = Cs compound, STM experiments discovered the signature of a pair-density wave (PDW) persisting across Tc into the normal state13. All of these exotic features call for a complete understanding of the electronic structure of this family of kagome metals.

A detailed study of the magnetic-quantum-oscillation spectrum in CsV3Sb5 suggests modification of the Fermi-surface (FS) topology induced by CDW order14,15. Nevertheless, while the correspondence between the main oscillation branches and the large FS orbits has been clarified, the identification of lower oscillation frequencies \((F < 200{{{{{\rm{T}}}}}})\) remains elusive. Recently, an intriguing proposal invoking a doped Chern insulator state in a kagome lattice suggested that some of these orbits stem from a set of small Chern Fermi pockets (CFPs)16,17. These CFPs host spontaneous orbital-current and large orbital magnetic moments, which contribute to the TRS breaking in the CDW state. Potentially, the large orbital moments are experimentally detectable; however, because the crystal lattice is inversion-symmetry invariant, the orbital moments align antiferromagnetically, with the thermodynamic magnetization nearly completely canceled at zero magnetic field16. Consequently, although the large Berry curvatures carried by CFPs may naturally explain the observations of the giant anomalous Hall18 and anomalous Nernst19,20 effects in CsV3Sb5, obtaining direct evidence of the presence of orbital moments (and therefore the CFPs) has proved challenging.

We address this problem by measuring the Zeeman effect in the target Fermi surface orbits. Given the large orbital magnetic moments, the Zeeman coupling will be significantly enhanced, leading to a large effective g-factor and profound spin-zero effect in the quantum oscillations. Furthermore, most orbits are shown to arise from magnetic breakdown, with the effective masses following the linear relationships expected for breakdown orbits. Finally, the angle dependence of one orbit (or a pair of orbits) reveals that the oscillation amplitude vanishes at two field orientations due to the spin-zero effect. This spin-zero effect yields a large apparent effective g-factor and shows that the orbit’s Zeeman effect is stronger than that of regular band electrons.

Results

Fermi-surface topology from quantum oscillations

Figure 1a shows the de Haas-van Alphen (dHvA) effect (i.e., quantum oscillations of the magnetization) observed using piezoresistive torque magnetometry; to better emphasize the higher dHvA frequencies, the derivative of the torque is shown. The field orientation angle is defined to be \(\theta =0\) for H \(\parallel\) c and θ = 90° for H lying in the ab plane. Using the Onsager relationship21, the dHvA frequencies F are given by \(F=\frac{\hslash }{2\pi e}S\), where \(S\) is a FS extremal-orbit cross-sectional area, \(\hslash\) is the Planck constant over 2π, and e is the electron charge. Therefore, by measuring the dHvA frequencies as θ varies, the sizes and shapes of the various FS sections can be mapped. Figure 1b shows fast-Fourier-transform (FFT) spectra, in which the dHvA peaks are observed at F up to 2000 T. \(F\alpha =20\,{{{{{\rm{T}}}}}}\) is consistent with previous torque and transport measurements22; it was attributed to a closed 3D FS pocket23. \({F}_{\beta }\approx 80\,{{{{{\rm{T}}}}}}\) was reported to have a nontrivial Berry phase in both torque22 and transport15. It is also identified as a small reconstructed Fermi pocket due to CDW band-folding in DFT calculations24 and ARPES25. The frequency near 200 T labeled with an “∗” mark; its origin is as yet unclear. A group of frequencies \(500\le F\le 1000\,{{{{{\rm{T}}}}}}\) results from the triangular FS section at the Brillouin zone corners, and their magnetic breakdown orbits with the small reconstructed FS β.

Fig. 1: dHvA oscillations.
figure 1

a The first derivative of the background subtracted torque as a function of magnetic field µ0H for H \(\parallel\) c. b Fourier transform spectra of the dHvA oscillations. The field ranges of the FFTs are set to \(5-10\,{{{{{\rm{T}}}}}}\) for frequencies below \(450\,{{{{{\rm{T}}}}}}\) and \(10-14\,{{{{{\rm{T}}}}}}\) for higher frequencies. c Illustration of Fermi surface based on the dHvA oscillations. d dHvA frequencies as a function of θ, the angle between the c−axis and H. The lines of \({\varepsilon }_{1}\) and \({\varepsilon }_{2}\) are from the DFT calculation of the Sb Pz orbital close to the Γ and A points separately, using the room-temperature lattice parameters without considering the CDW distortion.

Full size image

ARPES26,27 and STM13,28 experiments suggest the presence of multiple van Hove singularities (vHSs) close to the Fermi energy. To assess the potential impact of the vHSs it is essential to derive the Fermi energy precisely. The origin of the quantum oscillation frequencies \(\approx 2\,{{{{{\rm{kT}}}}}}\) are not yet understood. For example, ref. 29 and ref. 30 attributed the frequency \(F=2\,{{{{{\rm{kT}}}}}}\) to two dissimilar magnetic breakdown orbits.

Here we propose another possibility, that both \({F}_{{\varepsilon }_{1}}=1300\,\)T and \({F}_{{\varepsilon }_{2}}=2000\) T are from the Sb Pz orbital bands. It is known that the bands from the Sb Pz orbital close to the Γ and A points are robust against CDW distortion2,26. Consequently, it should be possible to infer the Fermi energy by mapping the warped cylindrical Fermi surface (Fig. 1c) at the center of the BZ. The band structure calculated using the room-temperature lattice parameters without considering the CDW distortion is given in Supplementary Fig. 1, whilst Fig. 1d shows the θ−dependent FFTs of the dHvA data; the pink curve \(({F}_{{\varepsilon }_{1}})\) and the purple curve \(({F}_{{\varepsilon }_{2}})\) are derived from the DFT calculations by using room temperature lattice parameters. (Note that \({\varepsilon }_{1}\) is the minimum area “neck” orbit at \({k}_{z}=0\), and \({\varepsilon }_{2}\) at \({k}_{z}=\pi /c\) is the maximum area “belly” orbit of this warped cylindrical FS.)

Reconstructed small Fermi surface and magnetic breakdown

\(F=560\,{{{{{\rm{T}}}}}}\) and \(650\,{{{{{\rm{T}}}}}}\) are the first two peaks in the FFT spectra between 500 and 1000 T [Fig. 1b], and are consistent with prior transport measurements in small magnetic fields14. By contrast, previous torque22 and resistivity15 measurements in fields of up to 35 T detected only two peaks in this range, at around 720 T and 800 T, while tunnel diode oscillator (TDO) data show a group of oscillations between \(500-1000\,{{{{{\rm{T}}}}}}\)31. Whilst these observations are at first sight apparently inconsistent, similar behavior is clearly seen across various magnetic field ranges, as shown in Fig. 2a and Supplementary Fig. 2 for different tilt angles.

Fig. 2: Magnetic breakdown orbits.
figure 2

a Fourier Transform spectra of dHvA and SdH oscillations for various FFT windows at \(\theta =-22^\circ\). b FFT amplitudes of dHvA oscillations at various temperatures at \(\theta =-22^\circ\). The field ranges for Fourier are 8-14 T. c Effective masses of γ \(\leftrightarrow\) β and δ \(\leftrightarrow\) \(\beta ^{\prime}\) breakdown orbits. Error bars reflect the error from fitting the temperature dependence of quantum oscillation amplitude to the Lifshitz-Kosevich formula. Insert: Sketch of magnetic breakdown orbit \(\gamma +\beta\) between the triangular shaped Fermi surface and the ellipsoid-shaped β pocket in the kZ = 0 plane. The arrow indicates the carriers’ k−space paths of the hole Fermi surfaces.

Full size image

Figure 2 present frequencies in the range \(500-1000\,{{{{{\rm{T}}}}}}\) at an angle of 22° between the c-axis and the applied magnetic field H; owing to the quasi-two dimensional nature of CsV3Sb5, the FFT peaks have larger separations compared to H \(\parallel\) c and are hence easier to view. The Fermi surface is illustrated in Fig. 1c; γ and δ are the triangular hole orbits at \({k}_{z}=0\) and \({k}_{z}=\pi /c\), respectively. Of the small reconstructed orbits due to the CDW, β is close to γ, and \({\beta }^{{\prime} }\) is near δ. These frequencies are in agreement with a 2 × 2 × 2 CDW DFT calculation24 and ARPES experiments25. Figure 2a shows the evolution of the frequencies over various field ranges. For \({\mu }_{0}H\le 10\,{{{{{\rm{T}}}}}}\), only Fγ and Fδ are observed, but as µ0H increases above 10 T, the probabilities of tunneling between γ and β or between δ and \({\beta }^{{\prime} }\) increase sufficiently for peaks at \({F}_{\gamma +n\beta }\) and \({F}_{\delta +{n}^{{\prime} }{\beta }^{{\prime} }}\) to appear in the FFTs (Fig. 2b); here, n, \({n}^{{\prime} }\) are integers, and \({F}_{\beta }\approx {F}_{{\beta }^{{\prime} }}\approx 80\,{{{{{\rm{T}}}}}}\). For a still higher-field Fourier window of \(18-45\,{{{{{\rm{T}}}}}}\), the \({F}_{\gamma +2\beta }\) and \({F}_{\gamma +3\beta }\) magnetic-breakdown orbits dominate the FFTs. Figure 2c shows that as the orbit areas increase in steps of \({F}_{\beta }\) or \({F}_{\beta {\prime} }\), the measured effective masses also increase in steps of \(\approx 0.1{m}_{{{{{{\rm{e}}}}}}}\), where \({m}_{{{{{{\rm{e}}}}}}}\) is the free-electron mass; the step size is the same as the effective mass of the reconstructed small β FS pocket on its own14,15. (Note that Lifshitz-Kosevich (LK) mass fits are shown in Supplementary Fig. 3.) These observations are entirely consistent with magnetic breakdown orbits32; the triangular FS orbits γ, δ and the reconstructed small FS orbits \(\beta\), \({\beta }^{{\prime} }\) are all hole orbits, so the frequencies and the effective masses of the breakdown orbits should be given by approximately by simple sums of the frequencies and masses of the component orbits (i.e. \(f={f}_{1}+{f}_{2},{m}^{* }={m}_{1}^{* }+{m}_{2}^{* }\), see Supplemental Note 1) especially given that the fact that the component orbits are close to each other in k-space).

Effective g factor determination

In order to determine the g-factor, the magnetic field must be tilted away from the c-axis21. Because the FS sections in CsV3Sb5 are either quasi-two-dimensional or very elongated in the c-direction, features such as the breakdown orbits will be displaced to higher fields (roughly \(\propto 1/\cos \theta\)) as θ increases. Hence, we turn to pulsed magnetic fields of up to 75 T to follow the features of interest in the magnetotransport to higher angles. However, measurements of the resistance of these CsV3Sb5 samples are challenging in pulsed fields because of the small resistivity of CsV3Sb5 (ρ0 ≈ 1µΩ cm), the morphology of the single crystals, which are also difficult to cut or shape, and the short duration (∼10 s of ms) of the magnet pulse. Therefore, the pulsed-field transport studies as a function of θ employ the contactless MHz Proximity-Detector-Oscillator (PDO) technique.

The crystals are fixed to small pancake coils coupled to the PDO circuit. Shifts \(\triangle f\) in the PDO’s resonant frequency f result from changes in the coil inductance caused in turn by changes in the sample skin-depth33,34; for small changes in resistivity, \(\triangle f\propto -\triangle \rho\). In Fig. 3a, f decreases with magnetic field, consistent with the positive magnetoresistance. Above 30 T, the breakdown orbits \({F}_{\gamma +2\beta }\) and \({F}_{\gamma +3\beta }\) dominate, and in Fig. 3b, the field is multiplied by \(\cos \theta\) to compare the amplitude and phase at various θ directly. Near \(\theta =17^\circ\) the amplitude of the oscillations vanishes, and they exhibit a π phase shift on crossing this angle. This angle dependence is made clearer using FFTs of the data; Fig. 3c gives the Fourier amplitudes of \(\gamma +2\beta\) (red) and \(\gamma +3\beta\) (blue), derived using a Gaussian fit, showing that both vanish around \(\theta =17^\circ\) and \(\theta =30^\circ -37^\circ\). (The two frequency values are fixed parameters derived from fitting the data to the LK formula. see Supplementary Fig. 4.) We use the following LK21,34 formula to model the SdH oscillations:

$$\Delta f=A{B}^{\frac{1}{2}}{R}_{T}{R}_{D}{R}_{S}\cos \left(\frac{2\pi F}{B}+\phi \right)$$
(1)
Fig. 3: Spin-zero methods.
figure 3

a The PDO frequency f for CsV3Sb5 at various tilt angle θ measured at \(T=1.5\,{{{{{\rm{K}}}}}}\). b Oscillatory component \(\triangle f\) versus \(1/({\mu }_{0}H\cos \theta )\) at various θ. The oscillatory amplitude vanishes and with the corresponding phase flips when crossing 17°, indicating a”spin-zero” around 17°. c FFT amplitudes of SdH oscillations at various angles θ in the Fourier window \(40-72\,{{{{{\rm{T}}}}}}\). The FFT amplitudes of \(\gamma +2\beta\) and \(\gamma +3\beta\) are derived by Gaussian fit with the frequencies are fixed by the LK fitting for ∆f versus \(1/{\mu }_{0}H\). d, e Oscillatory amplitudes as a function of angle θ of \(\gamma +2\beta\) and \(\gamma +3\beta\), separately. The black lines are the fitting curves which give \(g=15\) for \(\gamma +2\beta\) and \(g=18\) for \(\gamma +3\beta\). The effective mass \({m}_{\gamma +2\beta }^{* }\left(0^\circ \right)=0.7{m}_{e},{m}_{\gamma +3\beta }^{* }\left(0^\circ \right)=0.8{m}_{e}\), Dingle temperature\({T}_{D}(\gamma +2\beta )=27\,{{{{{\rm{K}}}}}}\), \({T}_{D}(\gamma +3\beta )=28.6\,{{{{{\rm{K}}}}}}\) are derived by LK formula at \(\theta =0^\circ\).

Full size image

Here, A is a scaling factor independent of \(B\approx {\mu }_{0}H\) and \(T\), \({R}_{T}=X/\sinh (X)\) is the thermal damping factor, where \(X=2{\pi }^{2}{k}_{B}{m}^{* }T/e\hslash B\), \({R}_{D}=\exp (-2{\pi }^{2}{k}_{B}{m}^{* }{T}_{D}/e\hslash B)\) is the Dingle damping factor, where \({T}_{D}=\hslash /2\pi {k}_{B}\tau\), \(\tau\) is the quasiparticle lifetime, and we assume that the quasi-two-dimensional nature of the FS sections results in a θ−dependent effective mass \({m}^{* }={m}^{* }(0^\circ )/\cos \theta\). The \({R}_{S}\) factor,

$${R}_{S}=\cos \left(\frac{\pi g{m}^{* }\left(0^\circ \right)}{2{m}_{e}\cos \theta }\right),$$
(2)

suppresses the quantum oscillation amplitude due to the interference between Zeeman-split Landau levels; g is the effective g-factor. The amplitude vanishes where “spin-zeros” \((i.e.,{R}_{S}=0)\) occur; here, \(g{m}^{* }(0^\circ )/\cos \theta =1+2n\) is satisfied, with n an integer. The phase flips when crossing these zeros. In Fig. 3d and Fig. 3e, the oscillatory amplitudes are plotted as a function of angle. The overall amplitudes are damped to zero at higher angles by the Dingle factor RD. Two “spin-zeros” due to the angle dependence of RS can be seen for \(\theta\, < \,40^\circ\) in both the \(\gamma +2\beta\) and \(\gamma +3\beta\) frequencies. The black lines represent the fits to the data, under the assumption that the Dingle temperature does not vary with angle. \({T}_{D}(\gamma +2\beta )=27\,{{{{{\rm{K}}}}}}\), \({T}_{D}(\gamma +3\beta )=28.6\,{{{{{\rm{K}}}}}}\) and the effective masses \({m}_{\gamma +2\beta }^{* }\left(0^\circ \right)=0.7\,{m}_{e}\) and \({m}_{\gamma +3\beta }^{* }\left(0^\circ \right)=0.8\,{m}_{e}\) are deduced by employing the LK formula at θ = 0°, see Supplementary Fig. 5. The fitting parameters are \({g}_{\gamma +2\beta }\) and \({g}_{\gamma +3\beta }\), resulting in \({g}_{\gamma +2\beta }=15\) and \({g}_{\gamma +3\beta }=18\).

Another simple approach for deriving the effective g-factor uses the two angles of spin-zeros for \(\gamma +2\beta\) and \(\gamma +3\beta\). Minima in the amplitudes are clearly seen around the “spin zero”, with the amplitude recovering at higher angles (Fig. 3d, e). Even if there is a magnetic field dependence of the magnetic breakdown probability, as long as the breakdown has a non-zero probability, these minima in the amplitudes occur at “spin-zeros”, values of θ at which \({Rs}\) = 0. [i.e., where \(g{m}^{* }(0)/{m}_{e}\cos \theta =2n+1\) is satisfied, with \(n\) an integer]; the oscillation phase also flips when crossing the zeros. For \(\gamma +2\beta\) the effective mass \({m}^{* }\left(0\right)\approx 0.7\,{m}_{e}\) and the two spin-zeros at \(\theta\) = 17° and 36°.

$$\left\{\begin{array}{c}0.7g/\cos \left(17^\circ \right)=2n^{\prime} +1\\ 0.7g/\cos \left(36^\circ \right)=2n^{\prime} +3\end{array}\right.$$
(3)

we can determine \({g}_{\gamma +2\beta }=15\) and in the same way derive \({g}_{\gamma +3\beta }=18,\) which is consistent with the fitting.

The above analysis assumes an isotropic g-factor; in reality, reflecting the anisotropic structure of CsV3Sb5, the g-factor may be a tensor. However, in order to reveal any possible effects of the g-factor tensor would require much stronger magnetic fields and a cleaner sample in order to resolve several higher-order spin-zeros.

We note that this double-dip θ−dependence of the oscillation amplitude is not due to the Yamaji effect frequently seen in quasi-two-dimensional metals35. The Yamaji effect is due to θ−dependent variations in the orbit areas of quasiparticles circling the FS sections36, and results in maxima in the quantum oscillation amplitude at angles θY that are periodic in \(\tan {\theta }^{Y}\). As shown in Supplementary Fig. 6, the maxima in the oscillation amplitudes are far from periodic in\(\tan \theta\). Moreover, unlike our experimental data, a π phase change in the quantum oscillations is not expected at the amplitude minima between Yamaji angles. Therefore, the varnishing of the oscillation amplitude in our data is most likely due to the spin-zero effect associated with a large effective g-factor.

Although the frequencies versus angle relationships of the warped cylindrical Fermi surfaces follow a \(1/\cos \theta\) dependence closely at small angles, subtle deviations of such FSs from ideal two-dimensionality could lead to phase shifts in the quantum oscillations as the sample is tilted in the field, see Supplementary Fig. 7. However, such phase shifts will be subtle for small changes in angle. By contrast, as shown in Supplementary Fig. 4, a comparison between the oscillation patterns at \(\theta =-2^\circ\) and those at \(\theta =27^\circ\) shows that the phase change is much larger, being π in one case \(({F}_{\gamma +2\beta })\) and close to \(\pi /2\) in the other \(({F}_{\gamma +3\beta })\). These phase shifts are consistent with a spin-zero occurring between the two angles but are unlikely to be due to the moderately warped FS.

Discussion

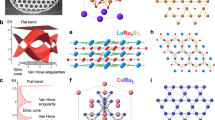
Time-reversal symmetry breaking scenario (loop current phase)

A likely cause is the proposed large orbital magnetic moment provided by the CFP16,17. According to Ref. 16, these FS pockets arise from the Chern number band and carry a large Berry curvature, leading to a significant orbital Zeeman effect16,37, see Supplementary Note 2. The spin contribution can be neglected in the effective Zeeman coupling as it is significantly smaller compared to the orbital part. However, since the spin-zero effect conventionally requires two sets (spin up and spin down) of Landau levels split by the field, the TRS breaking staggered loop-current order needs to be extended to include interlayer correlations. A possible realization is shown in Fig. 4a, where the loop-current order is stacked antiferromagnetically between the adjacent kagome layers. Such a 2 × 2 × 2 loop-current order is consistent with the observed 3D CDW3,38,39,40. The CFPs from adjacent layers form Z2 partners of TRS, and are split in opposite directions by the magnetic field with a large orbital g-factor, which can account for the observed spin-zero effect.

Fig. 4: Time-reversal symmetry breaking in Loop-current phase and time-reversal symmetry in loop- spin-current phase.
figure 4

a Schematic diagram of loop-current phase. The directions of the current j are opposite between two Kagome layers. b Schematic diagram of loop spin-current phase. Yellow (pink) arrows indicate the direction of the loop current from up (down) spin j↑ (j↓).

Full size image

Time-reversal symmetry preserving scenario

Another scenario is that the reconstructed small FS possesses TRS preserved loop-spin-current as shown in Fig. 4b. Analogously to the TRS breaking CFP scenario, the small FS induced by loop-spin-current also has a concentrated Berry curvature and therefore large orbital Zeeman effect. Nonetheless, the TRS bands should be characterized by spin Chern numbers41,42, resulting in the small reconstructed FS being identified as a spin Chern Fermi pocket (SCFP). Given the direction of the loop currents are opposite for spin-up and spin-down states, it becomes evident that spin-zero effect can occur via the interference of the spin-up and -down SCFPs.

For the magnetic breakdown orbits, the effective g factor can be estimated to be roughly \({g}_{\gamma +n\beta }{m}_{\gamma +n\beta }^{\ast }={g}_{\gamma }{m}_{\gamma }^{\ast }+n{g}_{\beta }{m}_{\beta }^{\ast }\). With the known values \({g}_{\gamma +2\beta }=15\) and \({g}_{\gamma +3\beta }=18\) as previously discussed, we can derive \({g}_{\gamma }=4.8\) and \({g}_{\beta }=40\).

Furthermore, despite the large g-factor, we do not observe a spin-zero effect for the small reconstructed β orbit (refer to Supplementary Fig. 8); this is probably because the small effective mass\((\approx 0.1m{{{{{\rm{e}}}}}})\) will push the first amplitude minimum out to a large angle where, because of fields limited to below 75 T we are unable to resolve the effect. Conversely, the “normal” γ orbit has a higher effective mass, but this will be compensated by a much smaller (unenhanced) \(g\approx 5\), again pushing the first spin-zero out to large θ. It is only when the larger effective mass of the breakdown orbit \((\approx 0.7-0.8{m}_{{{{{{\rm{e}}}}}}})\) is united with the large apparent g−factor \((\approx 15)\) that the spin-zero effect is shifted to lower values of θ, enabling a clear observation of CFP/SCFP physics.

Berry-curvature generated large orbital moments are usually concealed by other effects (e.g., antiferromagnetic alignment) described at the start of this paper; here, the breakdown orbits due to proximity to a “conventional” FS section allow them to be writ large in the magnetic quantum oscillations. This observation is part of an emerging trend where exotic quasiparticles are only clearly manifested via their interactions with relatively conventional charge carriers43. A recent example is the measurement of magnetic quantum oscillations in the electrical resistivity of Kondo insulators44,45,46; here the effects of the Landau level density of states of exotic electrically neutral fermions are measurable in the electrical resistivity because of their effect on the scattering of a small population of conventional electrons and holes.

We remark here that DFT electronic-structure modeling24 has shown that the spin-orbit-coupling (SOC) energy can be comparable to energy gaps in the band structure at certain k-space locations. The SOC can lead to Berry contributions to the orbital magnetic moment, which is usually only large around the K points. Time reversal symmetry breaking can generate Berry curvature and enhance the g-factor on the pockets around M, in addition to the contributions from SOC, though it is not yet clear whether this can produce large \(g\)-factor enhancement. It will be interesting to see if further development of the DFT (or perhaps other theoretical models based on SOC) can lead to a g-factor as large as 18.

In summary, magnetic quantum oscillations are observed in magnetic torque, resistivity, and AC conductivity of the kagome metal CsV3Sb5. Whilst the angular dependences of most of the observed orbit frequencies and the effective masses are consistent with simple, single-particle band-structure calculations, we also observe magnetic breakdown between regular Fermi-surface orbits and unconventional, correlation-driven Fermi-surface pockets for the first time. As expected, the breakdown orbits yield a sequence of equally spaced frequencies with corresponding equally spaced effective masses. More importantly, these orbits exhibit spin-zeros as a function of field orientation that yield a greatly enhanced apparent g-factor. This strongly suggests that the smaller of the two Fermi-surface sections involved possesses a greatly enhanced orbital moment, that can be described by CFP in TRS breaking or SCFP in TRS preserved kagome metals. Such large orbital moments usually cannot be measured directly, being concealed by other effects; here, the breakdown orbits allow them to be clearly manifested in the magnetic quantum oscillations.

Methods

Single crystals of CsV3Sb5 were synthesized via a self-flux growth method similar to that in previous reports2 and the same batch of the samples as in the ref. 18 were used with \({T}_{C}\) = 2.7 K and high residual resistivity ratio of 69.

Torque magnetometry measurements were performed using both capacitive cantilevers and piezoresistive micro-cantilevers. The high-field measurements were carried out in Quantum Design Physical Property Measurement Systems (PPMS Dynacool-14T) and the 45 T Hybrid Magnet in NHMFL, Tallahassee.

The AC conductivity experiments using Proximity Detector Oscillators (PDO) were carried out in the 75 T Duplex magnet of the NHMFL Pulsed-Field Facility at Los Alamos33,34,44. The shift in PDO frequency \(f\) due to \(H\) is written as \(\varDelta f=-a\varDelta L{-}b\varDelta R\) (where \(a\) and \(b\) are positive constants determined by the frequency plus the capacitances, resistances and inductances in the circuit; \(L\) is the coil inductance; and \(R\) is the resistance of the coil wire and cables). In the case of a metallic sample, the coil inductance \(L\) depends on the skin depth \(\lambda\) of the sample. If we assume that the sample magnetic permeability μ and coil length stay unchanged during a field pulse, we have \(\varDelta L\propto (r-\lambda )\varDelta \lambda\), where r is the sample radius. At angular frequency ω, the skin depth is proportional to the square root of resistivity ρ, i.e. \(\lambda =\sqrt{\frac{2\rho }{\omega \mu }}\). Therefore, for a metallic sample, the resonance shift \(\varDelta f\) reflects the sample magnetoresistance and the detected quantum oscillations are due to the SdH effect. For the typical size of frequency shifts in this paper, \(\Delta f\propto -\Delta \rho\)47.

Density functional-theory calculations were performed using WIEN2k48. The angular dependence of FS cross-sectional areas was computed by SKEAF49.