Abstract
Lead chalcogenides are known for their thermoelectric properties since the first work of Thomas Seebeck on the discovery of this phenomenon. Yet, the electronic properties of lead telluride are still of interest due to the incomplete understanding of the metal-to-semiconductor transition at temperatures around 230 °C. Here, a temperature-dependent atomic-resolution transmission electron microscopy study performed on a single crystal of lead telluride reveals structural reasons for this electronic transition. Below the transition temperature, the formation of a dislocation network due to shifts of the NaCl-like atomic slabs perpendicular to {100} was observed. The local structure modification leads to the appearance of in-gap electronic states and causes metal-like electronic transport behavior. The dislocation network disappears with increasing temperature, yielding semiconductor-like electrical conductivity, and re-appears after cooling to room temperature restoring the metal-like behavior. The structural defects coupled to the ordering of stereochemically active lone pairs of lead atoms are discussed in the context of dislocations' formation.
Similar content being viewed by others
Introduction
The interest in lead chalcogenides as thermoelectric materials goes back to T. Seebeck. Already in the first report about the discovery of thermoelectricity (at that time he called it thermomagnetism), he described Bleiglanz (the German name for galena, a natural form of lead sulfide) as a material yielding an electrical current (detected by its magnetic field) in the closed-circuit set when it is exposed to a temperature gradient (cf. experiment 381). T. A. Edison was reported to use a thermoelectric generator based on semiconducting lead and copper sulfides for optimizing the power generators for lighting in New York2. Lead telluride was suggested as thermoelectric material by A. E. Ioffe much later - in the thirties of the last century3. Using lead telluride-based p- and n-type materials in radioisotope thermoelectric generators, NASA successfully realized several space research programs4,5.
One of the challenges of the power generation with lead telluride at elevated temperatures is a non-monotonic change of relevant properties, like electrical resistivity and the Seebeck coefficient. Not only in the pristine material3,6,7,8 (and references therein), but also in iso-electronically substituted materials, e.g., Pb1−xEuxTe, the electrical resistivity ρ(Τ) changes slope from positive to negative at around 180–230 °C, while the Seebeck coefficient changes sign9. As a reason for such behavior, the resolution of excess atoms present after the single crystal growth by the Bridgman technique and the vaporization of tellurium from the specimens were discussed10,11. Furthermore, the creation and healing of defects due to mechanical milling and sintering, respectively, were assumed to change the effective charge carrier concentration8. For high-carrier-concentration samples, the simple two-valence-band model was applied to explain the general temperature variations of resistivity, although it was apparent that a complete analysis would require the more exact theory of transport in semiconductors with non-parabolic bands7. Excitation of electron-hole pairs with the formation of structural defects at elevated temperatures6 and temperature-dependent band crossing12 and references therein were also considered as reasons for the electronic transport behavior of PbTe. All these approaches assume that the crystal structure of PbTe (structure type NaCl, space group Fm\(\bar{3}\)m, a = 6.4611(3) Å)9 remains basically unchanged.
Several recent findings call the latter assumption into question. The powder XRD patterns of PbTe reveal unusual anisotropic peak broadening below 473 K indicating a structural disorder. The anisotropy disappears at elevated temperature, which correlates with the strong change in electron and phonon transport9. Such behavior was explained by an anisotropic microstrain13. Similar drastic changes of the electronic and thermoelectric properties are explained by off-center positions of the atoms or the presence of local structural dipoles that emerge from the undistorted ground state on heating14,15, but were called into question by a spectroscopic study16.
In general, the physical properties of semiconductors are strongly dependent on and determined by the underlying crystal structure. Furthermore, many other factors may play a role in understanding the observed properties, such as structural defects, diffusion processes, and recrystallization phenomena. E.g., non-stoichiometry on the atomic scale results in a larger amount of point defects in the crystal lattice17,18. These point defects may introduce a temperature-dependent concentration of acceptors or donors. During annealing, the point defects may diffuse from the regular sites toward the precipitation centers19,20. This leads to the formation of distributed agglomerations20,21.
Nowadays, atomic high-resolution transmission electron microscopy (HRTEM) and high-resolution scanning transmission electron microscopy (HRSTEM) are ideally suited for the direct observation of the real structure of materials, in particular, precipitations and point defects. Te-rich precipitates have been found by TEM in PbTe single crystals having stoichiometric, slightly Te-rich, and also 0.3% Pb excess compositions. For excess of 1.0% Pb, however, no Te-rich precipitates appear22. More recently, Pb-depleted disks (Pb-vacancy aggregates) in {100} planes and Pb nanocrystallites as precipitates in stoichiometric PbTe were discovered23,24.
In the present work, an atomic-resolution study on the local structure of PbTe single crystals under different thermal conditions is performed, which reveals the possible structural origin of the metal-to-semiconductor transition.
Results and discussion
Dislocation pattern and lone-pair model
The single crystal of p-type PbTe used in this study was grown on the Te-rich side of the homogeneity range more than 20 years ago25. It is known, that Pb-rich PbTe single crystals are hard to prepare, and all attempts lead rather to defect-rich, poor quality samples with a tendency to polycrystal behavior (cf. Supplementary Note 1). Furthermore, resistivity measurements on polycrystalline specimens on both sides of the homogeneity range reveal the metal-to-semiconductor transition only at the stoichiometric composition and on the Te-rich side. The behavior on the Pb-rich side seems to be much more complex (Supplementary Fig. 1). A part of the single crystal (Fig. 1a, left insert) is kept as pristine material. Two further specimens cut out of the same crystal were used to trace temperature-dependent differences of properties after annealing at 400 °C and 600 °C (cf. Methods). Further cut-out specimens were subjected to temperature-dependent HRTEM experiments.
(a) overview image of sub-μm scale (inset left shows the single crystal studied, inset right – selected area diffraction image of the region); (b) magnified image of the region with parallel dislocations; (c) HRTEM image of the dislocation mesh region; (d) atomic resolution image of the dislocation mesh region; positions of atoms in the initial layer are shown with square symbols; the position of shifted layers are visualized by white circles (inset shows FFT of the region); ideal NaCl-type atomic arrangement in PbTe (e) and the model with a shift of every second layer along [100] (f); electronic DOS of the ideal PbTe structure (g) and changes in DOS caused by the layer shifts above (h).
In parts of the pristine PbTe single crystal, the expected ordered crystal structure of the NaCl-type with regular structural pattern is present, while special strain caused features dislocations appear in other regions (cf. high-resolution images in Supplementary Fig. 2). The dislocations (thickness of about 50 nm) are superimposed with a periodicity of 80 nm in one direction and 90 nm in the other one, forming meshes (Fig. 1a–c). Diffraction analysis (Fig. 1a, right inset) and Fast Fourier transform (FFT, Fig. 1d, inset) of these regions indicate the presence of PbTe reflections solely. Atomic-resolution TEM reveals a shift of atomic slabs perpendicular to [001]. The layer shifts happen in different directions from [100] via [110] to [010] (Fig. 1d), i.e. the translation symmetry along [001] is strongly violated. Assuming the Burgers vector to be ½[101], the TEM images can be understood and modeled by the atomic arrangement with every second layer shifted along [100] perpendicular to [001] (Fig. 1e, f). Already such ‘simplest’ shifts by (x 0 0) cause marked changes in the electronic density of states: the bandgap characteristic for the pristine material (Fig. 1g) closes, i.e. in-gap states appear in comparison with the ideal NaCl-type structure (Fig. 1h, Supplementary Fig. 3). This explains on the one hand the reduced value of the experimentally measured bandgap in comparison with the calculated values and on the other hand the metallic behavior of the material below the transition temperature.
The influence of the layer shifts on the total energy of the system is evaluated for models with 8 atoms in the unit cell (equivalent to the content of the NaCl-type unit cell of the ideal structure, cf. Supplementary Table 1, Methods). For the shift (x 0 0), the total energy increases by 0.10–0.43 eV/f.u. PbTe depending on the value of x and on the lattice parameter ratio (Supplementary Fig. 3). A similar total energy increase of ca. 0.6 eV/f.u. PbTe is calculated for the diagonal shift (x x 0) with x = 0.25 (Burgers vector ½[111]), which can be also recognized in Fig. 1d.
Such layer shifts are known in inorganic structural chemistry as the route toward the formation of new atomic arrangements. In particular, the diagonal shift for the polymorphs of thallium iodide TlI. While the modification grown from the vapor on the appropriate single crystal substrate has the NaCl-type structure26, α-TlI, which is stable at ambient conditions reveals double-layer slabs shifted by (x x 0) with x = 0.25 (in the coordinate system of the NaCl structure), and each layer has one shifted and one non-shifted as stacking neighbors (27, Supplementary Fig. 4). From these experimental data, the NaCl-type modification should have higher energy, which is compensated by the growth on a rigid substrate. And, obviously, the shift of each third layer has a releasing influence reducing the energy of the system.
While the layer shifts are energetically disfavored for PbTe compared with the ideal NaCl-type structure, the energetic situation in PbTe changes in regions where structural defects are present. Lead telluride has a small homogeneity range, in the order of 10−4 at% on both sides of the stoichiometric (1:1) composition19,28,29,30,31,32,33. The investigated single crystal is grown on the Te-rich side of the homogeneity range and is a p-type conductor with a charge carrier concentration of 10.4 × 1017 cm−3; thus, the presence of defects is obvious. The formation and influence of defects on properties of lead telluride were widely studied experimentally and theoretically34 and references therein. The calculated formation energy in the order of eV × defect−1 is at least comparable with the total energy increase due to the layer shifts. E.g., for lead vacancies characteristic for p-type PbTe, the formation energy is 1.9–2.2 eV × defect−1, 1.68 eV × defect−1 was calculated for the Schottky pair and the lowest one of 1.21 eV × defect−1 is found for the Shottky dimers, i.e. larger defects causing extended deviation from translational symmetry35. In the regions containing such irregularities, locally, both atomic arrangements – pristine with defects and one with layer shifts – may become competitive by causing reductions of the system energy. In particular, the Shottky dimers may become the suitable starting point for the formation of a dislocation.
The layer shifts may be initialized and realized with the support of ordering of the stereochemically active lone pairs on lead atoms, which can be understood as a non-centrosymmetric distribution of the electron density around the nucleus. Lone pair formation was already discussed for lead chalcogenides from DFT calculations36,37, or - from another point of view – in form of the correlated local dipoles15. Their role in the structure increases due to the lower ionicity of the bonding: effective charge transfer in PbTe calculated from the Quantum Theory of Atoms In Molecules is 0.65 electrons of two formally possible per atom in comparison with 0.86 electrons of one formally possible per atom in NaCl. Indirectly, this is confirmed by the TEM observations, which do not reveal a formation of dislocations in essential concentrations in PbSe and PbS with higher charge transfer (0.83 and 0.87 electrons per atom, respectively).
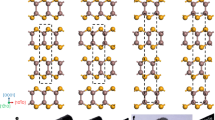
The possible scenario is as follows. At temperatures above the metal-to-semiconductor transition, the lone pairs are structurally inactive (disordered) and yield an average ordered picture of the cubic NaCl-type crystal structure of PbTe (Fig. 2a, b). By temperature reduction, they may order and support the gliding of neighboring atomic layers due to the repulsive interaction between the lone pairs (Fig. 2c, d). In this way, the atomic arrangement with shifted layers forms a structural basis of a dislocation (Fig. 2e, f).
(a) pristine atomic arrangement in NaCl-type PbTe; (b) disordered lone-pairs in the pristine structure; (c) lone-pair ordering allowing layers shifts in the (001) plane due lone-pair repulsive interaction; (d) atomic arrangement with layers shifted by (0.25 0 0) reducing the repulsion between the lone-pairs; (e, f) the resulting atomic arrangement (cf. Fig. 1). The stoichiometry and composition in all panels is 1:1. Orange spheres–lead, green–tellurium, gray spheres symbolize lone pairs at the orange Pb atoms. The larger size of the gray spheres is used to emphasize the enhanced volume need of the lone pairs.
Following this model, the heat treatment is expected to induce the reorganization of dislocations. To study the kinetics of the precipitation process, the single crystal was annealed at different temperatures. Annealing at 400 °C gives rise to a less ordered arrangement than the network of parallel running dislocations (Supplementary Fig. 5a). The periodicity of the latter is 50–100 nm, depending on the direction. After annealing at 600 °C, the existing dislocation network rearranges inside the cubic PbTe matrix, becomes denser than in the pristine single crystal, and develops a periodicity of about 60 nm (Supplementary Fig. 5b). As in previous cases, FFT shows only the reflections of PbTe and does not reveal other elemental structures. Evidently, holding the sample at 600 °C for 5 days is not sufficient to eliminate dislocations, but it is sufficient to change their density and size. The ex-situ experiments cannot fully clarify the dynamic character of the deviation of the real structure of lead telluride from the ideal NaCl-type lattice. Thus, in-situ heating in the TEM is applied to observe structural transformations in PbTe.
In-situ TEM experiments
When the lamella is gradually heated, the first change is observed at 200 °C (Fig. 3a). The dislocation picture becomes sharper (the specimen probably bends due to the heating changing the diffraction conditions). By further heating to 350 °C, some of the dislocations vanish, others start to condense and dissipate. Initially, dislocations vanish in the thinnest parts of the lamella, and then gradually in the thicker parts of the specimen. The threshold temperature is around 400 °C. At this temperature, only a few dislocations remain in the thick areas, and - above this temperature - the dislocations disappear. The longer treatment above 420 °C leads to sample disintegration by void growth (Fig. 3a). Additional temperature-dependent experiments finally confirm the reversibility of the structuring of PbTe. The initially present pattern starts to disappear at 350 °C, vanishes completely at 400 °C, and re-appears at room temperature (Fig. 3b). The initial structure does not show clustering of Pb or Te (Supplementary Fig. 5), thus the (incomplete) re-appearance of the dislocations at another place in the sample may not be caused by the (partial) evaporation of the components and is most probably connected with atomic redistribution within the dislocations (due to the layers movement) yielding back the ‘initial’ defects at another place. This behavior of the structure correlates with the earlier temperature-dependent powder diffraction data of a specimen with composition PbTe: below 200 °C, a strong anisotropy of reflection broadening is observed (the h00 peaks show a much smaller full width at half maximum in comparison to that of hk0 and hkl) which may be caused by a partial disorder in the structure; this anisotropy is strongly suppressed between 200 °C and 300 °C, and practically disappears above 300 °C (Supplementary Fig. 6)9.
(a) dislocation distribution in the single crystal lamella at different temperatures (LAADF STEM. experiment 1); (b) presence, disappearing, and re-appearing of lamella structuring in a heating-cooling cycle (ABF STEM, experiment 2). Black points are platinum islands recrystallized from the amorphous layer formed during the FIB preparation (Supplementary Figs. 7 and 8).
Ex-situ TEM experiments
The presence of lone pairs – being a part of atomic interactions in the structure (chemical bonding) - strongly influences the thermoelectric properties of materials, in particular the lattice thermal conductivity38,39. The structural behavior described above is also consistent with measurements of electrical resistivity (Fig. 4). The pristine material with a high-density dislocation network reveals the metal-to-semiconductor transition at around 230 °C (Fig. 4a). Annealing at 400 °C slightly reduces the dislocation density and shape; it also shifts the transition temperature to ca. 250 °C. As the annealing temperature is obviously too low to destroy the dislocations network completely, the resistivity does not change during the heating and cooling cycle below 270 °C (Fig. 4b). The thermal treatment at 600 °C increases the transition temperature to approx. 270 °C, but the dislocation structure is not stable. It tends to recover upon cooling toward the pristine state, but with other dislocation networks, reflected by the different resistivity behavior during the heating and cooling cycle (Fig. 4c).
Conclusions
In conclusion, the in-situ temperature-dependent high-resolution HRTEM and HRSTEM study on single crystalline lead telluride reveals a special structural feature – dislocations. The atomic-resolution experiments disclose shifts of atomic slabs perpendicular to {100} and point toward ordering of the stereochemically active lone pairs on lead atoms below the characteristic value of ca. 230 °C. This causes changes in the electronic structure. The gap in the band structure of the ideal PbTe rock salt-type structure closes, and the material behaves like a metal in electronic transport measurements. Temperature increase above the characteristic value leads to a lone-pair disorder, and the crystal structure recovers the NaCl lattice. Simultaneously, electronic transport becomes semiconducting. This state is not stable and heating-cooling cycling leads to the re-appearance of the metal-to-semiconductor transition at the characteristic temperature.
Methods
Crystal growth and TEM sample preparation
A single crystal of PbTe was grown by the vertical Bridgman-Stockbarger method. The melt composition was chosen to be near stoichiometric with a slight excess of Te (0.5%)40. Subsequently, the single crystal was cut into three pieces, from which two were annealed at 400 °C and 600 °C for 128 h in a closed glassy carbon tube within a sealed quartz tube held at 400 bars in an argon atmosphere. After annealing, tubes with samples were quenched in water. Next, the slices were polished with a 0.25 µm diamond polish solution. The focused ion beam (FIB) machine was used for removing a 200 µm thick slice of the damaged surface. For TEM investigations, FIB lift-out lamellas were prepared along the [001] direction. The amorphized layer, which was caused by the gallium milling, was removed at 5 kV acceleration voltage.
The in-situ TEM samples were prepared by site-specific focused ion beam (FIB) lift-out in a Scios2HiVac (Thermo Fisher Scientific) dual-beam instrument. The in-situ heating samples were first transferred to a Cu half grid for coarse thinning. Subsequently, the specimens were transferred to MEMS-based heating chips (DENSsolution Wildfire) and were finally thinned to electron transparency at 5 kV. The final polishing of the lamella during FIB preparation is performed by Ga ions with 5 kV acceleration voltage. The lamella is tilted at 60 and 45 degrees and polished from both sides. The polishing time was 45 s.
TEM
High-resolution TEM (HRTEM) analyses were performed using a JEM-ARM300F (Grand ARM, JEOL, Akishima, Tokyo, Japan) with double correction. The spherical aberration of the condenser and the objective lens were corrected by dodecapole correctors in the beam and the image forming system. TEM resolution is 0.5–0.7 Å depending on the resolution criterion applied. TEM images were recorded on a 4k × 4k pixel CCD array (Gatan US4000). Additional analysis was carried out on an FEI Tecnai F30-G2 with a Super-Twin lens (ThermoFischer, Eindhoven, NL) with a field emission gun at an acceleration voltage of 300 kV. The point resolution amounts to 2.0 Å, and the information limit to about 1.2 Å. The microscope is equipped with a wide-angle slow-scan CCD camera (MultiScan, 2 k × 2 k pixels; Gatan Inc., Pleasanton, CA, USA). Resolution of the spectrometer measured as the full width at half maximum of the zero-loss peaks amounts to 0.75 eV, dispersion of the spectrometer 0.3 eV per pixel. The datasets generated or analyzed during the current study are available from the corresponding author on reasonable request.
The in-situ heating experiments were conducted in a probe aberration-corrected Titan Themis 60-300 (Thermo Fisher Scientific) microscope operated at 300 kV. In STEM mode, a probe semi-convergence angle of 17 mrad and inner and outer semi-collection angles ranging from 8 to 13 mrad were chosen, respectively for annular bright-field (ABF) imaging; and a probe semi-convergence angle of 17 mrad and inner and outer semi-collection angles from 14–63 mrad were used, receptively for low-angle annular dark-field (LAADF)-STEM imaging. STEM-EDX was performed in HAADF mode. A double tilt heating/biasing holder (DENSsolution Lightning) was used for heating the sample mounted onto a MEMS-based heating chip (DENSsolution Wildfire). The in-situ heating experiment was performed at 23 °C, 50 °C, 100 °C and then with 20 °C-steps from 100 °C up to 350 °C, from 350 °C with 10 °C-steps till 420 °C. Dwell time for every step amounted to 10–15 s. Temperature accuracy is kept below 5% and temperature stability below 1 °C. The heating rate of the holder amounted to 200 °C per millisecond.
Transport properties
Electrical resistivity was measured with the ZEM-3 setup (Ulvac-Riko) in the temperature range from 300–760 K. The Hall effect (RH) was measured with a standard six-point ac technique in a physical property measurement system (PPMS, Quantum Design), with magnetic fields up to 9 T. The Hall carrier concentrations were calculated by 1/(RH·e), RH is the Hall coefficient, e is the charge of an electron.
Calculations
Electronic structure calculations were performed by using the all-electron, full-potential local orbital (FPLO) method41. All main results were obtained within the local density approximation (LDA) to the density functional theory through the Perdew-Wang parametrization for the exchange-correlation effects42. A mesh of 12 ×12 × 12 k points was used for calculations. The band structure of pristine PbTe was calculated using the lattice parameter of 6.4611 Å, space group Fm\(\bar{3}\)m, and atomic positions of the NaCl-type (Pb at 4(a) 0 0 0; Te at 4(b) 0 0 ½). For the modeling of the layer shifts the space group C1m1 with the pseudocubic unit cell a = b = c = 6.4611 Å and β = 90° was chosen with the following atomic positions: Pb1 in 2(a) 0.0 0 0.0; Pb2 in 2(a) x ½ 0.5; Te1 in 2(a) 0.0 ½ 0.0; Te2 in 2(a) x 0 0.5. The model with x = 0 corresponds to the NaCl-type structure, further models with x between 0.125 and 0.875 were calculated. For each value of x, first the optimization of the unit cell volume was performed, followed by the optimization of the c/a ratio, keeping the a and b parameters equal (Supplementary Table 1).
The topology of the calculated three-dimensional distributions of electron density (ED) was evaluated with the program DGrid43. The atomic charges from ED were obtained by its integration within the basins (space regions), bounded by zero-flux surfaces in according to gradient field. This procedure follows the quantum theory of atoms in molecules (QTAIM44).
Data availability
All data supporting the findings of this study are included into the paper and/or are available from the authors upon reasonable request.
References
Seebeck, T. Magnetische Polarisation der Metalle und Erze durch Temperatur-Differenz. Abhandlungen der Königlichen Akademie der Wissenschaften in Berlin, 265–373 (1822–1823).
Anatychuk, L. Film presentation at the 29th International Conference on Thermoelectrics, Shanghai (2016).
Ravich, Y. I., Efimova, B. A. & Smirnov. I. A. Semiconducting lead chalcogenides, Plenum Press (1970).
Atomic power in space, a history. U.S. Department of Energy (1987), https://fas.org/nuke/space/history.pdf.
LaLonde, A. D., Pei, Y., Wang, H. & Snyder, G. J. Lead telluride alloy thermoelectrics. Mat. Today 14, 526–532 (2011).
Miller, E., Komarek, K. & Cadoff, I. Interrelation of electronic properties and defect equilibria in PbTe. J. Appl. Phys. 32, 2457–2465 (1961).
Crocker, A. J. & Rogers, L. M. Interpretation of the Hall coefficient, electrical resistivity and Seebeck coefficient of p-type lead telluride. Br. J. Appl. Phys. 18, 563–573 (1967).
Schmitz, A. et al. Current assisted sintering of PbTe—Effects on thermoelectric and mechanical properties. Mater. Res. Bull. 86, 159–166 (2017).
Wang, X., Veremchuk, I., Bobnar, M., Zhao, J.-T. & Grin, Y. Solid solution Pb1−xEuxTe: constitution and thermoelectric behavior. Inorg. Chem. Front. 3, 1152–1159 (2016).
Kovalchik, T. L. & Maslakovets, I. P. Effect of impurities on the electrical properties of lead telluride. Sov. Physics-Technical Phys. 1, 2337–2349 (1956).
Smith, R. A. The electronic and optical properties of the lead sulphide group of semi-conductors. Physica 20, 910–929 (1954).
He, J.-A., Xia, Y., Naghavi, S. S., Ozoliņš, V. & Wolverton, C. Designing chemical analogs to PbTe with intrinsic high band degeneracy and low lattice thermal conductivity. Nature Comm. 10, 719–727 (2019).
Christensen, S., Bindzus, N., Sist, M., Takata, M. & Iversen, B. B. Structural disorder, anisotropic micro-strain and cation vacancies in thermo-electric lead chalcogenides. Phys. Chem. Chem. Phys. 18, 15874–15883 (2016).
Božin, E. S. et al. Entropically stabilized local dipole formation in lead chalcogenides. Science 330, 1660–1663 (2010).
Sangiorgio, B. et al. Correlated local dipoles in PbTe. Phys. Rev Mat. 2, 085402 (2018).
Keiber, T., Bridges, F. & Sales, B. C. Lead is not off center in PbTe: the importance of r-space phase information in extended X-ray absorption fine structure spectroscopy. Phys. Rev. Lett. 111, 095504 (2013).
Schenk, M., Berger, H., Klimakow, A., Mühlberg, M. & Wienecke, M. Nonstoichiometry and Point defects in PbTe. Cryst. Res. Tech. 23, 77–84 (1988).
Miller, J., Moody, J. & Himes, R. The Preparation of PbTe crystals. AIME Conference Papers 239, 342 (1967).
Brebrick, R. & Gubner, E. Composition stability limits of PbTe. II. J. Chem. Phys. 36, 1283–1289 (1962).
Mühlberg, M. & Hesse, D. TEM precipitation studies in Te‐rich as‐grown PbTe single crystals. Phys. Stat. Sol. 76, 513–524 (1983).
Scanlon, W. W. Precipitation of Te and Pb in PbTe crystals. Phys. Rev. 126, 509 (1962).
Levine, E. & Tauber, R. The preparation and examination of PbTe by transmission electron microscopy. J. Electrochem. Soc. 115, 107–108 (1968).
Wang, G., Shi, T. & Zhang, S. Microdefects in Te-Rich PbTe bulk crystal. Chin. Phys. Lett. 12, 469–472 (1995).
Wang, H. et al. Transmission electron microscopy study of Pb-depleted disks in PbTe-based alloys. J. Mat. Res. 26, 912–916 (2011).
Gille, P., Mühlberg, M., Parthier, L. & Rudolph, P. Crystal growth of PbTe and (Pb, Sn)Te by the Bridgman method and by THM. Cryst. Res. Technol. 19, 881–891 (1984).
Schulz, L. G. Polymorphism of cesium and thallium halides. Acta Crystallogr. 4, 487–489 (1951).
Helmholz, L. The crystal structure of the low temperature modification of thallous iodide. Z. Kristallogr. 95, 129–137 (1936).
Brebrick, R. F. & Allgaier, R. S. Composition limits of stability of PbTe. J. Chem. Phys. 32, 1826–1831 (1960).
Sealy, B. J. & Crocker, A. J. The P-T-x phase diagram of PbTe and PbSe. J. Mat. Sci. 8, 1737–1743 (1973).
Avetisov, I. K., Kharif, Y. L. & Kovtunenko, P. V. Determination of the range of homogeneity of lead telluride. Inorg. Mat. 23, 455–457 (1987).
Lin, J. C., Hsleh, K. C., Sharma, R. C. & Chang, Y. A. The Pb-Te (lead-tellurium) system. Bulletin of Alloy Phase Diagrams 10, 340–347 (1989).
Bajaj, S. et al. Ab initio study of intrinsic point defects in PbTe: an insight into phase stability. Acta Mater. 92, 72–80 (2015).
Masatomo, F. & Yasuo, S. PTx phase diagram of the lead telluride system. Jap. J. Appl. Phys. 5, 128–133 (1966).
Goyal, A., Gorai, P., Toberer, E. S. & Stevanović, V. First-principles calculation of intrinsic defect chemistry and self-doping in PbTe. npj Comp. Mat. 3, 42 (2017).
Li, W.-F., Fang, C.-M., Dijkstra, M. & van Huis, M. J. The role of point defects in PbS, PbSe and PbTe: a first principles study. J. Phys. Condens. Matter 27, 355801 (2015).
Waghmare, U. V., Spaldin, N. A., Kandpal, H. C. & Seshadri, R. First-principles indicators of metallicity and cation off-centricity in the IV-VI rocksalt chalcogenides of divalent Ge, Sn, and Pb. Phys. Rev. B67, 125111 (2003).
Walsh, A. & Watson, G. W. The origin of the stereochemically active Pb(II) lone pair: DFT calculations on PbO and PbS. J. Solid State Chem. 178, 1422–1428 (2005).
Nielsen, M. D., Ozolins, V. & Heremans, J. P. Lone pair electrons minimize lattice thermal conductivity. Energy Environ. Sci. 6, 570–578 (2013).
Grin, Y. Inhomogeneity and anisotropy of chemical bonding and thermoelectric properties of materials. J. Solid State Chem. 274, 329–336 (2019).
Breitsameter, B., Hartmann, W. & Löwe, H. Chemical lap polishing of PbTe and Pb1−xSnxTe crystals. Kristall und Technik 15, 497–503 (1980).
Koepernik, K. & Eschrig, H. Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme. Phys. Rev. B59, 1743–1757 (1999).
Perdew, J. P. & Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B45, 13244 (1992).
Kohout, M. DGrid, versions 4.6-5.0, (2018).
Bader, R. F. W. Atoms in molecules: A quantum theory. Oxford University Press, Oxford (1999).
Acknowledgements
The authors are grateful to Prof. M. Mühlberg (University of Cologne) for the single crystal specimen, Prof. P. Gille (Ludwig-Maximilian-University Munich), Dr. U. Schwarz, Dr. F. R. Wagner (MPI CPfS, Dresden), and Dr. Thierry Caillat (Caltech) for fruitful discussions. I. Zelenina thanks for funding to the International Max Planck Research School for Chemistry and Physics of Quantum Materials (IMPRS-CPQM) at MPI CPfS.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
I.Z. and P.S. designed and realized the conventional TEM experiments. I.Z., P.S., C.L., and Y.G. analyzed the TEM data. I.Z. carried out the FIB cut preparation needed for conventional TEM. M.B., X.W., and I.V. performed macroscopic sample preparations and physical measurements. W.L. and C.L. designed the in-situ TEM measurements. FIB preparation for in-situ STEM and the in-situ STEM experiment itself was carried out by W.L. Y.G. developed the concept, supervised the research, and wrote the paper together with P.S., I.Z., and C.L. Y.G. performed the electronic structure calculations and bonding analysis. All authors contributed to the discussion and paper preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests
Additional information
Peer review information Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Andreja Benčan Golob and Aldo Isidori.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zelenina, I., Simon, P., Veremchuk, I. et al. Structural complexity and the metal-to-semiconductor transition in lead telluride. Commun Mater 2, 99 (2021). https://doi.org/10.1038/s43246-021-00201-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00201-7