Quantifying the role of the lattice in metal–insulator phase transitions

Abstract

Many materials exhibit phase transitions at which both the electronic properties and the crystal structure change. Some authors have argued that the change in electronic order is primary, with the lattice distortion a relatively minor side-effect, and others have argued that the lattice distortions play an essential role in the energetics of the transition. In this paper, we introduce a formalism that resolves this long-standing problem. The methodology works with any electronic structure method that produces solutions of the equation of state determining the electronic order parameter as a function of lattice distortion. We use the formalism to settle the question of the physics of the metal–insulator transitions in the rare-earth perovskite nickelates (RNiO₃) and Ruddlesden–Popper calcium ruthenates (Ca₂RuO₄) in bulk, heterostructure, and epitaxially strained thin film forms, finding that electron-lattice coupling is key to stabilizing the insulating state in both classes of materials.

Introduction

The relative importance of electronic and lattice effects in driving phase transitions in quantum materials is the subject of long-standing interest and controversy. One issue of particular focus is the metal to insulator transition (MIT), which in many materials is accompanied by a change in atomic positions, in other words, by a lattice distortion¹. Multiple studies have addressed various aspects of the interplay between electronic and lattice contributions to the metal–insulator transition, both theoretically and experimentally. Some works have argued that the lattice plays a crucial role², while others have emphasize the electronic aspects³; recently, explicit attempts at disentangling the two have appeared^4,5,6. Information on the coupling of electronic and structural modes has been used to design and study new materials^7,8,9 and to help clarify their interconnected roles. Machine learning approaches are discovering features from comparison of MIT and non-MIT materials^10,11,12. Nonetheless, the problem remains an open topic of exploration with a wide variety of theoretical and experimental approaches^{2,3,4,5,6,7,8,9,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54}. Yet, the relative importance of electronic and lattice effects in producing a transition has remained unclear, in part because of the lack of an appropriate theoretical framework and of computational schema for evaluating the needed quantities.

Metal insulator transition phenomena are properly analyzed by constructing an energy landscape in the space of lattice distortions and electronic order parameters as shown in Fig. 1 for NdNiO₃. However, construction of the full energy landscape as a function of electronic order parameter and lattice configuration has not been feasible, as current quantum many-body methods do not allow the order parameters to be independently varied. Here we show how to avoid this difficulty by building the needed energy landscapes from solutions of the equation of state (electronic order parameter as a function of lattice configuration). This information is available from modern quantum many-body methods at reasonable computational expense.

Fig. 1: Energy Landscape for NdNiO₃ as a function of the electronic and ionic lattice disproportionation.

Energy landscape for NdNiO₃ as a function of electronic disproportionation ΔN and lattice distortion (bond disproportionation) Q as obtained from the energy functional methods introduced in this paper using data from ref. ⁴.

Our work was inspired by the pioneering work of Fisher and collaborators⁵⁵, who combined elegant experimental measurements with an insightful free energy analysis to show that the observed second order nematic transition in an iron pnictide material has an intrinsically electronic origin. Our work may be viewed as a generalization of the ideas of Fisher et al. to first order transitions, where a more global view of the energy landscape is required, and as an extension of the insightful equation of state analysis of Peil, Hampel, Ederer, and Georges⁶ to the computation and interpretation of the full free energy landscape. We make substantial use of concepts put forward in analyses of the metal–insulator transition in epitaxially strained Ca₂RuO₄⁵ and in nickelate heterostructures⁴. We apply the methodology developed here to two paradigmatic metal–insulator materials, the perovskite rare earth nickelates, and the Ruddlesden–Popper calcium ruthenates, settling a decades-old controversy by showing that in both cases the energetics associated with the lattice degrees of freedom are essential to the stabilization of the insulating phase.

Results

Framework

Following refs. ^4,5,6 we consider a free energy F(ΔN, Q) that depends on an electronic order parameter, ΔN, and a lattice distortion, Q. The precise definitions of ΔN and Q will depend on the specifics of the system. We choose (ΔN, Q) = (0, 0) as the equilibrium configuration of the metallic phase. The insulating state then corresponds to a configuration (ΔN, Q) ≠ (0, 0) and the question of the existence of a purely electronic transition relates to the properties of F as a function of ΔN at Q = 0.

A second order transition corresponds to a linear instability of the (ΔN, Q) = (0, 0) state, in other words to a change in sign of the smallest eigenvalue of the Hessian matrix ∂²F/∂²ΔN, Q evaluated at ΔN = Q = 0. In general, the eigenvector associated with the negative eigenvalue will have components along both ΔN and Q, indicating that the electronic and lattice orders are coupled. A purely electronically driven transition would correspond to a change in sign of ∂²F/∂²ΔN, a lattice-driven transition would correspond to a change in sign of ∂²F/∂²Q, and in a mixed situation, neither single derivative changes sign but the lowest eigenvalue of the Hessian matrix does change sign. In the case of the nematic transition in pnictides, Fisher and co-workers were able⁵⁵ to experimentally determine ∂²F(Q = 0)/∂ΔN² and show that it changed sign at a temperature only slightly lower than the observed nematic transition temperature, thereby establishing that a purely electronically driven nematic transition exists in these materials, with a transition temperature that is slightly enhanced by coupling to the lattice.

The transitions of interest in this paper are first order, characterized by the appearance of a new free energy minimum at which ΔN and Q are both different from zero (see e.g., Fig. 1). Study of first order transitions requires global knowledge of the free energy. One may say that the transition is electronically driven if F(ΔN, Q = 0) has an extremum at a ΔN ≠ 0 with ∂²F(ΔN, 0)/∂ΔN² > 0 and with energy lower than F(0, 0). One may say that the transition is lattice-assisted if F(ΔN, 0) has a local minimum at a ΔN ≠ 0 but that the lattice coupling is required to make this minimum the ground state. Finally, if F(ΔN, Q = 0) has only one minimum, at ΔN = 0 but exhibits a stable minimum with ΔN ≠ 0 at a Q ≠ 0 then we may say that the transition is not electronically driven. The energy functional shown in Fig. 1 shows a transition that is not electronically driven because the global minima are at a Q, ΔN ≠ 0 but along the line Q = 0 the functional has only one minimum, at the origin.

The global knowledge of F required to assess the relative importance of electronic and lattice effects in stabilizing the insulating state has been challenging to obtain. Available quantum many-body methods can, with reasonable computational cost, obtain estimates of the optimal ΔN that minimizes F at fixed atomic positions (Q), but finding the dependence of F on ΔN at fixed Q or on Q at fixed ΔN is difficult, both because it is not straightforward to control ΔN independently of Q and because calculations of energies are very expensive.

However, the metal–insulator transitions of greatest current experimental interest share two features that greatly simplify an analysis. First, the lattice energetics is to good approximation harmonic^4,5,6, as shown from calculations⁴ and by the observation that phonon frequencies change only very slightly (~1%) across the metal–insulator transition. Second, and closely related to the first point, the coupling between the electronic order parameter and lattice modes is linear and is well determined by standard theoretical methods^4,5,6, as are the lattice energetics. This means that we may write, schematically,^4,5,6:

$$F({{\Delta }}N,Q)=\frac{1}{2}K{Q}^{2}-\frac{1}{2}gQ{{\Delta }}N+{F}_{{{{{\rm{el}}}}}}({{\Delta }}N)$$

(1)

Requiring stationarity of F with respect to variations in ΔN and Q yields the equations of state^4,6

$$KQ=\frac{1}{2}g{{\Delta }}N$$

(2)

and

$$\frac{\partial {F}_{{{{{\rm{el}}}}}}({{\Delta }}N)}{\partial {{\Delta }}N}=\frac{1}{2}gQ$$

(3)

Because g and K are known, Eq. 2 can be solved. Substituting the solution back into Eq. 1 produces:

$$\bar{F}({{\Delta }}N)=-\frac{1}{8K}{\left(g{{\Delta }}N\right)}^{2}+{F}_{{{{{\rm{el}}}}}}({{\Delta }}N)$$

(4)

From this point of view, the key question is the magnitude of the lattice stabilization energy $\frac{1}{8K}{\left(g{{\Delta }}N\right)}^{2}$: is it large enough to create a new extremum at a ΔN ≠ 0? Is it large enough to ensure that the extremum at ΔN = 0 is unstable? Answering this question requires knowledge of F_el.

Peil, Hampel, Ederer, and Georges⁶ observed that existing many-body methods such as the dynamical mean field method enable computation of electronic properties at fixed lattice configuration Q, in effect solving Eq. 3. Here we take one further step: the ansatz for the electronic energy functional in Eq. 1 means that the computed ΔN(Q) determines dF_el(ΔN)/dΔN; the derivative can then be integrated, thereby constructing F, F_el itself. In practice, we perform the integration by fitting the ΔN(Q) results to a polynomial, which is analytically integrated. While this method requires a choice of polynomial form, we empirically find that the uncertainty thereby introduced is small, of the order of a few meV, comparable to the error in performing an explicit energy calculation. This approach is computationally inexpensive, relatively unaffected by noise, and the analytically specified functional forms provide additional insight, in particular enabling a straightforward examination of the global energy landscape.

The method is general: the electronic and lattice order parameters can be of scalar, vector, or tensor character, higher-order couplings can be included and any theoretical method that delivers an equation of state can be used in Eq. 1. The applicability of the model in its current form is, however, restricted to situations in which the orbital basis used to define the electronic order parameter can be clearly defined, and the order parameter energetics can be separated from the energetics of the rest of the material which can then be subsumed into the lattice stiffnesses K. We will discuss the limits of our method’s applicability in more detail in the “Discussion” section, and in the Conclusion mention other materials to which it may be applicable.

We use this approach to analyze the metal–insulator transitions occurring in the rare-earth nickelates and their heterostructures, and in bulk and epitaxially strained Ca₂RuO₄. We find that in all of these situations the metal–insulator transition is, in the sense defined above, not electronically driven.

It is important to emphasize that the distinction between electronically driven and lattice driven transitions is not the same as the distinction between weak and strong electron correlations. A material may be said to be weakly correlated if density functional band theory (DFT) methods (or their hybrid and +U extensions) adequately describe the behavior and may be said to be strongly correlated if beyond DFT methods are required for the correct description of materials properties. While the weak/strong correlation distinction is not the main focus of this paper we believe the available evidence indicates that beyond DFT methods are needed to properly calculate the electronic term F_el of the materials we study here.

Rare-earth nickelates

The perovskite rare-earth nickelates have the chemical formula RNiO₃; when synthesized in bulk form the materials with R = Lu, Y, Sm, Nd, Pr exhibit a first order transition from a high-temperature metal to a low-temperature insulator while LaNiO₃ remains metallic down to the lowest measured temperature⁵⁶. The material properties depend systematically on the choice of rare-earth ion, with LuNiO₃ exhibiting the highest metal insulator transition temperature T_MIT = 600 K, SmNiO₃ having T_MIT ≈ 400 K, NdNiO₃ having a T_MIT ≈ 200 K and PrNiO₃ having a T_MIT ≈ 130 K^17,57,58. The materials may also be grown in heterostructure form^{4,7,13,17,18,24,48,59,60}, with a small number of layers of RNiO₃ sandwiched between layers of other materials. The metal–insulator transition temperature in the heterostructures differs from that in the bulk.

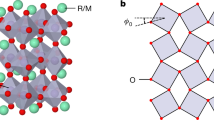
Except for the La-based compound, where the symmetry is slightly different, the high temperature metallic state forms in a Pbnm structure which for present purposes may be regarded as a pseudo-cubic lattice of Ni ions with an O ion at the midpoint of each Ni–Ni bond. The insulating state is characterized by a two-sublattice bond disproportionation, with one Ni sublattice having a short mean Ni–O bond length and the other by a long one, represented qualitatively in Fig. 2. The difference in mean Ni–O bond lengths defines the lattice mode Q appropriate to this transition.

Fig. 2: Schematic of the electronic and structural disproportionation in the insulating state in rare-earth nickelates.

NiO₆ octahedra disproportionate electronically and structurally in a three-dimensional checkerboard pattern in RNiO₃ metal–insulator transition compounds, with R a rare-earth. In the low-energy model of refs. ^4,6, the Ni ions corresponding to the larger octahedra have 1e⁻ $+\frac{{{\Delta }}N}{2}$ electrons (dark blue) in their e_g shell, while those corresponding to the smaller one (light blue) have 1e⁻ $-\frac{{{\Delta }}N}{2}$. The difference in average bond lengths defines Q for the nickelate materials. Red circles correspond to oxygen atoms, while the green arrow is a measure of the oxygen displacement along the Ni-Ni direction.

In the low T insulating state, the two Ni sublattices differ in electronic configuration. This difference has been characterized in various ways in the literature^{6,36,44,61,62,63}. We follow Peil and collaborators^4,6 and define the electronic change ΔN as the difference in the occupation of the e_g states obtained from a narrow window Wannier fit of the bands crossing the Fermi level, i.e.,

$${{\Delta }}N={N}_{{{{{\rm{HF}}}}}}-{N}_{{{{{\rm{LF}}}}}}$$

(5)

with N_HF (N_LF) the total e_g occupation on the octahedron with higher (lower) Ni occupation NiO₆ octahedra, while Q is defined as the average Ni–O bond length difference between the two, as shown in Fig. 2.

In Fig. 3 we present results for three different bulk-form rare earth nickelates, (LuNiO₃, SmNiO₃, PrNiO₃) as a function of Q, digitized from the calculations of ΔN presented in ref. ⁶. In this reference, the calculations performed are DFT+DMFT (DFT+Dynamical Mean Field Theory) calculations in the paramagnetic phase. In all compounds, two regimes are found, a low Q regime where ΔN is proportional to Q and a high Q regime where ΔN is large but weakly dependent on Q; the two regimes are separated by a discontinuity.

Fig. 3: Equation of state fit for bulk rare-earth nickelates, and corresponding electronic and total energies.

a Points: Electronic disproportionation as a function of bond disproportionation ΔN(Q) values used for the three RNiO₃ materials as obtained from Density Functional Theory + Dynamical Mean Field Theory calculations from ref. ⁶; Light lines: fits of the points to Eq. 7. Also shown is the Q(ΔN) line obtained from the Q equation of state Eq. 2. Note that the ratio of the lattice stiffness to the linear coupling K/g has the same value for all three materials. b Electronic energy, c total energy F_tot = F of three RNiO₃ compounds as a function of electronic order parameter ΔN, minimized over structural order parameter (bond disproportionation) Q. d Total energy as function of lattice distortion Q, minimized over ΔN. Energies per 10 atom unit cell.

To determine the free energy model to which the results should be fit we observe that the two sublattice nature of the insulating state means that the free energy must be invariant under simultaneous inversion Q ↔ −Q, ΔN ↔ −ΔN, so in particular, F_el(ΔN) must be even in ΔN. Motivated by the observed first-order nature of the transition we assume that F_el is a 6th order polynomial in ΔN:

$${F}_{{{{{\rm{el}}}}}}({{\Delta }}N)=\frac{1}{2}{\chi }_{0}^{-1}{{\Delta }}{N}^{2}+\frac{1}{4}\beta {{\Delta }}{N}^{4}+\frac{1}{6}\gamma {{\Delta }}{N}^{6}$$

(6)

Solving Eq. 2 and eliminating Q from the full free energy then changes the quadratic term ${\chi }_{0}^{-1}\to {\chi }_{0}^{-1}-\frac{{g}^{2}}{4K}$. Note that the shift in the quadratic term involves the parameter g²/K, which varies slightly across the RNiO₃ series although as noted in ref. ⁶ the ratio g/K is almost material-independent. The K for the Lu, Sm, and Pr materials were reported in ref. ⁶ to be 39.29, 41.45, and 44.47 eV/Ų, while the g are 3.75, 4.02, and 4.24 eV/Å.

Equation 6 implies that the equation of state Eq. 3 takes the explicit form

$$0=-gQ+{\chi }_{0}^{-1}{{\Delta }}N+\beta {{\Delta }}{N}^{3}+\gamma {{\Delta }}{N}^{5}$$

(7)

We fit the points in Fig. 3 to Eq. 7, using the g values presented in ref. ⁶, obtaining the light solid curves shown in Fig. 3 and the fit parameters given Table 1. It is important to note that the DMFT equation of state shown in Fig. 3 has two branches, with the solution discontinuously changing from one to the other as Q is varied. In our fits we only use the data points shown as symbols in Fig. 3; these points lie outside the region of multistability (i.e., where two ΔN solutions exist within DMFT for the same Q). However, our theoretical energy function correctly reproduces behavior that was not part of the original fit, for example, the locally stable large ΔN at Q = 0 solution for LuNiO₃⁶. Including points within the region of multistability does not lead to significant changes to our results. The free energy we obtain here may be thought of as the free energy that would be obtained from the two component Landau theory of ref. ⁶ if the metal–insulator variable were integrated out.

Table 1 Parameters that characterize the electronic and total energy of the three RNiO₃ materials, as extracted by fitting the data from ref. ⁶ to Eq. 7.

Panel b of Fig. 3 shows the purely electronic energy F_el corresponding to the fit parameters given in Table 1. We see that for all of the materials the purely electronic theory is characterized by a locally and globally stable metallic minimum at Q = 0. Only for LuNiO₃ does the purely electronic theory even exhibit a second, insulating extremum and even in this case it is not energetically favored. Panel c presents the total free energy as a function of ΔN obtained by minimization over the lattice degrees of freedom Q. We see that inclusion of the lattice coupling is necessary to stabilize the ΔN, Q ≠ 0 solution: in other words, it is the electron-lattice coupling that drives the transition.

Table 1 shows that as one moves across the RNiO₃ series from R = Lu (most insulating) to R = Pr (least insulating), the linear response electronic susceptibility of the metallic state decreases, consistent with the empirical observation that the Lu material is the strongest insulator and the Pr material is the weakest. We see also that the nonlinear terms in the energy are the same for the Lu and Sm compounds, which are the two strong insulators, but are different in the Pr compound, which is close to the metal–insulator transition. This shows that to understand composition-dependent changes one must consider more than just the variation in linear response susceptibilities. Results to be presented below for superlattices further confirm this point.

The present theory predicts that PrNiO₃ is undistorted and metallic, although close to the metal–insulator transition boundary, while the compound is empirically distorted and insulating, although again with a very low transition temperature. We believe this discrepancy arises because the transition in PrNiO₃ is from a paramagnetic metal to an antiferromagnetic insulator, in contrast to the Sm and Lu materials where the transition is between two paramagnetic phases. Inclusion of antiferromagnetism in the theory will yield a lower energy for the insulating phase of PrNiO₃ at the U, J values used here while a slightly different choice of interaction parameters would also push PrNiO₃ to the insulating side of the phase diagram.

We may take the analysis further by substituting the ΔN(Q) obtained from the solution of Eq. 7 into the full free energy expression to obtain the free energy as a function of the lattice coordinate Q shown in the panel d of Fig. 3. This is analogous to the energy that is usually calculated by electronic structure codes, which work at fixed atomic positions. The discontinuities arise from the different branches of the ΔN(Q) curves. The resulting free energy is, to a good approximation, the combination of two parabolic energy curves, one corresponding to the metallic state, and one to the insulating state. We see that in this theory the ΔN = 0, Q = 0 state is stable to lattice distortions for PrNiO₃, marginally stable for SmNiO₃, and unstable for LuNiO₃.

The analysis presented here is based on a fit of the computed ΔN(Q) to a free energy model. We emphasize that this fit is in no way essential to our method; one could simply numerically integrate a suitably dense set of ΔN(Q) data. But for the procedure used here the question of the sensitivity of the results to the choice of free energy arises. To quantify the uncertainties we have refit the PrNiO₃ data shown in Fig. 3, now constraining the 4th and 6th order coefficients to have the same values as found in SmNiO₃. Results are shown in Fig. 4. We see from panel a that this fit to the data is not quite as good, especially in the small to intermediate Q region. The fitted energy (panel b) is very similar to that shown in Fig. 3, with the value of ΔN at the minimum almost the same in the two cases and the energy of insulating solution in the constrained fit is now slightly lower than the energy of the metallic solution, placing paramagnetic PrNiO₃ slightly on the insulating side of the transition. These differences indicate that the systematic uncertainties in the method are not large.

Fig. 4: Assessing the accuracy of the method by comparing multiple fits.

Fits (a) and total energy (b) for PrNiO₃ based on Density Functional Theory + Dynamical Mean Field Theory data from ref. ⁶; green lines correspond to the optimal polynomial fit, red lines to 4th and 6th kept constant to the values extracted for SmNiO₃, and only the quadratic term fitted to the data.

Layered structures of NdNiO₃/NdAlO₃

An important modern direction in quantum materials science is heterostructuring: the ability to synthesize structures in which atomically thin planes of one material alternate with atomically thin planes of another. Previous experimental¹³ and theoretical⁴ work analyzed systems of the type shown schematically in Fig. 5 in which a few layers of metal–insulator transition compound NdNiO₃ were grown as a thin film sandwiched epitaxially between layers of the wide-gap insulator NdAlO₃. The few-layer systems had significantly higher transition temperatures than did bulk NdNiO₃. Theoretical DFT+DMFT results are available⁴ for three systems: bulk NdNiO₃ and two heterostructured systems with a 4 unit cell repeat distance: one layer of NdNiO₃ followed by three of NdAlO₃ (monolayer), and two layers of NdNiO₃ followed by two of NdAlO₃ (bilayer). The ΔN(Q) results are shown in Fig. 6

Fig. 5: Structural and electronic effects of layering NdNiO₃ with the band insulator NdAlO₃.

a Schematic of superlattice consisting of NdNiO₃ layered in between the band insulator NdAlO₃; b schematic view of two atomic layers of NdNiO₃ sandwiched between NdAlO₃ layers as described in ref. ⁴. Dashed line with red slash: forbidden electronic hopping path, indicating mechanism of dimensional confinement. Zig-zag lines connecting O (red circles) and Al atoms: representation of the increased stiffness to distortions of apical Ni–O bonds as a result of resistance from the Al–O bonds.

Fig. 6: Equation of state fit, and electronic and total energy for bulk NdNiO₃ and layered NdNiO₃/NdAlO₃ structures.

a Data showing electronic disproportionation as a function of structural distortion ΔN(Q), from⁴ (points) and the polynomials (light lines) obtained by fitting the data to the equation of state, Eq. 7. b Electronic and c total energy as functions of electronic order parameter ΔN for bulk NdNiO₃ and for superlattices consisting of a bilayer of NdNiO₃ alternating with NdAlO₃ and a monolayer of NdNiO₃ alternating with three layers of NdAlO₃ using data from ref. ⁴. d Total energy as function of octahedral distortion Q after minimizing over electronic disproportionation ΔN. Note change of y-axis scale between panel a and other two panels. Energy normalized to correspond to 10 atom unit cell for the bulk, and per two Ni atoms (one layer) of NdNiO₃ in the superlattices.

Two competing effects were found⁴: the electronic confinement of the electrons in the NdNiO₃ by the nearby NdAlO₃ layers favors a higher electronic disproportionation ΔN, while the energy cost of imposing a lattice distortion on the adjacent Al-O octahedra is equivalent to an increase in the stiffness K of the NiO₆ lattice with a K = 31.6914eV/Ų, for the bulk material, K = 35.6269 eV/Ų for the bilayer and K = 40.4753 eV/Ų for the monolayer; all energies per 10 atom unit cell. The values for g are those quoted in ref. ⁴; we reproduce them here for convenience: g = 3.2212 eV/Å for the bulk, g = 3.3465 eV/Å for the bilayer, and g = 3.3780 eV/Å for the monolayer. Performing an analysis similar to that presented in section “Rare-earth nickelates” leads to the energy curves presented in Fig. 6 and to the fit parameters shown in Table 2. The original data with the fit are presented for convenience in Fig. 6

Table 2 Parameters that characterize the electronic and total energy of NdNiO₃ and NdNiO₃/NdAlO₃ heterostructures consisting of a single or two layers of NdNiO₃ from ref. ⁴.

Turning first to the purely electronic correlation energy shown in the (b) panel of Fig. 6, we observe that neither NdNiO₃ nor the heterostructured materials show a purely electronically driven insulating state; however, hints of an inflection point, the precursor of the formation of a higher ΔN extremum, can be seen in bilayer and monolayer curves around ΔN = 1 reflecting the effect of quantum confinement in increasing electron correlation effects. Inclusion of the lattice energy produces a global, insulating minimum in all three materials. The monolayer and bilayer show a significantly larger energy difference between the insulating and the metallic states than does bulk NdNiO₃, in agreement with their higher T_MIT.

The origin of the differences between monolayer, bilayer, and bulk nickelates is surprising: the modest decrease in the magnitude of g²/K as we pass from bulk to bilayer to monolayer reflects the increase in lattice stiffness, opposing the order, and nearly counterbalances the modest decrease in ${\chi }_{0}^{-1}$ reflecting the increased correlation physics of the confined metallic state. The more important effect, however, is the change in the magnitude of the higher order (ΔN⁴, ΔN⁶) terms shown in Table 2. The change can be seen in Fig. 6 from the variation of the critical Q below which the insulating state is not stable. In the calculations presented in the previous subsection the higher order terms were also found to be different in PrNiO₃ (proximal to the metal–insulator transition) than in LuNiO₃ and SmNiO₃ (farther from the transition point).

Metal–insulator transition in bulk Ca₂RuO₄

Ca₂RuO₄ forms in a slightly distorted version of the n = 1 Ruddlesden–Popper structure, a layered structure consisting of RuO₂ planes separated by pairs of CaO layers. Each Ru is six-fold coordinated by oxygen, forming RuO₆ octahedra. The relevant electronic states (actually Ru–O antibonding states) may be thought of as Ru t_2g symmetry d-states (d_xy, d_xz, d_yz) with 4 t_2g electrons per Ru. Below 340 K the material undergoes a first-order transition from a high temperature metallic to a low temperature insulating phase. No symmetry is broken at the transition: the two phases share the same crystal symmetry but differ in the occupancies of the d orbitals and shape of the RuO₆ octahedra, and the relative occupancies of the d-levels. As sketched in Fig. 7, the metallic state is characterized by an approximately equal occupancy of the t_2g orbitals, while in the insulating state the xy orbitals are doubly occupied and the xz/yz orbitals each contain a single electron. The appropriate electronic order parameter is the occupancy difference between the xy and xz/yz orbitals

$${{\Delta }}N={n}_{xy}-\frac{1}{2}({n}_{xz}+{n}_{yz}).$$

(8)

No crystal symmetry protects the orbital occupancies in the high temperature metallic state, which is characterized by a ΔN = N_H close to, but not exactly, zero.

Fig. 7: Schematic of the electronic and structural disproportionation characterizing the metal–insulator transition of Ca₂RuO₄.

a In the metallic phase, all 3 t_2g orbitals of Ca₂RuO₄ are approximately equally occupied; ΔN ≈ 0. b In the insulating phase, the xy orbital is doubly occupied, while the yz and xz are singly occupied; ΔN = 1. c Representation of Q₀ structural mode, in which all bond lengths change equally. d Representation of structural mode Q₃ in which octahedral volume is preserved and the change in the two in-plane Ru–O bond lengths are equal, and opposite in sign to the change in the apical bond length. The electronic state in b is associated with a structural term of the form −(Q₃ − λ₀Q₀), with λ₀ > 0 Legend: a, b: black lines correspond to orbital energy levels, blue circles signify electrons; c, d: purple circle = Ru atom, red circle, O atom; arrows and dotted lines signify bonds and their changes with the two different structural modes.

The change in electron occupancy across the metal–insulator transition occurs simultaneously with a decrease in the Ru–O apical bond length and an increase in the in-plane Ru-O bond length (a flattening of the octahedra). At the transition, there is a change in the lattice constants, and rearrangements of other internal coordinates. The harmonic nature of the lattice Hamiltonian means that most of the lattice modes may be integrated out, leaving an effective theory involving two structural degrees of freedom. The two lattice degrees of freedom are needed, because if the point symmetry of the Ru ion is lower than cubic, then both the unit cell volume change and the relative octahedral distortion couple linearly to the differential level occupancy ΔN.

Following ref. ⁵ we write the two relevant structural degrees of freedom as a variable Q₃ parametrizing a volume preserving change in the c-direction Ru–O bonds relative to the average in-plane Ru–O bonds, and a change Q₀ in the octahedral volume and define the lattice variables such that in the high-T metallic state Q₃ = Q₀ = 0. In terms of changes δx, δy, δz to the three Ru–O bond lengths, defined as:

$${Q}_{0}=\frac{1}{\sqrt{3}}(\delta x+\delta y+\delta z)\,\,\,{Q}_{3}=\frac{1}{\sqrt{6}}(2\delta z-\delta x-\delta x)$$

(9)

We now build the free energy. We define the lattice distortion relative to the high-T metallic state as the vector $\overrightarrow{Q}=({Q}_{3},{Q}_{0})$; the lattice restoring term K is a 2 × 2 matrix with entries determined in previous work⁵ to be K₃₃ = 17.7, K₀₃ = 7.6, K₀₀ = 46.2 eV/Ų per formula unit. We write the linear combination of the Q that couples to the electronic disproportionation as $\overrightarrow{{{{{{{{\mathcal{F}}}}}}}}}\cdot \overrightarrow{Q}$ with $\overrightarrow{{{{{{{{\mathcal{F}}}}}}}}}={F}_{3}(1,-\lambda )$. Reference ⁵ finds F₃ = 2.8 eV/Å and λ = 0.45.

$$F({{\Delta }}N,Q)=\frac{1}{2}{{{{{{{{\bf{Q}}}}}}}}}^{T}{{{{{{{\bf{K}}}}}}}}{{{{{{{\bf{Q}}}}}}}}-\overrightarrow{{{{{{{{\mathcal{F}}}}}}}}}\cdot \overrightarrow{Q}({{\Delta }}N-{{\Delta }}{N}_{H})+{F}_{{{{{\rm{el}}}}}}({{\Delta }}N),$$

(10)

Here ΔN_H is the value of ΔN in the high temperature insulating phase; it is nearly, but not quite, zero.

For the purely electronic energy we chose the 4th order form:

$${F}_{el}({{\Delta }}N)=\frac{c{{\Delta }}{N}^{4}}{4}+\frac{b{{\Delta }}{N}^{3}}{3}+\frac{a{{\Delta }}{N}^{2}}{2}+{\sigma }_{0}{{\Delta }}N$$

(11)

Odd powers occur because no symmetry is broken at the transition.

Figure 8 shows previously published results⁵ for ΔN as a function of the relevant combination of lattice distortions along with our fit to Eq. 11. As in the previous section we have not used points in the coexistence region for the fit. We find σ₀ = −0.009, a = 0.70, b = −1.718, c = 1.28.

Fig. 8: Equation of state fit for bulk Ca₂RuO₄, the resulting energy, and energy as a function of epitaxial strain.

a Electronic disproportionation as a function of structural disproportionation ΔN(Q) from⁵ (heavy black points) and polynomial fit (solid line) used for the equation of state. b Correlated electron free energy, and total free energy as a function of the electronic disproportionation order parameter characterizing the orbital polarization: F_el(ΔN) and F_total(ΔN) for bulk Ca₂RuO₄. c Total energy plotted against orbital disproportionation ΔN for materials grown on four substrates indicated in the legend (NSAT is Nd_0.4Sr_0.6Al_0.7Ta_0.3O₃) which provide different strains relative to the metallic phase of Ca₂RuO₄. For compressive strain (NdAlO₃), the material is always metallic and the orbital polarization has the opposite sign from the insulating state. d Total free energy versus electronic disproportionation ΔN : F_total(ΔN) computed for bulk Ca₂RuO₄ different values of the linear coupling term F₃. e Phase diagram of epitaxially constrained Ca₂RuO₄ in plane of tensile strain (defined as difference of mean in-plane Ru–O bond length from value in the high temperature structure) in Å and electron-lattice coupling parameter F₃. Red dashed line: value of F₃ at which metal insulator transition occurs in bulk system. Arrows (red on line) indicate strain imposed by epitaxial growth.

The higher curve (blue) in Fig. 8, panel b, shows the purely electronic free energy resulting from the fit. We see that in the absence of lattice effects the metallic, undistorted state is energetically favored and that there is not even a metastable minimum corresponding to the insulating state, although there is a hint of an inflection point that is a precursor of a higher ΔN extremum. The lower trace (dark orange line) shows $\bar{F}$, the full free energy after the lattice modes have been integrated out. We see that the inclusion of the lattice energetics qualitatively changes the free energy, strongly favoring large ΔN. Indeed we see that the energy does not have a minimum in the physically allowed range ΔN ≤ 1; rather it is minimized at the boundary ΔN = 1, as ∣ΔN ≤ 1∣ is the largest allowed value. We again conclude that the transition in this compound is driven by the lattice contribution to the energetics.

Epitaxially constrained Ca₂RuO₄

Ca₂RuO₄ has also been grown expitaxially on insulating substrates. The epitaxial constraint means that the in-plane lattice parameters of Ca₂RuO₄ are forced to be equal to the in-plane lattice parameters of the substrate material. A priori, this constraint does not fix the values of the internal coordinates including the the Ru–O in-plane bond length of relevance here. Density functional theory calculations, however⁵, indicate that in practice the material adapts to the epitaxial constraint by adjusting the in-plane Ru–O bond lengths, rather than by rotating the Ru–O₆ octahedra, so that the percentage change in the in-plane Ru–O bond lengths is fixed by the percentage change in the in-plane lattice parameters. The z-direction lattice constants and Ru–O apical bond lengths are still of course free to relax. This means that the theory of the previous section can be simply adapted to the epitaxial case by a change of variables. We write:

$${Q}_{3}=\frac{1}{\sqrt{6}}(2\delta z-\delta {x}_{0}-\delta {y}_{0})$$

(12)

and

$${Q}_{0}=\frac{1}{3}(\delta z+\delta {x}_{0}+\delta {y}_{0})$$

(13)

with δx₀ and δy₀ fixed by the epitaxial constraint. It is also convenient to define the zero of δz to be the value

$$\delta {z}_{0}=-(\delta {x}_{0}+\delta {y}_{0})\frac{{K}_{00}-{K}_{33}+\frac{{K}_{30}}{\sqrt{2}}}{2{K}_{33}+2\sqrt{2}{K}_{30}+{K}_{00}}$$

(14)

that δz would take at ΔN = N_H.

We obtain:

$$F({{\Delta }}N,\delta z)=\frac{{K}^{\prime}}{2}\delta {z}^{2}+{g}^{\prime}\left(\delta z-\delta {z}^{\star }\right){{\Delta }}N+{F}_{el}({{\Delta }}N)$$

(15)

with

$${K}^{\prime}=\frac{2}{3}\left({K}_{33}+\sqrt{2}{K}_{30}+\frac{1}{2}{K}_{00}\right)$$

(16)

$${g}^{\prime}=\frac{{F}_{3}(2-\sqrt{2}{\lambda }_{0})}{\sqrt{6}}$$

(17)

and

$$\delta {z}^{\star }=(\delta {x}_{0}+\delta {y}_{0})\left(\frac{1+\sqrt{2}{\lambda }_{0}}{2-\sqrt{2}{\lambda }_{0}}+\frac{{K}_{00}-{K}_{33}+\frac{{K}_{30}}{\sqrt{2}}}{2{K}_{33}+2\sqrt{2}{K}_{30}+{K}_{00}}\right)$$

(18)

The epitaxial constraint thus has three effects: it increases the net stiffness to lattice distortions by preventing relaxations of the lattice coordinates associated with in-plane bond lengths, making the insulating phase more difficult to obtain. Second, it reduces the electron lattice coupling (Eq. 17) which also makes it more difficult to obtain an insulating phase. Finally, it provides a term linearly proportional to ΔN, which for positive epitaxial strain favors the insulating phase. Panel a of Fig. 9 shows the change in apical Ru–O bond length as a function of epitaxial strain; panel b the occupancy difference ΔN. The first order transition is evident. Note that for an epitaxial strain matching the in-plane lattice constant of the high temperature metallic phase, insufficient lattice energy is available to stabilize the insulating phase. As the tensile strain is increased, the octahedral deformation, which couples linearly to ΔN, increases, and beyond a critical value drives a first order transition.

Fig. 9: Structural and electronic disproportionation of Ca₂RuO₄ versus epitaxial strain.

Equilibrium electronic order parameter characterizing the orbital polarization ΔN (a) and Ni–O apical bond distortion δz (b) versus epitaxial strain defined as the difference in mean in-plane Ru–O bond length relative to the value in the high temperature structure of Ca₂RuO₄ as imposed through epitaxial strain via in-plane Ni–O bond changes away from the bulk values, δx₀, δy₀ where δx₀ = δy₀, computed as described in the main text.

Experiments (refs. ^64,65) have studied films grown epitaxially on substrates NdAlO₃, LaAlO₃, NSAT (Nd_0.4Sr_0.6Al_0.7Ta_0.3O₃), and NdGaO₃ corresponding to changes (relative to the high-T state, and assuming the Ru–O bond length exactly tracks the in-plane strain) in average in-plane Ru–O lattice parameters of −0.04, 0.008, .03, and 0.046  respectively. Figure 8 shows that the theory, with no adjustable parameters, predicts that for the theoretically predicted coupling F₃ = 2.8 eV/Å the films grown on NdAlO₃ and LaAlO₃ should be metallic, while the films grown on NSAT and NdGaO₃ should be insulating. In the experiment, the LaAlO₃-strained material has a transition at T ≈ 200 K from a high temperature metal to a low temperature weak insulator/bad metal, while the others are metallic and insulating as predicted by the theory. The qualitative agreement is good; the quantitative discrepancies may arise from a more subtle relation between Ru–O bond length and in plane lattice constant than was assumed in ref. ⁵ or from small systematic errors in the theory. The good correspondence between experiment and theory shows the utility of the methodology introduced here.

Temperature Dependence

The methods presented here provide some insight into the physics of the temperature-driven metal–insulator transition, indicating an important area for future research. We see from Figs. 3 and 6 that for the nickelates the low T energy landscape is characterized by two minima, with energy differences per formula unit ranging from 80 meV (LuNiO₃) to 25 meV (NdNiO₃). In the nickelates, as the temperature increases, a first order metal–insulator transition occurs. The lattice distortion Q exhibits negligible temperature dependence over the entire insulating phase, indicating that the minima remain robust and the transition is driven by an entropic effect that lifts up the free energy of the large ΔN extremum relative to that of the ΔN = 0 extremum.

To investigate whether the entropic effect arises from the local correlations captured by the dynamical mean field approximation, for bulk NdNiO₃ we have extended the calculations shown in Fig. 6 to much higher temperatures by performing calculations with the same methodology and interaction parameters as in⁴ but changing the electronic temperature. The parameters, as obtained from the fit for certain temperatures can be found in Table 3. Figure 10 shows the results: all of the parameters in the electronic free energy vary systematically with temperature, decreasing in magnitude as the temperature is increased from ~290 to 1000 K; the result is a very weakly first order transition at ≈1080 K (the model actually passes very close to the tricritical point at which the second and fourth order coefficients of the theory simultaneously change sign). This behavior, while theoretically interesting, is inconsistent with the observed strongly first order character and much lower transition temperature behavior, suggesting that either the single site dynamical mean field approximation does not adequately describe the temperature dependence of the electronic contribution to the free energy, or that an entropic effect associated with the lattice degrees of freedom plays an important role. Indeed the neglect of spatial fluctuations generically means that single-site DMFT approximations overestimate transition temperatures^66,67. It should also be noted that in this material antiferromagnetism plays an important role in the ordering, and that a direct computation⁴⁴ of the free energy F(ΔN, Q) using a different DMFT formalism places paramagnetic NdNiO₃ on the paramagnetic metal side of the transition and yields a stronger low T temperature dependence, and shows for LuNiO₃ a temperature dependence of F(ΔN, Q) in the range T < 500K very similar to that found here for NdNiO₃.

Table 3 Parameters that characterize the temperature dependence of the electronic energy as extracted by fitting the data in Supplementary Note 1; electronic energies presented in Fig. 10.

Fig. 10: Evolution of the electronic and total energy landscape of NdNiO₃ as a function of electronic temperature.

a Electronic free energy as function of electronic disproportionation ΔN computed for NdNiO₃ at temperatures from 290 to 1160 K. b Total free energy computed for bulk NdNiO₃ for the same temperature range. c Total expanded view of total free energy for bulk NdNiO₃ at temperatures close to the transition. d Optimal bond disproportionation Q, as obtained by a linear transformation from the electronic disproportionation ΔN, using the lattice stiffness K and electron-lattice coupling term g: Q(T) = ${{\Delta }}N(T)\frac{g}{2K}$. Data for fits provided in Supplementary Note 1.

Ca₂RuO₄ presents different issues. A substantial temperature dependence is observed⁶⁸ across the insulating phase. Since the electronic order parameter ΔN in this material is fixed at its largest possible value for a range of couplings, the temperature dependence must imply a temperature dependence of the electron-lattice coupling F₃ as proposed for related reasons in⁵. Within single-site dynamical mean field theory, there is no theoretical justification for a strongly temperature-dependent coupling parameter, but on the assumption that changes in electron-lattice coupling F₃ are a proxy for changes in temperature we show in Fig. 8, panel d, the energy computed for different values of F₃. We see that a first order transition occurs at an F₃ ≈ 1.58 ≈ 0.6 of the F₃ we estimated from the low temperature calculation. The phase diagram presented in Fig. 8 panels e, and c, then indicates that films grown on substrates with a tensile epitaxial constraint exhibit significantly higher transition temperatures than found in bulk, roughly consistent with experiment.

Discussion

It is important to critically examine the assumptions that underly our results. The first assumption enabling the construction is that the lattice energy is quadratic in deviations from an equilibrium position at fixed value of the electron order parameter, in other words that the physics controlling the relevant atomic force constants arises from chemical bonds inside the solid that are only weakly affected by the transition from metal to insulator. This and the harmonic nature of the lattice response are found in density functional calculations (see e.g., the supplementary material of ref. ⁴) and are further supported by the observation that phonon frequencies do not change much across the transitions of interest.

The second assumption is that the coupling between electronic and lattice degrees of freedom is linear, and may be determined a priori. This second assumption has been confirmed by explicit calculations (see, for example, the supplementary information in ref. ⁴). Further investigation of these assumptions, and identification of compounds in which they break down, is an important topic for future research. One important direction is a detailed comparison of results obtained along the lines indicated here to direct computations of energies and free energies^44,62,63,69.

Given these assumptions, a many-body calculation of electronic configuration as a function of lattice distortion may be used to construct free energies, essentially by integrating the equation of state. We accomplish the integration by fitting the equation of state results to a polynomial which is integrated analytically. This procedure is convenient because it avoids ambiguities associated with the coexistence region of the first order transition, but is not necessary.

We applied the methodology to two currently interesting families of compounds, that exhibit first order metal–insulator transitions as the temperature is decreased: the rare earth perovskite nickelates RNiO₃, and Ca₂RuO₄. The two materials were chosen because they exhibit qualitatively different electron-lattice couplings. The transition in the RNiO₃ is a symmetry-breaking transition leading to two inequivalent Ni sites and an alternating pattern of long and short Ni–O bond lengths. The transition in Ca₂RuO₄ is isosymmetric, with no broken crystal symmetries between the two states. In both materials, we find that if the lattice coordinate is set to the value appropriate to the high temperature metallic state, the resulting energy F(ΔN, Q = 0) has only one minimum, at ΔN = 0. It is only after the coupling to the lattice is included that the total functional F(ΔN, Q) acquires a minimum at a ΔN, Q ≠ 0. We, therefore, conclude that lattice effects are essential in driving the metal–insulator transition in both compounds, rather than being merely a minor consequence of a fundamentally electronically driven transition, thereby settling a long-standing controversy. It is important to note however that although the purely electronic theory does not produce a metal–insulator transition, the correlation contribution to the electronic energy is still important. DFT-level calculations would lead to a F_el, which rises so steeply with ΔN that the only extremum would be at ΔN = Q = 0. A beyond-DFT theory is needed to obtain an electronic energy which, although it does not by itself have a minimum at a non-zero ΔN, is “soft” enough to enable the lattice energies to produce the ordered state.

It is important to consider the limitations of our conclusions. First, while the approach introduced here will work with any method that calculates the electronic order parameter as a function of lattice distortion ΔN(Q), in practice the information available in the literature comes from the density functional plus dynamical mean field methodology. While this method successfully produces results that are consistent with many experiments, its precise quantitative accuracy is unknown. The method does require an identification of correlated orbitals, it relies on the assumption that density functional theory gives an adequate account of the energetics of the uncorrelated orbitals, it requires specification of interaction parameters, and its solution of the many body problem involves a stringent locality assumption. Cross checking via other methods (as for example was done for Ca₂RuO₄ in ref. ⁷⁰) would be desirable. Further, there are several variants of the DMFT plus DFT methodology, differing in the choice of energy window and the representation of correlated states⁷¹; the dependence of our conclusions on the implementation is an interesting question.

The specification of interaction parameters is of particular importance. As shown e.g., in refs. ^3,4, as the interaction parameters are increased in magnitude, a transition can be generated in the purely electronic theory. The precise statement made here is that with interaction parameters determined by reproducing physical properties including gaps, and effective masses, and structural distortion, the purely electronic theory does not exhibit a phase transition: electron-lattice coupling plays an essential role in stabilizing the insulating states.

It will also be noted that while the theory presented here reproduces trends and orders of magnitude very well, it has some quantitative deficiencies, for example predicting that PrNiO₃ is metallic but close to the phase boundary when in fact it is insulating but close to the phase boundary, with the lowest transition temperature of any bulk member of the RNiO₃ nickelate family. This deficiency is likely to be remedied by the inclusion of magnetism in the theory, since in PrNiO₃ and NdNiO₃, but not in the other compounds studied in this paper, the metal–insulator transition is accompanied by a magnetic transition. Similarly, the phase diagram of epitaxially constrained Ca₂RuO₄ films is qualitatively correct but exhibits quantitative discrepancies with experiment. We note that in this paper no attempt was made to adjust the parameters from the literature or to fine-tune the fits to obtain better agreement with the experiment. Small changes, reflecting moderate parameter uncertainties and modest systematic errors in the DFT+DMFT approach, would likely cure these discrepancies.

Conclusions

Electronic phase transitions in quantum materials are almost always accompanied by some form of lattice distortion, and in many specific cases, the question of whether the transition is driven by the lattice or by correlated electron energetics has been hotly debated. In theoretical terms, the answer is determined by the properties of a free energy functional F(ΔN, Q) that depends on suitably defined electronic (ΔN) and lattice (Q) modes. For second order transitions, the needed information can often be determined from symmetry arguments along with the values of a small number of parameters determined from the linear response of the symmetry-unbroken state. However, many transitions of current interest, in particular metal–insulator transitions, are first order, so that knowledge of the free energy landscape over a wide range is required. This information has been more difficult to obtain both because of the simple expense of computing an entire energy landscape and because these computations require fixing the electron order parameter at values that do not extremize the energy. In this paper, we proposed a method that constructs the needed free energy from the equation of state (electron order parameter as a function of lattice distortion). The method is computationally feasible and can be applied using any many-body method that obtains the equation of state. We demonstrate the power of the method by using it to resolve the long-standing question of the role of the lattice in the metal–insulator transitions in two representative classes of quantum materials, the perovskite rare earth nickelates, and the Ruddlesden–Popper calcium ruthenates. We find that in both materials the lattice degree of freedom is essential to the metal–insulator transition.

We also observe that while we presented results based on dynamical mean field calculations, the method is generic in nature and can easily be used with other electronic structure methods, including DFT, DFT+U^72,73, Gutzwiller^74,75, Auxiliary–Boson^76,77,78,79—particularly with the advent of new codes that calculate energy and naturally handle symmetry breaking^{80,81,82,83,84}, and quantum Monte Carlo⁸⁵.

The methods can be applied to quantify the importance of lattice effects in other systems of current interest, including CaFeO₃^86,87 which exhibits charge ordering and lattice disproportionation, perovskite titanates and vanadates, where lattice distortions couple to orbital ordering^88,89,90, VO₂ where a dimerization instability occurs⁹¹, V₂O₃ where the metal–insulator transition couples to the volume of the material⁹², and the rare earth manganites where electronic charge, orbital and magnetic ordering are tightly coupled to complex lattice distortions^93,94,95, two-dimensional correlated van der Waals dihalides and trihalides MX₂, MX₃, with M a transition metal ion and X a halogen^96,97,98,99, as well as in charge density waves in transition metal dichalcogenides^100,101.

The access to the free energy provided by our methods enables additional insights. Issues relating to temperature dependence were discussed in the temperature dependence section “Temperature Dependence”. The energy landscape shown in Fig. 1 makes it clear that only one narrowly defined path connects the metallic and insulating minima; this information may be used to investigate the kinetics of order parameter nucleation if the material is supercooled or superheated across the phase boundary. Further, the differing roles of the electronic and lattice degrees of freedom in defining the energy landscape make possible an analysis of the kinetics of state evolution after excitation. For example, excitation might rapidly heat the electrons (leading to changes in F_el) but only slowly heat the lattice degrees of freedom (which would in any event respond more slowly). Extension of the theory presented here to include the antiferromagnetism that occurs in the rare earth nickelates may help understand recent ultrafast experiments exploring the relation between antiferromagnetism, lattice distortions, and metallicity in NdNiO₃^102,103.

Methods

The new numerical ΔN(Q) data for NdNiO₃ used to build the electronic energies in this paper is obtained by using identical methodology and parameters as in our previous work (ref. ⁴). We’ve used Quantum Espresso¹⁰⁴ for density functional theory calculations, Wannier90¹⁰⁵ to build the low-energy Wannier model, and dynamical mean field theory calculations using the TRIQS implementation¹⁰⁶, using the continuous time hybridization¹⁰⁷ solver. We’ve used the exact same numerical and interaction parameters as in (ref. ⁴), but with a different electronic temperature which can be obtained by changing the parameter β.

The other DFT+DMFT data used in this work is digitized from previous work, namely from ref. ⁶ (bulk LuNiO₃, SmNiO₃, and PrNiO₃), from ref. ⁴ (for bulk NdNiO₃ and layered NdNiO₃/NdAlO₃), and from ref. ⁵ (Ca₂RuO₄).

Data obtained either from new calculations or digitizing from previous work, is fit using Matlab and built into our equation of state (3), as appropriate for each material.