Abstract
Three-dimensional (3D) chiral mechanical metamaterials enable behaviors not accessible in ordinary materials. In particular, a coupling between displacements and rotations can occur, which is symmetry-forbidden without chirality. In this work, we solve three open challenges of chiral metamaterials. First, we provide a simple analytical model, which we use to rationalize the design of the chiral characteristic length. Second, using rapid multi-photon multi-focus 3D laser microprinting, we manufacture samples with more than 105 micrometer-sized 3D chiral unit cells. This number surpasses previous work by more than two orders of magnitude. Third, using analytical and numerical modeling, we realize chiral characteristic lengths of the order of ten unit cells, changing the sample-size dependence qualitatively and quantitatively. In the small-sample limit, the twist per axial strain is initially proportional to the sample side length, reaching a maximum at the characteristic length. In the thermodynamic limit, the twist per axial strain is proportional to the square of the characteristic length. We show that chiral micropolar continuum elasticity can reproduce this behavior.
Similar content being viewed by others
Introduction
In ordinary elastic bulk solids, twist effects are of lesser importance than strains, or they are absent altogether. For example, transverse (TA) and longitudinal (LA) acoustic phonons appear in all bulk solids, whereas additional twist acoustic modes only appear in elastic achiral or chiral beams with finite cross-section1. As another example, the classical rank-four Cauchy elasticity tensor describes the generally rich connection between strains and stresses, whereas it completely neglects chiral twist effects. This asymmetry between strains and twists in elasticity is related to the fact that twist effects depend on the sample size. More specifically, in three-dimensional (3D) crystalline materials or metamaterials composed of a total of Nx × Ny × Nz unit cells with Nx ∝ Ny ∝ Nz ∝ N, the integer number N is decisive. In sharp contrast, usual strain-related effects do not depend on N.
On this background, our 2017 experiments on pronounced push-to-twist conversion effects in chiral architectures came as somewhat of a surprise2 (also see refs. 3,4). In these experiments2, we demonstrated large static twist effects in 3D cubic chiral metamaterials composed of moderately large total numbers of cubic unit cells of ≤500. We experimentally found a slow but monotonous decrease of the twist angle per axial strain, φ(N)/ϵzz at predescribed ϵzz, when increasing N from 1…5 for a fixed sample height-to-width aspect ratio of A = 2. For larger N, the computed asymptotic decrease followed the beam’s surface-to-volume-ratio ∝ 1/N. Later, the unit cell suggested in ref. 2 was systematically optimized in the sense of maximizing φ(1)/ϵzz for a single unit cell by using topology optimization5.
Three more recent independent conceptual studies6,7,8, loosely based on ref. 9, aimed toward systematically modifying and improving the qualitative and quantitative behavior of φ(N) with N ≫ 1 for metamaterial crystals composed of many unit cells. The results presented in refs. 6,7, both show that the behavior of twist versus N can be tailored by the coupling strength between chiral unit cells. In ref. 7, early model experiments on corresponding samples with a macroscale unit-cell size of axy = 2.4 cm, fabricated by macroscopic 3D printing, were reported as well.
On the level of effective continuum descriptions, the behavior of \(\varphi \left(N\right)\) has been described by generalized elasticity, e.g. by Eringen10 and Lakes11. Therein, several chiral and achiral characteristic length scales are defined. Different characteristic length scales for one metamaterial have also previously been discussed for two-dimensional achiral elastic metamaterials12,13. There, analytical expressions were derived12, relating the length scales to geometrical parameters of the microstructure. In the context of chiral 3D periodic elastic metamaterials, characteristic length scales have previously been discussed in generalized continuum theories beyond Cauchy elasticity, such as micropolar Eringen elasticity2,11 or Willis elasticity14. These length scales2,9 have been comparable to or even smaller than the unit cell size, or lattice constant, of the metamaterial crystal.
In the present paper, building on previous studies2,6, we design a feasible 3D tetragonal metamaterial crystal unit cell. We manufacture corresponding 3D metamaterial samples with a microscale unit cell size of axy = 74 µm and axy = 150 µm, respectively, characterize them under uniaxial compression, and compare the experimental results of the twist angle φ versus N to numerical calculations, to micropolar continuum elasticity following Eringen10, and to a simple analytical model. Within this model, the twist angle at fixed strain ϵzz and fixed sample height-to-width aspect ratio A linearly increases with N up to a certain maximum characteristic number Nc. Upon multiplication of Nc with the unit cell size, we obtain the characteristic length Lc. Beyond that maximum at N = Nc, the twist angle asymptotically decreases as ∝ 1/N. We reproduce this behavior by micropolar continuum elasticity. In our experiments, we achieve characteristic lengths that are on the order of ten times the unit cell size. This progress allows for much larger twist effects than previously2 for a total number of unit cells in the metamaterial >105—which has to be compared to <103 in previous works2,9. Thereby, this work brings twist effects closer to applications. One possible application is to combine such chiral metamaterials with a linear piezoelectric actuator, enabling to convert the actuator motion into a rotation (also cf. 15). There, overall millimeter-sized metamaterial crystals exhibiting large twist effects are desirable.
Results
Simple analytical model
Figure 1 shows the blueprint of the 3D chiral unit cell that we consider in this paper. This tetragonal cell is placed on a tetragonal translation lattice with lattice constants ax = ay ≠ az. The unit cell is composed of only a single simply connected constituent material and voids within (vacuum or air). The colors are for illustration only. The blue cubic part is intentionally identical to the cubic unit cell discussed in our earlier work2, therefore allowing for a direct comparison. As previously2, the indicated angle δ allows to control the degree of chirality. For δ = 0, the unit cell becomes achiral and twist effects are zero by symmetry. The red parts shown in Fig. 1 are the crucial novelty of the present paper with respect to ref. 2. These connectors determine how the twist angle builds up from a single unit cell to a 3D crystal (see right of Fig. 2a). This 3D metamaterial crystal is composed of a total of Nx × Ny × Nz unit cells with the choices N = Nx = Ny and Nz = 3Nx = 3N (see left of Fig. 2a).
a, b Different viewing directions. All are made from one material, the colors are for illustration only. Within the xy-plane, adjacent unit cells are connected only by the red arms of length 2c and width dT. In the z-direction, the unit cells are connected directly. The blue cubic part in the middle is identical to that in ref. 2 with radii r1, r2, and angle δ of the arms with respect to the cubic face diagonal. A non-zero δ makes the unit cell chiral. This tetragonal unit cell with lattice constants ax = ay = axy = 74 µm or axy = 150 µm (depending on the fabrication technique) and az = (2/3) × axy is placed on a tetragonal translation lattice. Further geometrical parameters used throughout this paper are: r1/axy = 21.3%, r2/axy = 26.7%, b/axy = 14.2%, c/axy = 34.2%, d/axy = dT/axy = 4%, h/axy = 14.2%, δ = 34.8°.
a Crystal lattices composed of Nx × Ny × Nz = 5 × 5 × 15 (left and right) and 1 × 1 × 15 (center) unit cells of the type shown in Fig. 1. Under compressive loading, the 1 × 1× 15 column twists by the indicated angle ϕ = φ(1, 15) < 0. The metamaterial crystal to the right twists under compressive loading by the indicated mean angle φ = φ(5) = φ(5, 15) < 0, which is generally different from ϕ. The difference of the two angles, mediated by the red connector arms (also see Fig. 1), leads to an important contribution to the total linear-elastic energy within the simple model. b Calculated twist angles φ(N) = φ(N, 3N) from our simple analytical model versus integer values of N (dots) for different characteristic numbers Nc = 1, 2, …10 (see legend). The straight lines between dots are merely guides to the eye. For Nc > 1, φ(N) / φ(1) monotonously increases as a function of N and reaches its maximum at Nc. For N > Nc, the twist angle approaches an ∝ 1/N decay.
In the following simple model, we consider the twist angle φ(Nx, Nz) which results from the predetermined axial compressive strain ϵzz within the linear elastic regime. We use traction-free boundary conditions for the four beam side faces and no external torques are applied. Edge effects are neglected. For Nx = 1, the twist angle ϕ = φ(1, Nz) can be seen as a “microtwist”. For Nx > 1, φ(Nx, Nz) is the twist angle of the overall metamaterial beam or the “macrotwist”. For fixed predetermined axial strain ϵzz, the twist angle of a single unit cell, φ(1, 1), is fixed and proportional to ϵzz. This angle φ(1, 1) is an input parameter of the model. For stapling Nz > 1 unit cells along the z-direction, the individual twist angles simply add up, i.e.,
Likewise, for stapling entire xy-planes of \({N}_{x}^{2}\) unit cells, the mean twist angles also add up
We consider three contributions to the linear elastic energy:
The first term, W1, is the usual compression energy given by
with coefficient c1. For simplicity, we have neglected the strains in the directions other than the z-direction, which is a good approximation if the effective Poisson’s ratio, ν, is small, ∣ν∣ ≪ 1. This condition is fulfilled for the architecture shown in Figs. 1 and 2a for loading along the z-direction. If the Poisson’s ratio should not be close to zero, the other strain components are proportional to ϵzz in the linear elastic regime. Hence, the other energy contributions can effectively be lumped into a renormalized coefficient c1 and the general form of the first term W1 stays the same. In any case, the contribution W1 does not enter directly into the resulting twist angle.
The second term, W2, is the twist energy of a (chiral or achiral) metamaterial beam, which is given by
with coefficient c2 (ref. 16).
The third term, W3, starts from the fact that the twist angle of a single unit cell, φ(1, 1), is generally different from that of an xy-plane of unit cells, i.e., φ(1, 1) ≠ φ(Nx, 1). That is, if a single unit cell alone wants to twist by the microtwist φ(1, 1) but the xy-plane twists by φ(Nx, 1), an elastic energy \({c}_{3}{(\varphi ({N}_{x},1)-\varphi (1,1))}^{2}\), with coefficient c3, results for each unit cell. Multiplication with the total number of unit cells \({N}_{x}^{2}{N}_{z}\) in the metamaterial beam leads us to
The resulting macrotwist angle φ(Nx, Nz) for fixed ϵzz is obtained from the minimum of the elastic energy W, i.e., from the condition
With the definition for the characteristic number Nc,
with the choice Nz = 3Ny = 3Nx = 3N as used in the below experiments (also see Fig. 2a), and using the shorter nomenclature φ(N) = φ(N, 3N), which is possible for fixed sample height-to-width aspect ratio A, we obtain
The behavior of φ(N) is determined by only two parameters. As introduced above, the parameter φ(1) = 3φ(1, 1) is given by the twist angle of a single unit cell φ(1, 1) for a given axial strain ϵzz in the linear elastic regime. φ(1) is obviously a property of an individual unit cell and not a property of how the unit cells are connected to a 3D crystal. The fit parameter Nc describes the effects resulting from the coupling of the cells in the x- and y-directions. Nc determines the shape of φ(N) versus N, whereas φ(1) is merely a prefactor. Exemplary curves of φ(N) for different values of Nc = 1, 2, …, 10 are depicted in Fig. 2b. For Nc ≫ 1, the function φ(N) starts ∝ N for N ≪ Nc, exhibits a maximum at N = Nc, and asymptotically decays ∝ 1/N for N ≫ Nc. For Nc ≈ 1 or even < 1, no maximum occurs any more for integer values N = 1, 2, …, and we rather obtain a monotonous decrease of φ(N) versus N, as in our previous work2. A direct comparison of φ(N)/ϵzz from the simple analytical model with microstructure-based simulations and micropolar continuum theory will be given in the “Discussion” section alongside the experiments.
Microstructure-based simulations
In the unit cell illustrated in Fig. 1, the characteristic number Nc is tailored by the red elongated rods of total length 2c and width d. To make the metamaterial unit cell compact, we have retracted the starting points of these elongated rods to the inside of the cubic blue part via the red “U”-shaped parts. In sharp contrast, the unit cells are connected without any intermediate element along the z-direction. This direct connection favors that the twist angle builds up linearly from one end of the metamaterial beam to the other. It is this wanted asymmetry between the z-direction and the xy-directions which makes the unit cell shown in Fig. 1 tetragonal rather than cubic. Our choice of the dimensions of the red parts are the result of a trade-off. If we left away the red parts (or give them zero stiffness), we would get c3 = 0, but also c2 = 0, leaving Nc undefined. If we replaced the red parts by a very much stiffer material than the blue parts, c3 would increase, but c2 would become very large, too6.
To evaluate whether 3D metamaterial crystals based on the 3D unit cell design depicted in Fig. 1 behave as expected from the simple analytical model outlined in the preceding section, we have performed finite-element numerical calculations. In a first approach, we have employed the standard finite-element software package Comsol (MUMPS solver). The used geometrical parameters are given in the caption of Fig. 1 and the parameters of the single constituent material are given in the “Methods” section. We fix the sample bottom and attach a plate at the top of the sample where we apply an uniaxial compression along the z-direction with prescribed displacement uz, and use traction-free boundary conditions for the four sample side faces. The twist angle φ is computed from the displacements of the corners of the top plate. The axial strain is defined by ϵzz = uz/Lz. We choose a sample height-to-width aspect ratio of A = Lz/Lx = Lz/Ly = 2. Together with the chosen lattice constants of ax = ay = axy and az = (2/3) × axy, this leads to Nz = 3 × Nx and Nx = Ny = N. Thus, the total number of unit cells in a metamaterial crystal with aspect ratio A and integer N is given by (ax/az)AN3 = 3N3. For the constituent material, we use a Young’s modulus of E = 2.6 GPa, and Poisson’s ratio of ν = 0.4. The obtained numerical results for N ≤ 6 (648 unit cells total) will be discussed and compared to our experiments below.
In our above discussion of the simple model, we have briefly mentioned the Poisson’s ratio. Therefore, we present numerically calculated Poisson’s ratios in Supplementary Fig. S1. Indeed, the Poisson’s ratios are close to zero.
However, our below experiments extend to integer values N as large as N = 27. Using the described continuum finite-element approach, values much larger than 6 are presently out of reach due to computational constraints. To obtain at least some qualitative theoretical guidance based on the metamaterial microstructure, we radically simplify the architecture shown in Fig. 1 by using Timoshenko beam elements. Details are described in the “Methods” section and Supplementary Fig. S2. By using roughly 2.2 × 106 beam elements, we have obtained convergent results for a total number of up to 24,000 unit cells (N = 20 and A = 2), while accounting for geometrical nonlinearities. It should be noted though that the Timoshenko beam approach grossly underestimates the effective Young’s modulus of the metamaterial. This aspect is expected because slender beams are a bad approximation for the regions in Fig. 1 where the arms merge into the rings, leading to a stiffening of these regions. However, the effective Young’s modulus does not directly enter into the observable φ(N)/ϵzz versus N that we focus on in this paper.
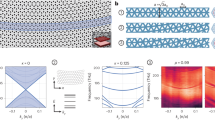
An example of calculated raw data from the Timoshenko beam approach within the linear elastic regime for N = 10 is depicted on the left-hand side of Fig. 3a. In Fig. 3b, we show the calculated φ(N)/ϵzz versus N for three different compressive axial strains and for three different beam diameters, dT, corresponding to the red beams in Fig. 1. The diameter of dT = 0.04 × axy ≈ 3 µm roughly mimics the parameters given in Fig. 1. The two other diameters dT depicted in Fig. 3b are different by merely about ±10%, equivalent to about ±0.3 µm for one of the later used lattice constant of axy = 74 µm. Two trends can be seen. First, for small strains of ϵzz = −0.1% toward the linear elastic regime, the behavior in Fig. 3b depends very sensitively on the beam diameter dT. As expected from our above qualitative discussion, thinner (thicker) beams lead to a larger (smaller) position of the maximum of φ(N)/ϵzz versus N, hence of the characteristic number Nc. However, the magnitude of the dependence on dT is obviously quite pronounced. The characteristic number changes likewise when changing the beam stiffness by changing its length c at otherwise fixed parameters. The corresponding behavior is depicted in Supplementary Fig. S3. Second, for all three dT, we find a pronounced dependence of φ(N)/ϵzz on the magnitude of the compressive axial strain when going from ϵzz = −0.1% via −0.5% to −1.0%. Pronounced geometrical nonlinearities are apparent, even for small strains ∣ϵzz∣ < 1%. This aspect has been discussed previously6 and we will come back to it in our discussion and comparison with experiments.
a Calculated behavior of a metamaterial beam as shown in Fig. 1 under compressive loading along the axial (z) direction. Left: Microstructure Timoshenko beam calculation for N = 10 (3N3 = 3000 unit cells total), ϵzz = −0.1%, dT/axy = 4.4%, and axy = 150 µm. Right: Calculation based on linear micropolar Eringen continuum elasticity (for parameters, see Supplementary Note 1). For clarity, all displacements are exaggerated by a factor of 15. The actual displacements are given by the false-color scale. b Derived twist per strain φ/ϵzz versus N for three different Timoshenko beam diameters dT and for three different axial strains ϵzz (see legend). For clarity, we have drawn continuous curves versus N, while only data at integer values of N have been calculated. The behavior can be compared to that of the simple model shown in Fig. 2b. To allow for a direct comparison with the experimental and with other theoretical data, the three black curves are reproduced in Fig. 5.
Micropolar continuum elasticity
The mapping of the metamaterial structure behavior onto an effective continuum description is important to us because it can be argued17 that calling a metamaterial a “material” requires that its properties can be mapped onto a suitable continuum description, containing effective material parameters that do not depend on size or conditions, but that are rather material specific. To avoid misunderstandings, we emphasize that such mapping does not imply by any means that we are able to determine the effective parameters uniquely (“parameter retrieval”). A unique effective parameter retrieval would necessitate to consider a large number of dissimilar deformation modes of the structure, which is well beyond the scope of this paper.
In brief, in micropolar elasticity10, the rank-two strain tensor \(\mathop{\epsilon}\limits^{\leftrightarrow}\) and the rank-two curvature tensor \(\mathop{\kappa}\limits^{\leftrightarrow}\) are connected to the rank-two stress tensor \(\mathop{\sigma}\limits^{\leftrightarrow}\) and couple stress tensor \(\mathop{m}\limits^{\leftrightarrow}\) via the four rank-four tensors \(\mathop{A}\limits^{\leftrightarrow}\), \(\mathop{B}\limits^{\leftrightarrow}\), \(\mathop{C}\limits^{\leftrightarrow}\), and \(\mathop{D}\limits^{\leftrightarrow}\). The tensors \(\mathop{B}\limits^{\leftrightarrow}\) and \(\mathop{D}\limits^{\leftrightarrow}\) are connected10. In components and using the Einstein summation convention, we have
with elastic energy density w. Note the order of subscript indices in Ajikl and Dklji. The reciprocity condition imposes the following major symmetries onto Cijkl and Aijkl10,
For the tetragonal crystal symmetry of interest in this paper, these four elasticity tensors can be parameterized by a total of 29 different non-zero scalar parameters. As explained in ref. 18 for the case of a cubic crystal, these parameters are connected via the condition that the elastic energy w must be positive for passive materials. Following along the lines of ref. 19, we arrive at a first guess for these parameters. Next, we numerically post-optimize them by a trial-and-error procedure. The resulting set of nonzero effective material parameters (see Supplementary Note 1) corresponds to the lattice constant of axy = 150 µm, az = 100 µm, a constituent material Young’s modulus of E = 2.6 GPa, and a Poisson’s ratio of ν = 0.4. An example calculation is shown on the right-hand side of Fig. 3a. It can be compared directly to the Timoshenko beam microstructure calculation on the left-hand side of Fig. 3a. The overall deformation of the metamaterial beam is well grasped by micropolar continuum elasticity. Numerical results for φ(N)/ϵzz versus N in the linear elastic regime are shown and compared to other data in the “Discussion” section.
Experiments
We have manufactured a large set of 3D chiral tetragonal microstructured metamaterials, including samples containing a very large number of unit cells by an approach that we have published recently20. This approach is based on multi-photon polymerization of a monomer photoresist, using a 3 × 3 array of laser foci instead of just a single focus, rapid scanning of the laser foci with a peak velocity of 0.4 ms−1, leading to a total peak printing rate of about 107 voxels s−1, and tight focusing of all femtosecond laser pulses by a microscope lens with a numerical aperture of NA = 1.4. With this setup, the total printing time (including all overheads and settling times) for the N = 27 sample, which contains a total of 2 × 3 × (27)3 = 118,098 > 105 unit cells, is about 30 h. Obviously, this setup only allows for values of N that are integer multiples of 3. For details of this home-built setup, we refer the reader to ref. 20 and the “Methods” section. For these samples, we have used the commercial photoresist IP-Dip (Nanoscribe GmbH), as in our previous work using this multi-focus setup20.
For the making of smaller samples with N = 1…6, we have used the same commercial 3D laser printer (Photonic Professional GT, Nanoscribe GmbH) as in our original work2,21,22. The lateral lattice constant for theses samples is ax = ay = axy = 150 µm. With this setup, the printing time for the N = 6 sample is about 19 h. For these samples, we have used the commercial photoresist IP-S (Nanoscribe GmbH), as in our original work2. In this manner, we also compare results of two different constituent materials. The constituent material properties are expected to drop out for the quasi-static twist angle per axial strain, φ/ϵzz11, which we will focus on in the “Discussion” section.
To avoid the need for sliding boundary conditions at the sample top, as previously2, we fabricate and characterize a left-handed metamaterial on top of a right-handed metamaterial or vice versa. Therefore, the total torque is zero. Thereby, the middle of the sample twists, whereas the top and the bottom of the sample do not twist. To monitor the twisting of the middle, we add marker areas in the middle of the sample edges. For very large samples, these markers are not necessary, hence we have partly left them away.
Figure 4 exhibits a gallery of electron micrographs of polymer samples with different values of N, revealing generally very high quality. Some of the samples, especially those with large N, are visibly twisted after the fabrication process. We assign this finding to sample shrinkage after the development process. If shrinkage was isotropic, all dimensions would shrink alike and no twist results. However, the mere fact that the metamaterial samples are fixed to the substrate breaks the symmetry. In addition, the slicing and hatching procedure in the 3D printing process (see “Methods” section) makes the polymer structure somewhat anisotropic locally. If, for example, the shrinkage in the axial z-direction was 10% and that in the lateral xy-directions was 9.9%, the relative difference of 1% would effectively act as an axial strain of ϵzz < 0, leading to sample twist angles on the order of up to 10° according to the mechanism discussed above. A relative asymmetry of 1% in polymer shrinkage is amazingly small and cannot be avoided to our experience. This pre-twist introduces a systematic error to our experimental data, the magnitude of which is difficult to estimate. If the resulting polymer is not pre-stressed after shrinkage, and if one assumes a linear behavior starting from the pre-twisted configuration, the pre-twist has no influence at all. The positive side of this unwanted pre-twist is that its presence already indicates that the aimed-at mechanism for achieving large values of φ(N)/ϵzz at large integers N works, because similar pre-twists were barely visible in our earlier experiments2.
a–d Optical micrographs of samples with N = 1, 2, 3, 6 fabricated using the Nanoscribe 3D printer. a N = 1, scale bar: 100 µm. b N = 2, scale bar: 200 µm. c N = 3, scale bar 300 µm. d N = 6, scale bar: 600 µm. e Scanning electron micrograph of one unit cell of the sample with N = 6 depicted in d, scale bar: 40 µm. f–i Optical micrographs of samples with N = 6, 9, 18, 27 fabricated using the multi-focus multi-photon 3D printer. f N = 6, scale bar: 300 µm. g N = 9, scale bar: 450 µm. h N = 18, scale bar: 900 µm. i N = 27, scale bar: 1350 µm. j Zoomed-in scanning electron micrograph of the sample with N = 27 depicted in i, scale bar: 300 µm.
Measurement results for φ(N)/ϵzz versus N for different chosen values of ϵzz are shown in Fig. 5. For small samples (i.e., N ≤ 10), relatively small strain values are prone to large experimental errors and hence not shown, whereas relatively large strain values are not accessible for large samples (i.e., N ≥ 10) due to irreversible sample deterioration. These results are further discussed in the following section.
a A metamaterial composed of unit cells as shown in Fig. 1 is subject to an axial compressive strain (cf. Fig. 3a). The resulting twist angle per axial strain, φ(N)/ϵzz, is plotted versus N. For the chosen lattice constants and chosen fixed sample height-to-width aspect ratio of A = 2, the resulting total number of metamaterial unit cells is given by NxNyNz = 3N3. In the experiments, the stacking of a left-handed and a right-handed sample part leads to a total number of NxNyNz = 2 × 3N3. Five types of results are summarized: experiments, microstructure calculations using beam elements (the three black curves are the same as in Fig. 3b for dT/axy = 4.4%), micropolar Eringen elasticity computations, and the simple analytical model. For experiment and microstructure calculations, results for different strain values are depicted (see symbols and legend). Dark-red (dark-blue) and light-red (light-blue) symbols at a given N correspond to experiments on different samples. Different measurements on the same sample are also shown. Eringen elasticity and the simple model are within the linear-elastic limit. For the simple model, we depict a range of curves corresponding to fixed φ(1)/ϵzz = 2.4°/% and varying Nc from 7 to 10, for the tetragonal case as considered here. For the case of ref. 2, we fit φ(1)/ϵzz = 2.0 and Nc = 1.7. b Same as a, plus microstructure calculations using volume elements and for a smaller range of N to improve the visibility of the large number of data points at small N.
Discussion
In Fig. 5, we summarize our results for the twist angle per axial strain, φ(N)/ϵzz, versus the integer number of unit cells N = Nx = Ny and Nz = 3N (hence sample height-to-width aspect ratio A = 2) in a chiral tetragonal metamaterial. Five independent data sets are depicted: (1) simple analytical model, (2) continuum finite-element microstructure calculations, (3) Timoshenko beam calculations, (4) Eringen micropolar continuum theory, and (5) experiment. For cases (1) and (3), for clarity and to distinguish from the experimental data points, we have drawn continuous curves versus N, while only the integer values of N are physically meaningful. For Eringen micropolar continuum theory, the depicted continuous curve versus N is meaningful, because N is defined via the sample side length Lx = 150 µm according to N = Lx/ax = Ly/ay, which can assume non-integer values.
First, the data (1)–(5) in Fig. 5 consistently exhibit an initial increase of φ(N)/ϵzz versus N, followed by a maximum, and a decrease. Achieving this behavior has been the main point of this paper. For the simple analytical model, we fix φ(1)/ϵzz = 2.4°/%, and depict a range of values for Nc from 7 to 10, leading to a peak twist angle per axial strain around 8–12°/%. This value is about 4–6 times larger than the maximum of 2°/% in ref. 2. More importantly, in the large-sample limit, for N → ∞, the twist angle per axial strain is \(\propto {N}_{{\rm{c}}}^{2}\). This leads to a 17–35 fold increase compared to the material in ref. 2. Values larger than 2°/% are achieved here at integers N as large as N = 27, for which the overall fabricated specimen contains a total of 2 × 3 × (27)3 = 118,098 unit cells, which compares to a total of 500 < 103 unit cells in ref. 2. The number of 118,098 complex 3D unit cells even surpasses previous record values for mechanical metamaterials20.
The blue symbols in Fig. 5 correspond to the photoresist IP-S (Nanoscribe GmbH) and axy = 150 µm, the red symbols to the photoresist IP-Dip (Nanoscribe GmbH) and axy = 74 µm. The blue and red data points agree for N = 3 and N = 6. This behavior confirms the theoretical expectation that, within the linear-elastic regime and for fixed unit-cell shape, φ(N)/ϵzz should neither depend on the Young’s modulus of the constituent material nor on the absolute value of the metamaterial lattice constant axy (ref. 6). The reproducibility of different measurements on the same sample can be assessed by comparing different symbols of the same kind and color and brightness at a given N. The reproducibility concerning different nominally identical samples can be seen by comparing the light-red and dark-red symbols, and the light-blue and dark-blue symbols, respectively.
A closer inspection of the data in Fig. 5 shows a strong influence of nonlinearities, even for absolute values of the axial strain significantly below 1% (cf. subsection “Microstructure-based simulations”). These nonlinearities are such that the twist angle per strain increases with increasing absolute values of the axial strain. At first sight, this strain dependence, which is encoded by the different symbols for the experiment, might be misinterpreted as errors or scattering in the experimental data. This general trend was already found in our original work2, but it was much less pronounced there. Here, this trend is also fairly small at integers smaller than N ≈ 5. However, it becomes quite prominent at around N ≈ 15, where the relative changes in twist angle per strain amount to relative 50% and more. The Timoshenko beam calculations (also see Fig. 3b) and the experiments qualitatively agree in regard to this trend, although the nonlinearities appear to be yet more pronounced in the experimental data. The origin of the corresponding quantitative differences between calculations and experiments is presently not clear. We can say, however, that we have not found any indication of irreversible modifications of our samples in the experiments shown in Fig. 5, in which six loading cycles have been performed subsequently. As discussed in subsection “Microstructure-based simulations”, we have only accounted for geometrical nonlinearities in the Timoshenko beam calculations. Due to computational limitations, these calculations have only been possible up to N = 20, whereas the experimental data go up to N = 27. We note that the magnitude and the sign of the geometrical nonlinearities are generally different for compressive or tensile axial strain, respectively6. The experiments reported here are restricted to compressive strain ϵzz < 0. Nonlinearities are neglected in the simple model as well as in linear micropolar elasticity.
Within the linear elastic regime, the simple analytical model, the continuum finite-element calculations, and the Timoshenko beam calculations for an axial strain of ϵzz = −0.1% agree well, indicating that the simple model qualitatively grasps the underlying physics. We recall that the simple model contains only two parameters, of which one, φ(1)/ϵzz, is merely a prefactor and the other one, the characteristic number Nc, solely determines the shape of the curve. Furthermore, linear Eringen micropolar elasticity also agrees well. Here, due to the large number of 29 different non-zero parameters, we are neither in a position to guarantee that we have achieved the best possible fit nor can we claim that our choice is unique. Nevertheless, we can say that we have found a reasonable set of parameters. It should also be stressed again that these 29 parameters are connected via the condition that the corresponding elastic energy needs to be positive definite. The existence of such material parameters appears important to us because it shows that the general behavior can be mapped onto an effective-medium description. In this description, the parameters of the four elasticity tensors are constant and do not depend on the sample size, whereas the behavior depicted in Fig. 5 is obviously very strongly dependent on sample size via the integer N. On this basis, the architectures discussed in this paper qualify as metamaterials in the strict sense17.
One may have expected that micropolar elasticity, which accounts for local displacements and local rotations, is not sufficient because the red parts of the unit cell in Fig. 1 are additionally deformed (sheared) when applying a compressive axial strain. Micromorphic Eringen elasticity (using nine elasticity tensors) is a generalization of micropolar Eringen elasticity (using four elasticity tensors) and explicitly accounts for such local shear deformations10. However, micromorphic Eringen elasticity does not appear to be necessary to understand the complex chiral metamaterial behavior presented here.
Finally, we note that the simple analytical model is not only able to describe the results presented here, but also our original 2017 results on cubic chiral metamaterials2. The simple model for the parameters φ(1) = 2.0 and Nc = 1.7 is shown by the green curve at the bottom of Fig. 5. This green dashed curve overlaps within the line thickness with the result of Eringen elasticity for the parameters in ref. 2, which is shown by the light-blue dashed curve. Effective values of Nc in between Nc = 1.7 (ref. 2) and Nc = 7.2 (this work) as well as yet larger values could be obtained by varying the thickness d of the red connector arms in Fig. 1, while fixing all other parameters (cf. Fig. 3b and ref. 6).
Conclusion
Chiral effects of artificial elastic solids called metamaterials have recently emerged, but are not accounted for on the level of classical textbook Cauchy elasticity. This fact is connected to the scale invariance of Cauchy elasticity, which means that it contains no characteristic length. Therefore, the elastic properties do depend on the material, but for a given material they do not depend on the sample size. In contrast, micropolar elasticity following Eringen does account for chiral effects and is not scale invariant. Therefore, certain elastic properties do depend on the sample size. This dependence can be expressed by introducing characteristic lengths, which determine from which point on the asymptotic behavior toward Cauchy elasticity begins.
In this paper, we have discussed a chiral 3D tetragonal mechanical metamaterial architecture that allows for tailoring the chiral characteristic length. In particular, we have shown here that the characteristic length scale can be made much larger than the metamaterial lattice constant of axy = 74 µm or axy = 150 µm, respectively. This step brings pronounced chiral effects to metamaterial crystals containing a much larger number of unit cells, >105, than previously. Corresponding analytical solutions of a simple and intuitive model, numerical volume finite-element calculations for 3D metamaterial microstructures, numerical Timoshenko beam calculations, numerical solutions of chiral micropolar continuum elasticity following Eringen, and extensive experiments on microstructured 3D mechanical metamaterials are in good qualitative agreement.
Methods
Microstructure calculations using volume elements
We utilized the commercial software package COMSOL Multiphysics to perform finite-element calculations of the microstructure. The microstructure was split up into tetrahedral mesh elements (up to 1.2 × 106 elements for N = 6). We solved the ordinary Cauchy continuum mechanics equations using quadratic Lagrange shape functions and the MUMPS solver. A linear elastic material with a Young’s modulus of 2.6 GPa and a Poisson’s ratio of 0.4 was assumed. To reduce the computational effort, only the bottom half of the structure, that is, only one handedness, was simulated. The mimic the experimental boundaries, we fixed all degrees of freedom at the bottom of the structure. As in the experiment, we attached a plate to the top of the structure with outer dimensions of Nxaxy × Nyaxy × 0.1az. Due to the generally large computational demands of this method, it was not possible to compute structures larger than N = 6, equivalent to a total of 6 × 6 × 3 × 6 = 648 unit cells.
Microstructure calculations using beam elements
As discussed in the main paper, the twist per strain versus N starts with an increase ∝ N, followed by a maximum, and a decrease \(\propto {N}_{{\rm{c}}}^{2}/N\). In our proposed structure, the maximum and the decrease occur for N > 6, where finite-element calculations of a microstructure meshed with continuum elements become infeasible. To support our findings to beyond N = 6, we simplified the structure by using Timoshenko beam elements (cf. Supplementary Fig. S2) and carried out geometrically nonlinear finite-element calculations of samples comprised of up to N = 20, equivalent to a total of 20 × 20 × 3 × 20 = 24,000 unit cells. For the simplified microstructure calculations, we used the software ABAQUS 3DEXPERIENCE R2018x and the beam element B32. We assumed a linear elastic behavior of the constituent material with a Young’s modulus of 2.6 GPa and a Poisson’s ratio of 0.4. We constrained all degrees of freedom at the bottom face of the sample. At the top face, we rigidly coupled all degrees of freedom to a single reference point located in the centroid of the top face. We applied a displacement uz in the vertical direction to this reference point such that a compressive engineering strain of ϵzz = uz/Lz = −1% was achieved. On all other surfaces, we applied traction-free boundary conditions. This choice of boundary conditions allowed us to only simulate one half of the samples, and the rotation of the reference point corresponds to the measurements discussed in the “Experiments” section.
A simplified extended unit cell is shown in Supplementary Fig. S1. All red beams of the unit cell have a cross-section of dT × dT. All blue beams have a cross-section of d × d, except for those constituting the octagons in the faces of the cube, that simplify the rings of the original unit cell (see Fig. 1). At the side faces, these beams have a cross-section of d × dR with dR = r2 − r1. In the bottom and the top face of the unit cell, the octagons of neighboring unit cells coincide when they are stacked along the z-axis. For these octagons, instead of defining two coinciding sets of elements and nodes and assigning each element a single beam width, we only defined one set of elements and assigned them double the beam width, leading to a cross-section of d × 2d. Thereby, we used less elements per unit cell and saved computational costs. With this procedure, parts of neighboring unit cells are already included in this extended unit cell. Therefore, when stacking unit cells along the z-axis, either the ring at the bottom or top had to be left away to avoid double counting of theses rings. The ABAQUS model of the unit cell (*.cae file), a python script creating simulation input decks (*.inp files) for different N and all individual input decks used to create the data in the main paper are provided in the repository given in the section on “Data availability”.
Sample fabrication
Three modifications of the multi-focus multi-photon 3D printer with respect to that in ref. 20 shall be noted here. First, we installed a motorized aperture in order to blank all but the central laser focus while 3D printing the marker arms attached to the plate located at the middle of the structure. Second, due to changes of one of the telescopes, the focus spacing and hence the lattice constant of the metamaterial is ax = ay = 74 µm here (compared to 80 µm previously20). Third, to make the 3D printer more compact, we have exchanged the prism dispersion-compensation unit. Here, we use only a single highly dispersive N-SF66 prism (instead of two previously20), which is Brewster-angle cut for 800 nm wavelength. The beam is back-folded onto this single prism, such that it passes the prism four times23, leading to an effective tip-tip distance of about 0.9 m (compared to 2 m previously20). The hatching distance is set to 200 nm, the slicing distance to 300 nm. We have used the commercial photoresist IP-Dip (Nanoscribe GmbH) and a 40× objective lens (numerical aperture NA = 1.4, Carl Zeiss).
For the smaller samples printed by the Nanoscribe 3D printer, the hatching distance is set to 300 nm, the slicing distance to 700 nm. We have used the commercial photoresist IP-S (Nanoscribe GmbH) and a 25× objective lens (numerical aperture NA = 0.8, Carl Zeiss).
Uniaxial loading experiments
The uniaxial loading experiments are performed with the same setup that we have used previously2, except that we have exchanged the force cell to a new one (K3D40 ± 2N, ME-Messsysteme, Germany). In this setup, a flat metal stamp in contact with the top of the metamaterial sample and moving along the z-direction contracts the sample. To control the process, we optically image the sample from the side and from the bottom. The axial strain of the sample is computed from the displacement uz at the top of the sample via ϵzz = uz/Lz, that is, compression corresponds to ϵzz < 0. Together with the handedness shown in Fig. 1, ϵzz < 0 leads to φ < 0. The twist angle is obtained from digital image processing of the bottom images using image cross-correlation analysis2,24,25 and averaging over the rotations obtained from the markers mentioned above (cf. Fig. 4). However, in contrast to our previous work (where we have fixed the sample side lengths LxLy, and Lz, hence changed a when varying N), we here fix all lattice constants ax, ay, and az, and change the side lengths LxLy, and Lz when varying N.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request and are published on the open access data repository of the Karlsruhe Institute of Technology (https://doi.org/10.5445/IR/1000126087).
Code availability
The code for simulation that support the findings of this study are available from the corresponding author upon reasonable request and are published on the open access data repository of the Karlsruhe Institute of Technology (KITopen).
References
Sommerfeld, A. Mechanics of Deformable Bodies: Lectures on Theoretical Physics Vol. 2 (Elsevier, 2016).
Frenzel, T., Kadic, M. & Wegener, M. Three-dimensional mechanical metamaterials with a twist. Science 358, 1072–1074 (2017).
Coulais, C. As the extension, so the twist. Science 358, 994–995 (2017).
Fernandez-Corbaton, I. et al. New twists of 3d chiral metamaterials. Adv. Mater. 31, 1807742 (2019).
Chen, W. & Huang, X. Topological design of 3D chiral metamaterials based on couple-stress homogenization. J. Mech. Phys. Solids 131, 372–386 (2019).
Ziemke, P., Frenzel, T., Wegener, M. & Gumbsch, P. Tailoring the characteristic length scale of 3d chiral mechanical metamaterials. Extreme Mech. Lett. 32, 100553 (2019).
Zhong, R., Fu, M., Chen, X., Zheng, B. & Hu, L. A novel three-dimensional mechanical metamaterial with compression-torsion properties. Compos. Struct. 226, 111232 (2019).
Wang, L. & Liu, H.-T. 3D compression-torsion cubic mechanical metamaterial with double inclined rods. Extreme Mech. Lett. 37, 100706 (2020).
Ha, C. S., Plesha, M. E. & Lakes, R. S. Chiral three-dimensional isotropic lattices with negative poisson’s ratio. Phys. Status Solidi B 253, 1243–1251 (2016).
Eringen, A. C. Microcontinuum Field Theories: I. Foundations and Solids (Springer Science & Business Media, 2012).
Lakes, R. S. & Benedict, R. L. Noncentrosymmetry in micropolar elasticity. Int. J. Eng. Sci. 20, 1161–1167 (1982).
Coulais, C., Kettenis, C. & van Hecke, M. A characteristic length scale causes anomalous size effects and boundary programmability in mechanical metamaterials. Nat. Phys. 14, 40 (2018).
Kadic, M., Frenzel, T. & Wegener, M. Mechanical metamaterials: when size matters. Nat. Phys. 14, 8 (2018).
Kadic, M., Diatta, A., Frenzel, T., Guenneau, S. & Wegener, M. Static chiral willis continuum mechanics for three-dimensional chiral mechanical metamaterials. Phys. Rev. B 99, 214101 (2019).
Köpfler, J., Frenzel, T., Kadic, M., Schmalian, J. & Wegener, M. Topologically protected twist edge states for a resonant mechanical laser-beam scanner. Phys. Rev. Appl. 11, 034059 (2019).
TimoŠenko, S. P. & Goodier, J. N. Theory of Elasticity 3rd edn (McGraw-Hill, Singapore, 1970).
Kadic, M., Milton, G. W., van Hecke, M. & Wegener, M. 3D metamaterials. Nat. Rev. Phys. 1, 198–210 (2019).
Chen, Y., Frenzel, T., Guenneau, S., Kadic, M. & Wegener, M. Mapping acoustical activity in 3D chiral mechanical metamaterials onto micropolar continuum elasticity. J. Mech. Phys. Solids 137, 103877 (2020).
Duan, S., Wen, W. & Fang, D. A predictive micropolar continuum model for a novel three-dimensional chiral lattice with size effect and tension-twist coupling behavior. J. Mech. Phys. Solids 121, 23–46 (2018).
Hahn, V. et al. Rapid assembly of small materials building blocks (voxels) into large functional 3D metamaterials. Adv. Funct. Mater. 30, 1907795 (2019).
Frenzel, T., Köpfler, J., Jung, E., Kadic, M. & Wegener, M. Ultrasound experiments on acoustical activity in chiral mechanical metamaterials. Nat. Commun. 10, 1–6 (2019).
Bückmann, T. et al. Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography. Adv. Mater. 24, 2710–2714 (2012).
Kong, L. & Cui, M. A high throughput (>90%), large compensation range, single-prism femtosecond pulse compressor. arXiv:1306.5011. Preprint at https://arxiv.org/pdf/1306.5011 (2013).
Bückmann, T., Thiel, M., Kadic, M., Schittny, R. & Wegener, M. An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nat. Commun. 5, 4130 (2014).
Eberl, C., Gianola, D. & Bundschuh, S. Free digital image correlation and tracking functions. https://www.mathworks.com/matlabcentral/fileexchange/12413 (2010).
Acknowledgements
We acknowledge discussions with Muamer Kadic (Karlsruhe and Besancon). This research has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy via the Excellence Cluster “3D Matter Made to Order” (EXC-2082/1–390761711), which has also been supported by the Carl Zeiss Foundation through the “Carl-Zeiss-Focus@HEiKA”, by the State of Baden-Württemberg, and by the Karlsruhe Institute of Technology (KIT). We further acknowledge support by the Max Planck School of Photonics (MPSP), by the Karlsruhe School of Optics & Photonics (KSOP), by the Helmholtz program “Materials System Engineering” (MSE), and by the associated KIT project “Virtual Materials Design” (VIRTMAT).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
T.F., V.H., and P.Z. contributed equally to this work. M.W. and P.G. supervised the work. T.F., P.Z., P.G., and M.W. conceived the experiments. T.F. and P.Z. designed the unit cell. T.F. and M.W. proposed the simple analytical model. T.F. and P.Z. performed the finite element microstructure calculations. P.Z. developed and performed the finite element microstructure calculations using the Timoshenko beam approximation. P.Z. and Y.C. implemented and performed the micropolar continuum simulations. V.H. and P.K. built the multi-focus multi-photon 3D printer. T.F., V.H., and J.L.G.S. fabricated the samples. T.F. and J.L.G.S. conducted the experiments. All authors discussed the results. M.W. wrote a first draft of the paper. All authors contributed to the final version of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Aldo Isidori.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frenzel, T., Hahn, V., Ziemke, P. et al. Large characteristic lengths in 3D chiral elastic metamaterials. Commun Mater 2, 4 (2021). https://doi.org/10.1038/s43246-020-00107-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00107-w
This article is cited by
-
Selective hinge removal strategy for architecting hierarchical auxetic metamaterials
Communications Materials (2022)
-
Rapid, continuous projection multi-photon 3D printing enabled by spatiotemporal focusing of femtosecond pulses
Light: Science & Applications (2021)
-
Monolithic piezoceramic actuators with a twist
Science China Materials (2021)