Main

Recent advances in deep learning have revolutionized computational imaging, microscopy and holography-related fields, with applications in biomedical imaging1, sensing2, diagnostics3 and three-dimensional (3D) displays4, also achieving benchmark results in various image translation and enhancement tasks, for example, super-resolution5,6,7,8,9,10,11,12, image denoising13,14,15,16 and virtual staining17,18,19,20,21,22,23, among others. The flexibility of deep learning models has also facilitated their widespread use in different imaging modalities, including bright-field24,25 and fluorescence8,11,12,15,26,27 microscopy. As another important example, digital holographic microscopy, a label-free imaging technique widely used in biomedical and physical sciences and engineering28,29,30,31,32,33,34,35,36,37, has also remarkably benefited from deep learning and neural networks4,38,39,40,41,42,43,44,45,46,47,48,49. Convolutional neural networks38,39,40,41,43,45,46,50,51 and recurrent neural networks47,52 have been used for holographic image reconstruction, presenting unique advantages over classical phase retrieval algorithms, such as using fewer measurements and achieving an extended depth of field. Researchers have also explored deep learning-enabled image analysis53,54,55,56,57,58 and transformations18,19,25,59,60 on holographic images to further leverage the quantitative phase information provided by digital holographic microscopy.

In these existing approaches, supervised learning models were utilized, demanding large-scale, high-quality and diverse training datasets (from various sources and types of object) with annotations and/or ground-truth experimental images. For microscopic imaging and holography, in general, such labelled training data can be acquired through classical algorithms that are treated as the ground-truth image reconstruction method38,39,43,47,48,49,52, or through registered image pairs (input versus ground truth) acquired by different imaging modalities8,17,18,25. These supervised learning methods require substantial labour, time and cost to acquire, align and pre-process the training images, and potentially introduce inference bias, resulting in limited generalization to new types of object never seen during the training. Generally speaking, existing supervised learning models demonstrated on microscopic imaging and holography tasks are highly dependent on the training image datasets acquired through experiments, which show variations due to the optical hardware, types of specimen and imaging (sample preparation) protocols. Although there have been efforts utilizing unsupervised learning61,62,63,64,65,66,67 and self-supervised learning16,68,69,70 to alleviate the reliance on large-scale experimental training data, the need for experimental measurements or sample labels with the same or similar features as the testing samples of interest is not entirely eliminated. Using labelled simulated data for network training is another possible solution; however, generating simulated data distributions to accurately represent the experimental sample distributions can be complicated and requires prior knowledge of the sample features and/or some initial measurements with the imaging set-up of interest6,10,71,72,73,74. For example, supervised learning-based deep neural networks for hologram reconstruction tasks demonstrated decent internal generalization to new samples of the same type as in the training dataset, while their external generalization to different sample types or imaging hardware was limited38,46,52.

A common practice to enhance the imaging performance of a supervised model is to apply transfer learning52,69,75,76,77, which trains the learned model on a subset of the new test data. However, the features learned through supervised transfer learning using a limited training data distribution, for example, specific types of sample, do not necessarily advance external generalization to other types of sample, considering that the sample features and imaging set-up may differ substantially in the blind testing phase. Furthermore, transfer learning requires additional labour and time to collect fresh data from the new testing data distribution and fine-tune the pre-trained model, which might bring practical challenges in different applications.

In addition, deep learning-based solutions for inverse problems in computational imaging generally lack the incorporation of explicit physical models in the training phase; this, in turn, limits the compatibility of the network’s inference with the physical laws that govern the light–matter interactions and wave propagation. Recent studies have demonstrated physics-informed neural networks70,78,79,80,81,82,83, where a physical loss was formulated to train the network in an unsupervised manner to solve partial differential equations. However, physics-informed neural network-based methods that can match (or come close to) the performance of supervised learning methods have not been reported yet for solving inverse problems in computational imaging with successful generalization to new types of sample.

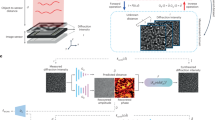
Here we demonstrate a self-supervised learning (SSL)-based deep neural network for zero-shot hologram reconstruction, which is trained without any experimental data or prior knowledge of the types or spatial features of the samples. We term it GedankenNet as the self-supervised training of our network model is based on randomly generated artificial images with no connection or resemblance to real samples at the micro- or macroscale, and therefore the spatial frequencies and the features of these images do not represent any real-world samples and are not related to any experimental set-up. As illustrated in Fig. 1a, the self-supervised learning scheme of GedankenNet adapts a physics-consistency loss between the input synthetic holograms of random, artificial objects and the numerically predicted holograms calculated using the GedankenNet output complex fields, without any reference to or use of the ground-truth object fields during the learning process. After its training, the self-supervised GedankenNet directly generalizes to experimental holograms of various types of sample even though it never saw any experimental data or used any information regarding the real samples. When blindly tested on experimental holograms of human tissue sections (lung, prostate and salivary gland tissue) and Pap smears, GedankenNet achieved better image reconstruction accuracy compared with supervised learning models using the same training datasets. We further demonstrated that GedankenNet can be widely applied to other training datasets, including simulations and experimental datasets, and achieves superior zero-shot generalization to unseen data distributions over supervised learning-based models.

Fig. 1: Diagrams of GedankenNet and other existing methods for solving holographic imaging problems.
figure 1

a, Diagrams of classical iterative hologram reconstruction algorithms, the self-supervised deep neural network (GedankenNet) and existing supervised deep neural networks. b, Self-supervised training pipeline of GedankenNet for hologram reconstruction.

Full size image

As GedankenNet’s self-supervised learning is based on a physics-consistency loss, its inference and the resulting output complex fields are compatible with the Maxwell’s equations and accurately reflect the physical wave propagation phenomenon in free space. By testing GedankenNet with experimental input holograms captured at shifted (unknown) axial positions, we showed that GedankenNet does not hallucinate and the object field at the sample plane can be accurately retrieved through wave propagation of the GedankenNet output field, without the need for retraining or fine-tuning its parameters. These results indicate that in addition to generalizing to experimental holograms of unseen sample types without seeing any experimental data or real object features, GedankenNet also implicitly acquired the physical information of wave propagation in free space and gained robustness towards defocused holograms or changes in the pixel size through the same self-supervised learning process. Furthermore, for phase-only objects (such as thin label-free samples), the GedankenNet framework also shows resilience to random unknown perturbations in the imaging system, including arbitrary shifts of the sample-to-sensor distances and unknown changes in the illumination wavelength, all of which make its generalization even broader without the need for any experimental data or ground-truth labels.

The success of GedankenNet eliminates three major challenges in existing deep learning-based holographic imaging approaches: (1) the need for large-scale, diverse and labelled training data, (2) the limited generalization to unseen sample types or shifted input data distributions, and (3) the lack of an interpretable connection and compatibility between the physical laws and models and the trained deep neural network. This work introduces a promising and powerful alternative to a wide variety of supervised learning-based methods that are currently applied in various microscopy, holography and computational imaging tasks.

Self-supervised learning of hologram reconstruction

The hologram reconstruction task, in general, can be formulated as an inverse problem44:

$$\hat{o}={\rm{arg }}\mathop{{\rm{min }}}\limits_{o}L(H(o),i)+R(o)$$

where \(i\in {{\mathbb{R}}}^{M{N}^{2}}\) represents the vectorized M measured holograms, each of which is of dimension N × N and \(o\in {{\mathbb{C}}}^{{N}^{2}}\) is the vectorized object complex field. H(⋅) is the forward imaging model, L(⋅) is the loss function and R(⋅) is the regularization term. Under spatially and temporally coherent illumination of a thin sample, H(⋅) can be simplified as:

$$H\left(o\right)=f({Ho})+\epsilon$$

where \(H\in {{\mathbb{C}}}^{M{N}^{2}\times {N}^{2}}\) is the free-space transformation matrix44,84, \(\epsilon \in {{\mathbb{R}}}^{M{N}^{2}}\) represents random detection noise and f(⋅) refers to the (opto-electronic) sensor-array sampling function, which records the intensity of the optical field.

Different schemes for solving holographic imaging inverse problems are summarized in Fig. 1. Existing methods for generalizable hologram reconstruction can be mainly classified into two categories, as shown in Fig. 1a: (1) iterative phase retrieval algorithms based on the physical forward model and iterative error-reduction; and (2) supervised deep learning-based inference methods that learn from training image pairs of input holograms i and the ground-truth object fields o. Similar to the iterative phase recovery algorithms listed under category 1, deep neural networks were also used to provide iterative approximations to the object field from a batch of hologram(s); however, these network models were iteratively optimized for each hologram batch separately, and cannot generalize to reconstruct holograms of other objects once they are optimized70,79,81 (Supplementary Note 2 and Extended Data Fig. 3).

Different from existing learning-based approaches, instead of directly comparing the output complex fields (\(\hat{o}\)) and the ground-truth object complex fields (o), GedankenNet infers the predicted holograms \(\hat{i}\) from its output complex fields \(\hat{o}\) using a deterministic physical forward model, and directly compares \(\hat{i}\) with i. Without the need to know the ground-truth object fields o, this forward model–network cycle establishes a physics-consistency loss (Lphysics-consistency) for gradient back-propagation and network parameter updates, which is defined as:

$${L}_{{{\mathrm{physics}}}-{{\mathrm{consistency}}}}\left(\hat{i},i\right)={\alpha L}_{{{\mathrm{FDMAE}}}}\left(\hat{i},i\right)+{\beta L}_{{{\mathrm{MSE}}}}\left(\hat{i},i\right),$$

where LFDMAE and LMSE are the Fourier domain mean absolute error (FDMAE) and the mean square error (MSE), respectively, calculated between the input holograms i and the predicted holograms \(\hat{i}\). α and β refer to the corresponding weights of each term (see Methods for the training and implementation details). The network architecture of GedankenNet is also detailed in Methods and Extended Data Fig. 1.

As emphasized in Fig. 1, GedankenNet eliminates the need for experimental, labelled training data and thus presents unique advantages over existing methods. The training dataset of GedankenNet only consists of artificial holograms generated from random images (with no connection or resemblance to real-world samples), which serve as the amplitude and phase channels of the object field (Methods and Fig. 1b). After its self-supervised training using artificial images without any experimental data or real-world specimens, GedankenNet can be directly used to reconstruct experimental holograms of various microscopic specimens, including, for example, densely connected tissue samples and Pap smears. GedankenNet also provides considerably faster reconstructions in a single forward inference without the need for numerical iterations, transfer learning or fine-tuning of its parameters on new testing samples.

Superior generalization of GedankenNet

To demonstrate the unique features of GedankenNet, we trained a series of self-supervised network models that take multiple input holograms (M ranging from 2 to 7), following the training process introduced in Fig. 1. Each GedankenNet model for a different M value was trained using artificial holograms generated from random synthetic images based on M different planes with designated sample-to-sensor distances zi, i = 1, 2, …, M. In the blind testing phase illustrated in Fig. 2a, M experimental holograms of human lung tissue sections were captured by a lens-free in-line holographic microscope (see Extended Data Fig. 1b and Methods for experimental details). We tested all the self-supervised GedankenNet models on 94 non-overlapping fields-of-view (FOVs) of tissue sections and quantified the image reconstruction quality in terms of the amplitude and phase structural similarity index measure (SSIM) values with respect to the ground-truth object fields (Fig. 2b). The ground-truth fields were retrieved by the multi-height phase retrieval (MHPR)85,86,87 algorithm using M = 8 raw holograms of each FOV. Our results indicate that all the GedankenNet models were able to reconstruct the sample fields with high fidelity even though they were trained using random, artificial images without any experimental data (Fig. 2c). In addition, Fig. 2 shows that the reconstruction quality of GedankenNet models increased with increasing number of input holograms M, which inherently points to a general trade-off between the image reconstruction quality and system throughput; depending on the level of reconstruction quality desired and the imaging application needs, M can be accordingly selected and optimized. In addition to the number of input holograms, we investigated the relationship between the sample-to-sensor distances and the reconstruction quality of GedankenNet (Extended Data Fig. 2 and Supplementary Note 1). Due to the reduced signal-to-noise ratio of the experimental in-line holograms acquired at large sample-to-sensor (axial) distances, GedankenNet models trained with larger sample-to-sensor distances show a relatively reduced reconstruction quality compared with the GedankenNet models trained with smaller axial distances.

Fig. 2: Hologram reconstruction performance of GedankenNet using multiple (M) input holograms.
figure 2

a, M holograms were selected from eight raw holograms as the inputs for GedankenNet. The ground-truth complex field (used only for comparison) was retrieved by MHPR using all the eight raw holograms. Scale bar, 50 μm. b, The amplitude and phase SSIM values between the reconstructed fields of GedankenNet and the ground-truth object fields. SSIM values were averaged on a testing set with 94 unique human lung tissue FOVs, and the SSIM standard deviations were calculated on 4 individual models for each M. c, Zoomed-in regions of the GedankenNet outputs and the ground-truth object fields. Scale bar, 20 μm.

Full size image

We also compared the generalization performance of self-supervised GedankenNet models against other supervised learning models and iterative phase recovery algorithms using experimental holograms of various types of human tissue section and Pap smears (Fig. 3). Although only seeing artificial holograms of random images in the training phase, GedankenNet (M = 2) was able to directly generalize to experimental holograms of Pap smears and human lung, salivary gland and prostate tissue sections. For comparison, we trained two supervised learning models using the same artificial image dataset, including the Fourier Imager Network (FIN)48 and a modified U-Net88 architecture (Methods). These supervised models were tested on the same experimental holograms to analyse their external generalization performance. Compared with these supervised learning methods, GedankenNet exhibited superior external generalization on all four types of sample (lung, salivary gland and prostate tissue sections and Pap smears), scoring higher enhanced correlation coefficient (ECC) values (Methods). A second comparative analysis was performed against a classical iterative phase recovery method, that is, MHPR85,86,87: GedankenNet inferred the object fields with less noise and higher image fidelity compared with MHPR (M = 2) that used the same input holograms (Fig. 3a,c). In addition, we compared GedankenNet image reconstruction results against deep image prior-based approaches70,79,81,89, also confirming its superior performance (Extended Data Fig. 3 and Supplementary Note 2).

Fig. 3: External generalization of GedankenNet on human tissue sections and Pap smears, and comparison with existing supervised learning models and MHPR.
figure 3

a, External generalization results of GedankenNet on human lung, salivary gland, prostate and Pap smear holograms. b, External generalization results of supervised learning methods on the same test datasets. The supervised models were trained on the same simulated hologram dataset as GedankenNet used. c, MHPR reconstruction results using the same M = 2 input holograms. d, Ground-truth object fields retrieved using eight raw holograms of each FOV. Scale bar, 50 μm.

Full size image

The inference time of each of these hologram reconstruction algorithms is summarized in Table 1, which indicates that GedankenNet accelerated the image reconstruction process by ~128 times compared with MHPR (M = 2). These holographic imaging experiments and resulting analyses successfully demonstrate GedankenNet’s unparalleled zero-shot generalization to experimental holograms of unknown, new types of sample without any prior knowledge about the samples or the use of experimental training data or labels.

Table 1 Holographic image inference time (for 1 mm2 sample area) for GedankenNet, supervised learning models and MHPR
Full size table

GedankenNet’s strong external generalization is due to its self-supervised learning scheme that employs the physics-consistency loss, which is further validated by the additional comparisons we performed between self-supervised learning and supervised learning schemes (Extended Data Fig. 4 and Supplementary Note 3). In addition to GedankenNet’s superior external generalization (from artificial random images to experimental holographic data), this framework can also be applied to other training datasets. To showcase this, we trained three GedankenNet models using (1) the artificial hologram dataset generated from random images, same as before; (2) a new artificial hologram dataset generated from a natural image dataset (common objects in context, COCO)90; and (3) an experimental hologram dataset of human tissue sections (see Methods for dataset preparation). Each one of these training datasets had ~100,000 training image pairs with M = 2, z1 = 300 μm and z2 = 375 μm. As shown in Fig. 4, these three individually trained GedankenNet models were tested on four testing datasets, including artificial holograms of (1) random synthetic images and (2) natural images as well as experimental holograms of (3) lung tissue sections and (4) Pap smears. Our results reveal that all the self-supervised GedankenNet models showed very good reconstruction quality for both internal and external generalization (Fig. 4a,b). When trained using the experimental holograms of lung tissue sections, the supervised hologram reconstruction model FIN (solid red bar) scored higher ECC values (P value of 7.5 × 10−38) than the GedankenNet (solid blue bar) on the same testing set of the lung tissue sections. However, when it comes to external generalization, as shown in Fig. 4b, GedankenNet (the blue shadow bar) achieved superior imaging performance (P value of 8.5 × 10−10) compared with FIN (the red shadow bar) on natural images (from the COCO dataset). One can also notice the overfitting of the supervised model (FIN) by the large performance gap observed between its internal and external generalization performance shown with the red bars in Fig. 4b. On the contrary, the self-supervised GedankenNet trained with artificial random images (the blue bars) showed very good generalization performance for both test datasets covering natural macroscale images as well as microscale tissue images. Also see Extended Data Fig. 5 and Supplementary Note 4 for additional results supporting the superior generalization performance of GedankenNet.

Fig. 4: Generalization of GedankenNet trained with different training datasets to various new testing datasets.
figure 4

a, Outputs of GedankenNet models trained on three different training datasets (artificially generated random synthetic images, natural images (COCO) and tissue sections, respectively). Scale bar, 50 μm. b, Quantitative performance analysis of GedankenNet models trained on three different datasets. The performances of a supervised deep neural network (trained on lung tissue sections) and MHPR are also included for comparison purposes. ECC mean ± s.d. values are presented and were calculated on lung and COCO test datasets with 94 and 100 unique FOVs, respectively.

Full size image

Compatibility of GedankenNet with the wave equation

Besides its generalization to unseen testing data distributions and experimental holograms, the inference of GedankenNet is also compatible with the wave equation. To demonstrate this, we tested the GedankenNet model (trained with the artificial hologram dataset generated from random synthetic images) on experimental holograms captured at shifted unknown axial positions \({z}_{1}^{{\prime} }\cong {z}_{1}+\Delta z\) and \({z}_{2}^{{\prime} }\cong {z}_{2}+\Delta z\), where z1 and z2 were the training axial positions and Δz is the unknown axial shift amount. The same model as in Fig. 3 was used for this analysis and blindly tested on lung tissue sections (that is, external generalization). Due to the unknown axial defocus distance (Δz), the direct output fields of GedankenNet do not match well with the ground truth, indicated by the orange curve in Fig. 5a. However, as GedankenNet was trained with the physics-consistency loss, its output fields are compatible with the wave equation in free space. Thus, the object fields at the sample plane can be accurately retrieved from the GedankenNet output fields by performing wave propagation by the corresponding axial defocus distance. After propagating the output fields of GedankenNet by −Δz using the angular spectrum approach, the propagated fields (blue curve) matched very well with the ground-truth fields across a large range of axial defocus values, Δz. These results are important because (1) they once again demonstrate the success of GedankenNet in generalizing to experimental holograms even though it was trained only by artificial holograms of random synthetic images; and (2) the physics-consistency based self-supervised training of GedankenNet encoded the wave equation into its inference process so that instead of hallucinating and creating non-physical random optical fields when tested with defocused holograms, GedankenNet outputs correct (physically consistent) defocused complex fields. In this sense, GedankenNet not only shows superior external generalization (from experiment- and data-free training to experimental holograms) but also very well generalized to work with defocused experimental holograms. To the best of our knowledge, these features have not been demonstrated before for any hologram reconstruction neural network in the literature.

Fig. 5: Compatibility of GedankenNet output images with the wave equation in free space.
figure 5

The GedankenNet model was trained to reconstruct M = 2 input holograms at z1 = 300 μm and z2 = 375 μm, but blindly tested on input holograms captured at \({z}_{1}^{{\prime} }=300+\Delta {z}\,{{\upmu}}{\rm{m}}\) and \({z}_{2}^{{\prime} }=375+\Delta {z}\,{{\upmu}}{\rm{m}}\) (orange curve). The resulting GedankenNet output complex fields are propagated in free space by −Δz using the wave equation, revealing a very good image quality (blue curve) across a wide range of axial defocus distances. The GedankenNet-Phase (green curve) was trained to reconstruct sample fields with M = 2 input holograms at arbitrary, unknown axial positions within [275, 400] μm. a, External generalization on stained human lung tissue sections. A, B represent testing results with Δz = −30 and 50 μm, respectively. b, External generalization on unstained, label-free human kidney tissue sections. C, D represent testing results with Δz = −30 and 40 μm, respectively. These results demonstrate that the GedankenNet framework not only has a superior external generalization to experimental holograms (using experiment- and data-free training) but also very well generalized to work with defocused experimental holograms, and encoded the wave equation into its inference process using the physics-consistency loss. Scale bars, 50 μm.

Full size image

Figure 5b shows another example of GedankenNet’s superior external generalization and its compatibility with the wave equation. The same trained GedankenNet model of Fig. 5a was blindly tested on experimental holograms of unstained (label free) human kidney tissue sections, which can be considered phase-only samples. Besides the success of GedankenNet’s generalization to experimental data of biological samples, the results shown in Fig. 5b demonstrate GedankenNet’s zero-shot generalization to another physical class of objects (that is, phase-only samples) that exhibit different physical properties than the synthetic, artificial random complex fields used in the training, which included random phase and amplitude patterns. Stated differently, although GedankenNet’s artificially generated random training images did not include any phase-only objects, it successfully reconstructed the experimental holograms of phase-only objects—the first time that they were seen. Furthermore, similar to Fig. 5a, we observe in Fig. 5b that by digitally propagating the GedankenNet outputs for defocused input holograms of the label-free tissue samples (orange curve) by an axial distance of −Δz, the resulting phase reconstructions (blue curve) showed good fidelity to the ground-truth phase images of the same samples.

Also refer to the Supplementary Note 5 and Extended Data Figs. 6–10 on the analysis of GedankenNet’s resilience to various sources of unknown perturbations, including the pixel pitch, signal-to-noise ratio, axial distances and the illumination wavelength. As detailed in Supplementary Note 5, this resilient performance of GedankenNet can be further enhanced using phase-only object priors; we termed this new model for phase-only object reconstruction as GedankenNet-Phase, which shows external generalization, reconstructing experimental holograms of unseen sample types, while simultaneously achieving autofocusing (Supplementary Note 5.3 and Extended Data Fig. 9).

Discussion

Compared with the existing supervised learning methods, GedankenNet has several unique advantages. It eliminates the dependence on labelled experimental training data in computational microscopy, which often come from other imaging modalities or classical algorithms and, therefore, inevitably introduce biases for external generalization performance of the trained network. The self-supervised, zero-shot learning scheme of GedankenNet also considerably relieves the cost and labour of collecting and preparing large-scale microscopic image datasets. For the inverse problem of hologram reconstruction, the reported physics-consistency loss that we used in self-supervised learning outperforms traditional structural loss functions commonly employed in supervised learning as they often overfit to specific image features that appear in the training dataset, resulting in generalization errors, especially for new types or classes of sample never seen before (Extended Data Fig. 4). In general, the residual errors that stochastically occur during the network training would be non-physical errors that are incompatible with the wave equation, for example, noise-like errors that do not follow wave propagation. In contrast to traditional structural loss functions that penalize these types of residual error based on the statistics of the sample type of interest (which requires experimental data and/or knowledge about the samples and their features), the physics-consistency loss function that we used focuses on physical inconsistencies, which is at the heart of the superior external generalization of GedankenNet framework as such physical errors are universally applicable, regardless of the type of sample or its physical properties or features (also refer to Supplementary Note 6). Furthermore, this physics-consistency loss benefits from multiple hologram planes (that is, M ≥ 2) so that it can also filter out twin-image-related artefacts that would normally appear in conventional in-line hologram reconstruction methods due to lack of direct phase information; stated differently, an artificial twin image that would be superimposed onto the complex-valued true image of the sample would be attacked by our self-consistency loss as it will create physical inconsistencies on at least M − 1 hologram planes as a result of the wave propagation step for M ≥ 2 planes. In addition to this, the large degrees of freedom provided by the artificially synthesized image datasets, with random phase and amplitude channels, also contribute to the effectiveness of the GedankenNet framework, as also highlighted in the ‘Superior Generalization of GedankenNet’ subsection, Extended Data Fig. 5 and Supplementary Note 4. Limited by the optical system, the experimental holographic imaging process applies a low-pass filter to the ground-truth object fields. Furthermore, the recurrent spatial features within the same type of sample further reduce the diversity of the experimental datasets. Thus, adapting simulated holograms of random, artificial image datasets presents a more effective solution when access to large amounts of experimental data is impractical (Fig. 4 and Extended Data Fig. 5). In addition, GedankenNet exhibits superior generalization to unseen data distributions than supervised models, and achieves better holographic image reconstruction for unseen, new types of sample (see, for example, Figs. 3 and 4).

Methods

Sample preparation and imaging

Human tissue samples used in this work were prepared and provided by the University of California Los Angeles (UCLA) Translational Pathology Core Laboratory. A fraction of tissue slides were stained with haematoxylin and eosin to reveal structural features in the amplitude channel and the other slides remained unstained to serve as phase-only objects. Stained Pap smears were acquired from the UCLA Department of Pathology. All slides were deidentified and prepared from existing specimens without links or identifiers to the patients.

The experimental holograms were captured on stained human lung, prostate, salivary gland, kidney, liver and oesophagus tissue sections, Pap smears, and unstained label-free human kidney tissue sections. Holographic microscopy imaging was implemented using a lens-free, in-line holographic microscope as illustrated in Extended Data Fig. 1b. The custom-designed microscope was equipped with a tunable light source (WhiteLase Micro, NKT Photonics) and an acousto-optic tunable filter. In the reported experiments, the acousto-optic tunable filter was set to filter the illumination light at λ0 = 530 nm wavelength unless otherwise specified. Raw holograms (~4,600 × 3,500 pixels) were recorded by a complementary metal–oxide semiconductor with a pixel size of 1.12 μm (IMX 081 RGB, Sony). A 6-axis 3D positioning stage (MAX606, Thorlabs) controlled the complementary metal–oxide semiconductor sensor to capture raw holograms consecutively for each FOV at various sample-to-sensor distances, which ranged from ~300 μm to ~600 μm in this work with an axial spacing of ~10–15 μm. A computer connected all the devices and automatically controlled the image acquisition process through a LabView script (LabView 2012, version 12.0) and AYA software tool (Sony).

Artificial hologram preparation and preprocessing

The artificial holograms used in this work for the training were simulated from either random images or natural images (from the COCO dataset). Random images (with no connection or resemblance to real-world samples) were generated using a Python package randimage, which coloured the pixels along a path found from a random grey-valued image to generate an artificial RGB image. Then we mapped the generated random RGB images to greyscale. Two independent images randomly selected from the dataset served as the amplitude and phase of the complex object field, and a small constant was added to the amplitude channel to avoid zero transmission and undefined phase issue. For the artificial random phase-only object fields, only the phase image was selected, and the amplitude was set as 1 everywhere. The object field was then propagated by the given sample-to-sensor distances using the angular spectrum approach84, and the intensity of the resulting complex field was calculated. The resulting holograms were cropped into 512 × 512 patches. Each of the two datasets (from either random images or COCO natural images) used ~100,000 images for training and a set of 100 images for validation and testing, which were excluded from training. All models in this work used the amplitude of the measured fields as the inputs.

Given a randomly selected amplitude (A) image and phase (ϕ) image, the simulated hologram i(x, y;z) at axial position z is generated by free-space propagation (FSP):

$$i\left(x,y{\rm{;}}\,z\right)=\left|{\rm{FSP}}\left(\left(A+\delta \right)\odot {{\mathrm{e}}}^{{\mathrm{i}}\uppi \phi }{\rm{;}}\,z\right)+\epsilon \right|$$

where \(\delta \,{\mathbb{\in }}\,{\mathbb{R}}\) stands for the added small constant, ⨀ represents element-wise multiplication and \(\epsilon \in {{\mathbb{C}}}^{N\times N}\) is the additional white Gaussian noise. For the phase-only objects, the simulated holograms can be expressed as:

$$i\left(x,y{\rm{;}}\,z\right)={\rm{|FSP}}\left({{\mathrm{e}}}^{{\mathrm{i}}\uppi \phi }{\rm{;}}\,z\right)+\epsilon {\rm{|}}$$

The FSP is implemented based on the angular spectrum propagation method84 by taking into account all the travelling waves in free space. The angular spectrum of a light field U(x, y;z0) at the axial position z0 can be expressed as

$$\widetilde{A}\left(\xi ,\eta {\rm{;}}\,{z}_{0}\right){\mathscr{=}}{\mathcal{F}}\left\{U\left(x,y{\rm{;}}\,{z}_{0}\right)\right\}$$

The angular spectrum of the propagated field at z is related to A(ξ, η; z0) by

\(\widetilde{A}\left(\xi ,\eta {;z}\right)=\left\{\begin{array}{c}{{\mathrm{e}}}^{{\mathrm{i}}\left(z-{z}_{0}\right)\sqrt{{k}^{2}-{\xi }^{\,2}-{\eta }^{2}}} \widetilde{A}\left(\xi ,\eta ;{z}_{0}\right),\,{\rm{if}\,}{\xi }^{\,2}+{\eta }^{2} < {k}^{2}\\ 0,\,{\rm{otherwise}}\end{array}\right.\)

Here \({\mathcal{F}}\) and \({{\mathcal{F}}}^{-1}\) are the fast Fourier transform (FFT) pairs (forward versus inverse). x, y and ξ, η are spatial and frequency domain coordinates, respectively. k is the wave number of the illumination light in the medium. The FSP then infers the propagated field at z by:

$${\rm{FSP}}\left(U\left(x,y{\rm{;}}\,{z}_{0}\right){\rm{;}}\,z-{z}_{0}\right)={{\mathcal{F}}}^{-1}\left\{\widetilde{A}\left(\xi ,\eta {\rm{;}}\,z\right)\right\}.$$

Experimental hologram dataset preparation and processing

Raw experimental holograms were pre-processed through pixel super-resolution and autofocusing algorithms to retrieve subpixel features of the samples. For this, a pixel super-resolution algorithm85,91 was applied to raw experimental holograms to obtain high-resolution holograms, resulting in a final effective pixel size of 0.37 μm. Then, an edge sparsity-based autofocusing algorithm92 was employed to determine the sample-to-sensor distances for each super-resolved hologram. The ground-truth sample field was retrieved from M = 8 super-resolved holograms of the same FOV using the MHPR algorithm85,86,87. The MHPR algorithm retrieves the sample complex field through iterations between eight input holograms. The initial guess of the sample complex field is propagated to each measurement plane using FSP and the corresponding sample-to-sensor distance. Then, the propagated field is updated by replacing the amplitude with the measured one and retaining the phase. One iteration is completed after all eight holograms have been used. The algorithm generally converges after 100 iterations.

Input–target pairs of 512 × 512 pixels were cropped from the super-resolved holograms and their corresponding retrieved ground-truth fields, forming the experimental hologram datasets. Standard data augmentation techniques were applied, including random rotations by 0°, ±45° and ±90°, and random vertical and horizontal flipping. The multi-height experimental hologram dataset of tissue sections contains ~100,000 input–target pairs of stained human lung, prostate, salivary gland, kidney, liver and oesophagus tissue sections. A subset of the lung, prostate, salivary gland slides from new patients and Pap smears were excluded from the training dataset and used as testing datasets, containing 94, 49, 49 and 47 unique FOVs, respectively. The holograms of the unstained (label free) kidney tissue thin sections (~3–4 µm thick) were used as our phase-only object test dataset containing 98 unique FOVs.

Network architecture

A sequence of M holograms is concatenated as the input image with M channels and the real and imaginary parts of the object complex field are generated at the output of GedankenNet. GedankenNet contains a series of spatial Fourier transformation (SPAF) blocks and a large-scale residual connection, in addition to two 1 × 1 convolution layers at the head and the tail of the network (Extended Data Fig. 1a). In each SPAF block, input tensors pass through two recursive SPAF modules with residual connections, which share the same parameters before entering the parametric rectified linear unit (PReLU) activation layer93. The PReLU activation function with respect to an input value \(x\,{\mathbb{\in}}\,{\mathbb{R}}\) is defined as:

$${\rm{PReLU}}\left(x\right)={\rm{max }}\left(0,x\right)+a\times {\rm{min }}(0,x)$$

where \(a\,{\mathbb{\in }}\,{\mathbb{R}}\) is a learnable parameter. Another residual connection passes the input tensor after the PReLU layer. The SPAF module consists of a 3 × 3 convolution layer and a branch performing linear transformation in the Fourier domain (Extended Data Fig. 1a). The input tensor with c channels to the SPAF module is first transformed into the frequency domain by a two-dimensional FFT and truncated by a window with a half size k to filter out higher-frequency components. The linear transformation in the frequency domain is realized through pixel-wise multiplication with a trainable weight tensor \(W\in {{\mathbb{R}}}^{c\times \left(2k+1\right)\times (2k+1)}\), that is

$${F}_{j,u,v}^{{\prime} }={W}_{j,u,v}\cdot \mathop{\sum }\limits_{i=1}^{c}{F}_{i,u,v},\,u,v=0,\pm 1,\ldots ,\pm k,\,j=1,\ldots ,c$$

where \(F\in {{\mathbb{C}}}^{c\times (2k+1)\times (2k+1)}\) are the truncated frequency components. The resulting tensor F′ is then transformed into the spatial domain through an inverse two-dimensional FFT. The same pyramid-like setting of half window size k as in ref. 82 was applied here such that k decreases for deeper SPAF blocks. This pyramid-like setting provides a mapping of the high-frequency information of the holographic diffraction patterns to low-frequency regions in the first few layers and passes this low-frequency information to the subsequent layers with a smaller window size, which better utilizes the spatial features at multiple scales and at the same time considerably reduces the model size, avoiding potential overfitting and generalization issues.

The architecture of GedankenNet was extended for two additional models, namely GedankenNet-Phase and GedankenNet-Phaseλ, as detailed in the Supplementary Note 5 and Extended Data Fig. 8a. Similar to GedankenNet, these models use a sequence of M holograms concatenated as the input image with M channels, but, instead of outputting real and imaginary parts, the GedankenNet-Phase and GedankenNet-Phaseλ only generate phase-only output images. The dynamic SPAF (dSPAF) modules49 inside GedankenNet-Phase and GedankenNet-Phaseλ exploit a shallow U-Net to dynamically generate weights W for each input tensor, and enable the capabilities of autofocusing and adapting to unknown shifts or changes in the illumination wavelengths. The dense links provide an efficient flow of information from the input layer to the output layer, so that every output tensor of the dSPAF group is appended and fed to the subsequent dSPAF groups, resulting in an economic and powerful network architecture.

Algorithm implementation

GedankenNet, GedankenNet-Phase and GedankenNet-Phaseλ were implemented using PyTorch94. We calculated the loss values based on the hologram amplitudes, that is:

$$\hat{i}={\rm{|FSP}}\left(\hat{o}{\rm{;}}\,{z}_{1},{z}_{2},\cdots ,{z}_{M}\right){\rm{|}}$$

The training loss consists of three individual terms: (1) FDMAE loss between the predicted holograms \(\hat{i}\) and the input holograms i; (2) MSE loss between \(\hat{i}\) and i; and (3) total variation (TV) loss on the output complex field \(\hat{o}\). The first two terms constitute the physics-consistency loss, and the total loss is a linear combination of the three terms, expressed as:

$$\begin{array}{l}{L}_{{{\mathrm{total}}}}={L}_{{{\mathrm{physics}}}-{{\mathrm{consistency}}}}\left(\hat{i},i\right)+\gamma {L}_{{{\mathrm{TV}}}}(\hat{o})\\\qquad\ =\alpha {L}_{{{\mathrm{FDMAE}}}}\left(\hat{i},i\right)+\beta {L}_{{{\mathrm{MSE}}}}\left(\hat{i},i\right)+\gamma {L}_{{{\mathrm{TV}}}}(\hat{o})\end{array}$$

where α, β and γ are loss weights empirically set as 0.1, 1 and 20.

The FDMAE loss is calculated as:

$${L}_{{{\mathrm{FDMAE}}}}(\hat{i},i)=\frac{1}{{N}^{2}}\mathop{\sum }\limits_{\xi =1}^{N}\mathop{\sum }\limits_{\eta =1}^{N}\left|{\mathcal{F}}\left\{\hat{i}\,\right\}\left(\xi ,\eta \right)\cdot w\,(\xi ,\eta)-{\mathcal{F}}\left\{i\right\}\left(\xi ,\eta \right)\cdot w\left(\xi ,\eta \right)\right|$$

Here \(w\in {{\mathbb{R}}}^{N\times N}\) is a two-dimensional Hann window95, and ξ, η are indices of frequency components. MSE and TV losses are computed using:

$${L}_{{{\mathrm{MSE}}}}\left(\hat{i},i\right)=\frac{1}{{N}^{\,2}}\mathop{\sum }\limits_{x=1}^{N}\mathop{\sum }\limits_{y=1}^{N}{\left|\hat{i}\left(x,y\right)-i\left(x,y\right)\right|}^{2}$$
$$\begin{array}{l}{L}_{{{\mathrm{TV}}}}(\hat{o})=\frac{1}{{2N}^{\,2}}\mathop{\sum }\limits_{x=1}^{N}\mathop{\sum }\limits_{y=1}^{N}\left|{\nabla }_{x}{\mathrm{Re}}\{\hat{o}\}\left(x,y\right)\right|+\left|{\nabla }_{y}{\mathrm{Re}}\{\hat{o}\}\left(x,y\right)\right|\\ \qquad \qquad+\left|{\nabla }_{x}{{\mathrm{Im}}}\{\hat{o}\}\left(x,y\right)\right|+\left|{\nabla }_{y}{{\mathrm{Im}}}\{\hat{o}\}(x,y)\right|\end{array}$$

Here x, y are spatial indices, \({\nabla }_{x}\), \({\nabla }_{y}\) refer to the differentiation operation along the horizontal and vertical axes, Re{⋅}, Im{⋅} return the real and imaginary parts of the complex fields, respectively.

For the GedankenNet-Phase and GedankenNet-Phaseλ, which generate phase-only output fields, the predicted hologram was calculated using:

$$\hat{i}=\left|{\rm{FSP}}\left({{\mathrm{e}}}^{{\mathrm{i}}\uppi \hat{p}}{\rm{;}}{z}_{1},{z}_{2},\ldots ,{z}_{M}\right)\right|$$

where \(\hat{p}\) is the output phase field. The TV loss was calculated by using:

$${L}_{{{\mathrm{TV}}}}(\,\hat{p})=\frac{1}{{N}^{\,2}}\mathop{\sum }\limits_{x=1}^{N}\mathop{\sum }\limits_{y=1}^{N}\left|{\nabla }_{x}\hat{p}\left(x,y\right)\right|+\left|{\nabla }_{y}\hat{p}\left(x,y\right)\right|$$

To avoid trivial ambiguities in phase retrieval96,97,98, the GedankenNet’s output was normalized using its complex mean; the outputs of GedankenNet-Phase and GedankenNet-Phaseλ were subtracted from their corresponding mean.

All the trainable parameters in GedankenNet were optimized using the Adam optimizer99. The learning rate follows a cosine annealing scheduler with an initial rate of 0.002. All the models went through ~0.75 million batches (equivalent to ~7.5 epochs) and the best model was preserved with the minimal validation loss. The training takes ~48 h for an M = 2 model on a computer equipped with an i9–12900F central processing unit, 64 GB random-access memory and an RTX 3090 graphics card. The inference time measurement (Table 1) was done on the same machine with GPU acceleration and a test batch size of 20 for GedankenNet, 12 for both GedankenNet-Phase and GedankenNet-Phaseλ.

The supervised FIN adopted the same architecture and parameters as in ref. 48. The U-Net architecture employed four convolutional blocks in the down-sampling and up-sampling paths separately, and each block contained two convolutional layers with batch normalization and ReLU activation. The input feature maps of the first convolutional block had 64 channels and each block in the down-sampling path doubled the number of channels. Supervised FIN and U-Net88 models adopted the same loss function as in ref. 48. The same Adam optimizer and learning rate were applied to the supervised learning models. Deep image prior adopted a U-Net architecture, an Adam optimizer and the loss function used in ref. 81.

Image reconstruction evaluation metrics

SSIM, root mean square error (RMSE) and ECC were used in our work to evaluate the reconstruction quality of the output fields with respect to the ground-truth fields. SSIM and RMSE are based on single-channel images. Denoting \(\hat{o}\in {{\mathbb{R}}}^{N\times N}\) as the reconstructed amplitude or phase image, and \(o\in {{\mathbb{R}}}^{N\times N}\) as the ground-truth amplitude or phase image, SSIM and RMSE values were calculated using the following equations:

$${\rm{SSIM}}\left(\hat{o},o\right)=\frac{\left(2{\mu }_{\hat{o}}{\mu }_{o}+{c}_{1}\right)\left(2{\sigma }_{\hat{o}o}+{c}_{2}\right)}{\left({\mu }_{\hat{o}}^{2}+{\mu }_{o}^{2}+{c}_{1}\right)\left({\sigma }_{\hat{o}}^{2}+{\sigma }_{o}^{2}+{c}_{2}\right)}$$
$${\rm{RMSE}}\left(\hat{o},o\right)=\sqrt{\frac{1}{{N}^{\,2}}\mathop{\sum }\limits_{x=1}^{N}\mathop{\sum }\limits_{y=1}^{N}{\left(\hat{o}\left(x,y\right)-o\left(x,y\right)\right)}^{2}}$$

Here \({\mu }_{\hat{o}}\) and μo stand for the mean of \(\hat{o}\) and o, respectively. \({\sigma }_{\hat{o}}^{2}\) and \({\sigma }_{o}^{2}\) stand for the variance of \(\hat{o}\) and o, respectively, and \({\sigma }_{\hat{o}o}\) is the covariance between \(\hat{o}\) and o. c1 = 2.552 and c2 = 7.652 are constants used for 8-bit images. x and y are two-dimensional coordinates of the image pixels.

The ECC is calculated based on the reconstructed complex field and the ground-truth field. \({\hat{o}}^{{\prime} }\in {{\mathbb{C}}}^{N\times N}\) is the reconstructed field obtained by subtracting \(\hat{o}\) with its mean value. \({o}^{{\prime} }\in {{\mathbb{C}}}^{N\times N}\) is the corresponding ground-truth field. The ECC can be calculated as:

$${{\mathrm{ECC}}}\left({\hat{o}}^{{\prime} },\,{o}^{{\prime} }\right)={\mathrm{Re}}\left\{\frac{{{\mathrm{vec}}}{\left({\hat{o}}^{{\prime} }\right)}^{H}\cdot {{\mathrm{vec}}}\left({o}^{{\prime} }\right)}{\Vert{{\mathrm{vec}}}\left(\hat{o}^{\prime} \right)\Vert\cdot \Vert{{\mathrm{vec}}}({o}^{{\prime} })\Vert}\right\}$$

Here \({{\mathrm{vec}}}{\left({\hat{o}}^{{\prime} }\right)}^{H}\) is the conjugate transpose of the vectorized \(\hat{o}^{\prime}\), and ||⋅|| is the Euclidean norm.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.