Abstract
Despite tremendous progress of generative models in the natural sciences, their controllability remains challenging. One fundamentally missing aspect of molecular or protein generative models is an inductive bias that can reflect continuous properties of interest. To that end, we propose the Regression Transformer (RT), a method that abstracts regression as a conditional sequence modelling problem. This introduces a new direction for multitask language models, seamlessly bridging sequence regression and conditional sequence generation. We demonstrate that, despite using a nominal-scale training objective, the RT matches or surpasses the performance of conventional regression models in property prediction of small molecules, proteins and chemical reactions. Critically, priming the same model with continuous properties yields a competitive conditional generative model that outperforms specialized approaches in a substructure-constrained, property-driven molecule generation benchmark. Our dichotomous approach is facilitated by an alternating training scheme that enables the model to decorate seed sequences on the basis of desired property constraints, for example, to optimize reaction yield. We expect that the RT’s capability to jointly tackle predictive and generative tasks in biochemistry can find applications in property-driven, local exploration of the chemical or protein space. Such multitask approaches will pave the road towards foundation models in materials design.
Similar content being viewed by others
Main
Transformers1 are now ubiquitous in natural language processing (NLP) and have also enjoyed large success in molecular2,3,4 and protein language modelling5,6. The invention of Transformers was in alignment with the steady decline of inductive biases in machine learning, a trend that started with the rise of deep learning: convolutional neural networks outperformed traditional feature descriptors in object recognition7, self-attention generalized dense layers to learn sample-dependent instead of static affine transformations8 and Transformers exploited self-attention to supersede recurrent neural networks as the de facto standard in NLP. The success of vision transformers has questioned the need for translation equivariance in image processing9, and now, even frozen Transformers pre-trained on text achieve state-of-the-art results in object detection and protein classification10. Given that Transformers are today’s most generic model (that is, graph neural networks with multihead attention as neighbourhood aggregation on complete graphs), it is not surprising that attempts have been made to abstract entire domains such as reinforcement learning to sequence modelling in order to leverage Transformers11.
A provocative next step towards reducing inductive biases might be to refrain from explicitly modelling target variables as functions of input variables. Instead of following this discriminative modelling approach when tuning task-specific language heads in Transformers, learning the joint distribution over input and target variables could effectively further blur the lines between predictive and conditional generative models. The feasibility of such an approach can be assessed via permutation language modelling (PLM), an extension of masked-language modelling to autoregressive models12. Such dichotomous models (that concurrently excel at regression and conditional sequence generation) are beyond applications in NLP of special interest for chemical and material design. Molecules are often labelled with continuous properties (for example, drug efficacy or protein solubility), and design tasks are intertwined with bio- or physicochemical properties. But despite the rise of deep generative models in molecular13,14 and protein design15,16, current approaches still develop property predictors and generative models independently. Transformer-based architectures have been used widely on chemical tasks but focused on either property prediction17,18 or conditional molecular design19,20,21. Typically, they employ large-scale self-supervised pre-training and then fine-tune on different tasks22,23, but only the Chemformer by ref. 22 addresses regression as well as targeted molecular generation. However, the ChemFormer tunes task-specific heads and thus does not pose a true multitask model that entangles both tasks seamlessly. This semantic gap persists across architectural flavours (for example, generative adversarial networks (GANs)24, reinforcement learning25, variational autoencoders (VAEs)26, graph neural networks (GNNs)19,27, flow28,29 and diffusion models30). However, some works performed property-driven generation through probabilistic reparameterization that directly optimize the input to a property prediction model, for example, gradient-based schemes such as PASITHEA31, differentiable scaffolding trees32 and activation maximization 33 or multi-objective Bayesian optimization34 that has been applied to peptide inhibitor35 and antibody design36. Still, to our knowledge, existing Transformers either tune task-specific heads (see, for example, refs. 22,23) or limit the communication between both modules to a reward/loss and thus fail to ‘entangle’ constrained structure generation with property prediction. This critically violates the intuitive expectation that a property-driven generative model should, in the first place, excel at recognizing this property.
In this Article, we aim to close this gap by reformulating regression as a sequence modelling task. We propose the Regression Transformer (RT), a novel multitask model that can be trained on combinations of numerical and textual tokens (Fig. 1). This circumvents the canonical way of addressing regression in Transformers, that is, tuning a designated regression head37. Despite solely relying on tokenization of numbers and cross-entropy loss, the RT can successfully solve regression tasks. Notably, the same model can conditionally generate text sequences given continuous properties. This is achieved simply by moving the [MASK] location and does not require fine-tuning specific heads, thus constituting a true multitask model. To equip the RT with an inductive bias for handling floating-point properties, numbers are first tokenized into a sequence of tokens preserving the decimal order. We then devise numerical encodings (NEs) to inform the model about the semantic proximity of these tokens. To allow for concurrent optimization of regression and conditional generation, we derive a PLM-inspired, alternating training scheme that includes a novel self-consistency (SC) loss for improved text generation based on continuous primers.
The RT is a multitask language model designed to handle combinations of text and numbers. a, Traditional approach in generative chemistry: property predictors and generative models are trained independently from another. b, Our approach: Training the RT yields a dichotomous model that seamlessly transitions between property prediction and conditional text generation. The model’s task is to fill the content behind the [MASK] tokens. Depending on the mask location, the same model either predicts numerical tokens given textual tokens, thus performing a regression task (blue stream, top), or predicts textual tokens given both numerical and textual tokens, thus performing a property-driven conditional generation (yellow stream, bottom). c–f, This novel formulation finds application across a wide range of domains. We demonstrate the flexibility of the RT in predictive and generative tasks in modelling small molecules, proteins and chemical reactions and note that it can even be applied to natural text.
In the remainder of this paper, we describe the capabilities of the RT on a diverse set of predictive and generative tasks in chemical and protein language modelling. We commence with small-molecule modelling, validate the RT on a synthetic dataset of drug likeness38 and then test it on three property prediction datasets from the MoleculeNet benchmark39. The property predictions results are compared with previous approaches relying on a regression loss and demonstrate that regression can be cast as conditional sequence generation task without losing accuracy. These experiments rely on SELFIES40, a chemical language devised for generative tasks that, as we show, has comparable predictive power to SMILES. Although we aim to concurrently excel at predicting properties and generating sequences conditioned on properties, we start training with the PLM objective12, which does not explicitly model those tasks. We then refine this objective and devise a training scheme that alternates between optimizing property prediction and text generation. For the latter, we derive a novel SC loss that exploits the dichotomy of the RT by querying itself with the generated candidate sequence. To assess performance in conditional sequence generation, we systematically vary the continuous properties of interest and investigate the model’s ability to adapt a seed sequence according to the primed property value. We show applications on property-driven local chemical space exploration by decorating scaffolds with a continuum of properties and evaluate the novel molecules using the RT itself as well as an independent property predictor41. The RT is then challenged against specialized molecular generative models on a property-driven molecular generation benchmark42, where it substantially outperforms prior art.
Next, the RT is investigated on protein sequence modelling where it matches the performance of conventional Transformers on two regression datasets from the TAPE (Tasks Assessing Protein Embeddings) benchmark43. In experiments on chemical reactions, we notice that the RT constitutes a generalization of forward reaction and retrosynthesis models. We then demonstrate on two reaction datasets that the RT can not only predict reaction yields with similar accuracy to conventional Transformers44, but that it can also substitute specific precursors and thus generate novel reactions with higher predicted yield than a seed reaction.
Results
Chemical language modelling
Initial validations—learning drug likeness
To test the feasibility of concurrent property prediction and conditional generation, we start with optimizing the vanilla permutation language objective (equation (3)) on a synthetic QED (quantitative estimation of drug-likeness) dataset (Extended Data Fig. 1 shows an illustration of the entire workflow, for example, the different objective functions and the autoregressive generation and how the mixed alphanumeric sequences are tokenized and embedded). Since this objective masks tokens randomly in the sequence, evaluating such models on property prediction (that is, masking only numerical tokens as shown in Fig. 1b (top)) does not closely mimic their training dynamics.
Despite this, as well as the unconventional formulation of a regression task as sequence modelling, all models generated sequences of numerical tokens that allowed decoding floats, and even achieved a root mean square error (RMSE) <0.06 (Table 1, top three rows). Instead, for the generative task, the same models were queried ten times for every validation molecule with property ‘primers’ equidistantly spaced in [0, 1] and 40% of masked textual tokens. Throughout this manuscript by ‘primers’ we mean that we replace the true property of a sequence with a desired property value. The high rank correlation ρ (between primers and QED of unique, generated molecules) values show that the model learned successfully to complete the corrupted sequences to produce full molecules with a desired QED. Notably, the novelty score (that is, the percentage of conditionally generated molecules not present in training data) was >99% for all models. This demonstrates that the RT can generate novel chemical matter that adheres to a continuous property of interest. Moreover, the NEs, an inductive bias to ease learning proximities of numbers (similar to positional encodings1), slightly improved performance in all tasks (for details, see “Numerical Encodings” subsection in Methods). Next, the SELFIES models with and without NEs were refined on the basis of our proposed training scheme with alternating objectives. For both models, two models were fine-tuned using the alternating objective (equation (7)), with (α = 1) and without (α = 0) the SC term in the text loss, respectively (Table 1, bottom section). Interestingly the performance in regression as well as conditional generation improved notably, demonstrating the effectiveness of the refined objectives.
Furthermore, the ablation studies on pre-training or fine-tuning on individual objectives (Table 1, middle) revealed that good performance can be achieved on singular tasks. But the alternating objective enables cross-task benefits that enable the multitask model to outperform single-task models in almost all cases. As might be expected, evaluation queries with large deltas between seed and primed QED lead to lower precision on the generation since they essentially pose an out-of-distribution setting (note that the model was only trained with seed = primer). This is shown in Extended Data Fig. 2, which also reveals that the SC model particularly shines for challenging queries whereas for a pure reconstruction task (that is, primer close to seed) the single-task ‘generate-only’ model is advantageous. Moreover, as we report in Extended Data Table 1, all configurations of the RT outperformed a baseline k-nearest neighbour (k-NN) regressor on extended connectivity fingerprints (ECFP45) and our best configuration even surpassed SMILES-BERT17, which achieved a mean absolute error of 0.02 with a regular regression loss and after pre-training on ~9 million SMILES.
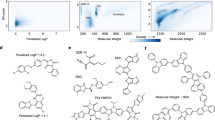
The SC term further improved the model’s ability to generate tailored ensembles of molecules and led to consistently higher correlation scores. This is exemplarily visualized in Fig. 2 (top) where a single seed molecule is decorated according to the property primers to cover the full range of QED scores.
For each row, the seed molecule is shown in the middle alongside its true property. On the basis of ten property primers, ten molecules were decoded but duplicates were discarded. Samples generated with the SC model. Top: QED dataset. Bottom: ESOL dataset of aquatic solubility. The solubility of the novel molecules was predicted by the RT itself and is externally validated by Grover41.
Generally, the better performance of the SC models (α = 1) in the generative tasks comes at the cost of slightly inferior regression performance (Table 1). Presumably, this is because the model weights in charge of the regression are confounded with the gradients from the self-evaluation (equation (7)). The novelty scores for the molecules generated in this setting were even slightly higher than for the PLM training (>99.3% for all models). A particularly challenging application for property-driven, local exploration of the chemical space is scaffold decoration (that is, adapting a seed molecule while preserving its core structure). For an example on this, see Supplementary Information Section 6.1. Here, the SELFIES models exceeded the SMILES models by far, because SMILES, unlike SELFIES, can be syntactically invalid (we found 60% validity). However, this number can hardly be compared to unseeded generative models because (1) the RT has to remediate a corrupted SMILES and cannot simply rely on its own internal states, (2) the concurrently provided property primers capture the entire range of low to high QED scores, thus incentivizing the model to decorate the sequence adventurously to adhere to the constrained property—a task that is often impossible and can easily lead to broken SMILES and (3) the RT training did not rely on teacher forcing. Due to the comparable results for property prediction (Table 1, top three rows), the remaining experiments focus exclusively on SELFIES. But even though SELFIES are designed to be always valid, they can also break by converting long sequences to short, stub-like molecules. We assessed the frequency of this scenario by defining a generation as defective if the obtained molecule had <50% of the atoms of the seed molecule. This yielded ~1.9% defective generations across ~300,000 generations. Regarding chemical sensibility, we observed that the 1,000 most common functional groups46 are reproduced in the generated molecules (Supplementary Fig. 1). Further ablation studies on different types of NE and related work on encoding numbers with Transformer are reported in Supplementary Information Section 1.
Learning embeddings of numbers
We sought to understand why the ablation studies on the NEs on the QED dataset (Table 1) reveal only mild superiority of models with NEs. Interestingly, as visualized in Extended Data Fig. 3, in the absence of static NEs, the model learns the natural ordering of digits from the data. A large number of embedding dimensions (47% and 36% for the decimal places −1 and −2, respectively) directly and significantly encoded the ordering of digits (that is, P < 0.05 and ∣PCC∣ >0.62 between the ten embedding values and a strictly monotonic vector). For example, in Extended Data Fig. 3 (left), the digit value is monotonically related to its embedding value. In general, attention weights in Transformers can capture complex semantics such as protein folding structure47 or atom mapping in chemical reactions4. For a qualitative comparison of the RT’s attention across the predictive and generative task, see Supplementary Information Section 2.
Regression benchmark (MoleculeNet)
After the successful initial experiments, we evaluated the RT on three regression benchmarks from MoleculeNet39. The regression performance on ESOL, FreeSolv and Lipophilicity is shown in Extended Data Table 2 and compared with prior work. The strongest baseline model from MoleculeNet, XGBoost, is outperformed by all our models on all tasks. Even the MPNN48, a message-passing GNN, is slightly surpassed on FreeSolv and Lipophilicity by some of our models. However, all our models are outperformed by BERT49 and BART22. Notably, these models leveraged large-scale self-supervised pre-training before fine-tuning a regression head, whereas we use a classification loss. Since these results might not be directly comparable to the RT with its XLNet backbone, we also fine-tuned a XLNet model with a conventional regression head. Notably, despite the absence of a regression loss, the RT is on par (Lipophilicity) or only mildly inferior (that is, within s.d. range; ESOL, FreeSolv) to XLNet.
However, in stark contrast to all those approaches, only the RT can also be used to conditionally generate molecules similar to the training samples (Extended Data Table 3). Since the properties of the generated molecules are intractable to evaluate in silico, we could predict them, handily, using the RT. However, as this might be a biased estimator, we additionally evaluated them using Grover41, a self-supervised Graph Transformer that relies on large-scale pre-training. Extended Data Table 3 presents the performance in conditional molecular generation, which underlines the benefit of the SC loss (α = 1) and demonstrates that the RT can adapt unseen seed molecules even according to complex molecular properties such as water solubility. Corroborative for our work is the high correlation of our property predictions (RT) with Grover’s for molecules generated by the ESOL, FreeSolv and Lipo models (0.86, 0.84 and 0.75, respectively). For a qualitative evaluation, we depict the generations for one exemplary seed molecule of the solubility dataset in Fig. 2 (bottom). Lastly, we found 1.3% defective generations, which is comparable to or lower than in the QED dataset.
Conditional molecular generation benchmark
To assess whether the RT is a powerful conditional generative model, we benchmarked it on a property-driven molecular generation task, namely penalized logP (plogP; definition in Methods) constrained optimization42. Given a seed molecule and a similarity constraint to the seed molecule (δ, given in Tanimoto similarity), the goal is to generate molecules with higher plogP values. The results in Table 2 demonstrate that, for both similarity thresholds δ, the RT performs competitive to state-of-the-art models; for example, it outperforms a Junction-Tree-VAE42 and a graph-convolutional policy network (GCPN)50 by 614% and 103% in average improvement, respectively.
It falls behind the Back Translation (BT) model51 on average improvement; however, care has to be taken on their results since other metrics and s.d. values are not reported. The RT performs comparably to the MoFlow model52, while our results for δ = 0.4 are inferior, the unconstrained generation results (δ = 0.0) are in favour of our method (Supplementary Information Section 3). Moreover, these comparisons are not truly fair because all competing methods have a training procedure that rewards generating molecules with high plogP and some methods even apply gradient optimization schemes at inference time (GCPN and JT-VAE). This is in stark contrast to the RT training, which rewards only if the reconstructed molecule has a similar (predicted) plogP to the seed molecule (we did not construct directed plogP queries for the training; they were used only at inference time). Thus, the RT is agnostic in valence and could equally be used to adapt molecules towards lower plogP. Overall, this experiment demonstrates that the RT is able to compete with specialized conditional generative models in goal-directed molecular generation. At the same time, the RT also predicted the plogP value with a Pearson’s correlation coefficient (PCC) of 0.92, a task that cannot be addressed with normal conditional generative models. The results in Table 2 were obtained with the RT including a SC loss, but for ablation studies on the RT and further results on δ = 0.2 and δ = 0, see Supplementary Information Section 3.
Protein sequence language modelling
Pre-training on potential protein interaction (Boman index)
To assess the generality of the RT beyond chemical languages, we benchmarked the RT in protein language modelling. On the synthetic pre-training data, the RT obtained nearly perfect results in predicting Boman’s index (Spearman’s ρ > 0.994; Table 3) and outperformed a baseline k-NN using Levenshtein distance53. But the RT also successfully generated peptides with a desired Boman index, given a partially corrupted amino acid sequence (Spearman’s ρ of 0.84; Table 3b). Moreover, a higher fraction of masked tokens lead to better results in protein generation tasks (Supplementary Fig. 2).
TAPE datasets (protein fluorescence and protein stability)
Next, the RT performed competitively on two realistic protein regression datasets from TAPE (Table 3). This is remarkable given that the TAPE models were pre-trained large scale on unlabelled protein sequences and fine-tuned with a regression loss. For example, the RT outperforms all reported methods in Spearman’s correlation on the fluorescence task, which has a distribution with two modes, for bright and dark proteins, respectively. Inspecting the predictions in more depth showed that the RT, compared with other methods, excels at recognizing the mode of a protein but struggles with intra-mode precision (Supplementary Information Section 7.2). Across both datasets, the RT performs on par or superior to the TAPE Transformer43, UniRep54 and the contemporary ProteinBERT55 model, pre-trained on 31 million, 24 million and 106 million protein sequences, respectively (2.6 million in our case). However, scaling this pre-training to evolutionary-scale protein language models would probably displace UniRep as well as the RT as evolutionary-scale protein language models was recently demonstrated to have strong zero-shot generalization performance56.
Overall, the competitive predictive performance of the RT demonstrates that the benefits of self-supervised pre-training can extend to numerically labelled datasets. This yields, en passant, a conditional generative model for property-driven local exploration of the protein sequence space. Evidence on this can be found in Table 3b: Whereas all TAPE models as well as the UniRep method are incapable of addressing this generation task, the RT was able to modify the test proteins such that their (predicted) stability correlated strongly with the primed property (ρ = 0.44).
Modelling chemical reactions
Language models advanced reaction chemistry dramatically4,57 and, among others, showed superior performance on yield prediction44, yet models incorporating yield into (partial) reaction generation are lacking entirely. Such models could be used to (1) identify entirely novel reactions by substituting a specific precursor type with a higher yield, (2) cure erroneous reactions by identifying missing precursors in databases of specific reaction types or (3) infer reagents or solvents in reactions that only specify main compounds.
We therefore optimized the RT for concurrent yield prediction and precursor generation on two reaction-yield datasets: Buchwald–Hartig aminations58 and Suzuki–Miyaura cross-couplings59. All experiments relied on the alternated training scheme with SC loss. On yield prediction, the RT (trained on SELFIES) outperforms fingerprint-based or quantum mechanics methods, and matches (Suzuki dataset) or almost matches (Buchwald dataset) the performance of language models such as Yield-BERT, trained with regression loss on SMILES (Table 4).
The same model learned to reconstruct missing precursors in Buchwald–Hartwig animations, which can be useful to infer missing solvents or reagents in automatically extracted reactions (Table 4b). This is partly achieved with great accuracy (for example, 98.2% for aryl-halides). Interestingly, inferring additives proved challenging, possibly because they are the dominant precursor type for the reaction yield58. However, upon masking the additive only partially (rather than completely), the reconstruction performance increases significantly (ablation study with pmask ∈ [0.25, 0.5, 1] in Supplementary Table 5). On the Suzuki couplings, the reconstruction results are more balanced among the five precursor types; the average Tanimoto similarity to the true precursor was >0.65 in all cases (Table 4b). Moreover, across both datasets we observed mild benefits in reconstruction performance when providing the true yield rather than masking it (Supplementary Tables 6 and 7). In addition to yield prediction and precursor reconstruction, the RT can also decorate existing reactions by adapting specific precursors towards a higher yield (Table 4b). Consistently among both datasets and all precursor types, 40–80% of the top-five predicted sequences contained reactions with entirely novel precursors and higher predicted yield.
Extended Data Fig. 4 visualizes exemplary adaptations of each precursor type of a BH amination with very low yield (<5%). Notably, for this unseen reaction, the RT found novel adaptations of each of the four precursor types that resulted in an increase of predicted yield by 11–85%. With the forward reaction prediction model in IBM RXN2, we confirmed that all reactions indeed result in the desired product. Notably, the confidence from the forward model rank-correlated almost perfectly with the yield predicted by the RT (ρ = 0.90, P < 0.05).
Discussion
The herein presented RT demonstrated that regression can be cast as conditional sequence learning task. We introduced a flexible multitask language model with wide application in scientific discovery. Our main contribution is a multitask transformer that bridges previously considered disjoint tasks (property prediction and conditional generation) without the need of tuning task-specific heads. This model shines at both tasks and facilitates highly customizable molecular generation (for details, see ‘Usage of trained models’ in the Code availability section). This could pave the road towards foundation models in material design.
Regarding molecular property prediction, we find that the RT learns continuous properties even from small datasets, surpasses conventional regression models on several benchmarks and sometimes competes with Transformers trained on regression loss. Remarkably, this is achieved without providing ratio-scale information about the property, potentially even challenging the necessity of using regression rather than classification objectives.
The experiments on conditional text generation underline the versatility of the RT. Across a wide range of tasks, we conditionally generated novel sequences (molecules, proteins and reactions) that seemingly adhere to primed, continuous properties. Our experiments on constrained molecular generation benchmark further demonstrate that the RT can surpass specialized conditional generative models. We foresee this to impact property-driven and substructure-constrained molecular or protein design tasks. In the recent work by ref. 60, the RT has been applied in polymer chemistry for the generation of novel ring-opening polymerization catalysts as well as block and statistical co-polymers. In both cases, successful experimental validation confirmed the ability of the RT to accelerate real discovery workflows.
Moreover, even though all experiments reported herein examined singular properties, the RT naturally scales to multi-property prediction (see ‘GUI Demo’ in the Code availability section on how to access pre-trained multi-property models).
While we build the RT upon XLNet, any decoder that combines the benefits of masked language modelling (MLM) and causal, autoregressive language modelling could serve as a backbone (for example, T5 with its sentinel tokens61, MPNet62, InCoder63 or FIM64). Future work could evaluate the RT on such backbones, intensify the work on reaction modelling (the RT effectively generalizes forward reaction and retrosynthesis models) or improve the ability of the RT to perform fine-grained regression (for an interesting failure mode, see Supplementary Information Section 7.1). Another prospect is to investigate property-constrained but unseeded molecular generation for more global chemical space exploration. Finally, our work resonates with the recent trend towards multitask Transformers65,66,67, and we envision it as a means to accelerate the development of foundation models for scientific discovery applications.
Methods
In this section we first describe the different components of our methodology (architectural choices, tokenization scheme, NEs and training objectives). We then describe the implementation details for both training and evaluation.
XLNet backbone
Language models utilize either a causal (that is, left-to-right), autoregressive training objective such as recurrent neural networks and GPT-3 (ref. 67) or use MLM such as BERT37. Autoregressive approaches are preferable for generating long sequences (for example, entire documents), but since such causal models only condition on previous tokens, they cannot be applied to text infilling tasks and cannot profit from MLM pre-training. Instead, MLMs such as BERT condition on the entire sequence to fill masked tokens, making them appear a good choice for infilling tasks; however, MLM approaches fail to generate longer sequences due to their independence assumption. To unify both worlds and retain the benefits of autoregressive modelling in combination with a bidirectional context, several methods have been proposed, with XLNet12 being the first prominent one. The RT is built upon an XLNet backbone that is an autoregressive language model, but due to its novel training objective, it, in expectation, obtains full bidirectional attention. This bidirectionality is critical because the RT is required to fill multiple tokens at arbitrary positions in a sequence while attending the full remaining sequence (for example, SMILES/SELFIES are non-local sequences such that masking functional groups usually implies masking disconnected tokens). Moreover, the independence assumption in bidirectional but non-autoregressive models (such as BERT) becomes increasingly disruptive as more masked tokens are filled, making XLNet a great choice. This limits BERT’s applicability for generative tasks in biochemistry such as scaffold decoration where large portions of a molecule might be masked and generation of individual atoms can critically alter the molecule’s functional properties. In general, it is important to notice that the proposed framework can be applied to all transformer flavours, but it certainly benefits from an autoregressive generation with full sequence attention even for discontiguous mask locations. Such approaches rely on either a PLM like XLNet or MPNet62 or on sentinel tokens replacing code spans that are then predicted at the end of a sequence with an autoregressive approach like in T5 (ref. 61), InCoder63 or fill-in-the-middle64. Further information on the implementation and the model hyperparameters can be found below in the “Model training and evaluation procedure” section.
Tokenization
This section describes the processing of alphanumeric sequences, that is, strings consisting of a mixture of numerical and textual symbols (for a visualization of the tokenization, see Extended Data Fig. 1, top). Unlike previous approaches that modelled 8-bit integers with a classifier68, we strive to represent real numbers with arbitrary floating point precision. Since representing every number as a single token is suboptimal due to a lack of generalization to new numbers and sparsity of the provided tokens, we formulated regression as sequential classification task. In turn, this necessitates a scheme for converting text representing numbers into a sequences of tokens. First, the following regular expression splits a string denoting a numerical:
Each of the resulting matches containing a number is converted to a token tv,p where \({v\in {\mathbb{N}}\cap [0..9]}\) is the value/digit and \(p\in {\mathbb{Z}}\) is the decimal place (for example, 12.3 is split into [1_1, 2_0., 3_-1]). We call these numerical tokens. This representation has the advantage that it allows easy decoding of the digit sequence but also distinguishes their decimal order by adhering to classic positional notation. Negative numbers are preceded with a special token. Regarding alphabetic tokens, we represent molecules as SELFIES40 strings and tokenized them with their internal tokenizer. In one ablation study, we instead use SMILES69 and tokenize with the regular expression from ref. 57. Protein sequences are tokenized per amino acid.
Numerical Encodings (NE)
Due to the inherent structure of numbers, learning the embeddings of numerical tokens in a purely data-driven way might be ineffective. Moreover, since the RT is trained with cross-entropy loss, no notion of similarity between numerical tokens is conveyed. As a remedy, we propose NEs, a simple inductive bias about the semantic proximity of numerical tokens, similar to positional encodings1. Our proposed NEs are zero vectors for all but numerical tokens of the dictionary. We follow positional notation as above. Given a token tv,p (with digit value v and decimal place p), the NE at embedding dimension j is defined as
Thus, the amplitude of the NE scales with the numerical value of the token. This scheme can be applied to any floating point value \(x\in {\mathbb{R}}\). The encodings are also independent of the sign of the number. Hence, they equally convey proximity between positive and negative numbers. The NEs are perfectly correlated among embedding dimensions but alternate between positive and negative values for even and odd dimensions and vanish for higher dimensions (see example in Extended Data Fig. 5a). Critically, the pairwise distances of the NEs are symmetric and decay monotonically with the float value (Extended Data Fig. 5b). In practice, we sum the NEs with regular word embeddings and relative positional encodings from XLNet (for workflow, see Extended Data Fig. 1). Note that we also experimented with integer-based NEs (for additional experiments, see Supplementary Material Section 1).
Training objectives
The input x for an RT is defined by a concatenation of k property tokens \({[{{{{\bf{x}}}}}^{\,p}]}_{k}\) and l textual tokens \({[{{{{\bf{x}}}}}^{t}]}_{l}\), such that \({{{\bf{x}}}}={[{{{\bf{{x}}}^{\,p}}},{{{{\bf{x}}}}}^{{{{\bf{t}}}}}]}_{T}={[{x}_{1}^{\,p},...,{x}_{k}^{\,p},{x}_{1}^{t},...,{x}_{l}^{t}]}_{T}\). The full sequence length is T = k + l, and xp and xt are property and textual tokens, respectively. For a high-level overview of the training objectives, see Extended Data Fig. 1 (bottom).
PLM objective
The idea of PLM12 is to fill masked tokens autoregressively by sampling a factorization order z for a sequence x at runtime. Decomposing the likelihood pθ(x) according to the facorization order yields, in expectation, a bidirectional autoregressive model. Let \({{{\bf{z}}}}\in {{{{\mathcal{Z}}}}}_{T}\) denote one of the T! permutations of our sequence x. If zi and z<i are the i-th and first i − 1 elements of z, the PLM objective is
In practice, partial prediction is performed. That is, only the last c tokens of the factorization order z are predicted. Following XLNet, z is split into a (masked) target subsequence z>c and an unmasked input sequence z≤c such that the objective becomes
where c is a hyperparameter, usually sampled per batch such that the fraction of masked tokens is roughly 1/c. We notice that equation (4) does not make any specific choices on xp and xt. It thus constitutes our baseline objective. While equation (4) is a generic objective, it is computationally exhaustive to optimize due to the permutations. Moreover, it is not ideal for our needs because it does not distinguish between textual and property tokens. Instead, we are aiming to develop a single model that can predict either numerical tokens (when given text sequences) or text tokens (when given a combination of numerical and text tokens). To that end, we propose to train on two alternating objectives, one designed for property prediction and one for text generation.
Property prediction objective
Instead of randomizing which tokens are masked, this objective exclusively masks all the property tokens. Specifically, we constrain the factorization order z by setting the first l elements to xt and fixing c = l. This guarantees that only property tokens are masked. Let \({{{{\mathcal{Z}}}}}_{T}^{p}\) denote the set of possible permutations. Under this constraint, the objective then becomes
where \({{{{\bf{x}}}}}_{{{{{\bf{z}}}}}_{\ > \ c < i}}^{\,p}\) denotes the c-th to the (i − 1)th element of the factorization order z. We emphasize that this ‘tailored’ property objective \({{{{\mathcal{L}}}}}_{\mathrm{p}}\) is still optimized with a cross-entropy loss in practice. Note that this loss cannot convey any notion on the qualitative proximity of the prediction to the labels because the level of measurement of tokens in a language model are on a nominal level. Thus, predicting a sequence of numerical tokens corresponding to a property score of 0.91 for a sample with a true property of 0.11 will not generally result in a higher loss than predicting 0.21. Instead, a traditional regression loss operates on a ratio scale.
Conditional text generation objective
This objective facilitates the generation of textual tokens given a property primer and textual tokens. We constrain the factorization order z by setting the first k elements to xp to and sampling the cut-off c, such that c ≥ k. This ensures that masking occurs only on textual tokens. With this constraint, we denote the set of permutations by \({{{{\mathcal{Z}}}}}_{T}^{t}\) and the objective becomes
Intuitively, this objective applies regular PLM while sparing the numerical tokens. It then aims to reconstruct the full text sequence (that is, molecule) given the uncorrupted property tokens and partially corrupted textual tokens.
Self-consistency (SC) objective
Standalone, the above conditional text generation objective (6) does not reward if the generated sequences adhere to the primed property. This is critical because in chemical as well as natural languages changes in single tokens (that is, atoms, amino acids or (sub)words) can drastically change the property (meaning) of a sequence (sentence). As a remedy, we extended the text generation objective \({{{{\mathcal{L}}}}}_\mathrm{G}\) by an SC term that exploits the dichotomy of the RT. The full objective is given by
where the second addend is the SC term, weighted by a factor α. Intuitively, it is given by the difference between the property of the sample and the predicted property of the generated sample \(\hat{{{{\bf{x}}}}}\). Here, \(\hat{{{{\bf{x}}}}}\) is obtained by greedy decoding of the masked tokens and combining it with the non-corrupted tokens of x. To be precise, \(\hat{{{{\bf{x}}}}}=[{{{{\bf{x}}}}}^{\,p},{\hat{{{{\bf{x}}}}}}^{t}]\) where \({\hat{{{{\bf{x}}}}}}^{t}=[{m}_{1}{\bar{x}}_{1}+(1-{m}_{i}){x}_{1},...,{m}_{l}{\bar{x}}_{l}+(1-{m}_{l}){x}_{l}]\). Here, m is an indicator vector for whether masking occurred at a given position and \(\bar{{{{\bf{x}}}}}=\arg \max \mathop{\sum }\nolimits_{i = c+1}^{T}\log {p}_{\theta }({x}_{{z}_{i}}^{t}| {{{{\bf{x}}}}}_{{{{{\bf{z}}}}}_{ < k}}^{\,p},{{{{\bf{x}}}}}_{{{{{\bf{z}}}}}_{\ > \ k < i}}^{t})\) is the result of greedy decoding. In such a formulation, the RT acts as an oracle during its own optimization, resembling an additional layer of self-supervision. While this scheme risks undesired side effects when the model performs poorly at property prediction, it introduces a notion of SC and rewards the generation of molecules that are different from training samples as long as they adhere to the property.
Model training and evaluation procedure
Implementation
All experiments build upon the XLNet12 implementation from the HuggingFace library70. We expanded the XLNet backbone with our proposed tokenization scheme, an additional encoding layer for the numerical embeddings (Ndim = 16) and the custom training objectives (Extended Data Fig. 1). Regarding architectural hyperparameters, we used 32 hidden layers in the Transformer encoder, with a dimensionality of 256 and 1,024 in the feed-forward layer and 16 attention heads (20% dropout). Altogether, this model has ~27 million trainable parameters (exact numbers vary dependent on vocabulary size). During evaluation, greedy decoding was used for property prediction and beam search decoding for conditional sequence generation. We used PyTorch 1.3.1 (ref. 71) and the XLNet backbone from Transformers 3.1.0 (ref. 70). Models were trained from scratch unless indicated otherwise. All models were trained on single graphics processing units (GPUs) (NVIDIA Tesla A100 or V100). In the following sections, we elaborate on the training procedures for each dataset.
Chemical language modelling
Drug likeness (QED)
Dataset. Starting from ~1.6 million bioactive molecules from ChEMBL72, we created a synthetic dataset by computing the QED38 score (q ∈ [0, 1]) for all molecules with RDKit and rounded to three decimal places. We used ~1.4 million molecules for training, 1,000 for validation and 10,000 for testing.
Procedure. We started training the models with the vanilla PLM objective (equation (4)) on the QED dataset until validation perplexity saturated (~4 days, single GPU). Thereafter, the models were further refined on the same dataset by alternating every 50 steps between objectives (equation (5) and equation (7)). We perform ablation studies on the SC loss, setting α in equation (7) to 0 and 1, respectively. The SELFIES/SMILES vocabulary had 509 and 724 tokens, respectively. During evaluation, greedy decoding was used for property prediction and beam search decoding for molecular generation. During evaluation, we set c = 2.5, which implies that roughly ~40% of the tokens were masked (maximum span: seven tokens).
MoleculeNet benchmark
Dataset. We focused on three regression datasets from the MoleculeNet benchmark39: ESOL, FreeSolv and Lipophilicity, where the task is to predict water solubility, hydration free energy and lipophilicity of a molecule, respectively. For each dataset, we performed three random splits (as recommended by ref. 39) with 15% validation data. Because the datasets are small (<5,000 samples), we used offline SMILES augmentation73 to augment the training dataset by a factor of 16.
Procedure. For the MoleculeNet datasets, the models were warm-started using the QED initialization and trained for only 50,000 steps (batch size 4) with early stopping. Since the QED pre-training utilized numerical values in [0, 1], we normalized the regression values of the entire MoleculeNet datasets to the same range (using training data only) and rounded them also to three decimal places. For all objectives, unless otherwise constrained, we set the masking hyperparameter c = 5 and restrict the span of consecutively masked tokens to a maximum of five tokens.
Property optimization benchmark
Dataset. This is a benchmark for property-driven, conditional molecular generation. The goal is to adapt a seed molecule such that a property is maximized while adhering to a fixed similarity constraint. We obtained the data from 42 which ships with a fixed split of 215,381 training and 799 test molecules and their penalized logP (pLogP) value 74. pLogP is the octanol-water partition coefficient (logP) penalized by the synthetic accessibility score and the number of cycles with > 6 atoms. Hence, pLogP just like QED can be computed deterministically from the molecule42.
Procedure. For this task, the models were also warm-started using the QED initialization and trained for 50,000 steps with early stopping on perplexity. To assemble the candidates for the optimization of one seed molecule, we tried to follow the process of ref. 42 as closely as possible. Reference 42 applied 80 gradient steps, then decoded 80 molecules and reported the molecule with the highest pLogP score that satisfies the similarity constraint δ. Instead, we form a pool of molecules by prompting 80 times with the same seed molecule but varying the fraction and the maximum span of masked tokens. From the pool of decodings we report the molecule with the highest pLogP, just like refs. 42,50.
Protein sequence language modelling
Protein interaction index (Boman)
Dataset. As a large-scale, labelled dataset for proteins we focused on the Boman index, a measure of potential protein interaction for peptides. It is the average of the solubility values of the residues75. We collected all 2,648,205 peptides with 15–45 amino acids from UniProt76, computed their Boman index and used 10,000 and 1,000 for testing and validation, respectively.
Procedure. To model protein sequences, we started with training on the Boman dataset. We trained three groups of models, one for the vanilla PLM objective (equation (4)) and two for the alternating objectives. We again alternated every 50 steps between optimizing (equation (5) and equation (7)) and trained one set of models with and one set without the SC loss, such that α = 1 and α = 0, respectively, in equation (7). Models were trained until validation perplexity saturated (~4 days, single GPU). The numerical values of the Boman index, originally in the range [−3.1, 6.1] were normalized to [0, 1] (using training data only) and rounded to three decimal places.
TAPE benchmark
Dataset. We focused on two datasets from the TAPE benchmark43: Fluorescence77 and Stability78. The goal is to predict, respectively, the fluorescence and intrinsic folding stability of a protein that is one to four mutations away from a training protein. Both datasets ship with fixed splits. The fluorescence (stability) dataset has 21,446 (53,416) training, 5,362 (2,512) validation and 27,217 (12,851) test samples.
Procedure. For both datasets, three models were warm-started using the Boman initialization (PLM objective) and trained until validation performance saturated (~100,000 steps). Experiments were conducted using three configurations; PLM objective, and alternated training with (\({{{{\mathcal{L}}}}}_{{\mathrm{SC}}}\)) and without (\({{{{\mathcal{L}}}}}_\mathrm{G}\)) the SC objective. The numerical values were again scaled to [0, 1]. On the Fluorescence data, a small value of Gaussian noise was added to some training samples due to an interesting failure mode (Supplementary Information Section 7.1). For the evaluation of the conditional generation task, the models were given more flexibility: 60% of the tokens were masked (that is, c = 1.7 in equation (3)) and the maximum span was seven amino acid residues. We did not evaluate the RT on conditional generation for the Fluorescence dataset because of a massive pre-training–fine-tuning mismatch: While the Boman dataset used for pre-training consisted of 15–45 residues (mean ± s.d., 36 ± 7), the fluorescence proteins were significantly larger (246 ± 0.2 residues, P < 0.001). Instead, the proteins in the stability dataset were similar in size to the pre-training data (45 ± 3 residues).
Chemical reaction modelling
Pre-training on USPTO
Dataset. We used reactions from the US Patent Office (USPTO), the largest open-source dataset about chemical reactions79 to learn generic reaction chemistry. Since no yield information was available, the utilized numerical property was the total molecular weight of all precursors. The dataset contained n = 2,830,616 reactions and was obtained from ref. 4.
Procedure. Since the two reaction yield datasets cover only narrow regions of the chemical space (one template applied to many precursor combinations), we warm up the model on broader reaction chemistry extracted from patents (USPTO). A total of 5,000 reactions were held out for validation, and the model was trained until validation performance on the two alternating objectives (equation (5) and equation (7) with α = 1) saturated. The masking hyperparameter c was set to 2.5, and the model were trained for ~2 days (single GPU). The vocabulary for reaction SELFIES contained 861 tokens.
Reaction yield datasets
Dataset. We investigated two high-throughput experimentation (HTE) yield datasets that examine specific reaction types: Buchwald–Hartig aminations 58 and Suzuki–Miyaura cross-coupling reactions59. Both datasets were investigated in the same ten random splits as examined in ref. 44 with a 70%/30% train/validation ratio.
The Buchwald–Hartwig dataset was produced by ref. 58 and investigates HTE of palladium-catalysed Buchwald–Hartwig C–N cross-coupling reactions. The reaction space comprises 3,955 reactions, spanned by 15 unique aryl and heteroaryl halides, 4 Buchwald ligands, 3 bases and 22 isoxazole additives. A palladium catalyst and a methylaniline are the fifth and sixth precursor, respectively; however, they are identical for all reactions. Each reaction is associated with a yield y ∈ [0, 100], and the ten random splits were identical to the ones released by ref. 80 that are also used by all competing methods in Supplementary Table 6. Yield is given in a range of [0, 100].
The Suzuki cross-coupling dataset was provided by ref. 59 and investigates HTE of Suzuki–Miyaura reactions across 15 pairs of electrophiles and nucleophiles, leading to different products, respectively. For each pair, a combination of 4 solvents, 12 ligands and 8 bases (reagents) was measured, resulting in a total of 5,760 reaction yields that we scale to the range [0, 100]. The catalyst is identical for all reactions; some reactions omitted the ligand or the base, while others contained electrophiles, nucleophiles, ligands, bases or solvents that were composed of different fragments (for example, salts).
Procedure. For both datasets, ten models were fine-tuned respectively on repeated random splits. The training objectives again alternated every 50 steps between property prediction (equation (5)) and conditional generation (equation (7) with α = 1) for a maximum of 50,000 steps (~1 day). Notably, during the conditional generation task we sampled one precursor per batch and then entirely but exclusively masked this precursor. Thus the objective for the model became to reconstruct a missing precursor from the remaining precursors and the reaction yield (or to produce an alternative precursor with a similar predicted yield).
Evaluation and performance metrics
Regression
For the regression (or property prediction) task, we convert the sequence of predicted (numerical) tokens into a floating-point prediction (the model never failed to predict a token sequence not corresponding to a valid numerical). We then report the RMSE, PCC or coefficient of determination (R2), dependent on the dataset and previous methods.
Conditional sequence generation
Dependent on the application domain, different metrics are utilized (see above).
Small molecule and protein modelling
We strive to assess the model’s ability to decorate an arbitrary, possibly discontiguous fractional input sequence (for example, a molecular scaffold) according to a property of interest. Therefore, we randomly mask a fraction of tokens of the text sequence and then query the model with ten equidistant property primers spanning the full range of property values. The metric is the average Spearman’s ρ between the ten primers and the actual properties. Spearman is favourable over Pearson because it is only rank sensitive. Note that, due to constraints induced by the fragmented sequence, covering the entire property spectrum is usually impossible such that, for example, RMSE is inappropriate for this task (for example, priming a highly toxic scaffold with low toxicity cannot yield a non-toxic molecule). As a sanity check, we also report 0-Var, that is, the percentage of test molecules/proteins for which the generation was unaffected by the primer, that is, upon priming with the ten equidistant property primers and the fractional sequences, the decoded molecules/proteins were all identical (the lower the better).
On the property optimization benchmark from ref. 42, we report the same metrics as in their work: the success rate in generating molecules with higher logP (while adhering to the similarity constraint δ), the Tanimoto similarity δ to the seed molecule and the average improvement in plogP.
Chemical reaction modelling
For the reaction yield datasets, we challenge the model by two sequence generation tasks. First, we fully reconstructed a precursor solely based on the remaining precursors and the reaction yield. The top-three predicted sequences (decoded via beam search) are considered, s.t. top-three accuracy is reported. Additionally we report the average Tanimoto similarity of the most similar of the top-three molecules to the seed molecule. We used RDKit Morgan fingerprints with radius 2 (roughly equivalent to ECFP4 (ref. 45)). Secondly, we measure the capability of decorating existing reactions to obtain a (potentially) higher yield. To that end, the model is prompted with incomplete reactions consisting of an increased yield, an entirely masked precursor and complete remaining precursors. We consider the top-three predicted sequences (decoded via beam search) and report the fraction of samples where one of the reactions had a higher (predicted) yield (success rate). The second response metric is the mean improvement in (predicted) reaction yield (yield y ∈ [0, 100]; the distributions are right-skewed). Note that we exclude trivial solutions by removing all predicted precursors that exist in the training dataset.
Baseline models
k-NN
For small-molecule and protein modelling we reported results in property prediction with the k-NN baseline model. For small molecules, the distance measure was (inverted) Tanimoto similarity81 of ECFP4 fingerprints45. For the protein language models, the Levenshtein distance between the protein sequences was used53. For the k-NN baseline models, k was determined on the basis of the best performance on the validation data. This led to k = 25 for the drug-likeness/QED task, k = 21 for the protein interaction (Boman index) task, k = 50 for the fluorescence and k = 15 for the stability task.
XLNet with regression head
For the molecular property prediction on the MoleculeNet datasets, we trained an XLNet12 model with a conventional regression loss. This maximizes comparability to the RT since it, unlike the other models in Extended Data Table 2, also uses an XLNet backbone. This model was initialized using the XLNet-base-cased weights from HuggingFace and subsequently the SequenceClassification head was fine-tuned with an L2 loss. The model contained ~93 million parameters and was fine-tuned for 200 epochs without any hyperparameter optimization. Early stopping was used to determine the best epoch.
Data availability
The data for the MoleculeNet experiments can be obtained from https://moleculenet.org/datasets-1. The data for the molecular optimization experiments can be obtained from https://github.com/wengong-jin/icml18-jtnn/tree/master/data/zinc. The data for the protein language modelling experiments can be obtained from https://github.com/songlab-cal/tape. The data for the reaction yield experiments can be obtained from https://github.com/rxn4chemistry/rxn_yields/tree/master/data.
Code availability
Usage of trained models
The RT is implemented in the Generative Toolkit for Scientific Discovery (GT4SD)82, which provides ready-to-use pipelines for inference on pre-trained models as well as training or fine-tuning on custom data. The GT4SD endpoint of the RT facilitates highly customizable local chemical space exploration. The user can decide to (1) make no assumptions about which tokens are being masked, (2) mask only specific types of atoms, (3) preserve certain structures while randomly masking on the rest, (4) mask certain moieties or (5) decide on a token-by-token basis on which atoms are masked. Via GT4SD, versions of the RT trained on the QED and ESOL datasets (small molecules), the stability dataset (proteins) and the USPTO-pre-trained reaction model are available. Moreover, GT4SD also distributes additional versions of the RT trained on multi-property prediction tasks not described herein, including but not limited to ring-opening polymerization catalysis and block copolymers (CITE REF 59) a logP as well as a combined logp-synthesizability model. A guide to use the RT be found on https://github.com/GT4SD/gt4sd-core/tree/main/examples/regression_transformer. A notebook with a short demo can be found under https://github.com/GT4SD/gt4sd-core/blob/main/notebooks/regression-transformer-demo.ipynb. The datasets used for benchmarking are available from the respectively referenced papers.
GUI Demo
A simple webapp of the RT for inference of pre-trained models has been made publicly available via HuggingFace spaces at https://huggingface.co/spaces/GT4SD/regression_transformer. The app was build with Gradio83 upon the GT4SD82 implementation.
Reproduction
The code base to facilitate reproduction of all experiments is publicly available at https://github.com/IBM/regression-transformer refs. 84,85,86,87,88,89,90,91.
References
Vaswani, A. et al. In Advances in Neural Information Processing Systems 30 (Eds Guyon, I. etal.) 5998–6008 (NIPS, 2017).
Schwaller, P. et al. Molecular transformer: a model for uncertainty-calibrated chemical reaction prediction. ACS Cent. Sci. 5, 1572–1583 (2019).
Schwaller, P. et al. Mapping the space of chemical reactions using attention-based neural networks. Nat. Mach. Intell. 3, 144–152 (2021).
Schwaller, P., Hoover, B., Reymond, Jean-Louis, Strobelt, H. & Laino, T. Extraction of organic chemistry grammar from unsupervised learning of chemical reactions. Sci. Adv. 7, eabe4166 (2021).
Rives, A. et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl Acad. Sci. USA 118, e2016239118 (2021).
Jumper, J. et al. Highly accurate protein structure prediction with alphafold. Nature 596, 583–589 (2021).
Krizhevsky, A., Sutskever, I. & Hinton, G. E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 25, 1097–1105 (2012).
Luong, M.-T., Pham, H. & Manning, C. D. Effective approaches to attention-based neural machine translation. In Proc. 2015 Conference on Empirical Methods in Natural Language Processing 1412–1421 (ACL, 2015).
Ramachandran, P. et al. Stand-alone self-attention in vision models. Adv. Neural Inf. Process. Syst. 32, 68–80 (2019).
Lu, K., Grover, A., Abbeel, P. & Mordatch, I. Frozen pretrained transformers as universal computation engines. In Proc. AAAI Conference on Artificial Intelligence 36, 7628–7636 (AAI Press, 2022).
Chen, L. et al. Decision transformer: reinforcement learning via sequence modeling. Adv. Neural Inf. Process. Syst. 34, 15084–15097 (2021).
Yang, Z. et al. Xlnet: Generalized autoregressive pretraining for language understanding. Adv. Neural Inf. Process. Syst., 32, 5753–5763 (2019).
Elton, D. C., Boukouvalas, Z., Fuge, M. D. & Chung, P. W. Deep learning for molecular design—a review of the state of the art. Mol. Syst. Des. Eng. 4, 828–849 (2019).
Chen, Z., Min, MartinRenqiang, Parthasarathy, S. & Ning, X. A deep generative model for molecule optimization via one fragment modification. Nat. Mach. Intell. 3, 1040–1049 (2021).
Wu, Z., Johnston, K. E., Arnold, F. H. & Yang, K. K. Protein sequence design with deep generative models. Curr. Opin. Chem. Biol. 65, 18–27 (2021).
Madani, A. et al. Large language models generate functional protein sequences across diverse families Nat. Biotechnol. (2023); https://doi.org/10.1038/s41587-022-01618-2
Wang, S., Guo, Y., Wang, Y., Sun, H. & Huang, J. Smiles-bert: large scale unsupervised pre-training for molecular property prediction. In Proc. 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics (Eds Shi, X.M. et al.) 429–436 (ACM, 2019).
Kim, H., Lee, J., Ahn, S. & Lee, J. R. A merged molecular representation learning for molecular properties prediction with a web-based service. Sci. Rep. 11, 1–9 (2021).
Mahmood, O., Mansimov, E., Bonneau, R. & Cho, K. Masked graph modeling for molecule generation. Nat. Commun. 12, 1–12 (2021).
Kotsias, P.-C. et al. Direct steering of de novo molecular generation with descriptor conditional recurrent neural networks. Nat. Mach. Intell. 2, 254–265 (2020).
Bagal, V., Aggarwal, R., Vinod, P. K. & Priyakumar, U. D. Molgpt: molecular generation using a transformer-decoder model. J. Chem. Inf. Model. 62, 2064–2076 (2021).
Irwin, R., Dimitriadis, S., He, J. & Bjerrum, E. J. Chemformer: a pre-trained transformer for computational chemistry. Mach. Learn. Sci. Technol. 3, 015022 (2021).
Lu, J. & Zhang, Y. Unified deep learning model for multitask reaction predictions with explanation. J. Chem. Inf. Model. 62, 1376–1387 (2022).
Méndez-Lucio, O., Baillif, B., Clevert, Djork-Arné, Rouquié, D. & Wichard, J. De novo generation of hit-like molecules from gene expression signatures using artificial intelligence. Nat. Commun. 11, 1–10 (2020).
Born, J. et al. Data-driven molecular design for discovery and synthesis of novel ligands: a case study on SARS-CoV-2. Mach. Learn. Sci. Technol. 2, 025024 (2021).
Gomez-Bombarelli, R. et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 4, 268–276 (2018).
Maziarz, K. et al. Learning to extend molecular scaffolds with structural motifs. In The Tenth International Conference on Learning Representations (ICLR, 2022).
Shi, C. et al. Graphaf: a flow-based autoregressive model for molecular graph generation. In 8th International Conference on Learning Representations (ICLR, 2020).
Jain, M. et al. Biological sequence design with gflownets. In International Conference on Machine Learning, pages 9786–9801 (PMLR, 2022).
Xu, M. et al. Geodiff: a geometric diffusion model for molecular conformation generation. In The Tenth International Conference on Learning Representations (ICLR, 2022).
Shen, C., Krenn, M., Eppel, S. & Aspuru-Guzik, A. Deep molecular dreaming: inverse machine learning for de-novo molecular design and interpretability with surjective representations. Mach. Learn. Sci. Technol. 2, 03LT02 (2021).
Fu, T. et al. Differentiable scaffolding tree for molecule optimization. In The Tenth International Conference on Learning Representations (ICLR, 2022).
Linder, J. & Seelig, G. Fast activation maximization for molecular sequence design. BMC Bioinformatics 22, 1–20 (2021).
Daulton, S. et al. Robust multi-objective Bayesian optimization under input noise. In International Conference on Machine Learning, ICML 2022, volume 162 of Proc. Machine Learning Research pages 4831–4866 (PMLR, 2022).
Yang, Z., Milas, K. A. & White, A. D. Now what sequence? Pre-trained ensembles for Bayesian optimization of protein sequences. Preprint at bioRxiv (2022); https://doi.org/10.1101/2022.08.05.502972
Khan, A. et al. Toward real-world automated antibody design with combinatorial Bayesian optimization. Cell Report Methods 3, 100374 (2023).
Devlin, J., Chang, M.-W., Lee, K. & Toutanova, K. BERT: pre-training of deep bidirectional transformers for language understanding. In Proc. 2019 Conference of the North American Chapter of the Association for Computational Linguistics pages 4171–4186 (ACL, 2019).
Bickerton, G. R., Paolini, G. V., Besnard, J. érémy, Muresan, S. & Hopkins, A. L. Quantifying the chemical beauty of drugs. Nat. Chem. 4, 90 (2012).
Wu, Z. et al. Moleculenet: a benchmark for molecular machine learning. Chem. Sci. 9, 513–530 (2018).
Krenn, M., Häse, F., Nigam, A. K., Friederich, P. & Aspuru-Guzik, A. Self-referencing embedded strings (SELFIES): a 100% robust molecular string representation. Mach. Learn. Sci. Technol. 1, 045024 (2020).
Rong, Y. et al. In Advances in Neural Information Processing Systems (Eds Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.-F. & Lin, H.-T.) 33 (2020).
Jin, W., Barzilay, R. & Jaakkola, T. Junction tree variational autoencoder for molecular graph generation. In International Conference on Machine Learning (Eds Dy, J. & Krause, A.) 2323–2332 (PMLR, 2018).
Rao, R. et al. In Advances in Neural Information Processing Systems (Eds Schölkopf, B. et al.) 9686–9698 (MIT Press, 2019).
Schwaller, P., Vaucher, A. C., Laino, T. & Reymond, J.-L. Prediction of chemical reaction yields using deep learning. Mach. Learn. Sci. Technol. 2, 015016 (2021).
Rogers, D. & Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Model. 50, 742–754 (2010).
Ertl, P. An algorithm to identify functional groups in organic molecules. J. Cheminform. 9, 1–7 (2017).
Vig, J. et al. Bertology meets biology: interpreting attention in protein language models. In 9th International Conference on Learning Representations (ICLR, 2021).
Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O. & Dahl, G. E. Neural message passing for quantum chemistry. In International Conference on Machine Learning (Eds Precup, D. & Tehpages, Y.W.) 1263–1272 (PMLR, 2017).
Fabian, B. et al. Molecular representation learning with language models and domain-relevant auxiliary tasks. Preprint at arXiv https://doi.org/10.48550/arXiv.2011.13230 (2020).
You, J., Liu, B., Ying, Z., Pande, V. & Leskovec, J. Graph convolutional policy network for goal-directed molecular graph generation. In Advances in Neural Information Processing Systems (Eds Bengio, S. & Wallach, H.M.) 6412–6422 (Curran Associates Inc., 2018).
Fan, Y. et al. Back translation for molecule generation. Bioinformatics 38, 1244–1251 (2022).
Zang, C. & Wang, F. Moflow: an invertible flow model for generating molecular graphs. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining pages 617–626 (Association for Computing Machinery, 2020).
Levenshtein, V. I. Binary codes capable of correcting deletions, insertions, and reversals. Sov. Phys. Doklady 10, 707–710 (1966).
Alley, E. C., Khimulya, G., Biswas, S., AlQuraishi, M. & Church, G. M. Unified rational protein engineering with sequence-based deep representation learning. Nat. Methods 16, 1315–1322 (2019).
Brandes, N., Ofer, D., Peleg, Y., Rappoport, N. & Linial, M. Proteinbert: a universal deep-learning model of protein sequence and function. Bioinformatics 38, 2102–2110 (2022).
Meier, J. et al. Language models enable zero-shot prediction of the effects of mutations on protein function. Adv. Neural Inf. Process. Syst. 34, 29287–29303 (2021).
Schwaller, P., Gaudin, T., Lanyi, D., Bekas, C. & Laino, T. Found in translation: predicting outcomes of complex organic chemistry reactions using neural sequence-to-sequence models. Chem. Sci. 9, 6091–6098 (2018).
Ahneman, D. T., Estrada, JesúsG., Lin, S., Dreher, S. D. & Doyle, A. G. Predicting reaction performance in C–N cross-coupling using machine learning. Science 360, 186–190 (2018).
Perera, D. et al. A platform for automated nanomole-scale reaction screening and micromole-scale synthesis in flow. Science 359, 429–434 (2018).
Park, N. et al. An extensible platform for enabling artificial intelligence guided design of catalysts and materials. Preprint at ChemRxiv https://doi.org/10.26434/chemrxiv-2022-811rl-v2 (2022). In Revision at Nature Communications
Raffel, C. et al. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 21, 1–67 (2020).
Song, K., Tan, X., Qin, T., Lu, J. & Liu, T.-Y. MPNet: Masked and Permuted Pre-training for Language Understanding. In Advances in Neural Information Processing Systems 33 (Eds Larochelle, H. et al.) (NeruIPS, 2020).
Fried, D. et al. Incoder: a generative model for code infilling and synthesis. Preprint at arXiv https://doi.org/10.48550/arXiv.2204.05999 (2022).
Bavarian, M. et al. Efficient training of language models to fill in the middle. Preprint at arXiv https://doi.org/10.48550/arXiv.2207.14255 (2022).
Sanh, V. et al. Multitask prompted training enables zero-shot task generalization. In International Conference on Learning Representations (OpenReview.net, 2022).
Lu, K., Grover, A., Abbeel, P. & Mordatch, I. Pretrained transformers as universal computation engines. In Proc. of the Thirty-Sixth AAAI Conference on Artificial Intelligence (AAAI-22) 7628–7636 (AAAI Press, 2022); (https://ojs.aaai.org/index.php/AAAI/article/view/20729/20488
Brown, Tom et al. In Advances in Neural Information Processing Systems Vol. 33, (Eds Schölkopf, B. et al.) 1877–1901 (MIT Press, 2020).
Van Oord, A., Kalchbrenner, N. & Kavukcuoglu, K. Pixel recurrent neural networks. In International Conference on Machine Learning (Eds Balcan, M.F. & Weinberger, K.Q.) 1747–1756 (PMLR, 2016).
Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 28, 31–36 (1988).
Wolf, T. et al. Transformers: state-of-the-art natural language processing. In Proc. 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations pages 38–45 (Association for Computational Linguistics, 2020).
Paszke, A. et al. Pytorch: an imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 32, 8026–8037 (2019).
Mendez, D. et al. Chembl: towards direct deposition of bioassay data. Nucleic Acids Res. 47, D930–D940 (2019).
Bjerrum, E. J. SMILES enumeration as data augmentation for neural network modeling of molecules. Preprint at arXiv https://doi.org/10.48550/arXiv.1703.07076 (2017).
Kusner, M. J, Paige, B. & Hernández-Lobato, J. M. Grammar variational autoencoder. In Proc. 34th International Conference on Machine Learning Vol. 70, 1945–1954 (JMLR, 2017).
Boman, H. G. Antibacterial peptides: basic facts and emerging concepts. J. Intern. Med. 254, 197–215 (2003).
The UniProt Consortium. UniProt: the universal protein knowledgebase in 2021. Nucleic Acids Res. 49, D480–D489 (2020).
Sarkisyan, K. S. et al. Local fitness landscape of the green fluorescent protein. Nature 533, 397 (2016).
Rocklin, G. J. et al. Global analysis of protein folding using massively parallel design, synthesis, and testing. Science 357, 168–175 (2017).
Lowe, D. Chemical reactions from US patents (1976-Sep2016). Figshare https://figshare.com/articles/dataset/Chemical_reactions_from_US_patents_1976-Sep2016_/5104873 (2017)
Sandfort, F., Strieth-Kalthoff, F., Kühnemund, M., Beecks, C. & Glorius, F. A structure-based platform for predicting chemical reactivity. Chem 6, 1379–1390 (2020).
Tanimoto, T. T. Elementary Mathematical Theory of Classification and Prediction (International Business Machines Corp., 1958).
Manica, M. et al. GT4SD: Generative toolkit for scientific discovery. GitHub https://github.com/GT4SD/gt4sd-core (2022).
Abid, A. et al. Gradio: hassle-free sharing and testing of ML models in the wild. Preprint at arXiv https://doi.org/10.48550/arXiv.1906.02569 (2019).
Born, J. & Manica, M. Regression transformer repository. Zenodo https://doi.org/10.5281/zenodo.7639206 (2023).
He, P., Liu, X., Gao, J. & Chen, W. Deberta: decoding-enhanced bert with disentangled attention. In 9th International Conference on Learning Representations (ICLR, 2021).
Dai, Z. et al. Transformer-xl: attentive language models beyond a fixed-length context. In Proc. 57th Annual Meeting of the Association for Computational Linguistics. 2978–2988 (Association for Computational Linguistics, 2019).
Bai, H. et al. Segatron: segment-aware transformer for language modeling and understanding. In Proc. AAAI Conference on Artificial Intelligence Vol. 35, 12526–12534 (AAAI Press, 2021).
Wang, Y.-A. & Chen, Y.-N. What do position embeddings learn? An empirical study of pre-trained language model positional encoding. In Proc. of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP) 6840–6849 (Association for Computational Linguistics, 2020).
Zhang, J., Mercado, Rocío, Engkvist, O. & Chen, H. Comparative study of deep generative models on chemical space coverage. J. Chem. Inf. Model. 61, 2572–2581 (2021).
Bemis, G. W. & Murcko, M. A. The properties of known drugs. 1. Molecular frameworks. J. Med. Chem. 39, 2887–2893 (1996).
Vig, J. A multiscale visualization of attention in the transformer model. In Proc. 57th Annual Meeting of the Association for Computational Linguistics: System Demonstrations pages 37–42 (Association for Computational Linguistics, 2019).
Acknowledgements
The authors thank the entire AI for Scientific Discovery Group at IBM and particularly C. Baldassari and A. Leonov for useful discussions on reaction chemistry. The authors especially thank E. J. Bjerrum but also the anonymous reviewers for their constructive and valuable feedback that helped improving the article tremendously.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Author information
Authors and Affiliations
Contributions
J.B. and M.M. conceived the initial idea for the project, set the scope of experiments and wrote the code base as well as the manuscript. J.B. further trained the models, performed the experiments, analysed the results, created the visualizations and devised the alternating training scheme with SC loss.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Machine Intelligence thanks Esben Jannik Bjerrum and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Workflow of the Regression Transformer (RT) model.
Based on the XLNet backbone, the RT is a dichotomous model designed to handle combinations of text and numbers. Top: An input sequence consisting of a molecular string (red) and two property tags (blue), each associated to a floating value (green). Numbers are tokenized into a sequence of tokens that preserve the decimal order of each character. The pipe (∣) is a separator token distinguishing numerical and text tokens. Middle: We propose numerical encodings that inform the model about the semantic proximity of these tokens and naturally integrate with relative positional encodings and classical learned embeddings. The RT relies on a XLNet backbone and follows permutation language modeling (PLM). Bottom: Multiple training objectives are proposed and combined (predicted tokens are emphasized in the figure). Following the vanilla PLM objective 12, masking occurs randomly throughout the sequence. In the property objective, masking occurs exclusively on the property tokens. In the generation objective, masking occurs exclusively on the textual tokens (here: SMILES). This objective can be augmented with a self-consistency term LSC that exploits the dichotomoy of the model. In practice, we use an alternating training scheme designed to concurrently excel at property prediction and conditional generation tasks. Note that the RT builds upon an XLNet-backbone which samples a token factorization order (following PML as proposed by Yang et al. 12; not shown). The dots indicate that the RT naturally scales to multiple property tags.
Extended Data Fig. 2 More distant queries are harder to decorate.
When gradually increasing task difficulty (that is, the distance between the QED of the seed molecule and the primed property), the distance between the QED of the generated molecule and the primed property increases linearly. Data presented as means, error bars denote 95% confidence intervals. For the blue, orange and green bars, a total of 880k, 239k and 207k generated molecules are evaluated respectively.
Extended Data Fig. 3 Learned embeddings of numerical tokens.
Left: For an exemplary dimension, embeddings for 20 tokens, corresponding to 10 digits and 2 decimal places are shown. Right: Embeddings for 20 exemplary dimensions across all ten digits. The stars indicate the significance level of the Pearson correlation. The analysis is based on a SELFIES model without any NEs (PLM objective).
Extended Data Fig. 4 Discovering novel, more effective reactions by adapting an unseen Buchwald-Hartwig amination.
Below an unseen BH amination (top) and its experimentally reported yield, we show four RT-generated reactions that selectively replace individual precursors. Upon priming the RT with a higher yield and a given precursor type, the RT generated reactions with higher yield, as predicted by the RT. The RXN confidence stems from the forward reaction prediction model by Schwaller et al. 2 which confirmed that the reaction would result in the shown product in all cases. Note that no adaptations of 4-Methylaniline and the Palladium-catalyst are generated since they are constanta cross the dataset.
Extended Data Fig. 5 Float-based numerical encodings.
a) Numerical encodings for an molecule with a QED of 0.179. b) Pairwise distances of numerical encodings for floats between 0 and 100 (the NEs of all tokens associated to a float are summed up).
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Born, J., Manica, M. Regression Transformer enables concurrent sequence regression and generation for molecular language modelling. Nat Mach Intell 5, 432–444 (2023). https://doi.org/10.1038/s42256-023-00639-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-023-00639-z