Geometric renormalization of weighted networks

Abstract

The geometric renormalization technique for complex networks has successfully revealed the multiscale self-similarity of real network topologies and can be applied to generate replicas at different length scales. Here, we extend the geometric renormalization framework to weighted networks, where the intensities of the interactions play a crucial role in their structural organization and function. Our findings demonstrate that the weighted organization of real networks exhibits multiscale self-similarity under a renormalization protocol that selects the connections with the maximum weight across increasingly longer length scales. We present a theory that elucidates this symmetry, and that sustains the selection of the maximum weight as a meaningful procedure. Based on our results, scaled-down replicas of weighted networks can be straightforwardly derived, facilitating the investigation of various size-dependent phenomena in downstream applications.

Introduction

Renormalization of real networks^1,2,3,4 can be performed on a geometric framework¹ by virtue of the discovery that the structure of complex networks is underlain by a latent hyperbolic geometry^5,6. The likelihood of interactions between nodes depends on their distances in the underlying space via a universal connectivity law that operates at all scales and simultaneously encodes short- and long-range connections. This geometric principle has been able to explain many features of the structure of real networks, including the small-world property, scale-free degree distributions, and clustering, as well as fundamental mechanisms such as preferential attachment in growing networks⁷ and the emergence of communities^8,9. It has also led to embedding techniques that produce a geometric representation of a complex network from its topologies^{10,11,12,13,14}.

Given a network map, geometric renormalization (GR) applies coarse-graining and rescaling steps on the topology of a network to produce a multiscale unfolding over progressively longer length scales¹. This transformation has revealed multiscale self-similarity to be a ubiquitous symmetry in the binarized structure of real networks, and allows to obtain scaled down replicas. However, the GR technique is restricted to unweighted network representations. Information about the intensities of interactions in networks can fundamentally change the picture that emerges from the bare connections^{15,16,17,18,19}. This poses the question of whether the GR methodology could be generalized to explore weighted networks at different resolutions, and whether their weighted structure is self-similarly preserved in that case.

Adding to GR on the grounds of our previous finding that the binarized structure of real networks is statistically self-similar when renormalized¹, the geometric renormalization of weights (GRW) should produce the multiscale unfolding of a network into a shell of scaled-down layers that preserves not only the binarized structure but also the weighted structure of the network in the renormalization flow. Here, we propose a theory for the renormalization of weighted networks that supports the selection of the maximum, or supreme, as an effective approximation to allocate weights in the renormalized layers of real networks. Our theory is sustained by the renormalizability of the W${{\mathbb{S}}}^{D}$ model²⁰, which entails that the GRW transformation should be a rescaled p-norm on the set of weights to be renormalized. Alternatively, the GR technique was recently extended to weighted networks using an ad hoc approach that treats weights as currents or resistances in a parallel circuit—renormalizing by the sum of the weights or by the inverse of the sum of their inverses, respectively²¹. The two methods are recovered as particular limits of our theory.

In this work, we present empirical evidence and a theoretical framework that supports the self-similar organization of weights in real networks when they are viewed at progressively longer length scales. We used three renormalization approaches: sup-GRW, that allocates the weight of new links in the renormalized layer by selecting the maximum weight of the renormalized links; ϕ-GRW, the geometric renormalization transformation for the weights in the W${{\mathbb{S}}}^{D}$ model, obtained by imposing the preservation of the relation between the strength and degree of nodes in the renormalization flow; and sum-GRW, the summation approach recently introduced in ref. ²¹. We found that, in practice, sup-GRW is a good approximation that presents some advantages over the theoretical ϕ-GRW approach, while sum-GRW only works under limited conditions. In addition, we leveraged the multiscale self-similarity of weighted networks to introduce a protocol that generates scaled down replicas.

Results

Evidence of geometric scaling in the weighted structure of real networks

First, we present evidence that weights in real networks show geometric scaling when conveniently coarse-grained and rescaled to produce renormalized versions. The technique assumes that real network topologies are well described by the geometric soft configuration model ${{\mathbb{S}}}^{1}$²², where each network node i has popularity κ_i and similarity θ_i coordinates. Popularities are hidden degrees that control expected degrees k in the network, and similarities are angular coordinates in a 1-sphere. Equivalently, the ${{\mathbb{S}}}^{1}$ model is isomorphic to a purely geometric model, the ${{\mathbb{H}}}^{2}$ model, where both the popularity and similarity attributes are encoded into the hyperbolic plane²³. In this representation, nodes reside in the hyperbolic plane where the popularity coordinate determines the radial position whereas the similarity (or angular) coordinate remains the same. In the ${{\mathbb{S}}}^{1}$ model, pairs of nodes are connected by a Fermi-like probability function, which is also gravity-like. This function grows with the product of popularities and decreases with the distance between the nodes in the latent similarity space. Real networks can be embedded in the latent space by employing statistical inference techniques to identify the coordinates of the nodes that maximize the likelihood that the topology of the network is reproduced by the model^10,14. These hyperbolic embeddings can be obtained using the mapping tool Mercator¹⁴.

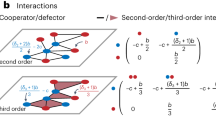
Once the geometric map of a real network has been produced and nodes have associated coordinates in the latent space, the GRW transformation proceeds in two steps. Figure 1 illustrates the process. First, we zoom out the resolution of the network by increasing the length scale at which it is observed by applying the GR technique for unweighted networks defined in ref. ¹. GR proceeds by defining non-overlapping consecutive blocks, or sectors, along the similarity circle of the network embedding. Each sector contains r consecutive nodes, independently of whether these nodes are connected. Given the distribution of nodes across the similarity space, sectors could exhibit varying angular spans. Sectors are then coarse-grained to form supernodes. The specific angular position of each supernode is not relevant as far as it lays within the angular region defined by the corresponding block so that the order of supernodes preserves the original order of nodes. Finally, two supernodes are connected if there is at least one connection between the nodes in one supernode and the nodes in the other so that, in general, several connections are renormalized into a single link between the two supernodes. In this way, GR produces a reduced self-similar version of the topology of the network. When applied iteratively (bounded to order $\log (N)$ steps due to the finite size of real networks), the transformation selects longer range connections in a progressive fashion, and the average degree becomes a relevant observable that grows in the renormalization flow¹. The GR transformation is valid for uneven supernode sizes as well.

Fig. 1: Geometric renormalization of weights (GRW).

Each layer is obtained after a GRW step with resolution r starting from the original network in l = 0. Each node i in red is placed at an angular position on the similarity circle and has a size proportional to the logarithm of its hidden degree. Straight solid lines represent the links in each layer with weights denoted by their thickness. Coarse-graining blocks correspond to the blue shadowed areas, and dashed lines connect nodes to their supernodes in layer l + 1. Two supernodes in layer l + 1 are connected if and only if some node of one supernode in layer l is connected to some node of the other, with the supremum among the weights of links between the constituent nodes as the weight of the new connection (dark blue links give an example). The GRW transformation has semigroup structure with respect to the composition. In the figure, the transformation with r = 4 goes from l = 0 to l = 2 in a single step.

The second step in GRW proceeds by assigning intensities to the links in the renormalized layer as a function of the weights in the original layer. To define weights in the renormalized layer, different prescriptions are possible. First, we define the weight of the link between two supernodes as the maximum, or supremum, of the weights among the existing links between their constituent nodes in the original layer. We name this prescription sup-GRW. The whole operation can be iterated starting from the original network at layer l = 0 and the set of sup-GRW network layers l—each r times smaller than the original one—forms a multiscale weighted shell of the original network.

We applied the sup-GRW technique with r = 2 to 12 different real weighted networks with heterogeneous degree distributions from very different domains, including biology, transportation, knowledge, and social systems. More details of the datasets are available in “Methods” and the main statistical properties are in Supplementary Table 1 in Supplementary Note 1. The features that characterize the weighted structure of two of the renormalized weighted networks are shown in Fig. 2 (see Supplementary Figs. 1–4 for the rest in Supplementary Notes 2 and 3.1, where we report the topological and weighted features of the real networks along the renormalization flow). Apart from the weights associated to the links, w_ij, we also considered the strength of nodes (sum of the weights of incident links), s_i = ∑_jω_ij, and the disparity, Y_i, which quantifies the local heterogeneity of the weights by measuring their variability in the links attached to a given node (see “Methods”). The complementary cumulative distribution functions of weights, P_c(ω), in Fig. 2a, i, and strengths, P_c(s), in Fig. 2b, j display heterogeneity and show self-similar behavior across layers l, meaning that the curves collapse once weights and strengths are rescaled by the average weight and by the average strength, respectively, in the corresponding layer. The power-law relations between strength and degree, s(k), in Fig. 2c, k also overlap once the degrees are rescaled by the average degree of the layer. We also show the disparity of the weights averaged over degree classes, Y(k), in Fig. 2d, l. This function shows a downward trend as a function of the degree and again remains statistically invariant across layers. Notice that, by construction, the average weight in the sup-GRW layers grows with l. While this behavior does not add fundamental information to characterize the description of the weighted structure of the network, it may still be interesting to know how 〈w〉(l) depends on the scale of observation l for some specific system, given that weights may be given in some real-world units (see Supplementary Figs. 5 and 6 for the rescaled and unrescaled flows of 〈w〉 and 〈s〉).

Fig. 2: Self-similarity of the geometric renormalization of weights (GRW) in real networks.

The complementary cumulative distribution functions of weights and strengths, the relation between strength and degree, and the disparity of weights in nodes are shown in (a–d) for sup-GRW and in (e–h) for sum-GRW of the Openfligts network. The same measures are in (i–l) for sup-GRW and in (m–p) for sum-GRW of the Collaboration network. The variables w_res, s_res, and k_res refer to the weights, strengths, and degrees k rescaled by the average weight, average strength, and average degree in the layer, respectively. The weighted renormalization scheme, sup-GRW, selects the weight of the link between two supernodes as the maximum, or supremum, of the weights among the existing links between their constituent nodes in the original layer. Alternatively, in the sum-GRW scheme, weights in the new layer are assigned by summing the weights of existing links between the nodes in supernodes. The number of layers in each system is determined by their original size, and r = 2 in all cases.

Note that the sup-GRW transformation has semigroup structure with respect to the composition, as fulfilled by GR in the unweighted case, meaning that a certain number of iterations with a given coarse-graining factor are equivalent to a single transformation with a higher coarse-graining factor (see Supplementary Fig. 7 in Supplementary Note 3.2 for results supporting this claim).

We also tested an alternative prescription, referred as sum-GRW, where weights in the new layer are assigned by summing the weights of existing links between the nodes in supernodes, following the prescription described in ref. ²¹. While this strategy proves effective for many real networks, there are certain cases in which self-similarity is not maintained in the renormalization flow. When sum-GRW is applied, the global distribution of weights, the local heterogeneity of weights in nodes, and the relation between strength and degree become increasingly heterogeneous compared to the original graph. This is observed in the Openflights and the scientific collaboration network, as illustrated in Fig. 2e–h, m–p (see Supplementary Figs. 8 and 9 in Supplementary Note 4 for the rest).

Geometric renormalization of the weighted geometric soft configuration model

We develop next the theoretical backup that predicts the obtained results and clarifies in which situations each of the two approaches works well, either selecting the supremum of the weights between supernodes or their sum.

Geometric renormalization transformation for the weights

The renormalization theory that allows to fully appreciate the observed self-similarity is based on the W${{\mathbb{S}}}^{D}$ model²⁰, which extends the geometric interpretation of real networks to the weighted organization. The W${{\mathbb{S}}}^{D}$ model couples the weights of a network to the same underlying metric space to which the topology is coupled in the ${{\mathbb{S}}}^{D}$ model, the generalization of the ${{\mathbb{S}}}^{1}$ model to D dimensions²².

As in the ${{\mathbb{S}}}^{1}$ model, in the ${{\mathbb{S}}}^{D}$ model the coordinates of the nodes in the latent space represent popularity and similarity dimensions and distances between nodes determine the probability of connection, that reads ${p}_{ij}=1/(1+{\chi }_{ij}^{\beta })$, where ${\chi }_{ij}={d}_{ij}/{(\mu {\kappa }_{i}{\kappa }_{j})}^{1/D}$, d_ij is the distance in ${{\mathbb{S}}}^{D}$ between nodes i and j, μ controls the average degree, β > D controls the clustering of the network ensemble and quantifies the level of coupling between the network topology and the metric space, and D is the dimensionality of the similarity space. The popularity dimension of node i is associated with its hidden degree κ_i such that higher hidden degree nodes have more chance to connect to others. The hidden degree is proportional to the expected degree, and it is equivalent to a radial coordinate in the purely geometric formulation of the model, the ${{\mathbb{H}}}^{D+1}$ model²³.

The embedding tool Mercator¹⁴ generates the real network embeddings based on the model in D = 1, where the similarity space is represented as a one-dimensional sphere or circle of radius R = N/(2π), so that the density of nodes is set to one. Every node i has an angular coordinate θ_i in the circle, and angular distances d_ij = RΔθ_ij between pairs of nodes stand for all factors other than degrees that affect the propensity of forming connections, such that nodes closer in the similarity space have a higher likelihood of being connected.

In the W${{\mathbb{S}}}^{D}$ model, weights are assigned on top of the topology generated by the ${{\mathbb{S}}}^{D}$ model. The weight between two connected nodes i and j is given by:

$${\omega }_{ij}={\epsilon }_{ij}\frac{\nu {\sigma }_{i}{\sigma }_{j}}{{\left({\kappa }_{i}{\kappa }_{j}\right)}^{1-\alpha /D}{d}_{ij}^{\alpha }}.$$

(1)

The hidden variable σ_i is named the hidden strength and it is related to the observed strength of node i, that is, the form of Eq. (1) and the convenient selection of the free parameter ν guarantees that the expected strength of node i in the generated networks, ${\bar{s}}_{i}$, is proportional to σ_i, ${\bar{s}}_{i}\propto {\sigma }_{i}$, in the same way as ${\bar{k}}_{i}\propto {\kappa }_{i}$ is guaranteed in the ${{\mathbb{S}}}^{D}$ model. The distance d_ij refers to the distance between the nodes in the similarity space, and 0 ⩽ α < D is the coupling of the weighted structure to the metric space such that if α = 0 weights are independent of the underlying geometry and maximally dependent on degrees, while α = D implies that weights are maximally coupled to the underlying metric space with no direct contribution of the degrees. Finally, ϵ_ij is a random variable with mean equal to one and the variance of which regulates the level of noise in the network. Further on, we will assume the noiseless version of the model to simplify analytical calculations, that is, ϵ_ij = 1  ∀ (i, j).

To control the correlation between strength and degree, which fixes the strength distribution, we assume a deterministic relation between hidden variables σ and κ of the form σ = aκ^η, yielding s(k) ~ ak^η as observed in real complex networks. Working under this assumption, a valid GRW transformation should preserve the relation between strength and degree, and in particular the exponent η, meaning that the renormalized hidden degree and strength should satisfy ${\sigma }^{{\prime} }={a}^{{\prime} }{({\kappa }^{{\prime} })}^{\eta }$ (to simplify notation, we have used prima to denote quantities in the renormalized layer).

To find this transformation, the geometric renormalization equations for the topology have to be combined with Eq. (1). From (1), the coordinates of supernodes ${\kappa }^{{\prime} }$ and ${\theta }^{{\prime} }$ in the renormalized map are:

$${\kappa }^{{\prime} }={\left[\mathop{\sum }\limits_{j = 1}^{r}{({\kappa }_{j})}^{\beta }\right]}^{1/\beta }\quad \,{{\mbox{and}}}\,\quad {\theta }^{{\prime} }={\left[\frac{\mathop{\sum }\nolimits_{j = 1}^{r}{({\theta }_{j}{\kappa }_{j})}^{\beta }}{\mathop{\sum }\nolimits_{j = 1}^{r}{({\kappa }_{j})}^{\beta }}\right]}^{1/\beta },$$

(2)

where the sums run over the r nodes that are coarse-grained to form the supernodes. Global parameters need to be rescaled as ${\mu }^{{\prime} }=\mu /r$, ${\beta }^{{\prime} }=\beta$, and ${R}^{{\prime} }=R/r$. By imposing the preservation of the relationship between strength and degree, and using Eq. (1), we obtain the following expression for the renormalized weights (see derivation in “Methods”):

$${\omega }_{ij}^{{\prime} }=C{\left[\mathop{\sum }\limits_{e = 1}^{{r}^{2}}{\left({w}_{mn}\right)}_{e}^{\phi }\right]}^{1/\phi },$$

(3)

where the sum runs over the links between nodes within supernodes i and j. The new variable $\phi \equiv \frac{\beta }{D(\eta -1)+\alpha }$ is a parameter that depends on the weighted and unweighted structure of the network, and $C=\frac{{\nu }^{{\prime} }}{\nu }{\left(\frac{{a}^{{\prime} }}{a}\right)}^{2}{r}^{\alpha /D}$. In practice, however, we rescale weights by the average weight in each layer, as explained above, so constant C plays no role. Notice that Eq. (3) is a p-norm (also related with a generalized mean), where p = ϕ. Therefore, the weighted model predicts that, given a network with a specific value of ϕ, the GRW transformation of weights Eq. (3), that we name ϕ-GRW, preserves the exponent η characterizing the relation between strength and degree. At the same time, since the distribution of hidden degrees is assumed to be preserved by GR, the distribution of hidden strengths and the distribution of weights are also preserved. This is valid as long as β > (γ − 1)/2. Otherwise, the power-law distribution of hidden degrees loses its self-similarity in the unweighted renormalization flow and this breaks the self-similarity of the statistical properties of the binarized network and the weighted counterpart. Also, note that the ϕ-GRW transformation has semigroup structure with respect to the composition for any value of ϕ, as also fulfilled by sum-GRW.

We validated our theoretical results for ϕ − GRW in the real networks analyzed in this work (Supplementary Figs. 10 and 11 in Supplementary Note 5.1). For all the networks, we estimated the exponent η and the parameter a that controls the coupling between strengths and degrees by adjusting a power-law to the empirical data. The coupling constant α and the level of noise were inferred by using the triangle inequality violation spectrum as described in ref. ²⁰. See Supplementary Table 1, where we report the specific values for each network.

We also checked ϕ − GRW, including its semigroup structure property, in synthetic networks with a scale-free degree distribution and realistic values of clustering, results are shown in Supplementary Figs. 12–16 in Supplementary Note 5.2. The synthetic networks were produced with the W${{\mathbb{S}}}^{1}$ model for different values of α and η obtaining, thus, different values of ϕ, which were calculated using the parameters employed to generate the networks.

For all the real and synthetic networks, we measured the distributions of weights and strengths, and the power-law relation between strength and degrees in the multiscale unfoldings obtained by applying ϕ − GRW (see Supplementary Figs. 10–16). In all cases, the self-similar behavior is clear across length scales, which validates our analytic calculations.

Flow of the average strength

The preservation of the relation σ = aκ^η allows us to approximate analytically the flow of the average strength from the flow of the average degree. In GR, the average degree changes from layer to layer approximately as 〈k〉^(l+1) = r^ξ〈k〉^(l), with a scaling factor ξ depending on the connectivity structure of the original network¹. Combining this with Eq. (3) and imposing that the rescaling constant of weights C does not change in the flow, we obtain:

$$\langle {\sigma }^{{\prime} }\rangle =\langle \sigma \rangle {r}^{\psi },\psi =\left(\frac{\alpha }{D}+2\eta -1\right)\xi -\frac{\alpha }{D},$$

(4)

which, due to the proportionality between observed and hidden strength, implies that the flow of the average observed strength follows the same scaling. Therefore, in D = 1, the strength increases with a factor that depends on the exponent η characterizing the scaling between strength and degree, the coupling α between topology and geometry, and the scaling factor ξ for the flow of the average degree, see the “Theoretical derivation of the renormalized weights” in “Methods” for details. As shown in Fig. 3, the analytic approximation for the relative growth of the average strength as a function of the average degree can be expressed as follows:

$${\langle s\rangle }^{(l)}={\langle s\rangle }^{(0)}{\left(\frac{{\langle k\rangle }^{(l)}}{{\langle s\rangle }^{(0)}}\right)}^{\frac{\psi }{\xi }},$$

(5)

which agrees with the measurements in synthetic networks where the average weight may increase, stay flat, or decrease in the flow.

Fig. 3: Analytic approximation vs. simulations.

a Unrescaled average weight for different layers l. b Average strength, 〈s〉 as a function of average degree 〈k〉, in which symbols are the simulated results and lines indicate the corresponding theoretical analysis from Eq. (5). The synthetic networks are generated with γ = 2.7, β = 1.5, α = 0.4 and η = 1.2 for Net 0; γ = 2.7, β = 1.5, α = 0.4 and η = 1.8 for Net 1; γ = 2.2, β = 2.0, α = 0.4 and η = 1.5 for Net 2; γ = 2.2, β = 2.0, α = 0.6 and η = 1.5 for Net 3. The other parameters are fixed as N = 64,000, 〈k〉 = 5, a = 100 and 〈ϵ²〉 = 1.0. Error bars representing the standard error of the estimated averages are smaller than the symbol size.

Reconciling sup-GRW and ϕ − GRW

Notice that the transformation in Eq. (3) is a ϕ-norm, a generalization of the Euclidean norm that becomes progressively dominated by the supremum of the (absolute values of the) terms w_mn in Eq. (3) as ϕ increases. In fact, the sup-GRW prescription is recovered in the limit ϕ = ∞ of ϕ-GRW. In addition, renormalizing by the sum is equivalent to setting ϕ = 1, and the renormalization of weights by the inverse of the sum of inverse values corresponds to ϕ = −1.

To clarify the efficacy of approximating ϕ − GRW as sup-GRW, we checked the asymptotic behavior of the ϕ-norm as a function of the number of elements E in the set {ω_mn} and of the level of heterogeneity in the weights (see Supplementary Note 6 for more details). We simulated weights using a distribution $p({\omega }_{mn}) \sim {\omega }_{mn}^{-\delta }$, where exponent δ allowed us to tune the level of heterogeneity, and produced sets of weights that were renormalized using Eq. (3) with C = 1 and different values of ϕ. We also renormalized the same sets using the alternative sum and supremum prescriptions, the results are shown in Supplementary Figs. 17 and 18 of Supplementary Note 6.1. In Fig. 4, we display the result of applying the supremum or the sum prescriptions as compared with the renormalized weight calculated for different values of ϕ using the distributions of weights in two of the real networks analyzed in this paper, see Supplementary Figs. 19 and 20 in Supplementary Note 6.2 for the rest.

Fig. 4: Asymptotics of the ϕ-norm in the geometric renormalization of weights (GRW).

The renormalized weight ${\omega }^{{\prime} }(\phi =1)$ and ${\omega }^{{\prime} }(\phi =\infty )$ versus ${\omega }^{{\prime} }({\phi }^{* })$, where ϕ^* is the inferred value ϕ^* = β/(η − 1 + α), for different number of links E between the constituent nodes of two supernodes are displayed in (a–c) for Openflights and in (d–f) for Collaboration. Note that when r = 2, the number of links E can have values 1, 2, 3 or 4, and that sum-GRW corresponds to the case ϕ = 1 while sup-GRW to ϕ = ∞. We used the sets {ω_mn} following the coarse-graining in the real network, and performed an iteration of ϕ − GRW to calculate the renormalized weight ${\omega }^{{\prime} }$ with Eq. (3).

In heterogeneous networks with a markedly scale-free character of the weight distribution, very small deviation from the supremum are observed only for very low values of ϕ and only for low values of the weights. As E becomes larger and the degree distribution becomes more homogeneous the deviations increase progressively. As expected, increasing values of ϕ decrease the divergence between the ϕ-norm and the supremum estimator. In any case, good agreement is found between the ϕ-norm and the selection of the supremum in a wide range of parameter values that include those for realistic networks and the deviation, when existing, is in general very mild. The curves for ϕ = 1 lying on the diagonal means that sup-GRW and sum-GRW lead to the same renormalized weights (for instance the JCN in Supplementary Figs. 19 and 20). This happens for some empirical weight distributions, which explains why there is no difference between sum-GRW and sup-GRW in some cases. However, in general the relation between hidden strength and hidden degree is not preserved under sum-GRW. See Methods for more details.

Finally, the random protocol for the selection of the weight between two supernodes would always result in self-similarity of the distribution of weights if links between nodes in the same supernode were also taken into account in the selection set, independently of the topological and weighted features of the network. However, those interactions are coarse-grained and the balance between the weights in links between nodes inside supernodes and in links between nodes in different supernodes, which determine the selection set, dictates in which situations the random selection works. Experiments in synthetic networks, Supplementary Figs. 21 and 22 in Supplementary Note 7.1, prove that heterogeneity in the distribution of weights, as found in many real networks, favors a better self-similar scaling of their distribution. Decreasing the coupling of weights with topology and geometry in the W${{\mathbb{S}}}^{D}$ model produces more homogeneous distributions of weights, which causes the loss of self-similarity in the flow. In E. coli, the distribution of weights is affected under the random prescription, see Supplementary Fig. 23 in Supplementary Note 7.2.

All together, the results imply that sup-GRW is a good approximation that presents some advantages over ϕ-GRW, like avoiding the estimation of parameters for the coupling between the weighted structure of the network and the underlying geometry which, in practice, is difficult to estimate.

In summary, renormalizing weights simply by the supremum is a good and convenient approximation for real networks. It is equivalent to setting ϕ = ∞ and due to the nature of the transformation it is effectively reached for relatively low values of ϕ. In addition, renormalizing by the sum is equivalent to setting ϕ = 1, which in general does not preserve the exponent η of the relation between σ and κ (see “Methods” for analytical calculations), and the same is valid for renormalizing weights by the inverse of the sum of inverse values, recovered when ϕ = −1.

Scaled down replicas of weighted networks

From the practical point of view, scaled down replicas of weighted networks are straightforwardly derived from the results with sup-GRW. The generation of a scaled-down replica involves obtaining a reduced version of the topology, as described in ref. ¹, and subsequently rescaling the weights in the renormalized network layer to match the level of the original network. The detailed procedure can be found in scale down replicas in Methods, and the results for the scaled-down replicas of real weighted networks are presented in Supplementary Figs. 24–27 in Supplementary Note 8.

Discussion

One of the big questions in science, and particularly important for the comprehension of complex systems, is to understand which are the scales relevant to a given phenomenon and how these scales are interrelated. The geometric renormalization of complex networks provides a powerful framework to disentangle the intricacy of length scales in their structure by progressively selecting longer range connections, and uncovers self-similarity as a ubiquitous symmetry in the multiscale organization of real networks. The generalization of the renormalization framework to weighted networks introduced in this manuscript proves that the multiscale self-similarity is still preserved in a wide variety of weighted real networks if the proper renormalization scheme is applied. In addition, weights are the result of processes determining the intensities of interactions and the self-similarity found in the weighted structure of real networks suggest that the same laws rule those processes at different length scales.

We offer here an effective explanation for the self-similar behavior observed in the real networks analyzed in this work based on two keystones: the goodness of the W${{\mathbb{S}}}^{D}$ model to reproduce the organization of real weighted networks, and its renormalizability under the ϕ-GRW transformation of weights, that preserves the relation between strength and degree across scales. Estimating the value of parameter ϕ in practice is, however, complicated and we have proved that using instead the sum-GRW prescription, which selects the maximum weight among the renormalizable links, is a very good and manageable approximation.

The weighted renormalization technique is, thus, well grounded on theoretical results that assume that weights display no noise. In general, this is not the case in real networks. In any case, it is remarkable that the transformation suggested by the models is approximated with high fidelity by connecting supernodes using the maximum weight between nodes belonging to them, an extremely simple transformation easily applicable to real networks despite the large levels of noise that they display. This justifies our view that noise will not change qualitatively the results reported here and the study of its role can be postponed for future work.

Beyond theoretical considerations, scaled down replicas of weighted networks can be straightforwardly produced using our weighted renormalization framework. These replicas could be used as testbeds for the scalability of expensive computational protocols or to study any process in which the scale or the size of real networks have a role, including for example finite size scaling analysis in phase transitions or size-dependent stochastic resonance phenomena. The generalization of the geometric branching growth model²⁴—that reverses GR to explain the self-similar evolution of real growing networks—to weighted networks will be needed to produce scaled up replicas.

Overall, the present work represents another important step forward toward an integral framework for the renormalization of network structure, a prerequisite for renormalizing dynamical processes on real networks in the geometric approach. In traditional real space renormalization schemes in physics, the spatial embedding in which the physical process takes place is trivially self-similar under length scale transformations and all the efforts can be directed toward the renormalization of the physical process and the corresponding Hamiltonian. In contrast, specific properties of complex networks, like a strong hierarchy of degrees and the small-world property, complicate the renormalization of network structure as the support of dynamical processes happening on top. It is, thus, crucial to design a renormalization scheme for the structure of networks, including weights, that produces self-similar renormalized versions as the analogous to the renormalization of space in physical processes.

In this context, GRW works in two steps, as explained above. First, GR is applied to the binarized structure of the network to produce a multiscale unfolding, and this step does not depend on the weights and the result is not changed once weights are added to the description. Once the GR backbone is obtained, GRW associates the weights to the renormalized links without changing the definition of length scales or the coarse graining. An interesting issue to explore in the future is the consistency of the introduced unpacking of scales and the one enabled by geometric network models and techniques where weights and links are integrated. The integrated model, currently missing, would allow to embed weighted networks in their hyperbolic latent space possibly defining an alternative similarity landscape and coarse graining. However, due to the findings in this work and the goodness of the W${{\mathbb{S}}}^{D}$ model to fit real networks, we do not expect divergent results. At the same time, the renormalization of network structure needs to not only account for the weights in the connections but also their directionality, which is a relevant information in most real systems. This, again, goes through extending hyperbolic network embedding methods, in this case to directed networks.

Methods

Description of empirical datasets

• Cargo ships: the international network of global cargo ship movements consists of the number of shipping journeys between pairs of major commercial ports in the world in 2007²⁵.

• E. coli: weights in the metabolic network of the bacteria E. coli K-12 MG1655 consist of the number of different metabolic reactions in which two metabolites participate^26,27.

• US commute: the commuting network reflects the daily flow of commuters between counties in the United States in 2000²⁸.

• Facebook-like Social Network (Facebook): the Facebook-like Social Network originate from an online community for students at University of California, Irvine, in the period between April to October 2004^29,30. In this network, the nodes are students and ties are established when online messages are exchanged between the students. The weight of a directed tie is defined as the number of messages sent from one student to another. We discard the directions for any link and preserve the weight ω_ij with the sum of bidirectional messages, i.e., ω_ij = ω_i→j + ω_j→i. Notice that we only consider the giant connected component of the undirected and weighted networks in this paper.

• Collaboration: this is the co-authorship network of based on preprints posted to Condensed Matter section of arXiv E-Print Archive between 1995 and 1999³¹. Authors are identified with nodes, and an edge exists between two scientists if they have coauthored at least one paper. The weights are the sum of joint papers. Notice that we only consider the giant connected component of the undirected and weighted networks in this paper.

• Openflights: network of flights among all commercial airports in the world, in 2010, derived from the Openflights.org database³². Nodes represent the airports. The weights in this network refer to the number of routes between two airports. We discard the directions for any link and preserve the weight ω_ij with the sum of bidirectional weights, i.e., ω_ij = ω_i→j + ω_j→i. Notice that we only consider the giant connected component of the undirected and weighted networks in this paper.

• Journal Citation Network (JCN): the citation networks from 1900 to 2013 were reconstructed from data on citations between scientific articles extracted from the Thomson Reuters Citation Index³³. A node corresponds to a journal with publications in the given time period. An edge is connected from journal i to journal j if an article in journal i cites an article in journal j, and the weight of this link is taken to be the number of such citations. In this work, we use undirected and weighted networks generated from 3 different time windows, 2008–2013, 1985–1990 and 1965–1975. The data are obtained from ref. ²⁴.

• New Zealand Collaboration Network (NZCN): this is a network of scientific collaborations among institutions in New Zealand. Nodes are institutions (universities, organizations, etc.) and edges represent collaborations between them. In particular, two nodes i, j are connected if Scopus lists at least one publication with authors at institutions i and j, in the period 2010–2015. The weights of edges record the number of such collaborations. The data are obtained from ref. ³⁴. Notice that we only consider the giant connected component of the undirected and weighted networks in this paper.

• Poppy and foxglove hypocotyl cellular interaction networks: these networks capture global cellular connectivity within the hypocotyl (embryonic stem) of poppy and foxglove. Nodes represent cells and edges are their physical associations in 3D space. Edges are weighted by the size of shared intercellular interfaces, and nodes annotated with cell type. The data are obtained from ref. ³⁵.

Network statistics can be found in Supplementary Table 1.

Network embedding to produce geometric network maps

We embed each considered network into hyperbolic space using the algorithm introduced in ref. ¹⁴, named Mercator. Mercator takes the network adjacency matrix A_ij (A_ij = A_ji = 1 if there is a link between nodes i and j, and A_ij = A_ji = 0 otherwise) as input and then returns inferred hidden degrees, angular positions of nodes and global model parameters. More precisely, the hyperbolic maps were inferred by finding the hidden degree and angular position of each node, {κ_i} and {θ_i}, that maximize the likelihood ${{{{{{{\mathcal{L}}}}}}}}$ that the structure of the network was generated by the ${{\mathbb{S}}}^{1}$ model, where

$${{{{{{{\mathcal{L}}}}}}}}=\mathop{\prod}\limits_{i < j}{\left[{p}_{ij}\right]}^{{A}_{ij}}{\left[1-{p}_{ij}\right]}^{1-{A}_{ij}}\,,$$

(6)

and ${p}_{ij}=1/(1+{\chi }_{ij}^{\beta })$ is the connected probability.

The definition of disparity

The disparity of a node i quantifies the local heterogeneity of the weights attached to it³⁶, and is defined as:

$$\begin{array}{r}{Y}_{i}=\mathop{\sum}\limits_{j}{\left(\frac{{\omega }_{ij}}{{\sum }_{j}{\omega }_{ij}}\right)}^{2}=\mathop{\sum}\limits_{j}{\left(\frac{{\omega }_{ij}}{{s}_{i}}\right)}^{2},\end{array}$$

(7)

where ω_ij is the weight of the link between node i and its neighbor j, and s_i is the strength of node i. From this definition, it is easy to see that the disparity scales as Y ~ k⁻¹ whenever the weights are homogeneously distributed among the links. Conversely, the disparity decreases slower than k⁻¹ whenever the weights are heterogeneously distributed.

Theoretical derivation of the renormalized weights

Under GR, the hidden variables of supernodes in the resulting layer, ${\kappa }^{{\prime} }$ and ${\theta }^{{\prime} }$, are calculated as a function of the hidden variables of the constituent nodes as:

$${\kappa }^{{\prime} }={\left[\mathop{\sum }\limits_{j = 1}^{r}{({\kappa }_{j})}^{\beta }\right]}^{1/\beta }\quad \,{{\mbox{and}}}\,\quad {\theta }^{{\prime} }={\left[\frac{\mathop{\sum }\nolimits_{j = 1}^{r}{({\theta }_{j}{\kappa }_{j})}^{\beta }}{\mathop{\sum }\nolimits_{j = 1}^{r}{({\kappa }_{j})}^{\beta }}\right]}^{1/\beta }.$$

(8)

The expressions above and Eq. (1) altogether imply that the renormalized weight should be:

$${\omega }_{ij}^{{\prime} } = \, \frac{{\nu }^{{\prime} }{\sigma }_{i}^{{\prime} }{\sigma }_{j}^{{\prime} }}{{\left({\kappa }_{i}^{{\prime} }{\kappa }_{j}^{{\prime} }\right)}^{1-{\alpha }^{{\prime} }/D}{d}_{ij}^{{}^{{\prime} }{\alpha }^{{\prime} }}}={\nu }^{{\prime} }{({a}^{{\prime} })}^{2}{d}_{ij}^{{\prime} }-{\alpha }^{{\prime} }{\left({\kappa }_{i}^{{\prime} }{\kappa }_{j}^{{\prime} }\right)}^{\eta -1+{\alpha }^{{\prime} }/D}\\ = \, {\epsilon }_{ij}^{{\prime} }{\nu }^{{\prime} }{({a}^{{\prime} })}^{2}{d}_{ij}^{{\prime} -{\alpha }^{{\prime} }}{\left[{\left({\kappa }_{i}^{{\prime} }{\kappa }_{j}^{{\prime} }\right)}^{\beta /D}\right]}^{\frac{D(\eta -1)+{\alpha }^{{\prime} }}{\beta }}\\ = \, {\nu }^{{\prime} }{({a}^{{\prime} })}^{2}{d}_{ij}^{{\prime} -{\alpha }^{{\prime} }}{\left[\mathop{\sum }\limits_{e = 1}^{{r}^{2}}{\left({\kappa }_{m}{\kappa }_{n}\right)}_{e}^{\beta /D}\right]}^{\frac{D(\eta -1)+{\alpha }^{{\prime} }}{\beta }}\\ = \, {\nu }^{{\prime} }{({a}^{{\prime} })}^{2}{d}_{ij}^{{\prime} -{\alpha }^{{\prime} }}{\left[\mathop{\sum }\limits_{e = 1}^{{r}^{2}}{\left(\frac{{w}_{mn}}{\nu {a}^{2}{d}_{mn}^{-\alpha }}\right)}_{e}^{\frac{\beta }{D(\eta -1)+\alpha }}\right]}^{\frac{D(\eta -1)+{\alpha }^{{\prime} }}{\beta }}.$$

(9)

In the last step, we have assumed that, for every pair of nodes (m, n), we can obtain the product κ_mκ_n from the corresponding weight ω_mn, which is not true in general, as some links might not exist. However, this should be a reasonable approximation, since it only misses the smallest products of hidden degrees. Now, the above transformation cannot be performed without the precise distances in the embedding, as it depends on d_mn. Recalling that d_mn = RΔθ_mn, where Δθ_mn stands for the angular separation between the nodes, and the fact that all such distances are approximately equal to the angular separation between the supernodes to which the nodes belong to ($\Delta {\theta }_{mn}\, \approx \, \Delta {\theta }_{ij}^{{\prime} }$), all dependency on the distance can be removed by fixing ${\alpha }^{{\prime} }=\alpha$:

$${\omega }_{ij}^{{\prime} } = \,{\nu }^{{\prime} }{({a}^{{\prime} })}^{2}{d}_{ij}^{{}^{{\prime} }-\alpha }{\left[\mathop{\sum }\limits_{e = 1}^{{r}^{2}}{\left(\frac{{w}_{mn}}{\nu {a}^{2}{d}_{mn}^{-\alpha }}\right)}_{e}^{\frac{\beta }{D(\eta -1)+\alpha }}\right]}^{\frac{D(\eta -1)+\alpha }{\beta }}\\ = \, \frac{{\nu }^{{\prime} }}{\nu }{\left(\frac{{a}^{{\prime} }}{a}\right)}^{2}{\left(\frac{R\Delta {\theta }_{ij}^{{\prime} }}{{R}^{{\prime} }\Delta {\theta }_{ij}^{{\prime} }}\right)}^{\alpha }{\left[\mathop{\sum }\limits_{e = 1}^{{r}^{2}}{\left({w}_{mn}\right)}_{e}^{\frac{\beta }{D(\eta -1)+\alpha }}\right]}^{\frac{D(\eta -1)+\alpha }{\beta }}\\ = \, \frac{{\nu }^{{\prime} }}{\nu }{\left(\frac{{a}^{{\prime} }}{a}\right)}^{2}{r}^{\alpha /D}{\left[\mathop{\sum }\limits_{e = 1}^{{r}^{2}}{\left({w}_{mn}\right)}_{e}^{\frac{\beta }{D(\eta -1)+\alpha }}\right]}^{\frac{D(\eta -1)+\alpha }{\beta }},$$

(10)

where we have used that ${R}^{{\prime} }=R/{r}^{1/D}$.

Finally, we can choose any appropriate relation between primed and unprimed global parameters leading to:

$${\omega }_{ij}^{{\prime} }=C{\left[\mathop{\sum }\limits_{e = 1}^{{r}^{2}}{\left({w}_{mn}\right)}_{e}^{\phi }\right]}^{1/\phi },$$

(11)

with $\phi \equiv \frac{\beta }{D(\eta -1)+\alpha }$ and $C=\frac{{\nu }^{{\prime} }}{\nu }{\left(\frac{{a}^{{\prime} }}{a}\right)}^{2}{r}^{\alpha /D}$. Therefore, the weighted model predicts that the exponent η characterizing the relation between strength and degree is preserved in the renormalized network if weights are transformed following Eq. (11) (in the noiseless case) and the value of ϕ that corresponds to the considered network is used.

Theoretical derivation of the flow of the average strength

We start from Eq. (3) (D = 1) and impose that the rescaling variable:

$$C=\frac{{\nu }^{{\prime} }}{\nu }{\left(\frac{{a}^{{\prime} }}{a}\right)}^{2}{r}^{\alpha }$$

is constant in the flow such that the transformation of weights keeps the same units in all scales of observation. The transformation of the relation between hidden strength and hidden degree is:

$$\frac{{a}^{{\prime} }}{a}=\frac{{\langle \sigma \rangle }^{{\prime} }}{\langle \sigma \rangle }\frac{\langle {\kappa }^{\eta }\rangle }{{\langle {\kappa }^{\eta }\rangle }^{{\prime} }}.$$

We can also obtain the transformation of the free parameter ν using its expression from ref. ²⁰ and the expression for the parameter μ:

$$\nu =\frac{\Gamma (1/2)}{2{\pi }^{1/2}{\mu }^{1-\alpha }{I}_{2}{I}_{3}\langle \sigma \rangle }\quad \mu =\frac{\Gamma (1/2)}{2{\pi }^{1/2}{I}_{1}\langle k\rangle },$$

which leads to:

$$\frac{{\nu }^{{\prime} }}{\nu }=\frac{\langle \sigma \rangle }{{\langle \sigma \rangle }^{{\prime} }}{\left(\frac{{\langle k\rangle }^{{\prime} }}{\langle k\rangle }\right)}^{1-\alpha }$$

and therefore to:

$$C=\frac{{\langle \sigma \rangle }^{{\prime} }}{\langle \sigma \rangle }{\left(\frac{\langle {\kappa }^{\eta }\rangle }{{\langle {\kappa }^{\eta }\rangle }^{{\prime} }}\right)}^{2}{r}^{\xi (1-\alpha )+\alpha },$$

where we have used the expression for the flow of the average degree. We use $\langle {\kappa }^{\eta }\rangle =\frac{\gamma -1}{\gamma -1-\eta }{\kappa }_{0}^{\eta }$ (η < γ − 1) to compute its flow, and we obtain:

$$\frac{{\langle {\kappa }^{\eta }\rangle }^{{\prime} }}{\langle {\kappa }^{\eta }\rangle }={r}^{\xi \eta }.$$

Finally,

$$C=\frac{{\langle \sigma \rangle }^{{\prime} }}{\langle \sigma \rangle }{r}^{\xi (1-2\eta -\alpha )+\alpha }=\frac{{\langle \sigma \rangle }^{{\prime} }}{\langle \sigma \rangle }{r}^{-\psi },$$

and we impose C = 1 to obtain Eq. (4), from which ψ > 0 implies an increasing average strength in the flow while it decreases if ψ < 0.

The transformation sum-GRW does not preserve the relation between strength and degree

The sum-GRW transformation is:

$${w}_{ij}^{{\prime} } = \mathop{\sum }\limits_{e=1}^{{r}^{2}}{\epsilon }_{mn}{w}_{mn}\\ = \, \nu {d}_{mn}^{-\alpha }\mathop{\sum }\limits_{e=1}^{{r}^{2}}{\epsilon }_{mn}{\sigma }_{m}{\sigma }_{n}{({\kappa }_{m}{\kappa }_{n})}^{\alpha /D-1},$$

(12)

where e runs over all pairs of nodes (m, n) with m in supernode i and n in supernode j and d_mn = RΔθ_mn, where Δθ_mn stands for the angular separation between the nodes. All such distances are approximately equal to the angular separation between the supernodes to which the nodes belong ($\Delta {\theta }_{mn}\, \approx \, \Delta {\theta }_{ij}^{{\prime} }$), and one can take ${\alpha }^{{\prime} }=\alpha$. Comparing Eq. (1) and (12), we can write:

$${\nu }^{{\prime} }{d}_{ij}^{{}^{{\prime} }-{\alpha }^{{\prime} }}=\nu {d}_{ij}^{-\alpha },$$

(13)

$${\epsilon }_{ij}^{{\prime} }{\sigma }_{i}^{{\prime} }{\sigma }_{j}^{{\prime} }{({\kappa }_{i}^{{\prime} }{\kappa }_{j}^{{\prime} })}^{{\alpha }^{{\prime} }/D-1}=\mathop{\sum }\limits_{e=1}^{{r}^{2}}{\epsilon }_{mn}{\sigma }_{m}{\sigma }_{n}{({\kappa }_{m}{\kappa }_{n})}^{\alpha /D-1},$$

(14)

and using ${R}^{{\prime} }=R/{r}^{1/D}$ and Eq. (13) altogether, we have:

$${\nu }^{{\prime} }=\nu {r}^{-\alpha /D}.$$

(15)

Therefore, in the noiseless version (ϵ_mn = 1  ∀ (m, n)), we can obtain the hidden strength ${\sigma }_{i}^{{\prime} }$ in the supernodes layer as:

$${\sigma }_{i}^{{\prime} }=\frac{\mathop{\sum }\nolimits_{m = 1}^{r}{\sigma }_{m}{\kappa }_{m}^{\alpha /D-1}}{{\kappa }_{i}^{{\prime} \alpha /D-1}}\,{\not\approx} \,{\kappa }_{i}^{{\prime} \eta },$$

(16)

which proves that, in general, the relation between hidden strength and hidden degree is not preserved under sum-GRW.

Scale down replicas

• (1) We obtain a renormalized network layer by applying the sup-GRW method with a given value of r and number of iterations to match the target network size.

• (2) Typically, the average degree of the renormalized network layer is higher than the original one. Thus, to obtain a scaled down network replica of the topology, we decrease the average degree in the renormalized layer to that in the original network as explained in ref. ¹, such that $\langle {k}_{{{{{{{{\rm{new}}}}}}}}}^{(l)}\rangle =\langle {k}^{(0)}\rangle$. The main idea is to reduce the value of μ^(l) to a new one ${\mu }_{new}^{(l)}$, which means that the connection probability of every pair of nodes (i, j), ${p}_{ij}^{(l)}$ decreases to ${p}_{ij,new}^{(l)}$. Therefore, the probability for a link to exist in the pruned network reads:

  $${p}_{ij,new}^{(l)}=\frac{1}{1+{\left(\frac{{d}_{ij}}{{\mu }_{new}^{(l)}{\kappa }_{i}{\kappa }_{j}}\right)}^{\beta }}.$$

  (17)

  In particular, we prune the links using ${\mu }_{{{{{{{{\rm{new}}}}}}}}}^{(l)}=h\frac{\langle {k}^{(0)}\rangle }{\langle {k}^{(l)}\rangle }{\mu }^{(l)}$ with h = 1 as initial value. After an iteration for all the links in the layer, we give h a new value h(1 − 0.1u) → h if $\langle {k}_{{{{{{{{\rm{new}}}}}}}}}^{(l)}\rangle \, > \, \langle {k}^{(0)}\rangle$, where u ∈ [0, 1) is a random variable from a uniform distribution. If $\langle {k}_{{{{{{{{\rm{new}}}}}}}}}^{(l)}\rangle \, < \, \langle {k}^{(0)}\rangle$, h(1 + 0.1u) → h. The procedure stops when $| \langle {k}_{{{{{{{{\rm{new}}}}}}}}}^{(l)}\rangle -\langle {k}^{(0)}\rangle |$ is below a given threshold, that we set to 0.1.

• (3) Finally, we rescale the weights in the resulting network by a global factor to match the average weight of the original network. Specifically, we calculate the average weight $\langle {w}_{{{{{{{{\rm{new}}}}}}}}}^{(l)}\rangle$ of the resulting network from step (2) and the average weight 〈w⁽⁰⁾〉 in the original network. Then we rescale the weight of each link by the factor $c=\frac{\langle {w}^{(0)}\rangle }{\langle {w}_{{{{{{{{\rm{new}}}}}}}}}^{(l)}\rangle }$.