Introduction

The rapid growth of big data has placed a premium on information storage and processing speed, leading the spintronic community to focus on investigating ultrafast spin dynamics. Recent advances in antiferromagnetic (AFM) spintronics1,2,3 have highlighted advantages over ferromagnetic (FM) materials, particularly in their ability to operate at terahertz (THz) frequencies, which is attributed to the strong anti-parallel exchange coupling that generates a large intrinsic exchange field4,5,6. However, due to lacking net magnetization, AFM materials for the magnetoresistance-based spintronic devices are limited by weak electrical signal outputs and inefficient electrical manipulation7,8. This impedes the practical applications of AFM in information devices.

To overcome this challenge, ferrimagnets (FiMs) offer a promising alternative for achieving ultrafast devices with feasible electrical-based tunability due to their AFM-like exchange coupling combined with a non-vanishing net magnetization9. When approaching the angular momentum compensation point (TA)10,11, the cancelation of the net angular momentum with the maintained net magnetization results in large domain wall (DW) velocities through spin-orbital torque (SOT)12,13 or spin transfer torque (STT)14,15 without Walker breakdown16,17. These properties make FiMs ideal for ultra-fast DW-based memory18 and logic devices19,20. Moreover, FiMs exhibit an enhanced magnon-magnon entanglement at the TA due to the finite Zeeman coupling, making them an excellent platform for quantum information processing21. Compared to AFMs, the spin torque-induced THz-oscillation in exchange mode can be self-stabilized in FiMs, with a reduced threshold current for triggering the oscillation due to the unbalanced sublattices22. In contrast, the AFM counterpart requires a dynamic feedback mechanism4,23 that combines spin pumping with spin torques to form a stable oscillation. GdFeCo is one of typical rare earth–transition metal ferrimagnets with different Landé g-factors10. Therefore, the GdFeCo ferrimagnets have distinguishable magnetization compensation point and angular momentum compensation point, providing a fertile materials platform to study pure antiferromagnetic spin dynamics at angular momentum compensation point with detectable and controllable uncompensated magnetization.

Currently, theoretical studies on the dynamics of Ferrimagnets (FiMs) have conventionally assumed the system as collinearly coupled sublattices15 or used the two-sublattice macro-spin model22 coupling two Landau-Lifshitz-Gilbert-Slonczewski (LLGS) equations24 to describe the magnetization evolution. Although these modeling contributed to understanding the spin dynamics in the FiM, they have limitations in describing the spin dynamics of non-uniform spin textures, such as magnons, skyrmions, and other exotic dynamics such as the asynchronous motion of different sublattices25. Therefore, there exists an imperative request for a multi-spin model26,27 that can account for individual and conjoint spin dynamics to investigate the inhomogeneous and asynchronous spin dynamics in FiMs. One recent simulation work28 reported the phenomenon of the non-uniform oscillation in a two-dimensional (2D) GdFeCo in which the Gd atoms randomly distributed among the FeCo atoms. However, such spatially inhomogeneous oscillation, stemmed from the AFM-like exchange interaction, remain incompletely understood. Considering this issue, it is significant to investigate the most fundamental case, the finite FiM spin-chain system, in that the spin-chain29,30 is a crucial system in studying far-reaching spin dynamics such as the Haldane phase transition31, surface/edge effect32 etc. Moreover, the advent of scanning tunneling microscopy (STM) and in-situ material synthesis have enabled the engineering of spin chains on an atomic scale.

In this study, we investigate the oscillation dynamics induced by STT in a designed FiM spin chain using a multi-spin model. We found that the oscillation properties in the 2D case28 are replicable in the spin-chain. Specifically, when excited by STT, the spin-chain oscillates in the exchange mode that exhibits three typical phases and all the oscillatory atoms share identical frequencies with the linear relation to the injected current densities, while the rest of atoms keep static. To find the fundamental reasons of the observed oscillation properties, firstly, a joint effective field (\({H}_{{joint}}\)) is derived to describe the conjoint frequency tunability in the spin-chain. Besides, a localized phase-dependent oscillation dynamics is observed that, even when the localized AFM phase occurs, the spinchain still maintains auto-oscillation, while in the vicinity of the localized FM limit, the frequency of the spin chain is sensitive to the STT strength. Furthermore, an anti-parallel exchange length (\({l}_{{AEX}}\)) is employed to quantitatively describe the spatially inhomogeneous oscillation profile of the spin-chain. The analytical results of the \({l}_{{AEX}}\) are consistent with the numerical results and reveal that the stronger AFM-like exchange coupling and smaller magnetization of the host material led to more remarkable inhomogeneity in the spin chain. The multi-spin model provides advantages over the two-sublattice macro-spin model by enabling us to observe the spin dynamics affected by the localized phase-effected and inhomogeneous oscillation properties. These findings reveal understandings of FiM spin dynamics and suggest strategies for material selection and doping to construct THz-spin nano oscillators.

Results and discussion

Frequency tunability

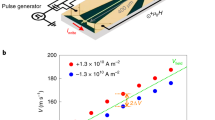
The FiM spin-chain is illustrated Fig. 1a, where the central spin is a down-spin from Gd, denoted as ‘0’, and the rest are 100 up-spins from FeCo, each labeled. The FiM chain is injected with spin-polarized electrons and thus exerted STT to the magnetic moment of every atom. Firstly, we explore the relationship between the oscillation characteristics and STT strength. As depicted in Fig. 1b, we can observe that when the FiM spin-chain is manipulated by STT with increasing strength, the exchange mode can be further classified into three regions: non-flipped exchange mode (region I), critical exchange mode (region II), and flipped exchange mode (region III). Throughout the entire exchange mode region, the frequency increased linearly as the current density (\({J}_{c}\)) increased, while the amplitude increased in region I, reached its plateau in region II, and decreased in region III. To figure out the STT-tuned oscillation characteristics, we look into the evolution of the exchange field (\({H}_{{ex}}\)) and the uniaxial anisotropy field (\({H}_{{ani}}\)) of every oscillatory atom. Figure 1c shows the \({H}_{{ex}}\) experienced by the oscillatory Gd and FeCo atoms under different current density. The \({H}_{{ex},{Gd}}\)-\({J}_{c}\) curve and the amplitude-\({J}_{c}\) curve exhibit the same trend, implying that the variation of the oscillation amplitude in the FiM system is dominated by the \({H}_{{ex},{Gd}}\). Specifically, according to the torque analysis28, the Gilbert damping and damping-like STT acting on the Gd atom are in opposite directions due to the opposite direction of the \({H}_{{ex},{Gd}}\) and spin polarization (\({P}_{{STT}}\)), whereas the two torques acting on the FeCo atom are in the same direction. The self-stabilized oscillation in the spin chain is stemmed from the precession of the Gd atom, where the Gilbert damping and damping-like torque can be balanced, while the FeCo atom is passively dragged into oscillation by the exchange interaction.

Fig. 1: Schematic of the spin-chain and its oscillation property manipulated by current.
figure 1

a Schematic of the multi-spin model which describes the Heisenberg spin-chain with 101 spins; b Frequency and Fast Fourier transform (FFT) amplitude as a function of the current density \({J}_{c}\); c The exchange field experienced by Gd and FeCo atoms, respectively. The color bar represents the atom index labeled in (a); d The analytical solution of the joint effective field \({H}_{{joint}}\) as a function of the current density \({J}_{c}\).

Full size image

For a homogeneous system, the oscillation frequency is directly determined by the effective field (\({H}_{{eff}}\)). However, in the inhomogeneous case, it is evident that each oscillatory atom experiences a different \({H}_{{eff}}\), and the corresponding Hex changes non-linearly with an increase in \({J}_{c}\), as shown in Fig. 1c. Despite this, all oscillatory atoms share the same frequency (see Supplementary Fig. 1) due to strong exchange coupling, which exhibits a linear relation with \({J}_{c}\). This frequency behavior can be explained by the configuration of \({H}_{{ex}}\) and \({H}_{{ani}}\), which can be tuned by the STT strength, i.e., the injected \({J}_{c}\).

To understand this physically, we derive an analytical solution from the LLGS equations to determine the specific configuration of \({H}_{{ex}}\) and \({H}_{{ani}}\), called the “joint effective field \(({H}_{{joint}})\)” that directly determines the oscillation frequency and can be expressed as follows:

$${H}_{{joint}}= \frac{1}{2}\left[\left({H}_{{{{{{\rm{ani}}}}}},{{{{{\rm{FeCo}}}}}}}-{H}_{{{{{{\rm{ex}}}}}},{{{{{\rm{Gd}}}}}}}\right)+\left({H}_{{{{{{\rm{ani}}}}}},{{{{{\rm{Gd}}}}}}}-2{H}_{{{{{{\rm{ex}}}}}},{{{{{\rm{FeCo}}}}}}}\right) \right.\\ + \left.\sqrt{{\left[\left({H}_{{{{{{\rm{ani}}}}}},{{{{{\rm{FeCo}}}}}}}-{H}_{{{{{{\rm{ex}}}}}},{{{{{\rm{Gd}}}}}}}\right)+\left({H}_{{{{{{\rm{ani}}}}}},{{{{{\rm{Gd}}}}}}}-2{H}_{{{{{{\rm{ex}}}}}},{{{{{\rm{FeCo}}}}}}}\right)\right]}^{2}-4{H}_{{{{{{\rm{ex}}}}}},{{{{{\rm{FeCo}}}}}}}\left(2{H}_{{{{{{\rm{ex}}}}}},{{{{{\rm{Gd}}}}}}}\right)}\right]$$
(1)

Substituting the corresponding \({H}_{{ex}}\) and \({H}_{{ani}}\) in Eq. (1), the \({H}_{{joint}}\) increases linearly with the increase of the \({J}_{c}\), as shown in Fig. 1d. The detailed derivation can be found in the Supplementary Note 1.

To further investigate how the oscillation behavior of the FiM spin chain is affected by the ratio (ξ) of individual spin angular momenta of the opposite spins, as shown in Fig. 2a. The ξ for the GdFeCo is 0.3 and then we conduct a parametric study by varying the magnetic moment of FeCo. It is worth noting that the extensive scope of ξ encompasses both diverse FiMs with varying chemical compositions but also physically intriguing aspects that cannot be reached by altering temperature, unveiling profound implications that might not necessarily be attainable in real materials. Figure 2b illustrates that the oscillation dynamics of the three types of exchange modes are consistent across different ξ values, in that they have the same variation tendency of FFT amplitude as that shown Fig. 1a. The inset of the Fig. 2b identifies the three exchange modes: \({s}_{z,{Gd}}\) < 0 (>0) represents the non-flipped (flipped) exchange mode, while \({s}_{z,{Gd}}\) around 0 represents the critical exchange mode (\({s}_{z,{Gd}}\) represents the \(\hat{{{{{{\boldsymbol{z}}}}}}}\) component of the spin angular momentum from Gd atom). When ξ is small, the spin chain exhibits a large amplitude excited by STT, as more atoms form a stable exchange oscillation. This will be discussed quantitatively later. In addition, larger ξ requires a stronger \({J}_{c}\) (i.e., STT strength) to overcome the strong co-linear exchange interaction and facilitate exchange mode oscillation. Figure 2c shows that frequency tunability is more sensitive to changes in \({J}_{c}\) when ξ is small. At small ξ, the FiM spin chain operates at a broad frequency range and low \({J}_{c}\). The inset of Fig. 2c summarizes the frequency tunability by manipulating \({J}_{c}\) and ξ. The increased frequency with the decreasing ξ can be demonstrated by the relation of the total net magnetization in the spin-chain and the frequency. Specifically, the definition of the \({H}_{{eff}}\) is expressed by the Eq. (2)

$${H}_{{eff}}=-\frac{1}{{\mu }_{0}{M}_{{net}}}\frac{\partial {{{{{\mathcal{H}}}}}}}{\partial m}$$
(2)

Where \({{{{{\mathcal{H}}}}}}\) is the Hamiltonian of the system (the detail of the \({{{{{\mathcal{H}}}}}}\) is demonstrated in the method). The smaller net magnetization \({M}_{{net}}\) leads larger \({H}_{{eff}}\) and therefore results in higher frequency. The conclusion that is drawn by the \({H}_{{joint}}\) is consistent with that of the definition of the \({H}_{{eff}}\). When the ξ is small, the small FM-magnetization results in the small exchange field (\({H}_{{{{{{\rm{ex}}}}}},{{{{{\rm{FeCo}}}}}}}\) in the Eq. 2) in the FM phase, and therefore the increased \({H}_{{joint}}\), which is proportional to the frequency. This regulation of the frequency tuned by the \({J}_{c}\) is also valid when ξ > 1. The frequency-current density curves of ξ = 1.2 comparing with the curves of ξ < 1 is shown in Supplementary Fig. 2. More importantly, the spin chain maintains self-stabilized oscillation even in the presence of localized AFM-phase, while near the localized FM-limit, the frequency of the spin chain is sensitive to STT strength. The localized phase-dependent oscillation dynamics observed in our multi-spin model is not considered in the two-sublattice macro-spin model.

Fig. 2: The oscillation phase diagrams of different spin-chain configurations.
figure 2

a Schematic of the spin configurations with different ratio of individual up-spin and down-spin ξ. Numerical results of (b) Fast Fourier transform (FFT) amplitude and c frequency associated with steady-state oscillations in the range of the current density \({J}_{c}\) (\(\times {10}^{12}A{m}^{-2}\))∈[0.3, 1.2] and ratio of individual up-spin and down-spin ξ ∈ [0.1, 1] for the spin chain. The insets are the \(\hat{{{{{{\boldsymbol{z}}}}}}}\) component of the magnetization of the Gd atom \({m}_{z,{Gd}}\) and frequency as a function of current density \({J}_{c}\) and ratio of individual up-spin and down-spin ξ, and the color bars represent the value of the \({m}_{z,{Gd}}\) and frequency, respectively.

Full size image

To close the discussion of frequency tunability, we would like to mention that the relation between the frequency of the nano oscillator and the spin wave dispersion is crucial for designing and optimizing spintronic devices based on spin nano oscillators33. By tuning the oscillator’s frequency to match specific spin wave modes, we can enhance the efficiency and performance of these devices. In our present work, we find the localized phase-dependent and inhomogeneous oscillation behaviors, and how these behaviors affect the spin wave would be an open question.

Inhomogeneous profile of the ferrimagnetic oscillation

In addition to the oscillation frequency, compared to the two-sublattice model, our multi-spin model also enables the ability to investigate inhomogeneous oscillation behavior in the spin chain system. As shown in Fig. 3a, when electrons with a parallel \({P}_{{STT}}\) are injected along the +z-axis, only specific spins near the opposite-spin spatial region exhibit a stable oscillation in the exchange mode. The remaining spins are stabilized by the \({P}_{{STT}}\) and remain static. We refer to the opposite-spin spatial region as the “oscillation core (OC)” since the oscillation arises from the antiferromagnetic exchange interaction in this area. Figure 3b demonstrates that the oscillation amplitude is maximal at the OC (corresponding to the atom with index 0) and decays as the atom moves away from the OC. This indicates that although we only consider the nearest neighbor exchange interaction in the spin chain, the anti-parallel exchange interaction (AEI) can indirectly influence the spins near the OC (corresponding to the atom with index 2, 3 and so on), resulting in the stable oscillation. Beyond the indirect influence range, the spins keep static. The amplitude distribution and identical frequency indicate that the spin closer to the OC exhibits a larger linear velocity and, thus requires more time to achieve stable oscillation, as demonstrated in Fig. 3c.

Fig. 3: Spatially inhomogeneous oscillation profile of the spin-chain.
figure 3

a Schematic of the spin motion in the ferrimagnetic spin-chain excited by spin transfer torque; b Fast Fourier transform (FFT) amplitude distribution. The color bar represents the value of FFT amplitude; and c the formation time with respect to spatial position in the spin chain operated under current density \({J}_{c}=0.7\times {10}^{12}A{m}^{-2}\).

Full size image

To investigate the inhomogeneous profile qualitatively, the amplitude distribution is further evaluated. The oscillation amplitude relates to the variation of the \(\hat{{{{{{\boldsymbol{z}}}}}}}\) component of the \({{{{{\boldsymbol{S}}}}}}\) (\(\left|{\Delta S}_{z}\right|\)) shown in Supplementary Fig. 3 and the \(\left|{\Delta S}_{z}\right|\) indicates the atoms that form stable oscillation (\(\left|{\Delta S}_{z}\right| \, \ne \, 0\)), or atoms that relax to the z-axis and remain static (\(\left|{\Delta S}_{z}\right|=0\)). By analyzing \(\left|{\Delta S}_{z}\right|\) shown in Fig. 4a, b, it was determined that the number of atoms that can be facilitated in stable oscillation state depends on ξ, which represents the ratio of individual spin angular momenta of the opposite spins. In the spin chain, the number of oscillatory atoms remains constant even when operated at different \({J}_{c}\), as long as ξ is fixed (see Supplementary Fig. 4). However, smaller ξ facilitates more atoms to oscillate due to more remarkable AEI. The spin chain with reduced ξ requires less time to form stable oscillation and exhibits a stable oscillatory phase within the range affected by the AEI, as shown in Fig. 4c, d. As shown in Fig. 4e and Supplementary Fig. 5, when ξ is further reduced, the dynamic phase involves a stable oscillation and a decaying oscillation, indicating that the effect of AEI still exists but is not strong enough to maintain the stable oscillation.

Fig. 4: Qualitative analysis of the spatially inhomogeneous oscillation.
figure 4

The variation of the \(\hat{{{{{{\boldsymbol{z}}}}}}}\) component of the spin angular momentum \(\left|{\triangle S}_{z}\right|\) as a function of atom index under the condition of (a) different current density \({J}_{c}\) (\(\times {10}^{12}A{m}^{-2}\)) with the ratio of individual up-spin and down-spin ξ = 0.3 and b the different ratio in non-flipped exchange mode. The formation time with respect to spatial position in the spin chain with (c) ξ = 1.0; d ξ = 0.5; and e ξ = 0.1.

Full size image

Furthermore, the inhomogeneous oscillation induced by the AEI can be understood quantitatively by the competition between the \({H}_{{ex}}\) and the \({H}_{{ani}}\), which is tuned by the STT strength. The internal Bloch structure, in principle, shares a similar physics principle to the Bloch domain wall, whose width can be described by the exchange length34:

$${l}_{{EX}}=\sqrt{{A}_{{EX}}/{K}_{u}}$$
(3)

The \({A}_{{EX}}\) is the exchange stiffness in the ferromagnetic system with the parallel exchange interaction, and the \({K}_{u}\) is the uniaxial anisotropy energy density. Hence, we calculate an anti-parallel exchange length (\({l}_{{AEX}}\)) expressed as follows:

$${l}_{{AEX}}=\sqrt{\frac{{{{{{\rm{|}}}}}}{J}_{A-B}{{{{{\rm{|}}}}}}}{a{\mu }_{0}{M}_{s,A}^{2}}}$$
(4)

The \({J}_{A-B}\) is the anti-parallel exchange factor, which is smaller than zero, wherein A is for the atom of the host material (FeCo in this case) and B is for the atom of doped material (Gd in this case). \({M}_{s,{A}}\) is the saturation magnetization of the atom A, \(a\) is the lattice constant, and \({\mu }_{0}\) is the permeability of vacuum. The detailed derivation for the \({l}_{{AEX}}\) can be found in the Supplementary Note 2. For the spin chain system, the number of atoms (N) within the \({l}_{{AEX}}\) can be calculated as \(N={l}_{{AEX}}/a\).To verify the analytical solution of the \({l}_{{AEX}}\), we not only investigate the spin chain composed of GdFeCo, but also change the value of \({J}_{A-B}\) for the parametric study. As shown in Fig. 5a, the analytical results (AR) are consistent with the numerical results (NR), and reveal that the larger anti-parallel exchange factor or smaller \({M}_{s}\) of the host material would result in longer \({l}_{{AEX}}\). Additionally, we find that the \({l}_{{AEX}}\) is independent of the position of the OC as shown Fig. 5b.

Fig. 5: Quantitatively analysis of the spatially inhomogeneous oscillation.
figure 5

a Comparation between the numerical (NR) and analytical results (AR) of the number of atoms within the anti-parallel exchange length (\({l}_{{AEX}}\)). Jex is the exchange factor of anti-parallel exchange coupling; b The \({l}_{{AEX}}\) of the different position of the oscillation core (OC).

Full size image

Conclusions

In summary, we investigated the tunable and inhomogeneous oscillation dynamics in the FiM spin-chain through qualitative and quantitative analysis using the multi-spin model. When triggered by the STT, the spin-chain exhibits oscillations in the exchange mode with an inhomogeneous profile. We classify the exchange mode into non-flipped, critical, and flipped exchange modes based on their different phases. The oscillatory atoms have identical frequencies that increase linearly with increasing STT strength. Additionally, our work demonstrates this frequency behavior through an analytical solution and defines a joint effective field (\({H}_{{joint}}\)) that represents the specific configuration of the exchange field (\({H}_{{ex}}\)) and anisotropy field (\({H}_{{ani}}\)), which can be tuned by the STT strength. We also studied the effect of the localized phase on the oscillation dynamics in the spin chain. Despite the occurrence of the localized AFM phase, the spin-chain still maintains self-stabilized oscillation. Nevertheless, in the vicinity of the localized FM-limit, the frequency of the spin chain becomes sensitive to the STT strength. Further, we implemented an anti-parallel exchange length (\({l}_{{AEX}}\)) to quantitatively analyze the inhomogeneity arising from the AFM-like exchange interaction. Our analytical and numerical results are in agreement, and they reveal that stronger AFM-like exchange coupling or smaller magnetization of the host material would enhance the inhomogeneity in the spin chain. We acknowledge that further studies are required for higher dimensions, which would be involved in more effects such as thickness, size and so on. Nonetheless, the fundamental physics of the inhomogeneous oscillation dynamics that we extracted from the 1D case are valid in the 2D and 3D cases, in that the shared physics principal for the observed phenomena among these systems. Our work provides insights into the FiM spin dynamics related to the localized phase-dependent and inhomogeneous profile. Moreover, the impact of these oscillation dynamics on the relationship between the frequency of the spin nano oscillator and the spin wave dispersion needs to be explored, in that it is crucial for designing and optimizing spintronic devices based on spin nano oscillators.

Methods

The FiM chain is injected with spin-polarized electrons and thus exerted STT to the magnetic moment of every atom, as is shown in Fig. 1a. The magnetization dynamics of the FiM chain is conducted by the coupled LLGS equations,

$$\frac{\partial {{{{{{\boldsymbol{S}}}}}}}_{i}}{\partial t}=-{{{{{{\rm{\gamma }}}}}}}_{{{{{{\rm{i}}}}}}}{{{{{{\boldsymbol{S}}}}}}}_{i}\times {{{{{{\boldsymbol{H}}}}}}}_{{eff},i}+{{{{{\rm{\alpha }}}}}}{{{{{{\boldsymbol{S}}}}}}}_{i}\times \frac{\partial {{{{{{\boldsymbol{S}}}}}}}_{i}}{\partial t}-{\gamma }_{i}{B}_{D,i}{{{{{{\boldsymbol{S}}}}}}}_{i}\times \left({{{{{{\boldsymbol{S}}}}}}}_{i}\times {{{{{{\boldsymbol{p}}}}}}}_{{{{{{\boldsymbol{STT}}}}}}}\right)$$
(5)

The three terms on the right-hand side of the LLGS equation represent the precession, the Gilbert damping and the damping-like STT, respectively. Besides, i denotes individual spins positioned at the atom side i. \({{{{{\boldsymbol{S}}}}}}\), \({{{{{\rm{\gamma }}}}}}\), \({{{{{\rm{\alpha }}}}}}\) are the unit vector of spin, the gyromagnetic ratio, and the Gilbert damping constant, respectively. With regards to the source of the auto-oscillations in the exchange mode being attributed to AFM-like exchange interactions22, it’s pivotal to underscore that our study is primarily oriented towards comprehending the impact of exchange interactions (with a specific emphasis on the AFM-like exchange interaction), uniaxial anisotropy, and STT, as well as their intricate interplay Therefore, the effective field (\({{{{{{\boldsymbol{H}}}}}}}_{{eff}}\)) is extracted from the Hamiltonian as is shown in Eq. (6):

$${{{{{\mathcal{H}}}}}}{{{{{\mathscr{=}}}}}}{{{{{{\rm{J}}}}}}}_{{{{{{\rm{ex}}}}}}}\mathop{\sum}\limits_{i}{{{{{{\boldsymbol{S}}}}}}}_{i}\cdot {{{{{{\boldsymbol{S}}}}}}}_{i+1}-{K}_{u}\mathop{\sum}\limits_{i}{\left({{{{{{\boldsymbol{S}}}}}}}_{i}\cdot \hat{{{{{{\boldsymbol{z}}}}}}}\right)}^{2}$$
(6)

The Hamiltonian includes the exchange interaction with the exchange constant \({J}_{{ex}}\) and the uniaxial anisotropy with the anisotropy constant \({K}_{u}\).

The strength of STT is described by Eq. (7):

$${B}_{D,i}=\frac{{{\hslash }}}{2}\frac{{J}_{c}{{{{{\rm{\eta }}}}}}}{{{{{{\rm{e}}}}}}{{{{{{\rm{M}}}}}}}_{{{{{{\rm{s}}}}}},{{{{{\rm{i}}}}}}}d}$$
(7)

Where d is the thickness of the FiM chain, \({J}_{c}\) is the charge current density, η is the spin transfer efficiency, and Ms is the saturation magnetization. \({{{{{{\boldsymbol{p}}}}}}}_{{{{{{\boldsymbol{STT}}}}}}}\) is the unit vector that represents the spin-polarization of the injected electrons. The material parameters of GdFeCo are extracted from both experimental and theoretical works35,36 and are listed in the Table 1. For simplification, we treated the FeCo sublattice as a unitary transition metal and ignored the parametric difference of Fe and Co atoms. This is reasonable in that the amount of Co used in experimental studies on GdFeCo is typically small10,34. Therefore, we restrict our discussion to the simplified case that GdFeCo is composed of a trace of Co. It should be noted that the GdFeCo is our beginning point for the simulation. Then we conducted a parametric study by changing the ratio of individual spin angular momenta of the opposite spins, with the aim to obtain the general oscillation dynamics in the spin-chain that beyond the scope of the GdFeCo. The magnetization dynamic study is performed by using a self-made code that numerically couples the LLGS equations and these equations are solved via the fourth-order Runge-Kutta method with a time step of 2 fs. All the magnetic moment are initially tilted at 5 degrees away from the +z ( − z) axis to assist the STT to drive the system, regarding the simulation approach issues. It takes about 40 picoseconds for the system to relax back to their ground state without STT (shown in Supplementary Fig. 6), ensuring that the initial angle would not change the static equilibrium state in the spin chain, so the deviation angle cannot influence our simulation results. Besides, the Hamiltonian that represents the dipolar interaction is shown in Eq. (8)

$${{{{{{\mathcal{H}}}}}}}_{{dipole}}=-\frac{{{{{{{\boldsymbol{\mu }}}}}}}_{{{{{{\bf{0}}}}}}}}{4}\mathop{\sum}\limits_{{{{{{\boldsymbol{i}}}}}}\ne {{{{{\boldsymbol{j}}}}}}}\frac{3\left({{{{{{\boldsymbol{R}}}}}}}_{{{{{{\boldsymbol{ij}}}}}}}\cdot {{{{{{\boldsymbol{\mu }}}}}}}_{{{{{{\boldsymbol{i}}}}}}}\right)\left({{{{{{\boldsymbol{R}}}}}}}_{{{{{{\boldsymbol{ij}}}}}}}\cdot {{{{{{\boldsymbol{\mu }}}}}}}_{{{{{{\boldsymbol{j}}}}}}}\right)}{{{{{{{\boldsymbol{R}}}}}}}_{{{{{{\boldsymbol{ij}}}}}}}^{{{{{{\bf{5}}}}}}}}-\frac{\,{{{{{{\boldsymbol{\mu }}}}}}}_{{{{{{\boldsymbol{i}}}}}}}\cdot {{{{{{\boldsymbol{\mu }}}}}}}_{{{{{{\boldsymbol{j}}}}}}}}{{{{{{{\boldsymbol{R}}}}}}}_{{{{{{\boldsymbol{ij}}}}}}}^{{{{{{\bf{3}}}}}}}}$$
(8)

Where \({{{{{{\boldsymbol{R}}}}}}}_{{{{{{\boldsymbol{ij}}}}}}}\) is the vector that connects magnetic moment \({{{{{{\boldsymbol{\mu }}}}}}}_{{{{{{\boldsymbol{i}}}}}}}\) and \({{{{{{\boldsymbol{\mu }}}}}}}_{{{{{{\boldsymbol{j}}}}}}}\). In the spin-chain, however, the dipolar field hardly effect the simulation results and can be ignored, in that each atom from all other 100 atoms is 103 times smaller than the exchange field.

Table 1 The parameters adopted in the simulation
Full size table