Topological high-harmonic spectroscopy

Abstract

Linearly polarized vector beams are structured lasers whose topology is characterized by a well-defined Poincaré index, which is a topological invariant during high-order harmonic generation. As such, harmonics are produced as extreme-ultraviolet vector beams that inherit the topology of the driver. This holds for isotropic targets such as noble gases, but analogous behaviour in crystalline solids is still open to discussion. Here, we demonstrate that this conservation rule breaks in crystalline solids, in virtue of their anisotropic non-linear susceptibility. We identify the topological properties of the harmonic field as unique probes, sensitive to both the microscopic and macroscopic features of the target’s complex non-linear response. Our simulations, performed in single-layer graphene, show that the harmonic field is split into a multi-beam structure whose topology encodes information about laser-driven electronic dynamics. Our work promotes the topological analysis of the high-order harmonic field as a spectroscopic tool to reveal the nonlinearities in the coupling of light and target symmetries.

Introduction

Nonlinear optics stands nowadays as a unique approach not only to up-convert laser radiation to higher frequencies but also to obtain information on the dynamics of laser-driven media. High-harmonic generation (HHG) is an exemplary manifestation of this phenomenon, capable of producing extreme-ultraviolet (EUV) to soft x-ray coherent radiation, as well as of unveiling electronic dynamics at the attosecond scale¹. In gases, HHG can be readily understood using a semiclassical point of view². According to it, first, an intense infrared laser field liberates an electronic wavepacket from the atom via tunnel ionization and accelerates it in the continuum. Then, upon reversal of the field amplitude, the electronic wavepacket is redirected to the parent ion, where it recombines emitting high-frequency radiation. The radiated spectrum contains unique information about the ultrafast non-perturbative electron dynamics during the interaction. As a result, high-harmonic spectroscopy has emerged as a main technique to access the ultrafast dynamics of matter subjected to intense laser fields^3,4,5.

It was not until recently that HHG in crystalline solids was demonstrated, so the full potentialities of these targets are currently being unraveled^6,7. For driving beams at grazing incidence, HHG from solids is mediated by electrons detached from the target and, therefore, has a resemblance to its atomic counterpart⁸. However, despite this parallelism, it has been shown that the periodicity of the crystal imprints a diffraction pattern in the electronic wavefunction, giving rise to Talbot revivals, with signatures in the harmonic spectrum⁹. In contrast, when driven at normal incidence, HHG from solids can be interpreted in terms of semi-classical trajectories of electron-hole pairs in the target, excited via tunneling or Landau-Zener transitions, which subsequently evolve accordingly to the band’s energy dispersion¹⁰. In this case, the harmonic emission takes place upon recombination of the electron-hole pair, following either perfect or imperfect recollisions^11,12,13. As in gas targets, high-harmonic spectroscopy of solids has emerged as a fundamental technique giving access to information about intraband currents in bulk solids¹⁴, the Berry curvature¹⁵, many-body dynamics in strongly correlated systems¹⁶, or the ultrafast dynamics of carriers^17,18, among others.

During the last decade, there has been considerable interest in driving HHG with structured laser beams, in order to obtain coherent short-wavelength radiation with controlled spin (SAM) and/or orbital (OAM) angular momentum. Whereas SAM is connected to the field polarization—characterized by the spin index, σ = −1 for right (RCP) and σ = +1 for left (LCP) circularly polarization states—OAM is associated with the beam’s azimuthal phase variation¹⁹, and it is characterized by the topological charge, a discrete index that can take infinite integer values. Such laser sources are valuable tools for the ultrafast control of electronic currents at the nanoscale^20,21.

It is not trivial to convey the angular momentum properties of the driving beam into high-order harmonic radiation. For instance, in the case of gaseous targets, the efficiency of HHG drops drastically when driven by elliptically polarized fields²². Nevertheless, it is still possible to produce harmonic radiation with on-demand SAM from atomic targets by using rather sophisticated driver geometries, such as bicircular fields²³ or noncollinear beams^24,25, among others^26,27,28,29. In contrast, the topological charge of the high-order harmonics driven by linearly polarized single-OAM beams scales linearly with that of the driving field^30,31,32. The deep understanding of OAM-SAM conversion in HHG from gaseous targets, which requires a macroscopic description, has inspired the engineering of a wide variety of schemes that allow for the fine spatiotemporal control of the intensity, phase and polarization properties of the high-order harmonics^{33,34,35,36,37,38}. In this context, vector beams are particularly interesting. These beams result from the combination of raveled SAM and OAM modes. Among them, linear-polarized vector beams (LPVB) present a transversal distribution of linearly polarized states with different tilt-angles³⁹. This azimuthally-varying orientation confers the beam with a topological character, with a well-defined Poincare index⁴⁰. In this sense, it has already been demonstrated that the up-conversion of LPVBs to high-order harmonics in gases preserves the topology of the driving field^41,42.

The general scenario of SAM-OAM conversion in HHG changes completely in the case of solid targets, in particular for crystals, where symmetries can introduce anisotropy in their nonlinear optical response^{43,44,45,46,47,48}. The exploration of the interplay of the electromagnetic field topology and the target symmetries in HHG remains barely explored, being limited to the study of OAM conservation in semiconductors⁴⁹, to the best of our knowledge. In this sense, we shall see that the analysis of the topological properties of high-order harmonics driven in solids stands as a promising route for high harmonic spectroscopy of condensed matter⁵⁰.

In this article, we identify light’s topology as a property sensitive to the electronic dynamics in crystals, which establishes the basis of a topological approach to high harmonic spectroscopy. To do so, we explore the up-conversion to high-harmonics of an LPVB driver by single-layer graphene (SLG). The investigation of the coupling of light’s topology with crystal symmetries finds a privileged scenario in HHG from two-dimensional crystals driven by LPVB. On the one hand, their atomic-thin thickness excludes the effects of the propagation inside the target. On the other hand, the target presents well-defined symmetries that play a relevant role. As an example, the nonlinear response of SLG is sensitive to the driver’s polarization tilt-angle, with π/3 periodicity according to the hexagonal symmetry of the lattice⁴⁷. As a main result, we find that HHG from SLG driven by LPVB produces harmonic beams composed of a central vector beam, that retains the topological characteristics of the driving field, surrounded by a topological cluster encoding specific information about the crystal’s anisotropic nonlinear response. Therefore, the conservation of the driver’s topology in HHG found in isotropic targets⁴¹ is broken in the generation of the topological cluster. We present an analytical model that demonstrates how the topological structure of the harmonic far-field encodes unique information about the crystal’s nonlinear response. Indeed, sub-cycle dynamics, such as those arising from interband and intraband transitions, can be also distinguished through the topological structure of the harmonic beam. Therefore, we envisage a spectroscopic method that uses the parameters of the far-field topology to unveil details of the nonlinear response of the target. In addition, our work demonstrates that crystalline solid targets presenting a non-linear anisotropic response are suitable for the generation of structured short-wavelength radiation with intertwined SAM and OAM properties.

Results and discussion

We perform theoretical simulations of HHG in SLG driven by LPVB (see “Methods”), corresponding to a superposition of two counter-rotating circularly-polarized Laguerre-Gauss beams with opposite topological charges. The driver’s transverse profile at the focus can be described as:

$${{{{{{{\bf{E}}}}}}}}(\rho ,\varphi ,t)={U}_{0}(\rho ){e}^{-i\omega t}\left[{e}^{-i(\ell \varphi -{\theta }_{0})}{{{{{{{{\bf{e}}}}}}}}}_{L}+{e}^{+i(\ell \varphi -{\theta }_{0})}{{{{{{{{\bf{e}}}}}}}}}_{R}\right]$$

(1)

where ρ is the radius, φ the azimuth angle, ℓ is the absolute value of the OAM charge of the modes composing the LPVB, e_L,R are the left/right polarization vectors, and θ₀ defines the geometry of the beam’s polarization. For the particular case of ℓ = 1, θ₀ = 0 describes a radial vector beam and θ₀ = ±π/2 an azimuthal one. In the following, we shall consider a radial LPBV, therefore ℓ = 1 and θ₀ = 0. Note that, due to the opposite values of OAM and SAM of the composing modes, LPVB are vectorial fields with no net OAM or SAM. However, they are topologically characterized by their Poincaré index, ${{{{{{{\mathcal{P}}}}}}}}$—the number of complete rotations of the polarization tilt along a closed loop around the axis⁴⁰—which coincides with the OAM charge of the RCP mode, i.e., ${{{{{{{\mathcal{P}}}}}}}}=\ell$.

In Fig. 1 we show an overview of the topological high-harmonic spectroscopy. The interaction geometry studied in this work is sketched in Fig. 1a. We consider an eight-cycle (28 fs full width at half maximum in intensity), 3 μm wavelength driving pulse, with ${\sin }^{2}$ envelope and peak intensity of 5 × 10¹⁰ W/cm². The driving field, structured as an LPVB with beam waist 30 μm, is aimed at normal incidence onto an SLG sheet. Note that tighter focusing conditions, where the paraxial approximation is broken, would induce a non-negligible on-axis longitudinal component⁵¹.

Fig. 1: Overview of topological high-harmonic spectroscopy in graphene and argon.

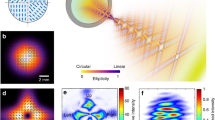
a Scheme of the interaction geometry for HHG in single-layer graphene driven by a mid-infrared (mid-IR) linearly-polarized vector beam (LPVB). The driving beam is aimed at a graphene sheet at normal incidence, where high-order harmonic generation (HHG) results in the emission of high-order harmonics. b Spatially-integrated far-field harmonic spectrum emitted by the graphene target when driven by an LPVB with Poincaré index ${{{{{{{\mathcal{P}}}}}}}}=1$—which corresponds to a radial vector beam. Total intensity and polarization profile of the driving LPVBs with Poincaré indices ${{{{{{{\mathcal{P}}}}}}}}=1$(c) and ${{{{{{{\mathcal{P}}}}}}}}=2$(d) for graphene and ${{{{{{{\mathcal{P}}}}}}}}=1$ for argon e Far-field total intensity (f–h) and polarization tilt-angle (i–k)—in the regions with an intensity over 10% of the maximum—for the 9th and 7th harmonics in graphene and the 25th harmonic in argon. The off-axis far-field intensity is magnified for the harmonics in graphene to show the details of the spatial profile.

We consider that, after generation at the graphene layer, the high-order harmonics are detected in the far field. Figure 1b depicts the spatially-integrated far-field harmonic spectrum generated in graphene by a radially polarized vector beam. As for gas targets, the spectrum presents a plateau of harmonics, a characteristic signature of the non-perturbative non-linear interaction. For the present driving field, the harmonic plateau extends up to the 9th order, followed by a cut-off frequency where harmonic efficiencies decrease at a ratio of approximately one order of magnitude per harmonic interval. The fundamental details of this structure can be understood in semiclassical terms, according to the recollision trajectories of electron-hole pairs excited at the neighborhood of the Dirac points¹².

We present in Fig. 1c, d, i the intensity and polarization profiles of the LPVB with ${{{{{{{\mathcal{P}}}}}}}}=1$ —which corresponds to a radially polarized vector beam—and ${{{{{{{\mathcal{P}}}}}}}}=2$ driving HHG in graphene and argon. The far-field intensity and linear-polarization tilt-angle distributions for two sample harmonics emitted from graphene (the 9th harmonic for the ${{{{{{{\mathcal{P}}}}}}}}=1$, and the 7th harmonic for the ${{{{{{{\mathcal{P}}}}}}}}=2$ driving fields) are shown in Fig. 1e–h. Results for the rest of the high-order harmonics are shown in Supplementary Note 3. For the sake of comparison, we show in Fig. 1j, k the far field of the 25th harmonic obtained in an Ar slab driven by a radially polarized beam (${{{{{{{\mathcal{P}}}}}}}}=1$). For this latter case, we have used standard parameters for HHG in Ar (50 μm-waist, 800 nm wavelength, peak intensity of 1.7 × 10¹⁴ W/cm² and same pulse envelope and duration as that used in graphene). While the vector beam character of the driver—intensity profile and ${{{{{{{\mathcal{P}}}}}}}}$—is translated into the harmonic emission in Ar, the up-conversion in graphene is much more complex.

To shed light on these results, we have analyzed in detail the two polarization components of the harmonic emission. Figure 2 shows the far-field intensity and phase distributions of the 9th and 7th harmonics depicted in Fig. 1 for the ${{{{{{{\mathcal{P}}}}}}}}=1$ and ${{{{{{{\mathcal{P}}}}}}}}=2$ LPVB drivers, decomposed into their LCP (see Fig. 2a, c, e, g) and RCP (see Fig. 2b, d, f, h) components.

Fig. 2: Far-field harmonic emission profiles of the left (LCP) and right (RCP) circularly polarized components.

Far-field intensity and phase distributions for the LCP and RCP components of the 9th (a–d) and 7th (e–h) harmonics for single layer graphene driven by the ${{{{{{{\mathcal{P}}}}}}}}=1$ and ${{{{{{{\mathcal{P}}}}}}}}=2$ linearly polarized vector beams, respectively.

The diffraction patterns of the two polarization components are displaced from each other. This demonstrates that SLG’s diffraction of the harmonic field is spin-dependent, a consequence of the anisotropic character of its non-linear response. Note also that only at low-divergence angles, both polarization modes fully overlap.

Further analysis of the harmonic far-field characteristics can be drawn by exploring the particular OAM composition of each of the polarization modes. To do so, we perform the Fourier Transform of the harmonic field along the azimuthal coordinate, and we integrate its modulus squared over the radial coordinate. In Fig. 3, we plot the OAM content of the LCP (red) and RCP (blue) harmonic emission in SLG driven by Fig. 3a a ${{{{{{{\mathcal{P}}}}}}}}=1$ and Fig. 3b a ${{{{{{{\mathcal{P}}}}}}}}=2$ LPVB as a function of the harmonic order. For the sake of comparison we include in Fig. 3c results in Ar driven by a ${{{{{{{\mathcal{P}}}}}}}}=1$ LPVB. In this latter case each polarization mode of the harmonic field is composed of the same OAM components as in the driving field⁴¹. It is worth mentioning that, for the same gas target driven by a vector-vortex beam, i.e., a vector beam with non-zero net topological charge, it has been shown that the harmonic topological charge scales linearly with the OAM charge of the driver^42,52. The comparison of the results in Fig. 3 demonstrates that the harmonic build-up in graphene is far more complex than in isotropic targets. The OAM content of each polarization mode is extended in steps Δℓ = ±6ℓ, a consequence of graphene’s 6-fold rotational symmetry. Note also that all harmonic orders present the same OAM content.

Fig. 3: Comparison of the orbital angular momentum (OAM) carried by the high-order harmonics emitted from anisotropic and isotropic targets.

OAM content of the left circularly polarized (LCP) and right circularly polarized (RCP) components of the HHG spectrum driven by a linearly polarized vector beam (LPVB) with ${{{{{{{\mathcal{P}}}}}}}}=1$(a) and with ${{{{{{{\mathcal{P}}}}}}}}=2$(b) in graphene. The interplay between the driving beam and crystal symmetries leads to the appearance of higher components—different from those of the driver—in the OAM content of the harmonic beams. For comparison, the OAM content obtained in argon driven by an LPVB with ${{{{{{{\mathcal{P}}}}}}}}=1$ is shown in (c). The OAM is extracted from the Fourier transform of the harmonic field along the azimuthal coordinate.

In order to understand the far-field characteristics of the harmonic emission presented in the previous section, we derive an analytical model by means of a Fraunhofer integration that demonstrates the coupling between the target symmetries and the driving field’s topology. Such understanding allows us to propose a topological harmonic spectroscopy scheme by solving the inverse problem: to identify the crystal’s nonlinear response properties through the topological structure of the far-field harmonic emission. This method is derived to consider any crystalline structure, though we have validated it in the case of SLG.

Understanding the coupling between the target symmetries and the driving field’s topology

In this section, we derive an analytical model for the high harmonic far-field profile that allows us to obtain and understand its properties from the near-field harmonic emission. We show the near-field total intensity (Fig. 4a, g) and ellipticity (Fig. 4b, h) distributions of the 9th and 7th harmonics obtained from our simulations of SLG, driven by ${{{{{{{\mathcal{P}}}}}}}}=1$ and ${{{{{{{\mathcal{P}}}}}}}}=2$ LPVBs, respectively, as well as the intensity and phase profiles of the LCP (Fig. 4c, d, i, j) and RCP (Fig. 4e, f, k, l) components. The amplitudes of both polarization components are connected by a mirror transformation, φ → −φ. This symmetry is inherited from the driving field, and it is preserved during HHG, as a consequence of the mirror reflection symmetry stemming from the point group of graphene, namely the dihedral group D_6h.

Fig. 4: Near-field harmonic emission profiles obtained in anisotropic and isotropic targets.

Near-field intensity, ellipticity and phase properties of the 9th (a–f) and 7th (g–l) harmonics in single-layer graphene driven by a ${{{{{{{\mathcal{P}}}}}}}}=1$ and ${{{{{{{\mathcal{P}}}}}}}}=2$ linearly polarized vector beam (LPVB), respectively. The decomposition into polarization components evidences the connection through a mirror transformation of the left circularly polarized (LCP) (c, d, i, j) and right circularly polarized (RCP) (e, f, k, l) intensity and phase distributions. For the sake of comparison, m, n show the near-field LCP component’s intensity and phase distributions of the 25th harmonic in argon driven by a ${{{{{{{\mathcal{P}}}}}}}}=1$ LPVB. The ellipticity ϵ is computed from the Stokes parameters, where ϵ = ±1 corresponds to LCP (+) and RCP (−) fields, respectively.

For the sake of comparison, we show in Fig. 4m, n the intensity and phase profiles of the LCP component of the 25th harmonic obtained in Ar driven by a ${{{{{{{\mathcal{P}}}}}}}}=1$ LPVB. In this case, as for any isotropic target, the RCP component shows an identical intensity profile as the LCP and conjugated phase. As a consequence, the superposition of both polarization modes results in an LPVB harmonic near-field with the same topology, same ${{{{{{{\mathcal{P}}}}}}}}$, as the driver. Therefore, HHG in gases can be regarded as a topologically invariant frequency up-conversion of the driving field—${{{{{{{\mathcal{P}}}}}}}}$ being the topological invariant—resulting from the isotropic character of the non-linear response of the gas.

In sharp contrast, the harmonic near-field intensity obtained from SLG is structured into a necklace pattern (Fig. 4a, g). The necklace beads correspond to target regions where the driver’s polarization tilt coincides with those angles where the SLG anisotropy shows a stronger non-linear response⁴⁷. In correspondence, the harmonic phase and ellipticity distributions are modulated, as shown in Fig. 4b, d, f, h, j, l. Note therefore that, as a result of the SLG anisotropic non-linear response, the harmonic near-field emitted by SLG does not correspond anymore to an LPVB, meaning that the ${{{{{{{\mathcal{P}}}}}}}}$ topological invariance in HHG is broken.

According to Fig. 3, the amplitude of each polarization mode of the harmonic field can be cast into a superposition of OAM modes. Thus, in the general case of a target of N-fold symmetry, the near field amplitude can be expressed as:

$${F}_{q}^{\pm }(\rho ,\varphi )={e}^{\pm i\ell \varphi }\mathop{\sum }\limits_{s=-\infty }^{\infty }{c}_{q,s}^{\pm }(\rho )\,{e}^{\pm iNs\ell \varphi },$$

(2)

where q is the harmonic order, and ${c}_{q,s}^{\pm }(\rho )$ are complex Fourier amplitudes. The upper/lower sign in Eq. (2) applies to the RCP/LCP components of the field, respectively. Factoring the near-field as a product of the driving field amplitude times the material response function (susceptibility)—i.e., the first factor and the sum term in Eq. (2)—the susceptibility χ_q of the non-linear response of the target is defined by the near-field amplitudes as:

$${\chi }_{q}^{\pm }(\rho ,\varphi )\propto \mathop{\sum }\limits_{s=-\infty }^{\infty }{c}_{q,s}^{\pm }(\rho )\,{e}^{\pm iNs\ell \varphi }$$

(3)

The rotational symmetry of the target response reflects the coupling between the target’s symmetry, C_N, and the driving field Poincaré’s topological index, ${{{{{{{\mathcal{P}}}}}}}}=\ell$, thus revealing the fundamental coupling between the target symmetries and the driving field’s topology in HHG.

Taking into account the near-field harmonic description, we now derive an analytical model to reproduce the far-field harmonic profile, in order to understand its topological properties. To do this, we simplify the near-field harmonic emission ${F}_{q}^{\pm }(\rho ,\varphi )$ in Eq. (2) to a circumference with amplitude ${F}_{q}^{\pm }({\rho }_{0},\varphi )$, ρ₀ corresponding to the radius of maximum intensity in Fig. 4a, g. We use this expression to compute the Fraunhofer integral for the far-field distribution (see Methods “Derivation of the analytical far-field model”), which reads as:

$${U}_{q}^{\pm }(\beta ,\phi )=\mathop{\sum}\limits_{s}{\eta }_{q,s}^{\pm }{J}_{\pm (Ns+1)\ell }\left(\kappa \beta \right){e}^{\pm i(Ns+1)\ell \phi }$$

(4)

where (β, ϕ) are the radial and azimuthal far-field angular coordinates, and κ = 2πqρ₀/λ, λ being the driver’s wavelength. The coefficients ${\eta }_{q,s}^{\pm }$ are complex amplitude factors proportional to the near-field Fourier components ${{c}_{q,s}}^{\pm }({\rho }_{0})$: ${\eta }_{q,s}^{\pm }=-2\pi i\frac{q{\rho }_{0}}{\lambda D}{e}^{i2\pi qD/\lambda }{c}_{q,s}^{\pm }({\rho }_{0}){e}^{\mp i(Ns+1)\ell \pi /2}$. In Fig. 5a, we plot the far-field intensity profile of the LCP component of the 9th harmonic from SLG computed from our model—Eq. (4) using N = 6. The excellent agreement between the main features of the results from our simplified model and the exact results (Fig. 2a) allows us to use this model to analyze the topological structure of the far-field harmonics.

Fig. 5: The inverse problem: retrieving the nonlinear response from the topological harmonic properties.

Harmonic far-field from our simplified model and its reconstruction using a topological cluster of vortices. a Intensity profile of the left circularly polarized (LCP) component of the 9th harmonic from single-layer graphene driven by a ${{{{{{{\mathcal{P}}}}}}}}=1$ LPVB, obtained from the analytical far-field model, given by Eq. (4). The resulting far-field profile can be decomposed into a topological cluster of vortices with ℓ = 1 and radius a₀, as depicted by the red lines in (b): a central vortex and a necklace of radius r₁ = 4.1a₀ composed of Nℓ = 6 vortices. The excellent agreement of the resulting far-field intensity profile reconstructed from the topological cluster in (b), given by Eq. (8), compared to (a) and Fig. 2a, demonstrates the working principle of topological harmonic spectroscopy.

Topological harmonic spectroscopy

Inspired by the results presented in Figs. 2 and 5a, we propose to decompose a general far-field harmonic profile into a topological cluster. Indeed, the far-field profile in Eq. (4) can be rewritten as the superposition of vortices. Such cluster is composed by the repetition of a single elemental vortex structure, with topological charge ℓ and radius a₀. First, the central component of the cluster propagates on axis, therefore it is given by:

$${U}_{q}^{\pm ,0}(r,\phi )={A}_{0}{J}_{\pm \ell }\left({z}_{\ell }\frac{r}{{a}_{0}}\right){e}^{\pm i\ell \phi },$$

(5)

where z_ℓ is the position of the first amplitude maximum of the Bessel function J_ℓ(z), and r and ϕ are the polar coordinates of the far-field plane. Note that the far-field divergence β and the radial coordinate r are related through the distance to the detector, D, by β ≈ r/D. Second, the other vortices composing the cluster, present diverging centers and are organized as set of necklaces with radii r_ν, ν > 0 being the necklace index (see red lines in Fig. 5a). Each necklace ν is composed by a regular distribution of Nℓ vortices, placed at azimuthal angles ${\phi }_{n,\nu }^{\pm }=2\pi n/N\ell \pm {\phi }_{0,\nu }$. Therefore, the ν necklace field is given by:

$${U}_{q}^{\pm ,\nu }(r,\phi )={A}_{\nu }\mathop{\sum }\limits_{n=0}^{N\ell -1}{J}_{\pm \ell }\left({z}_{\ell }\frac{\sqrt{{(x-{x}_{n}^{\pm ,\nu })}^{2}+{(y-{y}_{n}^{\pm ,\nu })}^{2}}}{{a}_{0}}\right){e}^{\pm i\ell \arctan \frac{y-{y}_{n}^{\pm ,\nu }}{x-{x}_{n}^{\pm ,\nu }}}$$

(6)

where $x=r\cos \phi$, $y=r\sin \phi$ are the far-field cartesian coordinates, and ${x}_{n}^{\pm ,\nu }={r}_{\nu }\cos {\phi }_{n}^{\pm }$ and ${y}_{n}^{\pm ,\nu }={r}_{\nu }\sin {\phi }_{n}^{\pm }$ denote the position of the vortex centers within the necklace. Figure 5b shows the resulting superposition of the central vortex and the first necklace, with the choices A₁/A₀ = 0.55e^−i0.45π, r₁ = 4.1a₀, and ϕ_0,1 = 12°. As it can be observed, an excellent description of the far-field harmonic profile can be given equivalently either by a polar distribution of a set of on-axis vortices—obtained through the analytical far-field model given by Eq. (4)—or by a topological cluster composed of identical vortices distributed as necklaces around a central one—given by Eq. (6). Note that from the practical viewpoint, this later representation is described by geometrical parameters: the vortex and necklace radii (a₀ and r_ν), and the necklace rotation (ϕ_0,ν), which can be well determined by a simple inspection of the far-field intensity profile. On the other hand, the contrast ratios A_ν/A₀ can be also found by best fit from the far-field intensity distribution.

The configuration of the far-field topological cluster, therefore, encodes the details of the non-linear response of the target, as depicted by Eq. (3), defining topology as a relevant spectroscopic observable. The suitability of the topological approach can be demonstrated by determining the direct relationship between the geometrical parameters of the far field vortices and the Fourier components (c_s) describing the material response (see Eq. (3)). To this aim, we use the equivalence between the far-field descriptions: the polar description of on-axis vortices—Eq. (4)—and the topological cluster composed of necklaces of displaced vortices—Eq. (6). As we demonstrate in the Methods section, the necklace of displaced vortices ν can be re-written as:

$${U}_{q}^{\pm ,\nu }(r,\phi )={A}_{\nu }N\ell {e}^{\pm i\ell \phi }\mathop{\sum}\limits_{s}{e}^{\pm iNs\ell (\phi \mp {\phi }_{0,\nu })}{J}_{\pm Ns\ell }\left({z}_{\ell }\frac{{r}_{\nu }}{{a}_{0}}\right){J}_{\pm (Ns+1)\ell }\left({z}_{\ell }\frac{r}{{a}_{0}}\right).$$

(7)

Considering the on-axis vortex, which is given by ${U}_{q}^{\pm ,0}(r,\phi )={A}_{0}{J}_{\pm \ell }\left({z}_{\ell }\frac{r}{{a}_{0}}\right){e}^{\pm i\ell \phi }$, the total far field can be expressed as:

$${U}_{q}^{\pm }(r,\phi ) = \mathop{\sum}\limits_{\nu }{U}_{q}^{\pm ,\nu }(r,\phi )\\ = \,N\ell \mathop{\sum}\limits_{s}\left[\mathop{\sum}\limits_{\nu > 0}{A}_{\nu }{e}^{-iNs\ell {\phi }_{0,\nu }}{J}_{\pm Ns\ell }\left({z}_{\ell }\frac{{r}_{\nu }}{{a}_{0}}\right)\right]{J}_{\pm (Ns+1)\ell }\left({z}_{\ell }\frac{r}{{a}_{0}}\right){e}^{\pm i(Ns+1)\ell \phi }\\ +{A}_{0}{J}_{\pm \ell }\left({z}_{\ell }\frac{r}{{a}_{0}}\right){e}^{\pm i\ell \phi }.$$

(8)

Comparing Eqs. (8) to (4), we find two relevant relationships. On the one hand, through inspection of the arguments of the Bessel functions of order ±(Ns + 1)ℓ we can extract the ratio between the radius of the elemental vortex composing the far-field topological cluster (a₀) and the distance from the target to the far-field plane (D) as:

$$\frac{{a}_{0}}{D}=\frac{{z}_{\ell }\lambda }{2\pi q{\rho }_{0}}.$$

(9)

This allows us to establish a direct relationship between the vortex radii, a₀, with the radius of the driving LPVB, ρ₀. On the other hand, a second condition is given by:

$${c}_{q,s}^{\pm }({\rho }_{0})={i}^{\pm Ns\ell }{K}_{\ell }^{\pm }N\ell \mathop{\sum}\limits_{\nu > 0}{A}_{\nu }{e}^{-iNs\ell {\phi }_{0,\nu }}{J}_{\pm Ns\ell }\left({z}_{\ell }\frac{{r}_{\nu }}{{a}_{0}}\right)\,{{\mbox{for}}}\,s\ , \ne \, 0$$

(10)

$${c}_{q,0}^{\pm }({\rho }_{0})={K}_{\ell }^{\pm }\left[{A}_{0}+N\ell \mathop{\sum}\limits_{\nu > 0}{A}_{\nu }{J}_{0}\left({z}_{\ell }\frac{{r}_{\nu }}{{a}_{0}}\right)\right],$$

(11)

with ${K}_{\ell }^{\pm }={i}^{\pm \ell +1}{e}^{-i2\pi qD/\lambda }{a}_{0}/{z}_{\ell }$. Thus, Eqs. (10) and (11) demonstrate that the target response, Eq. (3), is completely defined by the characteristics of the topological objects that describe the harmonic far field. Additionally, Eqs. (10) and (11) ground a basic procedure for topological spectroscopy: once the topological structure of the harmonic far-field is recorded, the nonlinear response of the target can be extracted. In particular, by measuring the number (ν) and rotation (ϕ_0,ν) of the necklaces, the necklace to vortex radii ratio (r_ν/a₀), and the amplitudes ratio of the necklace vortices to the central one (A_ν/A₀), and assuming vortices with Bessel profiles—as those shown in Eq. (6)—Eqs. (10) and (11) can be used to recover the Fourier components of the target response in a circle of radius ρ₀—i.e., the circle of intensity maxima of the driving LPVB. The direct map of the driver’s azimuth to the polarization, characteristic in an LPVB, allows using the inverse Fourier transform of the coefficients ${c}_{q,s}^{\mp }$ to recover the q-th harmonic non-linear anisotropic response of the target. In addition, it holds the potential to uncover the possible inhomogeneous response of the target response along the circle of maximum intensity of the driver.

As a proof of concept, we apply the above steps to the 9th order harmonic far field obtained numerically from an ${{{{{{{\mathcal{P}}}}}}}}=1$ LPVB driver with ρ₀ = 22 μm, as shown in Fig. 2a, c. As we mentioned above, a simple best-fit analysis yields a far-field cluster composed by an on-axis vortex and a single necklace of Nℓ = 6 vortices, with rotation ϕ_0,1 = 12^∘, an amplitude ratio A₁/A₀ = 0.55e^−i0.45π, and a radius r₁ = 4.1a₀. For these parameters, Eq. (9) gives a₀/D = 4.44 mrad. Feeding Eqs. (10) and (11) with these necklace and vortex parameters we can find the values of the 9th-harmonic response coefficients c_9,0, c_9,±1 defined in Eq. (3). The relative ratios found are c_9,1/c_9,0 = ±0.84 × e^i0.22π and c_9,−1/c_9,0 = ±0.83 × e^−i0.87π. Taking into account that the ratios between the Fourier components of the computed near-field shown in Fig. 5 are c_9,1/c_9,0 = 0.83 × e^i0.35π and c_9,−1/c_9,0 = 0.83 × e^−0.84π, and that we have only considered the central vortex, ν = 0 and the first necklace ν = 1, our results demonstrate the potentiality of topological high harmonic spectroscopy to extract information about the anisotropic crystal’s response. In Supplementary Note 2, we demonstrate that this method can be applied to identify the role of interband and intraband contributions to HHG. However, we note that the proposed method would highly benefit from further developments in retrieval algorithms that can infer the anisotropic response through topological far-field traces.

Conclusion

We have demonstrated a scenario for high-harmonic spectroscopy stemming from the interaction of structured driving beams with crystalline solid targets. In contrast to isotropic gaseous targets, we show that crystal symmetries couple with the driving beam’s topology during HHG. The signature of this coupling is encoded into a complex spatial structure in the emitted harmonics. Particularly, we unveil this intertwined photon conversion by studying HHG from single-layer graphene driven by LPVB. We show that, in contrast to the isotropic case, the harmonics generated from crystal targets can break the conservation of the driver’s topological structure, according to their constituent symmetries. We provide an analytical derivation that allows to (1) predict the topology of the high harmonic beams from the target’s anisotropic symmetry, and (2), retrieve the anisotropic response of the target from the topology of the high harmonic beams. As a consequence, high harmonic spectroscopy based on topology allows to extract spatially resolved information about the nonlinear response of the target, which can not be obtained with standard spectroscopic techniques.

Though we have demonstrated the interplay of the vector beam driver topology with the target’s symmetries in two-dimensional materials such as graphene, we believe our results open a general scenario for topological optics in which the target’s non-linear response is coupled with the topological structure of light. Note that propagation effects may play a relevant role in the case of HHG in bulk crystals^44,45. In general, any property that presents an anisotropic HHG response could be characterized. For example, interband and intraband contributions to HHG respond differently to the driver’s ellipticity in bulk silicon⁴⁴, and as such the nature of the harmonic’s contribution can be characterized through its topology when driven by properly chosen vector beams (see Supplementary Note 2). Finally, we believe that this technique can be further used to characterize more complex targets such as polycrystals^53,54 or heterostructures⁵⁵.

Methods

Numerical simulations of high-harmonic generation in graphene and in gases

HHG driven by structured beams requires the computation of the macroscopic response of the target. Our strategy follows the discrete-dipole approximation method presented in ref. ⁵⁶, which has been recently also applied to graphene polycrystals⁵⁴. In this method, the graphene target is divided into a set of elemental surfaces of dimensions small enough to assume the local field profile constant, but still enclosing a sufficient number of graphene’s lattice cells to allow the approximation of the Brillouin zone as a continuous region. Next, we integrate the Schrödinger equation to obtain the mean dipole acceleration in each elementary surface. The dipole acceleration is used to compute the time derivative of the current density, which is proportional to the radiated near-field, and used as a source for the electromagnetic field propagator, in order to find the far-field distribution. Dynamics of the SLG interaction with the driving field is integrated from the Schrödinger equation in the nearest neighbor tight-binding approximation^12,56. We have also implemented the laser-driven dynamics in SLG through the semiconductor Bloch equations (SBE). The comparison between the macroscopic TDSE and SBE simulations (see Supplementary Note 1) demonstrates that our results do not depend on the formalism used to calculate the current density.

In order to compare the results of HHG from SLG with that from an isotropic target, we have conducted calculations of HHG in an infinitely thin Ar gas jet. For this, we have followed the method presented in ref. ⁵⁷, that has been successfully validated against several experiments (see for example^{24,25,27,36,37,38,41,52}). Similarly to the procedure used for SLG, discussed in the above paragraph, the gas target is split into elemental emitters. The dipole acceleration in each emitter is computed using the strong field approximation, without resorting to the saddle-point approximation.

Derivation of the analytical far-field model

In our model we consider a simplified representation of the q-th harmonic near-field as a circumference of radius of maximal amplitude ρ₀, which also corresponds to the radius of maximum intensity of the driving field, as:

$${R}_{q}^{\pm }(\rho ,\varphi )={F}_{q}^{\pm }(\rho ,\varphi )\delta (\rho -{\rho }_{0}),$$

(12)

with ${F}_{q}^{\pm }(\rho ,\varphi )$ the near-field azimuthal profile, Eq. (2), and (ρ, φ) the near-field radial and azimuthal coordinates, respectively. In the results presented in this work for SLG, ρ₀ corresponds to 22 μm for the ${{{{{{{\mathcal{P}}}}}}}}=1$ LPVB, and 25 μm for the ${{{{{{{\mathcal{P}}}}}}}}=2$ LPVB.

We compute the harmonic far-field amplitude, ${U}_{q}^{\pm }(\beta ,\phi )$, from the Fraunhofer integral of the near-field ${R}_{q}^{\pm }(\rho ,\varphi )$. Using Eq. (2), and after the trivial radial integration, we obtain:

$${U}_{q}^{\pm }(\beta ,\phi )=-iq\frac{{e}^{i2\pi Dq/\lambda }}{\lambda D}{\rho }_{0}\mathop{\sum }\limits_{s=-\infty }^{\infty }{c}_{q,s}^{\pm }({\rho }_{0})\int\nolimits_{0}^{2\pi }d\varphi \,\,{e}^{\pm i(Ns+1)\ell \varphi }{e}^{-i\kappa \beta \cos (\phi -\varphi )}$$

(13)

with κ = 2πqρ₀/λ, λ being the driver’s wavelength, and (β, ϕ) the far-field divergence and azimuthal angles, respectively. Using the identity:

$${e}^{i\alpha \cos (\phi -\varphi )}=\mathop{\sum}\limits_{m}{i}^{m}{J}_{m}(\alpha ){e}^{im(\phi -\varphi )},$$

(14)

the azimuthal integral in Eq. (13) leads to the condition m = ∓(Ns + 1)ℓ, and thus Eq. (13) leads to Eq. (4).

Derivation of the topological cluster

A vortex necklace is a distribution of identical vortices with centers equally distributed along a ring of radius r_ν. To compute the polar form of such structure, we shall first find the polar expression of an off-axis vortex with center at an arbitrary coordinate (x_n, y_n), as:

$${V}_{\ell }^{({x}_{n},{y}_{n})}(x,y)={V}_{0}{J}_{\ell }\left(\frac{{z}_{\ell }}{{a}_{0}}\sqrt{{(x-{x}_{n})}^{2}+{(y-{y}_{n})}^{2}}\right){e}^{i\ell \arctan \frac{y-{y}_{n}}{x-{x}_{n}}},$$

(15)

where (x, y) are the far-field cartesian coordinates. Equation (15) corresponds to the translation of the on-axis vortex ${V}_{\ell }^{(0,0)}$ to the point (x_n, y_n). To compute the polar form of Eq. (15), we apply the translation as a phase shift in Fourier space:

$${\tilde{V}}_{\ell }^{({x}_{n},{y}_{n})}({k}_{x},{k}_{y})={e}^{-i{k}_{x}{x}_{n}}{e}^{-i{k}_{y}{y}_{n}}{\tilde{V}}_{\ell }^{(0,0)}({k}_{x},{k}_{y}).$$

(16)

Defining the far-field polar coordinates in real and Fourier spaces as (r, ϕ) and (k, φ), respectively, we use the coordinate transformations $x=r\cos \phi$, $y=r\sin \phi$, ${k}_{x}=k\cos \varphi$ and ${k}_{y}=k\sin \varphi$, to compute ${\tilde{V}}_{\ell }^{(0,0)}$ in polar coordinates as:

$${\tilde{V}}_{\ell }^{(0,0)}(k,\varphi ) =\frac{{V}_{0}}{2\pi }\iint {J}_{\ell }\left({z}_{\ell }\frac{r}{{a}_{0}}\right){e}^{i\ell \phi }{e}^{-ikr\cos (\phi -\varphi )}rdrd\phi \\ ={i}^{-\ell }{V}_{0}{e}^{i\ell \varphi }\int{J}_{\ell }\left({z}_{\ell }\frac{r}{{a}_{0}}\right){J}_{\ell }(kr)rdr \\ ={i}^{-\ell }{V}_{0}\frac{{a}_{0}}{{z}_{\ell }}\delta \left(\frac{{z}_{\ell }}{{a}_{0}}-k\right){e}^{i\ell \varphi }$$

(17)

where, for the last step, we have used the identity:

$$\frac{1}{x}\delta (x-a)=\int\nolimits_{0}^{\infty }{J}_{\ell }(xt){J}_{\ell }(at)tdt.$$

(18)

Defining ${x}_{n}={r}_{n}\cos {\phi }_{n}$ and ${y}_{n}={r}_{n}\sin {\phi }_{n}$, we can compute ${V}_{\ell }^{({x}_{n},{y}_{n})}$ in Eq. (15) in polar coordinates as the inverse Fourier transform of ${\tilde{V}}_{\ell }^{({x}_{n},{y}_{n})}$ in Eq. (16), leading to:

$${V}_{\ell }^{({r}_{n},{\phi }_{n})}(r,\phi )=\frac{1}{2\pi }\iint {\tilde{V}}_{\ell }^{(0,0)}(k,\varphi ){e}^{-ik{r}_{n}\cos (\varphi -{\phi }_{n})}{e}^{ikr\cos (\varphi -\phi )}kdkd\varphi .$$

(19)

Using Eqs. (17) and (14), we find from Eq. (19) the polar description for the vortex displaced to (x_n, y_n) as:

$${V}_{\ell }^{({r}_{n},{\phi }_{n})}(r,\phi )={(-1)}^{\ell }{V}_{0}{e}^{i\ell \phi }\mathop{\sum}\limits_{m}{e}^{-im(\phi -{\phi }_{n})}{J}_{m}\left(\frac{{z}_{\ell }}{{a}_{0}}{r}_{n}\right){J}_{m-\ell }\left(\frac{{z}_{\ell }}{{a}_{0}}r\right).$$

(20)

Correspondingly, using Eq. (20) the polar expression of the vortex necklace with radius r_ν defined in Eq. (6) is given by:

$${U}_{q}^{\pm ,\nu }(r,\phi ) =\mathop{\sum }\limits_{n=0}^{N\ell -1}{V}_{\pm \ell }^{({r}_{\nu },2\pi \ell \frac{n}{N}\mp {\phi }_{0,\nu })}(r,\phi )\\ ={A}_{\nu }N\ell {e}^{\pm i\ell \phi }\mathop{\sum}\limits_{s}{e}^{\pm iNs\ell (\phi \mp {\phi }_{0,\nu })}{J}_{\pm Ns\ell }\left(\frac{{z}_{\ell }}{{a}_{0}}{r}_{\nu }\right){J}_{\pm (Ns+1)\ell }\left(\frac{{z}_{\ell }}{{a}_{0}}r\right),$$

(21.)