Identifying key players in complex networks via network entanglement

Abstract

Empirical networks exhibit significant heterogeneity in node connections, resulting in a few vertices playing critical roles in various scenarios, including decision-making, viral marketing, and population immunization. Thus, identifying key vertices is a fundamental research problem in Network Science. In this paper, we introduce vertex entanglement (VE), an entanglement-based metric capable of quantifying the perturbations caused by individual vertices on spectral entropy, residing at the intersection of quantum information and network science. Our analytical analysis reveals that VE is closely related to network robustness and information transmission ability. As an application, VE offers an approach to the challenging problem of optimal network dismantling, and empirical experiments demonstrate its superiority over state-of-the-art algorithms. Furthermore, VE also contributes to the diagnosis of autism spectrum disorder (ASD), with significant distinctions in hub disruption indices based on VE between ASD and typical controls, promising a diagnostic role for VE in ASD assessment.

Introduction

Complex systems, such as ecological¹, social², neuronal³, and economic⁴ systems, are ubiquitous and can be abstracted and studied as networks⁵. Key players in a complex network refer to a small part of vertices that play a vital role in the structure and function of the network⁶. The study of identifying a set of key players helps answer a range of critical questions from biology to marketing to immunization: Which set of influential individuals should we choose as seeds to trigger a cascade in viral marketing²? Which kind of species could trigger dramatic changes to the entire ecosystem if they were to demise⁷? Which groups should be prioritized for vaccination given the limited number of vaccines available^8,9?

In practice, finding the optimal set of players in a given networked system has far-reaching effects in various disciplines. In previous studies, a great deal of work has been devoted to exploring how to find key players in specific networks^6,10,11. Most research ranks players using neighborhood-based centralities, path-based centralities, iterative refinement centralities, or dynamics-based methods^12,13,14. See Supplementary Note 1 for a detailed introduction. With the recent fast development of quantum-based processes on networks^15,16,17, identifying key players in complex networks via network entanglement presents a promising solution to these issues.

Quantum entanglement is a precious quantum resource for computation and communication¹⁸. The distance between quantum entangled states and the set of separable states is one of the quantum entanglement metrics^19,20,21. Inspired by quantum statistical mechanics and collective network entanglement¹⁶, this paper proposes an entanglement-based approach described by a Gibbsian-like density matrix. Spectral entropy captures the global topological feature of the network rather than a subset of the network’s descriptors²². Vertex entanglement reflects the spectral entropy variance between the v-control network and the original network, indicating changes caused by a single vertex to spectral entropy. The theoretical analysis and empirical experiments show that vertex entanglement is closely related to the dynamic diversity of information and network robustness. Specifically, the vertex entanglement tends to vanish in a transient diffusion time, while it coincides with the number of connected components at extremely large time scales. The proposed approach is partially based on the original framework of collective network entanglement (CNE)¹⁶, which essentially measures the difference between the original graph and the sum of two subgraphs, i.e., a star graph formed by a detached node with its edges and the remainder of the original graph. Therefore, CNE measures how subadditive the entropy of these networks is. However, in our approach, VE directly calculates the difference in terms of spectral entropy between the original network and the perturbed network, which is closer to the mathematical nature of quantum resource theory¹⁸ and is computationally more efficient.

The issue of optimal network dismantling or percolation is a non-deterministic polynomial-time hard (NP-hard) problem⁹. One critical application of vertex entanglement is network dismantling, where VE addresses two previously neglected but critical issues. The first concern pertains to network integrity, which refers to the network’s ability to maintain its normal inter-node communication and other functions in the face of an attack¹⁶. Comprehending the information propagation mechanism in a network goes beyond simply identifying the shortest path²³. Therefore, to thoroughly analyze how information propagates in networks and is affected by perturbations, we necessitate a multiscale framework that can distinguish network response from micro, meso, and macroscales. Secondly, most centrality metrics predominantly focus on partial aspects of a network’s structure or local topological features, such as degree and betweenness²⁴, rather than considering the global structure of the system as a whole. As a result, these measures may not accurately capture the full complexity of the network and are prone to miss important information. Vertex entanglement, which is based on the global properties of the network, provides a promising approach to address the network dismantling problem as it is closely correlated with network robustness and connectivity. By conducting targeted attack experiments on various empirical systems, we find that VE outperforms other state-of-the-art algorithms in network dismantling, and networks will collapse rapidly once highly entangled vertices fail or are attacked. Another essential application of vertex entanglement is to assist in the diagnosis of autism spectrum disorder (ASD)²⁵, a disorder caused by a developmental brain impairment^26,27. To be specific, significant differences are detected between ASD and typical controls on the hub disruption indices based on vertex entanglement. Moreover, the hub disruption indices display a significant positive correlation with the intelligence quotient (IQ) of ASD participants, suggesting that VE may contribute to the prediction of behavioral characteristics of ASD participants.

Results

In this section, we first introduce the required theoretical grounds for the new metric vertex entanglement and clarify its definition. Then we analyze the correlations between VE and four node centralities, and explore VE’s application in network dismantling and ASD diagnosis.

Network information theory

The possibility of extending theoretical measures of quantum information to complex systems has been investigated in terms of the statistical field theory of information dynamics^15,28. Take into account a network $G({{{{{{{\mathcal{V}}}}}}}},{{{{{{{\mathcal{E}}}}}}}})$ with a set of nodes ${{{{{{{\mathcal{V}}}}}}}}$ and a set of links ${{{{{{{\mathcal{E}}}}}}}}$. Its adjacency matrix A can fully encode the connectivity of the network, with entry A_ij being the link’s weight from node i to j. If a vector ψ(τ) encodes the amount of information about all nodes at a given time τ, then its evolution process can be described as ψ(τ) = e^−τLψ(0). Here, ψ(0) denotes the initial state, e^−τL is the diffusion propagator, L = D − A is the combinatorial graph Laplacian matrix, and D is the diagonal matrix with the degree sequence along the diagonal. D_ij is defined as δ_ijk_i, where δ_ij is Kronecker function and k_i = ∑_jA_ij.

Inspired by quantum information theory, the density matrix of network G, denoted as ρ, was proposed in terms of the normalized diffusion propagator²² as

$$\rho =\frac{{e}^{-\tau L}}{Z},$$

(1)

where $Z=tr\left({e}^{-\tau L}\right)$ is the partition function of the system, and the positive parameter τ encodes the diffusion propagation time. It can be easily confirmed that ρ is a semi-positive matrix with a trace equal to one, satisfying the same mathematical conditions as a density matrix²⁹, that is, ρ can be regarded as the density matrix for networks. Recently, a generalized network density representation has also been proposed, expanding the range of applicability of the framework to nonlinear dynamics³⁰.

One cardinal concept of classical information theory is Shannon entropy³¹, which is related to the amount of disorder and information in systems³². This concept can be extended to the quantum realm by replacing probability distributions with density operators and Shannon entropy with the von Neumann entropy³². Naturally, we are also interested in studying complex networks from the perspective of information processing.

When it comes to complex systems, several entropies have been introduced, such as the remaining degree³³ and shortest path distribution^34,35. However, these entropies merely take into account the network’s local properties. A cutting-edge research direction in complex networks is the integration of quantum information theory^15,16. Spectral entropy²² serves as a network counterpart of von Neumann entropy based on the network density matrix, and it follows that

$${S}_{\tau }\left(\rho \right)=-tr\left(\rho \,{\log }_{2}\rho \right).$$

(2)

Spectral entropy captures the global topological feature of the network, rather than a subset of the network’s descriptors, making it a more appropriate entropy metric for complex systems. It has also been discovered that the functional diversity among the vertices can be quantified by spectral entropy²⁸. For simplicity, the notion ${S}_{\tau }\left(G\right)={S}_{\tau }\left(\rho \right)$ is also adopted in this paper to denote the spectral entropy of the network G.

We analytically demonstrate that spectral entropy is a monotonic function and ${S}_{\tau }\in [{\log }_{2}C,{\log }_{2}N]$, where C denotes the number of disconnected components (see “Methods” for proof and explanation). Consequently, for connected networks, S_τ falls within the interval $[0,{\log }_{2}N]$.

Definition of vertex entanglement

Quantum entanglement is a kind of precious resource¹⁸, and the distance between quantum entangled states and a collection of separable states can be defined as entanglement. When it comes to complex systems, the influence of node removal on the largest eigenvalue of the adjacency matrix is defined as dynamic importance³⁶. Similarly, we can define entanglement as the effect of changes in the local structure of the network on spectral entropy. The network resulting from the local perturbation is referred to as the v-control network, denoted as G_v. The difference between the entropy of G_v and G captures the confusion due to the function of vertex v, and in mathematics, vertex entanglement (VE) can thus be defined as:

$${E}_{\tau }\left(v\right)={S}_{\tau }\left({G}_{v}\right)-{S}_{\tau }\left(G\right).$$

(3)

Here, diffusion time τ is a tunable parameter, enabling us to study the network entanglement from a time-varying perspective. In contrast to dynamical importance³⁶, which only considers the variation of maximum eigenvalues, our entanglement measure can quantitatively portray the importance of vertices to the overall network topology.

Vertex entanglement captures the effect of the perturbations caused by a single vertex on the spectral entropy of the network. It has been discovered that spectral entropy reflects the functional diversity in complex systems²⁸. Thereby, a vertex is supposed to be more important in our framework if it can affect the system’s functional diversity more severely. Vertex entanglement is thus a fundamental metric for the dynamic diversity of information and measures the importance of vertices in complex systems. In addition, diffusion time τ serves as a tunable parameter in the computation of VE, enabling us to study network response at micro, meso, and macroscales. We conducted an analytical study on the impact of τ on vertex entanglement with a mean-field approximation, and the results show that

• τ → 0: E₀ ≈ 0,

• $\tau \to \infty :{E}_{\infty }\approx {\log }_{2}{C}_{v}$.

Here, C_v denotes the number of connected components of G_v. In the mesoscale, where 0 < τ < ∞, vertex entanglement also captures the impact of topological perturbations (see “Methods”). The variations in the vertex entanglement with respect to diffusion time are depicted in Fig. 1.

Fig. 1: The variations of vertex entanglement ${E}_{\tau }\left(v\right)$ with the diffusion propagation time τ.

The curves are colored based on the degree of the detached vertex when constructing the v-control network G_v, with darker orange indicating a larger degree. It can be observed that ${E}_{0}\left(v\right)\to 0$ when diffusion is transient and ${E}_{\infty }\left(v\right)\to {\log }_{2}{C}_{v}$ on an extremely large time scale, where C_v denotes the number of connected components of G_v.

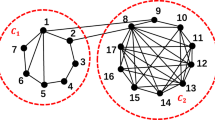
As the name indicates, G_v is under the control of vertex v. One of the possible methods to construct G_v is to detach vertex v crudely and without any other adjustments¹⁶. Nevertheless, this method will result in changes to many fundamental properties of the network, including the number of links M and the average degree 〈k〉. A nature principle associated with probabilistic dismantling is that G_v should preserve as much as possible the statistical properties of the original network G, such as M and 〈k〉. To achieve this, instead of detaching vertex v, we transform the subgraph formed by v and its neighboring vertices into a probabilistic complete graph, i.e., a graph where all possible edges between vertices are present with a certain probability, with the link relationships between other vertices remaining unchanged. The above process is analogous to shrinking v and its neighbors into one super vertex and evenly distributing the original weights within the super vertex. This strategy is visualized in Fig. 2. Intuitively, if a node’s neighbors are densely connected, this perturbation method tends to assign less importance to such a node because there are many alternative ways to interact and communicate with its neighbors. A thorough comparative analysis between this perturbation strategy and directly detaching nodes is deferred to Supplementary Note 2. Experiments conducted on several empirical networks have also indicated that better network dismantling results can be obtained with this strategy, also see Supplementary Note 2.

Fig. 2: Construction diagram of the v-control network G_v.

The process of constructing G_v is somewhat analogous to shrinking v and its neighbors into one super vertex and redistributing the original weights evenly within the super vertex. Specifically, the transition from G to G_v occurs merely in v and its neighbors, being restructured into a probabilistic complete graph. The weight of each link in the probabilistic complete graph is ${\omega }_{v}=\frac{{{{{{{{\rm{sum}}}}}}}}\,{{{{{{{\rm{of}}}}}}}}\,{{{{{{{\rm{link}}}}}}}}\,{{{{{{{\rm{weights}}}}}}}}\,{{{{{{{\rm{among}}}}}}}}\,v\,{{{{{{{\rm{and}}}}}}}}\,{{{{{{{\rm{its}}}}}}}}\,{{{{{{{\rm{neighbors}}}}}}}}}{{{{{{{{\rm{possible}}}}}}}}\,{{{{{{{\rm{links}}}}}}}}\,{{{{{{{\rm{number}}}}}}}}}=\frac{{k}_{v}+0.5{k}_{v}\left({k}_{v}-1\right){c}_{v}}{{k}_{v}\left({k}_{v}+1\right)}$$=\frac{{c}_{v}}{2}$ $-\, \frac{{c}_{v}+1}{{k}_{v}+1}$, with c_v presenting the clustering coefficient of G_v. For example, in the above network, ${\omega }_{v}=\frac{4}{6}=\frac{2}{3}$.

In order for vertex entanglement to capture the structural significance of individual players without relying on diffusion time, a logical assumption is that the connectivity of the v-control network is independent of diffusion time. Nevertheless, the impact of local perturbations on the global network topology is limited at smaller time scales. Conversely, longer diffusion time tends to cause a significant overlap between the flow vectors initiated from different nodes, resulting in a decrease in the ability to identify important nodes. Therefore, we seek to find τ that amplifies the potential impact of local control on information dynamics across various time scales. From Fig. 1, we can draw that the minimum value of vertex entanglement is negative, and this property is proved in “Methods”. Therefore, the preferred value of τ should be such that the vertex entanglement is minimized, and a new definition of vertex entanglement with independent diffusion time τ can be given as:

$$E\left(v\right)={E}_{{\tau }^{* }}\left(v\right)=\mathop{\min }\limits_{\tau }{E}_{\tau }\left(v\right).$$

(4)

An issue of central importance is whether such τ* exists. It would be inappropriate to dismantle networks based on vertex entanglement if τ* is nonexistent. The proof of the existence of τ* will be presented in the Methods Section. In addition, we introduce an efficient method for approximating vertex entanglement that significantly decreases the computational complexity by one order of magnitude in “Methods”, while maintaining a high degree of accuracy.

Correlation analysis

It is worth noting that the vertex entanglement contains rich information in addition to network centrality measures, such as degree and betweenness. In Fig. 3a–e, we illustrate the physicist collaboration network³⁷ corresponding to different node centralities, namely degree, Coreness³⁸, Collective Network Entanglement (CNE)¹⁶, Betweenness²⁴, and vertex entanglement (VE). The Pearson correlation matrix among all index pairs is depicted in Fig. 3f. Here, we adopt the opposite values to VE since VE is negative, ensuring that each metric has positive values, with larger values indicating greater importance.

Fig. 3: Visualization and correlation analysis of the ranking of five centrality indicators.

The physicist collaboration network is taken as an example. a–e The colors of vertices are proportional to the normalized values of the indicators. Here, min-max normalization is adopted. Since the values of VE are negative and smaller values of VE correspond to more important nodes, we perform an additional operation of taking the opposite of VE before normalizing it. This transformation is solely intended to ensure consistent interpretation across all metrics, where higher values indicate greater importance of nodes. f visualizes the pairwise Pearson correlation, with letters a–e in the abscissa and ordinate representing Degree, Coreness, CNE, Betweenness, and the opposite value of vertex entanglement, respectively. a–c illustrate that the vital nodes are tightly interconnected with each other, forming clusters in specific regions of the network. In contrast, d, e show a different pattern, where significant nodes are dispersed throughout the network, and in (e), the vital nodes are more evenly distributed than in (d).

As evidenced by the comparatively low correlations between vertex entanglement and the other four indicators, it is apparent that vertex entanglement encapsulates a plethora of information and is poised to provide fresh insights beyond those of established metrics. This serves as a noteworthy, albeit frequently overlooked, indicator of the potential metric of the VE metric. Additional correlation analyses will be presented in Supplementary Note 3.

Entanglement-based network dismantling

Discovering the minimum set of units that can drive a complex system to its collapse, also termed network dismantling, is a famous NP-hard problem. According to our discussion (see “Methods”), vertex entanglement is closely related to network connectivity, robustness, and information transfer efficiency. Therefore, the proposed vertex entanglement in this paper provides an effective framework for network dismantling.

To validate the applicability of the proposed metric, we conduct targeted attack experiments on four empirical systems, that is, the power-grid network (Grid)³⁹, crime network (Crime)³⁹, physicist collaboration network (Collaboration)³⁷, and Petster–Hamster online social network (PH)³⁹. We compare the proposed method with several state-of-the-art dismantling schemes, namely collective influence (CI)⁴⁰, Belief Propagation guided Decimation (BPD)⁴¹, Collective Network Entanglement (CNE)¹⁶, Generalized Network Dismantling with Reinsertion (GNDR)⁹, FINDER⁴², CoreHD⁴³, MinSum⁴⁴, and Betweenness centrality²⁴. In addition, as some strongly entangled vertices may aggregate and their contributions may overlap, there may be some difference between the dismantling result of attacking a small number of vertices and that of attacking a larger one. Therefore, we adopt the reinsertion algorithm⁴⁴, which is often used to improve an existing solution, to enhance the network dismantling performance of VE.

The size of giant connected components (GCC) is commonly used to indicate the robustness of the network against random or targeted attack⁴⁵, as giant clusters are generally necessary to ensure the proper functioning of the system. So, we utilize normalized GCC size to compare networks of various scales. Figure 4 exhibits the network dismantling processes of the nine dismantling schemes on the four empirical systems, enabling a visual and thorough comparison. We also list the proportion of attacked vertices when the dismantling target size is 1% in Table 1. It can be drawn that VE leads to a much faster collapse than other strategies.

Fig. 4: Dismantling process of different methods.

Targeted attack towards a power-grid network, b crime network, c physicist collaboration network, and d Petster–Hamster online social network with the dismantling target size of 1%. The x axis values represent the removed fraction of vertices, and the y axis values represent the size of giant connected components (GCC) after normalization. Compared with the other eight methods (see legend of panel a for the color code), the number of vertices attacked and the area beneath the curve for vertex entanglement (VE, red line) are comparably small in all cases, indicating superior dismantling performance. b Red nodes suggest that they are under direct attack, gray nodes indicate that they belong to various small connected components, and the colors of the remaining nodes signify how they are distributed among various large connected components.

Table 1 The efficiency performance of various network dismantling strategies.

The robustness measure R⁴⁶ is another index that quantitatively describes the performance of different network dismantling algorithms by measuring the area under the dismantling curve. Mathematically, R is defined as

$$R=\frac{1}{N}\mathop{\sum}\limits_{n}g(n),$$

(5)

where g(n) is the normalized GCC size after removing n vertices. The normalization factor $\frac{1}{N}$ allows R to be compared between networks of different sizes. Obviously, a smaller R corresponds to a more effective network dismantling strategy. Figure 5 shows the robustness value R of various attack strategies on four real-world networks. We conduct additional experiments in Supplementary Note 4 on more empirical networks, demonstrating the effectiveness and broad applicability of the proposed algorithm. In general, the proposed method is comparable to and even outperforms the others in terms of both dismantling efficiency and robustness.

Fig. 5: The robustness performance of various network dismantling strategies.

Per-method cumulative robustness measure R, which measures the area under the curve of network dismantling, with lower values indicating better performance. The dismantling target for each method is 1% of the network size, and all values are scaled to the one of VE for the same network.

Entanglement-based ancillary diagnosis of ASD

Autism spectrum disorder (ASD) is considered a lifelong neurological and genetic disorder²⁵, whose manifestations include impairments in social communication and interaction, sensory abnormalities, repetitive behaviors, and varying levels of intellectual disability. Early diagnosis of ASD is crucial because early intervention can make a difference and lead to superior treatment outcomes.

To enhance our comprehension of how information is transmitted within the brain of ASD patients, imaging techniques are extensively utilized to deduce the structural and functional interconnections between distinct brain regions, as demarcated by parcellation into regions of interest (ROI)⁴⁷. This enables brains to be effectively simplified into complex networks with much smaller sizes, which are subsequently scrutinized through the lens of network science⁴⁸. Specifically, the data about ASD and typical control (TC) participants used in this study comes from the second iteration of Autism Brain Imaging Data Exchange (ABIDE II)⁴⁹, which was openly released to the scientific community in June 2016. This study enrolls 40 participants, from ABIDE II-Indiana University site, 20 with ASD and 20 with TC. A 600 × 600 brain functional network is obtained for each participant. More details about data processing and network construction are delayed to Supplementary Note 5.

To detect differences in brain networks between ASD participants and TC participants, we utilize vertex entanglement and find a significant disparity in the hub disruption indices based on vertex entanglement between the two groups.

Specifically, we compute each subject’s hub disruption index (HDI)⁵⁰, a metric capturing the topological reorganization of the brain network. First, entanglement $E\left(v\right)$ is calculated for all ROIs in the functional brain network among all participants, consisting of ${E}^{a}\left(v\right)$ for ASD participants and ${E}^{t}\left(v\right)$ for TC participants. The average vertex entanglement of TC participants is denoted as 〈E^t(v)〉. Subsequently, each subject’s hub disruption index κ corresponds to the slope of the linear regression on the set of $\left\{(\langle {E}^{t}(v)\rangle ,E(v)-\langle {E}^{t}(v)\rangle )\right\}$. This means that for each participant, their HDI is calculated based on how their vertex entanglement compares to the average vertex entanglement of TC participants. Therefore, HDI captures the topological abnormalities in the functional brain network. Because different thresholds have different effects on the results, we calculated the average hub disruption index of five thresholds (ranging from 1 to 5% with a 1% interval) to obtain robust and comprehensive results. In addition, we compute the hub disruption indices based on other centrality metrics with the same approach.

As the statistical results shown in Fig. 6, the VE-based hub disruption index can clearly differentiate between ASD and TC participants. In this analysis, we focus on four metrics: VE, Betweenness²⁴, CNE¹⁶, and CoreHD⁴³, as the other methods employed in the previous experiments are primarily tailored for network dismantling tasks. Evidently, the hub disruption indices for individuals with ASD are significantly lower than those for TC subjects across various metrics, indicating that the brain networks of ASD patients may be more stable and adaptable, which could compensate for impairments of certain brain regions. This special feature of ASD patients’ brain network can be used to help diagnose ASD.

Fig. 6: Average hub disruption indices based on different centrality metrics.

The vertical coordinate of each dot is the average hub disruption index for five brain networks with a sparsity of 1% to 5% (1% interval).

Moreover, a significant positive correlation (r = 0.681, P = 0.001857) has been observed between ASD participants’ performance intelligence quotient (IQ) and the VE-based hub disruption index, while no significant correlations are detected between Performance IQ and the other three metrics, as shown in Fig. 7. In our study, we employ the Performance IQ, as ascertained by the Wechsler Abbreviated Scale of Intelligence (WASI), as a measure of cognitive ability, which has been widely used and recognized as a reliable tool in assessing cognitive abilities across various settings⁵¹. The relationship between the Performance IQ and the brain hub disruption index in Fig. 7 provides valuable insights into potential associations between cognitive abilities and disruptions in brain networks. Specifically, if the disruption of brain topology is more severe, then the individual’s Performance IQ tends to be lower. To perform these analyses, Shepherd’s pi correlation is employed here as it provides adequate statistical power and is less affected by outliers. This method is an extension of Spearman’s correlation and additionally incorporates a bootstrap-based estimation of the Mahalanobis distance, thereby enabling an unbiased detection and exclusion of outliers. Furthermore, Shepherd’s pi correlation⁵² analysis is particularly suited for small sample sizes⁵³. Detailed statistical analysis and the Spearman correlation analysis without moving outliers are deferred to Supplementary Note 5.

Fig. 7: The Shepherd’s pi correlations between average hub disruption indices (HDI) and intelligence quotient (IQ) of autism spectrum disorder participants.

The horizontal axes are the average hub disruption indices based on a Vertex Entanglement (VE), b Betweenness, c CNE, and d CoreHD, over brain networks with sparsity ranging from 1 to 5% (1% interval). The dashed line is obtained by least squares fitting.

Our findings align with the theory that ASD patients may have a different network organization compared to typically developing individuals⁵⁴. Specifically, individuals with ASD may experience functional activity suppression in some key brain areas, indicating the diminished importance of those key areas. In order to maintain essential brain activity, the functional connectivity of some limbic brain areas, i.e., vertices of lower importance, is likely to be enhanced to compensate for the suppression, thus increasing the significance of these limbic brain vertices. The combined effect of suppression and compensation mechanisms results in a smaller hub disruption index κ, and individuals with more severe ASD symptoms tend to have smaller κ.

Conclusion

In this study, we employ networks’ density matrices to measure the entanglement between vertices and their respective networks. Specifically, we propose an approach to key vertex identification by analyzing the effect of perturbations generated by a single vertex on the overall functionality of the network. In addition, entropy is found to be a functional diversity indicator of a node as a sender of information²⁸, and VE measures the change in the spectral entropy of the network resulting from the perturbations. Thereby, VE is an ideal metric for assessing the significance of vertices in terms of the functional diversity of the whole system.

The diffusion time τ is tunable when calculating VE, allowing the network response to be studied from micro, meso, and macroscales. As theoretical and experimental analysis reveals, vertex entanglement can effectively capture the transport properties and dynamic diversity of complex systems. To be specific, VE tends to zero when diffusion is transient and will converge to ${\log }_{2}{C}_{v}$ (C_v denotes the number of connected components of G_v) on an extremely large time scale. This advantageous property highlights the potential of our metric to address real-world issues and promises a wide range of practical applications. The multiscale property of VE renders it versatile in analysis, and we further introduce a reliable method for selecting τ in practical scenarios. Moreover, we propose an approximate calculation for vertex entanglement that effectively reduces the complexity by an order of magnitude without compromising its accuracy. This is particularly useful in applications where excessive overhead is a concern.

We perform correlation analysis before delving into VE’s ability to identify key vertices, and our findings indicate that VE offers valuable insights beyond traditional network centrality metrics by providing rich information. As an application, vertex entanglement can be applied to network dismantling tasks. We fine-tune the v-control network for the sake of an improved dismantling result, and find that targeted attacks on a few strongly entangled vertices in the network can lead to the collapse of the entire network. Empirical results demonstrate that VE outperforms other cutting-edge algorithms in dismantling tasks, highlighting its superior performance gains. Early diagnosis of ASD patients is quite daunting. As another significant application, entanglement offers significant contributions to its diagnosis. The hub disruption index based on vertex entanglement for ASD patients is significantly lower than that of typical controls. Moreover, the hub disruption indices exhibit a significant positive correlation with the intelligence quotient (IQ) of ASD participants, suggesting that VE promises to serve as a diagnostic tool for ASD.

This study explores the intersection of quantum information and complex systems at the research frontier, providing fresh insights into the intrinsic topological properties of complex systems. Specifically, key players are those that are robust against local perturbations. The proposed entanglement frame can be employed to identify key players in complex networks, including but not limited to identifying critical vertices. A less explored but promising research direction is to identify influential mesoscale structures, such as measuring the significance of simplices in simplicial complexes^11,55. Simplices are a natural extension in our framework as nodes can be seen as 0-simplices. Similarly, we can perturb simplices and their associated neighborhood structures in simplicial complexes to assess their impact on the structure and functional diversity. However, we note that perturbing larger subgraph structures will significantly affect entropy, resulting in greater inaccuracies in approximate analysis and computation. Therefore, more efficient analytical and computational methods are required. The extension of our framework to simplicial complexes introduces further potential applications, such as higher-order link prediction⁵⁶ and simplex information imputation⁵⁷.

Methods

Multiresolution analysis of entanglement

Time τ serves as a tunable parameter in the computation of VE, which enables the study of the network response at micro, meso, and macroscales. In this section, we conduct an analytical study of the properties of vertex entanglement across various diffusion time scales.

According to the definition²², spectral entropy can be figured out using the spectral decomposition theory that

$${S}_{\tau }\left(G\right)=-tr\left(\rho \,{\log }_{2}\rho \right)=-\mathop{\sum }\limits_{i=1}^{N}{\lambda }_{i}\left(\rho \right){\log }_{2}{\lambda }_{i}\left(\rho \right).$$

(6)

By applying ${\lambda }_{i}\left(\rho \right)={e}^{-\tau {\lambda }_{i}\left(L\right)}/Z$, it can be derived that

$${S}_{\tau }(G)=\frac{1}{Z\ln 2}\mathop{\sum }\limits_{i=1}^{N}{e}^{-\tau {\lambda }_{i}\left(L\right)}\left(\tau {\lambda }_{i}\left(L\right)+\ln Z\right)$$

(7)

$$=\frac{\tau }{\ln 2}\mathop{\sum }\limits_{i=1}^{N}{\lambda }_{i}\left(L\right){\lambda }_{i}\left(\rho \right)+{\log }_{2}Z$$

(8)

$$=\frac{\tau }{\ln 2}tr\left(L\rho \right)+{\log }_{2}Z,$$

(9)

where $Z=tr({e}^{-\tau L})=\mathop{\sum }\nolimits_{i = 1}^{N}{e}^{-\tau {\lambda }_{i}(L)}$ is the partition function. The last equation holds as L and ρ can be spectrally decomposed simultaneously. Mean-field approximations for network entropy have recently been suggested for the random walk-based⁵⁸ and continuous diffusion-based¹⁶ density matrices, together with analytical and numerical investigations demonstrating that this approximation is quite effective in approximating the dynamics of systems at the meso- and macroscales⁵⁸. Hence, the sum term in Eq. (8) can also be simplified with mean-field approximation^16,58 as follows:

$$\langle {\lambda }_{i}(L){\lambda }_{i}(\rho )\rangle = \langle {\lambda }_{i}(L)\rangle \langle {\lambda }_{i}(\rho )\rangle +\langle ({\lambda }_{i}(L)-\langle {\lambda }_{i}(L)\rangle )({\lambda }_{i}(\rho )-\langle {\lambda }_{i}(\rho )\rangle )\rangle \\ \approx \langle {\lambda }_{i}(L)\rangle \langle {\lambda }_{i}(\rho )\rangle .$$

(10)

Since the number of λ_i satisfying ${\lambda }_{i}\left(L\right)=0$ is equal to the connected components C⁵⁹, one can further obtain

$$\langle {\lambda }_{i}(L)\rangle =\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{\lambda }_{i}\left(L\right)=\frac{1}{N-C}\mathop{\sum }\limits_{i=C+1}^{N}{\lambda }_{i}\left(L\right)=\frac{2m}{N-C},$$

(11)

and the mean value for λ_i(ρ) follows that

$$\langle {\lambda }_{i}(\rho )\rangle =\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\frac{{e}^{-\tau {\lambda }_{i}\left(L\right)}}{Z}=\frac{1}{N-C}\mathop{\sum }\limits_{i=C+1}^{N}\frac{{e}^{-\tau {\lambda }_{i}\left(L\right)}}{Z}=\frac{1}{N-C}\left(1-\frac{C}{Z}\right).$$

(12)

A simplified form can thus be obtained through the mean-field approximation that

$${S}_{\tau }\left(G\right)\approx \frac{2m\tau }{\ln 2(N-C)}\left(1-\frac{C}{Z}\right)+{\log }_{2}Z.$$

(13)

Thereby, the vertex entanglement can be formulated as

$${E}_{\tau }\left(v\right) = {S}_{\tau }\left({G}_{v}\right)-{S}_{\tau }\left(G\right)\\ \approx \frac{2m\tau }{\ln 2(N-C)}\left(\frac{{C}_{v}}{{Z}_{v}}-\frac{C}{Z}\right)+{\log }_{2}\frac{{Z}_{v}}{Z},$$

(14)

where C_v is the number of connected components of G_v. Assuming that the v-control network maintains the number of connected components, i.e., C_v = C, and by performing the Taylor expanding, we can obtain

$${E}_{\tau }\left(v\right) = \frac{2m\tau C}{\ln 2\left(N-C\right)}\frac{Z-{Z}_{v}}{{Z}_{v}Z}+{\log }_{2}\frac{{Z}_{v}}{Z}\\ \approx \frac{2m\tau C}{\ln 2\left(N-C\right)}\frac{\Delta Z}{{Z}_{v}Z}+\frac{\Delta Z}{Z\ln 2},$$

(15)

where ΔZ = Z − Z_v.

Moreover, for large-scale networks, the vertex entanglement can be further approximated as

$${E}_{\tau }\left(v\right)=\frac{\Delta Z}{Z\ln 2}\left(1+\frac{\tau C\langle k\rangle }{{Z}_{v}}\right),$$

(16)

where 〈k〉 stands for the average vertex degree, and $\langle k\rangle =\frac{1}{N}\mathop{\sum }\nolimits_{i = 1}^{N}{k}_{i}=\frac{2m}{N}\approx \frac{2m}{N-C}$. The partition function Z captures the topological property of the system, indicating the average return probability of a random walker⁵⁸.

In the following, we will discuss the properties of vertex entanglement in the various diffusion time limits. As a preparation, we will demonstrate that the spectral entropy is monotonically decreasing with respect to diffusion time τ and ${S}_{\tau }\in \left[{\log }_{2}C,{\log }_{2}N\right]$.

Since

$$\frac{\partial {\log }_{2}Z}{\partial \tau }=\frac{1}{Z\ln 2}\frac{\partial Z}{\partial \tau }=\frac{1}{Z\ln 2}\left(\mathop{\sum }\limits_{i=1}^{N}-{\lambda }_{i}\left(L\right){e}^{-\tau {\lambda }_{i}\left(L\right)}\right)=-\frac{tr\left(L\rho \right)}{\ln 2},$$

(17)

according to Eq. (9), we can conclude that

$$\frac{\partial {S}_{\tau }}{\partial \tau } = \frac{tr\left(L\rho \right)}{\ln 2}+\frac{\tau }{\ln 2}\frac{\partial tr\left(L\rho \right)}{\partial \tau }-\frac{tr\left(L\rho \right)}{\ln 2}\\ = \frac{\tau }{\ln 2}\frac{\partial tr\left(L\rho \right)}{\partial \tau }\\ = \frac{\tau }{{Z}^{2}\ln 2}\left[-\mathop{\sum }\limits_{i=1}^{N}{\lambda }_{i}^{2}\left(L\right){e}^{-\tau {\lambda }_{i}\left(L\right)}\cdot \mathop{\sum }\limits_{i=1}^{N}{e}^{-\tau {\lambda }_{i}\left(L\right)}+{\left(\mathop{\sum }\limits_{i = 1}^{N}{\lambda }_{i}\left(L\right){e}^{-\tau {\lambda }_{i}\left(L\right)}\right)}^{2}\right]\\ < \,0.$$

(18)

The last inequality holds exploiting the Cauchy–Schwarz inequality. The process of entropy reduction is somewhat intriguing, but we find it explainable. As the diffusion time τ increases, there is a notable overlap between the flow vectors initiated from nodes, which results in lower spectral entropy²⁸.

When τ → ∞, it can be directedly obtained that Z → C and $\frac{\tau }{\ln 2}tr\left(L\rho \right)=\frac{\tau \mathop{\sum }\nolimits_{i = 1}^{N}{\lambda }_{i}\left(L\right){e}^{-\tau {\lambda }_{i}\left(L\right)}}{\ln 2C}\to 0$. Hence,

$${S}_{\infty }=\frac{\tau }{\ln 2}tr\left(L\rho \right)+{\log }_{2}Z={\log }_{2}C.$$

(19)

At this stage, the information has spread throughout the network. Additionally, when τ → 0, spectral entropy follows that

$${S}_{0}=\frac{\tau }{\ln 2}tr\left(L\rho \right)+{\log }_{2}Z={\log }_{2}N.$$

(20)

This result is consistent with the fact that when τ = 0, no signal propagation happens and thus the spectral entropy reaches its maximum value, as no information regarding the network structure is available.

Since we have proved that spectral entropy is monotonically decreasing concerning τ, it can be concluded that ${S}_{\tau }\in [{\log }_{2}C,{\log }_{2}N]$. In particular, ${S}_{\tau }\in [0,{\log }_{2}N]$ for those connected networks.

The diffusion time τ is a tunable parameter in the definition of vertex entanglement, and we will discuss asymptotic expressions for vertex entanglement.

When τ → 0,

$${E}_{0}\left(v\right)={S}_{0}\left({G}_{v}\right)-{S}_{0}\left(G\right)=0.$$

(21)

When τ → ∞,

$${E}_{\infty }\left(v\right)={S}_{\infty }\left({G}_{v}\right)-{S}_{\infty }\left(G\right)={\log }_{2}\frac{{C}_{v}}{C}.$$

(22)

In particular, for a connected network G, it further reduces to ${E}_{\infty }\left(v\right)={\log }_{2}{C}_{v}$.

From the above discussion, we can conclude that vertex entanglement is closely related to network connectivity and information transfer efficiency. Therefore, VE is an ideal metric for assessing the importance of vertices in terms of these properties.

Choosing a suitable diffusion time

Given our objective of assessing the significance of network players from a structural perspective, it makes sense to require that the connectivity of the v-control network be independent of τ. However, it is crucial to meticulously consider the impact of local perturbations on the global network topology, as this impact is limited at smaller time scales. Conversely, longer diffusion times tend to cause significant overlap between the flow vectors initiated from different nodes, thereby diminishing our ability to identify vital players. Therefore, we seek to amplify the possible impact of local control on the information dynamics at different time scales, and thus a suitable diffusion time τ* should satisfy

$${\tau }^{* }=\mathop{{{{{{\rm{arg}}}}}}\, {{{{{\rm{min}}}}}} }\limits _{\tau }{E}_{\tau }\left(x\right).$$

(23)

If there exists no such parameter τ* that satisfies Eq. (23), then it is infeasible to perform network dismantling and address other issues using vertex entanglement. In the following, we will prove the existence of τ* and that the vertex entanglement with τ* is less than 0.

Let

$$f\left(\tau \right)=\frac{{Z}^{{\prime} }}{Z}=\frac{\mathop{\sum }\nolimits_{i = 1}^{N}{e}^{-\tau {\lambda }_{i}^{{\prime} }(L)}}{\mathop{\sum }\nolimits_{i = 1}^{N}{e}^{-\tau {\lambda }_{i}(L)}}.$$

(24)

Since f is a continuous function and $f\left(0+\right)=1$, let $\gamma =\mathop{\max }\limits_{i}{e}^{-\tau ({\lambda }_{i}^{{\prime} }\left(L\right)-{\lambda }_{i}\left(L\right))}\ge 1$, then there exists τ > 0 such that $f\left(\tau \right)\le \gamma$. We can directly obtain that $\frac{{e}^{-\tau {\lambda }_{i}^{{\prime} }\left(L\right)}}{{Z}^{{\prime} }}\ge \frac{{e}^{-\tau {\lambda }_{i}\left(L\right)}}{Z}$. Hence,

$${E}_{\tau }\left(v\right)={S}_{\tau }\left({G}_{v}\right)-{S}_{\tau }\left(G\right)\le 0.$$

(25)

Since ${E}_{\tau }\left(v\right)={\log }_{2}{C}_{v}\ge 0$ for very large τ, $E\left(v\right)$ is doomed to exist and be non-positive. Moreover, a smaller value of $E\left(v\right)$ reflects the greater impact of v on the network connectivity and stronger entanglement. Intuitively, VE is negative can be explained by the fact that we perturb the subgraph consisting of node v and its direct neighbors into a probabilistic complete graph when constructing the v-control network, which obviously promotes the propagation of information within the network, thus leading to a decrease in entropy, i.e., ${S}_{\tau }\left({G}_{v}\right)\, < \,{S}_{\tau }\left(G\right)$. In addition, the diffusion time τ* should belong to $(0,\frac{1}{{\lambda }_{2}})$ as the time for the system to stabilize is inversely proportional to the smallest nonvanishing eigenvalue λ₂ of L⁶⁰.

Approximate calculation and complexity analysis

The most computationally intensive step to calculate entanglement is solving the spectrum problem, with complexity varying between ${{{{{{{\mathcal{O}}}}}}}}({N}^{2})$ and ${{{{{{{\mathcal{O}}}}}}}}({N}^{3})$ depending on the sparsity of the network. Worse still is the necessity to repeat spectral decomposition N + 1 times, since the entanglement of each vertex needs to be calculated.

The spectrum of the graph Laplacian matrix of G_v can be presented as ${\lambda }_{i}\left({L}^{{\prime} }\right)={{v}_{i}^{{\prime} }}^{T}{L}^{{\prime} }{v}_{i}^{{\prime} }$, where ${v}_{i}^{{\prime} }$ is the eigenvector corresponding to ${\lambda }_{i}\left({L}^{{\prime} }\right)$. Notice that the graph Laplacian matrix of each v-control network G_v is only slightly changed by several terms from G for large-scale sparse networks, and denote the change as $\Delta L(\Delta L={L}^{{\prime} }-L)$. This property enables an approximation algorithm for computing entanglement to avoid resolving the spectrum each time, thus resulting in a complexity reduction. Using the eigenvector v_i of L as an approximation instead of ${v}_{i}^{{\prime} }$ we can obtain

$${\lambda }_{i}\left({L}^{{\prime} }\right)={v}_{i}^{T}\left(L+\Delta L\right){v}_{i}={\lambda }_{i}\left(L\right)+{v}_{i}^{T}\Delta L{v}_{i}.$$

(26)

Since ΔL has only a few nonvanishing terms that need to be calculated, the complexity of calculating entanglement can be reduced to ${{{{{{{\mathcal{O}}}}}}}}\left(\left\langle {k}^{2}\right\rangle N\right)$ per vertex, where k indicates degree. As a result, a single eigenvalue decomposition for the original network is sufficient, eliminating the need for additional N decompositions and thus reducing the complexity of the algorithm by an order of magnitude. Moreover, empirical experiments suggest that this approximation also achieves impressive performance in both network dismantling and ASD diagnosis. Nevertheless, we admit that the efficiency of this approximation algorithm still lags behind other efficient centrality metrics. One potential avenue for breakthrough rests in leveraging partial eigenvalues, as opposed to the full spectrum, to approximate VE.

After that, the spectral entropy and vertex entanglement could be solved within ${{{{{{{\mathcal{O}}}}}}}}(N)$. When seeking the τ that minimizes $E\left(v\right)$, each trial can as well be completed in ${{{{{{{\mathcal{O}}}}}}}}(N)$ according to Eq. (7). Figure 8 presents a comparison between the approximate and exact results in Barabási–Albert (BA)⁶¹, Erdős–Rényi (ER)⁶² and Watts–Strogatz (WS)⁶³ networks. It can be drawn that the proposed strategy significantly reduces the complexity of the method by roughly one order of magnitude while maintaining a high level of accuracy.

Fig. 8: Approximation calculation.

Average spectral entropies of v-controlled networks G_v are compared between the exact and approximate values for three types of synthetic networks: a Erdős-Rényi network with P = 0.1, b Watts–Strogatz network with parameter K = 3 and P = 0.3, and c Barabási–Albert network with m = 3. In all cases, networks with N = 64 are considered. For (d–f), the horizontal and vertical coordinates of each dot are the exact and approximate values of vertex entanglement, and the Pearson correlations r between the exact and approximate VE values are reported at the top of each panel. Panels in (d–f) take the negative logarithm for negative values of VE (both exact and approximate values).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.