Introduction

In the last two decades, new ways of growing pristine nanoscopic wires have been developed enabling fields of research that facilitate the development of entirely new generations of sensors and electronic devices to unveil the physics at the nanoscale. Nanowires (NWs) have entered the research fields of electronics1, biosensors2, energy harvesting and storage3, drug delivery4, wearable devices5,6,7, environmental applications8, optical spectroscopy with nanometer resolution9, mass sensing10,11, and force sensing12,13,14,15,16. In addition, advancements in nanoscale characterization techniques have made it much easier to harness the potential of NWs.

For NW-based mass and force sensing, device geometries that support flexural vibrations of the NW are used where vibration properties such as eigenfrequencies or amplitudes respond to small interaction forces or attached masses. Singly-clamped NWs can be considered as miniaturized cantilever force transducers with a large dynamic range of linear operation17. The minimal measurable force of such NWs as limited by its thermal noise is given by \({F}_{\min }=\sqrt{4{k}_{{{{{{\rm{B}}}}}}}{TB}\varGamma }\) with \({k}_{{{{{{\rm{B}}}}}}}\) referring to the Boltzmann constant, \(T\) the temperature, \(B\) the measurement bandwidth and \(\varGamma\) the mechanical dissipation constant. Based on \(\varGamma ={\omega }_{0}{m}_{{{{{{\rm{eff}}}}}}}/Q\), where \({\omega }_{0}\) is the resonance frequency, \({m}_{{{{{{\rm{eff}}}}}}}\) the effective mass of the resonator, and \(Q\) the mechanical quality factor, it can be shown that \({F}_{\min }\propto d/\sqrt{l}\) where \(d\) is the NW diameter and \(l\) its length13. Hence, highly sensitive force measurements require thin and long cantilevers, requirements that are naturally satisfied by high aspect ratio NWs. In the case of NW-based devices for torque measurements, including approaches for nano-magnetometry18,19, the sensitivity is limited by the minimum detectable torque given by \({\tau }_{\min }={l}_{{{{{{\rm{eff}}}}}}}{F}_{\min }\propto d\sqrt{{l}_{{{{{{\rm{eff}}}}}}}}\) where \({l}_{{{{{{\rm{eff}}}}}}}\) is the effective length of the NW beam. Hence, for high-sensitivity torque measurements, a thin and short NW would be preferred. In general, further miniaturization of NWs’ dimensions holds great potential for achieving unprecedented sensitivity.

Deflections and flexural oscillations of singly-clamped NWs can be detected by interferometry for NW diameters above 50 nm20. Below this diameter detection becomes challenging. Detection of vibrations in the case of thinner NWs can be accomplished by the attachment of an optical scatterer at the free NW end21, by an NW interaction with a focused electron beam11,22, or by exploitation of field emission patterns23,24,25. However, the latter requires a sophisticated image analysis technique to interpret the oscillating emission pattern.

An alternative is the detection of flexural vibrations of the NW by mechanically coupling them to easy-to-detect cantilevers (CLs) and by the exploitation of coupled or hybrid vibration modes26,27,28,29. This approach is also referred to as the co-resonant detection concept since it relies on matched individual eigenfrequencies of NW and cantilever, i.e., \({\omega }_{{{{{{\rm{NW}}}}}}}\approx {\omega }_{{{{{{\rm{CL}}}}}}}\) where fundamental or higher-order flexural modes can be used. Even when considering two simple harmonic oscillators with one oscillation mode each, coupling of them leads to two new hybrid oscillation modes with eigenfrequencies \({\omega }_{{{{{{\rm{a}}}}}}}\) and \({\omega }_{{{{{{\rm{b}}}}}}}\). Such systems can be described as two degrees of freedom resonators30. In the case of matched individual eigenfrequencies, both coupled modes are detectable at the cantilever despite the huge size asymmetry \({{m}_{{{{{{\rm{CL}}}}}}}\gg m}_{{{{{{\rm{NW}}}}}}}\) of the subsystems where \({m}_{{{{{{\rm{CL}}}}}}}\) and \({m}_{{{{{{\rm{NW}}}}}}}\) are the masses of the cantilever and the NW, respectively26.

The key advantages of the co-resonant approach include: (i) The sensors can be read out with any conventional cantilever deflection detection setup as used in commercial scanning probe microscopy (SPM) equipment. (ii) It is based on a design, where the NW vibration is detected by purely mechanical coupling to a cantilever. Therefore, direct optical detection of the NW vibrations and its limitations in the case of small NW diameters are avoided. For example, optical heating of NWs due to interactions with the laser beam can be ruled out. (iii) Compared to focused electron-beam detection techniques, an optically detected co-resonant sensor is not subjected to the risk of unwanted deposition of contaminants or any electrical charging issues.

Other published sensor concepts based on the coupling of two oscillators with similar eigenfrequencies but very different spring constants include the Akiyama SPM probe31 consisting of a soft U-shaped cantilever coupled to a quartz tuning fork and stepped cantilevers32 for improved mass sensing.

Previously, it has been demonstrated that co-resonantly coupled oscillation systems enable high-sensitivity magnetometry of ferromagnetic nanoparticles even when using a cantilever with a spring constant as high as \({k}_{{{{{{\rm{CL}}}}}}}=1.4{{{{{\rm{N}}}}}}/{{{{{\rm{m}}}}}}\) as part of the coupled system28. Nevertheless, until now there is no conclusive experimental proof that a co-resonant sensor can, by design, detect smaller interactions than the standalone cantilever.

In this work, we show experimentally that small force derivatives, that are not detectable at a particular cantilever due to fundamental thermodynamical reasons, lead to clearly observable frequency shifts when measuring vibration modes of a co-resonantly coupled system consisting of the same cantilever and a silicon nanowire. The measured force derivatives are of the order of 10-9 N/m.

Results and discussion

Fabrication and frequency matching of coupled devices

For our devices, we used silicon nanowires (Si NWs) and tip-less Si cantilevers (see “Fabrication of coupled oscillator devices” in the “Methods” section). We prepared and characterized two coupled oscillator devices (device #1 and device #2, Fig. 1a, b, Table 1, and Supplementary Note 1).

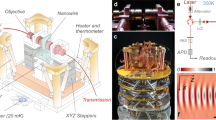
Fig. 1: Experimental setup and V-dependent frequency response.
figure 1

a Scheme of the detection technique where thermal fluctuations are read at the cantilever in a conventional scanning probe microscopy (SPM) device. b Scanning electron microscopy (SEM) image of a coupled oscillator consisting of a silicon nanowire (Si NW) and a tip-less Si cantilever (device #1). The lightning bolt symbol indicates a bias voltage-induced force derivative acting on the coupled oscillator as described by \({k}_{{{{{{\rm{bias}}}}}}}\). Inset: The same coupled oscillator after frequency matching by electron-beam-assisted deposition onto the NW free end. c Waterfall plot of cumulative curve fitting of the \(V\)-dependent power spectral density (PSD) of the thermal noise measured optically at the cantilever of device #1 at room temperature.

Full size image
Table 1 Properties of the Si cantilevers and nanowires.
Full size table

During the device fabrication process, we track the resonance frequencies of fundamental flexural vibration modes of both cantilever and NW by electron-beam-based mechanical motion detection22. Usually, two NW flexural resonances close to each other are detected that refer to orthogonal modes of vibration caused by slightly asymmetric NW cross-sections33,34. However, depending on the mode directions, their projections onto the SEM scanning plane may provide very different apparent amplitudes. Thus, we selected devices where the apparent amplitude of one of these orthogonal modes is at least 10 times larger than the other one. Since the cantilever is mounted on the SEM stage in such a way that its vibration direction is in the scanning plane, the observed dominant NW mode will be best suited to be coupled to the cantilever’s fundamental flexural mode. We achieve co-resonant coupling of the NW oscillator with the cantilever by changing the eigenfrequency of the selected NW mode (i.e., \({\omega }_{{{{{{\rm{NW}}}}}}}\approx {\omega }_{{{{{{\rm{CL}}}}}}}\) with \({\omega }_{i}=\sqrt{{k}_{i}/{m}_{i}}\)). The frequency matching is done by deposition of tungsten onto the free NW end (by electron-beam-assisted deposition and by attachment of small pieces of a tungsten nanomanipulator tip), which increases the NW’s effective mass \({m}_{{{{{{\rm{NW}}}}}}}\) (see Fig. S1 of Supplementary Information).

Measurement of coupled vibration modes

The coupled cantilever sensor is mounted at a tilt angle of \(10^\circ\) in a conventional high-vacuum SPM setup (NanoScan AG hrMFM) with cantilever detection by a laser beam deflection system (Fig. 1a). To tailor the coupled modes, a DC bias voltage \(V\) can be applied between the coupled device and a parallelly aligned Si substrate located 1 mm below. To capture and process the cantilever deflection signal we use a lock-in amplifier (Zurich Instruments HF2LI). An example of measured thermal displacement noise power spectral density (PSD) is shown in Fig. S2 (see Supplementary Note 2). The corresponding curve fitting is based on ref. 35

$${{{{{\rm{PSD}}}}}}\left(\omega \right) = \frac{A}{{\left(1-{\left(\omega /{\omega }_{{{{{{\rm{a}}}}}}}\right)}^{2}\right)}^{2}+{\left(\omega /\left({\omega }_{{{{{{\rm{a}}}}}}}{Q}_{{{{{{\rm{a}}}}}}}\right)\right)}^{2}}\\ +\frac{B}{{\left(1-{\left(\omega /{\omega }_{{{{{{\rm{b}}}}}}}\right)}^{2}\right)}^{2}+{\left(\omega /\left({\omega }_{{{{{{\rm{b}}}}}}}{Q}_{{{{{{\rm{b}}}}}}}\right)\right)}^{2}}$$
(1)

where \(A\) and \(B\) are constants.

Figure 1c presents the fitting of the \(V\)-dependent PSD of device #1. The electrostatic interaction imposed by the bias voltage \(V\) leads to a frequency increase which is in contrast to the usual frequency reduction caused by electrostatic attraction in typical cantilever-type SPM settings36. The voltage dependency of the coupled modes is mainly governed by the electrostatic interaction at the NW (see Supplementary Note 3).

Electrostatic interaction on the coupled devices

We model the electrostatic interaction acting on the NW end as a spring-like contribution \({{k}_{{{{{{\rm{bias}}}}}}}={rV}}^{2}\) where \(r\) is an electrostatic constant. For simplicity, we assume the electrostatic system is polarity independent and ignore contact potential differences (CPD) and further effects of asymmetries in the electrostatic system (see Supplementary Note 4). Note that we also neglect a bias dependency of \(r\) which might be caused by a \(V\) dependent static NW deflection (see Supplementary Note 3).

Neglecting damping and assuming simple one-dimensional spring-mass systems, the resonance frequencies of the coupled modes \({\omega }_{{{{{{\rm{a}}}}}},{{{{{\rm{b}}}}}}}\) read26,37

$${\omega }_{{{{{{\rm{a}}}}}},{{{{{\rm{b}}}}}}}^{2}=\frac{{\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}+{\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}}{2}\mp \sqrt{{\left(\frac{{\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}-{\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}}{2}\right)}^{2}+\frac{{k}_{{{{{{\rm{NW}}}}}}}^{2}}{{m}_{{{{{{\rm{CL}}}}}}}{m}_{{{{{{\rm{NW}}}}}}}}}$$
(2)

where \({\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}=\left({k}_{{{{{{\rm{CL}}}}}}}+{k}_{{{{{{\rm{NW}}}}}}}\right)/{m}_{{{{{{\rm{CL}}}}}}}\) and \({\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}=({k}_{{{{{{\rm{NW}}}}}}}+{k}_{{{{{{\rm{bias}}}}}}})/{m}_{{{{{{\rm{NW}}}}}}}\). Even if \({\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}\) and \({\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}\) intersect at a particular voltage (gray dashed lines in Fig. 2a), \({\omega }_{{{{{{\rm{a}}}}}}}\) and \({\omega }_{{{{{{\rm{b}}}}}}}\) show clear signatures of avoided level crossing or anticrossing37 as demonstrated in Fig. 1c and Fig. 2a for device #1. A minimal frequency gap \({\left({\omega }_{{{{{{\rm{b}}}}}}}^{2}-{\omega }_{{{{{{\rm{a}}}}}}}^{2}\right)}_{\min }\) is expected for \({\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}={\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}\).

Fig. 2: Frequencies of coupled modes.
figure 2

The measurements of device #1 are shown where spheres and solid lines refer to measurements and fitted curves, respectively. a Avoided level crossing of \({\omega }_{{{{{{\rm{a}}}}}}}\) (shown in blue) and \({\omega }_{{{{{{\rm{b}}}}}}}\) (shown in red) controlled by the bias voltage \(V\). The cantilever frequency and the nanowire (NW) frequency \({\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}=\left({k}_{{{{{{\rm{NW}}}}}}}+{k}_{{{{{{\rm{bias}}}}}}}\right)/{m}_{{{{{{\rm{NW}}}}}}}\) are indicated by gray dashed lines. b Magnified view of the section indicated by the dashed rectangle in a. The horizontal axis, i.e., the \(V\)-induced interaction, is represented as \({{k}_{{{{{{\rm{bias}}}}}}}={rV}}^{2}\). Here, \(r=5.4\times {10}^{-10}\,{{{{{\rm{N}}}}}}{{{{{{\rm{m}}}}}}}^{-1}{{{{{{\rm{V}}}}}}}^{-2}\) as extracted from curve fitting. In the inset, \({\omega }_{{{{{{\rm{b}}}}}}}\) residuals are shown.

Full size image

The measured frequency data presented in Fig. 2a allow for a precise curve fitting using Eq. 2. The sets of parameters that best fit our measurements include \({k}_{{{{{{\rm{NW}}}}}}}\), \({\omega }_{{{{{{\rm{CL}}}}}}}/2\pi\), \({\omega }_{{{{{{\rm{NW}}}}}}}/2\pi\) (see Table 2), and \(r\). When considering \({k}_{{{{{{\rm{bias}}}}}}}\) acting on the NW we may also expect a \(V\)-dependent effective reduction of the cantilever’s spring constant caused by the electrostatic attraction. However, this effect turns out to be negligible in our case (see Supplementary Note 3).

Table 2 Properties of individual and coupled oscillators.
Full size table

Figure 2b shows the \({\omega }_{{{{{{\rm{b}}}}}}}\left({k}_{{{{{{\rm{bias}}}}}}}\right)\) relation. For small increments \(\triangle {k}_{{{{{{\rm{bias}}}}}}}\) of the interaction force derivative where \(\left|\triangle {k}_{{{{{{\rm{bias}}}}}}}\right|\ll {k}_{{{{{{\rm{NW}}}}}}}+{k}_{{{{{{\rm{bias}}}}}}}\), we can assume a linear approximation for the corresponding shift in the frequency \({\triangle \omega }_{{{{{{\rm{b}}}}}}}\), which can be written by \({\triangle \omega }_{{{{{{\rm{b}}}}}}}/{\omega }_{{{{{{\rm{b}}}}}}}\approx \triangle {k}_{{{{{{\rm{bias}}}}}}}/2{k}_{{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}}\). Since \({k}_{{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}}\) describes the \({\triangle \omega }_{{{{{{\rm{b}}}}}}}\left(\triangle {k}_{{{{{{\rm{bias}}}}}}}\right)\) relation, it can be considered as an effective spring constant of the coupled system. Furthermore, \({k}_{{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}}\) can be approximated by \({2k}_{{{{{{\rm{NW}}}}}}}\) if the following requirements are fulfilled: (i) the cantilever spring constant is much larger than that of the NW, \({k}_{{{{{{\rm{CL}}}}}}}/{k}_{{{{{{\rm{NW}}}}}}}\gg 1\), and (ii) if the electrostatic interaction is tuned such that the system is driven to the minimum frequency gap \({\left({\omega }_{{{{{{\rm{b}}}}}}}^{2}-{\omega }_{{{{{{\rm{a}}}}}}}^{2}\right)}_{\min }\) in the anticrossing region38. Our measured data confirm this simple \({k}_{{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}}\approx {2k}_{{{{{{\rm{NW}}}}}}}\) relation which can also be applied to \({k}_{{{{{{\rm{a}}}}}}}^{{{{{{\rm{eff}}}}}}}\) for the first coupled mode. Note that \({k}_{{{{{{\rm{CL}}}}}}}/{k}_{{{{{{\rm{NW}}}}}}}\approx {{{{\mathrm{140,000}}}}}\) for device #1 (Table 2).

Minimal detectable force derivative

Our measurements demonstrate that a \(\triangle {k}_{{{{{{\rm{bias}}}}}}}\) increment as small as \(\approx 6\times {10}^{-10}{{{{{\rm{N}}}}}}/{{{{{\rm{m}}}}}}\) leads to a clearly detectable frequency shift \({\triangle \omega }_{{{{{{\rm{b}}}}}}}\approx 1.5 \, {{{{{\rm{Hz}}}}}}\) (Fig. 2b). The standard deviation of the \({\omega }_{{{{{{\rm{b}}}}}}}\) residuals (inset of Fig. 2b) is \(\approx 0.3 \, {{{{{\rm{Hz}}}}}}\) corresponding to a \({\triangle k}_{{{{{{\rm{bias}}}}}}}\) measurement uncertainty of \(\approx 1.1\times {10}^{-10}{{{{{\rm{N}}}}}}/{{{{{\rm{m}}}}}}\). Converted to a measurement scheme at a measurement bandwidth of 1 Hz (see Supplementary Note 5), the \(\triangle {k}_{{{{{{\rm{bias}}}}}}}\) measurement uncertainty for device #1 would be \(\approx 9\times {10}^{-10}{{{{{\rm{N}}}}}}/{{{{{\rm{m}}}}}}\).

We compare the measured force derivative uncertainty \(\triangle {k}_{{{{{{\rm{bias}}}}}}}\) to the minimal detectable force derivative \({{F{{\hbox{'}}}}}_{\min }\) as limited by thermal force fluctuations39,40 at room temperature. \({{F{{\hbox{'}}}}}_{\min }\) is given by

$${F}^{\prime} _{\min }=\sqrt{4{k}_{i}{k}_{{{{{{\rm{B}}}}}}}{TB}/({\omega }_{i}{Q}_{i}({\triangle z})^{2})}$$
(3)

Here, \(\triangle z\) is the sensor’s root-mean-square vibration amplitude. In our case, the thermal motion variance of the device, i.e., \(\triangle z=\sqrt{{k}_{{{{{{\rm{B}}}}}}}T/{k}_{i}}\) is used according to the equipartition theorem. Note that such calculated \({{F{{\hbox{'}}}}}_{\min }\) considers thermal limitations only and disregards various other noise contributions including detector noise. Therefore, it constitutes a theoretical lower limit that probably cannot be achieved experimentally.

Using Eq. 3, \({{F{{\hbox{'}}}}}_{\min }\) is calculated for the coupled devices, the isolated NWs, and the cantilevers (Table 2). We note that in the case of co-resonance, i.e., \({\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}={\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}\), the minimal detectable force derivative \({{F{{\hbox{'}}}}}_{\min }\) of the coupled devices is of the same order of magnitude as the corresponding quantity of the isolated NWs. In the case of device #1 the calculated \({{F{{\hbox{'}}}}}_{\min }=4.1\times {10}^{-10}{{{{{\rm{N}}}}}}/{{{{{\rm{m}}}}}}\) is only 45 % larger than that of the isolated NW, but at the same time, it is four orders of magnitude smaller than that of the corresponding standalone cantilever. Furthermore, the \({F}^{{\prime} }=\triangle {k}_{{{{{{\rm{bias}}}}}}}\) measurement uncertainty is approximately 2.2 times larger than \({{F{{\hbox{'}}}}}_{\min }\) for device #1 yet still roughly four orders of magnitude smaller than \({{F{{\hbox{'}}}}}_{\min }\) of the corresponding standalone cantilever. These findings are additionally confirmed by the analysis of device #2 (Table 2, Fig. 3, and Supplementary Note 7).

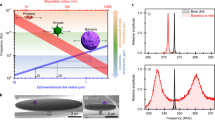
Fig. 3: Minimal detectable force derivative.
figure 3

The \({{F{{\hbox{'}}}}}_{\min }\) is shown as limited by thermal force fluctuations at a measurement bandwidth of \(B=1{{{{{\rm{Hz}}}}}}\) and at room temperature versus the typical width of the oscillator devices. Typical oscillator widths refer to the dimension of the optically detected sensor part, i.e., the diameter of the nanowire (NW) in the case of standalone NWs and the width of the cantilever in the case of standalone cantilevers and coupled devices. Calculated \({{F{{\hbox{'}}}}}_{\min }\) is given for the coupled devices, the standalone cantilevers and Si NWs of devices #1 and #2, and for singly-clamped NW and cantilever devices as reported in literature11,15,20,34,41,42,43,44,45,46. In addition, the measured force derivative uncertainty \(\triangle {k}_{{{{{{\rm{bias}}}}}}}\) of our coupled devices is shown. The light-green background indicates the expected trend for nano- and micro-scale cantilevers.

Full size image

In Fig. 3, \({{F{{\hbox{'}}}}}_{\min }\) is shown for the coupled devices, for the corresponding standalone cantilevers and Si NWs together with the measured force derivative uncertainty \(\triangle {k}_{{{{{{\rm{bias}}}}}}}\) and \({{F{{\hbox{'}}}}}_{\min }\) values derived from literature11,15,20,34,41,42,43,44,45,46. The data is arranged according to the respective typical widths of the sensors at a particular location where usually optical detection is performed. Therefore, a larger “typical width” is associated with easier detection of the signal (depicted by the arrow). Optical detection of our coupled systems is done at the cantilever near its free end where the NW is attached.

Note that the data points describing the devices and device components of this work are grouped in three clusters. If considered as standalone devices, the Si NWs are associated with high force derivative sensitivity but challenging direct detection (bottom left purple ellipse in Fig. 3). At the same time, the micron-sized cantilevers are associated with lower force derivative sensitivity but easy detectability (top right purple circle in Fig. 3). Our co-resonantly coupled devices (bottom right purple ellipse in Fig. 3) advantageously combine the NWs’ high sensitivity with the cantilevers’ easy detectability.

Now, we discuss the characteristics of the minimal detectable force derivative \({{F{{\hbox{'}}}}}_{\min }\) as limited by thermal force fluctuations (Eq. 3) when comparing a standalone NW to the same NW when co-resonantly coupled to a micro-cantilever. The doubled effective force constant, i.e., \({k}_{{{{{{\rm{a}}}}}}/{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}}\approx {2k}_{{{{{{\rm{NW}}}}}}}\), deteriorates \({{F{{\hbox{'}}}}}_{\min }\) by a factor of \(\sqrt{2}\), but at the same time, there is the advantage of increased quality factor, i.e., \({Q}_{{{{{{\rm{a}}}}}}/{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}} \, > \, {Q}_{{{{{{\rm{NW}}}}}}}\). The latter can be considered as the lending of the cantilever’s high quality factor to the co-resonantly coupled modes38. This effect has also been described for micron-sized drum resonators coupled to Si3N4 membranes47. For perfect frequency matching \({\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}\approx {\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}\) and very different individual quality factors \({Q}_{{{{{{\rm{CL}}}}}}}\gg {Q}_{{{{{{\rm{NW}}}}}}}\) like in our case, the effective quality factors \({Q}_{{{{{{\rm{a}}}}}}/{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}}\) are approximately doubled, i.e., \({Q}_{{{{{{\rm{a}}}}}}/{{{{{\rm{b}}}}}}}^{{{{{{\rm{eff}}}}}}}\approx 2{Q}_{{{{{{\rm{NW}}}}}}}\) (see Supplementary Note 6). Thus, the \({k}_{i}/{Q}_{i}\) ratio in Eq. 3 does not change upon co-resonant coupling of a NW. The moderate \({{F{{\hbox{'}}}}}_{\min }\) increase as apparent in Table 2 is caused by the decrease of the thermal motion variance upon coupling. In other words, \({{F{{\hbox{'}}}}}_{\min }\) would not deteriorate upon coupling if the systems were driven at constant \(\triangle z\).

Similar to Fig. 3, a compilation and comparison of force derivatives could also be done by considering vibration amplitudes \(\triangle z\) driven by periodic excitations that exploit the full dynamic range48 of the respective oscillators. However, the latter might only be appropriate where large oscillation amplitudes are compatible with the specific sensor application, e.g., in mass sensing17.

In order to understand the dependency of \({{F{{\hbox{'}}}}}_{\min }\) on the device dimensions we can divide \({F}_{\min }\propto d/\sqrt{l}\) by the thermal motion variance, i.e., \(\triangle z\propto \sqrt{1/{k}_{i}}\propto {l}^{3/2}/{d}^{2}\) resulting in \({{F{{\hbox{'}}}}}_{\min }\propto {d}^{3}/{l}^{2}\). Thus, devices comprising long and thin NWs will be the most sensitive. If we want to simultaneously maximize the frequencies and minimize \({{F{{\hbox{'}}}}}_{\min }\), all NW dimensions should be scaled down13. Here we specifically point to NW dimensions since \({{F{{\hbox{'}}}}}_{\min }\) of coupled devices is mainly defined by NW properties.

Possible mechanisms underlying the bias-induced NW frequency increase include a softening effect caused by the derivative of the attractive electrostatic force leading to a negative frequency shift, a pendulum-type effect that is expected for a NW tilted towards the counter electrode and exposed to an attractive force leading to a positive frequency shift, and an effective stiffening by bias-induced static NW bending taking into account geometrical nonlinearities. We calculated the sum of these contributions for device #1 at \(-6{{{{{\rm{V}}}}}}\). However, it accounts only for 10% of our experimentally obtained \({{k}_{{{{{{\rm{bias}}}}}}}={rV}}^{2}\) (see Supplementary Note 3). To provide a full analysis of the mechanism behind the voltage-dependent NW stiffening further studies are required.

Conclusions

Our results demonstrate that co-resonantly coupled NW-cantilever systems, i.e., systems with matched individual eigenfrequencies \({\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}\approx {\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}\), can detect small force derivatives of a similar order of magnitude to those of standalone NWs (Fig. 3). The coupled, hybrid modes of a NW-cantilever system reflect the vibration properties of the involved NW even if the coupled system is several orders of magnitude larger than the NW. At the same time, the coupled system can be read out by conventional cantilever detection methods that are widely used in commercial SPM setups.

The detection sensitivity of force and force derivative sensors based on coupled oscillators can be further improved by: (i) direct growth of NWs on cantilevers which will increase the NWs’ Q factors by several orders of magnitude20 and (ii) miniaturization of the coupled device, e.g., coupling a \({k=10}^{-9}{{{{{\rm{N}}}}}}/{{{{{\rm{m}}}}}}\) single-walled carbon nanotube to an interferometrically detected \({k=10}^{-4}{{{{{\rm{N}}}}}}/{{{{{\rm{m}}}}}}\) NW or soft cantilever.

A potential advantage of coupled NW-cantilever devices might be that they allow for sensing at much lower NW temperatures compared to optically detected NW-only sensors since the NWs of coupled devices are not exposed to optical heating.

There is a variety of possible implementations of the co-resonantly coupled sensor. A feasible mode of operation can be that the electrostatic interaction at the NW end is controlled by a feedback loop which keeps the frequencies of the coupled modes constant, preferably in the frequency-matching region \({\omega }_{{{{{{{\rm{CL}}}}}}}^{* }}^{2}={\omega }_{{{{{{{\rm{NW}}}}}}}^{* }}^{2}\). This would keep the overall interaction at the NW end constant and would ensure that the electrostatic interaction associated with the voltage would reflect changes in the external interaction.

The prospect for future applications of co-resonantly coupled NW-cantilever systems may include nano-torque magnetometry18 of single endohedral fullerene molecules or corresponding nano-crystallites49, sensing of ultra-small masses, and scanning probe microscopy approaches15,42,50. For the latter, the NW part of the sensor should be arranged in the pendulum geometry to avoid snap-in. Additionally, a straight NW shape would be necessary to ensure an adequate longitudinal NW stiffness.

Methods

Fabrication of coupled oscillator devices

We used As-doped Si NWs (diameters \(d\): 15 nm to 30 nm; lengths \(l\): 10 µm to 30 µm) grown by catalytic epitaxial chemical vapor deposition (CVD) using an Applied Materials P5000 cluster tool. The growth was carried out at a temperature of 450 °C and a pressure of 67 mbar. Details of the NW growth are described elsewhere51. The coupled oscillators were prepared using a micromanipulation device (Kleindiek micromanipulator) inside a combined scanning electron microscopy (SEM) and focused ion beam (FIB) instrument (ZEISS 1540 XB) equipped with a gas injection system. The NWs were glued to tip-less Si cantilevers (NanoWorld Arrow TL; triangular apex removed by FIB milling) by electron-beam-assisted deposition of tungsten (Fig. 1a, b).