Introduction

In quantum systems close to critical points, small variations of physical parameters can lead to drastic changes in the equilibrium-state properties1,2,3,4. An interesting class of quantum critical systems is provided by light-matter interaction models5,6,7,8, such as the quantum Rabi9,10 and Dicke models11,12,13,14,15,16,17,18 describing the interaction of single or many two-level atoms (atomic levels \(\left\vert g\right\rangle\) and \(\left\vert e\right\rangle\)) with a single-model cavity. The quantum Dicke model exhibits a superradiant quantum phase transition (QPT) in the thermodynamic limit of infinite atoms11,12,13,14,15,16,17. Such a thermodynamic limit leads to some difficulties in experimentally exploring the superradiant QPTs19,20,21,22,23,24,25,26. Instead, by replacing the thermodynamic limit with a scaling of the system parameters, the quantum Rabi model described by the Hamiltonian (hereafter ℏ = 1)

$${H}_{R}=\, \omega {a}^{{{{\dagger}}} }a(\left\vert e\right\rangle \langle e| +| g\rangle \langle g\vert )+\Omega \left\vert e\right\rangle \left\langle e\right\vert \\ -g(a+{a}^{{{{\dagger}}} })(\vert g\rangle \langle e| +| e\rangle \left\langle g\right\vert ),$$
(1)

can also exhibit a superradiant QPT9,10, where ω (Ω) is the cavity-mode (atomic-transition) frequency, a (a†) is the cavity-mode annihilation (creation) operator, and g is the light-matter coupling strength. We assume that the level frequency of the atomic state \(\vert g\rangle\) is zero. This superradiant QPT has been experimentally observed27,28 and is attracting increasing attention29,30,31,32,33,34. However, one of the most important critical phenomena in this system, i.e., a discontinuity of the derivative for the number of bare photons at the critical point, is hard to observe.

Unlike classical phase transitions, superradiant QPTs can occur when changing the system parameters at zero temperature5,6,16. Specifically, when g approaches the critical point, it was predicted10 that the mean photon number in the ground eigenstate of HR suddenly increases to infinity. This corresponds to a QPT from a normal phase (NP), where the ground state of the cavity field is not occupied, to a superradiant phase (SP), where the ground state is macroscopically occupied. However, experimentally exploring this critical phenomenon is challenging because: (i) the time required to prepare this equilibrium state diverges10; and (ii) these photons are virtual, so cannot be directly measured7,8. Especially, the difficulty (i) may make transition-edge sensing protocols35,36,37 not effective in detecting this kind of phase transitions.

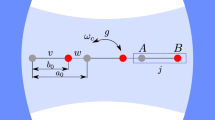
Here we show how to overcome these problems by introducing additional low-energy levels in the quantum Rabi model and driving transitions among these levels. We show that the stimulated emission effect of the whole system can directly reflect the change of the photon-number distributions of the quantum Rabi Hamiltonian. The process can be interpreted as a multi-photon down-conversion induced by stimulated Raman transitions (i.e., a pump photon is converted into a Stokes photon and multiple cavity photons, as shown in Fig. 1a)38,39,40,41. This parametric down-conversion process changes abruptly when the superradiant QPT occurs in the quantum Rabi Hamiltonian. Such a change can be observed by measuring the real photons continuously released from the cavity. Note that this parametric down-conversion process was initially studied by Huang et al. in 2014 for photon emission via vacuum-dressed intermediate states39. We find that such a photon emission can be useful in observing quantum critical phenomena. We predict that the steady-state output photon rate can reach \({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}} \sim 4\times 1{0}^{-3}\omega\) in the NP, then suddenly vanishes when tuning the Rabi Hamiltonian into the SP. This demonstrates a sudden change of the ground eigenstate of the quantum Rabi Hamiltonian, and indicates the occurrence of the superradiant QPT.

Fig. 1: Sketch and atomic level structure of the protocol.
figure 1

a Sketch of the parametric down-conversion process in an atom-cavity system. A pump pulse of frequency ωp is converted into a Stokes pulse of frequency ωs and multiple cavity photons of frequency ω. b Level structure of the atom. The upper two atomic levels \(\left\vert g\right\rangle\) and \(\left\vert e\right\rangle\) are ultrastrongly coupled to the cavity mode with strength g. The lower two levels \(\left\vert g\right\rangle\) and \(\left\vert \mu \right\rangle\) are off-resonantly driven by a composite pulse of two frequencies (ωp and ωs) and two amplitudes (Ωp and Ωs).

Full size image

Superadiant quantum phase transitions

Note that the theory of the superradiant phase transition in the quantum Rabi model was developed first in 20139 and then in 201510. For clarity, we first review the theory of the superradiant phase transition in the quantum Rabi model. In the limit of Ω/ω → ∞, following refs. 9,10, we can solve the Hamiltonian HR in Eq. (1) using a Schrieffer-Wolff transformation1,2:

$${U}_{{{{{{{{\rm{SW}}}}}}}}}=\exp \left[\left(\frac{g}{\Omega }\right)\left(a+{a}^{{{{\dagger}}} }\right)\left(\left\vert e\right\rangle \langle g| -| g\rangle \left\langle e\right\vert \right)\right].$$
(2)

For the transformed Hamiltonian, the transitions between the ground- and excited-qubit-state subspaces \(\{\vert n\rangle \vert g\rangle \}\) and \(\left\{\left\vert n\right\rangle \left\vert e\right\rangle \right\}\) are negligible. Thus, we perform a projection \(\langle g| {U}_{{{{{{{{\rm{SW}}}}}}}}}^{{{{\dagger}}} }{H}_{R}{U}_{{{{{{{{\rm{SW}}}}}}}}}| g\rangle\), resulting in

$${H}_{{{{{{{{\rm{np}}}}}}}}}=\omega {a}^{{{{\dagger}}} }a-\frac{\omega {g}_{c}^{2}}{4}{\left(a+{a}^{{{{\dagger}}} }\right)}^{2}+O({g}_{c}^{2}\omega /\Omega ),$$
(3)

where

$${g}_{c}=2g/\sqrt{\omega \Omega },$$

is the normalized coupling strength and \(O({g}_{c}^{2}\omega /\Omega )\) denotes negligible higher-order terms. The excitation energy of Hnp is

$${\varepsilon }_{{{{{{{{\rm{np}}}}}}}}}=\omega \sqrt{1-{g}_{c}^{2}},$$

which is real only for gc ≤ 1 and vanishes at gc = 1, i.e., in the NP10. The ground eigenstate of Hnp is \(\left\vert {E}_{0}\right\rangle =S({r}_{{{{{{{{\rm{np}}}}}}}}})\left\vert 0\right\rangle\), with

$$S({r}_{{{{{{{{\rm{np}}}}}}}}})=\exp \left[\frac{{r}_{{{{{{{{\rm{np}}}}}}}}}}{2}\left({a}^{{{{\dagger}}} 2}-{a}^{2}\right)\right],\,\,\,\,\,\,{{{{{{{\rm{and}}}}}}}}\,\,\,\,\,\,\,{r}_{{{{{{{{\rm{np}}}}}}}}}=-\frac{1}{4}\ln \left(1-{g}_{c}^{2}\right).$$
(4)

For gc > 1 and

$$\alpha =\frac{1}{2}\sqrt{\frac{\Omega }{\omega }\left({g}_{c}^{2}-{g}_{c}^{-2}\right)}\,\ge 0,$$
(5)

after displacing the cavity field with displacement operators

$$D(\pm \alpha )=\exp \left[\pm \alpha \left({a}^{{{{\dagger}}} }-a\right)\right],$$
(6)

we can employ the same procedure in deriving Hnp to obtain the Hamiltonian in the SP:

$${H}_{{{{{{{{\rm{sp}}}}}}}}}\approx \omega {a}^{{{{\dagger}}} }a-\frac{\omega }{4{g}_{c}^{4}}{\left(a+{a}^{{{{\dagger}}} }\right)}^{2}+\frac{\Omega }{2}\left(1-{g}_{c}^{2}\right)+\omega {\alpha }^{2}.$$
(7)

The excitation energy of Hsp is \({\varepsilon }_{{{{{{{{\rm{sp}}}}}}}}}=\omega \sqrt{1-{g}_{c}^{-4}}\) and the ground eigenstate of Hsp is \(S({r}_{{{{{{{{\rm{sp}}}}}}}}})\left\vert 0\right\rangle\), with

$${r}_{{{{{{{{\rm{sp}}}}}}}}}=-\frac{1}{4}\ln \left(1-{g}_{c}^{-4}\right).$$
(8)

Thus, in the lab frame, HR has two degenerate ground eigenstates

$$\left\vert {E}_{0}\right\rangle =D(\pm \alpha )S({r}_{{{{{{{{\rm{sp}}}}}}}}})\left\vert 0\right\rangle {\left\vert \downarrow \right\rangle }_{\pm },$$
(9)

where \({\left\vert \downarrow \right\rangle }_{\pm }\) are the ground eigenstates of

$${H}_{\pm }=\Omega \left\vert e\right\rangle \left\langle e\right\vert \mp 2g\alpha (\left\vert e\right\rangle \langle g| +| g\rangle \left\langle e\right\vert ).$$
(10)

This is because two different displacement parameters ± α result in an indentical spectrum9.

Demonstrating the critical phenomenon

The sudden change of \({\bar{n}}_{0}=\langle {E}_{0}| {a}^{{{{\dagger}}} }a| {E}_{0}\rangle\) at the critical point gc = 1 is the most important benchmark of the superradiant QPT. Specifically, when Ω/ω → ∞, the derivative \(d{\bar{n}}_{0}/d{g}_{c}\) is discontinuous at the critical point gc = 1 (see Fig. 2a), indicating the occurrence of the superradiant QPT. However, observing this critical phenomenon is still challenging in experiments mainly because: (i) it is difficult to prepare the ground state \(\left\vert {E}_{0}\right\rangle\) at the critical point; (ii) one cannot adiabatically tune control parameters across the critical point27,28 since the energy gap mostly closes at the critical point; and (iii) the photons in the ground eigenstate \(\left\vert {E}_{0}\right\rangle\) are virtual and cannot be directly measured7,8.

Fig. 2: Sudden change of photon number distribution.
figure 2

a Derivative \(d{\bar{n}}_{0}/d{g}_{c}\) of the virtual cavity excitation number \({\bar{n}}_{0}=\langle {E}_{0}| {a}^{{{{\dagger}}} }a| {E}_{0}\rangle\) calculated for different frequency rate Ω/ω. b Probability amplitudes ∣c2k∣ of the states \(\left\vert 2k\right\rangle \left\vert g\right\rangle\) in the eigenstate \(\left\vert {E}_{0}\right\rangle\) of HR in Eq. (1) when Ω = 106ω approximatively satisfying the condition Ω/ω → ∞. The green- and blue-shaded areas denote the normal phase (NP) and the superradiant phase (SP), respectively.

Full size image

Instead, in this manuscript, we propose to measure the sudden change of the photon number distributions of \(\left\vert {E}_{0}\right\rangle\), i.e., the probability amplitudes \({c}_{k}(\,{g}_{c})=\left\langle g\right\vert \langle k| {E}_{0}\rangle\). This is equivalent to measuring the change of 〈E0∣a†a∣E0〉 because it can be calculated using the photon number distributions. In the Ω/ω → ∞ limit, it is expected that α → ∞ and rsp ≠ 0 when gc > 1. Thus, when gc is tuned across the critical point, there is a sudden change in the amplitude c2k:

$$| {c}_{2k}({g}_{c})| \,\mathop{\longrightarrow }\limits^{{g}_{c}={1}^{-}}\,\left\vert \frac{{\left[-\tanh ({r}_{{{{{{{{\rm{np}}}}}}}}})\right]}^{k}\sqrt{(2k)!}}{{2}^{k}k!\sqrt{\cosh ({r}_{{{{{{{{\rm{np}}}}}}}}})}}\right\vert \, > \, 0,\\ | {c}_{2k}({g}_{c})| \,\mathop{\longrightarrow }\limits^{{g}_{c}={1}^{+}}\,\left\vert \frac{{(\tanh {r}_{{{{{{{{\rm{sp}}}}}}}}})}^{k}\exp \left[-\frac{{\alpha }^{2}}{2}(1+\tanh {r}_{{{{{{{{\rm{sp}}}}}}}}})\right]}{{2}^{k}\sqrt{(2k)!\cosh {r}_{{{{{{{{\rm{sp}}}}}}}}}}}{{{{{{{{\mathcal{H}}}}}}}}}_{{}_{n}}(x)\right\vert \longrightarrow 0,$$
(11)

where \({{{{{{{{\mathcal{H}}}}}}}}}_{n}(x)\) are the Hermite polynomials with

$$x=\frac{\alpha \exp ({r}_{{{{{{{{\rm{sp}}}}}}}}})}{\sqrt{\sinh 2{r}_{{{{{{{{\rm{sp}}}}}}}}}}}.$$
(12)

Such a change is obvious when k is small, because ∣c2k(gc → 1−)∣ is significant as shown in Fig. 2b. Especially, for k < 5, the components of the few-photon states in the eigenstate \(\left\vert {E}_{0}\right\rangle\) of HR suddenly vanish when gc is tuned across the critical point (see Fig. 2b). This coincides with the sudden changes of the photon number \({\bar{n}}_{0}\) and its derivative \(d{\bar{n}}_{0}/d{g}_{c}\) (see the red-solid curve in Fig. 2a).

To demonstrate the sudden change of c2k, following the idea in ref. 39, we introduce a third low-energy level \(\left\vert \mu \right\rangle\) with level frequency ωμ < 0 for the atom (see Fig. 1b). We assume that ∣ωμ∣ ≫ ω, so that the state \(\left\vert \mu \right\rangle\) is far off-resonance to the cavity bare frequency. The atom-cavity interaction becomes

$${H}_{0}={H}_{R}+{\omega }_{\mu }\left\vert \mu \right\rangle \langle \mu | +\omega {a}^{{{{\dagger}}} }a| \mu \rangle \left\langle \mu \right\vert ,$$
(13)

whose eigenstates \(\vert {\xi }_{j}\rangle\) can be separated into: (i) the noninteracting sectors \(\vert {\mu }_{n}\rangle =\vert n\rangle \vert \mu \rangle\) with eigenvalues nω + ωμ; and (ii) the eigenstates \(\vert {E}_{m}\rangle\) of HR with eigenvalues Em (j, n, m = 0, 1, 2, …). The ground state of the whole system becomes \(\vert {\mu }_{0}\rangle\), which is the initial state for the system dynamics hereafter.

Then, as shown in Fig. 1, we employ a composite pulse to drive the atomic transition \(\left\vert \mu \right\rangle \leftrightarrow \left\vert g\right\rangle\):

$${H}_{D}=\left[{\Omega }_{p}\cos ({\omega }_{p}t)+{\Omega }_{s}\cos ({\omega }_{s}t)\right]\left(\left\vert \mu \right\rangle \langle g| +| g\rangle \left\langle \mu \right\vert \right),$$
(14)

where Ωp,(s) and ωp,(s) are the driving amplitude and frequency, respectively. Focusing on the changes of few-photon components (k < 5), we choose ωp = E0 − ωμ and ωs = E0 − ωμ − 2lω, for l = 1, 2, …, resulting in the resonant transitions \(\vert {\mu }_{0}\rangle \leftrightarrow \vert {E}_{0}\rangle \leftrightarrow \vert {\mu }_{2l}\rangle\) in the subspace \(\{\vert {\xi }_{j}\rangle \}\). Specifically, for weak drivings Ωp,(s) ≪ ∣E2 − E0∣, the system dynamics is understood as the Raman transitions described by the effective Hamiltonian

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=\frac{1}{2}\left[{c}_{0}{\Omega }_{p}\left\vert {\mu }_{0}\right\rangle +{c}_{2l}{\Omega }_{s}\left\vert {\mu }_{2l}\right\rangle \right]\left\langle {E}_{0}\right\vert +{{{{{{{\rm{h}}}}}}}}.{{{{{{{\rm{c}}}}}}}}.,$$
(15)

which is obtained by performing \({e}^{i{H}_{0}t}{H}_{D}{e}^{-i{H}_{0}t}\) and neglecting fast-oscillating terms under the rotating-wave approximation (see Supplementary Note 1 for more details). Hereafter, we omit the explicit gc dependence of all the probability amplitudes ck for simplicity. The dynamics governed by Heff can be interpreted as a multi-photon down-conversion process (see Fig. 1a), with an efficiency controllable by the coefficients c0 and c2l. When the initial state is \(\left\vert {\mu }_{0}\right\rangle\), the probability amplitude of the state \(\left\vert {\mu }_{2l}\right\rangle\) at time t reads

$${P}_{2l} =\frac{{c}_{0}{\Omega }_{p}{c}_{2l}{\Omega }_{s}}{4{{{\Xi }}}^{2}}\left[\cos \left({{\Xi }}t\right)-1\right],\,\,\,\,{{{{{{{\rm{with}}}}}}}}\,\,\,\,{{{\Xi }}}^{2}\\ =\frac{1}{4}\left[{\left({c}_{0}{\Omega }_{p}\right)}^{2}+{\left({c}_{2l}{\Omega }_{s}\right)}^{2}\right].$$
(16)

Choosing t = π/Ξ, the probability amplitudeP2l and the mean photon number of the system both reach their maximum values. Then, as long as Ωp ≠ 0 and Ωs ≠ 0, P2l is measurable because c0 and c2l are significant. Accordingly, the theoretical prediction of the maximum photon number of the system after a finite-time evolution is

$${\bar{n}}_{\max }^{e}=2l| {P}_{2l}(t){| }^{2}=2l{\left\vert \frac{2{c}_{0}{\Omega }_{p}{c}_{2l}{\Omega }_{s}}{{({c}_{0}{\Omega }_{p})}^{2}+{\left({c}_{2l}{\Omega }_{s}\right)}^{2}}\right\vert }^{2}.\,\,\,\,\,\,({{{{{{{\rm{where}}}}}}}}\,t=\pi /\Xi )$$
(17)

However, when gc is tuned across the critical point, the needed evolution time to achieve the maximum photon number tends infinite due to Ξ → 0. To avoid such an infinite-time evolution, we impose t ≤ 106/ω in this protocol when Ξ → 0. In this limit, we obtain P2l → 0 because \(\cos (\Xi t)\to 1\) according to Eq. (16). Therefore, as shown in Fig. 3, we theoretically predict a sudden change of the mean photon number when gc → 1, indicating the occurrence of the superradiant QPT.

Fig. 3: Critical phenomenon.
figure 3

Theoretical prediction of the maximum photon number of the system after a finite-time evolution, according to Eqs. (16) and (17). For Ξ → 0, we impose t = 106/ω when π/Ξ → ∞, to avoid an infinite evolution time in the coherent dynamics. Parameters are: Ω = 106ω, \({\omega }_{\mu }={E}_{0}-\left[2({n}_{d}-l)+0.25\right]\omega\), Ωp = 0.005(E2 − E0), and Ωs = 2Ωp. For simplicity, we choose nd = 2 + l in the simulation.

Full size image

This demonstration can be interpreted as a partial quantum process tomography, which starts at preparing the initial state \(\vert {\mu }_{0}\rangle\) and fixing gc to a specific value, e.g., gc = 0.999. Then, turning on the drivings, one can detect the system dynamics (see the example in Fig. 4a). After the detection, the drives are turned off and the system is prepared to the state \(\left\vert {\mu }_{0}\right\rangle\). The next step is tuning gc to another value (e.g., gc = 1.001) through adjusting the frequencies Ω and ω. Thus, after the energy spectrum of the system stabilizes, one can turn on the drivings again and detect the system dynamics (see the example in Fig. 4b). By repeating these processes, we can know the system dynamics for an arbitrary gc and demonstrate the critical phenomenon as shown in Fig. 4c, which shows the maximum value \({\bar{n}}_{\max }\) of the mean photon number of the system in the evolution. Note that the mean photon number is no longer \(\bar{n}=\langle {a}^{{{{\dagger}}} }a\rangle\), but \(\bar{n}=\langle {X}^{-}{X}^{+}\rangle\), where X+ (X−) is the positive (negative) frequency component of the quadrature operator X = a + a†7,8,42,43. Otherwise, because of 〈E0∣a†a∣E0〉 ≠ 0, an observation of the stream of photons in the eigenstate \(\left\vert {E}_{0}\right\rangle\) of the Rabi model would give rise to a perpetuum mobile behavior38,42. Because these photons can be emitted and detected in a dissipative dynamics, a measurement of the population dynamics is not necessary.

Fig. 4: Dynamics of the model.
figure 4

Populations of the ground state \(\left\vert {\mu }_{0}\right\rangle\) and the four-photon state \(\left\vert {\mu }_{4}\right\rangle\) in (a) the normal phase (NP, green-shaded area) for gc = 0.999, and (b) the superradiant phase (SP, blue-shaded area) for gc = 1.001, calculated for the total Hamiltonian Htot = H0 + HD. c Maximum value (\({\bar{n}}_{\max }\) at the time t = π/Ξ) over time of the mean photon number in the evolution governed by Htot for l = 1, 2, 3, 4. Parameters are the same as those in Fig. 3. Here, nd ≥ l is used to tune the driving frequencies ωp and ωs; and for simplicity, we choose nd = 2 + l in the simulation. The eigenvalues E0 and E2 can be numerically calculated. The level frequency ωμ is chosen so that the state \(\left\vert {E}_{0}\right\rangle\) is the highest level in the dynamical evolution and the state \(\left\vert \mu \right\rangle\) is off-resonant to the cavity bare frequency. Thus, the system only has real cavity photons contributed by the state \(\left\vert {\mu }_{2l}\right\rangle\).

Full size image

Using the corresponding input-output theory39,43, we apply

$${X}^{+}=\mathop{\sum}\limits_{j,{j}^{{\prime} }}\langle {\xi }_{{j}^{{\prime} }}| \left(a+{a}^{{{{\dagger}}} }\right)| {\xi }_{j}\rangle \vert {\xi }_{{j}^{{\prime} }}\rangle \langle {\xi }_{j}\vert ,$$
(18)

and \({X}^{-}={\left({X}^{+}\right)}^{{{{\dagger}}} }\) with \({j}^{{\prime} }\, < \,j\). Here, Eq. (18) describes that a photon emission from the cavity is associated with the transition from a high-energy eigenstate \(\vert {\xi }_{j}\rangle\) to a low-energy eigenstate \(\vert {\xi }_{{j}^{{\prime} }}\rangle\) of H0. Note that in the subspace \(\{\vert {\mu }_{n}\rangle \}\), we can obtain \({\sum }_{n}\vert {\mu }_{n}\rangle \langle {\mu }_{n}| {X}^{+}{\sum }_{m}| {\mu }_{m}\rangle \langle {\mu }_{m}| =| \mu \rangle \langle \mu \vert \otimes a\). That is, the photons in the states \(\vert {\mu }_{2l}\rangle\) are real cavity photons, thus,

$${X}^{-}{X}^{+}\vert {\mu }_{2l}\rangle \equiv \vert \mu \rangle \langle \mu | \otimes {a}^{{{{\dagger}}} }a| {\mu }_{2l}\rangle ={a}^{{{{\dagger}}} }a\left\vert 2l\right\rangle \vert \mu \rangle .$$
(19)

Therefore, the system has maximum real photons at the time t = π/Ξ, when the state \(\vert {\mu }_{2l}\rangle\) is maximally populated according to Eq. (16). Figure 4c shows that \({\bar{n}}_{\max }\) reaches a maximum when gc → 1−, indicating a rapid increase of the mean photon number near the critical point. Then, when gc is tuned across the critical point, the photons suddenly vanish. The inset of Fig. 4 shows such changes more clearly, where we can see that \({\bar{n}}_{\max }\) changes sharply when slightly increasing gc from gc = 1 to gc = (1 + 10−4), demonstrating a sudden change of the photon-number distributions in \(\left\vert {E}_{0}\right\rangle\) (see also Supplementary Note 1). Obviously, the actual dynamics of the system shown in Fig. 4c coincides very well with the effective one shown in Fig. 3. As an example for l = 2, when gc = 0.99999, the theoretical prediction of the maximum photon number is \({\bar{n}}_{\max }^{e}\simeq 3.89\), and the actual number is \({\bar{n}}_{\max }\simeq 3.93\). When we change gc to gc = 1.0003, the theoretical prediction becomes \({\bar{n}}_{\max }^{e}\simeq 0.0018\) and the actual number is \({\bar{n}}_{\max }\simeq 0.04\). Both close to zero, indicating a sudden change of the mean photon number at the critical point. The sudden change in \({\bar{n}}_{\max }\) can be easily detected experimentally by measuring the rate of photons transmitted out of the cavity. Note that numerical results for actual dynamical evolution in this manuscript are obtained using the total Hamiltonian Htot = H0 + HD without approximations.

Output photon rate

A proper generalized input-output relation in the ultrastrong-coupling regime determines the output cavity photon rate38,39 by

$${\Phi }_{{{{{{{{\rm{out}}}}}}}}}=\kappa {{{{{{{\rm{Tr}}}}}}}}\left[{X}^{-}{X}^{+}\rho \right].$$
(20)

Here, κ is the cavity decay rate and ρ is the density matrix obeying the following master equation at zero temperature7,8,

$$\dot{\rho }=i\left[\rho ,{H}_{{{{{{{{\rm{tot}}}}}}}}}\right]+\mathop{\sum }\limits_{\nu =1}^{3}\mathop{\sum}\limits_{j,{j}^{{\prime} } < j}{\Gamma }_{j{j}^{{\prime} }}^{(\nu )}\left\{{{{{{{{\mathcal{D}}}}}}}}[\vert {\xi }_{{j}^{{\prime} }}\rangle \langle {\xi }_{j}\vert ]\rho \right\},$$
(21)

where Htot = H0 + HD is the total Hamiltonian and

$${{{{{{{\mathcal{D}}}}}}}}[o]\rho =o\rho {o}^{{{{\dagger}}} }-\frac{1}{2}\left({o}^{{{{\dagger}}} }o\rho +\rho {o}^{{{{\dagger}}} }o\right),$$
(22)

is the Lindblad superoperator. The relaxation coefficients \({{{\Gamma }}}_{jj{\prime} }^{(\nu )}\) can be written in compact forms as

$${\Gamma }_{j{j}^{{\prime} }}^{(1)} ={\gamma }_{1}| \langle {\xi }_{{j}^{{\prime} }}| (\vert \mu \rangle \langle g| +| g\rangle \langle \mu \vert )| {\xi }_{j}\rangle {| }^{2},\\ {\Gamma }_{j{j}^{{\prime} }}^{(2)} ={\gamma }_{2}| \langle {\xi }_{{j}^{{\prime} }}| (\vert g\rangle \langle e| +| e\rangle \langle g\vert )| {\xi }_{j}\rangle {| }^{2},\\ {\Gamma }_{j{j}^{{\prime} }}^{(3)} =\kappa | \langle {\xi }_{{j}^{{\prime} }}| (a+{a}^{{{{\dagger}}} })| {\xi }_{j}\rangle {| }^{2},$$
(23)

where γ1,(2) is the spontaneous emission rate of the transition \(\vert g\rangle \to \vert \mu \rangle\) (\(\left\vert e\right\rangle \to \vert g\rangle\)).

The steady-state output field can remain unchanged for a long time. This can reduce the difficulties in experiments to measure the emitted photons. Taking l = 2 as an example, in Fig. 5a, we show the steady-state output photon rates \({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}}={\Phi }_{{{{{{{{\rm{out}}}}}}}}}{| }_{t\to \infty }\), which is independent of the initial state. Focusing on Ω/ω = 104 (the black-solid curve in Fig. 5a), the peak value of steady-state output photon rate can reach \({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}} \, \gtrsim \, 4\times 1{0}^{-3}\omega\) in the NP near the critical point when the dissipation rates are κ = γ1 = γ2 = 0.01ω. We can choose ω ~ 2π × 5MHz and Ω ~ 2π × 50 GHz44,45, the cavity can transmit ~ 1.25 × 105 photons per second, which is detectable in cavity- and circuit-QED systems. The coupling strength is g ~ 2π × 250 MHz, and the driving amplitudes are Ωp ≳ 2π × 0.5 kHz and Ωs ≳ 2π × 1 kHz, which are feasible in current experiments7,8,46,47,48,49. When the parameter gc crosses the critical point, suddenly there is no photon released from the cavity. This indicates the drastic change of the photon number distributions and the occurrence of the QPT. The curves in Fig. 5a coincide well with those in Fig. 2a, proving that the steady-state output field is a good signature of the superradiant QPT.

Fig. 5: Photon output field.
figure 5

a Steady-state output photon rates \({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}}={\Phi }_{{{{{{{{\rm{out}}}}}}}}}{| }_{t\to \infty }\) defined in Eq. (20), and (b) the corresponding derivative \(d\left({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}}\right)/d{g}_{c}\) versus gc for l = 2. Dissipation rates are κ = γ1 = γ2 = 0.01ω. We choose relatively strong driving fields, i.e., Ωp = 0.05(E2 − E0) and Ωs = 2Ωp, to achieve relatively large output photon rates. Strong driving fields may cause small errors (via counter-rotating effects) in obtaining the effective Hamiltonian Heff, leading to oscillations in \({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}}\). These small errors do not affect the observation of the critical phenomenon, i.e., an extremum of \(d\left({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}}\right)/d{g}_{c}\) at gc → 1+. The blue, black, and red curves are plotted using frequency ratios Ω/ω = 102, Ω/ω = 104, and Ω/ω = 106, respectively. Other parameters are the same as those in Fig. 4.

Full size image

Finite-frequency effect

As mentioned above, for finite frequencies of Ω and ω, the higher-order terms \(O(\omega {g}_{c}^{2}/\Omega )\) cannot be ideally neglected but modify the eigenvalues and eigenstates of HR near the critical point. The influence of this finite-frequency effect is shown in Fig. 5. The first-order derivatives of \({\Phi }_{{{{{{{{\rm{out}}}}}}}}}^{{{{{{{{\rm{ss}}}}}}}}}\) versus gc are shown in Fig. 5b. For Ω/ω = 104 (black-solid curve in Fig. 5b) and Ω/ω = 106 (red-solid curve in Fig. 5b), we can see deep thin dips near the critical point of gc = 1, indicating the sudden changes of output photon rates. For Ω/ω = 102, the phenomenon becomes less pronounced (see the blue-solid curve in Fig. 5b).

Discussion

Our protocol does not need to control a parameter to adiabatically approach the critical point. Also, we do not need to prepare the equilibrium state, which is challenging in experiments because the time required diverges10,35. The critical phenomenon can be translated to a sudden change of the output photon rate, which can be easily detected in experiments. Thus, our protocol could be efficient to observe the critical phenomenon of the sudden change of photon number distributions in a superradiant QPT. Moreover, unlike dissipative phase transitions19,24,25,50,51,52, the drivings and dissipation in this manuscript are only used for quantum measurements and do not affect the QPT.

Our protocol could be implemented with superconducting circuits, which have realized the ultra- and deep-strong couplings between a single atom and a single-mode cavity44,45,53,54,55,56,57. One can couple, e.g., a flux qubit7,8,46,47,48,49, with a lumped-element resonator via Josephson junctions to reach a coupling strength of g/2π ~ 1 GHz44,45. To reduce the cavity frequency to ω = 2π × 5 MHz, one can use an array of dc superconducting quantum interference devices58 instead of the lumped-element resonator (see Supplementary Note 2). The level structure of the atom can be realized by adjusting the external magnetic flux through the qubit loop38,39,59. Moreover, simulated quantum Rabi models7,8,60,61,62,63,64,65, which work in the rotating frames of the Jaynes-Cummings models, can be another possible implementation of our protocol (see also Supplementary Note 3).

Conclusion

We have investigated a method to observe quantum critical phenomena: a sudden change of photon number distributions in a quantum phase transition exhibited by the quantum Rabi model. We can interpret the system dynamics as a multi-photon down-conversion process and study the outputs near the critical point. When the normalized coupling strength gc is tuned across the critical point, the output of the system changes abruptly. This reflects a sudden change of the eigenstate \(\left\vert {E}_{0}\right\rangle\) of the quantum Rabi model. Specifically, for the Rabi Hamiltonian in the NP, a pump pulse can be converted into a Stokes pulse and multiple cavity photons, while in the SP, it cannot. One can observe such a change by measuring the photons emitted out of the cavity continuously in the steady state. Moreover, for finite frequencies, we demonstrate that a small frequency ratio Ω/ω may lead to the disappearance of the critical phenomenon. We expect that our method can provide a useful tool to study various critical phenomena exhibited by quantum phase transitions without preparing their equilibrium states.