Linear optical response from the odd-parity Bardasis-Schrieffer mode in locally non-centrosymmetric superconductors

Abstract

On the recent report of a field-induced first order transition in the superconducting state of CeRh₂As₂, which is a possible indication of a parity-switching transition of the superconductor, the microscopic physics is still under investigation. However, if two competing paring channels of opposite parities do exist, a particle-particle collective mode referred to as the Bardasis-Schrieffer (BS) mode should generically exist below the pair-breaking continuum. The BS mode of the CeRh₂As₂ superconductor can couple to the light, as it arises from a pairing channel with the parity opposite to that of the superconducting condensate. Here, by using a generic model Hamiltonian we carry out a qualitative investigation on the excitation energy of the BS mode with respect to the out-of-plane magnetic fields and its contribution to the optical conductivity. Our findings indicate that the distinct coupling between the BS mode and the light can serve as evidence for the competing odd-parity channels of CeRh₂As₂ and other locally non-centrosymmetric superconductors.

Introduction

Discovering superconductors with odd-parity Cooper pairing has been a long-standing challenge in condensed matter physics, as they are rare in inversion symmetric solid-state systems. To name a few, UPt₃¹, UNi₂Al₃² and Sr₂RuO₄³ are the most notable candidates which have been suspected to host odd-parity Cooper pairings for a long time, though the case of a much studied candidate material Sr₂RuO₄ has grown more controversial in recent years^4,5,6,7,8.

Faced with this rarity of odd-parity superconducting materials, many researchers have endeavored to find realistic conditions favoring odd-parity superconductivity. For instance, the systems possessing a structural instability toward an inversion-symmetry-broken phase such as the pyrochlore oxide ${{{{{{{{\rm{Cd}}}}}}}}}_{2}{{{{{{{{\rm{Re}}}}}}}}}_{2}{{{{{{{{\rm{O}}}}}}}}}_{7}$ drew attention for a potential to host an odd-parity superconducting phase^9,10,11,12.

Another mechanism for odd-parity superconductivity is suggested by a recent experiment on CeRh₂As₂^13,14. There a transition is observed when the external magnetic fields are applied along the c-axis within the superconducting phase of CeRh₂As₂¹³. According to the preceding theoretical studies^15,16, the transition referred to as the even-to-odd transition seems to occur between two superconducting phases of opposite parities under an inversion. The Pauli paramagnetic pair-breaking effect^17,18 is a known mechanism for destroying the even-parity superconducting (eSC) phase. By contrast, an odd-parity superconducting (oSC) state can withstand the magnetic fields through an equal–(pseudo)spin pairing^13,19,20,21. It is noted that the combination of P4/nmm nonsymmorphic crystal structure and the heavy-fermion characteristic supports strong intralayer Rashba-type spin–orbit couplings that are known to favor equal-(pseudo)spin pairings²⁰.

An intriguing implication of the even-to-odd transition in CeRh₂As₂ is the presence of competing pairing channels with opposite parities. The potential transition temperature T_c,o of the oSC phase at zero field, which is preempted by the onset of the eSC phase in reality, is estimated to be close to the transition temperature T_c,e of the eSC phase¹³. Moreover, phenomenological studies have reproduced the overall superconducting phase diagram in CeRh₂As₂ with comparable coupling strengths for both pairing channels^13,22.

Even if most of the theories set forth so far support that the high-field superconducting phase of CeRh₂As₂ is odd in parity, counter-arguments have also been raised. For instance, a theoretical study proposed that the observed magnetic field-induced phase transition arises not from the parity switching of the superconducting gap but from the spin-flipping in the coexistent antiferromagnetic order parameter²³. Therefore, further experimental signatures need to be sought for the first-order transition that switches the parity of the superconducting gap. Of the many ways to find indisputable evidence for the symmetry of the superconducting phase, one is to investigate the collective modes in the superconducting phase²⁴. Historically, the detection of a number of the nearly degenerate collective modes in the superfluid B-phase of ³He proved to be the decisive evidence in favor of the spin–triplet pairing²⁵.

In this regard, we note that, if the first order transition is really associated with the parity-switching transition, T_c,o ≈ T_c,e not only implies the close competition between two pairing channels of opposite parities but also provides a favorable condition for a collective mode, known as the Bardasis–Schrieffer (BS) mode²⁶, to appear far from the pair-breaking continuum. The BS mode is an exciton-like collective mode in superconductors due to an uncondensed pairing channel and indicates an instability towards another superconducting phase breaking some symmetries of the superconducting ground state. As a precursor of the instability of the superconducting ground state, the BS mode softens as the uncondensed channel gets stronger so that the competition between the uncondensed pairing channel and the condensed pairing channel defining the superconducting ground state is enhanced. However, such closely competing pairing channels have rarely been found in superconductors, with one of a few exceptions being the iron-based superconductors, where the close competition between the s-wave and d-wave pairing channels has been confirmed by the Raman detection of the BS mode^27,28,29,30.

Besides the possible existence of the BS mode, it is worth noting that the collective mode can possess a non-zero optical coupling when the parity of the uncondensed pairing channel under inversion is the opposite of that of the superconducting ground state³¹. This feature makes the detection of the collective mode possible through the optical response in the linear response regime, which can be thought of as compelling proof for the existence of a strong odd-parity pairing channel. This is in sharp contrast to the Fe-based superconductors where the electronic Raman spectroscopy is used to detect the BS mode from the d-wave channel as this pairing channel and the s-wave ground state pairing share the same parity^{27,28,32,33,34}. Thus, in the case of CeRh₂As₂, the detection of the BS mode would be conclusive evidence for the occurrence of parity-switching at the observed transition between the two superconducting phases.

In this work, we conduct a qualitative study on the BS modes in the clean limit superconducting phase of a locally non-centrosymmetric system such as CeRh₂As₂, which arise from the odd-parity and even-parity pairing channel in the eSC state and oSC state, respectively. First, we demonstrate the even-to-odd parity transition by the Pauli paramagnetic effect at the zero-temperature at the level of a mean-field description. We then briefly introduce the generalized random phase approximation (GRPA)^35,36 which provides the basis of the analysis in this work. Also, it is shown that the BS mode from the uncondensed pairing channel can be linearly coupled to the light. This is ascribed to the origin of the BS mode whose parity is opposite to the condensed Cooper pairs. Using the GRPA, we investigate the softening of the BS modes under the external magnetic fields along the c-axis and its contribution to the optical conductivity.

Results

Mean-field analysis of the even-to-odd transition

We start our presentation by demonstrating the field-induced even-to-odd transition in the superconducting phase in a locally non-centrosymmetric layered structure by using a mean-field description at the zero-temperature. For results valid in a wider range of temperature and magnetic fields, we refer to refs. ^15,16,21,37.

To describe the normal phase of the representative locally non-centrosymmetric system, CeRh₂As₂, with the point group D_4h, we use a model Hamiltonian given by refs. ^13,16,20,21:

$${H}_{0}({{{{{{{\boldsymbol{k}}}}}}}})=\mathop{\sum }\limits_{i=0}^{2}{\varepsilon }_{i0}({{{{{{{\boldsymbol{k}}}}}}}}){\sigma }_{i}+\mathop{\sum }\limits_{i=1}^{3}{\varepsilon }_{3i}({{{{{{{\boldsymbol{k}}}}}}}}){\sigma }_{3}{s}_{i}-\mu$$

(1)

with

$${\varepsilon }_{00}({{{{{{{\boldsymbol{k}}}}}}}})=2t(2-\cos {k}_{x}-\cos {k}_{y}),$$

(2)

$${\varepsilon }_{10}({{{{{{{\boldsymbol{k}}}}}}}})={t}_{{{{{{{{\rm{c}}}}}}}},1}\cos \frac{{k}_{z}}{2}\cos \frac{{k}_{x}}{2}\cos \frac{{k}_{y}}{2},$$

(3)

$${\varepsilon }_{20}({{{{{{{\boldsymbol{k}}}}}}}})={t}_{{{{{{{{\rm{c}}}}}}}},2}\sin \frac{{k}_{z}}{2}\cos \frac{{k}_{x}}{2}\cos \frac{{k}_{y}}{2},$$

(4)

$${\varepsilon }_{31}({{{{{{{\boldsymbol{k}}}}}}}})=-{\alpha }_{{{{{{{{\rm{R}}}}}}}}}\sin {k}_{y},$$

(5)

$${\varepsilon }_{32}({{{{{{{\boldsymbol{k}}}}}}}})={\alpha }_{{{{{{{{\rm{R}}}}}}}}}\sin {k}_{x},$$

(6)

$${\varepsilon }_{33}({{{{{{{\boldsymbol{k}}}}}}}})={\lambda }_{{{{{{{{\rm{I}}}}}}}}}\sin {k}_{z}\sin {k}_{x}\sin {k}_{y}(\cos {k}_{x}-\cos {k}_{y}),$$

(7)

where σ_i and s_i are the Pauli matrices for the orbital and spin degrees of freedom, respectively. The eigenenergies ξ_i and eigenvectors $\left\vert i,\pm \right\rangle$ of H₀ for i = 1, 2 can be found in the subsection “Microscopic model” in the “Methods” section.

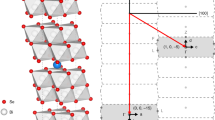
Note that two orbital degrees of freedom should be introduced to take account of the locally non-centrosymmetric feature of the system. The reason is easily understood by looking into the crystal structure of CeRh₂As₂³⁸. In Fig. 1a, the crystal structure is depicted with three {001} lattice planes composed of Ce atoms. The locally broken inversion symmetry around Ce atoms is easily noted in Fig. 1b where the crystal structure is viewed from the (100) direction. Still, there is a global inversion symmetry whose center is marked by the black star in Fig. 1, under which no individual atom is left invariant. This global inversion is represented by ${{{{{{{\mathcal{P}}}}}}}}={\sigma }_{1}{s}_{0}$ in the basis of the model Hamiltonian H₀(k) in Eq. (1).

Fig. 1: Crystal structure of CeRh₂As₂.

a Bird’s eye view of the structure. b A view from the (100) direction. An inversion center is marked by a black star.

t_c,1 and t_c,2 are the hoppings between the nearest-neighbor Ce layers depicted in Fig. 1. These hoppings endow the three-dimensional characteristics of the electronic structure. α_R and λ_I denote the intra-layer Rashba- and inter-layer Ising-type spin–orbit couplings, respectively. Note that the sign of the Rashba spin–orbit coupling alternates layer-by-layer, which reflects the locally non-centrosymmetric structure of the system shown in Fig. 1b.

Throughout this work, we ignore λ_I since this spin–orbit coupling corresponds to a spin-dependent inter-layer hopping between the two next-nearest-neighboring layers, and thus it is expected to be much weaker than the spin-independent inter-layer hoppings t_c,1 and t_c,2 between the nearest layers and the intra-layer Rashba spin–orbit coupling α_R.

In addition, we assume that the Rashba-type spin–orbit coupling α_R is much larger than the inter-layer hoppings t_c,1 and t_c,2 following refs. ^13,20. In this limit of large Rashba spin–orbit coupling, the difference between t_c,1 and t_c,2 has no significant effect on the band structure except for a weak modulation of the Fermi surface along the k_z-axis. Thus, t_c ≡ t_c,1 = t_c,2 is assumed throughout this work.

With this lattice model, we consider two spin–singlet pairing channels whose form factors are represented by σ₀ and σ_z. These are used to reproduce the magnetic field–temperature (H−T) phase diagram of CeRh₂As₂ in refs. ^13,20,21,37. The pairing channel represented by σ₀ describes a uniform s-wave pairing. Meanwhile, σ_z represents a pairing channel whose sign alternates layer-by-layer, in which way the two orbital degrees of freedom endow it with the odd parity with respect to the global inversion despite being singlet in the physical spin sector. Hence, we call the superconducting state, where the pairing channel σ₀ is condensed while σ_z is uncondensed, the eSC state. The opposite case is called the oSC state. Throughout this paper, we use for conciseness the nomenclature pSC state with p = e, o for the eSC and the oSC, respectively, and p = n for the normal state.

The Bogoliubov–de Gennes (BdG) Hamiltonian for the pSC state including the Zeeman term B ⋅ s is given by

$${H}_{{{\rm{BdG}}}}^{(p)}(B,{{{{{{{\boldsymbol{k}}}}}}}})={\tau }_{0}{{{{{{{\boldsymbol{B}}}}}}}}\cdot {{{{{{{\boldsymbol{s}}}}}}}}+{\tau }_{z}{H}_{0}({{{{{{{\boldsymbol{k}}}}}}}})+{\Delta }_{p}{\tau }_{x}^{(p)},$$

(8)

with ${\tau }_{i}^{({{{{{{{\rm{e}}}}}}}})}={\tau }_{i}{\sigma }_{0}$ and ${\tau }_{i}^{({{{{{{{\rm{o}}}}}}}})}={\tau }_{i}{\sigma }_{z}$ for i = x, y, z. Here, the basis field operator of the BdG Hamiltonian is ${\hat{\Psi }}_{{{{{{{{\boldsymbol{k}}}}}}}}}={({\hat{C}}_{{{{{{{{\boldsymbol{k}}}}}}}}},{\hat{C}}{\,\!}^{{{{\dagger}}} {\rm {T}}}_{-{{{{{{{\boldsymbol{k}}}}}}}}}(i{s}_{y}))}\!^{\rm {{T}}}$^39,40. The magnetic field along (perpendicular to) the c-axis in Fig. 1 is denoted by B_z(B_x) and it is referred to as the out-of-plane (in-plane) magnetic field in this work. The gap amplitude Δ_p, presumed to be real, is determined from the gap equation:

$${\Delta }_{p}=\frac{{g}_{p}}{2}\check{\mathop {\sum}\limits_{k}}\,{{\mbox{Tr}}}\,\left[{\tau }_{x}^{(p)}{G}_{k}^{(p)}\right],$$

(9)

with ${G}_{k}^{(p)}=i\omega -{H}_{{{\rm{BdG}}}}^{(p)}({{{{{{{\boldsymbol{k}}}}}}}})$, while ${\Delta }_{\bar{p}}=0$ where $\bar{p}$ denotes the uncondensed pairing channel in the pSC state. Here, ${\check{\sum }}_{k}={(\beta V)}^{-1}{\sum }_{k}$ is the normalized summation over a pair of Matsubara frequency and the three-dimensional momentum k = (iω, k), where β = 1/k_BT and V are the inverse of the temperature and the volume of the system, respectively. The coupling constants g_e and g_o are assumed to be constant for the simplicity of the presentation. This assumption is valid in the weak-coupling regime which is suitable for the qualitative study.

Though both pairing channels are spin–singlet pairings, the Pauli paramagnetism through the Zeeman term can induce an even-to-odd phase transition which can be shown by comparing the zero-temperature (Gibbs) free energies of eSC and oSC phases

$${F}_{p}({B}_{z})=\frac{{\Delta }_{p}^{2}}{4{g}_{p}}+\check{\mathop{\sum}\limits_{{{{{{{{\boldsymbol{k}}}}}}}}}}\frac{\,{{\mbox{Tr}}}\,[{H}_{0}({{{{{{{\boldsymbol{k}}}}}}}})]-\mathop{\sum}\nolimits_{n}{E}_{n}^{(p)}({B}_{z},{{{{{{{\boldsymbol{k}}}}}}}})}{2}.$$

(10)

Here, ${E}_{n}^{(p)}({B}_{z},{{{{{{{\boldsymbol{k}}}}}}}})$ (n = 1, 2) denotes a positive branch of the eigenvalues of the BdG Hamiltonian ${H}_{{{\rm{BdG}}}}^{(p)}({B}_{z},{{{{{{{\boldsymbol{k}}}}}}}})$ and ${\check{\sum }}_{{{{{{{{\boldsymbol{k}}}}}}}}}\equiv {V}^{-1}{\sum }_{{{{{{{{\boldsymbol{k}}}}}}}}}$. Figure 2a illustrates the free energies δF_p(B_z) ≡ F_p(B_z)−F_n(0) of the pSC state from which the zero-field normal phase free energy is subtracted. The parameters used are written in the caption of Fig. 2. The qualitative features of the system are well displayed with this set of parameters. g_e is chosen so that Δ_e = 0.004 is obtained by Eq. (9), which is used throughout this work unless otherwise noted.

Fig. 2: Magnetic field dependence of free energies of the normal state, even-parity and odd-parity superconducting states.

a Free energies versus the out-of-plane magnetic field B_z along the c-axis. b Free energies under the in-plane magnetic field B_x. Both magnetic fields are normalized by the Pauli limiting field B_z,P. The dashed line, and the black solid line depict the free energy of the normal state, and the even-parity superconducting state, respectively. The red, blue, and magenta lines correspond to the free energies of the odd-parity superconducting state for g_o/g_e = 1, 1.17, 1.2, respectively, where g_e and g_o are the coupling strengths for the even-parity pairing channel and the odd-parity pairing channel introduced in Eqs. (9) and (13). The parameters t = 2, μ = 0.5, t_c,1 = t_c,2 = 0.1, α_R = 0.34 and Δ_e = 0.004 are used.

Each curve in Fig. 2a is well described by

$${F}_{p}({B}_{z})={F}_{p}(0)-\frac{1}{2}{\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{(p)}{B}_{{z}}^{2},$$

(11)

where ${\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{(p)}$ is the spin susceptibility of the pSC state. The crossing point at the Pauli-limiting field B_z,P between the normal (black dashed line) and eSC (black line) phases marks a first-order transition between the normal and eSC phase. Using Eq. (11), B_z,P is given by

$${B}_{z,{{{{{{{\rm{P}}}}}}}}}=\sqrt{\frac{{F}_{{{{{{{{\rm{n}}}}}}}}}(0)-{F}_{{{{{{{{\rm{e}}}}}}}}}(0)}{({\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{({{{{{{{\rm{n}}}}}}}})}-{\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{({{{{{{{\rm{e}}}}}}}})})/2}}.$$

(12)

Compared to the conventional Pauli-limiting critical field referred to as the Chandrasekhar–Clogston field ${B}_{z,{{\rm{CC}}}}=\sqrt{2\{{F}_{{{{{{{{\rm{n}}}}}}}}}(0)-{F}_{{{{{{{{\rm{e}}}}}}}}}(0)\}/{\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{({{{{{{{\rm{n}}}}}}}})}}$, B_z,P is several times larger because of the non-vanishing ${\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{({{{{{{{\rm{e}}}}}}}})}$ due to the sizable Rashba spin–orbit couplings^15,41.

The red, blue, and green lines in Fig. 2b denote the free energies of the oSC states with g_o = g_e, g_o = 1.17g_e and g_o = 1.2g_e, respectively. Since ${\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{({{{{{{{\rm{o}}}}}}}})}={\chi }_{\,{{{{{{\mathrm{spin}}}}}}}\,}^{({{{{{{{\rm{n}}}}}}}})}$ as shown in Fig. 2a, a transition due to the Pauli paramagnetic depairing does not occur between the normal phase and the oSC state. The crossing point between the free energies of the eSC state and the oSC state for a given g_o indicates the even-to-odd transition observed in the experiment¹³. Moreover, the slopes of the lines are different at the crossing point, which means the transition is of the first order and the magnetization changes discontinuously at the transition.

Note that eSC state can be more stable than the oSC state at zero fields even if g_o > g_e, because the inter-layer spin-independent hoppings ε₁₀ and ε₂₀ effectively weaken the odd-parity pairing channel. For example, with the aforementioned parameters, we obtain 1.21 for the critical ratio r_c ≡ g_o,c/g_e at which the eSC and oSC states degenerate at zero fields. Above the critical ratio, the oSC state is the superconducting ground state of the system at zero field. In the two-dimensional limit in which the ratio α_R/max(∣t_c,1∣, ∣t_c,2∣) is infinite, the electrons do not discern the trivial gap function σ₀ from the sign-alternating gap function σ_z, and thus r_c → 1.

Though the effect of the out-of-plane magnetic fields is of main interest, we present the free energies under the in-plane magnetic fields as well. Figure 2b displays the free energies of the normal and superconducting phases under in-plane magnetic fields B_x. The free energies of the normal and the eSC phase cross at the Pauli-limiting in-plane magnetic field B_x,P which is smaller than B_z,P, and this is consistent with the experiment^13,42. When it comes to the oSC state, we do not see a first-order transition to the normal phase due to the Pauli depairing, while an exponential decrease of the gap function is seen with the increasing in-plane magnetic fields. (See Supplementary Note 1 for more details.).

Furthermore, the critical in-plane magnetic field at which the oSC state and the eSC state degenerate is very close to B_x,P for a fair range of g_o/g_e. As a result, up to the impurity and the finite-temperature effect, it can be challenging to detect the oSC state which would appear between the eSC and the normal phases. This is consistent with the experimental result where a phase transition into the oSC state by the in-plane magnetic field is not detected¹³.

Effective action for the pairing fluctuation

To study the BS mode, we use the generalized random phase approximation (GRPA)^26,35,36,43, which is one of the primary methods to incorporate the effect of the collective modes in the superconducting phase. Before applying the method to our case, we first briefly introduce the formulation of the GRPA.

Concerned with the linear optical response of the fluctuation from the uncondensed pairing channels around the (meta)stable superconducting condensate, we consider an attractive electronic interaction consistent with the gap equation in Eq. (9):

$$\hat{V}=-\frac{1}{2}\mathop{\sum}\limits_{p}\check{\mathop{\sum}\limits_{{k}_{1},{k}_{2},q}}{g}_{p}{\hat{\Pi }}_{p}({k}_{1},{k}_{1}-q)[{\hat{\Pi }}_{p}({k}_{2},{k}_{2}-q)]^{{{{\dagger}}} },$$

(13)

where ${\hat{\Pi }}_{p}({k}_{1},{k}_{2})={\hat{\Psi }}{\,\!}^{{{{\dagger}}} }_{{k}_{1}}{\tau }_{+}^{(p)}{\hat{\Psi }}_{{k}_{2}}$ with ${\tau }_{\pm }^{(p)}=({\tau }_{x}^{(p)}\pm i{\tau }_{y}^{(p)})/2$. ∑_p is the summation over the pairing channels represented by σ₀ and σ_z. We generally expect g_o ≠ g_e; one simplest case being the combination of the on-site attractive interaction and the pair hopping interaction between the Ce atoms on the neighboring layer. Other pairing channels such as those discussed in refs. ^21,41 do not couple linearly to the light because of the symmetries of H₀ with negligible λ_I as shown in the subsection “Other odd-parity channels” in the “Methods” section.

After adding $\hat{V}$ to the normal phase action ${{{{{{{{\mathcal{S}}}}}}}}}_{0}=\frac{1}{2}{\check{\sum }}_{k}{\hat{\Psi }}{\,\!}^{{{{\dagger}}} }_{k}(i\omega -{H}_{0}){\hat{\Psi }}_{k}$, we obtain the effective action for the pairing fluctuations under external electromagnetic fields in the pSC state through the standard procedure in the functional integral approach (see subsection “Macroscopic model” in the “Methods” section):

$${{{{{{{{\mathcal{S}}}}}}}}}_{{{\rm{eff}}}}^{(p)}=\, \frac{1}{2}\check{\mathop{\sum}\limits_{\Omega }}{({{{{{{{{\mathcal{A}}}}}}}}}_{0},{\eta }_{a}^{(p)})}_{{{\mbox{-}}}i\Omega }{\Lambda }_{p}(i\Omega ){\left(\begin{array}{c}{{{{{{{{\mathcal{A}}}}}}}}}_{0}\\ {\eta }_{b}^{(p)}\end{array}\right)}_{i\Omega }\\ +\frac{1}{2}\check{\mathop{\sum}\limits_{\Omega }}{({{{{{{{{\mathcal{A}}}}}}}}}_{i},{\eta }_{a}^{(\bar{p})})}_{{{\mbox{-}}}i\Omega }{\Lambda }_{\bar{p}}(i\Omega ){\left(\begin{array}{c}{{{{{{{{\mathcal{A}}}}}}}}}_{j}\\ {\eta }_{b}^{(\bar{p})}\end{array}\right)}_{i\Omega }.$$

(14)

The auxiliary bosonic fields ${\eta }_{a}^{(p)}$ with a = 1, 2 are introduced through the Hubbard–Stratonovich transformation. Associated with ${\tau }_{a}^{(p)}$, they represent the real and imaginary parts of the fluctuation in the condensed pairing channel, respectively. Importantly, they correspond to the amplitude and the phase fluctuation, respectively, when Δ_p is real. ${\eta }_{a}^{(\bar{p})}$ with a = 1, 2 associated with ${\tau }_{a}^{(\bar{p})}$ represent the fluctuations in the uncondensed pairing channel. The electromagnetic four-potential ${{{{{{{{\mathcal{A}}}}}}}}}_{\mu }=| e| (-i{A}_{0},{{{{{{{\boldsymbol{A}}}}}}}})$ is defined by multiplying the unit charge ∣e∣ to the conventional four-potential for conciseness. Note that we omit the momentum q dependence of η and ${{{{{{{\mathcal{A}}}}}}}}$ since the London limit (q → 0) of the linear response is our interest.

The kernels Λ_p and ${\Lambda }_{\bar{p}}$ in Eq. (14) are given as

$${\Lambda }_{p}=\left(\begin{array}{cc}{K}_{00}&{L}_{0b}^{(p)}\\ {R}_{a0}^{(p)}&{\tilde{\Pi }}_{ab}^{(p)}\end{array}\right),\quad {\Lambda }_{\bar{p}}=\left(\begin{array}{cc}{K}_{ij}&{L}_{ib}^{(\bar{p})}\\ {R}_{aj}^{(\bar{p})}&{\tilde{\Pi }}_{ab}^{(\bar{p})}\end{array}\right),$$

(15)

where the frequency dependence is omitted for conciseness (See the subsection “Macroscopic model” in the “Methods” section for the definition of the sub-blocks in Eq. (15)). The real-frequency kernels are obtained by the analytical continuation iΩ → Ω⁺ = Ω + iϵ. ϵ = 10⁻⁶ = 2.5 × 10⁻⁴ Δ_e is used throughout this work unless otherwise noted.

Note that the effective actions ${{{{{{{{\mathcal{S}}}}}}}}}_{{{\rm{eff}}}}^{(p)}$ for p = e and p = o are decomposed into two groups involving Λ_p and ${\Lambda }_{\bar{p}}$. This is because of the global inversion symmetry ${\tau }_{0}{{{{{{{\mathcal{I}}}}}}}}$ (${\tau }_{z}{{{{{{{\mathcal{I}}}}}}}}$) of the BdG Hamiltonian of the eSC (oSC) state. Also, Eqs. (14) and (15) explicitly show that the fluctuations of the uncondensed channel are involved in the optical response in the second block ${\Lambda }_{\bar{p}}$ in Eq. (15).

It also deserves to be noted that the effect of vortices in type-II superconductors is ignored since the critical fields H_c,2 of the eSC and oSC are about four times higher than the critical field for the even-to-odd transition¹³ which is our main focus.

Bardasis–Schrieffer mode at zero field

Given the effective action ${{{{{{{{\mathcal{S}}}}}}}}}_{{{\rm{eff}}}}^{(p)}$, we study the BS mode originating from the fluctuations ${\eta }_{1}^{(\bar{p})}$ and ${\eta }_{2}^{(\bar{p})}$ in the uncondensed pairing channel^{25,26,28,43,44}. The equation of motion for the BS mode is given by $0=\delta {{{{{{{{\mathcal{S}}}}}}}}}_{{{\rm{eff}}}}^{(p)}/\delta {\eta }^{(\bar{p})}$ which is rearranged into

$${\eta }^{(\bar{p})}=-[{\tilde{\Pi }}\,\!^{(\bar{p})}]^{-1}{R}^{(\bar{p})}{{{{{{{\mathcal{A}}}}}}}},$$

(16)

where ${\tilde{\Pi }}\,\!^{(\bar{p})}(\Omega )$ is the propagator of the fluctuations ${\eta }^{(\bar{p})}=({\eta }_{x}^{(\bar{p})},{\eta }_{y}^{(\bar{p})})$. Since the BS mode arises from this fluctuation, the gap of the mode can be obtained by finding the singularity of the right-hand side (RHS) in Eq. (16) by solving $\det [{\tilde{\Pi }}\,\!^{(\bar{p})}]=0$, which is denoted by Ω_BS throughout this work.

To figure out the physical implication of the BS mode, we analyze ${\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}$ based on our numerical and analytical results for the eSC state. As shown in Supplementary Note 2, ${[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{12}$ and ${[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{21}$ are vanishingly small, and ${[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{11}$ are finite for ∣Ω∣ < 2Δ_e. Thus, the zero of $\det [{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]\approx {[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{11}{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}$ is largely identical to the zero of ${[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}$ which can be understood as the propagator of the BS mode, and Ω_BS can be found by looking into the singular peak of the spectral function ${{{{{{{\rm{Im}}}}}}}}[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}]$. Figure 3a shows the spectral function $\,{{\mbox{Im}}}\,[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}]$ of the BS mode versus g_o/g_e in the eSC state at zero field. The gap of the BS mode Ω_BS is clearly identified. Increasing g_o/g_e drops Ω_BS, and Ω_BS becomes zero at the critical ratio r_c = g_o,c/g_e ~ 1.21. For larger g_o/g_e, the BS mode disappears, which is consistent with the free-energy analysis through the mean-field calculation.

Fig. 3: The spectral function ${{{{{{{\rm{Im}}}}}}}}[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}]}_{22}]$ of the Bardasis–Schrieffer (BS) mode.

${[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}]}_{22}$ is the propagator of the BS mode introduced in Eq. (16). a False color plot of the spectral function of the BS mode in the g_o/g_e−Ω plane. b The spectral function versus the frequency for the ratios g_o/g_e close to the critical ratio ~1.21 at which the BS mode becomes gapless as shown in (a). g_e and g_o are the coupling strengths for the even-parity pairing channel and the odd-parity pairing channel introduced in Eq. (9) and Eq. (13). Δ_e is the magnitude of the superconducting gap function in the even-parity superconducting state. Ω_BS, which is referred to as the gap of the BS mode in the main text, denotes the frequency where the peak of the spectral function is located. The inverse of the height of each peak is linearly dependent on Ω_BS as shown in the inset.

To relate the gap of the BS mode Ω_BS to the stability of the superconducting condensate against the condensation of the other pairing channel, we first derive a semi-analytical expression for Ω_BS which is given by

$$\frac{2y\arcsin y}{\sqrt{1-{y}^{2}}}=\frac{1}{{g}_{{{{{{{{\rm{o}}}}}}}}}{N}_{{{{{{{\mathrm{tot}}}}}}}}{\langle {\sin }^{2}\chi \rangle }_{{{{{{{\mathrm{FS}}}}}}}}}-\frac{1}{{g}_{{{{{{{{\rm{e}}}}}}}}}{N}_{{{{{{{\mathrm{tot}}}}}}}}}$$

(17)

$$=-\ln \frac{{T}_{{{{{{{{\rm{c}}}}}}}},{{{{{{{\rm{o}}}}}}}}}}{{T}_{{{{{{{{\rm{c}}}}}}}},{{{{{{{\rm{e}}}}}}}}}},$$

(18)

where y = Ω_BS/2Δ_e, $\sin \chi =\sqrt{{\varepsilon }_{31}^{2}({{{{{{{\boldsymbol{k}}}}}}}})+{\varepsilon }_{32}^{2}({{{{{{{\boldsymbol{k}}}}}}}})}/\sqrt{{\varepsilon }_{10}^{2}({{{{{{{\boldsymbol{k}}}}}}}})+{\varepsilon }_{20}^{2}({{{{{{{\boldsymbol{k}}}}}}}})+{\varepsilon }_{31}^{2}({{{{{{{\boldsymbol{k}}}}}}}})+{\varepsilon }_{32}^{2}({{{{{{{\boldsymbol{k}}}}}}}})}$, and N_tot = N₁ + N₂ with N_i=1,2 being the density of states of the i-th Fermi surface given by ξ_i = 0. [The total density of states is 2N_tot due to the Kramers’ degeneracy]. Here, ${\langle \cdots \rangle }_{{{{{{{\mathrm{FS}}}}}}}}=\mathop{\sum }\nolimits_{i = 1}^{2}{N}_{i}{\langle \cdots \rangle }_{{{{{{{\mathrm{FS}}}}}}},i}/({N}_{1}+{N}_{2})$ with 〈⋯ 〉_FS,i being the angular average over the ith Fermi surface (for the derivation, see the subsection “Relation between the critical temperatures and BS mode gap” in the “Methods” section). In the second line, the weak-coupling formulae of the superconducting transition temperature T_c for the eSC state and the preempted oSC state are used, which are given by ${g}_{{{{{{{{\rm{e}}}}}}}}}{N}_{{{{{{{\mathrm{tot}}}}}}}}=-1/\ln ({T}_{{{{{{{{\rm{c}}}}}}}},{{{{{{{\rm{e}}}}}}}}}/\Lambda )$ and $\langle {\sin }^{2}\chi \rangle {g}_{{{{{{{{\rm{o}}}}}}}}}{N}_{{{{{{{\mathrm{tot}}}}}}}}=-1/\ln ({T}_{{{{{{{{\rm{c}}}}}}}},{{{{{{{\rm{o}}}}}}}}}/\Lambda )$, respectively, with a cutoff Λ. Note that a real solution y exists only when T_c,o ≤ T_c,e. This implies that Ω_BS = 0 indicates a transition between two superconducting states, and, in turn, Ω_BS can be understood to tell how much more the superconducting condensate is stable than other superconducting states.

We now use Eq. (18) to estimate Ω_BS in CeRh₂As₂ at zero field. Adopting T_c,o/T_c,e = 0.87 as estimated for CeRh₂As₂ by ref. ¹³, we find Ω_BS ~ 0.51Δ_e; i.e. below the pair-breaking continuum. It should be stressed that this estimation of Ω_BS from Eq. (18) has nothing to do with our choice of the parameters such as t, μ, α_R; it is a model-independent result under weak-coupling assumption.

In Fig. 3b, the spectral functions $\,{{\mbox{Im}}}\,[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}]$ are drawn for several g_o/g_e around the critical ratio. The location of the peak of each curve corresponds to Ω_BS for each ratio g_o/g_e. The height of peak is enhanced as g_o/g_e → r_c. The inset clearly shows that the peak height is inversely proportional to Ω_BS for small Ω_BS.

This is a general consequence resulted from ${\Pi }^{({{{{{{{\rm{o}}}}}}}})}(\Omega )=[{\Pi }^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]^{{{{\dagger}}} }=[{\Pi }^{({{{{{{{\rm{o}}}}}}}})}(-\Omega )]^{{\rm {T}}}$⁴⁵ for Ω below the quasiparticle continuum, which ensures $\det \tilde{\Pi}\,\!^{({{\rm{o}}})}(\Omega )\propto \Omega_{{{\rm{BS}}}}^{2}-\Omega^{2}$ when Ω_BS and Ω are small. Given that the off-diagonal elements of ${\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}$ are small, then $\det {\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )$ and ${[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}$ are proportional, and we know $\,{{\mbox{Im}}}\,[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}]\propto \delta ({\Omega }_{{{\rm{BS}}}}^{2}-{\Omega }^{2})\propto \delta ({\Omega }_{{{\rm{BS}}}}-\Omega )/{\Omega }_{{{\rm{BS}}}}$, Thus, the intensity of the BS mode increases as Ω_BS approaches to zero. Note that this argument is applicable even when magnetic fields are applied and also applicable to the BS mode in the oSC state except that the BS mode appears only when g_o > g_o,c.

Bardasis–Schrieffer mode under B _z

We now study the effect of magnetic fields on the BS mode. Figure 4a and b show the imaginary part of the inverse of ${[{\tilde{\Pi }}\,\!^{(\bar{p})}({B}_{z},\Omega )]}_{22}$ in the pSC state for B_z. Here, g_o = 1.17g_e is used to make the features of figures more recognizable. The reddish region of each figure represents the BdG quasiparticle excitations. Below the quasiparticle continuum, the curves corresponding to the gap of the BS mode Ω_BS(B_z) in each pSC appear. The red and blue lines are drawn over the curves for a guide to the eye. The vertical dashed lines in both figures denote the even-to-odd critical field B_z,c identified in Fig. 2a.

Fig. 4: Spectral function of the Bardasis–Schrieffer (BS) mode for g_o = 1.17g_e in the plane of frequency and magnetic field B_z.

a False color plot of the spectral function ${{{{{{{\rm{Im}}}}}}}}[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}]}_{22}]$ of the BS mode in the even-parity superconducting state. b False color plot of the spectral function ${{{{{{{\rm{Im}}}}}}}}[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{e}}}}}}}})}]}_{22}]$ of the BS mode in the odd-parity superconducting state. Δ_o = 0.001 is used which is obtained from Eq. (9) with g_o = 1.17g_e. c The gaps of the BS modes. The red and blue lines are the lines of the same colors depicted in (a) and (b), respectively. The crossing point of the two curves does not coincide with the magnetic field B_z,c at the first-order transition. Δ_e is the magnitude of the superconducting gap function in the even-parity superconducting state. B_z,P is the Pauli limiting field. B_z,e and B_z,o are the magnetic fields at which the BS mode in each superconducting state becomes gapless.

It is clearly seen that Ω_BS(B_z) in eSC (oSC) phase is lowered (raised) as the external magnetic field B_z increases. Also, it has to be noted that Ω_BS exhibits a jump at the transition as shown in Fig. 4c, which is generally expected for a first-order transition^46,47,48. Furthermore, Ω_BS becomes zero at B_z = B_z,e > B_z,c (B_z = B_z,o < B_z,c) in eSC (oSC) phase. Recalling that the eSC (oSC) phase is the equilibrium ground state under B_z < B_z,c (B_z > B_z,c), Figure 4 shows that the softening of the BS mode occurs outside the thermodynamic equilibrium^31,49. Understood as a precursor of an instability of a superconducting condensate, B_z,e (B_z,o) could correspond to the termination of the metastability of the eSC (oSC) state. Note that this limiting field B_z,e (B_z,o) is to the transition into the oSC (eSC) state what the superheating field is to the vanishing of the energy barrier against the vortex formation in type-II superconductors.

Multiband-assisted optical coupling

The linear optical response function of the BS mode can be given as

$$\tilde{K}=K-{L}^{(\bar{p})}[{\tilde{\Pi }}\,\!^{(\bar{p})}]^{-1}[{L}^{(\bar{p})}]^{{{{\dagger}}} },$$

(19)

which is derived from ${{{{{{{{\mathcal{J}}}}}}}}}_{i}(i\Omega )/| e| =\delta {S}_{{{\rm{eff}}}}^{(p)}/\delta {{{{{{{{\mathcal{A}}}}}}}}}_{i}(-i\Omega )={K}_{ij}(i\Omega ){{{{{{{{\mathcal{A}}}}}}}}}_{j}(i\Omega )+{L}_{ia}^{(\bar{p})}(i\Omega ){\eta }_{a}(i\Omega )$, ${R}^{(p)}(i\Omega )=[{L}^{(p)}(-i\Omega )]^{{{{\dagger}}} }$ and Eq. (16) as exposed in the subsection “Derivation of $\tilde{K}$” in the “Methods” section. The imaginary part of $\tilde{K}(\Omega )\equiv \tilde{K}(i\Omega ){| }_{i\Omega \to {\Omega }^{+}}$ is related to the the real part of the optical conductivity tensor σ(Ω) = σ₁(Ω)−iσ₂(Ω) by ${\sigma }_{1}(\Omega )=\,{{\mbox{Im}}}\,[\tilde{K}(\Omega )]/\Omega$. Note that σ₁(Ω) involves the contribution of the BS mode contained in the second term in the RHS of Eq. (19), and the contribution is finite only when ${L}_{i,a}^{(\bar{p})}(\Omega )$ is finite. This is often overlooked in literature partially due to the fact that the matrix elements of the velocity operators vanish in the BCS model with a single electronic band⁵⁰.

However, the presence of multiple electronic bands can render ${L}_{i,a}^{(\bar{p})}(\Omega )$ finite⁵¹, as explained in detail below based on the analytical estimation of it in the eSC state at zero field.

Since the symmetry group of ${H}_{{{\rm{BdG}}}}^{({{{{{{{\rm{e}}}}}}}})}$ makes ${L}_{x,2}^{({{{{{{{\rm{o}}}}}}}})}$ and ${L}_{y,2}^{({{{{{{{\rm{o}}}}}}}})}$ vanish as shown in the subsection “Other odd-parity pairing channels” in the “Methods” section, we focus on ${L}_{z,2}^{({{{{{{{\rm{o}}}}}}}})}$. The spectral representation of it is given as ${L}_{z,2}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )=-\int{{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega ){{{\mbox{d}}}}^{\rm {{d}}}{{{{{{{\boldsymbol{k}}}}}}}}/{(2\pi )}^{\rm {{d}}}$ with

$${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega )=-\frac{1}{2}\mathop{\sum}\limits_{m,n}\frac{\left\langle m\right\vert {{{{{{{{\mathcal{V}}}}}}}}}_{z}\left\vert n\right\rangle \left\langle n\right\vert {\tau }_{y}{\sigma }_{z}\left\vert m\right\rangle }{{\Omega }^{+}-{E}_{m}+{E}_{n}}{\Theta }_{mn},$$

(20)

at the zero-temperature, where Θ_mn ≡ Θ(E_m)−Θ(E_n) with the Heaviside step function Θ(x). E_m and $\left\vert m\right\rangle$ denote the eigenenergies ${E}_{{{{{{{{\rm{c}}}}}}}},i}=-{E}_{{{{{{{{\rm{v}}}}}}}},i}=\sqrt{{\xi }_{i}^{2}+{\Delta }_{{{{{{{{\rm{e}}}}}}}}}^{2}}$ and the corresponding eigenvectors $\vert {{{{{{{\rm{c}}}}}}}}({{{{{{{\rm{v}}}}}}}}),i,u\rangle$ of the BdG Hamiltonian ${H}_{{{\rm{BdG}}}}^{({{{{{{{\rm{e}}}}}}}})}$, respectively, which are given in the subsection “Microscopic model” in the “Methods” section. The momentum dependence of E_m and $\left\vert m\right\rangle$ is omitted for conciseness.

The matrix element $\left\langle m\right\vert {{{{{{{{\mathcal{V}}}}}}}}}_{z}\left\vert n\right\rangle$ of the velocity operator, defined in the subsection “Macroscopic model” in the “Methods” section, relevant for calculating ${L}_{z,2}^{({{{{{{{\rm{o}}}}}}}})}$ at the zero-temperature is given by

$$\left\langle {{{{{{{\rm{c}}}}}}}},i,u\right\vert {{{{{{{{\mathcal{V}}}}}}}}}_{z}\vert {{{{{{{\rm{v}}}}}}}},j,v\rangle =\sin \frac{{\Xi }_{i}-{\Xi }_{j}}{2}\left\langle i,u\right\vert {\partial }_{z}{H}_{0}\vert j,v\rangle ,$$

(21)

where $\sin {\Xi }_{i}\equiv {\Delta }_{{{{{{{{\rm{e}}}}}}}}}/{E}_{{{{{{{{\rm{c}}}}}}}},i}$. Note that the RHS is zero when i = j, as it is in the single-band model. These forbidden elements $\left\langle {{{{{{{\rm{c}}}}}}}},i,u\right\vert {{{{{{{{\mathcal{V}}}}}}}}}_{z}\left\vert {{{{{{{\rm{v}}}}}}}},i,v\right\rangle$ for u, v = ± are marked by gray arrows in Fig. 5a, where the energy bands of the BdG quasiparticles are drawn. An explicit calculation using the eigenvectors $\left\vert i,u\right\rangle$ given in the subsection “Microscopic model” in the “Methods” section yields $\left\langle i,u\right\vert {\partial }_{z}{H}_{0}\vert j,v\rangle \propto {\delta }_{uv}$. Therefore, only $\left\langle {{{{{{{\rm{c}}}}}}}},i,u\right\vert {{{{{{{{\mathcal{V}}}}}}}}}_{z}\vert {{{{{{{\rm{v}}}}}}}},j,u\rangle$ with i ≠ j for i = 1, 2 and their complex conjugate are finite. The colored arrows in Fig. 5a represent the transitions related to these finite elements of the velocity operator. Comparing these to the interband transitions in the normal phase whose electronic band structure is displayed in Fig. 5b, these finite transitions associated with $\left\langle m\right\vert {{{{{{{{\mathcal{V}}}}}}}}}_{z}\left\vert n\right\rangle$ can be understood as the remnants of the interband transitions in the normal phase which are marked by arrows in Fig. 5b⁵¹.

Fig. 5: The band structure and the transitions between bands contributing to ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega )$ in Eq. (20).

a The band structure of the Bogoliubov–de Gennes quasiparticle and the transition relevant to ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega )$. The colored arrows depict the transitions contributing to ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega )$ in the even-parity superconducting state, while the gray arrows denote transitions to which have no contribution to ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega )$. b The electronic band structure is in the normal state. The interband transitions depicted by the colored arrows in (a) are inherited from the transitions depicted by the colored arrows in (b). For (a) and (b), the superconducting gap magnitude Δ_e = 0.05 is used. c ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},0)$ in the k_x−k_y plane. Δ_e = 0.004 is used for (c).

With $\langle {{{{{{{\rm{c}}}}}}}},j,u\vert {\tau }_{y}{\sigma }_{z}\left\vert {{{{{{{\rm{v}}}}}}}},i,u\right\rangle$ and their complex conjugate, one of which is given by

$$\left\langle {{{{{{{\rm{c}}}}}}}},2,u\right\vert {\tau }_{y}{\sigma }_{z}\left\vert {{{{{{{\rm{v}}}}}}}},1,u\right\rangle =\frac{{{\rm {e}}}^{i(\zeta +\phi )}{t}_{{{{{{{{\boldsymbol{k}}}}}}}}}\cos \chi }{2i}\cos \frac{{\Xi }_{2}-{\Xi }_{1}}{2},$$

(22)

we get

$${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega )=\frac{({E}_{{{{{{{{\rm{c}}}}}}}},1}+{E}_{{{{{{{{\rm{c}}}}}}}},2})t({{{{{{{\boldsymbol{k}}}}}}}})\cos \chi \sin ({\Xi }_{2}-{\Xi }_{1})}{{({E}_{{{{{{{{\rm{c}}}}}}}},1}+{E}_{{{{{{{{\rm{c}}}}}}}},2})}^{2}-{({\Omega }^{+})}^{2}}.$$

(23)

Note that the possible singularities of ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},\Omega )$ are located at ∣Ω∣ = Δ_e + ∣ξ_1,k − ξ_2,k∣ which are fairly distant from the region of interest ∣Ω∣ < 2Δ_e. Hence, it is a good approximation to set Ω = 0 in Eq. (23). We draw ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},0)$ in Fig. 5c. ${{{{{{{\mathcal{L}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}},0)$ has narrow positive peaks of height $\frac{{\Delta }_{{{{{{{{\rm{e}}}}}}}}}{\cos }^{2}\chi }{4{E}_{i}({{{{{{{\boldsymbol{k}}}}}}}})}$ on each ith Fermi surface, and thus

$${L}_{z,2}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )\approx -\frac{{\Delta }_{{{{{{{{\rm{e}}}}}}}}}{\langle {\cos }^{2}\chi \rangle }_{{{{{{{\mathrm{FS}}}}}}}}}{2{g}_{{{{{{{{\rm{e}}}}}}}}}}.$$

(24)

Here, we use the BCS gap equation $1/{g}_{{{{{{{{\rm{e}}}}}}}}}=({N}_{1}+{N}_{2})\int\,{{\mbox{d}}}\,\xi ({\xi}^{2}+{\Delta }^{2}_{{{\rm{e}}}})^{-1/2}$ with N_i the density of states of the ith Fermi surface given by ξ_i = 0. Note that ${L}_{z,2}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )$ is finite even at Ω = 0 as long as ${\langle {\cos }^{2}\chi \rangle }_{{{{{{{\mathrm{FS}}}}}}}}\, \ne \, 0$, which is approximately proportional to ${t}_{{{{{{{{\rm{c}}}}}}}}}^{2}/{\alpha }_{{{{{{{{\rm{R}}}}}}}}}^{2}$. Thus, the signature of the BS mode is expected to be observed in the optical conductivity along the z-direction ${[{\sigma }_{1}(\Omega )]}_{zz}$, or just σ₁(Ω) for short, at zero field.

Optical response

Given that the coupling between the fluctuations in the uncondensed channel and the light can be finite, the signature of the BS mode can be observed by measuring the optical conductivity σ₁(Ω). However, considering the experimental conditions by which the available range of frequency of the incident light is restricted, it is necessary to adjust the gap of the BS mode by tuning the external parameter, i.e. the magnetic field. Therefore, we present here our numerical results of σ₁(Ω) under B_z to provide a guide to future experiments.

For illustration, we use the case with g_o = 1.17g_e again. Figure 6a and b show σ₁(B_z, Ω) (normalized by σ₁(0, 2.5Δ_e)) in the log-scale in the eSC and the oSC states, respectively. It is easy to see the signature from the collective modes appearing in the spectral function of the BS mode $\,{{\mbox{Im}}}\,[1/{\tilde{\Pi }}\,\!^{(\bar{p})}_{22}({B}_{z},\Omega )]$ in Fig. 4a and b. As illustrated in Fig. 4c, the gap of BS mode is expected to change discontinuously when the first-order transition occurs, and thus, a sudden jump of the peak due to the BS mode can be observed in σ₁.

Fig. 6: The frequency and the magnetic field dependence of the real part of the optical conductivity σ = σ₁ + iσ₂.

a False color plot of σ₁ in the even-parity superconducting state. b False color plot of σ₁ in the odd-parity superconducting state. Δ_o = 0.001 is used which is obtained from Eq. (9) with g_o = 1.17g_e. c Frequency dependence of σ₁ for several magnetic fields B_z marked by green stars in (a). σ₁ is normalized by its magnitude at zero field and Ω = 2.5Δ_e. For c, the unity is added to plot σ₁ on the semi-log scale. B_z,c and B_z,P are the magnetic fields at the first-order transition and the Pauli limiting field, respectively. B_z,e and B_z,o are the magnetic fields at which the Bardasis–Schrieffer mode in each superconducting state becomes gapless.

Since ${L}_{z,a}^{(\bar{p})}({B}_{z},\Omega )$ is finite in the range of interest, the collective mode makes distinguished contributions to σ₁(B_z, Ω) which increases as Ω_BS → 0 like $\,{{\mbox{Im}}}\,[1/{[{\tilde{\Pi }}\,\!^{({{{{{{{\rm{o}}}}}}}})}(\Omega )]}_{22}]$ displayed in Fig. 3b. Figure 6c shows graphs of σ₁(B_z, Ω) for several B_z marked by stars in Fig. 6a, and we see that the peak height of σ₁(B_z, Ω) from the BS mode diverges like ${\Omega }_{{{\rm{BS}}}}^{-2}$ around the point where the gap of the BS mode vanishes and the metastability of the eSC state is terminated, which is in sharp contrast to the case in the iron-based superconductors where the spectral weight of BS mode in Raman measurement is predicted to diminish as the softening is approached^52,53,54. The diverging trend appears because ${L}_{z,a}^{(\bar{p})}({B}_{z},\Omega )$ is almost constant up to the critical magnetic field B_z,e (B_z,o) where the BS mode in the eSC (oSC) state becomes gapless. Consequently, using an incident light of lower frequency, a stronger peak from the BS mode is expected. The trend of σ₁(B_z, Ω) in the oSC state is qualitatively identical except that the peak height of the BS mode increases with decreasing B_z.

Discussion

We have investigated the linear optical response from the BS modes brought about by the uncondensed pairing channel with parity opposite to that of the condensed pairing. Our analysis shows the gap of the BS mode in the eSC (oSC) state is lowered with the increasing (decreasing) out-of-plane magnetic field and eventually becomes gapless at the termination of the metastability of the superconducting condensate which occurs around the first-order transition. In our analysis, the presence of the multiple orbital degrees of freedom intertwined by the inversion symmetry turns out to be crucial as it enables the linear coupling between the BS mode and the light which is generally allowed by the symmetry. As long as this coupling is finite, the contribution to the optical conductivity of the BS mode is much larger than that of the quasiparticle excitation in the clean limit and also can get enhanced as the BS mode softens. Therefore, we can expect the signature of the collective mode to be observed by measuring the linear optical response in the microwave regime for the superconductor CeRh₂As₂, where Ω_BS ~ 0.51Δ_e is expected at zero field^55,56,57,58.

It should be stressed that the detection of the BS modes via a linear optical response measurement is a compelling signature from the bulk of CeRh₂As₂ evidencing the competing odd-parity pairing channel. This is because linear optical coupling is possible only when the condensed and the competing uncondensed pairing channels are opposite in parity. Moreover, as discussed in the subsection “Other odd-parity channels” in the “Methods” section, the light selectively couples to a particular set of odd-parity pairings transforming as A_2u for D_4h symmetry to which the current operator along z belongs. Therefore, the detection of the BS modes not only can be taken as compelling proof, i.e. sufficient, for the existence of the odd-parity pairing channel but also can place restrictions on the form of the odd-parity pairing channels³¹. It also deserves to be noted that the gap of the BS mode in the oSC increases with increasing out-of-plane magnetic field. This feature may also be regarded as proof of the parity-switching at the first-order transition in the superconducting phase of CeRh₂As₂ because the gap of the BS mode should continue decreasing if it were not for the parity-switching.

Though the Pauli paramagnetic depairing is considered the primary cause of the first-order transition in the superconducting state of CeRh₂As₂, our findings and argument are applicable to any superconducting systems exhibiting parity-switching transitions regardless of the underlying mechanism and the transition order. An interesting application is superconductivity in a system hosting a structural instability^9,11,12,59, e.g. ferroelectric instability. We address the cases from the two perspectives. Firstly, if the even-to-odd transition is realized within the centrosymmetric state of this system, it is possible to have a soft BS mode at the transition, and a signature from it can appear in the linear optical response.

The second case is when such a transition occurs in the non-centrosymmetric state. In this case, the superconducting phase could host an intriguing topological phase transition between an even-parity dominant trivial superconductivity and an odd-parity dominant topological superconductivity, and a low-lying Leggett mode could appear at the transition^11,12. The existence of such a topological phase transition implies there are at least two competing pairing channels of opposite parities up to the parity mixing induced by the inversion-breaking order. This parity mixing blurs the the sharp distinction between even- and odd-parity pairings, which could lead both pairing channels to belonging to the same irreducible representation of the symmetry group of the state. As a result, the BS mode from the competing pairing channel will turn into the Leggett mode of refs. ^11,12. The absence of the inversion symmetry could allow the linear optical coupling of this Leggett mode to be nonzero⁵¹.

Lastly, a recent experiment suggests that the possibility of an inversion-breaking antiferromagnetic order coexisting with superconductivity in CeRh₂As₂^42,60. Since the antiferromagnetic order can reduce the symmetry group of the system, its potential effect on the BS modes and the optical response calls for further investigation.

Note added in proof: During the revision of this work for publication, ref. ⁶¹ appeared in arxiv. This work investigates the BS mode arising from the odd-parity pairing in a two-dimensional bilayer system and the consequence of the presence of strong interlayer Coulomb interaction.

Methods

Microscopic model

The two-fold degenerate eigenenergies of H₀(k) in Eq. (1) are given by

$${\xi }_{1}({{{{{{{\boldsymbol{k}}}}}}}})={\varepsilon }_{00}({{{{{{{\boldsymbol{k}}}}}}}})-\mu +\sqrt{t{({{{{{{{\boldsymbol{k}}}}}}}})}^{2}+\alpha {({{{{{{{\boldsymbol{k}}}}}}}})}^{2}},$$

(25)

$${\xi }_{2}({{{{{{{\boldsymbol{k}}}}}}}})={\varepsilon }_{00}({{{{{{{\boldsymbol{k}}}}}}}})-\mu -\sqrt{t{({{{{{{{\boldsymbol{k}}}}}}}})}^{2}+\alpha {({{{{{{{\boldsymbol{k}}}}}}}})}^{2}},$$

(26)

with $t({{{{{{{\boldsymbol{k}}}}}}}})=\sqrt{{\varepsilon }_{10}{({{{{{{{\boldsymbol{k}}}}}}}})}^{2}+{\varepsilon }_{20}{({{{{{{{\boldsymbol{k}}}}}}}})}^{2}}$ and $\alpha ({{{{{{{\boldsymbol{k}}}}}}}})=\sqrt{{\varepsilon }_{31}{({{{{{{{\boldsymbol{k}}}}}}}})}^{2}+{\varepsilon }_{32}{({{{{{{{\boldsymbol{k}}}}}}}})}^{2}}$. The eigenvectors of these eigenvalues are

$$\left\vert {\xi }_{1},+\right\rangle =\left(\begin{array}{c}\frac{\cos \frac{\chi }{2}}{\sqrt{2}}\\ \frac{{{\rm {e}}}^{i\phi }\sin \frac{\chi }{2}}{\sqrt{2}}\\ \frac{{{\rm {e}}}^{i\zeta }\cos \frac{\chi }{2}}{\sqrt{2}}\\ \frac{z\sin \frac{\chi }{2}}{-\sqrt{2}}\end{array}\right),\ \left\vert {\xi }_{1},-\right\rangle =\left(\begin{array}{c}\frac{\sin \frac{\chi }{2}}{z\sqrt{2}}\\ \frac{{{\rm {e}}}^{-i\zeta }\cos \frac{\chi }{2}}{\sqrt{2}}\\ \frac{{{\rm {e}}}^{-i\phi }\sin \frac{\chi }{2}}{-\sqrt{2}}\\ \frac{\cos \frac{\chi }{2}}{\sqrt{2}}\end{array}\right),$$

(27a)

$$\left\vert {\xi }_{2},+\right\rangle =\left(\begin{array}{c}\frac{\cos \frac{\chi }{2}}{z\sqrt{2}}\\ \frac{{{\rm {e}}}^{-i\zeta }\sin \frac{\chi }{2}}{-\sqrt{2}}\\ \frac{{{\rm {e}}}^{-i\phi }\cos \frac{\chi }{2}}{-\sqrt{2}}\\ \frac{\sin \frac{\chi }{2}}{-\sqrt{2}}\end{array}\right),\ \left\vert {\xi }_{2},-\right\rangle =\left(\begin{array}{c}\frac{\sin \frac{\chi }{2}}{\sqrt{2}}\\ \frac{{{\rm {e}}}^{i\phi }\cos \frac{\chi }{2}}{-\sqrt{2}}\\ \frac{{{\rm {e}}}^{i\zeta }\sin \frac{\chi }{2}}{\sqrt{2}}\\ \frac{z\cos \frac{\chi }{2}}{\sqrt{2}}\end{array}\right),$$

(27b)

with $\exp (i\chi )=\{t({{{{{{{\boldsymbol{k}}}}}}}})+i\alpha ({{{{{{{\boldsymbol{k}}}}}}}})\}/\sqrt{t{({{{{{{{\boldsymbol{k}}}}}}}})}^{2}+\alpha {({{{{{{{\boldsymbol{k}}}}}}}})}^{2}}$, $\exp (i\zeta )=\{{\varepsilon }_{10}({{{{{{{\boldsymbol{k}}}}}}}})+i{\varepsilon }_{20}({{{{{{{\boldsymbol{k}}}}}}}})\}/t({{{{{{{\boldsymbol{k}}}}}}}}),\,$$\exp (i\phi )=\{{\varepsilon }_{31}({{{{{{{\boldsymbol{k}}}}}}}})+i{\varepsilon }_{32}({{{{{{{\boldsymbol{k}}}}}}}})\}/\alpha ({{{{{{{\boldsymbol{k}}}}}}}})$, and $z=\exp [i(\zeta +\phi )]$.

The eigenenergies and eigenvectors of ${H}_{{{\rm{BdG}}}}^{({{{{{{{\rm{e}}}}}}}})}$ at zero field are given by ${E}_{{{{{{{{\rm{c}}}}}}}},i}=-{E}_{{{{{{{{\rm{v}}}}}}}},i}=\sqrt{{\xi }_{i}^{2}+{\Delta }_{{{{{{{{\rm{e}}}}}}}}}^{2}}$ for i = 1, 2 and

$$\left\vert {{{{{{{\rm{c}}}}}}}},i,u\right\rangle =\, \left(\begin{array}{c}\cos \frac{{\Xi }_{i}}{2}\left\vert {\xi }_{i},u\right\rangle \\ \sin \frac{{\Xi }_{i}}{2}\left\vert {\xi }_{i},u\right\rangle \end{array}\right),\\ \left\vert {{{{{{{\rm{v}}}}}}}},i,u\right\rangle =\, \left(\begin{array}{c}-\sin \frac{{\Xi }_{i}}{2}\left\vert {\xi }_{i},u\right\rangle \\ \cos \frac{{\Xi }_{i}}{2}\left\vert {\xi }_{i},u\right\rangle \end{array}\right),$$

(28)

for u = ± with ${\rm {{e}}}^{i{\Xi }_{i}}=({\xi }_{i}+i{\Delta }_{{{{{{{{\rm{e}}}}}}}}})/{E}_{{{{{{{{\rm{c}}}}}}}},i}$. These are used in the main text to derive the approximate expression for ${L}_{z,2}^{({{{{{{{\rm{e}}}}}}}})}(\Omega )$.

Macroscopic model

By adding

$$\hat{V}=-\frac{1}{2}\mathop{\sum}\limits_{p}\check{\mathop{\sum}\limits_{{k}_{1},{k}_{2},q}}{g}_{p}{\hat{\Pi }}_{p}({k}_{1},{k}_{1}-q)\,[{\hat{\Pi }}_{p}({k}_{2},{k}_{2}-q)]^{{{{\dagger}}} }$$

(29)

to the normal phase action ${{{{{{{{\mathcal{S}}}}}}}}}_{0}=\frac{1}{2}{\check{\sum }}_{k}{\hat{\Psi }}\,\!^{{{\dagger}}}_{k} (i\omega -{H}_{0}){\hat{\Psi }}_{k}$, and using the Hubbard–Stratonovich transformation, the microscopic action including the pairing fluctuations is obtained:

$${{{{{{{\mathcal{S}}}}}}}}={{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{e}}}}}}}}}^{(p)}+{{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{e}}}}}}}}-\eta }+{S}_{{{\mbox{}}}\eta {{\mbox{}}}}+{{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{e}}}}}}}}-A},$$

(30)

$${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{e}}}}}}}}}^{(p)}=\frac{1}{2}\check{\mathop{\sum}\limits_{k}}{\hat{\Psi }}\,\!^{{\dagger}}(k)\{-i\omega +{H}_{{{\rm{BdG}}}}^{(p)}({{{{{{{\boldsymbol{k}}}}}}}})\}\hat{\Psi }(k),$$

(31)

$${{{{{{{{\mathcal{S}}}}}}}}}_{\eta }=\frac{1}{2}\mathop{\sum}\limits_{p,a}\check{\mathop{\sum}\limits_{q}}\frac{{\hat{\eta }}_{a}^{(p)}(q){\hat{\eta }}_{a}^{(p)}(-q)}{{g}_{p}},$$

(32)

$${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{e}}}}}}}}-\eta }=\frac{1}{2}\mathop{\sum}\limits_{p,a}\check{\mathop{\sum}\limits_{k,q}}{\hat{\Psi }}{\,\!}^{{{{\dagger}}} }(k+q)\{{\eta }_{a}^{(p)}(q){\tau }_{a}^{(p)}\}\hat{\Psi }(k),$$

(33)

$${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{e}}}}}}}}-A}=\frac{1}{2}\check{\mathop{\sum}\limits_{k,q}}{\hat{\Psi }}{\,\!}^{{{{\dagger}}} }(k+q)\{{\Gamma }_{1}({{{{{{{\boldsymbol{k}}}}}}}},q)+{\Gamma }_{2}(k,q)\}\hat{\Psi }(k).$$

(34)

The auxiliary bosonic fields ${\eta }_{1}^{(p)}$ and ${\eta }_{2}^{(p)}$ represent the real and imaginary parts of the fluctuation in the condensed pairing channel of the pSC state, respectively. Γ₁ and Γ₂ are the paramagnetic and diamagnetic light-matter coupling vertices, respectively, and expressed in the uniform limit (q → 0) of the external electromagnetic fields as

$${\Gamma }_{1}({{{{{{{\boldsymbol{k}}}}}}}},q)=\mathop{\sum }\limits_{\mu =0}^{3}{{{{{{{{\mathcal{V}}}}}}}}}_{\mu }({{{{{{{\boldsymbol{k}}}}}}}}){{{{{{{{\mathcal{A}}}}}}}}}_{\mu }(q),$$

(35)

$${\Gamma }_{2}(k,q)=\check{\mathop{\sum}\limits_{{k}^{{\prime} }}}\mathop{\sum }\limits_{\mu ,\nu =0}^{3}{[{m}_{{{{{{{{\boldsymbol{k}}}}}}}}}^{-1}]}_{\mu \nu }{{{{{{{{\mathcal{A}}}}}}}}}_{\mu }(q-{k}^{{\prime} }){{{{{{{{\mathcal{A}}}}}}}}}_{\nu }({k}^{{\prime} }),$$

(36)

with the four-velocity operators ${{{{{{{{\mathcal{V}}}}}}}}}_{\mu }({{{{{{{\boldsymbol{k}}}}}}}})=(2{\tau }_{z},{\tau }_{0}{\partial }_{i}{H}_{0}({{{{{{{\boldsymbol{k}}}}}}}}))$ and the inverse of the mass matrix ${[{m}_{{{{{{{{\boldsymbol{k}}}}}}}}}^{-1}]}_{\mu \nu }={\tau }_{z}{\partial }_{\mu }{\partial }_{\nu }{H}_{0}({{{{{{{\boldsymbol{k}}}}}}}})$ which is zero when either of μ or ν is 0. Here, we define a four-potential ${{{{{{{{\mathcal{A}}}}}}}}}_{\mu }=| e| (-i{A}_{0},{{{{{{{\boldsymbol{A}}}}}}}})$ by multiplying the unit charge ∣e∣ to the conventional four-potential for conciseness.

By integrating out the fermionic degree of freedom $\hat{\Psi }$ and expanding the resultant action to the second order in ${{{{{{{{\mathcal{A}}}}}}}}}_{\mu }$ and ${\eta }_{a}^{(p)}$, we obtain an effective action for η and ${{{{{{{\mathcal{A}}}}}}}}$:

$${{{{{{{{\mathcal{S}}}}}}}}}_{{{\rm{eff}}}}^{(p)}=\, \frac{1}{2}\check{\mathop{\sum}\limits_{\Omega }}{({{{{{{{{\mathcal{A}}}}}}}}}_{0},{\eta }_{a}^{(p)})}_{{{\mbox{-}}}i\Omega }\left(\begin{array}{cc}{K}_{00}&{L}_{0b}^{(p)}\\ {R}_{0\nu }^{(p)}&{\tilde{\Pi }}_{ab}^{(p)}\end{array}\right){\left(\begin{array}{c}{{{{{{{{\mathcal{A}}}}}}}}}_{0}\\ {\eta }_{b}^{(p)}\end{array}\right)}_{i\Omega }\\ +\frac{1}{2}\check{\mathop{\sum }\limits_{\Omega }}{({{{{{{{{\mathcal{A}}}}}}}}}_{i},{\eta }_{a}^{(\bar{p})})}_{{{\mbox{-}}}i\Omega }\left(\begin{array}{cc}{K}_{ij}&{L}_{ib}^{(\bar{p})}\\ {R}_{aj}^{(\bar{p})}&{\tilde{\Pi }}_{ab}^{(\bar{p})}\end{array}\right){\left(\begin{array}{c}{{{{{{{{\mathcal{A}}}}}}}}}_{j}\\ {\eta }_{b}^{(\bar{p})}\end{array}\right)}_{i\Omega },$$

(37)

where $\bar{p}$ denotes the odd-parity(even-parity) pairing channel in eSC (oSC) state, which is the uncondensed pairing channel. Note that we omit the momentum q dependence of η and ${{{{{{{\mathcal{A}}}}}}}}$ since the London limit (q → 0) of the linear response is our interest. The sub-blocks K, L, R, and $\tilde{\Pi }$ are given by

$${K}_{\mu \nu }(q)=\, \frac{1}{2}\check{\mathop{\sum}\limits_{k}}\,{{\mbox{Tr}}}\,[{{{{{{{{\mathcal{V}}}}}}}}}_{\mu }({{{{{{{\boldsymbol{k}}}}}}}})G(k+q){{{{{{{{\mathcal{V}}}}}}}}}_{\nu }({{{{{{{\boldsymbol{k}}}}}}}})G(k)]\\ +\check{\mathop{\sum}\limits_{k}}\,{{\mbox{Tr}}}\,[G(k){[{m}_{{{{{{{{\boldsymbol{k}}}}}}}}}^{-1}]}_{\mu \nu }],$$

(38)

$${L}_{\mu a}^{(p)}(q)=\frac{1}{2}\check{\mathop{\sum }\limits_{k}}\,{{\mbox{Tr}}}\,[{{{{{{{{\mathcal{V}}}}}}}}}_{\mu }({{{{{{{\boldsymbol{k}}}}}}}})G(k+q){\tau }_{a}^{(p)}G(k)],$$

(39)

$${R}_{a\mu }^{(p)}(q)=\frac{1}{2}\check{\mathop{\sum }\limits_{k}}\,{{\mbox{Tr}}}\,[{\tau }_{a}^{(p)}G(k+q){{{{{{{{\mathcal{V}}}}}}}}}_{\mu }({{{{{{{\boldsymbol{k}}}}}}}})G(k)],$$

(40)

$${\tilde{\Pi }}\,\!^{(p)}_{ab}(q)=\frac{{\delta }_{ab}}{{g}_{p}}+\frac{1}{2}\check{\mathop{\sum}\limits_{k}}\,{{\mbox{Tr}}}\,[{\tau }_{a}^{(p)}G(k+q){\tau }_{b}^{(p)}G(k)],$$

(41)

with q = (iΩ, 0) and for p = e, o.

Derivation of $\tilde{K}$

The current J_i(Ω) in response to the external electromagnetic vector potential is derived by differentiating ${{{{{{{{\mathcal{S}}}}}}}}}_{{{\rm{eff}}}}^{(p)}$ with respect to the vector potential ${{{{{{{{\mathcal{A}}}}}}}}}_{i}(-i\Omega )$ and then taking the analytic continuation iΩ → Ω + iϵ.

$${J}_{i}(\Omega ) ={\left.\frac{\delta {{{{{{{{\mathcal{S}}}}}}}}}_{{{\rm{eff}}}}^{(p)}}{\delta {{{{{{{{\mathcal{A}}}}}}}}}_{i}(-i\Omega )}\right\vert }_{i\Omega \to \Omega +i\epsilon }\\ ={K}_{ij}(\Omega ){{{{{{{{\mathcal{A}}}}}}}}}_{j}(\Omega )+{L}_{ia}^{(\bar{p})}(\Omega ){\eta }_{a}^{(\bar{p})}(\Omega ),$$

(42)

where we use an identity K_ij(Ω) = K_ji(−Ω) and ${L}_{ia}^{(\bar{p})}(\Omega )={R}_{ai}^{(\bar{p})}(-\Omega )$. By substituting ${\eta }^{(\bar{p})}=-[{\tilde{\Pi }}\,\!^{(\bar{p})}]^{-1}{R}^{(\bar{p})}{{{{{{{\mathcal{A}}}}}}}}$ for ${\eta }^{(\bar{p})}$ in Eq. (42), we obtain

$${J}_{i}=\left\{{K}_{ij}-{[{L}^{(\bar{p})}[{\tilde{\Pi }}\,\!^{(\bar{p})}]^{-1}{R}^{(\bar{p})}]}_{ij}\right\}{{{{{{{{\mathcal{A}}}}}}}}}_{j},$$

(43)

where the argument Ω of each function is omitted for conciseness. Note that the term in parenthesis is nothing but $\tilde{K}$ in Eq. (19).

Spectral representation of ${L}_{z,2}^{(o)}$ in the eSC state

The spectral representation of ${L}_{\mu a}^{(p)}(q)$ is derived by carrying out the Matsubara frequency summation. Starting with the definition, we obtain

$${L}_{\mu a}^{(\bar{p})}(\Omega ) ={\left.\frac{1}{2}\check{\mathop{\sum}\limits_{k}}{{\mbox{Tr}}}[{{{{{{{{\mathcal{V}}}}}}}}}_{\mu ,{{{{{{{\boldsymbol{k}}}}}}}}}G(i{\omega }_{n}+i{\Omega }_{\nu },{{{{{{{\boldsymbol{k}}}}}}}}){\tau }_{a}^{(\bar{p})}G({{{{{{{\boldsymbol{k}}}}}}}})]\right\vert }_{i{\Omega }_{\nu }\to {\Omega }^{+}}\\ ={\left.\frac{1}{2}\check{\mathop{\sum}\limits_{k}}\frac{\langle m,{{{{{{{\boldsymbol{k}}}}}}}}| {{{{{{{{\mathcal{V}}}}}}}}}_{\mu ,{{{{{{{\boldsymbol{k}}}}}}}}}| n,{{{{{{{\boldsymbol{k}}}}}}}}\rangle \langle n,{{{{{{{\boldsymbol{k}}}}}}}}| {\tau }_{a}^{(\bar{p})}| m,{{{{{{{\boldsymbol{k}}}}}}}}\rangle }{(i{\omega }_{u}+i{\Omega }_{v}-{E}_{n,{{{{{{{\boldsymbol{k}}}}}}}}})(i{\omega }_{u}-{E}_{m,{{{{{{{\boldsymbol{k}}}}}}}}})}\right\vert }_{i{\Omega }_{\nu }\to {\Omega }^{+}}\\ = \frac{1}{2}\check{\mathop{\sum}\limits_{{{{{{{{\boldsymbol{k}}}}}}}}}}\frac{\langle m,{{{{{{{\boldsymbol{k}}}}}}}}| {{{{{{{{\mathcal{V}}}}}}}}}_{\mu ,{{{{{{{\boldsymbol{k}}}}}}}}}| n,{{{{{{{\boldsymbol{k}}}}}}}}\rangle \langle n,{{{{{{{\boldsymbol{k}}}}}}}}| {\tau }_{a}^{(\bar{p})}| m,{{{{{{{\boldsymbol{k}}}}}}}}\rangle }{{\Omega }^{+}-{E}_{n,{{{{{{{\boldsymbol{k}}}}}}}}}+{E}_{m,{{{{{{{\boldsymbol{k}}}}}}}}}}{\Theta }_{mn,{{{{{{{\boldsymbol{k}}}}}}}}},$$

(44)

where Θ_mn,k ≡ Θ(E_m,k) − Θ(E_n,k) and Ω⁺ = Ω + iϵ.

Other odd-parity channels

In this section, we discuss the linear couplings between the other odd-parity channels and the light (or the current) when the zero-field ground state is an even-parity state. We first note that the presence of an inversion ${{{{{{{\mathcal{I}}}}}}}}={\sigma }_{x}$ and a time-reversal symmetry ${{{{{{{\mathcal{T}}}}}}}}=i{s}_{y}{{{{{{{\mathcal{K}}}}}}}}$ forces the normal phase Hamiltonian to take the following form:

$${H}_{0}({{{{{{{\boldsymbol{k}}}}}}}})=\, {\varepsilon }_{00}({{{{{{{\boldsymbol{k}}}}}}}}){\sigma }_{0}{s}_{0}+({\varepsilon }_{10}({{{{{{{\boldsymbol{k}}}}}}}}){\sigma }_{x}+{\varepsilon }_{20}({{{{{{{\boldsymbol{k}}}}}}}}){\sigma }_{y}){s}_{0}\\ +{\sigma }_{z}({\varepsilon }_{31}({{{{{{{\boldsymbol{k}}}}}}}}){s}_{x}+{\varepsilon }_{32}({{{{{{{\boldsymbol{k}}}}}}}}){s}_{y}+{\varepsilon }_{33}({{{{{{{\boldsymbol{k}}}}}}}}){s}_{z})$$

(45)

where ε₀₀(k) and ε₁₀(k) are even functions under k → −k while ε₂₀(k) and ε_3i(k) are odd functions. The linear coupling between a pairing channel and the light is possible only when the pairing channel transforms like one of the current operators J_i under the symmetries of H₀(k). For CeRh₂As₂, the point group D_4h is the symmetry of the Hamiltonian at Γ in the Brillouin zone. By using the symmetries of the point group D_4h, we analyze the selection rule for odd-parity channels transforming like k_xs_y−k_ys_x, k_zs_z, k_zσ_xs_z, or k_xs_x + k_ys_y which are discussed in ref. ⁴¹.

Table 1 summarizes the parities of the current operators and the form factors of those odd-parity channels with respect to several two-fold symmetries in D_4h. The signs tell whether TO(k)T⁻¹ = +O(Tk) or TO(k)T⁻¹ = −O(Tk) where O represents one of the currents or the form factors in the first column of Table 1 and T represents a symmetry transformation in the first row.

Table 1 Symmetry properties of the current operators (J_x, J_y, J_z) and several odd-parity gap functions.

Firstly, the linear coupling between the in-plane currents J_x and J_y and the odd-parity gap functions in Table 1 is forbidden by, for example, C_2z. It is easy to see that the odd-party channels transforming like k_xs_x + k_ys_y or k_zs_z can not be linearly coupled to the light because of C_2z and C_2x. The odd-parity channel labeled by k_xs_y−k_ys_x transforms like J_z for all two-fold symmetries in D_4h. Indeed, J_z and k_xs_y−k_ys_x belong to the same irreducible representation, and thus k_xs_y−k_ys_x can be coupled to the light as σ_z can.

In the above symmetry-based analysis, however, the details of the electronic structure are not taken into consideration. For CeRh₂As₂, the large contribution to ε₃₃(k) may be supposed to originate from the Ising-type spin–orbit couplings between next-nearest-neighboring Ce atoms. As long as this Ising-type spin–orbit coupling is so negligible that ε₃₃ is also negligible compared to other ε_ij, the coupling between k_xs_y−k_ys_x and J_z is expected to be much smaller than that between σ_z and J_z.

To prove it, we first note that the non-trivial part of the normal phase Hamiltonian

$${\tilde{H}}_{0}({{{{{{{\boldsymbol{k}}}}}}}})\equiv {H}_{0}({{{{{{{\boldsymbol{k}}}}}}}})-{\varepsilon }_{00}({{{{{{{\boldsymbol{k}}}}}}}}){\sigma }_{0}{s}_{0}$$

(46)

is subject to an additional antiunitary antisymmetry ${{{{{{{\mathcal{A}}}}}}}}={U}_{{{{{{{{\mathcal{A}}}}}}}}}{{{{{{{\mathcal{K}}}}}}}}$ of ${\tilde{H}}_{0}({{{{{{{\boldsymbol{k}}}}}}}})$ with ${U}_{{{{{{{{\mathcal{A}}}}}}}}}=i{\sigma }_{y}{s}_{x}$. It transforms under ${{{{{{{\mathcal{A}}}}}}}}$ as ${U}_{{{{{{{{\mathcal{A}}}}}}}}}{\tilde{H}}_{0}{({{{{{{{\boldsymbol{k}}}}}}}})}^{* }{U}_{{{{{{{{\mathcal{A}}}}}}}}}^{{{{\dagger}}} }=-{\tilde{H}}_{0}({{{{{{{\boldsymbol{k}}}}}}}})$. By ${{{{{{{\mathcal{A}}}}}}}}$, the eigenvectors $\vert {\xi }_{1},\alpha \rangle$ and $\vert {\xi }_{1},\beta \rangle$ are related to $\vert {\xi }_{2},\alpha \rangle$ and $\vert {\xi }_{2},\beta \rangle$:

$${{{{{{{\mathcal{A}}}}}}}}\left\vert {\xi }_{1},\alpha \right\rangle =\mathop{\sum}\limits_{{\alpha }^{{\prime} }=\alpha ,\beta }{[{\Gamma }_{{{{{{{{\mathcal{A}}}}}}}}}]}_{{\alpha }^{{\prime} },\alpha }\left\vert {\xi }_{2},{\alpha }^{{\prime} }\right\rangle ,$$

(47)

$${{{{{{{\mathcal{A}}}}}}}}\left\vert {\xi }_{2},\alpha \right\rangle =\mathop{\sum}\limits_{{\alpha }^{{\prime} }=\alpha ,\beta }{[-{\Gamma }_{{{{{{{{\mathcal{A}}}}}}}}}^{T}]}_{{\alpha }^{{\prime} },\alpha }\left\vert {\xi }_{1},{\alpha }^{{\prime} }\right\rangle ,$$

(48)

where ${\Gamma }_{{{{{{{{\mathcal{A}}}}}}}}}$ is a 2 × 2 unitary matrix. Here, we use ${U}_{{{{{{{{\mathcal{A}}}}}}}}}=-{U}_{{{{{{{{\mathcal{A}}}}}}}}}^{\rm {{T}}}$.

The antiunitary antisymmetry of ${\tilde{H}}_{0}$ is especially useful when the linear coupling is computed between the current operator J_z and the pairing fluctuations with the form factor M_k in the eSC state with the trivial ground state gap function. In the calculation, we frequently encounter terms such as ${{{{{{{{\mathcal{I}}}}}}}}}_{m\bar{m}}={\sum }_{\alpha ,\beta }\langle m,\alpha | {J}_{z}| \bar{m},\beta \rangle \langle \bar{m},\beta | {M}_{{{{{{{{\boldsymbol{k}}}}}}}}}| m,\alpha \rangle$ with $\bar{m}=-m$ being 1 or 2, which determine the selection rule for the optical response. A tedious manipulation leads us to

$${{{{{{{{\mathcal{I}}}}}}}}}_{m\bar{m}}={\lambda }_{{J}_{z}}{\lambda }_{M}{{{{{{{{\mathcal{I}}}}}}}}}_{m\bar{m}},$$

(49)

where ${\lambda }_{{{{{{{{\mathcal{O}}}}}}}}}$ is the parity of the operator ${{{{{{{\mathcal{O}}}}}}}}$ with respect to ${{{{{{{\mathcal{A}}}}}}}}$. Thus, if ${\lambda }_{{J}_{z}}{\lambda }_{M}=-1$, the linear coupling between the light and the pairing fluctuation characterized by the form factor M_k is forbidden. Note that both J_z and σ_z are odd under ${{{{{{{\mathcal{A}}}}}}}}$ while k_xs_y−k_ys_x is even. Therefore, the linear coupling between the light and the fluctuation in the pairing channel k_xs_y−k_ys_x is negligible as long as the Ising-type spin–orbit coupling is negligible. This argument is also applicable even when the Zeeman term B_zs_z induced by the out-of-plane magnetic field is added to ${\tilde{H}}_{0}({{{{{{{\boldsymbol{k}}}}}}}})$.

For completeness, let us discuss the case discussed in ref. ²¹ in which it is proposed that the H−T phase diagram of the superconducting states of CeRh₂As₂ might be reproduced with inter-layer spin-triplet odd-parity gap functions. There, the low-field state is characterized by an odd-parity spin-triplet gap function transforming like ${k}_{x}{k}_{y}{k}_{z}({k}_{x}^{2}-{k}_{y}^{2}){\sigma }_{x}{s}_{z}$ that belongs to A_1u of D_4h. The gap function of the high-field state is another odd-parity spin-triplet gap function transforming σ_ys_z belonging to A_1u of D_4h. For this case, a BS mode should exist because both pairing channels belong to different irreducible representations. Since both pairing channels have the same inversion parity, however, the BS mode is inactive in the linear optical response.

Relation between the critical temperatures and BS mode gap

Eq. (17) is derived in this section. To derive it, it is sufficient to obtain the analytical expression of ${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )={g}_{\rm {{o}}}^{-1}-{\tilde{\Pi }}\,\!^{({{{\rm{o}}}})}_{22}(\Omega )$ for ∣Ω∣ < 2Δ_e. To get to the point first,

$${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )\approx -\langle {\sin }^{2}\chi \rangle \left\{\frac{1}{{g}_{{{{{{{{\rm{o}}}}}}}}}}+{N}_{{{{{{{\mathrm{tot}}}}}}}}\frac{2y\arcsin y}{\sqrt{1-{y}^{2}}}\right\}.$$

(50)

with y = Ω⁺/2Δ_e and N_tot = N₁ + N₂, which is used throughout this section. Here, N_i is the density of states at the Fermi surface from the band ξ_i. (Counting the Kramer degeneracy, 2N_tot is the total density of states).

For later use, we first evaluate ${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(0)$ using the identity

$$[{\tau }_{z}{\sigma }_{z},G{(k)}^{-1}]=-2i{\tau }_{y}^{({{{{{{{\rm{o}}}}}}}})}{{{{{{{\rm{Re}}}}}}}}[{\Delta }_{{{{{{{{\rm{e}}}}}}}}}]-4i{F}_{A}.$$

(51)

where 4iF_A ≡ [σ_z, H₀]. This commutator appears in literature that is concerned with the concept of superconducting fitness²¹. When the Ising-type spin–orbit coupling is ignored (λ_I = 0) in Eq. (1), F_A = J_z is satisfied. Given the self-consistent gap equation $2{{{{{{{\rm{Re}}}}}}}}[{\Delta }_{{{{{{{{\rm{e}}}}}}}}}]=-{g}_{{{{{{{{\rm{e}}}}}}}}}\,{{\mbox{Tr}}}\,[{\tau }_{x}G(k)]$ and F_A = J_z, we get

$${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(0)=-\frac{1}{{g}_{{{{{{{{\rm{e}}}}}}}}}}-\check{\mathop{\sum}\limits_{k}}\frac{\,{{\mbox{Tr}}}\,[{\tau }_{y}{\sigma }_{z}G(k){F}_{{{{{{{{\rm{A}}}}}}}}}({{{{{{{\boldsymbol{k}}}}}}}})G(k)]}{{{{{{{{\rm{Re}}}}}}}}[{\Delta }_{{{{{{{{\rm{e}}}}}}}}}]}$$

(52)

$$=-\frac{1}{{g}_{{{{{{{{\rm{e}}}}}}}}}}-\frac{2{L}_{z,2}^{({{{{{{{\rm{o}}}}}}}})}(0)}{{{{{{{{\rm{Re}}}}}}}}[{\Delta }_{{{{{{{{\rm{e}}}}}}}}}]}\approx -\frac{\langle {\sin }^{2}\chi \rangle }{{g}_{{{{{{{{\rm{e}}}}}}}}}},$$

(53)

where we use Eq. (24) for the last approximation.

To calculate ${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )$, let us first decompose ${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )$ at zero-temperature into the singular and regular parts as

$${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )={\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}},\,{{\rm{sig}}})}(\Omega )+{\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}},\,{{\rm{reg}}})}(\Omega ),$$

(54)

with

$${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}},\,{{\rm{sig}}})}(\Omega ) =\check{\mathop{\sum}\limits_{{{{{{{{\boldsymbol{k}}}}}}}}}}\mathop{\sum}\limits_{i=1,2}\frac{4{E}_{{{{{{{{\rm{c}}}}}}}},i}\,{\sin }^{2}\chi }{({\Omega }^{+})^{2}-4{E}_{{{{{{{{\rm{c}}}}}}}},i}^{2}},\\ {\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}},\,{{\rm{reg}}})}(\Omega ) =\check{\mathop{\sum}\limits_{{{{{{{{\boldsymbol{k}}}}}}}}}}\frac{4{\cos }^{2}\chi \,{\cos }^{2}\frac{{\Xi }_{1}-{\Xi }_{2}}{2}({E}_{{{{{{{{\rm{c}}}}}}}},1}+{E}_{{{{{{{{\rm{c}}}}}}}},2})}{({\Omega }^{+})^{2}-({E}_{{{{{{{{\rm{c}}}}}}}},1}+{E}_{{{{{{{{\rm{c}}}}}}}},2})^{2}},$$

(55)

where we use

$$| \langle {\xi }_{i},s| {\sigma }_{z}| {\xi }_{j},{s}^{{\prime} }\rangle | =(1-{\delta }_{s{s}^{{\prime} }})\left\{\begin{array}{ll}| \sin \chi | \quad &i=j\\ | \cos \chi | \quad &i\, \ne \, j\hfill\end{array}\right.,$$

(56)

$$\left\langle {{{{{{{\rm{c}}}}}}}},i,s\right\vert {\tau }_{y}^{(o)}\vert {{{{{{{\rm{v}}}}}}}},j,{s}^{{\prime} }\rangle =\frac{1}{i}\cos \frac{{\Xi }_{j}-{\Xi }_{i}}{2}\langle {\xi }_{i},s\vert {\sigma }_{z}\vert {\xi }_{j},{s}^{{\prime} }\rangle .$$

(57)

The potential singularities of ${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}},\,{{\rm{reg}}})}(\Omega )$ lie at Ω = E_c,1 + E_c,2 ≫ 2Δ_e, and thus it behaves regularly for ∣Ω∣ < 2Δ_e. Also, it is expected to be very small compared to the singular part ${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}},\,{{\rm{sig}}})}$. Thus, ignoring it can be justified as far as the semi-analytical expression for Ω_BS is concerned. This approximation, ${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )-{\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(0)$ is given by

$${\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )-{\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(0) =\check{\mathop{\sum}\limits_{{{{{{{{\boldsymbol{k}}}}}}}}}}\mathop{\sum}\limits_{i}\frac{{({\Omega }^{+})}^{2}{\sin }^{2}\chi }{{E}_{{{{{{{{\rm{c}}}}}}}},i}({({\Omega }^{+})}^{2}-4{E}_{{{{{{{{\rm{c}}}}}}}},i}^{2})}\\ =-\langle {\sin }^{2}\chi \rangle {N}_{{{{{{{\mathrm{tot}}}}}}}}\frac{2y\arcsin y}{\sqrt{1-{y}^{2}}}.$$

(58)

Therefore, we obtain

$${\tilde{\Pi }}\,\!^{({{{\rm{o}}}})}_{22}(\Omega ) =\frac{1}{{g}_{{{{{{{{\rm{o}}}}}}}}}}+{\Pi }_{22}^{({{{{{{{\rm{o}}}}}}}})}(\Omega )\\ =\frac{1}{{g}_{{{{{{{{\rm{o}}}}}}}}}}-\langle {\sin }^{2}\chi \rangle \left(\frac{1}{{g}_{{{{{{{{\rm{e}}}}}}}}}}+\frac{2{N}_{{{{{{{\mathrm{tot}}}}}}}}y\arcsin y}{\sqrt{1-{y}^{2}}}\right).$$

(59)