Introduction

Recent years have witnessed the success of artificial neural networks in solving real-world problems1,2,3 and also the rapid increase of structural complexity and the number of parameters in various neural network models4,5,6. Neural networks with a larger number of trainable parameters are more computationally and memory intensive, being difficult to deploy in embedded devices with limited hardware resources7. To address this limitation, there are increasing interests to sparsify neural networks, i.e., to iteratively reduce the number of weighted links (trainable parameters) by an order of magnitude, while maintaining their performance7,8,9,10,11,12. As shown in explorations of the Lottery Ticket Hypothesis, once initialized correctly, an optimal sub-network with similar predictive performance to the dense network can be found by iterative magnitude pruning13. For example, neural networks with sparsity level 0.9 (i.e., only 10% links’ weights trainable) are able to achieve comparable performance to their fully connected counterparts in computer vision, speech recognition, and natural language processing8,9,10. This phenomenon coincides with the fact that the biological brains of high intelligence and energy efficiency have actually very sparse neuronal networks. Indeed, the sparsity levels of Caenorhabditis elegans, Drosophila, and macaque brain connectome are about 0.88, 0.94 and 0.70, respectively14,15.

Neural networks can be sparsified by either pruning8,9,10 or rewiring11,12,16,17. The former starts from a fully connected network and intentionally removes its links during the training process. The latter starts from a sparse yet random network and gradually reorganizes its structure. From the renormalization group perspective, both can be viewed as inducing a flow in parameter space18. While these approaches can obtain optimized sparse networks, the resulting networks have different topologies19. Previous studies showed that topological properties of neural networks have a profound impact on their performance. For example, randomly wired neural networks with small-world attributes in connection patterns outperform random counterparts20; the performance of a deep neural network correlates highly with the clustering coefficient and the average path length of its graph structure21; the connection pattern of neurons on consecutive layers of sparse feed-forward neural networks tends to evolve towards scale-free topologies by evolutionary training11; trained multi-layer perceptrons are typically more clusterable than initially random networks, especially with dropout and weight pruning22; a fully connected network sparsified by iterative magnitude pruning can emerge with local connectivity patterns similar to convolutional neural networks23. While these results revealed the association between topological properties and the performance of neural networks, most of them focused on feed-forward neural networks, and there are currently few studies on the relationship between topological patterns and performance of sparse recurrent neural networks (RNNs). One exception is a recent study showing that the correlation between structural properties of RNNs and their performance could offer important insights into architectural search strategies24. However, a fundamental question remains open: Is there a universal topological patterns in well-performing sparse RNNs?

To address this question, we explore the mesoscopic structure of RNNs from the perspective of network science. Compared to previous studies that only focused on network topology, here we incorporate another dimension: the sign of weights, which has been shown to impact the performance of sparse networks25. We find that the topologies of sparse RNNs optimized by both pruning and rewiring approaches show a common profile of signed three-node motifs26,27. Our results also show that in the process of sparsification neural networks evolve towards configurations favouring feed-forward loops that are balanced, i.e., have an even number of negative weights, and this structural balance is helpful for achieving better performance of RNNs. These phenomena are consistent across many different tasks, and the emergence of structural balance is quite general, accommodating other state-of-the-art models such as neural ordinary differential equation networks28 (Neural ODEs) and continuous-time RNNs29,30 (CT-RNNs).

Results

Sparsifying RNNs

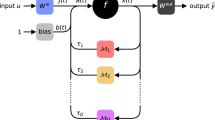
A typical RNN is shown in Fig. 1a, in which there are cyclic paths between the neurons. The connections can be excitatory or inhibitory, i.e., with positive or negative weights, respectively. RNNs have been successfully applied in natural language processing, time series prediction, cognitive neuroscience, and many other fields2,31,32.

Fig. 1: Sparsifying recurrent neural network (RNN).
figure 1

a An example of the RNN, typically characterized by cyclic links between the hidden neurons. b Sparsification by pruning, i.e., starting from a fully connected network and iteratively removing its links to obtain an optimized sparse network. c Sparsification by rewiring, i.e., starting from a sparse yet random network and iteratively rewiring its links to obtain an optimized sparse network. d Test accuracy vs. epochs for the MNIST task by different sparsification strategies. Black line represents the fully connected RNNs. Pruning I (blue line) and Pruning II (green line) refer to two pruning strategies, and DeepR (orange line) and SET (purple line) refer to two rewiring strategies. e Link weight distribution of the RNN hidden layer during the training process (the initial state, at the end of pruning, and the final state respectively). Orange (green) dots denote the links with positive (negative) weights, and blue dots represent the links whose weights have changed from positive to negative or from negative to positive from the end of pruning to the final state.

Full size image

A fully connected RNN can be sparsified by pruning, i.e., iteratively removing some connections or neurons (Fig. 1b), and a randomly wired RNN can be optimized by rewiring, i.e., shuffling the connections between neurons gradually (Fig. 1c). Here we employ two pruning methods9,10, called Pruning I and II hereafter (see “Methods” for details), and two rewiring methods, i.e., deep rewiring (DeepR)12 and sparse evolutionary training (SET)11, to sparsify the single hidden layer of our RNNs. The comparison between the sparse and the fully connected RNNs shows that, sparse RNNs, with only one tenth or twentieth of links, are able to achieve comparable performance to fully connected RNNs (Fig. 1d and Supplementary Table 1).

We analyze also the distribution of link weights during the training with pruning methods. At the initial state all link weights are drawn from a normal distribution with zero mean (Fig. 1e, left). In the pruning phase, unimportant links are iteratively removed in batches according to their weight rankings, hence, at the end of pruning the link weights obey a bimodal distribution, consistent with previous studies8. During the following fine-tuning phase, we fix the sparsified structure of the neural network and retrain it, finding that most links do not change their signs (Fig. 1e, right), i.e., only a few links change their weights from positive to negative or vice versa. This phenomenon is observed in diverse tasks and datasets, including MNIST, SMS spam classification (SMS), Mackey–Glass chaotic time series prediction (MG), hand gesture segmentation (HGS), and multi-task cognition (MTC) (see Supplementary Figs. 1 and 2).

Universal pattern of signed motifs in trained sparse RNNs

For a RNN with n neurons, the total number of potential links is n2. When the network is sparsified to have m links, taking into account the fact that each link can have a positive or negative weight, the total number of possible network configurations becomes \(\left({{n}^{2} \atop {m}}\right) \cdot {2}^{m}\). The sparsification methods described in the previous section, either by pruning or rewiring, lead to a subset of the large potential network configuration space. Hence, a fundamental yet unsolved problem is why such a subset of networks perform better than the rest, i.e., do these optimally trained sparse RNNs share any common structural patterns? Only very recent studies attempted to answer this question11,20,21,22,24,33,34,35,36. For example, neural networks trained by weight pruning are highly clusterable22, and artificial neural networks initialized with random sparse topologies tend to evolve to heavy-tailed topologies when adaptive sparse connectivity is allowed11.

Here we explore the regularities of well-performing sparse RNNs from the perspective of motif profile and structural balance. Motifs are subgraphs consisting of a few nodes, which can reveal the basic building blocks of complex networks37,38,39,40. To quantify the importance of a specific motif for a network, we calculate the number of this motif in the original network, No, and compare it with the numbers of this motif in degree-preserved randomized networks. The significance of this motif for the original network is captured by z-score38

$$z=\frac{{N}_{{{{{\mathrm{o}}}}}}-\langle {N}_{{{{{\mathrm{r}}}}}}\rangle }{{\sigma }_{{{{{\mathrm{r}}}}}}},$$
(1)

where 〈Nr〉 and σr are, respectively, the mean and the standard deviation of the numbers of this motif in degree-preserved randomized networks. If the z-score is positive and large, this motif is over-represented in the original network; If the z-score is negative and its absolute value is large, this motif is under-represented in the original network; otherwise, the motif is not significant for this network.

Because the weights of the links in RNNs can be positive or negative, here we consider signed motifs. As shown in Fig. 2a, b, there are eight feed-forward motifs consisting of three nodes i, j, and k. If sign(wij ⋅ wjk) = sign(wik), the motif is structurally balanced; otherwise unbalanced. The hidden layer of RNN is actually a directed weighted network (see Fig. 1a), and we investigate the profile of signed motifs in the networks sparsified by four strategies, i.e., Pruning I, Pruning II, DeepR, and SET, and for five different tasks. We find that, surprisingly, the motif profiles in all these diverse settings are consistent, even though we do not intentionally encourage this topological characteristic during sparsification. As shown in Fig. 2c–l, the balanced motifs are all over-represented while the unbalanced motifs are all under-represented in the well-performing sparse RNNs. Such a structural balance pattern emerges with iterative sparsification and is independent of sparsity level (sparsity s = 0.95 in Fig. 2c–g and s = 0.90 in Fig. 2h–l). We will show below that the structural pattern also exists in other state-of-the-art RNN models. To the best of our knowledge, this is the first time that such a universal pattern is discovered in sparse RNNs.

Fig. 2: Motif profile in optimized sparse recurrent neural networks (RNNs).
figure 2

a, b The balanced and unbalanced feed-forward motifs consisting of three nodes (i, j, and k). Positive and negative link weights are denoted by orange and green respectively. c–l Statistical significance, quantified by normalized z-score, of feed-forward motifs in the hidden layers of RNNs after training by four different sparsification strategies i.e., Pruning I (blue diamond), Pruning II (green triangle), DeepR (orange circle), and SET (purple inverted triangle), and for five different tasks (i.e., MNIST, SMS, MG, HGS, and MTC). The numbers of neurons in the hidden layer for these five tasks are 150, 100, 128, 128, and 256, respectively. Two sparsity levels, s = 95% (c–g) and s = 90% (h–l), are considered. The normalized z-scores are calculated over 20 independent runs, and the error bars represent standard deviation. Positive and negative z-scores mean motifs are over-represented and under-represented respectively. Other hyperparameters used in these experiments are listed in Supplementary Table 2.

Full size image

Emergence of overall structural balance in RNNs

In this section we explore the evolution of structural balance during the training process. To quantify the overall balance of a signed directed network, the most natural method27,41 is to incorporate both transitivity and sign consistency in the assessment of structural balance for each type of triad, i.e., a set of three nodes with at least one directed edge between each pair. Following a method41 previously used to measure the balance of signed directed networks, we consider four types of transitive triads, i.e., triads which either comprise a feed-forward loop, or can be decomposed into two or more feed-forward loops (see Fig. 3a). A triad is completely balanced (unbalanced) if and only if all of its decomposed feed-forward loops are balanced (unbalanced); If a triad decomposes to both balanced and unbalanced feed-forward loops then it is partially balanced. We calculate the balance ratio for the set of all transitive triads of each type, then the overall balance ratio η is calculated by averaging the balance ratios of all triad types across the network (see “Methods” for details).

Fig. 3: Emergence of structural balance during the training process.
figure 3

a Transitive triads that either contain a feed-forward loop, or can be decomposed into combinations of feed-forward loops. These four types of transitive triads are used to calculate the global structural balance ratio η of directed signed networks. b–f Structural balance ratio η of recurrent neural network (RNN) hidden layer over epochs for four sparsification strategies, i.e., Pruning I (blue diamond), Pruning II (green triangle), DeepR (orange circle), and SET (purple inverted triangle) and five different tasks (i.e., MNIST, SMS, MG, HGS, and MTC). Each plot is the averaging over 10 independent runs, and the error bars represent standard deviation. The sparsity level of hidden neurons is s = 95%. The hyperparameters used in these experiments are listed in Supplementary Table 2.

Full size image

We use this measure to examine the balance of RNNs during the training process with different sparsification strategies. We find that, for pruning strategies (both Pruning I and Pruning II), the overall balance ratio η increases quickly in the topology pruning phase, indicating that sparsification by pruning eliminates unbalanced links to promote the stability of the system, causing RNNs tend to evolve towards more structurally balanced configurations. In the subsequent phase of weight fine-tuning, the balance ratio does not increase further (while the sparsity level does not increase either). This phenomenon is consistent with our observation of that the signs of links barely change in the weight fine-tuning phase (see Fig. 1e). Similar results are found for rewiring strategies (both DeepR and SET). Indeed, while the initial topology is a random sparse network with an overall balance ratio η around 0.5, the η increases gradually or converges rapidly to a larger value, i.e., the network becomes more structurally balanced. The phenomena are independent of datasets and sparsity levels (s = 0.95 in Fig. 3b–f and s = 0.90 in Supplementary Fig. 3). These results demonstrate that the structural balance we found in sparse RNNs does not occur by chance but emerges during the sparsifying processes.

Better performance for structurally balanced networks

Since sparse neural networks tend to be structurally balanced, a question is whether structural balance can improve the performance of neural networks in real tasks. To investigate this question, here we compare the performance of sparse RNNs with balanced or random topologies. First, we generate balanced networks with higher balance ratios through the degree-preserving rewiring approach (see “Methods” for details). Then, we set the balanced and the random networks respectively as the hidden layer of RNN. Each link between the neurons in the hidden layer has a sign (+1 or −1) and its weight is drawn from the uniform distribution U(0, 1). During the training process, both the structure and the link weights of the hidden layer are fixed. Only the links between the inputs and the hidden layer, as well as those between the hidden layer and the outputs, are trainable. Such a setting ensures fair comparisons, because the only difference between these two models is that a model is structurally balanced and another is not.

We compute the performance of RNN that has a random-network hidden layer (i.e., whose balance ratio η ≈ 0.5) for four tasks and set the performance as respective baselines. We then increase the balance ratio η and obtain the change of RNN performance. Figure 4 displays the relative performance vs. the balance ratio, showing that structural balance is able to increase the prediction accuracy (Fig. 4a–c) or decrease the prediction error (Fig. 4d) with high probabilities. We have shown a correspondence between structural balance and improved performance, but are not implying that unbalanced motifs are irrelevant to function: performance decreases with the removal of unbalanced motifs (see Supplementary Fig. 4), and the estimated relative effect wij ⋅ wjk + wik of node i on node k (see “Methods”) is substantially different from zero in either the balanced or unbalanced case (see Supplementary Figs. 5–8). Furthermore, throughout training the distribution of weights in unbalanced motifs remains similar to the distribution in balanced motifs; although before the first pruning step weaker links are slightly more strongly represented in balanced motifs than in unbalanced motifs, this tendency disappears as training continues (see Supplementary Fig. 9).

Fig. 4: Performance comparison between recurrent neural networks (RNNs) with random or balanced networks.
figure 4

The change of accuracy (ACC) or mean square error (MSE) vs. structural balance ratio η for four real tasks, i.e., MNIST (a), SMS (b), HGS (c), and MG (d), where the baselines are the performance of RNNs with random networks. For each dataset, we show the results for 50 trials, each involving an independently generated random network and two balanced networks with identical degree sequences. Blue (yellow) dots correspond to improvement (loss) in network performance as a result of structural balancing. Purple dashed lines correspond to the median of the change in performance. The hyperparameters used in these experiments are listed in Supplementary Table 2.

Full size image

Structural balance in other recurrent network models

To assess whether structural balance patterns exist only in basic sparse RNNs or are general for sparse recurrent models, here we explore the sparse structure of CT-RNNs29 (see “Methods”) and Neural ODEs28 (see “Methods”). Specifically, we train a CT-RNN of 64 hidden neurons for two datasets, i.e., hand gesture segmentation and human activity recognition, by using the sparsification strategies of Pruning I and DeepR. After sparsification and training the link density among the neurons in the hidden layer is 5%, i.e., the sparsity s = 95%. We find that the sparse CT-RNN can achieve comparable or even better performance than its counterpart that has a fully connected network (Fig. 5a). The increase of the balance ratio during sparsification shows that the same structural balance patterns emerge in the well-performing sparse CT-RNNs for both tasks, regardless of which sparsification strategy is used (Fig. 5b for pruning and Fig. 5c for rewiring). Similarly, sparse Neural ODE can achieve comparable or even better performance than the fully connected counterpart, and the sparse networks are also structurally balanced.

Fig. 5: Structural balance of neural ordinary differential equation network (Neural ODE) and continuous-time recurrent neural network (CT-RNN).
figure 5

a Accuracy results of sparse (blue and green) and fully connected (purple) networks for both CT-RNNs and Neural ODEs. The two tasks are hand gesture segmentation (HGS) and human activity recognition (HAR). CT-RNN networks are sparsified by Pruning I (Pruning) and SET (Rewiring), and Neural ODE networks are sparsified by Pruning I (Pruning) and DeepR (Rewiring). The sparsity level is s = 95%. b, c The evolution of structural balance ratio of CT-RNN and Neural ODE networks during the training process. The sparsification strategies are Pruning (b) and Rewiring (c), respectively. Each dot in these curves is the averaging of 20 independent runs, and the error bars represent standard deviation. The hyperparameters used in these experiments are listed in Supplementary Table 3.

Full size image

Discussion

In this paper, we studied the structure of sparsified RNNs and proposed a motif-based method, inspired by social balance theory, to quantify the balance ratio of these signed networks. Our analysis unveiled a universal structurally balanced pattern in well-performing sparse RNNs, and showed that such structural balance does not occur by chance but emerges during training processes, independent of sparsification strategies, sparsity levels and specific tasks. Despite differences between sparsification strategies, particularly when comparing neural networks trained using the pruning method (which successively reduces the number of edges) and the rewiring method (which maintains a fixed number of edges), common structural features consistently emerge and impact the performance of sparse RNNs. To the best of our knowledge, this is the first time that a universal pattern has been discovered in sparse RNN models, which has the potential not only to improve network performance but also to offer insights for optimal architecture searching.

Our work bridged two fields, network science and artificial neural network, that have been independently developing previously, raising questions worthy of future pursuit. First, in this paper we focused on recurrent network models. Exploring structural patterns in other types or more complicated network models would be an important future work. Second, we found the structural balance phenomenon and the next aim is to uncover the underlying mechanism from the perspective of statistical physics26. Third, our findings suggest promising directions for optimization.

Methods

Sparsification strategies

Pruning I9

This approach sparsifies the network by setting all parameters that are lower than the threshold to zero during the training of the model. The threshold is a monotonically increasing quantity ϵ determined by a set of hyperparameters

$$\epsilon =\left\{\begin{array}{ll}\theta \times (\iota_{{{{{\mathrm{current}}}}}}-\iota_{{{{{\mathrm{start}}}}}}+1) /f \hfill &{{{{\mathrm{if}}}}}\,\,\iota_{{{{{\mathrm{start}}}}}} < \iota_{{{{{\mathrm{current}}}}}} < \iota_{{{{{\mathrm{ramp}}}}}}\\ \theta \times (\iota_{{{{{\mathrm{ramp}}}}}}-\iota_{{{{{\mathrm{start}}}}}}+1)+\frac{3}{2}\theta \\ \times (\iota_{{{{{\mathrm{current}}}}}}-\iota_{{{{{\mathrm{ramp}}}}}}+1)/f&\,{{{{\mathrm{if}}}}}\,\,\iota_{{{{{\mathrm{ramp}}}}}}\le \iota_{{{{{\mathrm{current}}}}}} < \iota_{{{{{\mathrm{end}}}}}}\end{array}\right.,$$
(2)

where \({\iota }_{\,{{{{\mathrm{start}}}}}}\) is the number of iterations before pruning, \({\iota }_{\,{{{{\mathrm{current}}}}}}\) is the number of current iterations, \({\iota }_{{{{{\mathrm{ramp}}}}}}=\frac{1}{4}({{{{\mathrm{total}}}}\; {{{\mathrm{epochs}}}}})\) is the number of iterations before increasing the rate of pruning, and \({\iota }_{{{{{\mathrm{end}}}}}}=\frac{1}{2}({{{{\mathrm{total}}}}\; {{{\mathrm{epochs}}}}})\) is the number of iterations before stopping pruning, and f is the number of iterations between updates of ϵ. The value of θ can be calculated as

$$\theta =\frac{2\times q\times f}{2\times (\iota_{{{{{\mathrm{ramp}}}}}}-\iota_{{{{{\mathrm{start}}}}}})+3\times (\iota_{{{{{\mathrm{end}}}}}}-\iota_{{{{{\mathrm{ramp}}}}}})},$$
(3)

where q is the threshold for absolute values of weights to achieve the target sparsity s.

Pruning II10

This approach starts from a fully connected network and reduces the number of non-zero parameters by gradually increasing the sparsity s of the model. The gradual sparsity function satisfies

$${s}^{(t)}={s}_{{{{{\mathrm{f}}}}}}+({s}_{{{{{\mathrm{i}}}}}}-{s}_{{{{{\mathrm{f}}}}}}){\left(1-\frac{t}{T}\right)}^{3}\quad \,{{{{\mathrm{for}}}}}\,\quad t\in 0,1,...,T,$$
(4)

where t is the index of the iterations, si is the initial sparsity (usually 0), sf is the target sparsity, and T is the number of pruning steps. Pruning II increases the sparsity level of neural networks faster than Pruning I, see Supplementary Fig. 10.

Deep rewiring (DeepR)12

DeepR simultaneously optimizes the connection weights and the connectivity graphs of sparsely connected neural networks. It combines gradient descent with random walk in the parameter space and guarantees connectivity under the given constraints. This is implemented by the following weight update policy applied to active connections (connections i with non-zero weights wi)

$${w}_{i}^{{\prime} }={w}_{i}-\epsilon \frac{\partial {{{{{{{\mathcal{L}}}}}}}}(f(X,{{{{{{{\boldsymbol{\theta }}}}}}}});Y)}{\partial {w}_{i}}-\epsilon \alpha +\sqrt{2\epsilon T}{\nu }_{i},$$
(5)

where ϵ is learning rate; \({{{{{{{\mathcal{L}}}}}}}}(f(X,{{{{{{{\boldsymbol{\theta }}}}}}}});Y)\) is a loss function of input X, target output Y and model parameters θ with derivative computed by backpropagation; −ϵα is a regularization term; and the noise \(\sqrt{2\epsilon T}{\nu }_{i}\) enables a random walk in parameter space, where νi is a standard Gaussian random variable and T controls strength of the noise. If \({w}_{i}^{{\prime} }\, \times {w}_{i} \, < \, 0\), deactivate connection i and set its update weight to \({w}_{i}^{{\prime} }=0\). Once a connection deactivated, a new connection \({i}^{{\prime} }\) will be randomly selected from the inactive connections, activated and initialized to \({w}_{{i}^{{\prime} }}=0\).

Sparse evolutionary training (SET)11

SET is a heuristic algorithm for training sparse neural networks with a fixed number of parameters. It starts from a random sparse network, and at each training epoch, a small fraction of connections whose weights are closest to zero are removed, and an equal number of new connections are added randomly and initialized to 0.

Recurrent network models

Neural ODE28

Recurrent neural networks with continuous dynamics of hidden neurons can be characterized by ordinary differential equations (ODEs)

$$\frac{d{h}_{t}}{dt}=f({h}_{t},{x}_{t},t,\theta ),$$
(6)

where ht is the RNN’s hidden state, and θ is model parameter. Instead of specifying a discrete sequence of hidden layers, the hidden unit dynamics can be obtained by numerically solving Eq. (6) with given inputs xt. We use the fourth-order Runge–Kutta method with a time step of 1/6 to solve the differential equations for Neural ODE.

Continuous-time RNN29

Continuous-time recurrent neural networks (CT-RNNs) have become popular due to their extensive ability to approximate dynamical time-variant systems. They usually use the ODE system to model the effects of time series on neurons

$$\frac{d{h}_{t}}{dt}=-\frac{{h}_{t}}{\tau }+f({h}_{t},{x}_{t},t,\theta ),$$
(7)

where τ is a time constant. We use τ = 1 in hand gesture segmentation task and τ = 0.5 in human activity recognition task. To simulate the differential equations for CT-RNNs, we use the Euler method, for which the time step is set to 1/6.

Measuring overall balance

To evaluate the balance of a signed directed network, we adopt a measure that satisfies transitivity and sign consistency. Similarly to the universal method27,41, we first need to quantify the balance of transitive triads (as shown in Fig. 3a), which are triads which contain only feed-forward loops (also called transitive semicycles27,41). For each type i of transitive triad, we calculate the fraction T(i) of decomposed feed-forward loops which are balanced, and then average T(i) over all triad types (i = 1, 2, 3, 4) to obtain the overall balance ratio η of the network. In our analysis, we use FANMOD42, a tool for fast detection of motifs in the network, to obtain the profile of triads and assess their balance based on the NumPy and NetworkX libraries in Python.

Tuning structural balance ratio

To generate RNNs with structurally balanced configuration, we start from a directed random network, and independently assign each edge a positive or negative sign with equal probability. To increase the global structural balance, we use the degree-preserving rewiring algorithm with rewiring probabilities determined by the local structural balance ratio χ, that is, the proportion of the balanced feed-forward motifs within the triples associated with candidate edges. Specifically, the rewiring method is inspired by simulated annealing to minimize the energy E(χ) = ∣1 − χ∣: (1) selecting two edges with uniform probability and calculating E(χ) corresponding to the current state; (2) rewiring these two edges and calculating the E(χ*) of the resulting state; (3) if E(χ*) < E(χ), then accepting the new state, otherwise accepting the new candidate state with the probability of e−βΔE, where ΔE = E(χ*) − E(χ) and β is the inverse temperature; (4) repeating the above steps while gradually increasing β, and stopping if temperature reaches the predefined value.

Motif lesion experiments

To explore the impact of unbalanced feed-forward motifs on network performance, we generate directed networks of n + 2m nodes consisting of a network core of n nodes together with m tangent feed-forward motifs. The network core comprises a random directed network the nodes of which are connected in each direction with edge density p. Tangent feed-forward motifs are so-called because they coincide with the network core at only one point, and each comprise one node randomly chosen from among the n nodes of the network core, and two nodes that are only connected to other nodes in the tangent feed-forward motif (as shown in Supplementary Fig. 4a). We set these networks as the hidden layer of RNNs, which we train on the MNIST and MG datasets with the network structure fixed. After training, we damage unbalanced tangent feed-forward motifs one by one, in a random order, by removing their edges, and then evaluate the performance of the damaged RNNs without further training.

Estimating the effect of a single feedforward loop

To estimate the effect of a single feed-forward loop with edges i → j, j → k and i → k (see Fig. 2a, b), we assume the biases of nodes j, k are zero and isolate them from other nodes. Fixing the state of node i at a constant value hi, the state of node k will approach \({h}^{k}=\sigma \left({w}_{ik}{h}^{i}+{w}_{jk}\sigma ({w}_{ij}{h}^{i})\right)\), where σ is the activation function. Using a Taylor expansion about hi = 0, the state hk can be approximated as \({h}^{k}=\sigma \left({w}_{jk}\sigma (0)\right)+\left({w}_{ik}+{w}_{ij}\cdot {w}_{jk}{\sigma }^{{\prime} }(0)\right){\sigma }^{{\prime} }\left({w}_{jk}\sigma (0)\right){h}^{i}\). Assuming that the activation function satisfies σ(0) = 0 and \({\sigma }^{{\prime} }(0)=1\), as is the case for our choice, \(\sigma (x)=\tanh (x)\), the relative effect of node i on node k can be estimated as hk/hi = wij ⋅ wjk + wik.

Data description

SMS spam classification

The SMS spam collection dataset contains 5574 tagged English messages, which are pre-processed by removing special characters, converting all texts to lowercase, extracting words with spaces, and other standard text processing procedures. The maximum length of each text is set to 25, only words that appear more than 10 times will be considered, and each word is embedded in a trainable vector of size 50. In the SMS classification experiment, we split the data into training and test sets by a ratio of 8:2.

Mackey–Glass chaotic time series prediction (MG)

Mackey–Glass time series is a benchmark task to test the forecasting performance of neural networks. It satisfies the following delay differential equation

$$\frac{dx(t)}{dt}=\beta \cdot \frac{x(t-\tau )}{1+x{(t-\tau )}^{n}}-\gamma x(t),$$
(8)

our experiments use τ = 23, n = 10, β = 0.2, γ = 0.1. For each data series, we generate \(\frac{\tau }{\gamma }=230\) random values uniformly distributed between 1.1 and 1.3, then solve Eq. (8) numerically with a stepsize of 10, with the first 1000 points discarded to eliminate initial transient. We generate a time series of length 50,000, of which 40,000 time points are used for training and the remaining 10,000 time points for testing. We predict the next 50 time steps based on the given 500 time steps, and use the mean squared error of the predicted values as a metric to measure the performance of neural networks.

Multi-task cognition (MTC)

The dataset of cognitive multi-tasks is commonly used in neuroscience studies of animals and contains 20 cognitive tasks related to working memory, decision making, categorization and inhibitory control32. We evaluate the network performance by the average of the behavioral performance across all tasks.

Hand gesture segmentation (HGS)

The gesture phase segmentation task records seven videos of people gesturing, where each sample contains 32 input features and a corresponding output phase (i.e., rest position, preparation, stroke, hold and retraction). We split the dataset into training (75%), validation (10%), and test (15%) sets, and divide the sequences of these three sets into overlapping sub-sequences of exactly 32 time steps. We evaluate the network on the validation set every training epoch, and save the weight configuration that achieves the optimal validation metric throughout the training process. At the end of training, we restore the previously saved optimal weights and evaluate the network performance on the test set.

Human activity recognition (HAR)

This task concerns the recognition of human activities, such as walking, sitting, and lying. For each sample, the input variables are pre-processed with seven features, and the output variable represents one of the seven activity categories. The data has been split into training set and test set, we select 10% of the training set as the validation set and align the sequences of these three sets into overlapping sub-sequences of exactly 32 time steps. We calculate the validation and test metrics after each training epoch and take the classification accuracy on the test set when the network achieves the best validation metric during the whole training process as the network performance.