Introduction

Although mass vaccination is one of the most powerful ways to quell a pandemic, it has been proven challenging to achieve universal vaccination and to predict the course of the pandemic as many sociopolitical factors come into play and variants emerge1,2,3,4. These factors include highly unequal vaccine allocation across locations5, heterogeneous vaccine acceptance across social groups3, and their mixing patterns6,7 in social and mobility networks. Here, by taking a network perspective, our study shows how this vaccination heterogeneity affects epidemic outcomes.

Our study investigates the effect of vaccination heterogeneity through large-scale epidemic simulations on the US mobility network. Departing from highly aggregated models to understand vaccination performance8,9,10,11, we employ a data-driven approach to study the impact of spatial vaccination heterogeneity. Specifically, we leverage fine-grained human mobility, vaccination, and census data in the US, along with an epidemiological model12,13,14, to illustrate how different hypothetical vaccination distributions can lead to largely different country-wide outcomes.

If vaccination heterogeneity indeed leads to different outcomes, the distribution of a marginal increase in country-wide vaccination over different administrative units should have substantial implications on case counts. Using an agent-based epidemiological model on large-scale mobility networks, we compare the following scenarios for distributing a fixed number of extra vaccines over current vaccination status in the US: uniformly increasing the vaccination rates of all administrative units, greatly increasing the vaccination rates in a small number of randomly selected units, the least vaccinated units or highly central units in the US mobility network. The simulations imply about 200% variation in overall case count reductions among these scenarios selecting the highly central units to achieve the largest case reduction.

To further explore the potential of leveraging vaccination heterogeneity to reduce case counts and to illustrate the upper bound for its impact, we develop an efficient algorithm to optimize the distribution of extra vaccines that leads to the maximum reduction in case numbers. It is computationally challenging to search over all possible vaccination strategies based on transmission simulations for 200,000 administrative units (census block groups (CBGs)). Our algorithm solves these challenges by using gradient-based optimization on a differentiable surrogate objective. We estimate that a large increase in the vaccination rates of the units selected by this algorithm can reduce the number of cases by 9.5% while fixing the overall increase in country-wide vaccination rate at 1%. Close examination of the administrative units selected by our algorithm suggests that they tend to be central units in the mobility network or surrounded by neighboring clusters with low vaccination rates. While the current literature already discusses targeted vaccination strategies15,16, only a few of these studies are as heavily reliant on granular mobility data at the CBG level as our study. Overall, our results suggest that understanding geographic patterns of vaccine uptake could be just as important as improving the overall vaccination rate.

From a policy perspective, we should not be only concerned about case counts but also about the implications of vaccination heterogeneity for equity. Hence, we examine how different distribution scenarios affect case counts across demographic and geographic groups, finding that selecting administrative units informed by our algorithm may even reduce case counts in vulnerable or disadvantaged groups more than in other scenarios.

Overall, our contribution is twofold. First, we significantly advance the understanding of the roles of mobility hubs and vaccine adoption assortativity in disease transmission through detailed CBG-level epidemic simulations using high-resolution mobility data. This process verifies hypotheses derived from theoretical literature on hub and assortativity effects, as discussed in17,18. Second, we present an algorithm that can identify the most critical locations-those that yield the largest reduction in cases with a given amount of additional vaccination for curbing disease transmission. Furthermore, our study offers strategies for accommodating various situations and priorities, such as new variants and social equity.

Results

Visualization of the prevalence of vaccination heterogeneity

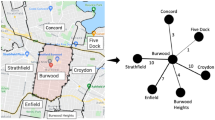
We begin by presenting the county-level COVID-19 vaccination rates to understand the prevalence of vaccination heterogeneity in mobility networks, as presented in Fig. 1. To ease the visualization, we retain the top five neighbors with the largest edge weights (Eq. (1)) in the plot.

Fig. 1: Illustration of the average vaccination rate in each county and the county-level mobility network backbone.
figure 1

a The network among all U.S. counties. b The network for Hennepin County in Minnesota (MN) and its adjacent counties. c The network for Dallas County in Texas (TX) and its adjacent counties. Nodes correspond to counties and are colored according to their vaccination rate, ranging from red (low) to blue (high), and are positioned according to the Fruchterman–Reingold layout41. The node size reflects its weighted degree centrality scores.

Full size image

We observe two drivers for the spatial heterogeneity of COVID-19 vaccination. The first driver is assortativity, a phenomenon of the clustering of similar people, either due to sorting, social contagion, or local regulations6,19. In our context, assortativity captures the fact that vaccination rates are similar among geographically close or socially connected locations20,21. Panel (a) illustrates strong homophily, shown as localized clusters of blue and red. For example, we see “blue clusters” for counties close to New York County in NY and Middlesex County in MA, while we observe “red clusters” for counties close to Dallas County in TX and Fayette County in KY. A high level of assortativity in vaccination leads to clusters of the unvaccinated, which may trigger localized outbreaks and produce more cases than expected by the overall vaccination rate.

The second network effect is the hub effect, where the vaccination rate of central and highly mobile places can have a disproportionate impact on the case count22,23. Panels (b) and (c) are the local networks for Hennepin County in MN and Dallas County in TX, respectively, where we observe that these hub counties that are connected to many other counties tend to have a higher vaccination rate than their adjacent counties. Due to various reasons, such as the urban–rural divide, hubs in the US generally have a higher vaccination rate24,25,26, which may potentially reduce the severity of outbreaks.

Baseline strategies and case-optimized strategy

We next construct the US nationwide mobility network between users’ home CBGs determined through their mobile phone usage and the points of interests (POIs) they visit on an hourly basis. We develop a fine-grained computational model based on the one proposed by 14 with CBG-level vaccination rates as its input to investigate the impact of spatial vaccination heterogeneity in the mobility network on case counts, as described in “Methods”. Note that we use two-dose vaccination rates as the input, though our results are robust when we change it to one-dose vaccination rates or booster rates. We employ Bayesian neural networks to infer CBG-level vaccination rates as only county-level vaccination rates are publicly available, but we run high-resolution simulations at the CBG level. We show that the prediction performance of this neural network model does not severely change our main conclusion. This agent-based model allows us to investigate the impact of heterogeneity in vaccination distribution on case counts. The heterogeneity we study involves various scenarios that increase the overall vaccination count by a fixed amount (1% of the US population), thus allowing for a fair comparison, but differ in how the extra vaccines are distributed among the CBGs:

  1. 1.

    Uniform: increasing the vaccination rates of all CBGs by 1%.

  2. 2.

    Random: increasing the vaccination rate of randomly chosen CBGs by 10% until an additional 1% of the US population is vaccinated.

  3. 3.

    Least vaccinated: increasing the vaccination rate of CBGs with the lowest vaccination rate in increasing order by 10% until an additional 1% of the US population is vaccinated.

  4. 4.

    Most central: increasing the vaccination rate of CBGs with the highest weighted degree centrality (see Eq. (2)) in the mobility network in decreasing order by 10% until an additional 1% of the US population is targeted. Existing studies such as11 also propose targeting central locations to substantially reduce transmission; however, they have examined this empirically at a resolution several orders of magnitude coarser than this work which covers over 200,000 CBGs across the US.

Figure 2 presents our main simulation results, given the vaccination state as of January 2022. We also tested the result as of July 2021 with the perfect vaccine efficacy assumption, the discrepancy in case counts across distributions doubles (see Supplementary Note 4). The uniform and the random selection approaches exhibit the worst outcome, with only a 2.7% reduction in case counts compared to the baseline of no extra vaccines. Selecting the least vaccinated CBGs achieves a slightly better outcome, whereas selecting the most central CBGs is much more effective and reduces the number of cases by 8.1%.

Fig. 2: Simulation outcomes of five census-block-group-level targeting distributions.
figure 2

The y-axis is the relative change in case counts, which compares the simulation result of a selection approach versus the simulation result using the original vaccination rates. Error bars are standard deviations of the 25 runs of simulations.

Full size image

The variation in transmission rates induced by heterogeneous vaccination distribution suggests that there may exist a hypothetical distribution that leads to a maximal reduction in the case count given the same fixed increase in the overall vaccination rate. Thus, we study a case-optimized strategy as follows.

This optimal distribution essentially boils down to the selection of a small number of CBGs whose vaccination rates should increase subject to the constraint in the number of extra vaccines. Deriving the case-optimized CBG targets is a significant computational challenge because it involves testing numerous combinations of tens of thousands of CBGs out of over 200,000 CBGs in total. Our main technical contribution here is an algorithm that addresses this challenge by using the projected gradient descent27 to optimize a computationally feasible surrogate objective.

As shown in Fig. 2, targeting these CBGs reduces the number of cases by 9.5% over the most central CBG selection scenario. This result implies a promising method for identifying a small number of the most pivotal locations. We show that, when targeted, the increased vaccination in these locations has a disproportionate effect on suppressing the epidemic.

We perform a series of robustness checks in Supplementary Note 4 and demonstrate our results remain consistent across various settings.

Impact on demographic and geographic subgroups

Our proposed strategy emphasizes that, besides decreasing cases, it is crucial to safeguard vulnerable populations and not exacerbate existing social inequalities. For instance, prioritizing vaccination efforts for the elderly, who are more susceptible to severe illness or death, could be of greater importance. Moreover, it is imperative to avoid a vaccination campaign that solely benefits high-income groups. The case-optimized strategy we explore in this study focuses on a limited number of locations, particularly hub cities, making it essential to assess its effects on various sub-populations, with an emphasis on disadvantaged groups. To further evaluate our strategy’s influence on equity, we provide simulated case counts across diverse demographic and geographic categories in Fig. 3. Here, we provide definitions of the subgroups:

  1. 1.

    Race. W = White, non-Hispanic; B = Black or African American, non-Hispanic, A = Asian, non-Hispanic, I = American Indian or Alaska Native, non-Hispanic, P = Native Hawaiian or Other Pacific Islander, non-Hispanic, and H (Hispanic).

  2. 2.

    Age group. We assign a numerical value to each age group provided by the US census data (9 groups in total). The first group is 0–10, followed by 20–30, ... until >80.

  3. 3.

    Income group. We assign a numerical value to each income group provided by the US census data (16 groups in total). One indicates the lowest income group, whereas 16 indicates the highest income group.

  4. 4.

    Vaccination rate group. We divide the CBG-level vaccination rates (inferred by our Bayesian deep learning algorithm) into 10 equal-sized groups. One represents the lowest vaccinated decile of CBGs, whereas 10 represents the highest vaccinated decile of CBGs.

  5. 5.

    Population density. We calculate density as the population divided by the area where both the CBG population and its area (computed using CBG polygon information) are provided by the US census data. We then divide CBG-level population densities into 10 equal-sized groups. One represents the lowest density decile of CBGs, whereas 10 represents the highest density decile of CBGs.

Fig. 3: Outcomes are conditional on different demographic and geographic groups.
figure 3

The outcomes for different racial or ethnic groups, age groups, different income groups, different deciles of census-block-group-level vaccination rate, different deciles of population density. The curves for “uniform” and “random” are largely overlapped. Error bars are standard deviations calculated in 25 runs of simulations.

Full size image

We find that this hypothetical strategy Pareto-dominates baseline strategies, i.e., the case-optimized strategy reduces comparable or more case counts than baseline strategies on every demographic group that we could examine by virtue of substantially suppressing the epidemic. Moreover, compared with the strategy targeting the least vaccinated CBGs, this hypothetical strategy can protect the CBGs with the lowest vaccination rates even better.

However, we should also note that this strategy, along with the strategy that targets the most central CBGs, tends to disproportionately benefit the high-income groups. Although this is beyond the scope of this paper, this issue can be addressed by modifying the objective function to account for vaccine equity (e.g., the variance in case reduction across subgroups).

Understanding the CBGs targeted by this algorithm

Next, we aim to understand what CBGs are selected by our case-optimized algorithm. To begin with, Fig. 4 illustrates the geographic distribution of the CBGs selected by our algorithm and compares them against those selected by the centrality-based targeting. There is only a 46% overlap between CBGs selected by the centrality-based targeting and those by our algorithm to have more than a 5% increase in their vaccination rate. Specifically, our algorithm avoids targeting highly affluent areas in the Northeast and Bay area, which are central in the mobility network but presumably have high vaccination rates. Instead, it selects more central locations with low vaccination rates in the South.

Fig. 4: Interactive map illustration for our algorithm.
figure 4

Dots are targeted CBGs with >5% increase in vaccination selected by the optimization algorithm, centrality-based targeting, or the least vaccinated targeting. Please refer to the Section “Interactive Map for Targeted CBGs” for the link to the website.

Full size image

Figure 5 provides a simple description of the optimally selected CBGs by comparing them against those not selected along two important factors for transmission: centrality and average neighborhood vaccination rate as defined by Eq. (2) and Eq. (3). Centrality affects how one case in a CBG can severely impact potentially many other CBGs, and average neighborhood vaccination rate affects how a CBG’s neighbors are vulnerable to its cases. This figure suggests CBGs with both low average neighborhood vaccination rates and high centrality are much more likely to be selected by the targeting algorithm.

Fig. 5: The kernel density estimate (KDE) plot for census block groups (CBGs) being selected by our algorithm versus those not selected.
figure 5

“log_centrality” and “neighbor_vax” represent the logarithm of weighted degree centrality of the CBG and the average neighborhood vaccination rate of its neighboring CBGs, respectively.

Full size image

To further investigate what factors influence how locations are targeted by our optimization algorithm, we deploy a random forest algorithm to interpret what features contribute more to the selection of our algorithm. We find that centrality and neighborhood vaccination rates remain the features of the largest importance scores. See Supplementary Note 5 for details.

In Supplementary Note 6, we also perform a set of experiments that further demonstrates how hub and assortativity effects have played a role in reshaping the historical COVID-19 transmission.

Conclusions

Our results from simulating 200,000 US CBGs highlight the importance of spatial heterogeneity of additional vaccine uptake. There may even be a large, untapped potential to utilize the underlying network effects and improve the effectiveness of a vaccination campaign. The optimal targeting algorithm allocates a marginal dose of vaccines to areas that tend to be more central or surrounded by CBGs that have less vaccination. These findings suggest the presence of two network-based mechanisms in transmission: hubness in the mobility network and local assortativity in low vaccination. CBGs with both such characteristics play a disproportionate role in transmission, and targeting them protects the whole population better than common strategies without necessarily disadvantaging certain social groups. These results may inform policymakers in designing geo-targeted campaigns such as vaccination advertisements or convenient vaccine stations.

Our methodology can be adapted to future pandemics by modifying several parameters that should be consistently monitored and readily available during future outbreaks. These include updating vaccination rates and tallying the number of individuals who are susceptible, exposed, infected, or recovered to accommodate new pathogens, variants, and fluctuating social conditions. In the face of future pandemics, provided the fundamental attributes of the new infectious disease are determined (i.e., suitable disease models and a plausible range of epidemic parameters are identified), we can adjust the model parameters and conduct the simulation. Although we may need to update the mobility networks based on the primary modes of transmission, models rooted in these networks will continue to be crucial for any infectious diseases. Furthermore, considering our case-optimized algorithm consistently outpaces naive baselines, it would be intriguing to investigate this method’s potential for initial dose allocation.

However, we urge that our results be carefully interpreted and applied by considering diverse contexts, socioeconomic inequalities, and other ethical concerns. Any vaccination plan must consider numerous ethical issues, such as equitable vaccine distribution, before real-world implementation. Note that the optimization algorithm discussed here is flexible and can easily incorporate societal values such as hospitalization or vaccine equity, which we leave as future directions. In addition, while our results provide valuable insights into the allocation of extra doses, policymakers should carefully consider societal factors, such as equity, when using our model as a basis for decision-making. With moderate revisions to our optimization model and a comprehensive understanding of these factors, our approach can be informative and useful. Finally, before implementing a policy informed by our algorithm, we should carefully consider how to further improve the quality of mobility and vaccination data to better the fidelity of our simulation models.

Methods

In summary, our study extended the SEIR-based model presented in14 to simulate the spread of COVID-19, incorporating the vaccination status of individuals at the CBG level, which is inferred using a Bayesian machine learning model, breakthrough infections, and reinfections. Our model aims to examine how vaccination heterogeneity affects the frequency of infections. We introduce a case-optimized algorithm that finds the optimal distribution of vaccinations to minimize the growth of cases, taking into account central hubs and assortativity of vaccination rates in mobility networks.

In “Data collection”, we discuss the data sources and the pre-processing procedure. In “Inferring CBG-level vaccination rate with machine learning”, we describe the use of Bayesian neural networks to infer the vaccination rate at the CBG level. “Constructing mobility network of CBGs” provides details on how we construct the mobility network that forms the basis for the transmission dynamics. Combining the inferred vaccination rates from “Inferring CBG-level vaccination rate with machine learning” and the mobility network introduced in “Constructing mobility network of CBGs”, COVID-19 Transmission simulation extends the model in14 by accounting for CBG-level vaccination rates, among other factors, to model the transmission dynamics. In “The case-optimized algorithm”, we design a case-optimized algorithm that explores how to reduce case counts given a limited marginal increase in overall vaccination rates, which is verified by the SEIR-based model (introduced in “COVID-19 Transmission simulation”). The results from the agent-based model can illustrate the effectiveness of the solution proposed by the algorithm.

The notation table is presented in Supplementary Note 1.

Data collection

We collect the US mobility data from SafeGraph, a company that provides aggregated data collected from mobile applications. All data is anonymized and aggregated by the company so that individual information is not re-identifiable. This dataset has been widely adopted to study human mobility patterns, particularly during the COVID pandemic14,19,28,29,30,31,32. SafeGraph receives the location data from “third-party data partners such as mobile application developers, through APIs and other delivery methods and aggregates them.” This data reflects the frequency of mobility between all POIs and the CBGs in the United States. Specifically, the data contains information on the number of people at a CBG who visit a POI on a certain day or at a certain hour. The data also contains the information for each CBG’s area, median dwell times, as well as geo-locations of all CBGs and POIs. In total, there are 214,697 CBGs and 4,310,261 POIs in the United States. We mainly use the 2019 mobility data to reflect the scenario when all businesses were to fully reopen, though we also examine 2020 and 2021 mobility data as robustness checks.

We also collect the latest US census data from the SafeGraph database (the complete US Census and American Community Survey data from 2016 to 2019). The data contains the demographic features of each CBG, such as the fractions of each sex, age group, racial and ethnic group, education level, and income level. The vaccination data come from the Centers for Disease Control and Prevention (CDC, https://covid.cdc.gov/covid-data-tracker), which provides daily vaccination records on all states except Hawaii. Note that the vaccination data from Hawaii is not available, thus excluded from our analysis. Given that it is an island with limited mobility to the rest of the US and its population makes up a tiny fraction of the US, we believe that its impact on the country-level outcomes could be marginal compared to other states. Since the vaccination rates are only available at the county level, we develop a deep learning approach to infer the CBG level using additional census demographic and spatial features.

Inferring CBG-level vaccination rate with machine learning

Since counties cover relatively large areas, with significant heterogeneity in terms of demographic factors and vaccination rates, our epidemic model is formulated at the level of CBGs, which offers a much higher resolution than county-level models and can predict epidemic growth with high accuracy. However, the CDC provides data on vaccination rates only at the county level, and fine-grained CBG-level vaccination rates are unavailable. Therefore, we train a neural network model to estimate the CBG-level vaccination rates from county-level data.

This problem is called “small area estimation”33, where the goal is to use aggregated statistics (such as county-level vaccination rate) and socio-demographic characteristics to infer corresponding statistics at a more fine-grained resolution (such as CBG-level vaccination rate). To enable accurate inferences, we use demographic and geographic features such as sex, age, race and ethnicity, income level, education level, and geographical coordinates, which are available for all the CBGs in the prediction model. Note that we acknowledge political ideology is also predictive, but we cannot use them to impute CBG-level vaccination rates as voting data are not available on the CBG level. The assumption is that CBGs that are similar in these features should have similar vaccination rates. This problem is akin to a latent data imputation problem where the observed variables are county-level vaccination rates and CBG-level features, while the latent variables are the CBG-level vaccination rates.

We design a Bayesian model shown in Fig. 6 to impute the CBG-level vaccination rates. The benefit of the Bayesian approach is that once we define the data generation process, we can compute the Bayesian posterior over the latent variables given the observed variables with standard inference methods34. We define the following data generation process: for each CBG, we observe the demographic and geographic features; the features are inputs to a Bayesian neural network35 with unknown parameter Θ, which outputs the vaccination rate of the CBG. Finally, we average the vaccination rates of all CBGs in a county to obtain the overall vaccination rate of that county. Since the posterior inference is approximate, the weighted average of CBG-level vaccination rates in a county does not exactly match the ground truth vaccination rate for that county. Thus, we rescale the inferred vaccination rates to match the ground truth county-level vaccination rate. The algorithm is run for all CBGs in the U.S. simultaneously. Finally, we further improve performance slightly by ensembling multiple inferred vaccination rates from randomly initialized approximate inference procedures. In Supplementary Note 2, we present examples of our inferred results. The interpolated CBG-level vaccination rates are used as the input for the downstream simulation tasks.

Fig. 6: A Bayesian latent variable model to impute the census-block-group-level vaccination rate from the county-level vaccination rate.
figure 6

For each county (indexed by i), we observe the county-level average vaccination rate; for each census-block-group, we observe demographic and geographic features (proportions of different sex, age, racial or ethnic, income, and education groups as well as the geo-locations). The latent variables (which we need to impute) are the vaccination rate for each census block group. We model the mapping from each census block group’s feature to vaccination rate as a Bayesian neural network with unknown parameters Θ. Given the observed variables (blue boxes), we infer the posterior distribution of the latent variables (yellow boxes).

Full size image

A major challenge is the performance evaluation because no CBG-level ground truth data is available. We thus resort to validating the zip code level ground truth data. A county typically consists of multiple zip codes, and a zip code corresponds to multiple CBGs. We aggregate predicted CBG-level vaccination rates to the predicted zip-code-level vaccination rate. Then we compare our predictions with the ground truth on the zip code level. As of January 21st, 2022, the following states provide zip code-level vaccination rates: California, Idaho, Illinois, Maine, New York, Oregon, Pennsylvania, and Texas. We thus test the model prediction on the value from these states. Our approach has a mean absolute error, or MAE (weighted by zip code population) of 8.9%, which accounts for 9.1%’s improvement over directly using the county-level vaccination rates on the relative scale. In Supplementary Note 2, we provide more details of this validation process and results.

Constructing mobility network of CBGs

We first construct a mobility bipartite network between US CBGs and POIs. The edges in the bipartite network are between POIs (denoted by the set \({{{{{{{\mathcal{P}}}}}}}}\)) and CBGs (denoted by the set \({{{{{{{\mathcal{C}}}}}}}}\)). The edge weight between a POI \(p\in {{{{{{{\mathcal{P}}}}}}}}\) and a CBG \(c\in {{{{{{{\mathcal{C}}}}}}}}\) corresponds to the number of people who live in CBG c and visit POI p. The bipartite network can vary over time according to the SafeGraph mobility data, and in fact14 used the hourly mobility data, which provides a snapshot of the network per hour. However, for the purposes of simplicity and our particular study, we have elected to amalgamate the hourly visitation data between all CBG–POI pairs, thus creating a single bipartite network that represents average mobility throughout the year. This methodology aligns with our aim to elucidate and harness the overarching influence of vaccination heterogeneity on disease transmission. While recognizing that specific seasonal patterns in mobility could alter our estimations, we posit that such modifications will not impede our primary objective of studying vaccination heterogeneity. Importantly, our approach retains a high degree of adaptability and can be applied in real-time to accommodate fluctuations in the mobility network.

Given the bipartite network described above, the actual undirected mobility network among CBGs, which forms the basis of the analysis, is derived by projecting the aforementioned bipartite graph, considering the areas and dwell times of each POI. Effectively, we assume that the edge weight between two CBGs is measured by the total number of co-visits of their residents. In this network, the edges between two CBGs c and \({c}^{{\prime} }\) have weights as

$${w}_{c,{c}^{{\prime} }}={\sum }_{p\in {{{{{{{\mathcal{P}}}}}}}}}\frac{{d}_{p}V(c,p)V({c}^{{\prime} },p)}{{a}_{p}}.$$
(1)

where p corresponds to a POI, V(c, p) is the hourly average number of visitors from CBG c at POI p, ap is the area of POI p. dp is the probability of two people visiting the POI p at the same time, derived from the median dwell time at the POI. The edge weight is proportional to the number of people in CBG c who get infected from CBG \({c}^{{\prime} }\) assuming the equal ratio of infections across all CBGs. Given the edge definition above, we define CBG-level centrality as:

$${{{{{{{\rm{centrality}}}}}}}}(c)={\sum }_{{c}^{{\prime} }}{w}_{c,{c}^{{\prime} }}.$$
(2)

Thus, the centrality of a CBG is its weighted degree or the sum of edge weights adjacent to it or weighted degree centrality. Intuitively, a more mobile and populous CBG, or a CBG connected to many other CBGs (through mutually visited POIs), should have a higher centrality score. There are different ways of defining the edge weights. We choose this edge weight because it directly reflects the extent of transmission between two CBGs, as it corresponds to Eq. (4). Thus, a more mobile CBG is considered more central as it is more vulnerable to contracting the disease. Similarly, there are other valid choices for the centrality score36. However, since our study examines a mobility network of more than 200,000 CBGs (with edges present among a significant fraction of pairs), calculating other centrality measures (such as eigenvector centrality or betweenness centrality) becomes computationally expensive. Nevertheless, as previous work has shown, degree centrality is highly correlated with other centrality measures, specifically eigenvector centrality37. Thus we do not expect the choice of centrality measure to significantly change our conclusions. In general, our observation is that CBGs that are closer to large cities (such as Los Angeles and San Francisco in California and Dallas and Houston in Texas) have larger centrality scores.

Figure 5 also includes the average neighborhood vaccination rate, which is defined as an average weighted by edge weights to each neighbor:

$${{{{{{{\rm{neighbor}}}}}}}}\_{{{{{{{\rm{vax}}}}}}}}(c)=\frac{{\sum }_{{c}^{{\prime} }}{w}_{c,{c}^{{\prime} }}{{{{{{{\rm{vax}}}}}}}}({c}^{{\prime} })}{{\sum }_{{c}^{{\prime} }}{w}_{c,{c}^{{\prime} }}}.$$
(3)

Here \({{{{{{{\rm{vax}}}}}}}}({c}^{{\prime} })\) is the vaccination rate of CBG \({c}^{{\prime} }\). If a CBG is highly connected to many CBGs with low vaccination, it would have a low average neighborhood vaccination rate. This is an indicator of being embedded in a geographic cluster with low vaccination. It measures how severe a case in CBG c would affect people in other neighboring CBGs.

COVID-19 transmission simulation

We extend the model in14 to simulate the spreading of COVID-19. The model is essentially an SEIR model38, but it is based on the full human mobility data at the level of CBGs, and the key parameters in the SEIR model are estimated from the mobility network using machine learning tools. Susceptible individuals (S) first get exposed (E) to the disease with a certain probability after contacting infected people; then exposed people develop symptoms (I, infected) after a period of time; finally, the infected people get recovered or removed (R) after a period of time. In our model, we also include the possibility of breakthrough infections by transitioning from recovered (R) to susceptible (S). The exact details of our simulation model and points of departure from14 are described in Supplementary Note 3. Here, we briefly describe important assumptions, parameters, and the mechanics of the model.

The key difference between our algorithm and the SEIR-based model in14 is that we also incorporate the vaccination status of individuals in the model using the CBG-level vaccination rate. For example, if a CBG c has a vaccination rate vc, we assume that a fraction (αvc) of individuals in the CBG are “recovered” at time 0. This implies that the vaccine efficacy is α, which under this scenario has an “all-or-nothing” property. This definition implies that a fraction of 1 − α vaccinated people do not receive any protection from the vaccine. The remaining α fraction, however, can develop breakthrough infections, which is a separate process from the perfect protection they receive from the vaccine. The lack of more fine-grained data implies that we cannot consider heterogeneity within a CBG—we assume all individuals within a CBG have an equal probability of getting vaccinated or infected.

The number of people in CBG c who newly get exposed (and then infected) at time t from POI p follows a Poisson distribution:

$${{{{{{{\rm{Pois}}}}}}}}\left(\phi \mathop{\sum}\limits_{{c}^{{\prime} }\in {{{{{{{\mathcal{C}}}}}}}}}\frac{{d}_{p}{S}_{c}^{(t)}{I}_{{c}^{{\prime} }}^{(t)}}{{a}_{p}{N}_{c}{N}_{{c}^{{\prime} }}}V(c,p)V({c}^{{\prime} },p)\right).$$
(4)

Definitions of the variables above are consistent with Eq. (1). Nc and \({N}_{{c}^{{\prime} }}\) are the number of people who reside in CBG c and \({c}^{{\prime} }\), respectively. We follow the convention, using \({S}_{c}^{(t)}\), \({E}_{c}^{(t)}\), \({I}_{c}^{(t)}\), \({R}_{c}^{(t)}\) to denote the number of people in CBG c who are susceptible, exposed, infectious, and removed at the time stamp (i.e., hour) t, respectively. ϕ is the transmission rate hyperparameter. The model assumes that all exposed people will eventually become infectious, and all infectious will eventually become “recovered.” Moreover, our study takes into account breakthrough infection in previously vaccinated individuals and reinfection in previously infected individuals, which were not considered in the original model in14. Reinfection in our model implies that recovered cases, either naturally or vaccine-induced, can eventually return to the “susceptible” state. Specifically, the number of people in CBG c who switch from “recovered” to “susceptible” follows a Binomial distribution:

$${{{{{{{\rm{Bin}}}}}}}}\left({R}_{c}^{(t)},\frac{1}{{l}_{imm}}\right).$$
(5)

where the parameter limm indicates the average length of the immunity period after recovery or vaccination.

We now describe the details of the parameters in the simulations. For the US country-level simulation, we set the initial ratio of infections to 0.1%, the country-wide cross-CBG transmission rate to ϕ = 1500, and within-CBG transmission to ϕ = 0.005. These numbers are the result of cross-validation from14, which has been shown to have the best fit into the real-world data. The average natural immunity period and vaccine wear-off period (limm) are set as 90 days as of January 2022; The vaccine efficacy (α) is set to be 0.7. The choice of these values is informed by their estimates in the ten major metro areas studied in14. Marginal changes to these values would not alter our main conclusions significantly. As for the hourly average number of visitors to a POI, V(c, p), we use the hourly average number of visits in 2019 rather than any other period. This choice is made explicitly to examine how vaccination heterogeneity affects the frequency of infections when human mobility returns to pre-pandemic levels.

To check the robustness of our findings, we examined the model results under different scenarios, including the aforementioned ones, in Supplementary Note 4. Here we list a few examples. First, we investigated scenarios with or without the reinfection/breakthrough infection scenario and full vaccine efficacy. These results show that our main conclusions are consistently robust—regardless of vaccine efficacy or the consideration of reinfection and breakthrough infection. The relative magnitudes of different distributions remain consistent. These simulation results also suggest that in real-world scenarios, our conclusions on the two network effects would also be likely robust to different transmission dynamics variants and vaccine efficacy levels. Finally, our main results are based on the simulations over a period of 30 days. However, simulations over a longer period lead to similar conclusions. See Supplementary Note 4 for details on the robustness checks.

The case-optimized algorithm

Due to the computational complexity of directly optimizing the allocation using the simulation model, we propose an algorithm that optimizes a surrogate objective, which serves as a suitable approximation of the simulation outcomes. We subsequently employ the simulation algorithm introduced in “COVID-19 transmission simulation” to validate the effectiveness of our optimization approach. Let u be the vector of the initial fraction of unvaccinated for each CBG (i.e., one minus the vaccination rate), and v be the increase in the vaccination rate under the campaign. Thus, u − v is the unvaccinated fraction vector after the campaign. Our goal is to find the optimal v* that decreases case counts as much as possible.

The quantity (u − v)TW(u − v) is our objective function, which captures the growth of the cases, where matrix W is \(| {{{{{{{\mathcal{C}}}}}}}}| \times | {{{{{{{\mathcal{C}}}}}}}}|\) and each element is defined by Eq. (1). In addition, we impose several feasibility constraints. Specifically, we assume that u − v ≽ 0, which means that no CBG’s unvaccination rate is negative, and v ≽ 0, which indicates that we only reduce unvaccination rate and never increase it. Since it is very difficult to decrease the unvaccation rate of a CBG by a large amount, we require v ≼ 0.1 for practical implementation, i.e., the proposed unvaccination reduction of each CBG is capped at 10%. Finally, to model finite resources, we limit the total number of vaccine doses to administer by θ, that is 〈v, m〉 ≤ θ, where each element in vector m is the population residing in its corresponding CBG. For our results, we set θ to 1% of the total population of the country (0.01 × US population); in other words, our algorithm increases the country-wide vaccination rate by at most 1%. Accordingly, we formulate the following optimization problem.

$${\min }_{v}\hskip 10pt{(u-v)}^{T}W(u-v)$$
(6)
$$s.t.\hskip 10pt\langle v,m\rangle \le \theta \hskip 1.4pc$$
(7)
$$\hskip 3.4pc u-v\succcurlyeq 0,0\preccurlyeq v\preccurlyeq 0.1$$
(8)

We begin by providing intuition for the case-optimized algorithm. First, from Eq. (4), we know that the number of people in CBG c who get infected from people in CBG \({c}^{{\prime} }\) is proportional to \(\frac{{S}_{c}^{(t)}}{{N}_{c}}\frac{{I}_{{c}^{{\prime} }}^{(t)}}{{N}_{{c}^{{\prime} }}}{w}_{c,{c}^{{\prime} }}\). Under the “perfect” vaccination (i.e., vaccinated people do not get infected), we assume \(\frac{{I}_{{c}^{{\prime} }}^{(t)}}{{N}_{{c}^{{\prime} }}}\) is highly correlated with (or approximately proportional to) the fraction of unvaccinated in \({c}^{{\prime} }\), which is (\({u}_{{c}^{{\prime} }}-{v}_{{c}^{{\prime} }}\)); and \(\frac{{S}_{c}^{(t)}}{{N}_{c}}\) is highly correlated with (or approximately proportional to) the unvaccination rate of c, which is (uc − vc). In other words, the unvaccination rate of a CBG predicts its fractions of susceptible and infected populations. Therefore, the value \(({u}_{c}-{v}_{c}){w}_{c,{c}^{{\prime} }}({u}_{{c}^{{\prime} }}-{v}_{{c}^{{\prime} }})\) reflects the transmission from CBG c to \({c}^{{\prime} }\) up to a constant. Using the matrix notation, (u − v)TW(u − v) is approximately proportional to the total transmission for all possible \(c,{c}^{{\prime} }\) pairs, or the number of new cases.

This objective function aims to consider two network effects—central hubs and assortativity of vaccination rates in mobility networks. First, the increase in the vaccination rate of a CBG (by vc) reduces the objective function by vc times the mobility centrality score of the CBG. Therefore, the optimization tends to improve the vaccination rates of more central CBGs. Second, an increase in a CBG c’s vaccination rate results in a decrease in the objective function that is proportional to \({w}_{c,{c}^{{\prime} }}({u}_{{c}^{{\prime} }}-{v}_{{c}^{{\prime} }})\) for all other \({c}^{{\prime} }\) that are connected to c. Therefore, reducing the vaccination rate of one CBG spills over to the adjacent CBGs. The spillover effect is larger if the targeted CBG c is in a cluster of CBGs with similarly low vaccination rates. Thus, the optimization can exploit the assortativity of vaccination rates by targeting clusters of low vaccination and further reducing the objective function by the spillover effect.

We solve the optimization problem by projected gradient descent27,39 At each step, we take a gradient step to minimize (u − v)TW(u − v). The resulting v might be infeasible, i.e., fail to satisfy the constraints in Eq. (7) and Eq. (8), so we project v back to the feasible set. In particular, to satisfy Eq. (7), we can compute the projection by

$${v}^{{\prime} }=\left\{\begin{array}{ll}v&{{{{{{{\rm{if}}}}}}}}\;{m}^{T}v\le \theta \\ v-\frac{{m}^{T}v-\theta }{\parallel m{\parallel }_{2}^{2}}m&{{{{{{{\rm{if}}}}}}}}\;{m}^{T}v \, > \,\theta \end{array}\right.$$
(9)

To satisfy Eq. (8), we can compute the projection by

$${v}^{{\prime}{\prime}}:=\min (\min (\max ({v}^{{\prime} },0),0.1),u).$$
(10)

Intuitively, we lower bound vc by 0 and upper bound it by the smaller of 0.1 and uc.

Formally, the algorithm is as follows:

  1. 1.

    Initialize v0, λ0 = 0, γ0 = 0;

  2. 2.

    For t = 0, … , T:

    1. (a)

      \({v}^{t+1}:={v}^{t}+{\eta }_{t}\left(2W(u-{v}^{(t)})\right.\);

    2. (b)

      Set \({v}^{t+1}:=\min (\min (\max ({v}^{t+1},0),0.1),u)\);

    3. (c)

      Set \({v}^{t+1}:={v}^{t+1}-\frac{{m}^{T}{v}^{t+1}-\theta }{{\left\Vert m\right\Vert }_{2}^{2}}m\), if mTvt+1 > θ.

The algorithm must converge with a suitably selected learning rate ηt based on standard results in optimization theory27,39 (i.e., because each step in the algorithm does not increase the L2 distance to the optimal solution). Upon convergence, the resulting vT is the optimal solution (v*) to the optimization problem in Eq. (6), as shown by the following theorem.

Theorem 1

If we choose \({\eta }_{t}=C/\sqrt{t}\) for any \(C\in {{\mathbb{R}}}^{+}\), the algorithm above converges to the global optimum of the optimization problem in Eq. (6).

Proof

We first prove that the optimization problem is convex. First, observe that the matrix W in Eq. (6) is a positive semi-definite matrix. This is because there exists matrix U such that W = UUT. Concretely, we can construct U by

$${W}_{c,{c}^{{\prime} }}=\mathop{\sum}\limits_{p\in {{{{{{{\mathcal{P}}}}}}}}}\frac{{d}_{p}V(c,p)V({c}^{{\prime} },p)}{{a}_{p}},{U}_{cp}=\frac{\sqrt{{d}_{p}}V(c,p)}{\sqrt{{a}_{p}}}.$$
(11)

Second, Eq. (7) is a linear inequality, and Eq. (8) are both linear inequalities. Therefore, the objective Eq. (6) and the constraints Eq. (7) and Eq. (8) are all convex or linear. Hence the problem is convex.

In addition, because the optimization objective Eq. (6) is a Lipschitz function, therefore, by standard results40, projected gradient descent converges to the global minimum of the optimization problem.

Note that this case-optimized algorithm assumes that the cost of vaccinating an additional person is constant. In supplementary Note 7, we introduce an approach to account for the heterogeneity of the cost term.