Abstract
Magnetic resonance imaging is a three-dimensional imaging technique, where a gradient of the magnetic field is used to interrogate spin resonances with spatial resolution. The application of this technique to probe the coherence of atoms with good three-dimensional resolution is a challenging application. We propose and demonstrate an optical method to probe spin resonances via a two-photon Raman transition, reconstructing the 3D-structure of an atomic ensemble’s coherence, which is itself subject to external fields. Our method relies on a single time-and-space resolved heterodyne measurement, allowing the reconstruction of a complex 3D coherence profile. Owing to the optical interface, we reach a tomographic image resolution of 14 × 14 × 36 μm3. The technique allows to probe any transparent medium with a resonance structure and provides a robust diagnostic tool for atom-based quantum information protocols. As such, it is a viable technique for application to magnetometry, electrometry, and imaging of electromagnetic fields.
Similar content being viewed by others
Introduction
It has always been the primary task of optics to deliver images. Three-dimensional (3D) imaging is now one of the essential tools in modern sciences, medicine, and technology. The ability to inspect the internal structure of an object not only fulfills the basic cognitive curiosity but also constitutes a robust and direct diagnostic method. Tomography, which nowadays appears in a plethora of variants, revolutionized medicine and has been widely adopted in natural and applied sciences1,2,3,4. The key example is magnetic resonance imaging (MRI)5,6 that allows volumetric inspection of biological samples5,6 by detecting space-dependent radio frequency signals generated by precessing nuclear spins placed in a magnetic field gradient. An optical version of MRI has been proposed as a technique to dramatically increase the spatial resolution of the system7. In physics, 3D imaging has been used to reveal and study microscopic features in quantum fluids8 and solids9,10,11, to detect and localize single spins12,13,14,15, and to visualize classical10,16,17,18 and quantum electromagnetic fields19.
Here we employ a cold-atoms-based memory and demonstrate a method to optically resolve a three-dimensional spatial distribution of coherence between two atomic spin states, in its full complex form. We directly demonstrate and benchmark the sensitivity of our method by phase-modulating the coherence with a predetermined pattern. Finally, we show the ability to detect a magnetic field structure by reconstructing its phase footprint on the coherence. This achievement is relevant to all countless protocols that process quantum information carried in such a coherence20,21,22. Via this coherence, we are able to measure external fields influencing the atoms in three dimensions, which in our case include optical and magnetic fields23,24, but possibly could be extended to microwave or terahertz sensing via Rydberg states25,26, imaging of interactions27,28, or as an alternative technique and a three-dimensional extension to quantum gas microscopes29,30. The technique could also be mapped to solid-state resonant systems that can be optically probed, including the example of color centers in diamonds31,32. Furthermore, our method is a practical tool for testing optical quantum memories, providing means to verify phase homogeneity, which is particularly relevant if specific interference of emissions from all atoms is desired, such as for example in the case of superradiance.
Results
Operating principle
The key idea behind our method is to map the coherence to light in a way that preserves information about its three-dimensional structure. Many atom-light interfaces, such as Electromagnetically Induced Transparency (EIT)33, Autler-Townes splitting21, or Raman scattering34 allow restoring the shape of the coherence in dimensions transverse to the propagation axis. The structure along the ensemble is however lost in the mapping process. The way to prevent this is to alter the atoms-to-light mapping process, so different components along the propagation direction are mapped to different frequency components of the emitted light. This is one of the key features of the Gradient Echo Memory (GEM)35 protocol in which atomic transition frequencies are altered by a magnetic field gradient causing Zeeman shifts. For a linear gradient, during the readout, the coherence along the ensemble is mapped linearly to the spectrum of the emitted signal pulse. At the same time, the transverse components are directly mapped to the corresponding distribution of the optical field. In reciprocal coordinates the readout process couples Fourier components of atomic coherence with wavevector (kx, ky, kz) to chunks of readout signal light described by coordinates (kx, ky, tR), i.e., emitted at a certain time with matching perpendicular wavevector components. The longitudinal direction z is both the direction of the propagation of the signal, as well as the direction of the magnetic field gradient. The correspondence between the time tR and kz is determined by the amount of time a magnetic field gradient β = ∂zBz needs to decelerate the atoms with momenta ℏkz to rest. In the spectral and real space coordinates this correspondence translates directly to the linearly changing Zeeman shift caused by the gradient μBβz ↔ ωℏ, where μB is the Bohr magneton. By measuring the amplitude and phase of the signal light as a function of (kx, ky, tR) all the information on initial atomic coherence can be recovered.
Protocol
In order to recover the profile of the atomic coherence from the optical measurement, we need to first understand the intricacies behind the interaction. In essence, the spatial dependence will be recovered by means of a multi-dimensional Fourier transform. However, effects such as diffraction necessitate careful theoretical treatment. To simplify the derivation of position-dependent coupling factors and phases introduced by diffraction let us consider the following protocol. At time t = 0 we are given an atomic sample with an unknown coherence ϱhg(x, y, z) between two levels \(\left\vert \,{{\mbox{g}}}\,\right\rangle\), \(\left\vert \,{{\mbox{h}}}\,\right\rangle\) (see Fig. 1a) that we assume to be long-lived. The coherence must be magnetically sensitive i.e. by applying a magnetic field gradient along the ensemble we are able to introduce a position-dependent phase to the coherence. Specifically:
where ωL = μBβ(t)(z − zg)/ℏ is the time and space-dependent Larmor frequency, with β(t) denoting the gradient along z and zg the point in space where splitting vanishes (naturally outside atomic ensemble due to bias field). This equation can be readily solved to yield
with \(\phi (z,t)=(z-{z}_{{{\mbox{g}}}})\int\nolimits_{0}^{t}\beta (t^{\prime} )dt^{\prime}\) denoting spatiotemporal GEM phase shift. We chose to split the total phase shift into a sum of dominant linear terms and corrections \(\phi (z,t)=\bar{\beta }zt+{\bar{\omega }}_{{{\mbox{L}}}}t+{{{{{{{\mathcal{O}}}}}}}}(z,t)\).
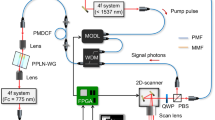
a Light-atoms interface used to generate, modulate and retrieve the atomic coherence (spin wave). The right-hand circularly polarized (σ+) control (red) and left-hand circularly polarized (σ−) signal (yellow) fields couple a two-photon transition \(\left\vert \,{{\mbox{h}}}\,\right\rangle \to \left\vert \,{{\mbox{g}}}\,\right\rangle\) between states of total angular momentum F = 2 and F = 1, respectively. This enables the mapping of the signal field onto atomic coherence. The off-resonant AC-Stark linearly polarized (π) laser (pink, SSM) is used to imprint phase profiles onto the created coherence. b The light emitted from the atomic cloud that stores a phase-modulated (QOT UW inscription) atomic coherence is detected in the far field of the ensemble using a spatially-resolved heterodyne detector enabled by the interference of the signal (sig) light with a local oscillator (LO). The temporal shape of the emitted signal contains information associated with the longitudinal coherence wavevector. The three-dimensional Fourier transform (represented as FFT block) of the collected heterodyne frames allows the reconstruction of the atomic coherence. The coherence can be created by sending to the atoms an input signal (sig-in) accompanied by a control field (ctrl) pulse.
At the time tR we send a short strong control pulse (red arrow in Fig. 1b) through the atomic ensemble that converts the coherence ϱhg to signal light Ωs. The control pulse with Rabi frequency ΩC and signal light with Rabi frequency Ωs together drive a two-photon transition from \(\left\vert \,{{\mbox{h}}}\,\right\rangle\) through \(\left\vert \,{{\mbox{e}}}\,\right\rangle\) to \(\left\vert \,{{\mbox{g}}}\,\right\rangle\), as depicted in Fig. 1a. We assume that both fields are co-propagating along z. In GEM protocol we work far from resonance (Δ/Γ > optical depth, with Δ being single photon detuning and Γ being the decay rate of the \(\left\vert \,{{\mbox{e}}}\,\right\rangle\) state), thus we neglect the single photon absorption and dispersion of the signal field. Under those conditions, the growth of the signal field Ωs along the atomic ensemble is governed by the equation:
where n(x, y, x) is the atomic density, dge is the relevant transition dipole moment, and k0 is the signal field wavevector length. For simplicity, we assume that the change of coherence due to the two-photon transition, expressed by the equation \({\dot{\varrho }}_{{{\mbox{hg}}}}=-{{{{{{{\rm{i}}}}}}}}{\Omega }_{{{\mbox{s}}}}{\Omega }_{{{\mbox{C}}}\,}^{* }/(4\Delta +2{{{{{{{\rm{i}}}}}}}}\Gamma )\), can be neglected, and we combine the coherence term with atomic density into a spin wave: \({{{{{{{\mathcal{S}}}}}}}}(x,y,z)=n(x,y,z){\varrho }_{{{\mbox{hg}}}}(x,y,z)\). Then equation (3) is integrated with two steps. First, transverse dimensions x and y are Fourier transformed. This affects only the diffraction term \({\nabla }_{\perp }^{2}\to -{k}_{\perp }^{2}\). We obtain:
Next, we integrate the equation along the atomic cloud, extending from −L to 0:
where the source term \(\tilde{{{{{{{{\mathcal{S}}}}}}}}}\) is a Fourier transform of the spin wave along x and y:
In equation (6) the z integral can be extended to infinity, since the source term is anyway nonzero only inside the atomic cloud. The \(\bar{\beta }zt\) term of GEM phase shift ϕ(z, t) enables recasting the integral into a 3D Fourier transform:
where we explicitly write the dominant part of the \({{{{{{{\mathcal{O}}}}}}}}(z,t)\) GEM phase correction which is a result of the slow decay of the magnetic field gradient β(t) = β0 − ξt with ξtR ≪ β0.
Now the above relation is reversible. In the experiment, we use spatial heterodyne detection to measure the amplitude and phase of the read-out light Ωs in the far field for each value of tR, i.e., exactly the left-hand side of the above equation. To recover the atomic part \({{{{{{{\mathcal{S}}}}}}}}(x,y,z)\) a series of multiplications and inverse Fourier transform is simply applied. Proper operation of the algorithm requires calibration of both the essential (such as the gradient) as well as nuisance (such as the rate of gradient decay) parameters.
Implementation
The base of the experiment is a pencil-shaped (10 × 0.3 × 0.3 mm3) cloud of 87Rb atoms formed in a magneto-optical trap (MOT) placed in a constant magnetic field along z-axis: \({{{{{{{\bf{B}}}}}}}}=\hat{z}{B}_{{{\mbox{0}}}}\), with B0 ≈ 1G. Atoms released from the trap are optically pumped to \(\left\vert \,{{\mbox{g}}}\right\rangle =5{{{\mbox{S}}}}_{{{\mbox{1/2}}}},{{\mbox{F}}}=2,{{{\mbox{m}}}}_{{{\mbox{F}}}}=2\) state, where F denotes the total angular momentum and mF denotes a projection of the total angular momentum onto quantization (z) axis.
After pumping, a strong atomic coherence ϱhg between \(\left\vert \,{{\mbox{g}}}\,\right\rangle\) and \(\left\vert \,{{\mbox{h}}}\right\rangle =5{{{\mbox{S}}}}_{{{\mbox{1/2}}}},{{\mbox{F}}}=1,{{{\mbox{m}}}}_{{{\mbox{F}}}}=0\) states is generated in a Λ scheme with excited state \(\left\vert \,{{\mbox{e}}}\right\rangle =5{{{\mbox{P}}}}_{{{\mbox{1/2}}}},{{\mbox{F}}}=2,{{{\mbox{m}}}}_{{{\mbox{F}}}}=1\), coupled with mutually coherent input signal pulse (at \(\left\vert \,{{\mbox{g}}}\,\right\rangle \to \left\vert \,{{\mbox{e}}}\,\right\rangle\) transition) and the control beam (at \(\left\vert \,{{\mbox{e}}}\,\right\rangle \to \left\vert \,{{\mbox{h}}}\,\right\rangle\) transition), as shown in Fig. 1a.
To benchmark the tomography protocol we generate a flat atomic coherence across the whole atomic ensemble by writing in a very short 200 ns input signal pulse accompanied by a control pulse of the same duration. Such a short pulse populates spin waves along the entire length of the cloud evenly, as the bandwidth of the input signal pulse is much larger than the magnetically (inhomogeneously) broadened two-photon absorption spectrum of the cloud. This was verified in the measurement shown in Fig. 2a where we compare the Fourier magnitude of heterodyne detected input and output signals. Here, we used a single point, differential photodiode (DPD) detector. The measurement yields bandwidths of about 8 MHz for the input signal and about 1.4 MHz for the registered output signal that directly corresponds to the GEM bandwidth induced by the Zeeman splitting gradient of around 2π × 1.4 MHz cm−1. The Fourier magnitude of the input signal is flat across the GEM spectrum which guarantees the creation of a flat spin wave. The narrow peak visible around 25 MHz corresponds to the two-photon clock transition mF = 1 → mF = −1 that due to the same Zeeman shift for the ground state sublevels is not affected by the magnetic field. Moreover, in Fig. 2b we show a zoomed-in plot of the Fourier magnitude of the read-out signal that corresponds to the (x, y)-averaged atomic density along the z-axis.
a Amplitude of 200 ns write-in pulse (blue) and read-out signal (red) measured with heterodyne detection. The spectrum of the write-in signal is much wider than the bandwidth of the atomic cloud. The Zeeman splitting between the two-photon clock transition (mF = 1 → mF = −1, the narrow peak) and the memory transition (mF = 2 → mF = 0), caused by the magnetic field bias, is also visible. b Zoomed-in spectrum of the read-out signal from panel a. c Temporal shape of the signal pulse registered by a point heterodyne (DPD). The red-shaded region represents the control pulse gating in the camera measurement.
For the full 3D reconstruction of \({{{{{{{\mathcal{S}}}}}}}}(x,y,z)\) we replaced the DPD with an sCMOS camera located in the far field of the ensemble with an effective focal length of about 250 mm. The two components of the heterodyne optical signal are registered on two separate regions of the camera that are then precisely aligned and subtracted to yield differential images. The camera has a very limited temporal resolution (exposure time of the order of 1 ms corresponds to 1 kHz bandwidth) which would spoil the z-resolution. However, in GEM the temporal structure of the read-out signal can be probed using a very short control pulse, as illustrated in Fig. 2c where we show the temporal shape of the typical heterodyne trace registered by the DPD with the sampling period represented by ht red-shaded region. The full 3D spin wave tomography is then realized in a sequence of measurements. In a single step, the control is turned on for only 200 ns, during which the read-out signal is generated and registered by the camera. For each probing time tR we collect 100 frames that are Fourier-filtered and coherently averaged in real time. The filtering and averaging strongly decrease the noise that is not correlated with the signal. The Fourier filtering step in this coherent detection process corresponds to only taking into account the signal which originated from the atoms and neglecting the components that could not be created within the cloud transverse area. Then, to reconstruct the entire \({{{{{{{\mathcal{S}}}}}}}}(x,y,z)\), we register a read-out signal for 600 distinct control pulse delays at a step of 100 ns. Finally, we get a three-dimensional array, which is a full Fourier transform of the spin waves stored in the atomic ensemble.
Calibration
The correct 3D reconstruction of the spin wave phase and amplitude requires calibration of the heterodyne camera setup. To benchmark and calibrate our device we use an ac-Stark spatial spin wave phase modulator (SSM). Using a spatial light modulator (SLM) and the camera, we are able to prepare a beam with an arbitrarily chosen intensity distribution, which illuminates atoms for 3 μs after creating the coherence. Thanks to the ac-Stark effect, the atomic coherence gets an additional phase which is proportional to the intensity of illuminating light. A detailed description of this technique can be found in the works that utilize SSM for various protocols36,37,38.
Figure 3a presents a checkerboard intensity profile of the ac-Stark beam, which we use for calibration. Figure 3b shows the phase cross-section of the full Fourier transform of the signal registered by the camera (without any compensation). In Fig. 3d we show a corresponding result of numerical simulation. In both cases, the checkerboard can be recognized, but the retrieved image is blurred. In order to obtain a sharp pattern, two phenomena must be taken into account. The first one is diffraction which manifests as an additional quadratic phase in a Fourier domain that each slice attains during propagation. The phase is \((z-{z}_{{{\mbox{0}}}})({k}_{x}^{2}+{k}_{y}^{2})/(2{k}_{{{\mbox{0}}}})\), where k0 is the wave number of emitted signal and kx,y are transverse components of the wavevector. In real space, this results in the blurred retrieved distribution in (x, y) subspace. The second phenomenon is caused by a slow decrease in magnetic field gradient strength during the read-out process. This effectively chirps the output signal. In other words, the signal gets an additional quadratic phase in the temporal domain, that results in a blur in z-direction. The temporal phase to be compensated is ζt2 with ζ = − 0.01rad × μs−2. Figure 3c (and numerical simulation in Fig. 3e) presents the retrieved phase checkerboard pattern after both compensations. We finally see that the image is in focus and sharp. The parameters (z0 and ζ) for optimal phase profiles have been determined to obtain the best sharpness of the resulting images. Moreover, as the test pattern is prepared in real space coordinates, the calibration procedure also yields the scaling factors and rotation for x, y, z axes. For this measurement, we extended the measurement time window by collecting data for 1000 control pulse delays spanning a range of 100 μs. The absolute phase value is obtained by subtracting the reference (ref) image that was acquired without the SSM modulation. The amplitude and the phase images are masked to display only the points that correspond to an atomic coherence magnitude much above the noise level \(| {{{{{{{{\mathcal{S}}}}}}}}}^{{{{{{{{\rm{ref}}}}}}}}}(x,y,z)| > 0.1\) and thus with a well-defined phase.
a Checkerboard phase profile used for calibration imprinted onto atomic coherence before reading out the signal. b The phase of raw three-dimensional Fourier transform of the read-out signal. c The phase of the three-dimensional Fourier transform of the read-out signal with compensation of both diffraction and temporal phase. The right column (d, e) corresponds to a numerical simulation of the results from the left column (b, c). All panels share the same color scale.
Exemplary results
With the calibration completed, we finally show some exemplary reconstructed phase and amplitude patterns of the atomic coherence. Figure 4 shows retrieved phase and amplitude profiles of a flat spin wave phase modulated with an inscription “QOT UW” (abbreviation of Quantum Optical Technologies, University of Warsaw). Figure 4a represents the displayed SSM pattern in phase (rad) units. In Fig. 4b we show the retrieved phase profile that well matches the target profile. Additionally, in Fig. 4c we show retrieved spatial amplitude which in this case (flat spin wave) corresponds to the atomic concentration. The full three-dimensional distribution of reconstructed phase and amplitude in the form of interactive visualization and a movie is available in Supplementary Data 1 and Supplementary Movie 139.
a “QOT UW” inscription phase profile imprinted onto atomic coherence. b Phase of three-dimensional Fourier transform of the measured signal with compensation of both diffraction and temporal phase. c Amplitude of fully compensated three-dimensional Fourier transform of the signal, which corresponds to atomic concentration.
To demonstrate the ability to reconstruct an amplitude pattern of the spin wave we replace the flat spin wave with a modulated one. This is accomplished by using two short (200 ns) input signal pulses (200 ns) separated by a delay of δt = 8 μs. The spectrum of two pulses of the same shape yet different amplitudes, separated in time by δt is a phase and amplitude modulated single pulse spectrum, given by the Fourier transform:
Due to the spectrum-to-position mapping feature of GEM40,41 combined with the large input signal bandwidth (see Fig. 2) this yields uniformly modulated coherence \({\varrho }_{{{\mbox{hg}}}}\propto (1+\alpha {{{{{{{{\rm{e}}}}}}}}}^{2\pi {{{{{{{\rm{i}}}}}}}}{\delta }_{t}\beta z})\). Figure 5a presents a two-dimensional magnitude slice ∣ϱhg(x, z)∣ of the retrieved and fully compensated spin-wave pattern normalized to a flat spin-wave: \({\varrho }_{{{\mbox{hg}}}}(x,y,z)={{{{{{{\mathcal{S}}}}}}}}(x,y,z)/{{{{{{{{\mathcal{S}}}}}}}}}^{{{{{{{{\rm{ref}}}}}}}}}(x,y,z)\). The magnitude, as expected, resembles a modulus of cosine function \(| {\varrho }_{{{\mbox{hg}}}}(x,z)| \propto | \cos (2\pi \delta t\beta z)|\) as the relative amplitude ratio is close to unity α ≈ 1. Figure 5b represents the normalized absolute value of the coherence slice ∣ϱhg(x, z)∣ averaged over the x-axis.
Slice of fully compensated three-dimensional Fourier transform of the signal corresponding to the coherence generated by two 200 ns input signal pulses separated by 8 μs. a Magnitude of two-dimensional z-x slice of the normalized spin wave \({{{{{{{\mathcal{S}}}}}}}}(x,y,z)/{{{{{{{{\mathcal{S}}}}}}}}}^{{{{{{{{\rm{ref}}}}}}}}}(x,y,z)\). b Average of the magnitude over the x-axis, revealing the amplitude modulation. The shaded region represents the standard deviation of the sample’s average.
Let us now shortly discuss the resolution limitation of the demonstrated 3D imaging method. The resolution in the perpendicular coordinates (x, y) is limited by the optical imaging system, namely its numerical aperture. From the calibration image in Fig. 3c, we can estimate the resolution as the half-width of the phase slope, which amounts to about 1 px. That equals to δx, δy ≈ 14 μm. The resolution along the propagation axis is however limited by the duration of the measurement window Tmeas = 100 μs that yields the minimal width of a feature in the spectral domain δω ≃ 2π × 1/T, combined with the magnitude of the magnetic field gradient μBβ/ℏ = 2π × 1.4 MHz cm−1 that facilitates the spectrum-to-position mapping μBβz/ℏ ↔ ω. The longitudinal resolution could be thus estimated by taking half of the inverse of the product of the measurement window and Zeeman splitting gradient: δz ≃ 0.5/(TmeasβμB/ℏ) ≈ 36 μm. In the calibration images (Fig. 3c) we see that the width of the phase slope in the z-direction spans approximately 2 px. This yields 44 μm of resolution. The maximal duration of the measurement window is in fact limited by the thermal motion of the atoms inside the ensemble42,43. By measuring the output signal intensity for a range of storage times (time between creation and retrieval of the coherence) we estimate that after 120 μs the read-out efficiency drops by 50%, which corresponds to an ensemble with a temperature of T = 265 ± 15 μK (see Methods). This is significantly larger than a typical ultracold system such as a Bose-Einstein condensate (with Rb atoms), which demonstrates that our method does not require extreme levels of optical cooling, and performs excellently with only roughly Doppler-limited cooling.
Finally, we demonstrate the potential for application in 3D magnetometry by detecting a spin wave phase modulation caused by the magnetic field generated by a small coil placed above the atomic ensemble (outside the vacuum chamber). The coil is turned on for a short period in the sequence after the creation of the coherence. The inhomogeneous magnetic field generated by the coil imprints a phase that is proportional to the total magnitude of the magnetic field ∣B∣ and the interaction time tc. The accumulated phase is \(\varphi ={\mu }_{{{{{{{{\rm{B}}}}}}}}}| {{{{{{{\bf{B}}}}}}}}+\hat{z}{B}_{0}| {t}_{{{{{{{{\rm{c}}}}}}}}}/\hslash\). The presence of the constant magnetic field along the z-axis makes the phase sensitive to mostly the changes of the field along the z-axis. However, one could easily imagine a more advanced protocol in which for the time of the measurement the constant field component is switched off. In such a scenario additionally to the phase modulation, one should observe amplitude modulation caused by the atomic spin rotation that yields different projections onto the z-axis and modifies the read-out process efficiency (the coherence is partially transferred to a different magnetic sublevel, that is not coupled by the control laser). Figure 6 shows the retrieved phase profile of the magnetically modulated coherence. The constant phase value lines correspond to the constant values of the local magnetic field.
Conclusions
We have demonstrated how to reconstruct a 3D complex spatial distribution of atomic coherence stored in the atomic ensemble. Our method employs a magnetic field gradient to map the longitudinal components of the coherence onto the optical signal frequency. A single spatiotemporally resolved heterodyne measurement of the signal light allows reconstruction of the full complex distribution of the atomic coherence S(x, y, z) = n(x, y, z)ϱhg(x, y, z). The unwinding of phase accumulated due to diffraction and compensating for distortions enables the faithful reconstruction of the complex atomic coherence.
Here, for the detection, we use a time-gated camera that requires many (short) measurements corresponding to different components in the reciprocal space of the propagation axis. However, a 2D array of photodiodes coupled with fast analog to digital converters would allow a single-shot measurement of the full 3D distribution. Moreover, a much simpler 1D array could be used in a hybrid measurement scheme with one of the axes resolved using a rainbow heterodyning technique44 enabled by a multi-frequency LO with a frequency gradient along the given (orthogonal to the array) axis. Finally, the demonstrated 3D magnetometry protocol could be extended to enable a 3D tomography of electric and electromagnetic fields in the microwave regime45, opening a new kind of atom-based metrology. Although our demonstration covers a millimeter-scale cold ensemble the protocol could be implemented in larger systems such as glass cells containing warm atoms, enabling centimeter-scale tomography. Beyond measuring external influences, the three-dimensional structure of Rydberg-atom interactions and propagation of Rydberg polaritons could be interrogated with the presented method, in order to generate exotic states of matter such as Efimov states46 efficiently.
Methods
Quantum memory setup
The GEM is based on a cold rubidium-87 ensemble prepared in a magneto-optical trap (MOT). The MOT utilizes quadruple coils and 3 pairs of counter-propagating trapping and cooling beams, which generate a strong symmetric trapping potential in the x and y axes. The trapping potential along the propagation (z) axis is much weaker. The resulting ensemble is thus elongated in the z-direction with approximate dimensions of 10 × 0.3 × 0.3 mm3. The trap is held in a bias magnetic field along the z-axis of \({{{{{{{\bf{B}}}}}}}}=\hat{z}{B}_{{{\mbox{0}}}}\), with B0 ≈ 1 G, that cancels the magnetic sublevels degeneration. After the trapping period (ca. 20 ms) we optically pump the atoms to \(\left\vert \,{{\mbox{g}}}\right\rangle =5{{{\mbox{S}}}}_{{{\mbox{1/2}}}},{{\mbox{F}}}=2,{{{\mbox{m}}}}_{{{\mbox{F}}}}=2\) state. This is achieved by illuminating the cloud with two laser beams for 15 μs. The first beam at 795 nm is tuned to 5S1/2, F = 1 → 5P1/2, F = 2 transition and illuminates the cloud from 4 sides. The beam provides hyperfine pumping by emptying the 5S1/2, F = 1 ground level. The second σ+ circularly polarized beam at 780 nm is tuned to 5S1/2, F = 2 → 5P3/2, F = 2 transition and illuminates the atoms along the propagation axis, providing magnetic sublevel pumping within the 5S1/2, F = 2 manifold, ideally populating only the \(\left\vert \,{{\mbox{g}}}\,\right\rangle\) state. The GEM coils are square-shaped with 10 cm side length, and are separated by 18 cm. They produce a linear magnetic field gradient along the cloud of approximately 1Gcm−1, which can be rapidly (0.35G cm−1 μs−1) switched to the opposite.
Heterodyne camera
The heterodyne camera setup incorporates a single Scientific-CMOS (sCMOS) camera (Andor Zyla) located in the far field of the atomic ensemble. The camera pane is divided into two regions (two ports of the heterodyne) that are precisely aligned and subtracted during measurements. The local oscillator (LO) is derived from the same laser as the control and signal fields, and is shifted in frequency by around 1 MHz. Moreover the LO is slightly angled with respect to the signal field, which produces spatial interference fringes in the measurement (spatial heterodyne). The spatial and temporal frequency shifts allow us to separate the genuine signal from background noises. The differential heterodyne frames are coherently averaged for each measurement point. The averaging is possible thanks to an additional reference frame preceding each signal frame. For this, we set the camera in the Particle Imaging Velocimetry (PIV) mode which enables the collection of two frames separated by a very short delay (2 μs). The first frame collects light from the incoming signal pulse that is used to create atomic coherence, and provides a phase reference for the second frame containing the read-out signal. For coherent averaging, we first unwind the phase of each signal frame according to the reference frame and then simply sum all the signal frames for a given measurement time tR. It is worth noting here that the phase fluctuations that we are compensating this way are solely caused by the signal-control-LO optical path length difference fluctuations, and not the laser itself (as all the beams are coming from the same laser, and the global phase fluctuations cancel out in the heterodyne measurement).
Thermal decoherence
To estimate the rate of thermal decoherence caused by the atomic motion, we measured the output signal amplitude for a range of read-out times tR. The results are presented in Fig. 7. The measurements were performed with and without a magnetic field gradient. The thermal decoherence of spin waves in an atomic ensemble without the magnetic field gradient is well known and yields a Gaussian decay42. In the GEM, due to the magnetic field gradient, atoms traveling along the ensemble enter regions with different values of the magnetic field and attain additional phase. Namely, each group of atoms with velocity vz gains an additional phase factor of \(\exp ({{{{{{{\rm{i}}}}}}}}\beta {v}_{z}{t}_{\,{{\mbox{R}}}\,}^{2}/4)\). That, after averaging with Maxwell velocity distribution, gives additional exponential decoherence term with time in the fourth power. The full expression for the read-out decay reads:
where \({k}_{{{{{{{{\mathcal{S}}}}}}}}}\) is the spin wave wavevector, kb is Boltzmann constant, m is 87Rb mass and T is the temperature of the atomic cloud. The solid curves in Fig. 7 correspond to the above model fitted to the experimental data. From the measurement without magnetic field gradient, we recover the characteristic time τk = 173 ± 5 μs. This for the angle between the control and the write-in signal beam of 4.6mrad corresponds to a temperature of T = 265 ± 15 μK. The second measurement with the gradient turned on yields τβ = 175.4 ± 2.5 μs. To compensate for this decay in the reconstruction procedure we divide the measured signal \({{{{{{{\mathcal{A}}}}}}}}({t}_{{{\mbox{R}}}})\) by the factor ηk,β(tR).
The data (points) represents the decay of the retrieved signal field without (\(\langle | {{{{{{{{\mathcal{A}}}}}}}}}_{{{{{{{{\rm{k}}}}}}}}}{| }^{2}\rangle\), red) and with GEM protocol (\(\langle | {{{{{{{{\mathcal{A}}}}}}}}}_{{{{{{{{\rm{k}}}}}}}},\beta }{| }^{2}\rangle\), blue). The solid lines correspond to fitted theoretical curves \({\eta }_{{{{{{{{\rm{k}}}}}}}}}^{2}\) (orange) and \({\eta }_{{{{{{{{\rm{k}}}}}}}},\beta }^{2}\) (blue). Measured lifetimes are equal τk ≈ 173 μs and τβ ≈ 175 μs, which corresponds to 265 ± 15 μK. The error bars represent the standard deviation of the data.
Data availability
The data presented in the figures of this manuscript has been deposited in ref. 47.
References
Shin, S. et al. Tomographic measurement of dielectric tensors at optical frequency. Nat. Mater. 21, 317 (2022).
Engström, D. et al. Three-dimensional imaging of liquid crystal structures and defects by means of holographic manipulation of colloidal nanowires with faceted sidewalls. Soft Matter 7, 6304 (2011).
Sung, Y. Snapshot three-dimensional absorption imaging of microscopic specimens. Phys. Rev. Appl. 15, 064065 (2021).
Xiao, X., Javidi, B., Martinez-Corral, M. & Stern, A. Advances in three-dimensional integral imaging: sensing, display, and applications [Invited]. Appl. Opt. 52, 546 (2013).
Lauterbur, P. C. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature 242, 190 (1973).
Feinberg, D. A. et al. Multiplexed echo planar imaging for sub-second whole brain fmri and fast diffusion imaging. PLoS ONE 5, e15710 (2010).
Allodi, M. A. et al. Optical resonance imaging: an optical analog to mri with subdiffraction-limited capabilities. ACS Photonics 3, 2445 (2016).
Kasai, J., Okamoto, Y., Nishioka, K., Takagi, T. & Sasaki, Y. Chiral domain structure in superfluid 3He-A studied by magnetic resonance imaging. Phys. Rev. Lett. 120, 205301 (2018).
Karpov, D. et al. Three-dimensional imaging of vortex structure in a ferroelectric nanoparticle driven by an electric field. Nat. Commun. 8, 280 (2017).
Kardjilov, N. et al. Three-dimensional imaging of magnetic fields with polarized neutrons. Nat. Phys. 4, 399 (2008).
Kim, C. et al. Three-dimensional imaging of phase ordering in an Fe-Al alloy by Bragg ptychography. Phys. Rev. Lett. 121, 256101 (2018).
Rugar, D., Budakian, R., Mamin, H. J. & Chui, B. W. Single spin detection by magnetic resonance force microscopy. Nature 430, 329 (2004).
Streed, E. W., Jechow, A., Norton, B. G. & Kielpinski, D. Absorption imaging of a single atom. Nature Commun. 3, 933 (2012).
Willke, P., Yang, K., Bae, Y., Heinrich, A. J. & Lutz, C. P. Magnetic resonance imaging of single atoms on a surface. Nat. Phys. 15, 1005 (2019).
Zopes, J. et al. Three-dimensional localization spectroscopy of individual nuclear spins with sub-Angstrom resolution. Nat. Commun. 9, 4678 (2018).
Appel, P., Ganzhorn, M., Neu, E. & Maletinsky, P. Nanoscale microwave imaging with a single electron spin in diamond. N. J. Phys. 17, 112001 (2015).
Böhi, P., Riedel, M. F., Hänsch, T. W. & Treutlein, P. Imaging of microwave fields using ultracold atoms. Appl. Phys. Lett. 97, 051101 (2010).
Horsley, A., Du, G.-X. & Treutlein, P. Widefield microwave imaging in alkali vapor cells with sub-100 μm resolution. N. J. Phys. 17, 112002 (2015).
Lee, M. et al. Three-dimensional imaging of cavity vacuum with single atoms localized by a nanohole array. Nat. Commun. 5, 3441 (2014).
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nat. Photon. 3, 706 (2009).
Saglamyurek, E., Hrushevskyi, T., Rastogi, A., Heshami, K. & LeBlanc, L. J. Coherent storage and manipulation of broadband photons via dynamically controlled Autler-Townes splitting. Nat. Photon. 12, 774 (2018).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413 (2001).
Castellucci, F., Clark, T. W., Selyem, A., Wang, J. & Franke-Arnold, S. Atomic compass: detecting 3D magnetic field alignment with vector vortex light. Phys. Rev. Lett. 127, 233202 (2021).
Xu, S. et al. Submillimeter-resolution magnetic resonance imaging at the Earth’s magnetic field with an atomic magnetometer. Phys. Rev. A 78, 013404 (2008).
Jing, M. et al. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 16, 911 (2020).
Downes, L. A. et al. Full-field terahertz imaging at kilohertz frame rates using atomic vapor. Phys. Rev. X 10, 011027 (2020).
Sompet, P. et al. Realizing the symmetry-protected Haldane phase in Fermi-Hubbard ladders. Nature 606, 484 (2022).
Ferreira-Cao, M. et al. Depletion imaging of rydberg atoms in cold atomic gases. J. Phys. B-At. Mol. Opt. 53, 084004 (2020).
Bakr, W. S., Gillen, J. I., Peng, A., Fölling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 462, 74 (2009).
Cheuk, L. W. et al. Quantum-gas microscope for fermionic atoms. Phys. Rev. Lett. 114, 193001 (2015).
Balasubramanian, G. et al. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 455, 648 (2008).
Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012 (1997).
Hsiao, Y.-F. et al. Highly efficient coherent optical memory based on electromagnetically induced transparency. Phys. Rev. Lett. 120, 183602 (2018).
Guo, J. et al. High-performance Raman quantum memory with optimal control in room temperature atoms. Nat. Commun. 10, 148 (2019).
Cho, Y.-W. et al. Highly efficient optical quantum memory with long coherence time in cold atoms. Optica 3, 100 (2016).
Lipka, M., Leszczyński, A., Mazelanik, M., Parniak, M. & Wasilewski, W. Spatial spin-wave modulator for quantum-memory-assisted adaptive measurements. Phys. Rev. Appl. 11, 034049 (2019).
Mazelanik, M., Parniak, M., Leszczyński, A., Lipka, M. & Wasilewski, W. Coherent spin-wave processor of stored optical pulses. npj Quantum Inf. 5, 22 (2019).
Parniak, M. et al. Quantum optics of spin waves through ac stark modulation. Phys. Rev. Lett. 122, 063604 (2019).
Mazelanik, M., Leszczyński, A., Szawełło, T. & Parniak, M. Supplementary media for: coherent optical two-photon resonance tomographic imaging in three dimensions. figshare https://doi.org/10.6084/m9.figshare.21804069 (2023a).
Mazelanik, M., Leszczyński, A., Lipka, M., Parniak, M. & Wasilewski, W. Temporal imaging for ultra-narrowband few-photon states of light. Optica 7, 203 (2020).
Mazelanik, M., Leszczyński, A. & Parniak, M. Optical-domain spectral super-resolution via a quantum-memory-based time-frequency processor. Nat. Commun. 13, 691 (2022).
Parniak, M. et al. Wavevector multiplexed atomic quantum memory via spatially-resolved single-photon detection. Nat. Commun. 8, 2140 (2017).
Lipka, M., Mazelanik, M., Leszczyński, A., Wasilewski, W. & Parniak, M. Massively-multiplexed generation of Bell-type entanglement using a quantum memory. Commun. Phys. 4, 46 (2021).
Strauss, C. E. M. Synthetic-array heterodyne detection: a single-element detector acts as an array. Opt. Lett. 19, 1609 (1994).
Sedlacek, J. A. et al. Microwave electrometry with rydberg atoms in a vapour cell using bright atomic resonances. Nat. Phys. 8, 819 (2012).
Gullans, M. J. et al. Efimov states of strongly interacting photons. Phys. Rev. Lett. 119, 233601 (2017).
Mazelanik, M., Leszczyński, A., Szawełło, T. & Parniak, M. Data for: coherent optical two-photon resonance tomographic imaging in three dimensions. https://doi.org/10.7910/DVN/HOMGFB (2023b).
Acknowledgements
We thank K. Banaszek and W. Wasilewski for their support and K. Jachymski and S. Borówka for insightful discussions. The “Quantum Optical Technologies” (MAB/2018/4) project is carried out within the International Research Agendas program of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund. MM was also supported by the Foundation for Polish Science via the START scholarship. This research was funded in whole or in part by National Science Centre, Poland grant no. 2021/43/D/ST2/03114 and by the Office of Naval Research Global grant no. N62909-19-1-2127.
Author information
Authors and Affiliations
Contributions
M.M. and M.P. conceived the protocol and experimental implementation. M.M., A.L., and M.P. contributed to the experimental setup and data collection. M.M. analyzed the data and prepared figures with help from A.L. M.M., A.L., and M.P. developed the theory for which T.S. and A.L. performed the numerical simulations. M.M., A.L., and M.P. wrote the manuscript with contributions from T.S. M.M. and M.P. managed the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mazelanik, M., Leszczyński, A., Szawełło, T. et al. Coherent optical two-photon resonance tomographic imaging in three dimensions. Commun Phys 6, 165 (2023). https://doi.org/10.1038/s42005-023-01284-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01284-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.