Introduction

In recent years, various nano-sensors, most prominently magnetic resonance force microscopy (MRFM) and nitrogen-vacancy (NV) centers, have enabled the detection of small ensembles of electron1,2 and nuclear3,4,5 spins, partially down to the level of single spins. Translating this power from a mere detection to a three-dimensional imaging technique promises transformative applications. Three-dimensional imaging of color centers would enable selective addressing and readout of networks of coherently coupled color centers in densely doped samples6,7, or the detection of elementary particles by high-resolution mapping of the crystal strain they induce upon impact8. Applied to electron spins, it would enable three-dimensional imaging of spin-labeled proteins. Such a technique would in particular provide distance constraints for label distances of >80 Å and for proteins labeled with arbitrary many electron spins, filling two blind spots of present electron spin resonance spectroscopy. Applied to nuclear spins, it would provide an ultimate microscope, able to image within opaque samples with label-free chemical contrast.

Conceptually, the step from detection to imaging is straightforward. Applying a magnetic field gradient is all it takes to turn a magnetic resonance spectrum into a one-dimensional image. Multiple gradients along linearly independent directions can encode multi-dimensional images, most beautifully illustrated in the output of clinical magnetic resonance imaging scanners. If the gradients can be switched faster than the duration of the spectroscopy sequence, Fourier-accelerated techniques can acquire extended volumes in reasonable time9. In clinical scanners, these comprise thousands of voxels, and similar data volumes are expected for particle detectors or imaging of a densely spin-labeled protein. Yet, three-dimensional Fourier-accelerated imaging at the nanoscale has remained elusive.

Imaging by less scalable techniques has been demonstrated multiple times. Three-dimensional imaging of nuclear spins with atomic resolution has been achieved using the intrinsic field gradient emerging from the magnetic dipole field of a color center10,11. However, only the closest few nanometers around a defect can be imaged by this approach so that it is limited to intrinsic spins in the diamond so far. One-dimensional and two-dimensional12 imaging in static gradients has been demonstrated, including resolving two adjacent centers by the gradient field of a hard-drive write head13. Three-dimensional images of intrinsic electron spins in a diamond have been obtained using a static gradient positioned by a scanning probe14. Fourier acceleration has remained out of reach of these approaches where gradients cannot be switched within a spectroscopy sequence.

Fourier acceleration of imaging has been demonstrated7,9 using quickly switchable conductors as gradient sources, but experiments with nanoscale resolution have remained limited to one- and two-dimensional proofs of the concept. One-dimensional imaging in MRFM by current-driven gradients has very recently even achieved sub-Ångstrom resolution15.

Results and discussion

Device

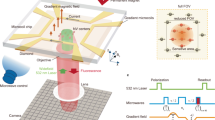
Here we demonstrate Fourier-accelerated three-dimensional imaging with nanometer-scale resolution. The key is a device to produce three linearly independent magnetic field gradients from a two-dimensional layout of conductors (Fig. 1a). Three microfabricated wires, arranged in a U-shape structure, create linearly independent gradient fields in a plane few microns beneath the structure, of around ∣∇(B ⋅ e111)∣ ≈ 2 Gμm−1 = 2 ⋅ 102 Tm−1. This device is fabricated via lift-off photolithography on a diamond substrate hosting a densely doped ensemble of NV centers (Element Six General Grade CVD diamond, [NV] ≈ 0.13 ppb, Fig. 1a). “Densely” here is to be understood in the sense that NV centers sit closer together than the diffraction limit. The U-microstructure consists of a 200 nm gold film on top of a 10 nm thick chromium layer. Each of its three arms is 5 μm long and 500 nm wide. The top arm also serves as a microwave antenna to implement single-qubit gates. We generate switchable magnetic field gradients by sending currents, labeled I1, I2, and I3 in Fig. 1a, into the three arms of the U microstructure. All currents are terminated with a 50 Ω resistance at the same vertex of the U structure. In all measurements a homogeneous bias magnetic field of B0 ≈ 76 G is applied along one of the four NV axes. This device is used to implement gradient echo pulse sequences, like the one-dimensional example shown in Fig. 1b−d. A Hahn echo sequences decouples the NV centers from static and slowly fluctuating background fields, to enable T2-limited sensing. A magnetic field gradient pulse, created by the current I1, is applied during one half of the echo sequence. This phase-encodes the position, because an NV center at point \(\bf{x}\) acquires a position-dependent phase shift

$$\phi ({{{\bf{x}}}},t)=\int\nolimits_{0}^{t}\omega ({{{{\bf{B}}}}}_{I}({{{\bf{x}}}},\tau ))d\tau \approx \omega ({{{{\bf{B}}}}}_{I}({{{\bf{x}}}}))t$$
(1)

where ω(BI(x, τ)) denotes the shift in the Larmor frequency induced by the current I and the approximation holds for pulses close to a rectangular shape. At the end of the Hahn echo sequence, this phase shift translates into an oscillatory spin signal

$$\langle {\hat{S}}_{z}\rangle (t)=\left\{\begin{array}{ll}(1+\cos (\omega ({{{\bf{x}}}})t))/2\quad &{{{\rm{trailing}}}}\,{\pi }_{x}/2\,{{{\rm{pulse}}}}\\ (1+\sin (\omega ({{{\bf{x}}}})t))/2\quad &{{{\rm{trailing}}}}\,{\pi }_{y}/2\,{{{\rm{pulse}}}}\end{array}\right.$$
(2)

For a distribution of N NV centers, the oscillatory signals of all centers will linearly superpose to a characteristic beating pattern

$$\langle {\hat{S}}_{z}\rangle (t)=\mathop{\sum}\limits_{{{{{{\bf{x}}}}}}_{{{{\rm{NV}}}}}}\left(1+ \cos (\omega ({{{{\bf{x}}}}}_{{{{\rm{NV}}}}})t)\right)/2N$$
(3)

(assuming a trailing πx/2 pulse). The various ω(xNV) can be recovered from this signal by an inverse Fourier transform, creating a one-dimensional image of the NV centers Fig. 1d. In the terminology of magnetic resonance imaging, the time domain of our experiment is k-space, whereas the frequency domain is real space.

Fig. 1: Experimental setup and one-dimensional magnetic resonance tomography of NV centers.
figure 1

a Electron micrograph of a device as used in the present study. Currents in the three gold wires of a microfabricated U-Structure create three linearly independent magnetic field gradients in the densely doped diamond below the structure. b Pulse sequence for one-dimensional imaging. A magnetic gradient pulse (length teff) inserted into a Hahn echo sequence phase-encodes position. The NV spin state is initialized and the spin projection \(\langle {\hat{S}}_{z}\rangle\) is read out optically. c Measurement result of (b). π/2x and π/2y denote the phase of the trailing π/2 pulse in (b). d Fourier transform of a dataset like (c) extending to t = 60 μs. Every NV center gives rise to one peak at the Larmor frequency set by the magnetic field \({B}_{{I}_{1}}(d)\) of the wire. d denotes the distance from the centroid of the NV center’s cluster (e) Experimental setup. A single microwave generator, a 90∘ splitter and two microwave switches are used to implement the Hahn Echo sequence. A confocal microscope with an avalanche photodiode (APD) as a detector is used for NV center polarization and readout. The gradient currents I1, I2, I3 are created from a constant voltage source and can be pulsed by a fast switch (ic-Haus HGP), which has a current rising and falling time of 1 ns. The voltage drop across the resistor is recorded by an A/D-converter and the pulse integral ∫ Idt is saved for every single current pulse.

Full size image

One major challenge of this experiment consists in creating sufficiently rectangular pulses to satisfy the approximation of Eq. (1). This requires a stable current supply that moreover has to be controlled with a fast (100 MHz) bandwidth to ensure that the rising and falling edges are quasi-instantaneous, i.e., much shorter than one period of the current-induced Larmor frequency ω(BI). Stability within every current pulse is required, because any variation of ω(BI(x, τ)) over the pulse will introduce a chirp in the time domain signal (Fig. 1c), which will blur the image in the frequency domain (Fig. 1d). Stability between successive experimental repetitions is required, because shot-to-shot fluctuations of the magnetic field induce decoherence (see below).

We experimentally address these constraints by two means (Fig. 1e). First, the current pulses are generated by switching a stable voltage source (Keithley 2230G-30-6) using fast switches (ic-Haus HGP), ensuring high stability of the pulse height and a nearly rectangular pulse shape. Second, we correct for residual nonlinearities and fluctuations by measurement and online post-processing. We acquire the current integral \(\int\nolimits_{0}^{t}I(\tau )d\tau\) for every pulse of every experimental repetition by hardware-integration on a fast A/D converter (Spectrum M4i.4451-x8), and use this value to define a new time axis for all photonic measurements that removes chirps. Specifically, we make the following approximation (valid for nearly rectangular pulses and a nearly linear Zeeman shift)

$$\int\nolimits_{0}^{t}\omega ({{{{\bf{B}}}}}_{I}({{{\bf{x}}}},\tau ))d\tau \approx {\omega }_{{{{\rm{I}}}},{{{\rm{ref}}}}}\frac{\int\nolimits_{0}^{t}I(\tau )d\tau }{{I}_{0}}={\omega }_{{{{\rm{I}}}},{{{\rm{ref}}}}}{t}_{{{{\rm{eff}}}}}$$
(4)

Here, ωI,ref(x) is the shift in Larmor frequency induced by some reference current I0 and teff denotes an “effective pulse duration”. We thus absorb minor fluctuations of the current over the pulse into this redefined time coordinate teff. All time-domain plots in this paper will use teff as time axis unless noted otherwise. This correction also suppresses shot-to-shot fluctuations, improving coherence16.

Three dimensional imaging

We now extend this one-dimensional magnetic resonance tomography to three dimensions, employing the three magnetic field gradients provided by the currents I1, I2, I3 of our device. Note that these gradients are linearly independent if the focal spot of the microscope is placed a few micrometers below the plane of the U-structure. This linear independence enables three-dimensional imaging despite the fact that the wire layout is two-dimensional. All following experiments have been performed in the lateral center of the U-structure, and ≈ 6 μm beneath the diamond surface.

During the Hahn Echo sequence the pulses of these three currents are applied consecutively (see Fig. 2a). Since the accumulated phase will add up linearly, the resulting spin signal is given by:

$$\langle {\hat{S}}_{z}\rangle (t)=\mathop{\sum}\limits_{{{{{{\bf{x}}}}}}_{{{{\rm{NV}}}}}}\left(1+\cos ({\omega }_{{I}_{1}}({{{{\bf{x}}}}}_{{{{\rm{NV}}}}}){t}_{1}+{\omega }_{{I}_{2}}({{{{\bf{x}}}}}_{{{{\rm{NV}}}}}){t}_{2}+{\omega }_{{I}_{3}}({{{{\bf{x}}}}}_{{{{\rm{NV}}}}}){t}_{3})\right)/2N$$
(5)

(assuming a trailing πx/2 pulse).

Fig. 2: Three-dimensional magnetic resonance tomography.
figure 2

a Pulse sequence. The sequence of Fig. 1 is extended to contain three magnetic gradient pulses from different wires. b Time domain data recorded from the sequence of (a) ending with π/2x. c Three-dimensional Fourier transform of the data in (b). The plot shows the square of the absolute value (spectral power) of the Fourier transform. d1, d2, d3 denote the distance to the respective wire (see Supplementary Discussion 3). The bottom, left, and back faces show projections of the 3D data.

Full size image

In analogy to one-dimensional tomography the set of (\({\omega }_{{{{{\rm{I}}}}}_{1}}({{{{\bf{x}}}}}_{{{{\rm{NV}}}}})\), \({\omega }_{{{{{\rm{I}}}}}_{2}}({{{{\bf{x}}}}}_{{{{\rm{NV}}}}})\), \({\omega }_{{{{{\rm{I}}}}}_{3}}({{{{\bf{x}}}}}_{{{{\rm{NV}}}}})\)) can be recovered from the three-dimensional time domain data (Fig. 2b) by a 3D inverse Fourier transform, forming a three-dimensional image. We note that this resulting image is distorted because the gradients, while linearly independent, are not fully orthogonal. While this distortion can in principle be corrected by computing and inverting the exact spatial distribution of the frequency shift ωI(x), the raw result of the Fourier transform is still a true three-dimensional image. This resulting image reveals individual NV centers in the diamond. Note that only NV centers within the confocal volume of the microscope contribute to the optically detected spin signal and can therefore be imaged. For the given NV density 5−15 centers are expected to be seen.

Sparse sampling

One challenge of such multidimensional measurements is the large number of required data points in Fourier space, e.g., 106 points in Fig. 2, which places strong demands on memory and sequencing hardware. This number can be reduced by compressed sensing, where only a subset of points is acquired, and the image is reconstructed by numerical techniques like L1 minimization, exploiting the a priori knowledge that the signal is a sparse set of discrete points9. Interestingly, our experimental setting allows for another compressed sensing approach. It does not require elaborate numerical reconstruction and exploits a different kind of a priori knowledge: that the signal is restricted to a narrow region of interest, i.e., a narrow band in frequency space. In this special case, we can implement an effective “zoom” into this region of interest by undersampling the signal in the time domain, lowering the amount of data points. Undersampling leads to aliasing of the signal in frequency space. For suitable parameters, this will shift the signal frequency band to a contiguous low frequency window where it can still be recovered by the inverse Fourier transform, effectively implementing a zoom. While this idea has already been explored in macroscale magnetic resonance17, introducing it to nanoscale magnetic resonance addresses two outstanding issues in this field. First, analog techniques for band-pass filtering like heterodyne detection cannot be used at the nanoscale, because the signal here is inherently digital, measuring e.g., the spin state of an NV center detector at one specific moment in time rather than a continuous electric voltage proportional to nuclear magnetization. Second, the sample volume (e.g., a single protein) is frequently much smaller than the volume spanned by the gradient conductors, so the acquisition of the full volume would require excessive resources. We demonstrate a proof of concept of this idea in Fig. 3. The simulated one-dimensional time and frequency domain plots (left part Fig. 3a) display a limited frequency band. When the time-domain signal is undersampled, i.e., sampled at a rate that the Nyquist frequency fNyq is smaller than the highest signal frequency, any signal at f > fNyq will be aliased to a frequency

$${f}_{{{{\rm{obs}}}}}=| f-2N\cdot {f}_{{{{\rm{Nyq}}}}}| ,$$
(6)

where N is the integer minimizing ∣f − 2NfNyq∣. In (Fig. 3a, middle plot), the signal band (around f ≈ 30 MHz) is close to twice the Nyquist frequency (2 ⋅ fNyq = 35 MHz) and hence aliased to a region close to f = 0 MHz. Note that the aliasing involves mirroring of the signal band, because the signal is at a lower frequency than the closest even multiple of fNyq.

Fig. 3: Aliasing magnification and speed-up of Fourier magnetic imaging.
figure 3

The plots in (a) show a simulated signal consisting of three distinct frequency components at (19.0, 20.3, 21.4) MHz, and its Fourier transform. Going through the columns from left to right the sampling rate is reduced resulting in a slower oscillation (red trace) and a lower Nyquist frequency (black-dashed line). Aliasing around the closest even multiple of the undersampled Nyquist frequency shifts the signal to a window close to f = 0, but does not change its shape. The Nyquist frequency of the undersampled signal has to be chosen large enough to cover the entire signal bandwidth. The signal is shifted to negative frequencies, and hence appears flipped in a frequency axis using ∣f∣, if it sits on the left of the closest even multiple of the Nyquist frequency. Panels (b–g) display measured 2D images of NV centers acquired by taking the FFT of the time domain signal (b, d, f) or by doing an L1 minimization of the time domain signal (c, e, g, see Supplementary Discussion 5 for details). (b, c) The Nyquist frequencies for each gradient direction (x and y axes) were set to be larger than the highest frequency in that direction (no aliasing). For (d, e) and (f, g) the measurement was done using an aliased grid, the aliased factor for each direction can be read in orange above FFT panel of each measurement. In (d, e) the undersampling parameters are such that the signal is flipped in both axes. For (f, g) the signal is flipped in the horizontal axis, but remains unflipped in the vertical axis. The aliased measurement (f, g) reduces the acquisition time by a factor of 10.

Full size image

We show this concept by acquiring three separate two-dimensional measurements (Fig. 3b−g), which display NV centers in a limited region of interest (upper right corner in Fig. 3b, c), defined by the confocal volume of the microscope. This process of undersampling and aliasing implements a zoom into the region of interest (Fig. 3d, e). Note that this process requires the signal to be confined to a limited window of frequencies. Since frequencies equal up to an integer multiple of 2fNyq will appear at the same fobs (Eq. 6), signals outside the zoom window will fold back into the signal of interest. To prevent contamination of the resulting image, the signal should be bandpass limited, i.e., values outside the frequency range of the signal should be zero and the Nyquist frequency should not fall below the bandwidth of the NV signal spectrum. For a suitable parameter choice of the undersampling, a zoom can be achieved that exactly covers the region of interest (Fig. 3f, g), allowing for the acquisition of a full image with a greatly reduced number of data points. In the specific example (Fig. 3f, g), the two dimensions are undersampled by a factor of 6 and 3, reducing the number of data points by a factor of 18, i.e., more than an order of magnitude. Note that reconstruction and visualization are still feasible by an inverse Fourier transform (Fig. 3f). L1 minimization is not required for reconstruction, but can still be implemented to improve the quality of the image and/or further reduce the number of data points required (Fig. 3c, e, g). We finally note a constraint of the technique. The undersampled data points have to be placed equidistantly in time, since any jitter or chirp will lead to a spectral broadening in the frequency-space image. Since a variation of the gradient current over the duration of a pulse is indistinguishable from a variation in timing, this also places higher demands on the constancy of currents, i.e., the requirement of rectangular current pulses discussed above.

Spatial resolution

We finally analyze the spatial resolution that is achieved in our measurement. This is defined by the magnitude of the magnetic field gradient, and the spectral resolution of the spectroscopy. The frequency resolution of Fourier-transformed data is given as the inverse of the length of the time domain signal. Analogous to that, the frequency (and thus spatial) resolution of our magnetic resonance tomography depends on how long we can make the gradient pulse length and still observe an oscillatory spin signal. The longest usable pulse is limited by the fact that the spin signal decays over time on a timescale of ≈ 10 μs (see e.g., Fig. 4a, b) because of shot-to-shot fluctuations of the gradient currents, which result in the decoherence of the NV centers. Denoting the timescale of this decay by T2,I (i.e., the coherence time in the presence of the gradient current), the frequency resolution is

$$\Delta f=\frac{\sqrt{2}}{\pi {T}_{2,I}}$$
(7)

where Δf denotes full width at half-maximum (FWHM) of the peak in frequency space. See Supplementary Discussion 7 for explanation of the \(\frac{\sqrt{2}}{\pi }\) factor. We extract T2,I from a long 1D tomography data set, extending to several multiples of T2,I. We calculate the Fourier transform for a short time window and “slide” this window over the whole range of the time domain signal. The resulting spectrogram (Fig. 4b) shows the evolution of the NV spectrum with increasing gradient pulse lengths. The signal from a single spin appears as a horizontal line in a specific frequency band. The decaying power of the signal with increasing time in this band defines the SNR over the measurement (see Supplementary Discussion 4). We fit the SNR curve (Fig. 4c) with a Gaussian (\({e}^{-{t}_{{{{\rm{eff}}}}}^{2}/2{T}_{2,I}^{2}}\)) to obtain T2,I. For the data of Fig. 4 we thus arrive at a coherence time of \({T}_{2,{I}_{2}}=8.64\pm 0.1\,\mu {{{\rm{s}}}}\). Taking into account the field gradients (described by a Jacobian taken at the centroid of the cluster, see Supplementary Discussion 3 for details about resolution derivation), uncertainties in frequency can be translated into uncertainties in space as \(\Delta \overrightarrow{x}=(5.9,9.9,14.7)\) nm. This resolution could be limited by several effects. First, shot-to-shot fluctuations of the current could shorten T2,I. We try to suppress this by hardware integrating every single current pulse (see above) and applying post-processing corrections, but this process is equally limited by electronic noise at a lower level. Second, a spatial drift of the current path between successive experimental repetitions can equally lead to a decrease of T2,I. A spatial drift could arise from heat expansion of the diamond and the conductors, but an expansion on the level of 10−3 would require a temperature difference of ≈1000 K which seems unlikely. A drift of the current path within the conductor, due to local heating, appears more reasonable. Intriguingly the product of ωNVT2,I, i.e., the relative stability of the gradient field, differs between the three wires. This tentatively suggests that spatial drifts of the current in the wires are the limiting factor rather than electrical fluctuations, which would be expected to be the same in all wires.

Fig. 4: Benchmarking of the spatial resolution for I2.
figure 4

a time-domain signal of a one-dimensional tomography (sequence of Fig. 1b). Excerpts at different time windows are shown. b Spectrogram (windowed Fourier transform) of (a). The signal produced by the NV centers decays over a timescale of ≈10 μs. c Signal-to-noise ratio of (b), computed by integrating the power in the signal window marked in (b) and referencing it to the noise observed outside this window (see Supplementary Discussion 4). c A Gaussian fit to the data yields a decay timescale \({T}_{2,{I}_{2}}=8.64\pm 0.1\,\mu {{{\rm{s}}}}\). d Fourier transform (absolute value) of the time domain signal in (a). Abbreviations in the figure: (f) frequency, (teff) length of a rectangular current pulse, (SNR) signal to noise ratio, (PL) Photoluminescence.

Full size image

Summary

In summary, we have demonstrated Fourier-accelerated 3D imaging of single spins with nanoscale resolution. We have also presented a compressed sensing scheme, which exploits a limited field of view, rather than sparseness of the data. Our experiments demonstrate that resolution in the sub-10 nm range can be achieved by switchable magnetic field gradients, thus establishing a three-dimensional superresolution imaging method for optically readable spin qubits.

Notably, the resolution we obtain is among the best results ever achieved in superresolution imaging, It outperforms standard methods of localization microscopy (PALM, STORM), which typically achieve ≈20 nm lateral and ≈50 nm axial resolution18. Only highly sophisticated techniques like MINFLUX19 and COLD20 have claimed even higher resolutions, but have not found widespread adoption yet and have partially been criticized for subtle pitfalls21. Already at the present level (Fig. 5a), our technique can find numerous applications. It can enable spin manipulation in quantum registers, e.g., by addressing a subset of coherently coupled qubits in a densely doped ensemble of NV centers. Resolving individual NV centers in a densely doped diamond also demonstrates an essential missing component for proposals to use NV centers as particle detectors8. Our technique could finally be applied to NV centers in nanodiamonds, e.g., to enable super-resolved tracking to measure and image forces at the nanoscale22,23.

Fig. 5: Possible applications of our technique.
figure 5

a present device. Three-dimensional super-resolution addressing of NV centers can find use in quantum registers, particle detectors, or tracking of nano-diamonds. b single-molecule MRI device. Applying gradient imaging to electron spin labels could enable direct real-space imaging of spin-labeled proteins. A single nitrogen vacancy can here be used as a detector for the electron spin signal, but would not be imaged itself.

Full size image

Moving beyond NV centers inside the diamond, the device and measurement technique could equally be applied to dark spins outside of the diamond (Fig. 5b). Here a single NV center would merely serve as a detector to enable electron/nuclear spin spectroscopy on spins, while the entire process of imaging could be performed by the device presented here. Our compressed sensing technique of “Fourier zooming” will be especially advantageous in this setting where all the spins are confined to the nanoscale detection volume of a shallow NV center. Such a direct 3D imaging technique could image an arbitrary number of spins and constrain inter-spin distances larger than 80 Å, which is not possible by current electron spin resonance spectroscopy. Shrinking the structure by one order of magnitude would even push the resolution into the range of Å. Notably the T2 of established spin labels is sufficiently long for the spectroscopy presented here24. As a final vision, we express our hope that future research will identify a fluorescent molecule with an optically readable electron spin, on which the technique could then be applied without any further modification.