Realistic scheme for quantum simulation of ${{\mathbb{Z}}}_{2}$ lattice gauge theories with dynamical matter in (2 + 1)D

Abstract

Gauge fields coupled to dynamical matter are ubiquitous in many disciplines of physics, ranging from particle to condensed matter physics, but their implementation in large-scale quantum simulators remains challenging. Here we propose a realistic scheme for Rydberg atom array experiments in which a ${{\mathbb{Z}}}_{2}$ gauge structure with dynamical charges emerges on experimentally relevant timescales from only local two-body interactions and one-body terms in two spatial dimensions. The scheme enables the experimental study of a variety of models, including (2 + 1)D ${{\mathbb{Z}}}_{2}$ lattice gauge theories coupled to different types of dynamical matter and quantum dimer models on the honeycomb lattice, for which we derive effective Hamiltonians. We discuss ground-state phase diagrams of the experimentally most relevant effective ${{\mathbb{Z}}}_{2}$ lattice gauge theories with dynamical matter featuring various confined and deconfined, quantum spin liquid phases. Further, we present selected probes with immediate experimental relevance, including signatures of disorder-free localization and a thermal deconfinement transition of two charges.

Introduction

It has been a long sought goal to faithfully study lattice gauge theories (LGTs) with dynamical matter in the realm of strong coupling. Since their discovery, ${{\mathbb{Z}}}_{2}$ LGTs have sparked the interest of physicists from various different fields including high-energy¹, condensed matter^2,3,4 or biophysics⁵. The seminal work by Fradkin and Shenker⁶ in 1979 predicted the existence of two phases in their model, in which ${{\mathbb{Z}}}_{2}$ charged particles are either confined or deconfined in (2 + 1)D. This insight made it a particularly promising candidate theory that could capture some of the essential physics of quark confinement in QCD¹ while hosting a much simpler gauge group. Likewise, it provides one of the most fundamental instances of the Higgs mechanism. Since then the study of ${{\mathbb{Z}}}_{2}$ LGTs has inspired physicists because of their intimate relation to topological order⁷, quantum spin liquids^8,9 and quantum information¹⁰, to name a few. While the physics of these models could give insights into outstanding problems, e.g., how to define confinement in the presence of dynamical matter, the numerical (e.g. refs. ^{11,12,13,14,15}) and experimental exploration is at the same time very challenging beyond (1 + 1)D (e.g. refs. ^16,17,18,19).

The experimental developments over the past years have driven the field of analog quantum simulation toward exploring many-body physics in system sizes out of reach for any numerical simulation and offering a new toolbox to approach complex, physical phenomena such as quantum spin liquids²⁰. The difficulty to implement gauge constraints and robustness against ever-present gauge-breaking errors in analog quantum simulators, however, has hindered the field to push forward into the aforementioned direction and a scalable, reliable implementation of LGTs with dynamical matter in (2 + 1)D remains a central goal.

The rich structure of gauge theories emerges from locally constraining the Hilbert space. This constraint can be formulated by Gauss’s law, which requires all physical states $\left\vert \psi \right\rangle$ to fulfill ${\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert \psi \right\rangle ={g}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert \psi \right\rangle$. For the ${{\mathbb{Z}}}_{2}$ LGT with dynamical matter (${{\mathbb{Z}}}_{2}$ mLGT) we consider in this work the symmetry generators ${\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ are given by:

$${\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}={(-1)}^{{\hat{n}}_{{{{{{{{\boldsymbol{j}}}}}}}}}}\mathop{\prod}\limits_{{{{{{{{\boldsymbol{i}}}}}}}}:\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x},$$

(1)

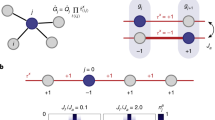
where ${\hat{n}}_{{{{{{{{\boldsymbol{j}}}}}}}}}={\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}^{{{{\dagger}}} }{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ is the number operator for (hard-core) matter on site j and the Pauli matrix ${\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}$ defines the electric field on the link between site i and j; hence g_j = ±1. Our starting point throughout this work are link and site qubits on a two-dimensional honeycomb lattice, see Fig. 1a.

Fig. 1: Constraint-based implementation of ${{\mathbb{Z}}}_{2}$ mLGT with qubits.

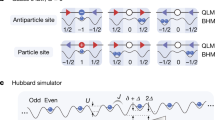
The ${{\mathbb{Z}}}_{2}$ gauge structure emerges from the dominant local-pseudogenerator (LPG) interaction on the honeycomb lattice introduced in (a). A vertex contains matter ${\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ qubits (blue) and shares link ${\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}$ qubits (red) with neighboring vertices. All qubits connected to a vertex interact pairwise with strength 2V. In a Rydberg atom array experiment the qubits are implemented by individual atoms in optical tweezers, which are assigned the role of matter or link depending on the position in the lattice. Here, the ground- and Rydberg state of the atoms, $\left\vert g\right\rangle$ and $\left\vert r\right\rangle$, encode qubit states, which are coupled by an off-resonant drive Ω to induce effective interactions. To realize equal strength nearest neighbor, two-body Rydberg–Rydberg interactions, the matter atoms can be elevated out of plane. In (b) we introduce the notation for the ${{\mathbb{Z}}}_{2}$ mLGT, for which the Hilbert space constraint is given by Gauss’s law ${\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}=+1$. We illustrate the electric field ${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=+1$ (${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=-1$) with flat (wavy) red lines and the matter site occupation n_j = 0 (n_j = 1) with empty (full) blue dots. c shows the notation for the QDM subspace with exactly one dimer per vertex. d illustrates how the distinct subspaces are energetically separated by the LPG term $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$. The two quantum dimer subspaces are disconnected when the matter is static, which can be exactly realized by the absence of matter atoms in (a) and setting $(2{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}^{{{{\dagger}}} }{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}-1)=\pm \!1$ in $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$.

We propose to realize matter and link variables as qubits, implementable e.g., by the ground $\vert g \rangle$ and Rydberg $\left\vert r\right\rangle$ states of atoms in optical tweezers^{20,21,22,23,24,25}, see Fig. 1a–c. Thus, the product in Eq. (1) measures the parity of qubit excitations of matter and links around vertex j.

By encoding the degrees-of-freedom in qubits the enlarged Hilbert space contains physical (g_j = +1) and unphysical (g_j = −1) states: The latter do not fulfill Gauss’s law. Since any local perturbations present in a realistic quantum simulation experiment mix the two subspaces, quantum simulations can become unreliable, effectively breaking gauge-invariance. Nevertheless, by energetically separating the physical from unphysical states transitions into the latter can be suppressed and the gauge structure emerges from the enlarged Hilbert space.

The simplest way, theoretically, to achieve such gauge protection, is by adding $-V{\sum }_{{{{{{{{\boldsymbol{j}}}}}}}}}{\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ to the Hamiltonian with large V > 0^26,27,28. But since this would require “strong four-body interactions”, it is experimentally not feasible in current experimental platforms.

Here we demonstrate that simple two-body Ising-type interactions, which are readily available in e.g., Rydberg tweezer arrays^{20,21,22,23,24,25}, combined with longitudinal and weak transverse fields provide a minimal set of ingredients which allow to robustly implement a variety of LGTs with dynamical matter⁹. The scheme we propose not only offers inherent protection against arbitrary gauge-breaking errors; it also provides a surprising degree of flexibility, including cases with global conserved particle number, global number-parity conservation, and quantum dimer models on a bipartite lattice which map to U(1) gauge theories.

In the following, we show that readily available Ising-type two-body interactions, in addition to local fields, are sufficient to protect Gauss’s law on experimentally relevant timescales by employing the so-called local pseudogenerator (LPG) method²⁹. Moreover, we show that the proposed protection scheme provides a generic means to engineer a variety of effective ${{\mathbb{Z}}}_{2}$ mLGT Hamiltonians by weakly driving the qubits. As an example, we demonstrate how this allows to realize the celebrated Fradkin–Shenker model⁶, and discuss the phase diagrams of several related effective Hamiltonians. Finally, we elaborate on some realistic experimental probes that we view as most realistic in state-of-the-art quantum simulators.

Results

Local pseudogenerator on the honeycomb lattice

The main ingredient of the experimental scheme proposed in this Article is the local pseudogenerator (LPG) interaction term $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$. As shown in Fig. 1a, $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ consists of equal-strength 2V interactions among all qubits (matter and gauge) around vertex j, taking the form:

$$V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}=\frac{V}{4}{\left[(2{\hat{n}}_{{{{{{{{\boldsymbol{j}}}}}}}}}-1)+\mathop{\sum}\limits_{{{{{{{{\boldsymbol{i}}}}}}}}:\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}\right]}^{2}.$$

(2)

We assume that V defines the largest energy scale in the problem, which separates the Hilbert space into constrained subspaces. This overcomes the most challenging step, imposing different gauge constraints in the emerging subspaces (Supplementary Note 1).

We obtain three distinct eigenspaces of the LPG term: (1) Two (distinct) quantum dimer model (QDM) subspaces with static matter at low-energy, (2) physical states of a ${{\mathbb{Z}}}_{2}$ mLGT at intermediate energies, and (3) trivial, polarized states at high energy, see Fig. 1b–d.

The LPG method requires that $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ acts identical to the full protection term on all physical states in the target gauge sector, i.e., ${\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert \psi \right\rangle ={\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert \psi \right\rangle$. For unphysical states, instead, the LPG term splits into many manifolds that can be energetically above and below the target sector²⁹. This construction allows to reduce experimental complexity from four- to two-body interactions.

Experimentally, we propose to implement strong LPG terms in the Hamiltonian such that quantum dynamics are constrained to remain in LPG eigenspaces by large energy barriers enabling the large-scale quantum simulation of ${{\mathbb{Z}}}_{2}$ mLGTs in (2 + 1)D. To introduce constraint-preserving dynamics within the LPG subspaces, the latter are coupled by weak on-site driving terms of strength Ω ≪ V as discussed below. Through the constrained dynamics, a ${{\mathbb{Z}}}_{2}$ mLGT emerges in an intermediate-energy eigenspace of $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$, which is accessible in quantum simulation platforms and which distinguishes our work from previous studies on emergent gauge symmetries, e.g. refs. ^30,31,32.

The LPG method is built upon stabilizing a high-energy sector of the spectrum, which comes with the caveat that a few unphysical states are resonantly coupled when considering the entire lattice. In particular, there is a subset of unphysical states that violate Gauss’s law on four vertices with energy lowered on three vertices and raised on one vertex; hence these states are on resonance with physical states. However, numerical simulations in small systems suggest that these gauge-breaking terms only play a subdominant role and gauge-invariance remains intact (Supplementary Note 2).

Ultimately, the problem of resonances with a few unphysical states can be remedied by promoting V → V_j to be site-dependent such that high-energy sectors can be faithfully protected^33,34 against potential gauge non-invariant processes described above (see Methods section). Site-dependent protection terms do not require any additional experimental capabilities in our protocol described below. Even more, experimental imperfections inherently give disorder stabilizing the gauge sectors further. It is also important to note that the presence of only weak disorder (compared to the energy scale V) is enough, which does not alter the effective couplings in the emergent gauge-invariant effective Hamiltonian.

In the following, we introduce the microscopic model that we propose to implement in an experiment. From the microscopic model, effective Hamiltonians for the ${{\mathbb{Z}}}_{2}$ mLGT and QDM subspaces can be derived by a Schrieffer–Wolff transformation (Supplementary Note 2 and 4). On realistic timescales of experiments, the effective models are gauge-invariant by construction and studied further below.

Experimental realization in Rydberg atom arrays

Here, we propose the microscopic model ${\hat{{{{{{{{\mathcal{H}}}}}}}}}}^{{{{{{{{\rm{mic}}}}}}}}}$ which can be directly implemented in state-of-the-art Rydberg atom arrays in optical tweezers, see Fig. 1a.

The constituents are qubits, which can be modeled by the ground $\vert g \rangle$ and Rydberg $\vert r \rangle$ states of individual atoms. As shown in Fig. 1a, we label the atoms as matter atom or link atom depending on their position on the lattice. The ${{\mathbb{Z}}}_{2}$ gauge structure then emerges from nearest-neighbor Ising interactions V realized by Rydberg–Rydberg interactions and hence the real space geometric arrangement plays a key role. The dynamics is induced by a weak transverse field Ω_m (Ω_l), which corresponds to a homogeneous drive between the ground and Rydberg states of the matter (link) atoms. Moreover, tunability of parameters defining the phase diagram is achieved by a longitudinal field or detuning Δ_m (Δ_l) of the weak drive.

The interesting physics emerges in different energy subsectors of the LPG protection term $\propto V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ in Eq. (2); in particular the ${{\mathbb{Z}}}_{2}$ mLGT is a sector in the middle of the spectrum of ${\hat{{{{{{{{\mathcal{H}}}}}}}}}}^{{{{{{{{\rm{mic}}}}}}}}}$. The suitability for Rydberg atom arrays comes from the flexibility in geometric arrangement required for the LPG term as well as from the natural energy scales V ≫ Ω in the system, which we use to derive the effective models below, see Eqs. (4) and (5).

Matter atoms ${\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ form the sites of a honeycomb lattice and we map the empty $\vert {n}_{{{{{{{{\boldsymbol{j}}}}}}}}}=0 \rangle$ (occupied $\vert {n}_{{{{{{{{\boldsymbol{j}}}}}}}}}=1 \rangle$) state on the ground state $\vert g \rangle_{{{{{{{{\boldsymbol{j}}}}}}}}}$ (Rydberg state $\vert r \rangle {\left. \right)}_{{{{{{{{\boldsymbol{j}}}}}}}}}$) of the atoms. Link atoms ${\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}$ are located on the links of the honeycomb lattice, i.e., a Kagome lattice, and analogously we map the ${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=+1$ (${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=-1$) state on the atomic state ${ \vert g \rangle }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }$ (${ \vert r \rangle }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }={\hat{a}}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{{{{\dagger}}} }{ \vert g \rangle }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }$). Moreover, we want the matter and link atoms to be in different layers and those layers should be vertically slightly apart in real space to ensure equal two-body interactions between matter and link atoms (Supplementary Note 5). Using the out-of-plane direction has the advantage that it only requires atoms of the same species and with the same internal states. However, the equal strength interaction can also be achieved in-plane by using e.g., two atomic species or different (suitable) internal Rydberg states for the matter and link atoms.

We first propose a non gauge-invariant microscopic Hamiltonian from which we later derive an effective model with only gauge-invariant terms. To lowest order in perturbation theory and on experimentally relevant timescales, the system evolves under an emergent gauge-invariant Hamiltonian. The microscopic Hamiltonian is given by:

$${\hat{{{{{{{{\mathcal{H}}}}}}}}}}^{{{{{{{{\rm{mic}}}}}}}}}= V\mathop{\sum}\limits_{{{{{{{{\boldsymbol{j}}}}}}}}}{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}-{\Delta }_{m}\mathop{\sum}\limits_{{{{{{{{\boldsymbol{j}}}}}}}}}{\hat{n}}_{{{{{{{{\boldsymbol{j}}}}}}}}}-\frac{{\Delta }_{l}}{2}\mathop{\sum}\limits_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}\\ +{\Omega }_{m}\mathop{\sum}\limits_{{{{{{{{\boldsymbol{j}}}}}}}}}({\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}+{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}^{{{{\dagger}}} })+{\Omega }_{l}\mathop{\sum}\limits_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }({\hat{a}}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }+{\hat{a}}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{{{{\dagger}}} }),$$

(3)

where bosonic operators ${\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}^{{{{\dagger}}} }$ and ${\hat{a}}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{({{{\dagger}}} )}$ annihilate (create) excitations on the matter and link atoms, respectively; ${\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ is the LPG term introduced in the main text Eq. (2). The last two terms describe driving of matter (${ \vert g \rangle }_{{{{{{{{\boldsymbol{j}}}}}}}}}\leftrightarrow {\left\vert r\right\rangle }_{{{{{{{{\boldsymbol{j}}}}}}}}}$) and link atoms (${ \vert g \rangle }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }\leftrightarrow {\vert r \rangle }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }$) in the rotating frame. Rewriting (3) in the atomic basis yields Rydberg–Rydberg interactions of strength 2V and renormalized, large detunings ${\tilde{\Delta }}_{m}=-3V+{\Delta }_{m}$ and ${\tilde{\Delta }}_{l}=-3V+{\Delta }_{l}$. In a Rydberg setup the driving terms can be realized by an external laser, which couples $\vert g \rangle \leftrightarrow \vert r \rangle$, while the detunings Δ_m, Δ_l of the laser relative to the resonance frequency controls the electric field Δ_l and chemical potential Δ_m in the rotating frame.

In the limit Ω_m,  Ω_l ≪ V, the energy subspaces defined by the LPG term $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$, Eq. (2), are weakly coupled by the drive to induce effective interactions and it is convenient but not required to choose Ω_m = Ω_l = Ω. The ${{\mathbb{Z}}}_{2}$ mLGT emerges as an intermediate-energy eigenspace of the LPG term $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$. The effective interactions in the constrained ${{\mathbb{Z}}}_{2}$ mLGT and QDM subspaces of ${\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ can be derived by a Schrieffer–Wolff transformation (Supplementary Note 2 and 4) and yielding the models discussed in the next section.

In the experiment we propose, the Rydberg–Rydberg interactions are not only restricted to nearest neighbors but are long ranged. We emphasize that beyond nearest neighbor interactions are inherently gauge invariant and hence do neither influence the LPG gauge protection scheme nor the Schrieffer–Wolff transformation. However, the long-range interactions can have strong influence on the ${{\mathbb{Z}}}_{2}$ invariant dynamics. While the interaction strength decreases as 1/R⁶, where R is the distance between atoms, the interaction is still comparable to the effective perturbative dynamics (Supplementary Note 5). We note that the dynamics might be slowed down but the qualitative features of the ${{\mathbb{Z}}}_{2}$ mLGT remain intact.

Effective ${{\mathbb{Z}}}_{2}$ mLGT model

A model is locally ${{\mathbb{Z}}}_{2}$ invariant if its Hamiltonian $\hat{{{{{{{{\mathcal{H}}}}}}}}}$ commutes with all symmetry generators ${\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$, i.e., $[\hat{{{{{{{{\mathcal{H}}}}}}}}},{\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}]=0$ for all j. This ensures that all dynamics is constrained to the physical subspace without leaking into unphysical states. In Eq. (2), the target sector is g_j = +1 for all j but our scheme can be easily adapted for any ${\{{g}_{{{{{{{{\boldsymbol{j}}}}}}}}}\}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ (Supplementary Note 1).

In the presence of strong LPG protection, the system is energetically enforced to remain in a target gauge sector and unphysical states are only virtually occupied by the drive Ω. To be precise, resonant couplings to unphysical sectors are suppressed by the (experimentally feasible) disorder protection scheme discussed above and in the “Methods” section. Otherwise emergent gauge-breaking terms appear in third-order perturbation theory. However, in small systems we have numerically confirmed that even without disorder in the LPG terms Gauss’s law is well conserved (Supplementary Note 2), which in larger systems we expect to crossover to an approximate gauge invariance. In the following we assume disorder protection or small systems, where leading order gauge-breaking terms are absent or can be neglect, respectively.

For the proposed on-site driving terms discussed above and shown in Fig. 1a, we derive the following effective Hamiltonian from the microscopic model (3) in the intermediate-energy LPG eigenspace (Supplementary Note 2):

$${\hat{{{{{{{{\mathcal{H}}}}}}}}}}_{{{\mathbb{Z}}}_{2}}^{{{{{{{{\rm{eff}}}}}}}}}= \mathop{\sum}\limits_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }\left(t{\hat{a}}_{{{{{{{{\boldsymbol{i}}}}}}}}}^{{{{\dagger}}} }{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}+{\Delta }_{1}{\hat{a}}_{{{{{{{{\boldsymbol{i}}}}}}}}}^{{{{\dagger}}} }{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}^{{{{\dagger}}} }+{\Delta }_{2}{\hat{a}}_{{{{{{{{\boldsymbol{i}}}}}}}}}^{{{{\dagger}}} }{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}^{{{{\dagger}}} }+{{{{{{{\rm{H.c.}}}}}}}}\right) \\ - J\mathop{\sum}\limits_{\hexagon}\mathop{\prod}\limits_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle \in {\hexagon}}{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}-h\mathop{\sum}\limits_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}-\mu \mathop{\sum}\limits_{{{{{{{{\boldsymbol{j}}}}}}}}}{\hat{n}}_{{{{{{{{\boldsymbol{j}}}}}}}}}.$$

(4)

The first terms in Eq. (4) describe gauge-invariant hopping of matter excitations with amplitude t and (anomalous) pairing ∝ Δ₁ (∝ Δ₂). The term ∝J is the magnetic plaquette interaction on the honeycomb lattice. The last two terms are referred to as electric field term h and chemical potential μ, respectively. Note that deriving Hamiltonian (4) from the microscopic model in Eq. (3) yields additional higher-order terms $\propto {\hat{\tau }}^{x}{\hat{\tau }}^{x},\,{\hat{\tau }}^{x}\hat{n}$, etc. In the effective model ${\hat{{{{{{{{\mathcal{H}}}}}}}}}}_{{{\mathbb{Z}}}_{2}}^{{{{{{{{\rm{eff}}}}}}}}}$ we treat these higher-order terms on a mean-field level of the electric field and matter density (Supplementary Note 2). Moreover, we emphasize that the effective model is solely derived from the microscopic Hamiltonian, which only requires a simple set of one- and two-body interactions between the constituents.

For any site j, one can take ${\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\to -{\hat{a}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ and ${\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}\to -{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}$; hence the effective Hamiltonian (4) has a local ${{\mathbb{Z}}}_{2}$ symmetry, $[{\hat{{{{{{{{\mathcal{H}}}}}}}}}}_{{{\mathbb{Z}}}_{2}}^{{{{{{{{\rm{eff}}}}}}}}},{\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}]=0\forall {{{{{{{\boldsymbol{j}}}}}}}}$, qualifying it as ${{\mathbb{Z}}}_{2}$ mLGT in (2 + 1)D. In particular, in our proposed scheme we do not have to apply involved steps to engineer ${{\mathbb{Z}}}_{2}$-invariant interactions but rather we exploit the intrinsic gauge protection by dominant LPG terms, which enforces any weak perturbation to yield an effective ${{\mathbb{Z}}}_{2}$ mLGT. This approach also inherently implies robustness against gauge-symmetry breaking terms in experimental realizations.

In the following, we discuss the rich physics of the effective model (4). However, due to the complexity of the system, it is challenging to conduct faithful numerical studies in extended systems. As a first step, we examine well-known limits of the model and conjecture T = 0 phase diagrams of the effective Hamiltonian when the ${{\mathbb{Z}}}_{2}$ gauge field is coupled to U(1) or quantum-${{\mathbb{Z}}}_{2}$ dynamical matter, respectively. We note that the strength of the plaquette interaction can only be estimated (Supplementary Note 2) and competes with the long-range Rydberg interactions. Moreover, the disorder protection scheme underlying the derivation of the effective Hamiltonian ensures gauge-invariance of the leading order contributions but higher-order gauge breaking terms can in principle appear and affect the physics at very long timescales.

Our effective model describes the physics of experimental system sizes and timescales; the efficiency of the LPG gauge protection in the thermodynamic limit is a subtle open question. Hence, in the following we discuss phases of the effective model (4) that may (or may not) emerge from the microscopic model (3).

U(1) matter

By fixing the number of matter excitations in the system, i.e., Δ₁ = Δ₂ = 0 in Hamiltonian (4), the model has a global U(1) symmetry of the matter (hard-core) bosons, which can be achieved by choosing the detuning at the matter sites Δ_m comparable to V in our proposed experimental scheme Eq. (3). Here, we consider the phase diagram when the filling of matter excitations is controlled by the chemical potential μ. To map out different possible phases, we fix the hopping t and study limiting cases.

First, we consider the pure gauge theory with no matter excitations (μ → −∞), see Fig. 2a (bottom). The Hamiltonian then reduces to the pure Ising LGT² with matter vacuum—an even ${{\mathbb{Z}}}_{2}$ LGT. The dual of this model exhibits a continuous (2 + 1)D Ising phase transition, corresponding to a confined (deconfined) phase below (above) a critical (J/h)_c, respectively^2,4. At the toric code point (J/h = ∞) the system is exactly solvable³⁵ and the gapped ground state has topological order.

Fig. 2: Conjectured ground-state phase diagrams.

We show two qualitative sketches of phase diagrams for the effective model (4). In (a), we consider U(1) matter (Δ₁ = Δ₂ = 0) coupled to a dynamical ${{\mathbb{Z}}}_{2}$ gauge field as discussed in the main text. Along the vertical direction the filling is tuned, which yields an even (odd) ${{\mathbb{Z}}}_{2}$ pure gauge theory in the vacuum (Mott insulator) illustrated by the gray regions. In between the matter and gauge degrees-of-freedom interplay, for which we examined the limiting cases. Above the deconfined region, we expect a superfluid regime (yellow), while above the confined region composite mesons of ${{\mathbb{Z}}}_{2}$ charges may condense (red). In (b), we show the phase diagram for an Ising ${{\mathbb{Z}}}_{2}$ LGT as proposed by Fradkin and Shenker⁶. The 2D quantum Hamiltonian of the Ising ${{\mathbb{Z}}}_{2}$ mLGT has equal hopping t and pairing Δ₁ strength and can thus be mapped on a classical 3D Ising theory. Because our model with quantum ${{\mathbb{Z}}}_{2}$ matter coupled to dynamical ${{\mathbb{Z}}}_{2}$ gauge fields has slight anisotropy between hopping and pairing, t ≠ Δ₁, as well as additional anomalous pairing terms Δ₂, the classical mapping can only work approximately. We anticipate that the phase diagram should be qualitatively very similar to (b).

Because for J/h = ∞ the gauge field has no fluctuations, we can fix the gauge by setting ${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}=+1$ and map out the pure matter theory in Fig. 2a (right). For finite μ we find a model with free hopping of hard-core bosons, for which the filling can be tuned by changing the chemical potential μ. Hence, for increasing μ and results based on the square lattice^36,37 we expect two continuous phase transitions: vacuum-to-superfluid and superfluid-to-Mott insulator. The Mott insulator phase is an odd ${{\mathbb{Z}}}_{2}$ LGT because the matter is static and acts as background charge and thus can be treated as a pure gauge theory with g_j = −1⁹. In the opposite limit J/h = 0, the same Mott state gives rise to a hard-core quantum dimer constraint for the ${{\mathbb{Z}}}_{2}$ electric field lines. On the square lattice, the quantum dimer model and odd ${{\mathbb{Z}}}_{2}$ LGT exhibit a phase transition from a confined to deconfined phase¹⁵. The honeycomb lattice and next-nearest neighbor Rydberg–Rydberg interactions might feature additional symmetry-broken phases. Hence it requires a sophisticated analysis to map out the substructure of the Mott insulating phase in Fig. 2a.

In the limit of low fillings and small but finite J/h ≪ 1, the matter excitations form two-body mesonic bound states¹⁵, which are ${{\mathbb{Z}}}_{2}$-charge neutral and can be considered as point-like particles. We can derive an effective meson model yielding hard-core bosons on the sites of a Kagome lattice (Supplementary Note 3).

At T = 0 and sufficiently low densities, the mesons can condense and spontaneously break the emergent global U(1) symmetry associated with meson number conservation. To determine the phase boundary of the meson condensate, we consider a single pair of matter excitations doped into the vacuum. This pair cannot alter the pure gauge phases and thus the two charges can be considered as probes for the (de)confined regime. For the latter, the matter excitations are bound into mesons, in contrast to free excitations above the deconfined regime. Hence, the effective description of bound mesonic pairs breaks down at the phase transition of the pure gauge theory indicating the phase boundary of the meson condensate phase at small filling.

At higher densities, dimer-dimer interactions and fluctuations of the gauge field play a role, requiring a more sophisticated analysis to predict the ground state. We emphasize that the rich physics in this model emerges from the gauge constraint generated by the LPG terms. Moreover, we note that by lifting the hard-core boson constraint, which is beyond our experimental scheme, the model maps onto a classical XY model coupled to a ${{\mathbb{Z}}}_{2}$ gauge field⁹. This model has been studied on the square lattice in the context of topological phases of matter⁹ and high-Tc superconductivity^38,39,40, to name a few.

Classical mapping

For t = Δ₁ and Δ₂ = 0 the model is well-studied and maps onto a classical Ising lattice gauge theory coupled to Ising ${{\mathbb{Z}}}_{2}$ matter⁶. In our experimental proposal Δ₁ and Δ₂ cannot be independently tuned, but due to the relevance of the model and its proximity to our effective model we briefly summarize the most important results for the square lattice here, see Fig. 2b.

In the limit with frozen gauge fields (pure matter axis, J/h = ∞) the resulting pure matter theory corresponds to a transverse field Ising model with a global ${{\mathbb{Z}}}_{2}$ symmetry, which maps to a classical 3D Ising model and exhibits a continuous phase transition. On the pure gauge axis (t/μ = 0) the model exhibits a topological phase transition without local order parameters². Instead, the scaling of non-local Wegner-Wilson loops with their area/perimeter distinguishes the confined from the deconfined phase. Remarkably, the pure gauge model is also dual to a classical 3D Ising model, rendering the pure gauge axis dual to the pure matter axis. The same pure gauge phases are realized for μ → −∞ in the case with U(1) matter.

For more general J/h, the model’s self-duality yields a symmetry in the phase diagram, which allows to study the pure gauge and matter theory in Fig. 2b but does not reveal the interior away from the axis. Fradkin’s and Shenker’s accomplishment was to show the existence of two distinct, extended phases: the confined and deconfined “free charge” phase, which have been confirmed numerically^12,13. From today’s perspective, the latter would be characterized as topological phase of matter in the toric code universality class.

Quantum-${{\mathbb{Z}}}_{2}$ matter

Now, we consider the full effective Hamiltonian (4), where hopping and pairing are anisotropic t ≠ Δ₁ and the pairing strength can depend on the electric field configuration Δ₂ ≠ 0, and relate it to Fig. 2b. Here, the pure matter theory can no longer be mapped on the classical 3D Ising model. Hence, we introduce the term quantum-${{\mathbb{Z}}}_{2}$ matter, which emphasizes the matter’s ${{\mathbb{Z}}}_{2}$ symmetry group but points out that a mapping to a known classical model is lacking.

We note that close to the toric code point (J/h = ∞ and t/μ = 0) in Fig. 2b, the expectation value of the electric field vanishes, $\langle {\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}\rangle =0$, and thus in mean-field approximation the anomalous terms should be negligible and renormalize the pairing ${\Delta }_{1}\to {\tilde{\Delta }}_{1}$. For the pure gauge theory it has been shown¹¹ that the expectation value $\langle {\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}\rangle$ continuously changes by tuning the electric field term h. Hence, by performing a mean-field approximation in the electric field, the quantum-${{\mathbb{Z}}}_{2}$ mLGT maps onto the classical Ising ${{\mathbb{Z}}}_{2}$ mLGT (Supplementary Note 2C).

Due to its proximity to the Ising ${{\mathbb{Z}}}_{2}$ mLGT and its common symmetries generated by the proposed LPG term, we anticipate that the phase diagram of the quantum-${{\mathbb{Z}}}_{2}$ mLGT shares all essential features of the Ising ${{\mathbb{Z}}}_{2}$ mLGT as shown in Fig. 2b.

Quantum dimer model (QDM)

Rokhsar and Kivelson introduced the QDM in the context of high-T_c superconductivity, which has the constraint that exactly one dimer is attached to each vertex^41,42. The QDM is an odd ${{\mathbb{Z}}}_{2}$ LGT, i.e., a pure gauge theory with g_j = +1 replaced by g_j = −1 ∀ j, with h → ∞, and its fundamental monomer excitations are gapped and can only be created in pairs.

Our proposed scheme allows to directly implement the gauge constraint of the QDM experimentally by preparing the system in the ground-state manifold of the LPG term as shown in Fig. 1b, d. Note that the LPG term splits the ground-state manifold into two distinct subspaces, QDM₁ and QDM₂, which can be seen by entirely removing the matter atoms and setting ${\hat{n}}_{{{{{{{{\boldsymbol{j}}}}}}}}}=0,1$ in Eq. (2), such that only the link atom Kagome lattice remains; hence it can be implemented in-plane. A dimer then corresponds to either ${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=-1$ (QDM₁) or ${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=+1$ (QDM₂). Due to the LPG protection the QDM subspaces are energetically protected and monomer excitations cost a finite energy 2V.

By weakly driving the system, the motion of virtual, gapped monomer pairs perturbatively induces plaquette terms of strength J_QDM, and we can derive an effective model (Supplementary Note 4) given by:

$${\hat{{{{{{{{\mathcal{H}}}}}}}}}}_{{{{{{{{\rm{QDM}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}=-{J}_{{{{{{{{\rm{QDM}}}}}}}}}\mathop{\sum}\limits_{\hexagon}\mathop{\prod}\limits_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle \in \hexagon}{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{z}+K\mathop{\sum}\limits_{{{{{{{{\rm{NNN}}}}}}}}}{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}{\hat{\tau }}_{\langle {{{{{{{\boldsymbol{m}}}}}}}},{{{{{{{\boldsymbol{n}}}}}}}}\rangle }^{x}.$$

(5)

Here, the NNN link–link interaction K can be tuned by the blockade radius of the Rydberg–Rydberg interactions.

Experimental²⁰ and theoretical^32,43,44,45 studies of QDMs in Rydberg atom arrays for different geometries and parameters regimes have shown to be an promising playground to probe ${{\mathbb{Z}}}_{2}$ spin liquids. Our proposed setup is a promising candidate to further study QDMs due to its versatility and its inherent protection by the LPG term and the phase diagram of Hamiltonian (5) remains to be explored

Here, we examine two limiting cases of Hamiltonian (5). For J_QDM/K ≫ 1, the system is in the so-called plaquette phase⁴⁶, which is characterized by a maximal number of flippable plaquettes and resonating dimers. On the other hand, for J_QDM/K ≪ 1 we find a classical Ising antiferromagnet on the Kagome lattice with NN and NNN interactions from the hard-core dimer constraint and K-term, respectively.

Experimental probes

In the following, we discuss potential signatures of the rich physics that can be readily explored with the proposed experimental setup Eq. (3).

Disorder-free localization

Recently, the idea of disorder-free localization (DFL), where averaging over gauge sectors induces disorder, has sparked theoretical interest^47,48. DFL is an example where the entire ${{\mathbb{Z}}}_{2}$ mLGT Hilbert space participates in the dynamics including sectors with g_j ≠ +1. It has been demonstrated that the (2 + 1)D U(1) quantum link models can show DFL^49,50; further it was proposed that in a (1 + 1)D ${{\mathbb{Z}}}_{2}$ LGT, LPG protection leads to enhanced localization³⁴. However, experimental evidence is still lacking. The scheme we propose is suitable to experimentally study ergodicity breaking without disorder in a strongly interacting (2 + 1)D system with U(1) matter.

In Fig. 3a we show results of a small-scale exact diagonalization (ED) study using realistic parameters for the experimentally relevant microscopic Hamiltonian (Supplementary Note 6). The system is prepared in two different initial states: (1) A gauge-invariant state $\left\vert {\psi }^{{{{{{{{\rm{inv}}}}}}}}}\right\rangle$, and (2) a gauge-noninvariant state $\left\vert {\psi }^{{{{{{{{\rm{ninv}}}}}}}}}\right\rangle$, both with (without) localized matter excitations in subsystem A (B).

Fig. 3: Experimental probes.

We analyze several observables that could be probed experimentally. a, b show results from ED simulations of the time-evolution of the microscopic model (3) with experimentally realistic parameters in a system with coordination number z = 3 (see inset). In (a) we observe disorder-free localization by initializing the system in a gauge-invariant (blue curve) and gauge-noninvariant (red curve) initial state with two matter excitations localized in subsystem A and calculating the time-averaged imbalance between subsystem A and B as shown. In (b), we probe the Schwinger effect by quenching the vacuum state with the microscopic model for different experimentally relevant parameters: matter detuning Δ_m (chemical potential) and link detuning Δ_l (electric field). We find lines of resonance, where the production of matter excitations out of the vacuum is large. In (c), we plot the average U(1) matter density (blue curve) obtained from DMRG calculations on a ladder with J < 0. We can qualitatively understand the sharp decay of matter as a transition into the vacuum phase as discussed in Fig. 2a. Additionally, a kink in the plaquette expectation value (red curve) signals a phase transition. In (d), we use two fluctuating test charges to probe a temperature-induced deconfinement transition in a classical limit of our effective model using Monte Carlo simulations. Both in the percolation strength (red curve) and the Euclidean distance of two matter excitations (blue curve), we find that above a certain temperature T/h the system undergoes a percolation transition.

We find distinctly different behaviors for the time-averaged matter occupation imbalance between subsystem A and B (Supplementary Note 6): While the gauge-invariant state $\left\vert {\psi }^{{{{{{{{\rm{inv}}}}}}}}}\right\rangle$ thermalizes, the gauge-noninvariant state $\left\vert {\psi }^{{{{{{{{\rm{ninv}}}}}}}}}\right\rangle$ breaks ergodicity on experimentally relevant timescales. Experimentally much larger systems can be addressed.

Schwinger effect

The Schwinger effect describes the creation of pairwise matter excitations from vacuum in strongly-coupled gauge theories⁵¹. Here, we use the Schwinger effect to test the validity of our LPG scheme. Starting from the microscopic model (3), we time-evolve the vacuum state with no matter excitations and extract the maximum number of created matter excitations in the initial gauge sector g_j = +1 ∀ j. As shown in Fig. 3b, by tuning the electric field and chemical potential we find resonance lines, where many matter excitations are produced in the system, and we verify that gauge-invariant processes dominate (Supplementary Note 7).

Phase transitions in a ladder geometry

Our proposed scheme is suitable for any geometry with coordination number z = 3; hence one can experimentally study square ladders of coupled 1D chains. Here, we have examined the ground state of Hamiltonian (4) with U(1) matter using the density matrix renormalization group (DMRG) technique⁵² (Supplementary Note 8) on a ladder and we find signatures of a quantum phase transition. As shown in Fig. 3c, both the average density of matter excitations and the plaquette terms, which are experimentally directly accessible by projective measurements, change abruptly by tuning the electric field h indicating a transition into the vacuum phase. We emphasize that the ladder geometry is different from the (2 + 1)D model studied in Fig. 2a, however numerical simulations suggest the presence of a phase transition and hence the ladder geometry offers a numerically and experimentally realistic playground for future studies of our model.

Thermal deconfinement from string percolation

We examine a temperature-induced deconfinement transition in a classical limit of our effective model (4), which neglects charge and gauge dynamics t = Δ_1,2 = J = 0. We use Monte Carlo simulations on a 35 × 35 honeycomb lattice (Supplementary Note 9).

To study thermal deconfinement, we consider exactly two matter excitations which, due to Gauss’s law, have to be connected by a string Σ of electric field lines; i.e., Σ is a path of links with electric fields ${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=-1$ for 〈i, j〉 ∈ Σ. This setting can be used as a probe of a deconfined (confined) phase, in which the ${{\mathbb{Z}}}_{2}$ matter is free (bound)⁵³.

To determine the classical equilibrium state, we note the following: (1) Due to the electric field term h in the Hamiltonian, a string of flipped electric fields ${\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}=-1$ costs an energy 2h ⋅ ℓ, where ℓ is the length of the string. (2) Gauss’s law enforces that at least one string is connected to each matter excitation.

Hence, in the classical ground state the two matter excitations form a mesonic bound state on nearest neighbor lattice sites. Therefore, the matter excitations are confined by a linear string potential. In the co-moving frame of one matter excitation, this model can approximately be described as a particle in a linear confining potential.

At non-zero temperature T > 0, the entropy contribution to the free energy F = E − TS must also be considered. Even though the electric field term h yields an approximately linear string tension, the two charges can separate infinitely in thermal equilibrium provided that $E(\ell ) \, < \, T\log ({N}_{\ell })$ for ℓ → ∞, where $\log ({N}_{\ell })=S$ denotes the entropy S of all the string states N_ℓ with length ℓ (setting k_B = 1) and E(ℓ) is their typical energy⁵³. This happens beyond a critical temperature T > T_c, when a percolating net of ${{\mathbb{Z}}}_{2}$ electric strings forms.

At the critical temperature T_c we anticipate a thermal deconfinement transition, where matter excitations become free ${{\mathbb{Z}}}_{2}$ charges (bound mesons) for T > T_c (T < T_c). To study this transition we use the percolation strength—a measure for the spatial extend of a global string net (see “Methods”)—as an order parameter for the deconfined phase. For experimentally realistic parameters, we find a sharp transition for both the percolation strength and Euclidean distance between two matter excitations around (T/h)_c ≈ 2 as shown in Fig. 3d. Although our classical simulation neglects quantum fluctuations, we expect that the revealed finite-temperature deconfinement transition is qualitatively captured.

For a finite density of matter excitations in the system, the Euclidean distance is not a reasonable measure anymore. However, we speculate that a percolation transition might be related to (de)confinement at finite densities. How this transition is related to the quantum deconfinement transition at T = 0^54,55, driven by quantum fluctuations, will be subject of our future research. Hence, experimentally exploring this transition not only in the classical case, but also in the presence of quantum fluctuations could give insights in the mechanism of charge (de)confinement.

Conclusion

We introduced an experimentally feasible protection scheme for ${{\mathbb{Z}}}_{2}$ mLGTs and QDMs in (2 + 1)D based on two-body interactions, where the ${{\mathbb{Z}}}_{2}$ gauge structure emerges from well-defined subspaces at high and low energy, respectively. The scheme not only allows reliable quantum simulation of gauge theories but provides an accessible approach to engineer gauge-invariant Hamiltonians. We derived an effective ${{\mathbb{Z}}}_{2}$ mLGT, Eq. (4), and QDM, Eq. (5), and discussed some of their rich physics. In particular, we suggested several experimental probes, for which we provide numerical analysis using ED of the experimentally relevant microscopic model (3) as well as DMRG and Monte Carlo simulations of the effective models. Experimentally, we anticipate that significantly larger systems are accessible.

Our proposed scheme is not only suitable and realistic to be implemented in Rydberg atom arrays, see Eq. (3), but it is also of high interest for future theoretical and numerical studies. Hard-core bosonic matter coupled to ${{\mathbb{Z}}}_{2}$ gauge fields in (2 + 1)D plays a role in theoretical models, e.g., in the context of high-Tc superconductivity³⁸. While certain limits such as the fine-tuned, classical limit studied by Fradkin and Shenker⁶ or coupling to fermionic matter^14,15 are well-understood, surprisingly little is known about the physics of our proposed model. What are the implications of anisotropic hopping and pairing t ≠ Δ₁ or anomalous pairing terms Δ₂, i.e., when the classical mapping fails? How can (de)confinement in the presence of dynamical matter be captured? Is disorder-free localization a mechanism for ergodicity breaking in (2 + 1)D? The possibility to study these questions experimentally will spark future theoretical interest.

Methods

Local pseudogenerators for ${{\mathbb{Z}}}_{2}$ mLGTs

The implementation of LGTs in quantum simulation platforms have two inherent challenges to overcome:

• (1) The physical Hilbert space of gauge theories is highly constrained and given by the gauge constraint ${\hat{G}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert {\psi }^{{{{{{{{\rm{physical}}}}}}}}}\right\rangle ={g}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert {\psi }^{{{{{{{{\rm{physical}}}}}}}}}\right\rangle$. In contrast the Hilbert space of the experimental setup is larger and also contains unphysical states $\left\vert {\psi }^{{{{{{{{\rm{unphysical}}}}}}}}}\right\rangle$, which do not satisfy Gauss’s law. Therefore, the dynamics of the system is fragile in the presence of experimental errors which couple physical and unphysical states. However, it has been shown that this can be reliably overcome by energetically gapping the physical from unphysical states using stabilizer/protection terms in the Hamiltonian^27,28. These strong stabilizer terms can be understood as “strong projectors” onto its energy eigenspaces, which are chosen to be the physical subsectors of a ${{\mathbb{Z}}}_{2}$ gauge theory in our case; hence the effective dynamics is constraint to quantum Zeno subspaces⁵⁶. Note that here the quantum Zeno effect is fully determined by a unitary time-evolution and not driven by dissipation, in agreement with the original effect⁵⁶.

  The obvious choice of such a protection term is the symmetry generator, Eq. (1). However, this requires strong and hence unfeasible multi-body interactions. In contrast, the LPG term ${\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$, Eq. (2), only contains two- and one-body terms and is engineered such that an energy gap between the physical and unphysical states is introduced under the reasonable condition that only one (target) gauge sector is protected. In particular, the LPG term in the 2D honeycomb lattice fulfills the condition:

  $$V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert {\psi }^{{{{{{{{\rm{physical}}}}}}}}}\right\rangle =+V\left\vert {\psi }^{{{{{{{{\rm{physical}}}}}}}}}\right\rangle$$

  (6)
  $$V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\left\vert {\psi }^{{{{{{{{\rm{unphysical}}}}}}}}}\right\rangle =\left\{\begin{array}{l}+4V\left\vert {\psi }^{{{{{{{{\rm{unphysical}}}}}}}}}\right\rangle \quad \\ 0V\left\vert {\psi }^{{{{{{{{\rm{unphysical}}}}}}}}}\right\rangle \quad \end{array}\right.,$$

  (7)

  where V is the strength of the LPG term. The spectrum of ${\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ for the gauge choice g_j = + 1 is illustrated in Fig. 1c.

• (2) To study gauge theories, a ${{\mathbb{Z}}}_{2}$-invariant Hamiltonian has to be engineered first, e.g., the Hamiltonian (4) discussed in the main text. In our scheme we exploit the LPG term with its large gap between energy sectors to construct an effective Hamiltonian perturbatively as explained in Supplementary Note 2.

To faithfully stabilize large systems for—in principle—infinitely long times, we want to discuss the stabilization of high-energy sectors by considering undesired instabilities/resonances in the spectrum $V{\sum }_{{{{{{{{\boldsymbol{j}}}}}}}}}{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$. The eigenvalues of $V{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ are w_j = (0,  V,  4V) and we want to protect a sector with intermediate energies. If the interaction strength V is equally strong at each vertex gauge-symmetry breaking can occur. For example, by exciting vertex j₀ and simultaneously de-exciting three vertices j₁, j₂ and j₃. This process has a net energy difference of ΔE = +3V − 3 ⋅ V = 0 and the resonance between the two states can lead to an instability toward unphysical states, hence gauge-symmetry breaking (Supplementary Note 2G).

Therefore, the LPG method without disorder cannot energetically protect against some states that break Gauss’s law on four vertices. An efficient way to stabilize the gauge theory even against such scenarios is to introduce disorder in the coupling strengths by $\hat{W}={\sum }_{{{{{{{{\boldsymbol{j}}}}}}}}}{V}_{{{{{{{{\boldsymbol{j}}}}}}}}}{\hat{W}}_{{{{{{{{\boldsymbol{j}}}}}}}}}$ with V_j = V + δV_j. The couplings δV_j are random and form a so-called compliant sequence^27,29. In 1D systems, this has been shown to faithfully protect ${{\mathbb{Z}}}_{2}$ LGTs also for extremely long times, see ref. ²⁹ for a detailed discussion of (non)compliant sequences. Moreover, we note that for small system sizes and experimentally relevant timescales even noncompliant sequences such as the simple choice V_j = V ∀ j lead to only small errors (Supplementary Note 2G).

For our (2 + 1)D model, we illustrate the effect of disordered protection terms in Fig. 4, which shows that only the gauge non-invariant states are shifted out of resonance. Moreover, we propose to use weak disorder such that the overall perturbative couplings remain unchanged in leading order. We emphasize that the disorder scheme does not require any additional experimental capabilities but only arbitrary control over the geometry as well as local detuning patterns. Even more, an experimental realization will always encounter slight disorder, i.e., the gauge non-invariant processes might already be sufficiently suppressed in experiment.

Fig. 4: Disorder-based protection scheme.

We calculate the spectrum of the minimal model studied in Fig. 3a, b with Ω = 0 and plot all eigenstates around energy E = 4V. Green (red) dots are states that fulfill (break) Gauss’s law as illustrated with two examples in the inset of (a). Without disorder, i.e., V_j = V for all j, the physical and unphysical states are on resonance. In (b), we show the effect of disordered protection terms V_j = V + δV_j, which only shifts the unphysical states out of resonance and hence fully stabilizes the gauge theory. We note that even without disorder, the emergent gauge structure is remarkably robust (Supplementary Note 2G).

We further note that the example above, where Gauss’s law is violated on four vertices, yields gauge-breaking terms in third-order perturbation theory. Ensuring that none of the protection terms V_j have gauge-breaking resonances within such a nearest-neighbor cluster, these terms can be suppressed. However, now it remains space for fifth-order breaking terms on next-nearest neighbor vertices. Hence, the non-resonance condition is now desired on a larger cluster and so forth. Therefore, systematically choosing the disorder potentials can suppress gauge-breaking terms to arbitrary finite order and stabilize gauge invariance up to exponential times. Its fate in the thermodynamic limit, however, is an open question beyond the scope of this study.

Percolating strings from classical Monte Carlo

The finite temperature percolation transition in Fig. 3d is obtained from classical Monte Carlo simulations on the honeycomb lattice with matter and link variables. In this section, we discuss the percolation strength order parameter⁵⁷ and details of the numerical simulations in more detail.

The classical model we consider is motivated by the microscopic Hamiltonian (3) and its effective model (4)—in particular we used the precise effective model as derived in Eq. (S13) of Supplementary Note 2 for Ω/V = 1/8, Δ_m = V/2 and Δ_l/V ≈ 0.044. For elevated temperatures T ≲ V, we expect that classical fluctuations dominate in the system while the Gauss’s law constraint is still satisfied due to the LPG protection. Therefore, we neglect quantum fluctuations and set t = Δ₁ = Δ₂ = J = 0. Hence, the resulting matter-excitation conserving Hamiltonian is purely classical and a configuration is fully determined by the distribution of matter and electric field lines under the Gauss’s law constraint, i.e., $\{({n}_{{{{{{{{\boldsymbol{j}}}}}}}}},{\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x})| {(-1)}^{{n}_{{{{{{{{\boldsymbol{j}}}}}}}}}}={g}_{{{{{{{{\boldsymbol{j}}}}}}}}}{\prod }_{{{{{{{{\boldsymbol{i}}}}}}}}:\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }{\tau }_{\langle {{{{{{{\boldsymbol{i}}}}}}}},{{{{{{{\boldsymbol{j}}}}}}}}\rangle }^{x}\forall {{{{{{{\boldsymbol{j}}}}}}}}\}$ and we consider the sector with g_j = +1 ∀ j.

From the numerical Monte Carlo simulation, we want to quantify the features discussed in the main text: (1) string net formation and (2) bound versus free matter excitations. To this end, we define the percolation strength as the number of strings in the largest percolating cluster of ${{\mathbb{Z}}}_{2}$ electric strings, normalized to the system size. Furthermore, we consider the Euclidean distance between two matter excitation and show that an abrupt change of behavior in this quantity indicates the disappearance of the bound state.

The Monte Carlo simulations are performed on a 35 × 35 honeycomb lattice (in units of lattice spacing) using classical Metropolis-Hastings sampling (Supplementary Note 9). Further analysis of the obtained samples allows to extract the number of strings in the largest percolating cluster to calculate the percolation strength. As shown in Fig. 3d, we find that for low temperatures T the percolation strength vanishes. At a critical temperature (T/h)_c ≈ 2, the percolation strength abruptly increases, i.e., the string net percolates. Moreover, at the same critical temperature (T/h)_c ≈ 2 the Euclidean distance shows a drastic change of behavior and saturates at about 30 for high temperatures. This saturation can be explained by the finite system size.