Polarization bases compensation towards advantages in satellite-based QKD without active feedback

Abstract

Long-distance photonic implementations of quantum key distribution protocols have gained increased interest due to the promise of information-theoretic security against unauthorized eavesdropping. However, a significant challenge in this endeavor is photon-polarization getting affected due to the birefringence of fibers in fiber-based implementations, or variation of reference frames due to satellite movement in long-haul demonstrations. Conventionally, active feedback-based mechanisms are employed for real-time polarization tracking. Here, we propose and demonstrate an alternative approach via a proof-of-principle experiment over an in-lab entanglement-based (BBM92) protocol. In this approach, we perform a quantum state tomography to arrive at optimal measurement bases for any one party resulting in maximal (anti-)correlation in measurement outcomes of both parties. Our polarization-entangled bi-photons have 94% fidelity with a singlet state and a Concurrence of 0.92. By considering a representative 1 ns coincidence window span, we achieve a quantum-bit-error-rate (QBER) of ≈5%, and a key rate of ≈35 Kbps. The performance of our implementation is independent of any local polarization rotation. Finally, using optimization methods we achieve the best trade-off between the key rate, QBER, and balanced key symmetry. Our approach obviates the need for active polarization tracking. It is also applicable to such demonstrations with non-maximally entangled states and prepare-and-measure-based protocols with partially polarized single-photon sources.

Introduction

State-of-the-art classical (public key) cryptosystems, based upon Rivest-Shamir-Adleman (RSA) algorithm¹, offer security dependent upon computational assumptions, which can be easily broken once large-scale quantum computers become available². The solution to this threat is offered by a relatively new cryptographic primitive: quantum key distribution (QKD). The security offered by it is free from any algorithmic or computational advancements³. The first QKD protocol was experimentally demonstrated over a 30 cm long free-space optical channel^4,5. Over the years, several sophisticated methods for performing QKD have been proposed^6,7,8,9 and successfully implemented within laboratory environment^{3,10,11,12,13}. Beyond the shielded lab atmosphere, on one hand, several experiments have been performed to test the practical limits of wide-scale deployment of QKD between the two communicating parties, commonly known as Alice (sender) and Bob (receiver), using optical fibers^2,14. However, it has been reported that the attenuation loss and background noise suffered in fiber-based QKD transmissions prohibit achieving sufficiently large key rates beyond metropolitan-scale networks^15,16. On the other hand, satellite-based QKD serves as a promising technique for overcoming this transmission distance scaling issue. Hence, over the last decade, many free-space experiments have been performed to test QKD implementations with a moving platform including hot-air balloon¹⁷, truck¹⁸, aircraft^19,20, and drone²¹. Furthermore, the progress in the Quantum Experiments at Space Scale project has enabled worldwide efforts toward realizing full QKD demonstrations in free-space using orbiting satellites^15,22.

The polarization of light is a commonly used degree of freedom to achieve the above-mentioned practical implementations of the QKD protocols. However, maintaining the polarization of light over long-distance QKD protocols has practical challenges. For optical fiber-based QKD protocols, the polarization state is affected due to randomly varying birefringence of the optical fiber^23,24. In the case of free space, although the polarization is comparatively robust against atmospheric turbulence^25,26,27,28, the reference frame of the satellite plays a detrimental role—polarization changes according to the movement of the satellite. Hence, it is important to circumvent such polarization changes in both free-space and fiber-based QKD. Conventional mitigation techniques involve active polarization tracking devices^{16,29,30,31,32,33}. For instance, Lee et al.²⁹ used a robotized polarization correction based on an active control system. Again, Toyoshima et al.¹⁶ established a 1 km free space QKD link with an active control system-based polarization tracking jitter error of 0.092°. In the above protocols, the authors calibrated the polarization change during the QKD session. In an alternative approach, Ding et al.³⁰ tracked the polarization basis using the sifted keys revealed during the QKD error-correction procedure. In the case of fiber-based protocols, the polarization compensation was done by Xavier et al.³¹, where the single photons were wavelength-multiplexed with two classical beams. The classical beams reveal information regarding polarization fluctuation. Based on the polarization fluctuation, the authors used an active polarization control system to compensate for the polarization change. Again Shi et al.³⁴ employed a stochastic algorithm in a feedback loop to dynamically compensate for any fiber-induced polarization state fluctuations. Fast feedback-based polarization controlling over an aerial fiber has been demonstrated by Li et al.³². These conventional approaches to mitigate polarization fluctuation require active control systems.

In this work, we propose an alternative solution where instead of correcting polarization fluctuation of the encoded state, we optimize the measurement bases at the receiver end. Using an in-lab single-photon-based BBM92 protocol implementation^8,12, we demonstrate that our approach mitigates any performance limitations of the protocol otherwise posed upon by polarization fluctuations of the entangled photons. In this implementation, we first produce polarization-entangled single-photon pairs using a Sagnac interferometer-based type-II Spontaneous Parametric Downconversion (SPDC) source³⁵. Through the optical fibers, we transmit the generated polarization-entangled single-photon pairs to two modules. The operations performed at the modules represent the operations by the communicating parties, henceforth we will refer to these modules as Alice and Bob. In a conventional BBM92 protocol, Alice and Bob agree on two out of three mutually unbiased measurement bases, ${\sigma }_{1}:\{\left\vert D\right\rangle ,\left\vert A\right\rangle \}$, ${\sigma }_{2}:\{\left\vert R\right\rangle ,\left\vert L\right\rangle \}$, and ${\sigma }_{3}:\{\left\vert H\right\rangle ,\left\vert V\right\rangle \}$. Here σ_i is the Pauli operator, and the corresponding measurement bases are the eigenstates of the Pauli operator. On every incoming photon, the parties randomly measure the polarization in σ_i or σ_j bases to generate the time-stamps on which the cross-correlation is performed to detect the (anti-)correlations. However, the fiber birefringence affects the polarization states of both Alice and Bob. This jeopardizes the expected coincidence counts after the measurements. To mitigate this effect and thus achieve high coincidences, we evaluate the optimal measurement bases on Bob’s side.

A significant aspect of our work involves optimization techniques for single-photon-based BBM92 protocol implementation. The details of these techniques have been discussed in the subsection “Optimization methods” under the section “Methods”. In the case of the BBM92 protocol, once the communicating parties generate the time-stamps after measuring the entangled photons in the desired and undesired bases, our optimization techniques find the optimal coincidence window spans required for determining the maximal (desired) signal and minimal noise (undesired) coincidences. We quantify the performance of our BBM92 protocol implementation by using three standard measures: key rate, quantum-bit-error-rate (QBER), and asymmetry of the obtained key string³. Key rate is the average number of key-bits generated per second (for exact expression, refer Eq. (14a)). QBER is the ratio of error rate to key rate (for exact expression, refer Eq. (14b)). Asymmetry (or key symmetry) quantifies the disparity between the number of 0 and 1 bits in the generated key string (for exact expression, refer Eq. (14c)). Using our optimization technique, we are able to achieve a higher key rate while maintaining an information-theoretically secure QBER (<11%)^36,37. Nevertheless it is important to mention that even without employing these optimization techniques, irrespective of the output polarization state, our choice of optimal measurement bases allows us to achieve around 5% QBER and 35 Kbps key rate for 1 ns coincidence window span, and around 10% QBER and 50 Kbps key rate for 4 ns coincidence window span. Upon further optimization, we are also able to restrict the individual QBERs for all four measurement pairs below 11% bound, while restricting the overall QBER to around 8.5%.

Our method overcomes a number of challenges associated with active feedback systems. Firstly, while the aim of active feedback systems is to compensate for any instabilities in the properties of an input state, often such control systems have more elements than the raw system, which incurs additional costs. Furthermore, active control systems have more parts than the raw system. Hence they are more prone to faults, which can lead to instability of the closed loop. In addition, such control systems often employ trial and error methods to nullify the output deviations. This approach often leads to the oscillatory response of the closed loop. We overcome the above challenges by the following procedure. We first perform a quantum state tomography (QST) at the output. Then, from the tomographically reconstructed density matrix, we evaluate the receiver’s optimal choice of measurement bases such that the measurement outcomes lead to a high (anti-)correlation that is required for successful key generation. Although demonstrated over a single-photon-based BBM92 protocol implementation, it is important to note that our method can be generalized toward any QKD protocol.

Results

Theory for optimized measurement bases

In this subsection, we describe our method to construct the optimal measurement bases to overcome polarization fluctuation during the transmission of single photons over a long distance. In practice, the polarization state of both photons would be affected. However, the polarization fluctuation of two subsystems could be mitigated by addressing only one of the subsystems. We convey this in the following lemma where we show that two local unitary operations on each subsystem of a maximally-entangled state are equivalent to a single unitary operation in one of the subsystems.

Lemma 1. The action of local unitary operations U and V on each subsystem of a Bell state ${\left\vert \psi \right\rangle }_{i}^{AB}$ is equivalent to a single local unitary operation W = Vσ_iU^Tσ_i on the subsystem B, i.e., $({U}^{A}\otimes {V}^{B}){\left\vert \psi \right\rangle }_{i}^{AB}=({{\mathbb{1}}}^{A}\otimes {W}^{B}){\left\vert \psi \right\rangle }_{i}^{AB}$.

Proof Firstly, let us consider the Bell-state ${\left\vert \psi \right\rangle }_{0}=1/\sqrt{2}(\left\vert 00\right\rangle +\left\vert 11\right\rangle )$. It is well-known³⁸ that any unitary operation U acting on one subsystem of ${\left\vert \psi \right\rangle }_{0}$ is equivalent to the transpose of the same unitary U^T acting on the other subsystem:

$$(U\otimes {\mathbb{1}}){\left\vert \psi \right\rangle }_{0}=({\mathbb{1}}\otimes {U}^{T}){\left\vert \psi \right\rangle }_{0}.$$

(1)

Hence, for two local unitary operations U and V on each subsystem of ${\left\vert \psi \right\rangle }_{0}$:

$$(U\otimes V){\left\vert \psi \right\rangle }_{0}=({\mathbb{1}}\otimes V).(U\otimes {\mathbb{1}}){\left\vert \psi \right\rangle }_{0}=({\mathbb{1}}\otimes V{U}^{T}){\left\vert \psi \right\rangle }_{0}.$$

(2)

Now, let us consider other Bell-states $\{{\left\vert \psi \right\rangle }_{i}\}$ which are related to ${\left\vert \psi \right\rangle }_{0}$ by local Pauli operations {σ_i}:

$${\left\vert \psi \right\rangle }_{i}=({\mathbb{1}}\otimes {\sigma }_{i}){\left\vert \psi \right\rangle }_{0}.$$

(3)

As Pauli matrices are self-inverse, we also have:

$${\left\vert \psi \right\rangle }_{0}=({\mathbb{1}}\otimes {\sigma }_{i}){\left\vert \psi \right\rangle }_{i}.$$

(4)

For the sake of consistency, we assume σ₀ to be the identity operation. Now, for two local unitary operations U and V acting on ${\left\vert \psi \right\rangle }_{i}$, we can write:

$$\begin{array}{ll}(U\otimes V){\left\vert \psi \right\rangle }_{i}&=(U\otimes V{\sigma }_{i}){\left\vert \psi \right\rangle }_{0}=({\mathbb{1}}\otimes V{\sigma }_{i}{U}^{T}){\left\vert \psi \right\rangle }_{0}\\ &=({\mathbb{1}}\otimes V{\sigma }_{i}{U}^{T}{\sigma }_{i}){\left\vert \psi \right\rangle }_{i}=({\mathbb{1}}\otimes W){\left\vert \psi \right\rangle }_{i}.\end{array}$$

(5)

Here, W = Vσ_iU^Tσ_i. The first, second and third equalities are due to Eqs. (2)–(4), respectively. This concludes our Lemma.

Motivated by the above lemma, if we could infer the relevant unitary operation W, we could absorb W in our measurement, i.e., if the desired measurement basis were $\{\left\vert \alpha \right\rangle ,\left\vert {\alpha }^{\perp }\right\rangle \}$, to mitigate the effect of W, we would have to measure in $\{{W}^{{{\dagger}} }\left\vert \alpha \right\rangle ,{W}^{{{\dagger}} }\left\vert {\alpha }^{\perp }\right\rangle \}$ basis. However, in practice, the photon sources have non-ideal purity. Hence, to estimate the unitary, or equivalently the nearest pure state after the action of the unitary W, we first perform quantum state tomography at the output. Let us assume the tomographically reconstructed density matrix is ρ. Next, we evaluate the nearest pure state of ρ, this nearest pure state will basically be the bell state affected by the unitary W. Next, based on the nearest pure state, we find the optimal measurement bases at Bob’s end: Bob’s $\{\left\vert {\phi }_{H}\right\rangle ,\left\vert {\phi }_{H}^{\perp }\right\rangle \}$ measurement basis showing the maximum (anti-)correlation with Alice’s $\{\left\vert H\right\rangle ,\left\vert V\right\rangle \}$ measurement basis, and Bob’s $\{\left\vert {\phi }_{D}\right\rangle ,\left\vert {\phi }_{D}^{\perp }\right\rangle \}$ basis showing the maximum correlation with Alice’s $\{\left\vert D\right\rangle ,\left\vert A\right\rangle \}$ measurement. In the next subsection, we show the method to find the nearest pure state.

Nearest pure state from the eigendecomposition

The nearest pure state of a density matrix is, as the name suggests, the state that has the maximum overlap to the said density matrix. In our case, we are using fidelity to define the overlap. Formally, the pure state $\vert {\psi }_{\rho }\rangle$ is the ‘nearest’ to the density matrix ρ when their fidelity F satisfies:

$$F=\left\langle {\psi }_{\rho }\right\vert \rho \left\vert {\psi }_{\rho }\right\rangle \ge \left\langle \alpha \right\vert \rho \left\vert \alpha \right\rangle ,\,\,{{{{{\rm{for}}}}}}\,{{{{{\rm{any}}}}}}\,{{{{{\rm{pure}}}}}}\,{{{{{\rm{state}}}}}}\,\left\vert \alpha \right\rangle .$$

(6)

To find the nearest pure state, we perform eigendecomposition of the density matrix ρ. The nearest pure state would be the eigenvector corresponding to the maximum eigenvalue. Formally, if the eigendecomposition of $\rho ={\sum }_{i}{\lambda }_{i}\left\vert {\lambda }_{i}\rangle \langle {\lambda }_{i}\right\vert$, with {λ_i} being the eigenvalues and $\{\left\vert {\lambda }_{i}\right\rangle \}$ being the corresponding eigenvectors. Without loss of generality, we also assume that {λ_i} are arranged in descending order: λ_i≥λ_j for i < j. Hence, according to our notation, λ₁ is the maximum eigenvalue and $\left\vert {\lambda }_{1}\right\rangle$ is the nearest pure state. In the following lemma, we will prove $\left\vert {\lambda }_{1}\right\rangle$ indeed has the maximum overlap with ρ.

Lemma 2. For a density matrix ρ having eigendecomposition $\rho ={\sum }_{i}{\lambda }_{i}\left\vert {\lambda }_{i}\rangle \langle {\lambda }_{i}\right\vert$, with λ_i≥λ_j for i < j, the nearest pure state of the density matrix is $\left\vert {\lambda }_{1}\right\rangle$.

Proof Let us consider an arbitrary pure state $\left\vert \alpha \right\rangle$ expressed in $\left\vert {\lambda }_{i}\right\rangle$ basis, $\left\vert \alpha \right\rangle ={\sum }_{i}{a}_{i}\left\vert {\lambda }_{i}\right\rangle$, with ∑_i∣a_i∣² = 1. The fidelity between the state $\left\vert \alpha \right\rangle$ and ρ is:

$$\left\langle \alpha \right\vert \rho \left\vert \alpha \right\rangle = \mathop{\sum}\limits_{i,j}{a}_{i}^{* }{a}_{j}\langle {\lambda }_{i}\vert \rho \vert {\lambda }_{j}\rangle \\ = \mathop{\sum}\limits_{i,j,k}{a}_{i}^{* }{a}_{j}{\lambda }_{k}\langle {\lambda }_{i}| {\lambda }_{k}\rangle \langle {\lambda }_{k}| {\lambda }_{j}\rangle =\mathop{\sum}\limits_{i}{\lambda }_{i}| {a}_{i}{| }^{2}.$$

(7)

Note that the set {∣a_i∣²} form a probability distribution: ∑_i∣a_i∣² = 1 and 0 ≤ ∣a_i∣² ≤ 1, hence Eq. (7) represents a convex combination of the eigenvalues of ρ. We know that the convex combination of scalars is bounded by the maximum of such scalars³⁹. Hence, the set {λ_i} being in descending order, the quantity ∑_iλ_i∣a_i∣² is maximum if and only if a₁ = 1 and a_i≠1 = 0. In that case, $\left\vert \alpha \right\rangle =\left\vert {\lambda }_{1}\right\rangle$: the eigenvector corresponding to the maximum eigenvalue.

Optimal measurement bases for BBM92 protocol

From our tomographically obtained density matrix ρ^AB, we find the nearest pure state ${\left\vert \psi \right\rangle }_{\rho }^{AB}$. We can express the nearest pure state in the form:

$${\left\vert \psi \right\rangle }_{\rho }^{AB}=\frac{1}{\sqrt{2}}\left({\left\vert H\right\rangle }^{A}{\left\vert {\phi }_{H}\right\rangle }^{B}+{\left\vert V\right\rangle }^{A}{\left\vert {\phi }_{V}\right\rangle }^{B}\right).$$

(8)

In an ideal scenario of maximally entangled state, $\left\vert {\phi }_{H}\right\rangle$ and $\left\vert {\phi }_{V}\right\rangle$ are orthogonal to each other, i.e., ∣〈ϕ_H∣ϕ_V〉∣² = 0. However, depending on the Concurrence of our estimated nearest pure state, $\left\vert {\phi }_{V}\right\rangle$ will have a small contribution from $\left\vert {\phi }_{H}\right\rangle$. In our experiment, however, the Concurrence of the estimated nearest pure state is ~0.99. This ensures that $\left\vert {\phi }_{H}\right\rangle$ and $\left\vert {\phi }_{V}\right\rangle$ are almost orthogonal, i.e., we have ∣〈ϕ_H∣ϕ_V〉∣² ≈ 0. From Eq. (8), we can see when Alice measures in $\{\left\vert H\right\rangle ,\left\vert V\right\rangle \}$, Bob gets maximum (anti-)correlation while measuring in $\{\left\vert {\phi }_{H}\right\rangle ,\left\vert {\phi }_{H}^{\perp }\right\rangle \}$ basis.

Similarly, when Alice measures in a different basis, we can calculate the corresponding rotated mutually unbiased basis. For instance, when we express the nearest pure state in diagonal/anti-diagonal basis:

$${\left\vert \psi \right\rangle }_{\rho }^{AB}=\frac{1}{\sqrt{2}}\left({\left\vert D\right\rangle }^{A}{\left\vert {\phi }_{D}\right\rangle }^{B}+{\left\vert A\right\rangle }^{A}{\left\vert {\phi }_{A}\right\rangle }^{B}\right),$$

(9)

we can see that when Alice is measuring in $\{\left\vert D\right\rangle ,\left\vert A\right\rangle \}$ basis, Bob has to measure in $\{\left\vert {\phi }_{D}\right\rangle ,\left\vert {\phi }_{D}^{\perp }\right\rangle \}$ basis to get the highest (anti-)correlation. Note that, $\left\vert {\phi }_{D}\right\rangle =1/\sqrt{2}(\left\vert {\phi }_{H}\right\rangle +\left\vert {\phi }_{V}\right\rangle )$ and $\left\vert {\phi }_{A}\right\rangle =1/\sqrt{2}(\left\vert {\phi }_{H}\right\rangle -\left\vert {\phi }_{V}\right\rangle )$. As discussed, 0.99 Concurrence of our estimated nearest pure state ensures ∣〈ϕ_A∣ϕ_D〉∣² ≈ 0. In the next subsection, we are going to discuss our experimental results.

Experimental outcome

We implement the BBM92 protocol using a polarization-entangled bi-photon source (PEBS) based upon a doubly-pumped type-II SPDC process in a Sagnac loop³⁵. An abridged schematic of our experimental setup has been provided in the figure titled “Experimental schematic for the source module” under the section “Methods”. Our source produces polarization-entangled single-photon pairs having 94% fidelity with the Bell-state ${\left\vert \psi \right\rangle }_{1}=1/\sqrt{2}(\left\vert HV\right\rangle +\left\vert VH\right\rangle )$, and a Concurrence of 0.92. We transmit the single photons to Alice and Bob module through two optical fibers. Each optical fiber is accompanied by a fiber-bench Polarization Controller Kit by Thorlabs (PC-FFB-780), see the figure titled “Experimental schematic for the BBM92 protocol” under the section “Methods”. For a detailed description of the experimental schematic, see the subsection “Experimental schematic” under the section “Methods”. Our objective is to have a controlled polarization change introduced in the experiment to demonstrate the efficacy of our correction mechanism for different cases. The introduction of the polarization controller enables the introduction of polarization fluctuation in both single photons, to essentially manipulate/control the fidelity of the two-qubit state with the ideal $\left\vert {\psi }_{1}\right\rangle$ state at the output end. For each altered polarization state, we perform a quantum state tomography at the output. From the tomographically reconstructed density matrix, we estimate the nearest pure state using Lemma 2. Next, we evaluate the measurement basis at Bob’s end, giving maximum (anti-) correlation with Alice’s σ₃ basis:$\{\left\vert {\phi }_{H}\right\rangle ,\left\vert {\phi }_{H}^{\perp }\right\rangle \}$ as in Eq. (8) and with Alice’s σ₁ basis: $\{\left\vert {\phi }_{D}\right\rangle ,\left\vert {\phi }_{D}^{\perp }\right\rangle \}$ as in Eq. (9). To complete the protocol, one of the parties (say Alice) sends his/her time-stamp information to the other party (say Bob) via a publicly accessible classical channel. Bob then performs a cross-correlation between his time-stamp and Alice’s time-stamp to generate the coincidence peaks. He further runs the optimization methods (see the subsection “Optimization methods” under the section “Methods”. for details) to optimize the window sizes for each coincidence peak to optimize the key rate, Eq. (14a), and QBER, Eq. (14b). Based on the optimized window choices, Bob informs Alice, via the public classical channel, which of her time-stamps needs to be discarded. From the remaining time-stamps, the two parties can reconstruct their respective keys from the information about their measurement outcomes. Note that, these measurement outcomes are private to the individual parties.

In our result, we first show how optimizing measurement bases could result in low QBER irrespective of the polarization rotation through the single-mode fibers. This is in stark contrast to the conventional approach, where we restrict our choice of measurement to Pauli bases. In such cases, we would see higher QBER for lower fidelity.

Next, we use our optimization methods for further improvement of the performance of BBM92 protocol, (see the subsection “Optimization methods” under the section “Methods”). To summarize, the goals of the three optimization methods are classified as follows. In method A, we maximize the keyrate (14a) while maintaining an information-theoretically secure bound of less than 11% QBER (14b) and ensuring symmetry in the obtained key bits. It is important to highlight that the optimized coincidence time window spans along each measurement bases need not be equal in this case. In method B, we relax the key symmetry constraint but enforce equal coincidence time window spans along the individual measurement bases. Finally, in method C, we retain the constraints of method B and in addition, maintain the QBERs of each individual measurement bases below the 11%.

We show the advantages of finding the optimal measurement bases in Fig. 1 where the orange circles represent QBERs for different fidelities with ${\left\vert \psi \right\rangle }_{1}$ for optimal measurement bases. We see how the optimal measurements can lower the QBERs below 11% independent of the fidelity of the output state. In contrast, the blue circles represent the QBERs for different fidelities for conventional measurement bases (σ₁ and σ₃ bases). We note that the QBERs increase with lower fidelity. We note that the decrease of the QBERs is not monotonic, as in the case of the fidelities in the range of 40–60% and 70–80%. This is because we are using the fixed Pauli bases of σ₁ and σ₃ for all the fidelity points. However, choosing a different Pauli bases turn out to be more optimal in certain scenarios. To provide a specific example, below we write the tomographically reconstructed density matrix having 60% fidelity with the state ${\left\vert \psi \right\rangle }_{1}$:

$${\rho }_{60 \% }=\left[\begin{array}{cccc}0.12&-0.14-0.14i&0.18+0.04i&0.08+0.1i\\ -0.14+0.14i&0.36&-0.27+0.19i&-0.23-0.06\\ 0.18-0.04i&-0.27-0.19i&0.3&0.12+0.16i\\ 0.08-0.1i&-0.23+0.06i&0.12-0.16i&0.22\\ \end{array}\right].$$

(10)

Fig. 1: Unoptimized QBERs vs. fidelity with the singlet state ${\left\vert \psi \right\rangle }_{1}$.

The blue dots represent our experimentally measured QBERs with the conventional bases of measurement (i.e., σ₁ and σ₃). It can be observed that the experimentally obtained QBERs are not monotonically decreasing, i.e., the QBERs portray an increasing trend for the fidelity of 40–60% and 70–80%. However, a monotonic graph (i.e., the cyan crosses) can be obtained, when we choose the pair of Pauli measurement bases (i.e., any two out of σ₁, σ₂, and σ₃) that offers the best signal-to-noise ratio at each fidelity point. Nevertheless, it can be noted that the optimized measurement bases outperform the conventional measurement bases by offering a lower QBER (orange dots) irrespective of their fidelity with the singlet state. At each fidelity point, we measured ten datasets, the mean of them represents the data points, while their standard deviation has been indicated with error bars. Note that the standard deviations being very small, result in error bars being even shorter than the diameter of the data points, and hence they are not observable against those points.

For the above density matrix, when both parties measure in σ₁, σ₂, and σ₃ bases, the associated visibilities (see Eq. (13b)) are 37%, 65%, and 24% respectively. Naturally, choosing the measurement bases associated with higher visibilities, i.e., σ₁ and σ₂ bases (instead of σ₁ and σ₃) leads to lower QBER of 25%. The cyan crosses in Fig. 1 convey the idea, where we use the tomographically reconstructed density matrix to estimate the QBERs for two optimal Pauli bases, and achieve a monotonically decreasing set of QBERs. In all such cases, the optimal choice of measurement bases outperforms conventional measurement bases.

In Fig. 2, we present the unoptimized results and show how varying coincidence window sizes lead to different QBERs and key rate. In both Fig. 2a, b, the red circles represent the data for 1 ns wide coincidence windows, the blue circles represent the data for 4 ns wide coincidence windows. We can see for the 1 ns coincidence window, both QBERs (≈5%) and key rate (≈35 Kbps) are lower compared to the 4 ns coincidence window where we have QBERs of ≈10% and key rate of ≈50 Kbps. To achieve optimal window sizes resulting in a better trade-off between QBER and key rate, i.e., low QBER and high key rate, we use the optimization methods.

Fig. 2: Unoptimized QBER and keyrate vs. fidelity with a singlet state.

a represents the unoptimized QBER (in %) vs. fidelity (in %) with the ${\left\vert \psi \right\rangle }_{1}$ state for two different coincidence window spans. b represents the unoptimized key rate (in Kbps) vs. fidelity (in %) with the ${\left\vert \psi \right\rangle }_{1}$ state plot for two different coincidence window spans. The red and blue dots represent values corresponding to 1 ns and 4 ns coincidence window spans, respectively. For each fidelity point, the mean and standard deviation has been obtained over ten measurement runs. The data points represent the mean of those runs, while the standard deviation in them has been indicated by the corresponding error bars. Note that for a few data points in (a) the standard deviations being very small, result in error bars being even shorter than the diameter of the points, and hence they are not observable against those points.

In Fig. 3a, we show the advantages of the optimization methods. The green circles represent optimized overall QBERs for the overall key string, however, in such cases the QBERs for individual bases are not optimized (optimization method B). The magenta circles represent the optimized overall QBERs where the individual QBERs are optimized as well (optimization method C). Using optimization, we could reduce the overall QBER while maintaining a high key rate of ~50 Kbps. In Fig. 3b, we show how the optimization methods take QBERs for individual measurement bases into account. It is possible that while maintaining the overall QBER below 11%, the QBERs for individual measurement bases may shoot up above 11% leading to leakage of information to the eavesdropper. To avoid this, it is important to contain the individual QBERs below 11%. In Fig. 3b, the green circles represent the maximum unoptimized QBERs for the individual measurement bases. The magenta circles represent the optimized QBERs for the individual measurement bases. We note that the optimization methods ensure that the individual QBERs lie below 11%. Enforcing such restrictions on the individual QBERs leads to relatively lower overall QBERs at 60 and 80% fidelities, see Fig. 3a. This results from the presence of relatively higher unoptimized individual QBERs along certain projection bases, see the green datapoints at those two fidelities in Fig. 3b. Hence, compared to other datapoints, the optimization method C uses smaller coincidence window spans to bring the individual QBERs down to 11%, resulting in lower overall QBER.

Fig. 3: Optimized and unoptimized QBER vs. fidelity with a singlet state.

Plots highlighting the advantages of our optimization methods. a plots overall QBERs (in %) after considering coincidence measurements among both MUB vs. fidelity (in %) with the ${\left\vert \psi \right\rangle }_{1}$ state. b plots maximal QBERs (in %) considering coincidence measurements for a particular (i.e., individual) MUB vs. fidelity (in %) with the ${\left\vert \psi \right\rangle }_{1}$ state, corresponding to the two results depicted in (a). The green dots result from the optimization method in which the QBERs for each individual measurement basis were not optimized (optimization method B), while the magenta dots are obtained from another variant of the optimization method in which the individual QBERs were restricted below 11% (optimization method C). Note that in (b), the information-theoretically secure bound of 11% has been indicated with the black dashed line. Using our optimization methods, we could reduce the overall QBER while maintaining a high key rate of ≈50 Kbps. For each data point against a given fidelity, the mean and standard deviation has been obtained over ten measurement runs similar to Fig. 2 (although in these cases for optimized window spans). Again, the data points represent the mean of those runs, while the standard deviation in them has been indicated by the corresponding error bars. Note that for some data points the standard deviations being very small, result in error bars being even shorter than the diameter of the points, and hence they are not observable against those points.

A parallel aim of our BBM92 protocol implementation is also to simultaneously attain a balanced key symmetry while maintaining a high key rate, along with an information-theoretically secure QBER. We achieve this goal via the use of optimization method A (for methodology details, refer the subsection “Optimization methods” under the section “Methods”). The performance of method A in contrast to methods B and C is presented Table 1. We particularly show considering two representative fidelity points at the boundaries of the measured range of fidelities: 91 and 9%, to convey that we obtain an improved key symmetry, i.e., 50.98 : 49.02 for 91% fidelity and 50.99 : 49.01 for 9% fidelity, while restricting the overall QBERs within the information-theoretically secure threshold and extracting comparable key rates, by using optimization method A.

Table 1 Optimized results of the average key rate, QBER, and asymmetry (i.e., key symmetry).

Resource requirement

For performing projective measurements along rectilinear/diagonal polarization bases in any conventional BBM92 protocol implementation, half-wave plates (HWPs) are required along with polarizing beam-splitters (PBSs). In terms of resources, our approach only requires the inclusion of quarter-wave plates (QWPs) in front of the HWPs. This helps in performing the QST at two such projective measurement setups and finally also the protocol measurements along rotated (optimized) projection bases. Furthermore, it may be efficient to mount the waveplates involved in QST on motorized rotation stages. In our QST measurement, we perform 36 coincidence detections of the entangled photons transmitted to Alice and Bob detection modules, from an over-complete tomography measurement set. Considering the minimal acquisition time of 1 s for our time-tagging unit, an upper bound on the overall time estimated by us to perform a QST and then infer the optimal measurement bases, loosely amounts to about 12 min. This time window required for evaluating the optimal measurement bases being solely dependent on the duration of performing the tomography of the output state can be significantly shortened with efficient tomography techniques that offer faster convergence rates based on Bayesian learning^40,41, or machine learning-based approaches^42,43,44, as well as fast polarization controllers like electro-optic modulators.

Conclusions

In summary, we have addressed the practical challenges of long-distance QKD protocols utilizing the polarization of photons to encode the quantum state. The polarization state of light is inevitably affected during long-distance transmission. The conventional active feedback system-based polarization tracking techniques are resource intensive, resulting in additional maintenance costs. We have shown that instead of active polarization correction, we can construct optimal measurement bases to achieve low QBER and high key rate irrespective of the polarization fluctuation. As a proof-of-principle demonstration, we have used the BBM92 protocol using polarization-entangled photon pairs. We overcome the polarization fluctuations of the single-photons during transmission through optical fibers by performing optimal measurements. As our approach is based on the general principle of state preparation and measurement duality, the method can easily be extended to other QKD protocols. To construct the optimal choice of measurements, the parties perform a quantum state tomography on the received two-qubit state before each QKD session. Based upon the tomographically reconstructed density matrix, Bob arrives at his choice of measurement bases through the techniques introduced in the subsection “Theory for optimized measurement bases” under the section “Results”. Our approach overcomes the need for active feedback-based control systems. Another advantage of our protocol could be found in scenarios where the entangled photon source is itself not perfect. In principle, the generated entangled state could be either partially mixed or non-maximally entangled. Our technique provides a recipe to construct optimal measurement bases even in such non-ideal conditions. Our technique could be particularly advantageous in downlink-based QKD protocols, e.g., the quantum experiments using the Micius satellite⁴⁵ where the photon sources, being in the satellite, are not readily accessible to the experimentalists. In such cases, altering the more easily accessible measurement bases of only one party could overcome the detrimental effects of polarization fluctuation. To implement such large-scale quantum communication protocols, it is important to conduct follow-up studies, e.g., on efficient synchronized quantum state tomography between two distant measurement stations, the role of finite-key effect⁴⁶, and the effect of the photon loss due to free-space channel. However, our proposed method opens a new paradigm for resource-efficient polarization bases compensation techniques without active feedback in long-distance quantum communication including satellite-based approaches. It is important to point out that a similar approach to choosing a suitable measurement basis has been reported by Tannous et al.⁴⁷. The authors consider a 6 state–4 state QKD protocol, i.e., where one party measures in six measurement bases: rectilinear, diagonal and circular polarization bases; and the other party measures in four measurement bases: rectilinear and diagonal polarization bases. These 24 measurements ensure the correction of arbitrary relative phase ϕ in the singlet state $1/\sqrt{2}(\left\vert {{{\rm{HV}}}}\right\rangle +{e}^{i\phi }\left\vert {{{\rm{VH}}}}\right\rangle )$. However, note that authors only consider a specific type of polarization fluctuation constrained by the photons traveling through polarization-maintaining fibers. In practice, the photons might experience more general polarization fluctuations resulting in unconstrained local operations. We propose a method to mitigate the effects of such general local unitary operation in our work, ensured by single-mode non-polarization-maintaining fibers. To address such arbitrary polarization fluctuation, we need to perform additional measurements to tomographically reconstruct the entangled density matrix. The primary objective of our work is to obviate the need for maintaining the polarization state of the photons using resource-intensive control systems. So far, we are constructing the optimal measurement bases using a tomographically complete dataset. As a future direction, it would be interesting to see if such optimization of measurement bases is possible without performing a full quantum state tomography.

Methods

Notations

We introduce the relevant notations used in this paper. We denote the Pauli group as {σ_i∣i ∈ {0, 1, 2, 3}} where ${\sigma }_{0}={\mathbb{1}}$ is the identity operation and σ₁, σ₂ and σ₃ are Pauli X, Y and Z respectively. To denote the Bell states, note that all Bell states are related by local Pauli operations, hence we use an indexed notation of the Bell states as $\{{\left\vert \psi \right\rangle }_{i}| i\in \{0,1,2,3\}\}$, such that ${\left\vert \psi \right\rangle }_{i}=({\mathbb{1}}\otimes {\sigma }_{i}){\left\vert \psi \right\rangle }_{0}$. In this way, our indexed Bell states are:

$$\begin{array}{l}{\left\vert \psi \right\rangle }_{0}=\frac{1}{\sqrt{2}}(\left\vert 00\right\rangle +\left\vert 11\right\rangle ),\,\,{\left\vert \psi \right\rangle }_{1}=\frac{1}{\sqrt{2}}(\left\vert 01\right\rangle +\left\vert 10\right\rangle ),\\ {\left\vert \psi \right\rangle }_{2}=\frac{1}{\sqrt{2}}(\left\vert 01\right\rangle -\left\vert 10\right\rangle ),\,\,{\left\vert \psi \right\rangle }_{3}=\frac{1}{\sqrt{2}}(\left\vert 00\right\rangle -\left\vert 11\right\rangle ).\end{array}$$

(11)

As we use the polarization degree of freedom of the photons to encode the quantum state—horizontal polarization $\left\vert H\right\rangle \to \left\vert 0\right\rangle$, and vertical polarization $\left\vert V\right\rangle \to \left\vert 1\right\rangle$,—we will interchangeably use standard notations for polarization to denote our quantum states:

$$\left\vert H\right\rangle \equiv \left\vert 0\right\rangle ,\,\,\left\vert V\right\rangle \equiv \left\vert 1\right\rangle ,\\ \left\vert D\right\rangle \equiv \frac{1}{\sqrt{2}}(\left\vert 0\right\rangle +\left\vert 1\right\rangle ),\,\,\left\vert A\right\rangle \equiv \frac{1}{\sqrt{2}}(\left\vert 0\right\rangle -\left\vert 1\right\rangle ),\\ \left\vert R\right\rangle \equiv \frac{1}{\sqrt{2}}(\left\vert 0\right\rangle +i\left\vert 1\right\rangle ),\,\,\left\vert L\right\rangle \equiv \frac{1}{\sqrt{2}}(\left\vert 0\right\rangle -i\left\vert 1\right\rangle ).$$

(12)

Experimental schematic

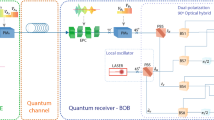
Our experimental setup for implementing the BBM92 protocol contains a PEBS, which generates polarization-entangled photons pairs via spontaneous parametric down-conversion (SPDC) process, from a doubly-pumped type-II periodically-poled KTP (PPKTP) crystal in a Sagnac configuration as schematically represented in Fig. 4³⁵. More specifically, we use a continuous-wave pump beam at 405 nm through a type-II PPKTP crystal with 10 μm poling period as indicated in Fig. 4. Passing the pump beam through the crystal produces down-converted, degenerate single-photon pairs with a central wavelength of 810 nm. The single photons are then separated from the pump beam via two dichroic mirrors. In case of the perfect alignment of the setup, a horizontally polarized ($\left\vert H\right\rangle$) pump beam produces two down-converted single photons of polarization state $\left\vert HV\right\rangle$. A vertically polarized ($\left\vert V\right\rangle$) pump beam, on the other hand, produces single photons with polarization state $\left\vert VH\right\rangle$. By changing the pump polarization, we can get a polarization-entangled state ${\left\vert \psi \right\rangle }_{\phi }=1/\sqrt{2}(\left\vert {{{\rm{HV}}}}\right\rangle +{e}^{i\phi }\left\vert {{{\rm{VH}}}}\right\rangle )$. The relative phase ϕ can be (adjusted) set to zero by varying the pump polarization using the quater-wave plate (QWP) and half-wave plate (HWP) placed at the entry of the interferometer, i.e., in principle oriented at 0° and 22.5°, respectively, in order to produce at singlet state as shown in Fig. 4.

Fig. 4: Experimental schematic for the source module.

We use a Sagnac interferometer-based setup to implement a polarization-entangled bi-photon source. Inside the Sagnac loop, we have a type-II periodically-poled KTP (PPKTP) crystal, with a 10 μm poling period. The crystal is pumped by a diagonally polarized 405 nm beam from both directions. At the output of the Sagnac configuration, we have degenerate 810 nm polarization-entangled photons pairs produced via the spontaneous parametric down-conversion (SPDC) process. We use dichroic mirrors to separate the pump beam and single photons, and then perform a quantum state tomography to characterize the output quantum state. The resulting polarization-entangled photon state has 94% fidelity with the singlet state ${\left\vert \psi \right\rangle }_{1}$ and a Concurrence of 0.92. In this figure, QWP, HWP, and PBS represent quarter-wave plate, half-wave plate, and polarizing beam splitter, respectively.

To characterize our state, we perform a quantum state tomography at the output of the source. Our source has a 91% purity, 94% fidelity with respect to ${\left\vert \psi \right\rangle }_{1}=1/\sqrt{2}(\left\vert {{{\rm{HV}}}}\right\rangle +\left\vert {{{\rm{VH}}}}\right\rangle )$, and a concurrence of 0.92. After developing the source, we dispatch the photons through two optical fibers to two setups (each ~5 meters apart from the source), referred to as Alice and Bob modules as introduced in the subsection “Experimental outcome” under the section “Results”. An abridged schematic of the setup that we used to perform the BBM92 measurements has been provided in Fig. 5.

Fig. 5: Experimental schematic for the BBM92 protocol.

In this setup, the polarization-entangled photon pairs are transferred to the eight single-photon avalanche detectors (SPADs) to implement the relevant measurement bases for the protocol. The paired terms (H1, V1) and (V2, H2), indicated in red, represent the corresponding polarization of the daughter photons emerging, from each pump photon striking the crystal, in two different directions. In this figure, QWP, HWP, PBS and BS represent quarter-wave plate, half-wave plate, polarizing beam splitter, and beam splitter, respectively.

During transmission, the polarization of the photons at Alice and Bob modules is affected. To mitigate this, on one hand in the Alice module, we randomly measure the stream of incoming source-photons along the rectilinear and diagonal projection bases (i.e., say, at SPADs-A1 to A4 in Fig. 5). On the other hand, in the Bob module, we randomly measure the polarization of incoming source-photons along the “rotated rectilinear” projection bases, $\{\left\vert {\phi }_{H}\right\rangle ,\left\vert {\phi }_{H}^{\perp }\right\rangle \}$, and “rotated diagonal” projection bases, $\{\left\vert {\phi }_{D}\right\rangle ,\left\vert {\phi }_{D}^{\perp }\right\rangle \}$ (i.e., say, at SPADs-B1 to B4 in Fig. 5). We implement the random choice of measurements using 50:50 beam-splitters and perform the projections with the QWP and HWP combination in front of each PBS. Each of these basis projections can lead to either of the two outcomes: detection of the photon along the transmitted arm ($\left\vert H\right\rangle \,\left\langle H\right\vert$ at SPAD-A1 or $\left\vert D\right\rangle \,\left\langle D\right\vert$ at SPAD-A3, and $\left\vert {\phi }_{H}\right\rangle \,\left\langle {\phi }_{H}\right\vert$ at SPAD-B1 or $\left\vert {\phi }_{D}\right\rangle \,\left\langle {\phi }_{D}\right\vert$ at SPAD-B3), or other along the reflected arm ($\left\vert V\right\rangle \,\left\langle V\right\vert$ at SPAD-A2 or $\left\vert A\right\rangle \,\left\langle A\right\vert$ at SPAD-A4, and $\left\vert {\phi }_{H}^{\perp }\right\rangle \,\left\langle {\phi }_{H}^{\perp }\right\vert$ at SPAD-B2 or $\left\vert {\phi }_{D}^{\perp }\right\rangle \,\left\langle {\phi }_{D}^{\perp }\right\vert$ at SPAD-B4) of the PBS. More specifically, Alice’s $\left\vert H\right\rangle \,\left\langle H\right\vert \,$$\left(\left\vert V\right\rangle \,\left\langle V\right\vert \right)$ detection is highly correlated to Bob’s $\left\vert {\phi }_{H}\right\rangle \,\left\langle {\phi }_{H}\right\vert$$\left(\left\vert {\phi }_{H}^{\perp }\right\rangle \,\left\langle {\phi }_{H}^{\perp }\right\vert \right)$ detection, and Alice’s $\left\vert D\right\rangle \,\left\langle D\right\vert \,$$\left(\left\vert A\right\rangle \,\left\langle A\right\vert \right)$ detection is highly correlated to Bob’s $\left\vert {\phi }_{D}\right\rangle \,\left\langle {\phi }_{D}\right\vert$$\left(\left\vert {\phi }_{D}^{\perp }\right\rangle \,\left\langle {\phi }_{D}^{\perp }\right\vert \right)$ detection. In this way, we end up performing a total of eight coincidence detections between Alice’s and Bob’s SPADs. Now considering that in our approach we produce two photons entangled in the polarization degree of freedom when SPAD-A1(2, 3, 4) clicks then ideally the other photon from that pair should go and always produce a click at the SPAD-B1(2, 3, 4). We term these coincidence detections as signal coincidences since they belong to the desired set. More specifically, they provide a signature that the photons were indeed entangled and thus collapsed to the expected polarization state on measurement. However, due to experimental imperfections and non-orthogonal projections, there is a non-zero probability that the other photon in that pair can collapse at the undesired detector. Such detections contribute to erroneous coincidences, and so they are called the noise coincidences. In a nutshell, four out of the eight coincidence detections form the desirable set (signal), while the other four form the undesirable set (noise). A special parameter of interest in such QKD protocol implementations using entangled photons is the visibility of the coincidences along the rectilinear and diagonal bases since it acts as a performance indicator for both the PEBS and the protocol. For our measurement bases optimization approach, these visibilities: Vis₁ along the rectilinear (for Alice) and rotated rectilinear (for Bob) bases, and Vis₂ along the diagonal (for Alice) and rotated diagonal bases can be expressed as:

$${{{{{{\rm{Vis}}}}}}}_{{{{{{\rm{1}}}}}}}=\frac{C\left(\left\vert H{\phi }_{H}\rangle \langle H{\phi }_{H}\right\vert \right)+C\left(\left\vert V{\phi }_{H}^{\perp }\rangle \langle V{\phi }_{H}^{\perp }\right\vert \right)-C\left(\left\vert H{\phi }_{H}^{\perp }\rangle \langle H{\phi }_{H}^{\perp }\right\vert \right)-C\left(\left\vert V{\phi }_{H}\rangle \langle V{\phi }_{H}\right\vert \right)}{C\left(\left\vert H{\phi }_{H}\rangle \langle H{\phi }_{H}\right\vert \right)+C\left(\left\vert V{\phi }_{H}^{\perp }\rangle \langle V{\phi }_{H}^{\perp }\right\vert \right)+C\left(\left\vert H{\phi }_{H}^{\perp }\rangle \langle H{\phi }_{H}^{\perp }\right\vert \right)+C\left(\left\vert V{\phi }_{H}\rangle \langle V{\phi }_{H}\right\vert \right)},{{{{{\rm{and}}}}}}$$

(13a)

$${{{{{{\rm{Vis}}}}}}}_{{{{{{\rm{2}}}}}}}=\frac{C\left(\left\vert D{\phi }_{D}\rangle \langle D{\phi }_{D}\right\vert \right)+C\left(\left\vert A{\phi }_{D}^{\perp }\rangle \langle A{\phi }_{D}^{\perp }\right\vert \right)-C\left(\left\vert D{\phi }_{D}^{\perp }\rangle \langle D{\phi }_{D}^{\perp }\right\vert \right)-C\left(\left\vert A{\phi }_{D}\rangle \langle A{\phi }_{D}\right\vert \right)}{C\left(\left\vert D{\phi }_{D}\rangle \langle D{\phi }_{D}\right\vert \right)+C\left(\left\vert A{\phi }_{D}^{\perp }\rangle \langle A{\phi }_{D}^{\perp }\right\vert \right)+C\left(\left\vert D{\phi }_{D}^{\perp }\rangle \langle D{\phi }_{D}^{\perp }\right\vert \right)+C\left(\left\vert A{\phi }_{D}\rangle \langle A{\phi }_{D}\right\vert \right)},$$

(13b)

respectively, where $C\left(\left\vert x\,y\rangle \langle x\,y\right\vert \right)$ captures the outcome of a bi-photon coincidence detection along $\left\vert x\rangle \langle x\right\vert$ and $\left\vert y\rangle \langle y\right\vert$ basis within a certain time window.

In the data processing stage, we calculate the number of coincidences in these sets by analyzing the signal-to-noise ratios (SNRs), through the consideration of suitably optimized window spans (see the subsection “Optimization methods” under the section “Methods”. for details) around the peak maxima. Given that, the three parameters (namely, the raw key rate, the quantum-bit-error-rate (QBER), and the asymmetry of the raw key string) can be used to assess the performance of any QKD protocol implementation³, the signal and the noise values thus obtained within the optimal window regions are then used to compute these figures of merit for our BBM92 experimentation. More specifically, key rate can be measured as the average number of bits in the sifted key (including error bits) generated per second. In BBM92 protocol, sifting includes post-processing of the dataset, where Alice and Bob both select only those coincidence events which occur within the chosen time window. In principle, Alice and Bob should have identical key strings after the protocol’s completion. However, in practice, they are not identical owing to the presence of noise in the transmission channel, any other experimental imperfections, and eavesdropping activity. Hence, the number of error bits can be obtained by comparing each bit value for the same bit position in these two key strings. The number of error bits divided by the total key length thus provides us with the QBER. Finally, any mismatch between the number of 0 and 1 bits in the sifted key of either Alice or Bob is captured by the asymmetry (or key symmetry) parameter. In context to these definitions, the three figures of merit can then be analytically expressed as:

$${{{{{\rm{key}}}}}}\,{{{{{\rm{rate}}}}}}= \frac{{{{{{\rm{coincidences}}}}}}\,{{{{{\rm{from}}}}}}\,{{{{{\rm{all}}}}}}\,{{{{{\rm{the}}}}}}\,{{{{{\rm{eight}}}}}}\,{{{{{\rm{coincidence}}}}}}\,{{{{{\rm{detections}}}}}}}{{{{{{\rm{runtime}}}}}}\,{{{{{\rm{of}}}}}}\,{{{{{\rm{the}}}}}}\,{{{{{\rm{protocol}}}}}}}\,\,\left({{{{{\rm{bps}}}}}}\right),\\ = \frac{1}{T}\,\left\{C\left(\left\vert H{\phi }_{H}\rangle \langle H{\phi }_{H}\right\vert \right)+C\left(\left\vert V{\phi }_{H}^{\perp }\rangle \langle V{\phi }_{H}^{\perp }\right\vert \right)+C\left(\left\vert H{\phi }_{H}^{\perp }\rangle \langle H{\phi }_{H}^{\perp }\right\vert \right)+C\left(\left\vert V{\phi }_{H}\rangle \langle V{\phi }_{H}\right\vert \right)\right.\\ \left.+C\left(\left\vert D{\phi }_{D}\rangle \langle D{\phi }_{D}\right\vert \right)+C\left(\left\vert A{\phi }_{D}^{\perp }\rangle \langle A{\phi }_{D}^{\perp }\right\vert \right)+C\left(\left\vert D{\phi }_{D}^{\perp }\rangle \langle D{\phi }_{D}^{\perp }\right\vert \right)+C\left(\left\vert A{\phi }_{D}\rangle \langle A{\phi }_{D}\right\vert \right)\right\}\,\,\left({{{{{\rm{bps}}}}}}\right),$$

(14a)

$${{{{{\rm{QBER}}}}}}= \frac{{{{{{\rm{coincidences}}}}}}\,{{{{{\rm{from}}}}}}\,{{{{{\rm{the}}}}}}\,{{{{{\rm{four}}}}}}\,{{{{{\rm{undesired}}}}}}\,{{{{{\rm{coincidence}}}}}}\,{{{{{\rm{detections}}}}}}\times 100}{{{{{{\rm{coincidences}}}}}}\,{{{{{\rm{from}}}}}}\,{{{{{\rm{all}}}}}}\,{{{{{\rm{the}}}}}}\,{{{{{\rm{eight}}}}}}\,{{{{{\rm{coincidence}}}}}}\,{{{{{\rm{detections}}}}}}}\,\,\left( \% \right),\\ = \frac{\left\{C\left(\left\vert H{\phi }_{H}^{\perp }\rangle \langle H{\phi }_{H}^{\perp }\right\vert \right)+C\left(\left\vert V{\phi }_{H}\rangle \langle V{\phi }_{H}\right\vert \right)+C\left(\left\vert D{\phi }_{D}^{\perp }\rangle \langle D{\phi }_{D}^{\perp }\right\vert \right)+C\left(\left\vert A{\phi }_{D}\rangle \langle A{\phi }_{D}\right\vert \right)\right\}\times 100}{T\times {{{{{\rm{key}}}}}}\,{{{{{\rm{rate}}}}}}}\,\,\left( \% \right),$$

(14b)

$$\begin{array}{ll}{{{{{\rm{key}}}}}}\,{{{{{\rm{symmetry}}}}}}&=\frac{{{{{{\rm{coincidences}}}}}}\,{{{{{\rm{detected}}}}}}\,{{{{{\rm{along}}}}}}\,{{{{{\rm{diagonal}}}}}}\,({{{{{\rm{for}}}}}}\,{{{{{\rm{Alice}}}}}})\,{{{{{\rm{and}}}}}}\,{{{{{\rm{rotated}}}}}}\,{{{{{\rm{diagonal}}}}}}\,({{{{{\rm{for}}}}}}\,{{{{{\rm{Bob}}}}}})\,{{{{{\rm{bases}}}}}}\times 100}{{{{{{\rm{coincidences}}}}}}\,{{{{{\rm{from}}}}}}\,{{{{{\rm{all}}}}}}\,{{{{{\rm{the}}}}}}\,{{{{{\rm{eight}}}}}}\,{{{{{\rm{coincidence}}}}}}\,{{{{{\rm{detections}}}}}}},\\ &=\frac{C\left(\left\vert D{\phi }_{D}\rangle \langle D{\phi }_{D}\right\vert \right)\,+\,C\left(\left\vert A{\phi }_{D}^{\perp }\rangle \langle A{\phi }_{D}^{\perp }\right\vert \right)\,+\,C\left(\left\vert D{\phi }_{D}^{\perp }\rangle \langle D{\phi }_{D}^{\perp }\right\vert \right)\,+\,C\left(\left\vert A{\phi }_{D}\rangle \langle A{\phi }_{D}\right\vert \right)}{T\times {{{{{\rm{key}}}}}}\,{{{{{\rm{rate}}}}}}},\end{array}$$

(14c)

where only the coincidences lying within the optimized window spans have been considered and T stands for the protocol runtime.

Optimization methods

In this subsection, we provide a qualitative overview of three optimization strategies: A, B, and C. We have developed these methods to obtain optimal values of the quantifiers (i.e., key rate, QBER, and asymmetry) that collectively assess the performance of entangled photon-based BBM92 protocol implementation.

From the discussion provided in the previous subsection, we recall that out of eight coincidence detections—four contribute to signal coincidences, while others supply noise coincidences. These coincidence detections actually produce either of the two coincidence distributions (also, denoted by “coincidence curves”), i.e., blue (signal) or red (noise), as schematically sketched in Fig. 6. More specifically, in all three optimization methodologies—to generate these curves, at the beginning the time-stamping data recorded by the two participating SPADs (i.e., one from Alice and the other from Bob module) are compared and plotted as a function of their relative time difference. Note that each “coincidence curve set” consists of two coincidence distributions or peaks: a signal coincidence peak and its corresponding noise coincidence peak, as represented with blue and red curves, respectively, in Fig. 6. For instance, if the coincidence curve set involving SPAD-A1 is considered then its coincidence detections with SPAD-B1 will contribute to the blue signal peak, while those with SPAD-B2 will form the red noise peak. Thus, corresponding to four SPADs in the Alice module, in summary, we end up having four such coincidence curve sets—each containing two peaks.

Fig. 6: Schematic of a representative coincidence curve set.

Each curve set consists of two coincidence peaks: signal (blue) and noise (red). The coincidences measured by performing projective measurements at the SPAD-A1(2, 3, 4) and SPAD-B1(2, 3, 4) contribute to the signal peak, while those measured at the SPAD-A1(2, 3, 4) and SPAD-B2(1, 4, 3) contribute to the noise peak. The background noise zone indicated below the flat portions of the blue and red curve represents the unwanted coincident detection from stray light sources, leaked pump photons, and dark noise of the SPADs. The symbols “l” and “r” represent the left and right panes (or edges) of the common time window considered around the maximal coincidence point of the signal and the corresponding noise coincidence peak. The total coincidences within the chosen window span, i.e., from “l” to “r” around the central maximum, from blue peak, contribute to the error-free key rate (or signal—shaded in purple); while from the red peak, i.e., including the background noise zone, contribute to the QBER (or noise—shaded in gray). Note that in practice, the coincidence curves are not typically smooth functions and contain a lot of kinks (local optimal points) around a central global maximum. In principle, for a perfectly entangled state having 100% fidelity with ${\left\vert \psi \right\rangle }_{1}$ state, the noise curve (or peak) should be flat as represented by the dashed red line. However, in practice, due to various experimental non-idealities, the fidelity always remains less than 100%, leading to a non-vanishing peaked distribution as indicated with the solid red line.

Commonly, for all three optimization methods, we maximize the key rate (as computed by Eq. (14a)) while constraining the overall QBER (as given by Eq. (14b)) to <11%, based upon the information-theoretic security threshold^36,37. To achieve this, we optimize the signal-to-noise ratio (SNR) at each step, while increasing the coincidence window span. From an overall perspective, this general idea is to consider two window edges (also referred to as panes in Fig. 6): left (l) and right (r), as indicated with green dotted vertical lines in the figure, at around the maximal point of the coincidence curve set, i.e., preferably at the top of the blue (signal) peak. Thereafter, move them outwards with a regular step size to increase the span.

For explaining the specifics of each method, we can start with the conventional kind, namely method “B”. It is assumed to be conventional in its approach, in the sense that it uses optimized identical window spans in each coincidence curve set. In this methodology, to optimize the SNR on each coincidence curve set—we shift the two window edges outwards, by the highest achievable resolution (say, 1 ps), and in turn, maximize the SNR at each step. This procedure is sequentially reiterated until the individual QBER value, for that coincidence curve sets, reaches the threshold upper limit of 11%. When the iteration stops for all the curve sets, the corresponding edge positions report the optimized SNRs for each of them. It is important to note that the resultant individual window spans in each curve set can be different at this point. In order to make them identical, the smaller spans are then matched to the largest one among them. Finally, all four spans are again iteratively adjusted with equal step size, until the overall QBER reaches just below the 11% threshold. Within those final spans, the sifted (or raw) key rate, the overall QBER, and the key symmetry values for the given dataset are then computed using Eqs. (14a)–(14c), respectively. In summary, this strategy optimizes the individual SNRs to achieve a maximal key rate that is information-theoretically secure, without worrying about the symmetry in key bits and the security aspect of the final individual QBERs in each coincidence curve set.

In the next method named “C”, we retain the optimization procedure followed by B, while including an additional constraint that the individual QBERs, for each coincidence curve set, should also remain below the information-theoretically secure bound of 11% at the output. In order to ascertain this requirement, while adjusting all four spans iteratively with equal step size, the iterations are continued until all four individual QBERs cross below 11% threshold. It is important to highlight that in this method, if one of the coincidence curve set (or projection bases) contains a significantly higher noise peak (or erroneous/undesired coincidences), then the overall QBER as well as the other individual QBERs at the output can reach values much less than 11%, resulting into a considerably lower sifted key rate. Therefore, this method can be advantageous over B, in the light that it prohibits any partial leakage of information to the eavesdropper even from the analysis of the individual coincidence curve sets.

In order to maintain a balanced symmetry among the “0” and “1” bits in the generated key string, while ensuring that it remains information-theoretically secure, we employ a much different optimization strategy as compared to methods: B and C. We refer to this strategy as method A. In this methodology, to optimize the overall SNR we shift the two edges outwards, on each coincidence curve set, by the maximal achievable resolution (say, 1 ps) and then calculate the SNR at each step. Out of all those eight SNR values (i.e., at the 2 edges for each of the 4 coincidence curve sets), the edge position corresponding to the maximum SNR is retained, while the others are reverted to their original position. This procedure is sequentially reiterated until the updated QBER value reaches the threshold upper limit of 11% and the key symmetry remains within a desired bound (i.e., around 50:50). When the iteration stops, the corresponding edge positions report the optimized SNRs for each coincidence curve set. Similar to methods: B and C, based upon those positions, finally, the sifted (or raw) key rate, the overall QBER, and the key symmetry values are calculated as per Eqs. (14a)–(14c), respectively. In summary, this method optimizes the SNRs to achieve a maximal key length that is information-theoretically secure, while also ensuring a symmetric distribution of “0” and “1” bits in that key string. In contrast to the previous optimization methods: B and C, this method (A) of analyzing the performance of BBM92 implementations are particularly valuable from the consideration that having a balanced or imbalanced key symmetry can both lead to important security implications, as explained by Chatterjee et al.³.

These optimization methods can be easily used for analyzing conventional BBM92 protocol measurements, even with the entangled (source) photon state having highly imperfect (≪90%) fidelity with ${\left\vert \psi \right\rangle }_{1}$ state. However, it is important to note that for evaluating such datasets measured in the conventional projection bases, the QBER threshold (and also the key symmetry thresholds—if applicable) may need to be relaxed by a small step size at each iteration of unsuccessful optimization, to reach convergence and assess the insecure but optimized key rate. In that light, these optimization methods can be generalized to any single-photon (or entangled-photons) based QKD protocol implementation with quick customization.