Introduction

The world around us includes a variety of complex systems that comprise many interacting components. In these complex systems, diverse macroscopic collective behaviors can emerge. Among them, the phenomenon that complex systems switch abruptly from one state to another, termed “critical transition,” are ubiquitous in physical and biological systems ranging from molecular crystals to neural networks and ecosystems. Anticipating such critical transitions suggests the opportunity to promote the desired transitions or to reduce the risks of unwanted transitions. In spite of great achievements in the quest for understanding and predicting the behaviors of complex systems and networks1,2,3,4,5, formulating an effective framework to predict critical transitions remains an open area of research across disciplines.

Transition phenomena in complex systems are one of the most fascinating topics in physics, known as phase transitions. The study of phase transitions was originally limited to equilibrium systems, and the fundamental regularities and laws for equilibrium phase transition phenomena have been characterized in the context of equilibrium thermodynamics and statistical mechanics1,2,3. In classical equilibrium phase transition theory, phase transitions emerge from the competition between the order induced by interactions and the disorder induced by thermal motions, which can be quantitatively characterized by the discontinuity in the first/second derivative of the free energy. Subsequently, the behaviors of the non-equilibrium systems have received more and more attention4,5,6,7,8,9,10,11. This is because most of the complex systems in nature, such as biological systems, are out of equilibrium, in which the detailed balance is broken by the fluxes of energy or materials across the systems. The fluxes can be caused by differences in chemical potentials, concentrations, temperature, etc. The transition phenomena in these non-equilibrium systems with broken detailed balance are termed non-equilibrium phase transitions. For instance, a major class of non-equilibrium transitions is absorbing state transitions, in which the system cannot return to its original state after the transition has occurred6. The notion of phase transitions has been extended even outside the realm of natural sciences to economics and sociology. However, despite the great efforts for a better understanding of transition phenomena in non-equilibrium systems such as the laser and the Belousov–Zhabotinskii reaction12,13, a complete theory that systematically describes the “thermodynamic” of non-equilibrium phase transitions is still challenging (although the thermodynamic quantities of temperature and work cannot be easily defined in the complex systems such as social networks and financial markets, we can still construct a metaphorical idea of “thermodynamics” to explore the corresponding macroscopic properties with the concepts and methods developed in the classical thermodynamics).

In recent years, nonlinear dynamics and bifurcation theory have been exploited to describe and predict the critical transitions in complex systems9,10,11. In many models, critical transitions correspond to bifurcations. Although studies in different scientific fields suggest that critical transitions in a myriad of systems may be signaled by the phenomenon of “critical slowing down”14,15, slowing down is still far from being a universal warning signal for predicting an approaching critical transition16. For instance, critical slowing down typically occurs very close to the bifurcation or phase transition point. When the external condition/control parameter varies slowly to the underlying tipping point, it is possible to prepare for the upcoming transitions (preventing the unwanted transition or promoting the desired transition) through the warning signals based on the critical slowing down9,16. However, the abrupt shift induced by a sudden significant impact, which may drive the system across the border between the attractors of the underlying alternative stable states or may drive the system across the tipping point directly, cannot easily be predicted by these warning signals. If we can detect the warning signals early enough sufficiently far from the bifurcation/tipping point, e.g., at the location where the critical transitions are less likely to happen even with a huge external impact, we will still have the opportunity to prepare in advance. An interesting question is whether the crucial signals can be detected earlier than the ones suggested in previous works based on critical slowing down.

Motivated by the great practical importance of predicting critical transitions in real systems, we developed a general non-equilibrium dynamical and thermodynamic framework to extend the thermodynamic quantities and phase transition theory in equilibrium systems to general non-equilibrium systems. This is inspired by the hints that phase transitions in the equilibrium systems can be clearly characterized by the behaviors of specific thermodynamic quantities, which are only dependent on the statistical distributions of the system states rather than the time-varying dynamics. Therefore, the specific behaviors of thermodynamic quantities in general non-equilibrium complex systems may be potential warning signals for anticipating critical transitions. Thermodynamic quantities such as non-equilibrium free energy, entropy, and heat capacity in our framework are defined in analogy to the ones in equilibrium systems based on the non-equilibrium steady-state (NESS) probability distributions. The NESS probability distributions are closely associated with the non-equilibrium intrinsic potential ϕ0 under the small noise limit, which is a Lyapunov function decreasing monotonically with time along the dynamical trajectories17,18. Such an intrinsic potential function having the property of the Lyapunov function reflects the dynamical nature of non-equilibrium systems and can be used to quantify global stability. Moreover, the corresponding generalized non-equilibrium first and second laws of thermodynamics can be formulated17,18.

To demonstrate the practicality of our framework in predicting critical transitions, we explored two popular non-equilibrium models with fold and Hopf bifurcations, which correspond to various types of critical transitions8. We found that the discontinuity in the non-equilibrium entropy and heat capacity defined in our framework as the first- and second-order derivative of the non-equilibrium free energy in the small-noise limit can characterize the discontinuous and continuous non-equilibrium thermodynamic phase transitions. In addition, the entropy production rate, which reflects the degree of the irreversibility or detailed balance breaking of a non-equilibrium system, can also characterize the discontinuous and continuous non-equilibrium thermodynamic phase transitions. Furthermore, our results suggest that the specific behaviors of the non-equilibrium thermodynamic quantities can serve as early-warning signals for predicting critical transitions which correspond to different types of bifurcations termed non-equilibrium dynamical transitions. Moreover, the irreversibility of the observed time series correlates strongly to the behaviors of the entropy production rate of the non-equilibrium systems and thus can provide a practical way to predict critical transitions in complex systems.

Results

An equilibrium system can always be described by a thermodynamic potential function, e.g., the free energy. Given the potential function, we know all the static thermodynamic properties of the system. At the same time, when the system deviates from the equilibrium state, the Lyapunov property of the potential function also gives the direction of the dynamic evolution of the system. The equilibrium state that corresponds to the minimum of the thermodynamic potential function is considered a “phase” in physics. As a given control parameter is changed, the state with the potential minimum can become unstable and be replaced by a new, qualitatively different type of state. That is, a phase transition happens. However, to understand and predict transitions in realistic, complex systems, the traditional equilibrium phase transition theory often does not apply. This is because real systems are usually out of equilibrium and exchange materials, energy, and information with the surrounding environments. The dynamics that are not involved in the equilibrium thermodynamics theory are crucial in such non-equilibrium systems. Complex dynamics such as limit cycle oscillations and dissipative chaos can only emerge in systems far from thermal equilibrium4,5,12. In addition, classical equilibrium thermodynamics theory shows that thermodynamic systems display sharp phase transitions only in the thermodynamic limit when the number of components becomes very large1,2,3. Contrary to the internal fluctuations, which can safely be neglected for macroscopically large systems, the intensity of the fluctuations due to environmental randomness, in general, does not scale with the inverse power of the system size. In some cases, environmental fluctuations play an essential role in the behavior of the non-equilibrium systems, e.g., noise-induced phase transitions19. Due to the difficulty in characterizing non-equilibrium phase transitions with a potential function, researchers use a different strategy to explore these transition phenomena in non-equilibrium complex systems8,20. The basic approach involves the consideration of a fundamental property: stability. A transition in a complex system occurs if the steady state of the system changes qualitatively. Therefore, it is natural to explore changes in the behavior of complex systems in terms of changes in their stability, which can be described by the corresponding bifurcation diagram.

Challenges in predicting critical transitions based on critical slowing down

In dynamical models, sharp transitions from one state to another are usually associated with bifurcations. In the vicinity of many types of bifurcation points, there is a general phenomenon that the recovery rate of a system from small perturbations becomes very slow, known as critical slowing down14,15. Such a phenomenon occurs when the basin of attraction that the system settles shrinks and becomes shallower and is often accompanied by increased autocorrelation and increased variance in the corresponding time series. Figure 1 describes a simple example (fold catastrophe) illustrating this.

Fig. 1: The schematic diagram of a dynamical model with the fold bifurcation and underlying potential landscapes for different conditions.
figure 1

a The phase diagram. The system can have different dynamical equilibria for different conditions, either stable or unstable, indicated by the solid lines and dashed lines, respectively. When the system is near the bifurcation point (e.g., point T1), a small change in the condition may lead to a sharp transition from the stable state on the upper branch to the lower branch. For a given control parameter, the dynamical attractors and the corresponding basins in the state space are fixed. The perturbations can also drive the system across the boundary (indicated by the dashed line) between the attraction basins. b–d The underlying potential landscapes are marked with the same colors as the colored bars for different conditions/control parameters in (a). Far from the bifurcation point T1, the attractor that the system settles into is strong, and the rate of recovery from the perturbations is relatively high (b). When the system is closer to the transition point T1 (from the left of T1 as shown in (a)), the attractor becomes weakened and shallower while the rate of recovery from small perturbations is lower (c), at this time, either a small perturbation that can drive the system across the boundary between the attraction basins (c) or a sudden change in the external conditions that destabilize the current attractor in the underlying potential landscape (d) can induce the critical transitions. The data in this example are generated with a model describing the dynamics of a harvested population: dX/dt = X(12X/K) − (X2/(X2 + 1)), and the parameter K is set to 10.

Full size image

However, these warning signals in the dynamics usually can only be significantly detected when the system is very close to a bifurcation point. This is because only when the dominant attractor is going to disappear as the corresponding eigenvalue characterizing the rates of change around the equilibrium approaches zero can the critical slowing down be observed. At this point, a sudden change in the control parameter or the state variables induced by external perturbations may lead to abrupt unanticipated transitions (Fig. 1). Since stochastic perturbations which may trigger a transition before a bifurcation point is reached are ubiquitous in complex systems, the practical applications of predicting critical transitions require that the warning signal can be detected sufficiently early. For instance, as illustrated in Fig. 1a, if a signal can appear around point T0, the unwanted transition around point T1 may be avoided even when a sudden large external impact is presented.

In the previous theoretical framework based on critical slowing down, it is not easy to provide warning signals sufficiently far enough from the actual transition point. In facing this challenge, we pay attention to the possible behaviors of the thermodynamic quantities during critical transition phenomena. We know that in equilibrium phase transition theory, different types of phase transitions can be characterized by the specific behaviors of thermodynamic quantities, such as entropy and heat capacity, and these thermodynamic quantities are only dependent on the steady-state probability distributions of the state variables. The question is whether we can define the non-equilibrium analogs of the thermodynamic quantities in equilibrium thermodynamics, which can provide us with new insights into predicting critical transitions in non-equilibrium complex systems.

Non-equilibrium thermodynamic framework for dynamical systems

To answer this question, we extend the well-established theory of phase transitions in systems at equilibrium to the ones in non-equilibrium regimes. In equilibrium statistical mechanics, the Boltzmann–Gibbs distribution, which is determined by certain a priori known Hamiltonian or an energy function, can provide all the information. The equilibrium phase transitions can usually be described in terms of free energy derived from the given probability distribution. When the free energy of the current state ceases to be a global minimum or a minimum at all, a phase transition emerges. A natural way to try to extend the ideas explaining the equilibrium phase transitions to non-equilibrium situations is to investigate whether the macroscopic behavior of a non-equilibrium complex system can be expressed in terms of a potential function, which plays the role of the equilibrium free energy.

For a simple one-dimensional system, we can always construct a potential function to clearly illustrate the characteristics of corresponding phase transitions, as shown in Fig. 1b–d. Real non-equilibrium complex systems are always multidimensional, and therefore it is not easy to construct such a potential function. Considering the fact that a transition occurs when the underlying potential function changes qualitatively and such qualitative change can be unambiguously reflected in the steady state probability distributions (PSS), we can introduce a “probabilistic” potential to estimate how the stability properties of the system change with varying control parameters. In analogy with the picture of a particle moving on a landscape (Fig. 1b–d), the maxima of PSS correspond to the valleys of the potential. Furthermore, non-equilibrium thermodynamics can be developed based on the non-equilibrium steady state (NESS) probability distributions in analogy to equilibrium thermodynamics17,18,21,22,23,24. However, in contrast to the equilibrium case, where the system is static, and no equation of motion has to be solved to uncover its thermodynamic nature, the dynamics play a central role in non-equilibrium systems. In addition, the fluctuations cannot be simply neglected. Although a non-equilibrium system can reach a steady state with stationary probability distributions, such NESS is, from the dynamical point of view, an emergent one from the underlying fluctuating, stochastic process involving the stochastic transitions among the multiple underlying microscopic stable states. The non-equilibrium analogs of the Gibbs ensemble can only be obtained as the stationary probability measure in the long time limit of the corresponding stochastic dynamics.

Non-equilibrium dynamics determined by landscape and flux

For a realistic complex system consisting of a large number of interacting components, it is usually difficult to keep track of all the microscopic trajectories of every component by solving the corresponding dynamical equations. Nevertheless, the macroscopic emergent behaviors of the system can often be approximately described by the dynamical evolution of several macroscopic observables with the deterministic driving forces and the random forces that represent the effects of the microscopic degrees of freedom on the macroscopic observables25. A well-known example is the stochastic Langevin particle dynamics. We consider a system whose dynamics can be described by a set of the Langevin equations:

$$\frac{d{{{{{\bf{x}}}}}}}{dt}={{{{{\bf{F}}}}}}({{{{{\bf{x}}}}}})+{{{{{\boldsymbol{\zeta }}}}}}.$$
(1)

x denotes the vector whose components are the variables representing the state of the system. F(x) is a vector representing the corresponding driving force. ζ is a Gaussian white noise with zero mean 〈ζ〉 = 0 and the autocorrelations \( < {{{{{\boldsymbol{\zeta }}}}}}({{{{{\bf{x}}}}}},t){{{{{\boldsymbol{\zeta }}}}}}({{{{{\bf{x}}}}}},{t}^{{\prime} }) > =2D{{{{{\bf{D}}}}}}({{{{{\bf{x}}}}}})\delta (t-{t}^{{\prime} })\), where D is a scale factor representing the magnitude of the fluctuations and D(x) is the diffusion tensor or matrix. The trajectories x usually follow a nonlinear law and are also stochastic. They are unpredictable.

The associated Fokker–Planck equation, which provides the time evolution of the corresponding probability distributions of the dynamic variables P(x, t)), is given by17,18,21,22,23,24:

$$\partial P({{{{{\bf{x}}}}}},t)/\partial t= \, \nabla \cdot (\nabla \cdot (D{{{{{\bf{D}}}}}}({{{{{\bf{x}}}}}})P({{{{{\bf{x}}}}}},t)))\\ -\nabla \cdot ({{{{{\bf{F}}}}}}({{{{{\bf{x}}}}}})P({{{{{\bf{x}}}}}},t))$$
(2)

When a system is at the steady state, the corresponding steady-state probability distributions can be solved through the equation:

$$\nabla \cdot (({{{{{\bf{F}}}}}}({{{{{\bf{x}}}}}}){P}_{ss}({{{{{\bf{x}}}}}}))-\nabla \cdot (D{{{{{\bf{D}}}}}}({{{{{\bf{x}}}}}}){P}_{ss}({{{{{\bf{x}}}}}})))=0$$
(3)

Further, we can define the non-equilibrium potential function U = −lnPss(x) in analogy to the Boltzmann law in equilibrium statistical mechanics. The corresponding Fokker–Planck equation can be written in the form of ∂P(x, t)/∂t = − ∇ ⋅ J, where the probability flux is defined as J = (F(x)*P(x, t)) − ∇ ⋅ (DDP(x, t)). The change of the local probability P(x, t) in time is determined by the net probability flux J in or out of that region. This guarantees the local conservation of probability. The local probability remains constant if the net probability flux vanishes. Notably, the divergence of the flux is zero at long times when a steady state emerges. However, it is not necessary for the flux itself to be zero even under this divergence-free condition. A non-zero flux means that there is a net flux that breaks the detailed balance. This indicates that the system is no longer in equilibrium. Moreover, the divergence-free flux implies that there are no sources and sinks for the probability of going to or coming from. Therefore, locally the flux must be rotational. Furthermore, we can decompose the driving force as:

$${{{{{\bf{F}}}}}} = {{{{{{\bf{J}}}}}}}_{ss}/{P}_{ss}+D{{{{{\bf{D}}}}}}\cdot \nabla ({P}_{ss})/{P}_{ss}+\nabla \cdot D{{{{{\bf{D}}}}}}\\ = {{{{{{\bf{J}}}}}}}_{ss}/{P}_{ss}-D{{{{{\bf{D}}}}}}\cdot \nabla U+\nabla \cdot D{{{{{\bf{D}}}}}}.$$
(4)

In contrast to the dynamics of the equilibrium systems, which are fully ruled by the gradient of the underlying energy function (zero net flux), the dynamics of the non-equilibrium systems are not only determined by the potential gradient but also by the curl flux. The non-equilibrium potential U can be used to quantify the global behavior of the non-equilibrium systems. However, it is not a monotonically decreasing Lyapunov function. Nevertheless, studies suggested that the non-equilibrium potential U can be expanded with respect to the scale of the fluctuations D for the case of the weak fluctuations(D ≪ 1) as17,18:

$$U=\frac{1}{D}\phi =\frac{1}{D}\mathop{\sum}\limits_{i=0}{D}^{i}{\phi }_{i}.$$
(5)

By substituting the expression of Pss from the small fluctuation expansions into the steady state Fokker-Planck equation and comparing the corresponding coefficients with the same powers of D on both sides of the equation, the equation of the leading order expansion D−1 can be obtained, which gives rise to the Hamilton–Jacobian (HJ) equation analogous to the classical mechanics17,18:

$${{{{{\boldsymbol{F}}}}}}\cdot \nabla {\phi }_{0}+\nabla {\phi }_{0}\cdot {{{{{\bf{D}}}}}}\cdot \nabla {\phi }_{0}=0$$
(6)

At the zero fluctuation limit, the temporal evolution \(\dot{{{{{{\bf{x}}}}}}}\) can be approximately written as F(x), neglecting the noise term ζ. Then one can obtain the time evolution dynamics of ϕ017,18:

$$\frac{d{\phi }_{0}({{{{{\bf{x}}}}}})}{dt}=\nabla {\phi }_{0}\cdot {{{{{\boldsymbol{F}}}}}}=-\nabla {\phi }_{0}\cdot {{{{{\bf{D}}}}}}\cdot \nabla {\phi }_{0}\le 0$$
(7)

Since ϕ0 monotonically decreases along the deterministic trajectory, thus it can be defined as a Lyapunov function. The Lyapunov function ϕ0, which can be given as the solution of the complicated HJ equation, is closely associated with the steady-state probability Pss ∝ exp(−ϕ0/D). Therefore, the Lyapunov function ϕ0 characterizing the steady state weights globally can serve as the intrinsic non-equilibrium potential landscape, which can be used to determine the direction of dynamical evolution and the global stability of a non-equilibrium system.

Non-equilibrium thermodynamics

To uncover the effective indicators which can predict the non-equilibrium phase transitions, we introduce the assumption of a small noise limit(D ⪡ 1) rather than the exact thermodynamic limit. We can then quantify the steady state probability PSS(x) as

$${P}_{SS}({{{{{\bf{x}}}}}})=\exp (-{\phi }_{0}/D)/Z,$$
(8)

where the non-equilibrium partition function can be naturally defined as:

$$Z=\int\exp (-{\phi }_{0}/D)d{{{{{\bf{x}}}}}}.$$
(9)

The diffusion scale D measures the strength of the fluctuations and here plays the role of the effective kBT in Boltzmann’s formula. The thermodynamic quantities such as the non-equilibrium entropy, energy, and free energy can be defined in analogy to that in the equilibrium system as

$$S=-\int\,P({{{{{\bf{x}}}}}},t){{{{\ln }}}}P({{{{{\bf{x}}}}}},t)d{{{{{\bf{x}}}}}}$$
(10)
$${{{{{\mathcal{E}}}}}}=\int{\phi }_{0}({{{{{\bf{x}}}}}})P\left({{{{{\bf{x}}}}}},t\right)d{{{{{\bf{x}}}}}}=-{{{{{\rm{D}}}}}}\int\ln (Z{P}_{SS}({{{{{\bf{x}}}}}}))P\left({{{{{\bf{x}}}}}},t\right){{{{{\bf{dx}}}}}}$$
(11)
$${{{{{\mathcal{F}}}}}}={{{{{\mathcal{E}}}}}}-D{{{{{\mathcal{S}}}}}}=D\left(\int\,P\ln \left(P/{P}_{SS}\right)d{{{{{\bf{x}}}}}}-\ln Z\right)$$
(12)

Here, P(x, t) represents the probability function in time. At the non-equilibrium steady state, \({{{{{{\mathcal{F}}}}}}}_{{{{{{\mathcal{SS}}}}}}}=-DlnZ\). The entropy S of the non-equilibrium system at steady state equals the derivative of the free energy\({{{{{\mathcal{F}}}}}}\) with respect to D (serving as the effective temperature): \({S}_{SS}=-\partial {{{{{{\mathcal{F}}}}}}}_{{{{{{\mathcal{SS}}}}}}}/\partial D\). Furthermore, the heat capacity can be defined as

$$C={\partial }^{2}F/\partial {D}^{2}=-\partial S/\partial D$$
(13)

This definition is analogous to the one in equilibrium thermodynamics.

In addition, a non-equilibrium thermodynamic system in the stationary state is characterized by a continuous production of entropy. Although the entropy of a non-equilibrium system at a steady state is invariant in time, there’s a flow of the entropy to the outside which is equal to the entropy spontaneously generated inside the system. To define entropy production, we can focus on the entropy relating to the time-dependent probability distribution. Using the Fokker-Planck equation and the definition of probability flux J(x), the time derivative of the system entropy dS/dt can be easily written in two terms:

$$\frac{d}{dt}S(t)=\int\,d{{{{{\bf{x}}}}}}({{{{{\bf{J}}}}}}\cdot {(D{{{{{\bf{D}}}}}})}^{-1}\cdot {{{{{\bf{J}}}}}})/P-\int\,d{{{{{\bf{x}}}}}}({{{{{\bf{J}}}}}}\cdot {(D{{{{{\bf{D}}}}}})}^{-1}\cdot ({{{{{\bf{F}}}}}}-D\nabla {{{{{\bf{D}}}}}})).$$
(14)

Notice that the first term on the right-hand side of the equation is always larger or equal to zero due to the positive definite diffusion matrix D. Therefore, it can be identified as the total entropy production rate18,26,27:

$${{{\rm{EPR}}}}={\dot{S}}_{{{\rm{tot}}}}=\int\,d{{{{{\bf{x}}}}}}({{{{{\bf{J}}}}}}\cdot {(D{{{{{\bf{D}}}}}})}^{-1}\cdot {{{{{\bf{J}}}}}})/P.$$
(15)

The second term on the right-hand side of the equation can then be regarded as the entropy flux from the system to the environment:

$${\dot{S}}_{{{\rm{env}}}}=\int\,d{{{{{\bf{x}}}}}}({{{{{\bf{J}}}}}}\cdot {(D{{{{{\bf{D}}}}}})}^{-1}\cdot ({{{{{\bf{F}}}}}}-D\nabla {{{{{\bf{D}}}}}})).$$
(16)

This leads to the total entropy change is equal to the sum of the entropy change of the system and that of the environment. We can see the emergence of the generalized non-equilibrium first law of thermodynamics:

$${\dot{S}}_{{{\rm{tot}}}}={{{\rm{EPR}}}}={\dot{S}}_{{{\rm{sys}}}}+{\dot{S}}_{{{\rm{env}}}}.$$
(17)

The entropy change of the non-equilibrium system can either be increased or decreased due to the entropy flow to the environments, while EPR, whose physical meaning is the total entropy change of the system and the environments is always non-negative. This leads to the generalized non-equilibrium thermodynamic second law:

$${\dot{S}}_{{{\rm{tot}}}}\ge 0.$$
(18)

The thermodynamic quantities defined in our non-equilibrium thermodynamic framework are dependent on the corresponding dynamical driving force. Both the intrinsic potential function ϕ0 and the non-equilibrium steady state probability distribution Pss are determined by the non-conservative driving force of the corresponding non-equilibrium system. Therefore, the thermodynamic quantities, such as the non-equilibrium entropy and heat capacity in our framework, intrinsically include non-equilibrium natures, which are different from the equilibrium analogies. In addition, the entropy production rate can explicitly reflect the degree of the irreversibility or detailed balance breaking of a non-equilibrium system. It is interesting to explore whether early warning signals for predicting critical transitions (bifurcations) in complex systems can be detected from the behaviors of the thermodynamic quantities in our non-equilibrium thermodynamic framework.

Early-warning indicators for non-equilibrium phase transitions

In order to verify the ability of our non-equilibrium thermodynamic framework to predict critical transitions, we applied this theory to two typical non-equilibrium systems where different types of bifurcations can emerge.

Wilson–Cowan model for neural network dynamics

We first consider the well-known Wilson–Cowan model, which is the first mean-field model to describe the collective behaviors of a cluster of neurons28. These behaviors are related to several key brain functions, such as working memory, decision-making, and the control of breathing, heartbeat, and circadian rhythms. The special functions of the brain emerge from the collective network dynamics of the interacting neurons rather than the isolated individual neurons. However, the search space for exploring neural network dynamics is extremely large. One way to overcome this difficulty is by the use of statistical approaches, including coarse-graining and mean-field approximations29. The Wilson–Cowan model, in the mean-field spirit, considers a localized neural population composed of an excitatory subpopulation and an inhibitory subpopulation (Fig. 2a). The evolution of the average activities can be described by the following two ordinary differentials equations28,30:

$$\frac{d{x}_{E}}{dt}= -{x}_{E}+({k}_{e}-{r}_{e}{x}_{E}){R}_{e}({w}_{EE}{x}_{E}-{w}_{IE}{x}_{I}+{I}_{E})\\ \frac{d{x}_{I}}{dt}= -{x}_{I}+({k}_{i}-{r}_{i}{x}_{I}){R}_{i}({w}_{EI}{x}_{E}-{w}_{II}{x}_{I}+{I}_{I})$$

where xE(t) and xI(t) are the average activities of the excitatory and the inhibitory subpopulations, wEE, wIE, wEI, wII are the connectivity weights, re and ri are the refractory constants, and IE and II are the external inputs to the excitatory and the inhibitory subpopulations. The subpopulation response function R(x) is chosen in the same form as the sigmoid function from the model of Wilson and Cowan28: R(x) = 1/(1 + exp(−b(x − θ))) − 1/(1 + exp(bθ)). Here b and θ are the parameters, the former determining the value of the maximum slope through the relationship: \({{{\rm{max}}}}[{R}^{{\prime} }(x)]={S}^{{\prime} }(\theta )=b/4\) and the latter giving the location of the maximum slope28.

Fig. 2: Critical transitions predicted by the specific behaviors of thermodynamic quantities in the Wilson–Cowan model.
figure 2

a Diagram of the Wilson–Cowan circuit. Panel b shows the phase diagrams by varying the parameters IE. Two saddle-node bifurcations can emerge at the parameter IE ≈ −0.82 and 1.08. Panel c shows the changes in the free energy with the IE = −0.4, −0.8, and −0.82, respectively, indicated by different colored lines. Here the free energy depends only on the variable xE because the contributions of different values of the variable xI on the summation of the partition function are integrated first. Top panels d–f show the non-equilibrium quantities, the non-equilibrium entropy, heat capacity, and entropy production rate derived from the intrinsic potential ϕ0 versus external input IE. Bottom panels g–i depict the case when the finite noise is present, and the thermodynamic quantities are derived directly from the corresponding steady-state probability distributions. The changes in the thermodynamic quantities are smoother in the case with finite noise (indicated by the red curves) than the ones in the case with the zero-noise limit (indicated by the blue curves). The vertical dot-dashed lines indicate the set of transition points. The values of other fixed parameters in this model are: wEE = 16, wIE = 12, wEI = 4, wII = 3, θe = 4, be = 1.3, θi = 3.7, bi = 2, re = 1, ri = 1, II = 0. The diffusion coefficient D that measures the magnitude of the noise is chosen as D = 0.0002 and D = 0.0032 for the small noise limit and finite-noise situations, respectively.

Full size image

The population dynamics described by the above equations can be analyzed upon the parameter variations (Fig. 2b). In this bifurcation diagram, the upper and lower branches correspond to stable states (the activity of population E is high, and the activity of population I is low, or vice versa). Here these steady states can be termed “up” states and “down” states for simplicity. We can see that these steady states not only change quantitatively, as the model parameter IE is varied. Instead, they can change their stability qualitatively, disappear, or emerge. Two saddle-node/fold bifurcations related to such qualitative change can emerge, separating the single fixed-point phase from the phase with bi-stable fixed points.

To address whether the non-equilibrium thermodynamics quantities can predict these critical transitions /bifurcations, we solved the intrinsic potential function ϕ0 numerically and calculated the corresponding steady-state probability distributions, free energy \({{{{{\mathcal{F}}}}}}\), entropy S, heat capacity, and the entropy production rate (EPR) as the parameters IE is varied. The corresponding main results are summarized in Fig. 2c–f. Figure 2c shows the changes in the free energy when the system goes from being bistable to monostable as the parameter IE is decreased. At IE ≈ −0.82, the local minimum F(x1) loses stability, and the system will spontaneously change from the “up” state to the “down” state. As shown in Fig. 2d, there is a peak in the entropy S at the location between the two bifurcation points where IE ≈ 0. In fact, it is not difficult to prove that once the zero-noise limit is introduced, there is a discontinuity in the entropy S at the location where the two alternative attractors/stable states have the same weight (the corresponding details and discussions are shown in the Supplementary Note 1). Moreover, there is also a discontinuity in the EPR at such a location (the numerical result is shown in Fig. 2f, and the theoretical proof is shown in Supplementary Note 1). According to the classification in classical equilibrium phase transition theory31, the present phase transition with a discontinuity in the entropy (first derivative of the free energy) and therefore involves a latent heat can be considered as the first order. Our result is also consistent with previous works showing that the entropy production rate is discontinuous when the transition is first-order32,33.

Notably, when the zero-noise limit is introduced, even though the underlying Lyapunov function ϕ0 exhibits multi-minima, only one of them with the smallest value of the potential function gives the dominant probability contribution. The significant changes in the thermodynamic quantities, such as the entropy, emerge at the location where the minima of the underlying potentials have the same values. The corresponding transitions are analogous to the classical equilibrium phase transitions, and therefore they can be termed “non-equilibrium thermodynamic phase transitions.” Since the critical transitions that we are concerned with in complex systems emerge at different locations (where bifurcations emerge9,16,34) in contrast to the locations of equilibrium thermodynamic phase transitions, the specific behaviors of the thermodynamic quantities defined in our framework provide the opportunities to predict critical transitions (can be termed as “non-equilibrium dynamical phase transitions”) in complex systems. Figure 3 shows the different locations of the thermodynamic phase transitions in the thermodynamic limit and bifurcations, taking the Wilson–Cowan model as an example (see more details and discussions in Supplementary Note 1). The early-warning indicators in our thermodynamic framework are in contrast to the ones in the previous works on the basis of nonlinear dynamics and the bifurcation theory. For instance, if we are concern about the transition from the “up” state to the “down” state, the specific behaviors of the thermodynamic quantities defined in our non-equilibrium thermodynamic framework can be detected much earlier around the location where the stable “down” state is going to be more preferred (IE ≈ 0) than the position where the current “up” state is going to disappear (IE ≈ −0.82) and the “down” state becomes dominant.

Fig. 3: Non-equilibrium thermodynamic phase transitions and dynamical bifurcations occur at different locations.
figure 3

In this phase diagram, the red dashed line indicates the location of the thermodynamic phase transition in the thermodynamic limit. The black dashed lines indicate the locations of the dynamical bifurcations. The red solid curve in the middle and two black solid curves on two sides show the underlying potential landscapes when the thermodynamic phase transition and critical transitions/bifurcations happen, respectively.

Full size image

Although the specific behaviors of the thermodynamic quantities here can serve as alternate early-warning signals for predicting critical transitions, they can only be quantified when the dynamical driving force that determines the evolution of the complex system with time is known. Very often in practice, we can only get the data about the steady-state probability density distributions of a system or even only limited individual time-dependent dynamic trajectories. To test if our framework can contribute to predicting critical transitions for these general situations, we try to explore the behaviors of the thermodynamic quantities derived directly from steady-state probability distributions when the transition occurs. As shown in Fig. 2g–i, one peak in the entropy and the EPR and two peaks in the heat capacity can be observed between two bifurcation points with varied parameter IE. We can find that there are no discontinuities in these thermodynamic quantities due to the effects of noises. but the corresponding specific behaviors upon varying control parameters (peaks in entropy, heat capacity, and EPR) can also serve as early warning signals for transitions.

Furthermore, even if the full information about the system is not quite available, we can still obtain some hints from our predictions on the changes in the EPR before and after the critical transitions. In fact, the EPR reflects the dissipative pattern of a non-equilibrium system, which is related to the degree of time-irreversibility or detailed balance breaking, as discussed in the above section. Inspired by the studies showing that the degree of the time irreversibility can be measured by the differences in the cross-correlations between the forward and the backward directions in time of the two-state variable time series of a non-equilibrium system35, which is termed as ΔC here for simplicity, we investigate how the irreversibility quantified by ΔC changes when the system approaches a bifurcation (the details about the cross-correlation function are shown in the “Materials and methods” section).

The ΔC is derived from the time series and depends on the state of the system. As shown in Fig. 4a, the system initiates at the stable “up” state, and a sharp transition to the “down” state occurs as the parameter IE is decreased. Meanwhile, the ΔC increases gradually first and then decreases significantly (Fig. 4b). The changes in ΔC for varying control parameter IE are similar to the changes in EPR under finite noise, which is consistent with the theoretical prediction that the degree of the time irreversibility can be measured by either EPR or ΔC. To compare the warning signal in our cross-correlation approach and the ones based on critical slowing down in previous works, we show how the autocorrelation and variance of the time series of the state of population E change with varying control parameter IE (Fig. 4c, d) (The divergence of the recovery time according to the power law around the transition point is shown in the Supplementary Note 2). As we have introduced above, both the autocorrelation and variance increase as the system approaches the bifurcation point (indicated by the dashed line where IE ≈ − 0.82). From the viewpoint of warning signals, the increasing trend of ΔC in our cross-correlation approach is more obvious than the ones of autocorrelation and variance. More importantly, there is an obvious inflection point before the bifurcation point is reached. These results suggest that the warning signals in our cross-correlation approach are better than previous ones based on critical slowing down. The cross-correlation approach can provide a more practical early-warning signal for predicting critical transitions since only the individual dynamical trajectories rather than the underlying mechanisms that drive the complex system are required.

Fig. 4: Early-warning signals in a time series generated by the Wilson–Cowan model is driven slowly across a fold bifurcation.
figure 4

a The state of the system (indicated by the blue circle) shifts abruptly from the “up” state to the “down” state as the parameter IE is decreased across the bifurcation point. b The differences in the cross-correlations forward and backward in time (ΔC) increases gradually at first and then decrease significantly as the control parameter IE is decreased. The gray band indicates the transition phase, where transitions from “up” to “down” may occur due to the finite noise. The transition can be predicted by the increased trend both in the autocorrelation (c) and variance (d), suggested as the early warning signals in previous works based on critical slowing down. The obvious increasing trend in ΔC before approaching the tipping point can be detected earlier than the ones in both autocorrelation and variance. There is also an obvious inflection point before the bifurcation point is reached. The dot-dashed lines indicate the positions of the bifurcation point.

Full size image

A dynamical model for biochemical oscillations

Non-equilibrium conditions can lead to richer transition behaviors than the equilibrium ones, such as the transition to sustained periodic behavior known as the limit cycle. To test our framework in predicting critical transitions for such transitions, we explore another paradigmatic non-equilibrium phase transition model for biochemical oscillations derived from glycolysis and the Brusselator36:

$$A\mathop{\rightleftharpoons }\limits_{{k}_{-1}}^{{k}_{1}} X,\quad B\mathop{\to }\limits^{{k}_{2}}Y,\quad 2X+Y\mathop{\to }\limits^{{k}_{3}}3X$$
(19)

X and Y are two intermediate species. In contact with external baths which contain two chemical species A and B, at fixed concentrations, this system can be driven out of the equilibrium due to a difference in chemical potential: \(\Delta G={k}_{B}Tln\frac{{{{{{{\mathcal{J}}}}}}}_{+}}{{{{{{{\mathcal{J}}}}}}}_{-}}={k}_{B}Tln\frac{[B]{k}_{2}{k}_{3}{k}_{-1}}{[A]{k}_{-1}}\). k1, k−1, k2, k3 are chemical reaction transition rates and \({{{{{{\mathcal{J}}}}}}}_{+}\)/\({{{{{{\mathcal{J}}}}}}}_{-}\) are the forward-/ backward-reaction flux. The chemical equilibrium (detailed balance) is broken when the chemical-potential difference ΔG ≠ 0 with a sustained non-zero net-reaction flux \({{{{{\mathcal{J}}}}}}={{{{{{\mathcal{J}}}}}}}_{+}-{{{{{{\mathcal{J}}}}}}}_{-}\). The state of the system is determined by the two variables, the total number of X molecules nX and the total number of Y molecules nY, and their dynamics are described as:

$$\frac{d{n}_{x}}{dt}= \, {k}_{1}{n}_{A}-{k}_{-1}{n}_{x}+{k}_{3}{n}_{x}^{2}{n}_{y}\\ \frac{d{n}_{y}}{dt}= \, {k}_{2}{n}_{B}-{k}_{3}{n}_{x}^{2}{n}_{y}$$
(20)

This set of ordinary differential equations can be scaled and non-dimensionalized with \(u=\sigma {n}_{x},v=\sigma {n}_{y},\sigma =\sqrt{{k}_{3}/{k}_{-1}},\tau ={k}_{-1}t\), and become

$$\frac{du}{d\tau }= \, a-u+{u}^{2}v\\ \frac{dv}{d\tau }= \, b-{u}^{2}v$$
(21)

where \(a=({k}_{1}/{k}_{-1})\sqrt{{k}_{3}/{k}_{-1}}{n}_{A},b=\sqrt{{k}_{2}/{k}_{-1}}{n}_{B}\).

The concentration ratio of molecule B vs. molecule A b/a acting as a chemical energy pump gives rise to an effective chemical potential difference for driving the non-equilibrium dynamics24. For different b/a, this non-equilibrium system can be either in a monostable phase or in a stable limit cycle separated by a Hopf-bifurcation.

Figure 5 depicts the main results for the non-equilibrium phase transition from the mono-stability phase to the limit-cycle phase for b = 0.4, along with the decrease of the control parameter a. Figure 5a shows the phase diagram with the varied parameter a. As shown in Fig. 5b, only one free energy minimum when a > 0.192 ceases to be the global minimum, and two new minima on both sides emerge when a < 0.192. Such change in the free energy is similar to the well-known second-order/continuous phase transitions in the classical equilibrium phase transition theory. The slope of the curve for the entropy S, which is the first derivative of the free energy, is smooth when the transition/Hopf bifurcation occurs(Fig. 5c). However, the heat capacity, which is related to the second derivative of the free energy diverges around the transition point (Fig. 5d). Figure 5e, f shows that the entropy production rate is continuous, with a jump in its first derivative. From the point of view of early-warning signals, the behaviours of the thermodynamic quantities here might not appear to be very helpful for predicting tipping points since certain discontinuity can be observed only when the transition occurs.

Fig. 5: Critical transitions characterized by the specific behaviors of thermodynamic quantities in the biochemical oscillation model.
figure 5

a The phase diagram varying the parameter a. b The changes in the non-equilibrium free energy around the Hopf bifurcation with the control parameter a = 0.19, 0.192, 0.195, respectively, indicated by different colored lines. We integrated the partition function with respect to the dynamical variable v, and then we can obtain the partition function and further the free energy as the functions depending only on the variable u. c–f Non-equilibrium entropy, heat capacity (the derivative of entropy with respect to the diffusion strength), the entropy production rate, and its first derivative \(ep{r}^{{\prime} }=\frac{\partial epr}{\partial a}\) versus the control parameter a. The vertical dot-dashed lines denote the associated transition points. The entropy and the entropy production rate are continuous at the bifurcation point, while their first derivatives show a discontinuity.

Full size image

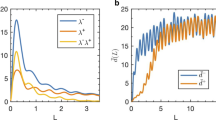
However, it is notable that the non-equilibrium flux, which also reflects the degree of time-reversal symmetry breaking, serves as the main part of the driving force of oscillations. Real systems are permanently subject to natural perturbations. Subtle changes, e.g., smaller transient oscillatory behaviors can occur before the bifurcation point. This implies an opportunity to predict the continuous transitions through monitoring the changes in variance and the differences in the cross-correlations ΔC as the system is approaching the bifurcation point. Figure 6 show trends in ΔC with varied control parameter a and comparisons with the trends in warning signals of the autocorrelation and variance. As shown in Fig. 5, the EPR increases gradually from the mono-stable phase to the oscillatory phase across the Hopf bifurcation, which corresponds to the continuous non-equilibrium phase transition. Therefore, Fig. 6a shows that there is no obvious inflection point in ΔC before the bifurcation point is reached comparing to the case of the dis-continuous non-equilibrium phase transition. The increasing trend in ΔC is slightly more obvious than the one in the autocorrelation. Figure 6b shows that the obvious increase in ΔC can be detected earlier than the one in the variance.

Fig. 6: Early-warning signals for the continuous transitions.
figure 6

The transitions from the mono-stable state to oscillation across a Hopf bifurcation are preceded by an increase in autocorrelation, variance, and the differences in the cross-correlations ΔC as the system is approaching the bifurcation point indicated by the dot-dashed line (a, b). a The increasing trend in ΔC is just slightly more obvious than the one in the autocorrelation. b The obvious increase in ΔC can be detected earlier than the one in the variance. When the system is closer to the Hopf bifurcation, perturbations can lead to longer transient oscillations. This can be reflected through the slower decay rates in the amplitudes of the correlation functions with respect to the delay time, which is indicated by lower decay rates in (c). c The obvious decrease (steeper slope) in the decay rates derived from the cross-correlation difference can be detected earlier (farther from the bifurcation point) than the one derived from the autocorrelation function.

Full size image

Since slowing down causes the intrinsic rates of change in the system to decrease, the state of the system at any given moment becomes more and more like its past state. The resulting increase in memory of the system can be measured through the magnitude of the autocorrelation within the fixed delay time, e.g., the lag-1 autocorrelation, as shown in Fig. 4c of the present work and previous works9. In fact, the changes in autocorrelation and cross-correlation can also be measured from another dimension by estimating the regression rates in the amplitudes of the correlation functions with respect to the delay time. Therefore, we computed the decay rate in the amplitudes of both the autocorrelation function and the cross-correlation difference with respect to the delay time (see details in the Methods section). The smaller decay factor indicates system states in time series are more strongly correlated with slower decay in the amplitudes of the correlation functions. As shown in Fig. 6c, both the decay factors derived from the autocorrelation function and the cross-correlation difference decrease when the system approaches the Hopf bifurcation point. However, the obvious decrease (steeper slope) in the decay factor derived from the cross-correlation difference can be detected earlier (farther from the bifurcation point) than the one derived from the autocorrelation function. This is because the decrease in the former one is induced by the increased non-equilibrium flux (the degree of the time irreversibility) that can emerge far from the bifurcation point, while the latter one is induced by the critical slowing down that usually occurs when the system is getting close to the bifurcation point. Our results suggest that our cross-correlation approach associated with the time irreversibility nature of non-equilibrium systems can provide better warning signals than the ones in previous works based on the critical slowing down.

Discussion

Critical transitions in complex systems are commonly described as dynamic phenomena within the framework of nonlinear dynamics and bifurcation theory due to the lack of a systematic treatment from the thermodynamic perspective9,10,11. A general phenomenon known as critical slowing down in the vicinity of many types of tipping points is used to be seen as an indicator for tipping points. However, critical slowing down is far from being a universal warning signal for abrupt shifts. The warning signals based on critical slowing down can only be detected when the system is very close to an approaching transition/bifurcation point, A sharp shift in system state resulting from a sudden big external impact, which may drive the system across the tipping point, cannot be easily predicted by the critical slowing down since they are close to the tipping point. Due to the fact that the conventional equilibrium phase transitions can be characterized by the specific behaviors of the thermodynamic quantities, we wonder whether one can define the non-equilibrium analogs of the thermodynamic quantities in equilibrium thermodynamics, which may provide us new insights in predicting critical transitions in non-equilibrium complex systems. Motivated by this challenge, we developed a non-equilibrium thermodynamic framework for general complex systems and suggested that critical transitions can be predicted through the specific behaviors of the thermodynamic quantities defined in our non-equilibrium dynamical and thermodynamic framework.

The equilibrium phase transitions are usually explored in the regime of the thermodynamic limit. Once the thermodynamic limit is introduced, even though the underlying Lyapunov function, e.g., equilibrium free energy, may exhibit multi-minima, only one of them with the smallest value of the free energy gives the dominant probability contribution. For example, the first-order equilibrium phase transition in the thermodynamic limit emerges at the location (specific control parameter) where both the minima of the underlying potentials have the same values, and the significant changes in the thermodynamic quantities such as the entropy also only emerge at this location. Although the specific behaviors of the thermodynamic quantities can serve as indicators for thermodynamic phase transitions in equilibrium systems, they may not be early enough to predict these thermodynamic phase transitions.

In our framework, the thermodynamic quantities for a general non-equilibrium system are dependent on the corresponding dynamical driving force, which determines the underlying intrinsic non-equilibrium potential function and the associated steady-state probability distributions. Applying this framework to two well-known non-equilibrium systems, we found that there is a discontinuity in the first/second-order derivative of the non-equilibrium free energy in the small noise limit. Therefore, these transitions in the small noise limit characterized by the specific behaviors of the thermodynamic quantities can be considered as the first/second-order or discontinuous/continuous non-equilibrium thermodynamic phase transitions, in analogy to the equilibrium phase transition theory. However, it is necessary to clarify that the critical transitions in general non-equilibrium systems concerned in the present work and previous works9,16,34 are distinctly different from the well-known thermodynamic phase transitions in equilibrium systems. To be brief and to the point, stochastic dynamics plays a major role in real systems that are subject to perturbations. The steady-state probability distributions in real systems are emergent that can only be obtained from the corresponding stochastic dynamics37. Such emergence arises from an infinitely long time (the steady-state probability distribution PSS = Pt→∞). Since the thermodynamic quantities defined in our non-equilibrium thermodynamic framework are dependent on the non-conserved dynamical driving force, they intrinsically include the non-equilibrium natures, which are different from the equilibrium analogies. As suggested in the previous works9,16,34, the critical transitions in complex systems correspond to different classes of bifurcations. Such critical transitions in non-equilibrium systems can be termed “non-equilibrium dynamical phase transitions.” Figure 3 shows the different locations of the first-order thermodynamic phase transitions in the thermodynamic limit and dynamical phase transitions/ saddle-node bifurcations, taking the Wilson–Cowan model as an example.

Since the critical transitions or dynamical bifurcations that we are concerned with in complex systems occur at different locations (where bifurcations emerge) in contrast with the locations of equilibrium thermodynamic phase transitions, the specific behaviors of the thermodynamic quantities defined in our framework provide the opportunities to predict critical transitions in complex systems. Despite the fact that noise could potentially reveal the presence of an impending transition through a stochastic resonance-like effect, the noise, which is almost ubiquitous in real systems, seems to have adverse effects on detecting the warning signals, such as increased autocorrelation for predicting the impending transitions based on the critical slowing down in previous approaches9,16. Nevertheless, the limited noise in complex systems can be beneficial to predict critical transitions in our framework. As suggested in the above section, in the small noise limit, the significant changes in our thermodynamic quantities across fold bifurcations can be detected at the location where an alternative stable state begins to be dominant. This is much earlier from the occurrence of the possible critical transitions and beyond the location where the current stable state is going to disappear. If finite noise is presented, there are also indicators (peaks in the entropy and heat capacity), which can be observed far from the approach transition point (Fig. 2g–i).

Previous works explored the architectural features that may create abrupt transitions in complex systems in addition to the warning signals, which provide alternative angles for diagnosis and potential action of critical transitions16. It is worth noting that sharp transitions in real complex systems such as ecosystems or societies may often be caused by changes in external conditions. For instance, the models in the present work show the transitions are the results of the changes in the external input signals or chemical potential differences. The steady states in such open systems are maintained through the constant exchange of entropy or energy with the outside environment. Therefore, the critical transitions that occur in open systems are usually accompanied by significant changes in the dissipative patterns, which can be measured by the entropy production rate (EPR)32,38,39,40. As we stated earlier from our previous findings that the driving force for the dynamics of a non-equilibrium system is determined by both the gradient of the landscape and the steady-state probability flux. While the gradient force tends to attract and stabilize the system to the point attractor, the flux force being rotational, tends to destabilize the point attractor and form a stable limit cycle, oscillatory attractor. Therefore, the increase of the flux force can destabilize a stable state. This gives the dynamical origin for a bifurcation or non-equilibrium dynamical phase transition. The non-equilibrium flux, which measures the degree of irreversibility or detailed balance breaking, provides the dynamical basis of the thermodynamic costs or dissipations in terms of the EPR in the open systems. Since the flux or irreversibility requires the thermodynamic cost to sustain, the EPR or dissipative cost gives the thermodynamic origin of the bifurcation or non-equilibrium phase transition. In the general case that finite noise is presented, the specific change in EPR can serve as warning signals for predicting critical transitions.

Inspired by these facts, we found that the specific behavior in the differences in the cross-correlations between the forward and backward directions in time of the two-state variables in the obtained time series, which is associated with the degree of time-reversal symmetry breaking of a non-equilibrium system, can serve as early-warning signals for predicting critical transitions. Our results suggest that such indicators can be detected earlier than the ones based on critical slowing down for both the critical transitions associated with the fold and Hopf bifurcations. In a more general sense, it is not easy to get all the details of the underlying mechanisms that drive a complex system. Therefore, the cross-correlation approach can provide a more practical early-warning signal for predicting critical transitions since only the time series of the state variables are required. Moreover, monitoring the behavior of the non-equilibrium flux and then steering the system through manipulating the specific control parameters (external conditions), which can induce efficient changes in the flux and further the EPR, may suggest an alternative way to prepare for anticipated change.

The directed percolation process, along with the related absorbing phase transitions, is a very important class of non-equilibrium phase transition6. These types of transitions are characterized by the presence of the absorbing state that can be reached by the system but from which the system cannot escape. It appears that there are no divergent-free non-equilibrium fluxes in the steady state after the system falls into a so-called absorbing state. This is different from the general cases that the non-equilibrium steady states always carry certain flux. So, the percolation is often characterized by the non-equilibrium in time rather than the non-equilibrium at steady state. For such cases, it may be challenging to detect early-warning signals with our cross-correlation approach. This is because the increased differences in the cross-correlation before an approaching critical transition/bifurcation can be detected from the time series of the system state variables often in steady states, while similar information cannot be obtained from the steady state of the system with the absorbing phase transitions. It will be very interesting to uncover practical early-warning signals for predicting such non-equilibrium phase transitions in future work.

For the directed percolation process, we can simulate this process using a computer since we know the short-ranged dynamical rules that dominate the evolution of the system. We can define an explicit order parameter and then use concepts and methods which were developed for equilibrium critical phenomena to explore such transitions. However, for many complex dynamical systems, ranging from ecosystems to the human brain, financial markets, and the climate, we may have a relatively poor understanding of the mechanisms that drive the dynamics. We cannot directly write down the corresponding master equations, Langevin equations, or Fokker–Plank equations. We may not even get enough information about the probability distributions involving sufficient transitions between alternative stable states. What we can obtain may only be the time series of the state variables. Then how can we predict the possible critical transitions in such systems? Here, we tried to provide a general yet practical approach for predicting critical transitions in such complex systems. The core idea of our approach is that the changes in the non-equilibrium flux, which plays an essential role in non-equilibrium phase transition, can be obtained from the detectable time series. This approach can provide a more practical early-warning signal for predicting critical transitions even if we do not understand all the details of the underlying mechanisms that drive the complex system, which is the significance of the current work.

In summary, motivated by the challenges of predicting the ubiquitous critical transitions in complex systems, our approach used the analogy to the well-established concepts and conventional statistical treatment for equilibrium phase transitions, while the natures of the non-equilibrium dynamics are considered and reflected in the thermodynamic quantities. In our framework, warning signals based on the thermodynamic quantities can be detected much earlier than the ones explored in the previous works on the basis of nonlinear dynamics and the bifurcation theory9. Notably, our cross-correlation approach can provide a more practical early-warning signal for predicting the critical transitions since only the observed time series of the state variables are required. Such warning signals reflect the time-irreversibility or the degree of the detailed balance breaking in the non-equilibrium complex systems. They can only be detected in non-equilibrium phase transitions rather than equilibrium phase transitions. The general approach exemplified by the models with fold/Hopf bifurcations in the present work is applicable to complex systems where critical transitions such as asthma attacks, epileptic seizures, abrupt shifts in ecosystems, and financial market crashes can occur9,41,42,43,44,45,46,47,48. Our approach can provide warning signals for approaching critical transitions in such complex systems. Since the behaviors of the entropy production rate have been suggested in previous works across various complex systems49,50,51,52, our work provides a general and unified approach for exploring the collective behaviors in non-equilibrium systems such as bifurcations and phase transitions.

Methods

To test the ability of our non-equilibrium thermodynamic framework to characterize and predict critical transitions in general non-equilibrium systems, we explored two typical non-equilibrium systems where different types of bifurcations can emerge. The details of these two models have been shown in the Results section. In order to obtain the non-equilibrium quantities such as the non-equilibrium free energy, entropy, and heat capacity that are defined on the basis of the NESS probability distributions derived from the intrinsic potential function ϕ0. We need to solve the corresponding Hamilton-Jacobi equation(Eq. (3)). The Hamilton–Jacobi equation is difficult to solve exactly with an analytic solution. To get the numerical solution of the Hamilton–Jacobi equation, a numerical method: the level set method, was devised and developed. In the present work, we use the Mitchells level-set toolbox53 to solve the Hamilton–Jacobi equation for intrinsic potential ϕ0.

However, the corresponding complex Hamilton–Jacobian (HJ) equations are difficult to be solved for some systems, e.g., the biochemical reactions where the diffusion coefficients are dependent on the state variables. For such cases as the biochemical oscillations model explored in the present work, we can calculate the NESS probability directly from the associated Fokker–Planck equation. Once the fluctuations are introduced, the corresponding driving forces should be written as:

$$\frac{du}{d\tau }= \, a-u+{u}^{2}v-(1/V)* ((1/2+2* u* v-{u}^{2}/2))\\ \frac{dv}{d\tau }= \, b-{u}^{2}v+(1/V)* (2* u* v-{u}^{2}/2)$$
(22)

Here V is the volume of the biochemical system. The diffusion matrix is:

$$D{{{{{\bf{D}}}}}}=\frac{1}{V}\left[\begin{array}{cc}a+u+{u}^{2}v&-{u}^{2}v\\ -{u}^{2}v&b+{u}^{2}v\end{array}\right]$$
(23)

Here the \(\frac{1}{V}=D\) measures the magnitude of the fluctuations. In the present work, we choose V = 10,000. We found significant changes in the thermodynamic quantities based on the NESS probability distributions, which are calculated directly from the associated Fokker–Planck equation in the vicinity of the transition points.

Most of the complex systems in nature, such as biological systems, are coupled to an environment far from thermodynamic equilibrium. In these non-equilibrium systems, the non-zero non-equilibrium flux induces the time-reversal symmetry breaking. Recent studies show that the degree of time-irreversibility or detailed balance breaking is measured by the cross-correlation difference between the forward and backward directions in time35. In contrast to an equilibrium system where the time-forward cross-correlation function between two signals equals the time-backward one, a non-equilibrium system shows asymmetry in the cross-correlation between the forward and the backward directions in time. As discussed in the main text, the flux part of the driving force in a non-equilibrium system is rotational and tends to destabilize the current fixed point/attractor state against the gradient part of the driving force. Therefore, the destabilization of the current state approaching a bifurcation or transition point may be reflected through the changes in the non-equilibrium flux and, further, more practically, the cross-correlation between the forward and the backward directions in time.

Here we first calculated the dynamical trajectories for the two-state variables of a non-equilibrium system by firstly solving the corresponding Langevin equations, e.g., the activities in the excitatory and the inhibitory subpopulations xE(t) and xI(t) in the Wilson-Cowan model. Then we can obtain the cross-correlation difference between the forward and the backward directions in time (ΔC(τ) = 〈xE(0)xI(τ)〉 − 〈xI(0)xE(τ)〉) according to the time series. After that, we calculated the average \(\Delta C=\int\nolimits_{0}^{t}C(\tau )d\tau \), which is no longer a function of the time delay τ. Here t is the length of the dynamical trajectory in time. For the case with the fold bifurcation, we calculated the cross-correlation difference at lag-1 (t is each time interval between the neighboring points in the time series). For the case where oscillations happen, the cross-correlation difference is calculated through the integral of the time series, including several periods of the corresponding oscillations. Due to the stochastic nature of the system, we may get different ΔC for different trajectories. Therefore, we repeated this process 10,000 times to obtain the final ΔC by averaging these results.

The ΔC is derived from the time series and depends on the state of the system. To test whether the changes in ΔC can serve as an early-warning signal for predicting critical transitions, the time series describing the destabilization of the current state approaching a bifurcation or transition point is required. For instance, if we are concerned about the transition from the “up” state to the “down” state in the Wilson-Cowan model, we need to collect the time series of xE(t) and xI(t) that fluctuate around the “up” state due to the noises as the control parameter IE is decreased. For different specific values of the control parameter IE, we can calculate the corresponding ΔC. Then the trends of the ΔC as the system approaches a transition point can be obtained. Our results suggest that the cross-correlation difference between the forward and the backward directions in time is closely related to the non-equilibrium flux and further the entropy production rate. The cross-correlation approach can serve as a more practical early-warning signal for predicting critical transitions, which can be detected much earlier before the actual corresponding transition point.

In addition to the magnitude of the autocorrelation within the fixed delay time, e.g., the lag-1 autocorrelation, the changes in the autocorrelation and cross-correlation can also be measured from another dimension by estimating the decay rates in the amplitudes of the correlation functions with respect to the delay time. For the case with the Hopf bifurcation, we computed the decay rate in the amplitudes of both the autocorrelation function and the cross-correlation difference with respect to the delay time. The decay in the amplitudes of the oscillatory cross-correlation difference with respect to the time delay τ is approximately exponential in a limited length of the time delay. The decay rate, therefore, can be calculated by fitting the exponential curves on the data about the amplitudes of the oscillatory cross-correlation difference with respect to the delay time. The decay rates are calculated using the MATLAB toolbox Curve Fitting. The lower decay rate indicates system states in time series are more strongly correlated with slower decay in the amplitudes of the correlation functions.