Introduction

Envisioned by Feynman1 and later formalized by Deutsch2 and others3, quantum computing has been perceived by many as the natural simulator of quantum mechanical processes that govern natural phenomena. It became more popular with the discovery of powerful algorithms like Shor’s integer factorization4 and Grover’s search5 offering significant theoretical speedup over their classical counterpart. A different flavor of quantum computing was also theorized in Refs. 6,7,8,9 which makes use of the adiabatic theorem10. It was later shown that these two flavors of quantum computing are equivalent11. The technological difficulties of realizing noiseless qubits with coherent interactions among the qubits have focused recent efforts on the Noisy Intermediate Scale Quantum (NISQ) regime12 and serious progress has been made in recent years13,14,15,16,17,18,19.

In the absence of general-purpose quantum computers, quantum Monte Carlo (QMC) still remains the standard tool to understand quantum many-body systems and to investigate a wide range of quantum phenomena—including magnetic phase transitions, molecular dynamics, and astrophysics20,21,22,23. Much effort has been made to develop efficient QMC algorithms of various sorts22,23,24,25,26,27,28,29,30,31 which can be suitably implemented on standard general-purpose classical processors (CPU). Interestingly for many important quantum problems, the efficiency of QMC is significantly affected by the notorious sign problem32. The sign problem manifests itself as an exponential increase in the number of Monte Carlo (MC) sweeps required to reach convergence33. The origin of the problem is that qubit wavefunctions can destructively interfere in the Hilbert space. Quantum problems that do not pose a sign problem are given a special name stoquastic and it is believed non-stoquasticity is an essential ingredient for adiabatic quantum computing (AQC) to be universal11 and to provide significant speedup over classical computers34,35. Recently in ref. 36, King et al. demonstrated that with a physical quantum annealing (QA) processor, it is possible to achieve 3 million times speed up with scaling advantage over an optimized cluster-based continuous time (CT) path integral Monte Carlo (PIMC) code simulated on CPU. In a surprising demonstration37,38, King et al. applied the Transverse Field Ising (TFI) Hamiltonian on a geometrically frustrated lattice initialized with a topologically obstructed state. Note that this is a different type of obstruction than the one commonly discussed in the related literature (see ref. 39 for example). This obstruction makes it difficult for an algorithm based on local update schemes to escape the obstruction, whereas a quantum annealer might help escape the obstruction faster. This is interesting because until this result, results on TFI, a well-known stoquastic Hamiltonian, have been routinely benchmarked with quantum Monte Carlo algorithms40 with no clear scaling differences for practical problems41. In the theoretical computer science community, the possibility of obtaining a scaling advantage for AQC with sign- problem-free Hamiltonians (such as TFI) is still being actively discussed42,43.

PIMC, one of many variations of QMC, is the state-of-the-art tool for simulating and estimating the equilibrium properties of these quantum problems. Powerful and efficient cluster-based algorithms exist for ferromagnetic spin lattices44. However, it is known that the efficiency of the cluster algorithms drops when frustrations are introduced in the lattice although alternative approaches that compromise between local and global updates were explored45 in the context of the classical Ising model.

In recent years, a lot of new devices and domain-specific hardware have emerged to augment the performance of classical computing/simulations in stark contrast with building quantum computers: which is a complete paradigm shift. In this paper, we explore the possibility of hardware accelerating QMC with one such technology that exploits classical and probabilistic resources, namely, a processor based on probabilistic bits (p-bits) which can be viewed as a classical counterpart of the QA processor46. A p-bit is a robust, classical, and room-temperature entity that continuously fluctuates between two logic states and the rate of this fluctuation can be controlled via an input signal applied to a third terminal47. p-bits can also be made very compact and can provide true randomness (important for the problem we address in this paper, see Supplementary Note 5) instead of pseudo-random generators, commonly used in software-based solutions. First appeared as a hardware realization of a binary stochastic neuron in ref. 47, later a proof-of-concept p-computer was first demonstrated in ref. 48. p-bit-based hardware solutions have been proposed to improve performance for optimization problems49, classical and quantum Monte Carlo50, Bayesian inference51 and machine learning52.

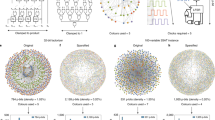
In this study, we demonstrate hardware acceleration using p-bits by an optimized probabilistic computer. This system employs the discrete-time (DT) Path Integral Monte Carlo (PIMC) approach, using the Suzuki-Trotter approximation, and features a sufficient number of replicas to ensure satisfactory accuracy. This design uses massive parallelism and suitable synapses to maximize the number of sweeps collected per clock cycle, resulting in a three-order-of-magnitude improvement in convergence time on a moderately sized programmable gate array (FPGA) compared to a CPU. This design strategy also enables the easy translation of the digital circuit into a clockless mixed-signal design featuring fast resistive synapses and low barrier magnet (LBM) based compact p-bits. Using SPICE (simulation program with integrated circuit emphasis) simulations grounded in experimentally benchmarked models, we anticipate an additional two to three orders of magnitude speedup. Figure 1 summarizes our approach, illustrating the four different hardware types and their expected relative performances. Overall, our demonstration offers a roadmap for achieving five to six orders of magnitude acceleration for a transverse field Ising model (TFIM) and has the potential to extend to other QMC models as well. The clockless analog hardware can be considered the classical counterpart of the quantum annealer, delivering performance within a factor of less than 10 of the latter. The convergence time for the clockless analog hardware scales with the number of qubits as approximately N, which is superior to the ~ N2 scaling for CPU implementations but appears worse than that reported for quantum annealers.

Fig. 1: Performance of specially designed p-computers, digital and clockless, relative to a CPU and a quantum annealer.
figure 1

a We use an example problem consisting of a lattice of qubits described by a transverse field Ising model. We simulate it classically using the Suzuki-Trotter transformation and calculate a pre-defined order parameter using three different types of hardware whose relative convergence times are sketched in b. The variations in performances due to variations in implementation technologies are indicated with thick lines. The four types of hardware are also shown schematically—c a von Neumann machine (CPU)—which simulates the problem by breaking down the problem into a series of instructions and executing them sequentially one after another, d a physical quantum annealing processor (QA) that maps the problem onto an interconnected network of rf-SQUIDs (radio-frequency-superconducting quantum interference devices) emulating qubits and rf-couplers coupling those qubits e a digital p-computer built using field programmable gate array (FPGA) to lay out a spatial network of interconnected probabilistic p-bits and f a clockless p-computer constructed by interconnecting a network of p-bits through resistors. The quantum annealing processor image has been taken from Harris et al. Phase transitions in a programmable quantum spin glass simulator. Science 361, 162–165 (2018). Reprinted with permission from AAAS.

Full size image

Results and discussion

We emulate a quantum problem from a recent work36 where a Transverse Field Ising Hamiltonian (which is stoquastic)

$${{{{{{{\mathcal{{H}}}}}}}_{{{{{{{{\rm{Q}}}}}}}}}}}=-\left(\mathop{\sum}\limits_{\langle ij\rangle }{J}_{ij}{\sigma }_{i}^{{{{{{{{\rm{z}}}}}}}}}{\sigma }_{j}^{{{{{{{{\rm{z}}}}}}}}}+\Gamma \mathop{\sum}\limits_{i}{\sigma }_{i}^{{{{{{{{\rm{x}}}}}}}}}\right)$$
(1)

is applied over a two-dimensional square-octagonal qubit lattice as shown in Fig. 2a. The exotic physics offered by this qubit lattice is of practical interest and has been described in ref. 36,53. The square-octagonal lattice can be viewed as a (2L − 6) × L antiferromagnetically (AFM) coupled triangular lattice with a four ferromagnetically (FM) coupled spin basis, giving rise to a total of 4L(2L − 6) qubits in the lattice. The resulting lattice consists of square and octagonal plaquettes which are periodically connected along one direction and it has open boundaries in the other direction. In the bulk of the lattice, each qubit is connected to three other neighbors whereas, at the open boundary, some qubits are connected to just one neighbor, and others are connected to two neighbors. To increase the degeneracy of the classical ground state, the AFM couplings at the open boundary are also reduced to half of that in the bulk.

Fig. 2: Example problem addressed in this paper following King et al.36.
figure 2

a quantum problem solved on quantum annealing processor involves a two-dimensional square octagonal lattice of qubits having 2L qubits in one direction and 2(2L − 6) qubits in the other direction (illustration shows L = 6). The blue bond between two qubits denotes ferromagnetic (FM) coupling (JFM = − 1.8) and yellow bond indicates antiferromagnetic (AFM) coupling (JAFM = 1.0). The AFM couplings at the open boundary have JAFM = 0.5, b Trotterized mapping solved on classical computers, c Trotter error with 10 replicas: (Upper panel) Equilibrium values predicted from 10 replica probabilistic computer emulation and four qubit continuous time path integral Monte Carlo (4q CT-PIMC) algorithm developed in ref. 36 (red hollow circles: p-computer data, blue hollow squares: 4q CT-PIMC data). (Lower panel) Absolute (blue hollow circles) and relative errors (red hollow squares) in predicting equilibrium values between the two methods are shown.

Full size image

Each square or octagonal plaquette in this lattice is composed of qubits from three different sublattices and has three (an odd number) AFM bonds (for both octagonal and square plaquettes). This leads to a frustrated lattice since it is impossible to satisfy all the bonds simultaneously. Three different qubit sublattices within the lattice are indicated by the red, green, and blue colors in Fig. 2a.

In this benchmark study, we observe the average equilibration speed of the average order parameter when initialized with a particular classical state (in this study we will be referring to two particular initial states: counterclockwise (CCW) and ordered, see Supplementary Note 1 for more details) in probabilistic computer which is based on discrete-time path integral Monte Carlo (DT-PIMC) with many interconnected replicas of the original qubit lattice but the qubits are replaced by p-bits (see Methods section). We will compare this result against the general-purpose processor (CPU) and with the quantum annealing processor from36. The procedure to obtain the average order parameter was defined in ref. 36 and has been outlined in the Methods section.

Design considerations for the probabilistic emulator

We start the process of designing our p-computer with the trotterization of the qubit lattice using 10 replicas and involving 40L(2L − 6) p-bits, ranging up to 14,400 p-bits for L = 15. Traditional Gibbs sampling or single-flip Monte Carlo sampling takes too long to converge for such a large network and we need a scheme that allows us to simultaneously update many p-bits. But it is also well-known that updating two p-bits simultaneously which are connected to each other leads to erroneous output. We realized that the limited connections among the p-bits in the replicated network could be utilized to achieve massive parallelism where many p-bits can be updated in parallel and therefore can be used to speedup the convergence. To obtain such massive parallelism, we next applied graph coloring on the replicated p-bit network, as recently explored in ref. 49 for general and irregular lattices.

Graph coloring assigns different colors to p-bits that are connected to each other and ensures that no two p-bits that are connected to each other have the same color thus enabling us to update all p-bits in the same color group simultaneously. Although not immediately obvious to many, it can be easily checked that the qubits of the square-octagonal lattice under consideration can be colored using just two colors (i.e., the lattice is bipartite). If we always choose an even number of replicas (which is what we do in this work), then we found that the translated p-network can also be colored using just two colors (i.e., the p-bit network also remains bipartite), as shown in Fig. 2b. Hence with just two colors, half of the p-bit network can be updated in one clock cycle and the other half of the network in another, producing one sweep in every two clock cycles. In general, compared to a single flip Monte Carlo implementation which updates one spin in one clock cycle, this graph-colored approach can reduce the number of clock periods required to converge by a factor of ~ nr/C (nr is the number of p-bits and C is the number of colors) assuming same clock period for both cases.

This leads us to argue that a p-computer should exhibit weaker dependence with the increasing size of the network compared to the CPU because even though the number of p-bit increases in the network, one can also proportionally increase the number of p-bits (we estimate that up to one million of p-bits can be integrated on a chip with a reasonable power budget54) to be updated in a given clock, yielding a factor of n ( = number of p-bits in the network) improvement in scaling over CPU. This demonstrates the power of a properly architected p-computer over a CPU where the scope of such parallelization is very limited.

Results from digital p-computer emulation on FPGA

To demonstrate the utility of such massively parallel architecture, we next emulate this graph-colored p-bit network by implementing it on FPGA using Amazon Web Services F1 instance (more details of the FPGA implementation can be found in Supplementary Note 2). Various implementations of p-bits including digital and analog have been discussed in refs. 54,55. The digital implementations of p-bits are costly in terms of resources and require thousands of transistors per p-bit and so we have only been able to fit the smallest lattice size (L = 6) with the resources provided therein. But we expect that when replaced with nanomagnet-based stochastic MTJs, the situation would improve drastically. It is also equally important to carefully design the synapse that can provide updated information to p-bits by quickly responding to any changes in the state of neighboring p-bits. In the spirit of ref. 56, we carefully choose our synapse to update nrf/C p-bits per second providing f/C sweeps per second. The clock period 1/f needs to be minimized carefully so that the synapse can correctly calculate the response while providing maximum throughput. This choice of FPGA implementation also provides a unique way that permits a clear pathway to a mixed signal circuit. The FPGA is less than an ASIC (application-specific integrated circuit), but the mixed signal especially with MTJs would be much more than an ASIC.

In our FPGA demonstration, we have been able to run the smallest lattice with an 8 ns clock period (16 ns per sweep since we have two colors) and we believe that given enough resources we should also be able to run the bigger lattices at the same clock frequency. We project convergence times for other lattice sizes based on CPU simulations. These ‘projections’ are based on actual implementation with real devices and should be reliable, given our digital architecture and the fact that we did not use the largest FPGA available today.

For the other lattice sizes, we obtain the average order parameter versus the number of sweeps plots via running MATLAB on CPU (a verification of FPGA output matching MATLAB output is also provided in Supplementary Note 2) and then multiply the x axis of that plot by 16 ns per sweep. These lead to the curves in Fig. 3a, where we report the average order parameter, 〈m(t)〉 versus time curves obtained from p-computer emulation for the same four lattice sizes of square-octagonal lattice and with the same parameters as in ref. 36 but only with counterclockwise (CCW) wound initial condition. The curves with clockwise wound (CW) initial condition are similar to these CCW curves (slightly faster than CCW) whereas curves for ordered initial condition (not shown) show much faster convergence.

Fig. 3: Extracting convergence times from simulation results following the protocol described in ref. 36.
figure 3

a Average order parameter 〈m〉 as defined in Eq. (2) (Eq. (2) in ref. 36) are obtained for four different lattice sizes (blue: 6 × 6, red: 12 × 9, yellow: 18 × 12, purple: 24 × 15) using the mapped p-bit network. We have used Γ = 0.736, and β = 1/0.244 for which the scaling difference was reported to be maximum. We show results only for the counterclockwise wound initial condition as explained in the Supplementary Note 1. Only the curve labeled as 6 × 6 is obtained through actual field programmable gate array emulation and the others are projected based on CPU simulation. All data points are averaged over 1000 different runs and the errorbars correspond to 95% confidence interval around the mean. Filled circles represent data points while the solid lines represent \(a\exp (-bx)+c\exp (-dx)+g\) type fit. b Mean squared error (MSE) plot for each lattice size (blue: 6 × 6, red: 12 × 9, yellow: 18 × 12, purple: 24 × 15; hollow circles: data, dashed lines: fit) calculated from their corresponding `g' values in a. The scaling is more clearly visible in this plot. Also shown is the 0.0025 threshold in dashed green which is used to define convergence.

Full size image

In Fig. 2c, we report the error in predicting the saturation value from using finite replica in our p-computer emulations. We compare our results against the 4q CT-PIMC algorithm developed in ref. 36. To ensure fidelity, we use the same C++ codes provided therein. With 10 replicas, we reproduce the CT-PIMC results with an absolute difference of 0.01–0.03 from the smallest to the largest lattice sizes (see Supplementary Note 4 for CT-PIMC results). As reported in ref. 36, we do not observe systematic changes in Trotter errors with lattice sizes.

Clockless autonomous operation

In the last subsection, we have presented a digital implementation of a p-computer based on the graph-colored architecture. Even though it is not immediately obvious to many, in that architecture, we managed to use just two colors which happen to be the minimum number of colors possible and thus maximizes the number of p-bits that can be updated simultaneously. This allowed us to greatly reduce the convergence time compared to single-flip Monte Carlo which updates just one p-bit at a given clock period and thus converges very slowly. However, there are two problems associated with this graph-colored digital implementation: first, a fully digital implementation of a p-bit requires thousands of transistors which increases the hardware footprint per p-bit quite significantly. This can be mitigated somewhat through the use of nano-magnet-based compact p-bits which uses just three transistors and an MTJ. However, this also requires the use of digital to analog converters for each p-bit since the input to such compact p-bits is analog. The second issue with the digital implementation is that to perform a colored update, all p-bits need to be synchronized through a global clock, the distribution of such clock throughout the chip becomes complicated with the increasing number of p-bits and also slows down the frequency with which the system can be operated.

To circumvent the above issues, we next visit a fully analog implementation of a p-computer with a clockless autonomous architecture. The clockless architecture is inspired by nature: natural processes do not use clocks. In clockless autonomous architecture, we do not put any restrictions on the updating of p-bits. Each p-bit can attempt to update at any point in time without ever requiring a clock to guide them. Of course, errors will be incurred if two connected p-bits update themselves simultaneously, and therefore with this scheme, it is essential to minimize the probability of happening that. If there are d neighbors to each p-bit then the probability that two connected p-bit will update simultaneously is roughly d × s2 where s = τs/τN, 1/τN is the frequency with which a p-bit attempt to update itself and τs is the time required to propagate the information of a p-bit update to its neighbors. To make this clockless autonomous operation work it is essential to have s ≪ 1 (usually s ≈ 0.1 works well). This interesting possibility of clockless autonomous operation was introduced in ref. 54 where a digital demonstration was made using FPGA. However, in this work, we use a simple resistive synapse-based architecture. Since resistors can instantaneously respond to the change in applied voltage, this type of synapse should be very fast compared to the average fluctuation time of s-MTJ-based p-bits ( ~ 100 ps). We demonstrate the validity of this scheme by showing a SPICE simulation of a 6 × 6 triangular AFM lattice with classical spins as shown in Fig. 4a. As mentioned earlier, the triangular lattice is the base lattice of the square-octagonal lattice we have used so far. A partial view of the analog circuit simulated in SPICE which corresponds to the lattice above is also shown in Fig. 4d. We only show the resistive analog synapse providing the input for a single p-bit as marked. We use similar parameter values and the same boundary conditions as we have used for the square-octagonal lattice (the same AFM coupling strength (∣JAFM∣ = 1) inside the lattice and ∣JAFM∣ = 0.5 at the open boundaries). We also use the same definition for the order parameter. To keep it similar to what we have done in the previous section, we also use CCW initial condition in this example. Doing these help us to solve the problem in SPICE within a reasonable amount of time.

Fig. 4: Comparing digital to clockless p-computer.
figure 4

a A 6 × 6 antiferromagnetically (AFM) coupled triangular lattice with classical spins is shown. b The convergences of the order parameter for the lattice shown in a are plotted for two different p-computer design approaches (red solid line: graph-colored based digital design and blue solid line: nanomagnets based analog design) discussed in this work. We have used β = 2 in this example. For SPICE simulation, we averaged results over 500 different runs whereas for the graph-colored result, we averaged over 1000 different runs. c The graph-colored (GC) based digital p-computer design where the convergence is estimated from MATLAB simulations assuming c × fc (c = 3 for triangular lattice) sweeps are collected every per second, fc being the clock frequency. d The clockless p-computer design which is simulated using SPICE simulator.

Full size image

Figure 4b shows the relaxation of the order parameter with time for the example described in Fig. 4a. We use the same SPICE p-bit model used in ref. 57. We also show the relaxation curve obtained via a 3-graph-colored architecture (the triangular lattice in this example is 3-colorable). The graph-colored system as shown in Fig. 4c converges (based on the criterion we have used so far) around 72 sweeps. In 125 MHz FPGA that we have used earlier, this would take around 72 × 3 × 8 ns = 1.73 μs, whereas the corresponding analog circuit implementation converges in around 5 ns, converging around 400 times faster than similar digital implementation used earlier. Although the circuit used here is not programmable, it nicely illustrates the principle that around two orders of additional speed-up can be obtained with the use of a properly designed fully analog and clockless p-computer.

Convergence time scaling results

Finally, we show the time scaling for four different hardware in Fig. 5. We directly adopt the optimized 4q CT-PIMC (in CPU) and QA processor data from ref. 36. A simple curve fitting to CPU data reveals a roughly \({N}_{Q}^{2}\) scaling where NQ = 4L(2L − 6) is the total number of qubits in the lattice. On the other hand, the p-computer results show a prefactor improvement and an improvement in scaling compared to a CPU. For a more direct comparison, we also show the scaling of our graph-colored algorithm simulated on CPU which also shows an \(\sim {N}_{Q}^{2}\) scaling behavior. We observe an ~ NQ scaling for p-computer and as noted before, the reason for such a scaling improvement is due to the exploitation of massive parallelism where the number of p-bits that can be updated also increases with the lattice size and this is not due to an algorithmic improvement (the scaling with the number of p-bits is provided in Supplementary Note 6).

Fig. 5: Convergence time for problems of increasing size using different hardware implementations.
figure 5

The convergence time is extracted using the protocol described in Data fitting and convergence criterion subsection of Method section for the problem defined in Fig. 2. The data for optimized CPU (yellow cross) (mean of counterclockwise and clockwise wound initial states) and quantum annealing processor (red triangles) (for counter clockwise wound initial state only) are extracted from the information provided in King et al.36 (Fig. 4 and supplementary Fig. 13 therein), while the results for graph-colored MATLAB (blue circles) (simulated on CPU), digital (purple star) and clockless p-computers (green squares) are obtained in this paper as described in the text. This CPU simulation of graph colored algorithm is performed with a vectorized MATLAB code running on Intel(R) Core(TM) i7-10750H CPU (2.60 GHz, 16 GB RAM, Windows 11 Home operating system and single thread simulation are used). As mentioned in the caption of Fig. 3, only the leftmost data point on the p-computer (FPGA: field programmable gate array) curve is obtained from actual FPGA emulation. The rest of the points on the curve are projections based on the simulations on the CPU. The slope of the p-computer curve is clearly different (and smaller) from the graph-colored MATLAB (CPU) and optimized four qubit continuous time path integral Monte Carlo algorithm (simulated on CPU) curves (the exact slopes found using curve fitting are listed in Supplementary Note 7).

Full size image

In our perspective, any CPU-based solution is unlikely to achieve the same level of parallelism as our p-computer, as this would necessitate the use of “N” processors or threads. While we acknowledge that specialized CPU implementations employing multiple threads and/or processors might approximate the parallelism achieved with our custom hardware, our optimized implementation suggests that achieving such parallelism (scaling with N-threads) is not trivial. Additionally, beyond digital implementations, nanodevice-based ASICs could support millions of p-bits54, taking N to unprecedented levels. This degree of parallelism may be challenging to replicate in conventional digital hardware, at least from a practical standpoint.

We note here that we are investigating a quantum sampling problem in this work that measures the equilibration time of a specially prepared lattice. The measured convergence time does not depend on the number of replicas run in parallel. This is because the reported time is the ‘average’ obtained from R identically prepared trials. Whether these trials are taken in parallel or in series does not affect the convergence time we (or King et al.) report. Increasing the number of replicas simply reduces the variance of the random variable we are estimating and has no effect on the reported wall-clock times or convergence times in any of the platforms (annealer, CPU, p-computer). For the same reason, we do not fit as many parallel replicas in our FPGA as possible to make our measurements, even for smaller lattice sizes.

On the contrary, in optimization-type problems where the quantity of interest is “time to solution” (TTS), it makes sense to utilize a p-bit/qubit system to the fullest by running as many parallel instances as possible in one run (to reduce TTS linearly by reducing the number of repetitions necessary). In such cases, appropriate care must be taken when comparing the performance of specialized hardware with CPU performance which is usually utilized fully (see ref. 58 for example).

Our results for the digital implementation of p-computer emulated on 125 MHz FPGA show that for the largest lattice size (L = 15) that has been emulated in ref. 36, we should get a ~ 1000 × improvement over a single thread implementation on CPU. But as it stands, the current FPGA emulations of our p-computer are ~ 3 orders of magnitude worse than the physical quantum annealing processor. We expect another one order of magnitude improvement might be possible with this approach by using a customized mixed-signal ASIC design with stochastic magnetic tunnel junction (sMTJ)-based p-bits. However, based on the example of clockless operation shown in Results and discussion, we project another two orders of magnitude improvement in convergence time. This brings the gap with the quantum annealing processor down to one order or less. The operation of the quantum annealing processor might be governed by non-local quantum processes leading to the \(\sqrt{{N}_{Q}}\) scaling predicted in ref. 59, though there are not enough data points to be certain.

Although we did not do a direct GPU (graphics processing unit) implementation of the problem under consideration, we looked for the GPU emulations of bipartite (2-colorable) graphs (like the one being simulated in this work) in the literature. In a typical GPU one gets around 10–30 flips/ns (the key metric used to compare the performance and the higher flips/ns gives better performance)60,61,62,63 for such graphs whereas our designs get 90 flips/ns (1440/2 = 720 p-bits being flipped at every 8 ns) from the actual FPGA design for the smallest lattice size and will increase as we enable ourselves to integrate more and more p-bits.

Conclusion

In this work, we have presented a roadmap for hardware acceleration of QMC which is ubiquitously used in the scientific community to study the properties of many-body quantum systems. We have mapped a recently studied quantum problem into a carefully designed autonomous probabilistic computer and projected 5–6 orders of magnitude improvement in convergence time which is within a factor of 10 of what has been obtained from a physical quantum annealer. The massively parallel operation of a probabilistic computer together with the clockless asynchronous dynamics provides a significant scaling advantage compared to a CPU implementation. Robustness, room-temperature operation, low power consumption, and ultra-fast sampling—these features make it interesting to investigate the applicability of probabilistic computers to other quantum problems beyond the TFI Hamiltonian studied in this work.

Methods

Procedure to calculate average order parameter

For the sake of completeness, we provide the details of the calculation of average order parameter in the following:

  1. 1.

    Average of four FM-coupled qubits is computed for each basis in the lattice. Depending on the sublattice the basis belongs to, these averages are denoted as mav,red, mav,green or mav,blue (see Fig. 2). As mentioned earlier, averaging over basis turns the lattice into an AFM-coupled triangular lattice.

  2. 2.

    For each triangular plaquette in the transformed triangular lattice (including those formed from the periodic boundary), compute the complex-valued quantity known as pseudospin which is defined as follows:

    $${\zeta }_{{{{{{{{\rm{pl}}}}}}}}}=\frac{1}{\sqrt{3}}\left({m}_{{{{{{{{\rm{av}}}}}}}},{{{{{{{\rm{red}}}}}}}}}+{{{{{{{{\rm{e}}}}}}}}}^{2\pi {{{{{{{\rm{i}}}}}}}}/3}{m}_{{{{{{{{\rm{av}}}}}}}},{{{{{{{\rm{green}}}}}}}}}+{{{{{{{{\rm{e}}}}}}}}}^{4\pi {{{{{{{\rm{i}}}}}}}}/3}{m}_{{{{{{{{\rm{av}}}}}}}},{{{{{{{\rm{blue}}}}}}}}}\right).$$
    (2)
  3. 3.

    Average over all triangular plaquettes, i.e.,

    $${\zeta }_{{{{{{{{\rm{conf}}}}}}}}}=\frac{1}{{N}_{{{{{{{{\rm{pl}}}}}}}}}}\mathop{\sum}\limits_{i}{\zeta }_{{{{{{{{\rm{pl}}}}}}}},i},$$
    (3)

    where Npl is the number of plaquettes (including periodic boundaries in the quantum lattice).

  4. 4.

    Obtain the average order parameter by taking the average of absolute values for different configurations of the lattice, i.e.,

    $$\langle m\rangle =\mathop{\sum}\limits_{k}{p}_{k}\left\vert {\zeta }_{{{{{{{{\rm{conf}}}}}}}},k}\right\vert ,$$
    (4)

    where pk is the probability of occurrence for configuration k.

Discrete-time path integral Monte Carlo

Our p-computer is a discrete-time path integral Monte Carlo (DT-PIMC) emulator based on the Suzuki-Trotter approximation64. The idea of such a hardware emulator for QMC was first proposed in ref. 46. In this scheme, one tries to approximate the partition function of the quantum Hamiltonian, ZQ:

$${Z}_{{{{{{{{\rm{Q}}}}}}}}}={{{{{{{\rm{tr}}}}}}}}\left[\exp \left(-\beta {H}_{{{{{{{{\rm{Q}}}}}}}}}\right)\right]$$
(5)

with a classical Hamiltonian, HCl such that the partition function corresponding to HCl is equal to ZQ. For the quantum Hamiltonian in Eq. (1), one finds that the following classical Hamiltonian, HCl:

$${H}_{{{{{{{{\rm{Cl}}}}}}}}}=-\mathop{\sum }\limits_{k=1}^{r}\left[\mathop{\sum}\limits_{i < j}{J}_{\parallel ,ij}{m}_{i,k}{m}_{j,k}+\mathop{\sum}\limits_{i}{J}_{\perp }{m}_{i,k}{m}_{i,k+1}\right]$$
(6)

with

$${J}_{\parallel ,ij}={J}_{ij}/r,$$
(7)
$${J}_{\perp }=-(0.5/\beta )\ln \left[\tanh \left(\beta \Gamma /r\right)\right]$$
(8)

and mi,j ∈ { − 1, + 1} yields the same ZQ in the limit r → ∞. The error goes down as \({{{{{{{\mathcal{O}}}}}}}}(1/{r}^{2})\) and in practice, one can find a reasonably good approximation with a finite number of replicas in many cases.

Data fitting and convergence criterion

Each curve in Fig. 3(a) is then fitted with ae−bx + ce−dx + g type fitting model (a justification for using this fitting model is provided in the Supplementary Note 3) where g represents the prediction for equilibrium value of average order parameter from p-computer emulation. Figure 3b shows the decay in mean squared error (MSE) as time increases. It also clearly shows that the time required to reach a fixed MSE level increases as the size of the lattice increases. We define convergence time as the time required to reach an MSE level of 0.0025, which is equivalent to finding the time required to reach g − 0.05 in Fig. 3a and was used to define convergence in ref. 36.

Averaging over sweeps from parallel runs to avoid autocorrelation

We note that to get the true average convergence time of the p-bit network, we run each lattice emulation many times each time with different seed in random number generator and compute the average order parameter at each time point by taking an average of the absolute value of the order parameter calculated at the same time point from all the runs only. This allows us to eliminate the correlation between sweeps taken from the same run which yields longer convergence times and does not represent the actual convergence time of the network.

More about the implementation of the clockless p-computer circuit

To simulate the analog circuit in Fig. 4d, we have used a simple voltage divider based synapse with R0 = 15MΩ, Rr = R0/10, Rb = R0/4 (for bias inputs) and R1 = R0/3.5 (for the AFM weight of magnitude 1). For p-bits on the border along horizontal direction (open boundary condition), we have used \({R}_{1}^{{\prime} }={R}_{0}/2\) (to represent the AFM weight of magnitude 1) and \({R}_{1}^{{\prime\prime} }={R}_{0}\) (to represent the AFM weight of magnitude 0.5).