Maximally modular structure of growing hyperbolic networks

Abstract

Hyperbolic network models provide a particularly successful approach to explain many peculiar features of real complex networks including, for instance, the small-world and scale-free properties, or the relatively high clustering coefficient. Here we show that for the popularity-similarity optimisation (PSO) model from this family, the generated networks become also extremely modular in the thermodynamic limit, despite lacking any explicitly built-in community formation mechanism in the model definition. In particular, our analytical calculations indicate that the modularity in PSO networks can get arbitrarily close to its maximal value of 1 as the network size is increased. We also derive the convergence rate, which turns out to be dependent on the popularity fading parameter controlling the degree decay exponent of the generated networks.

Introduction

Networks representing the patterns of interactions between the fundamental units of complex systems can show immensely rich behaviour as demonstrated by a vast number of studies, forming the core subject of an interdisciplinary field that became widely popular in the last two decades^1,2,3,4,5. The most important features of complex networks that show a great deal of universality across systems ranging from the metabolic networks within cells to the level of the entire society are the inhomogeneous scale-free nature of the degree distribution^6,7, the high local transitivity characterised by a relatively large average clustering coefficient⁸, and the small-world property^9,10. Furthermore, most real networks also display an intricate community structure^11,12,13, corresponding to the presence of denser modules in the network topology, in a similar fashion to families and friendship circles in the society. Capturing the most essential properties of complex networks with the help of simple mathematical models has always been one of the key goals in this field, and a notable approach in this respect is given by hyperbolic models^{14,15,16,17,18,19,20,21}, centred around the idea of placing the nodes in hyperbolic space and connecting node pairs with a probability depending on the hyperbolic distance.

A fundamental model based on this idea is the popularity-similarity optimisation (PSO) model¹⁵, which simulates the growth of networks in the two-dimensional hyperbolic space ${{\mathbb{H}}}^{2}$. In this approach, we keep adding nodes one by one into the native disk representation of ${{\mathbb{H}}}^{2}$¹⁴ until there is altogether N number of nodes in the system. New nodes always appear with logarithmically increasing radial and uniformly random angular coordinates, and once arrived, they establish connections with previously added nodes according to a hyperbolic proximity rule. More precisely, node i after its appearance on the disk gets connected to node j < i with a probability decaying as a function of the hyperbolic distance x_ij as

$$p({x}_{ij})=\frac{1}{1+{e}^{\frac{\zeta }{2T}({x}_{ij}-{R}_{i})}},$$

(1)

where $\zeta =\sqrt{-K}$ parametrises the curvature K < 0 of the hyperbolic space (where usually ζ = 1 is used), T ≥ 0 is a model parameter called temperature, and R_i is the cutoff distance of the connection probability at the arrival of node i. The latter is adjusted in such a way that the expected number of links formed between the new node i and the rest of the system is equal to m≥1 that acts as an additional model parameter related to the average degree of the network $\bar{k}$ where $\bar{k}\approx 2m$. Note that due to the decaying nature of p(x_ij) in Eq. (1), nodes that are closer to each other in the hyperbolic sense are more likely to become connected than the ones found at large distances. This tendency that newly-appearing nodes favour hyperbolically closer nodes to connect can be regarded as an optimisation of a trade-off between the popularity (reflected by the radial coordinate) of a possible candidate to connect and its similarity (the angular distance) compared to the newly arriving node¹⁵. Owing to the hyperbolic nature of the underlying geometry, the radial coordinate of the nodes has a very strong effect on the degree, with the most inner nodes usually becoming hubs in the long run. In order to allow control over the degree distribution, an outward shift of the nodes is also introduced as

$${r}_{ji}=\beta {r}_{jj}+(1-\beta ){r}_{ii},$$

(2)

where r_ji denotes the radial coordinate of node j at the appearance of node i, and β ∈ (0, 1] is a further model parameter often referred to as the popularity fading parameter. In particular, with the update rule of the radial coordinates given by Eq. (2), the degree distribution of the generated networks follows a scaling form, that is,

$${{{{{{{\mathcal{P}}}}}}}}(k) \sim {k}^{-\gamma },$$

(3)

where the degree decay exponent γ is related to the popularity fading parameter β as $\gamma =1+\frac{1}{\beta }$.

In the past couple of years, the original PSO model has been extended in various directions. Examples include the E-PSO model that can inherently account for the creation of internal links, i.e. connections that emerge between old nodes in the network¹⁶. Another paradigmatic example is given by the nonuniform popularity-similarity optimisation (nPSO) model¹⁸ that, by assuming a heterogeneous angular distribution of the nodes, allows the generation of networks with an adjustable community structure. Quite recently, the original PSO model has been generalised to higher-dimensional hyperbolic spaces as well²¹.

In the present article, we provide further insights into the architecture of PSO networks with a special emphasis on their extremely modular structure. One of the main reasons behind the success of the PSO model is that the networks generated by this approach simultaneously show the most ubiquitous features of real networks, e.g. the small-world property, high clustering coefficient, and the scale-free degree distribution. Quite recently, however, numerical studies have revealed that PSO networks inherently possess strong community structures as well for a wide range of parameter settings^22,23,24,25, albeit there is no clear analytical explanation for that. Motivated by this lack, the present paper brings the research focusing on the community structure of hyperbolic networks to a new level by showing analytically that the modularity in PSO networks can get arbitrarily close to 1 in the thermodynamic limit.

Results

In order to characterise the modular structure of PSO networks, we applied the modularity Q that corresponds to the most commonly used quality measure for quantifying the strength of communities^11,12,26. This quantity basically compares a given partitioning of a network to a random baseline based on the difference between the observed fraction of links inside the modules and its expected value in the random null model. In the most basic form, this model corresponds to the configuration model and Q can be written as

$$Q=\mathop{\sum }\limits_{c=1}^{q}\left[\frac{{l}_{c}}{E}-{\left(\frac{{\sum }_{i\in c}{k}_{i}}{2E}\right)}^{2}\right],$$

(4)

where the summation runs over the communities, l_c denotes the number of links inside module c, k_i is the degree of the community member i, and E stands for the total number of links in the network. Introducing b_i as the number of intra-community links of node i, we can express Q also as

$$Q=\mathop{\sum }\limits_{c=1}^{q}\left[\frac{{\sum }_{i\in c}{b}_{i}}{2E}-{\left(\frac{{\sum }_{i\in c}{k}_{i}}{2E}\right)}^{2}\right].$$

(5)

Partitions defined by equally sized angular sectors

Earlier works on the modular structure of hyperbolic networks pointed out that state-of-the-art community finding methods usually identify modules that correspond mostly to separated angular regions on the hyperbolic disk^22,23,24,25 (often referred to as angular sectors). This angular separation of the communities is particularly interesting since these community-finding methods are completely unaware of the underlying hyperbolic metric. Somewhat simplifying, but still trying to capture the key point of the previous observations, here we define the partitioning of the PSO network according to the angular coordinates of the nodes and divide the native disk into q number of communities of equal angular width given by 2π/q (where we assume that q ≥ 2 and q ≪ N, allowing at least a few members in each community). The boundary between the first and the second community can be placed at any arbitrary angle α, and once this is fixed, the rest of the community boundaries are found at α + i2π/q, where i runs up to q − 1. This uniform partitioning scheme of the hyperbolic disk is illustrated in Fig. 1.

Fig. 1: Visualisation of two different uniform partitioning schemes of the same PSO network with an average degree $\bar{k}=8$ and N = 100 nodes, generated at β = 0.6, T = 0.1.

In both panels, the red dashed lines indicate the boundaries of the modules obtained by dividing the entire hyperbolic disk into equally sized angular sectors. In panel a we used q = 4 and α = 0, whereas panel b depicts a partitioning where the parameters were set to q = 6 and α = 0.3.

Naturally, the modularity Q depends on the chosen value of q and, up to a certain variation, also on α – see the Supplementary Note 1. However, by assuming that nodes and links are distributed among the communities evenly, Q can be approximated as

$$Q(q)\approx \frac{\left(\mathop{\sum }\nolimits_{i = 1}^{N}{b}_{i}\right)}{2E}-q\frac{{\left(\left(\mathop{\sum }\nolimits_{i = 1}^{N}{k}_{i}\right)/q\right)}^{2}}{{(2E)}^{2}}.$$

(6)

Replacing b_i with the expected number of internal links of node i (denoted by ${\bar{b}}_{i}(q)$) and using that the sum of the node degrees in the negative term is equal to 2E, the expected value of the modularity can be given as

$$\bar{Q}(q)\approx \frac{1}{2E}\mathop{\sum }\limits_{i=1}^{N}{\bar{b}}_{i}(q)-\frac{1}{q}.$$

(7)

Note that up to this point, nothing but the assumption of uniform angular coordinates has been used; therefore, the approximation in Eq. (7) applies to any hyperbolic model, where the angular coordinates of the nodes are distributed uniformly at random.

The expected modularity in PSO networks

Following a similar line of derivation as in the work by Papadopoulos et al.¹⁶ for the expected degree ${\bar{k}}_{i}(t)$ of node i appearing at time t = i as a function of t during the network generation process, the expected internal degree for the same node, denoted by ${\bar{b}}_{i}(t)$, can also be calculated. The main idea is to focus only on the links that appear between node i and other members of the community of node i by replacing the connection probability with a conditional probability conditioned on that the other node falls into the same angular region as node i. Taking additionally into account that the angular distance of the nodes Δθ is no longer uniformly distributed inside the communities, but instead follows the distribution given by

$$\varrho (\Delta \theta )=\frac{q}{\pi }-\frac{1}{2}{\left(\frac{q}{\pi }\right)}^{2}\Delta \theta ,$$

(8)

we obtain for the expected internal degree of any node i

$${\bar{b}}_{i}(t)\approx {\bar{k}}_{i}(t)-q{m}^{2}\frac{\tan (T\pi )}{4\pi T}\frac{\left({\left(\frac{i}{t}\right)}^{1-2\beta }-1\right)}{i(2\beta -1){I}_{t}^{2}},$$

(9)

which holds for T < 1/2, where ${I}_{t}=\frac{1-{t}^{-(1-\beta )}}{1-\beta }$. For the sake of simplicity, the details of the calculation are moved to the “Methods” section. Naturally, we are interested in the result for ${\bar{b}}_{i}(t)$ at the end of the network generation process where t = N, and the above approximation works best for N → ∞. Substituting Eq. (9) into Eq. (7), we arrive to one of the main results of the paper:

$$\bar{Q}(q)\approx 1-{C}_{1}q-\frac{1}{q},$$

(10)

where C₁ = C₁(N, m, T, β) is independent of the number of communities q and can be written as

$$\begin{array}{rcl}&&{C}_{1}=\frac{m}{2(2\beta -1)N{I}_{N}^{2}}\frac{\tan (\pi T)}{4\pi T}\mathop{\sum }\limits_{i=1}^{N}\frac{1}{i}\left({\left(\frac{i}{N}\right)}^{1-2\beta }-1\right)\\ &&\mathop{=}\limits^{N\to \infty }\,\frac{m}{2}\frac{\tan (\pi T)}{4\pi T}\frac{\frac{1}{1-2\beta } \,+ \, \left(\frac{1}{2}-\frac{1}{1-2\beta }\right){N}^{2\beta -1}-\ln N}{N\frac{2\beta -1}{{(1-\beta )}^{2}}}\end{array}$$

(11)

Before discussing the consequences of the above results, let us examine how well Eq. (10) approximates the average modularity measured in networks generated by the PSO model with uniform angular partitioning into q communities. In Fig. 2a, we depict the size-dependence of both the measured and the expected modularity calculated according to Eq. (4) and Eq. (10), respectively. Besides, Fig. 2b shows the relative error δQ as a function of the network size N at different q values and fixed m, β, T parameters, displaying a clear decreasing tendency. The similar behaviour of the absolute error for the same parameter setting is presented in the Supplementary Note 2, along with further δQ(N) curves at various other values of the m, β, T parameters. Altogether, these results clearly suggest that Eq. (10) provides a remarkably good approximation for large networks and becomes exact in the N → ∞ thermodynamic limit.

Fig. 2: The measured and the predicted modularity values in PSO networks along with the relative error of the prediction as a function of the network size N.

The colours indicate the number q of equally sized communities into which the networks were divided. The examined PSO networks were generated with parameters m = 2, β = 0.6 and T = 0.1. In panel a, we show both the theoretical prediction for the expected modularity $\bar{Q}(q)$ along with the exact modularity Q(q) averaged over the studied PSO networks. Panel b depicts the relative error of the prediction, which is defined as $\delta Q=[\bar{Q}(q)- \langle Q(q) \rangle ]/ \langle Q(q) \rangle$. The number of samples considered in $\langle Q(q)\rangle$ decreases with the number of nodes N from 10000 at N = 10² to 50 at N = 10⁵. In both panels, the inset shows the corresponding curves at the optimal (N-dependent) q_* value, where the expected modularity is maximal.

Perhaps the most striking consequence of Eq. (10) emerges when compared to the results appearing in the article of Fortunato and Barthelemy²⁷. Therein the authors addressed the very general question of how to design a connected network with N number of nodes and E number of links which (with an appropriate choice of partitioning) yields the highest possible modularity. They have shown that under the assumption of connected networks this can be achieved by a simple ring-like configuration that consists of multiple modules being connected by a minimal number of links. More precisely, the maximal Q_M is realised when all modules contain the same number of links yielding

$${Q}_{M}(n)=1-\frac{n}{E}-\frac{1}{n},$$

(12)

where n denotes the number of modules in the above-mentioned ring-like configuration²⁷. Note that the form in Eq. (12) is quite reminiscent of the one appearing in Eq. (10) obtained for PSO networks with the only cardinal difference that the coefficient of the linear term in Eq. (10) is apparently different. Although it may seem insignificant, this difference guarantees that for given values of N and q the modularity of PSO networks remains always below the modularity of ring-like configurations, i.e

$${Q}_{M}(q) \, > \, \bar{Q}(q),$$

(13)

in perfect accordance with our expectations (see the “Methods” section for more details). Nevertheless, the formal analogy between Eq. (10) and Eq. (12) leads us to the conclusion that PSO networks in the thermodynamic limit start to behave in a similar way as maximally modular objects realised by the above-discussed ring-like configurations.

Optimal number of modules q _*

According to Eq. (10), the expected modularity is highly sensitive to the number of communities the network is divided into. A reasonable choice is to consider ${q}_{* }={\max }_{q}\bar{Q}(q)$, i.e. the value of q for which the expected modularity is maximised in Eq. (10). Treating q as a continuous parameter and taking the derivative of Eq. (10) with respect to q, one gets that

$${q}_{* }={C}_{1}^{-1/2}.$$

(14)

By substituting back into Eq. (10), we obtain that the maximal value of the modularity is given by

$$\bar{Q}({q}_{* })=1-2{C}_{1}^{1/2}.$$

(15)

In the inset of Fig. 2, we show the relative error of $\bar{Q}({q}_{* })$ based on Eq. (15), displaying a decreasing tendency with N in a fashion similar to the main plot.

Number of modules at the resolution limit

It is a well-known result that the maximisation of the modularity in sufficiently large networks would fail to resolve smaller communities²⁷. This can be quantified by the resolution limit ${l}_{{{{{{{{\rm{res}}}}}}}}}=\sqrt{E/2}$ providing a lower bound for the number of internal links in single modules below which merging any pair of connected communities will certainly increase the value of Q. Related to that, one can easily realise that for sufficiently large values of q, the angular sectors and, consequently, the corresponding modules become so small that the number of their internal links might drop below ${l}_{{{{{{{{\rm{res}}}}}}}}}$. This naturally allows us to rephrase the number of internal links at the resolution limit as

$${l}_{{{{{{{{\rm{res}}}}}}}}}\approx \frac{\mathop{\sum }\nolimits_{i = 1}^{N}{\bar{b}}_{i}({q}_{{{{{{{{\rm{res}}}}}}}}})}{2{q}_{{{{{{{{\rm{res}}}}}}}}}},$$

(16)

where ${q}_{{{{{{{{\rm{res}}}}}}}}}$ specifies an upper limit on the number of sectors: using values of q larger than ${q}_{{{{{{{{\rm{res}}}}}}}}}$ would result in the communities being unresolvable based on Q. Recalling Eq. (9), the expected number of intra-community links at ${q}_{{{{{{{{\rm{res}}}}}}}}}$ can be calculated using Eq. (16) too (the details are given in the “Methods” section), yielding

$${q}_{{{{{{{{\rm{res}}}}}}}}}=\frac{\sqrt{2E}}{1+{C}_{1}\sqrt{2E}}=\frac{{q}_{* }^{2}}{1+\frac{{q}_{* }^{2}}{\sqrt{2E}}}.$$

(17)

Maximally modular structure of PSO networks in the thermodynamic limit

Let us now turn to the behaviour of the modularity itself by plotting $1-\bar{Q}(q)$ in Fig. 3 as a function of both N and q, where $\bar{Q}(q)$ is obtained from Eq. (10). The heat map clearly indicates that the expected modularity approaches 1 if N is increased and q is in the vicinity of q_*(N). According to the calculations, the modularity of PSO networks can surpass 0.9 already at N = 10⁴, and even 0.99 at N = 10⁶, which is smaller only by 1% compared to the theoretically possible maximum value of 1.

Fig. 3: The expected modularity as a function of N and q.

For a better visibility, we plot $1-\bar{Q}$ with the help of the colourmap, showing that $\bar{Q}$ can get very close to 1 already in the examined network size range. The continuous line corresponds to q_*(N), whereas the dashed line shows ${q}_{{{{{{{{\rm{res}}}}}}}}}(N)$.

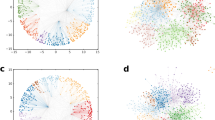
Next, as an illustration, we show in Fig. 4a a PSO network of N = 1000 number of nodes with the communities located by the Louvain algorithm²⁸ (corresponding to a very popular community finding method built on modularity maximisation), compared to the partitioning of the same network in Fig. 4b according to the setup studied here, where the communities are defined by q_* number of angular sectors of equal size. Apparently, the modules found by Louvain have varying sizes, and in general, the total number of communities can also be different in the two cases. Nevertheless, the overall look of the two partitionings is quite similar, and the modularity of the setup with q_* equally sized communities is also in the same order of magnitude as the modularity of the partitioning found by the Louvain algorithm. These results altogether show that the proposed division of PSO networks into communities based on equally sized angular sectors is not far from optimal already at such small network sizes. We note however that the true optimum of the modularity is expected to be higher compared to the Q measured for our uniform partitioning at finite network sizes, since angular sectors of varying sizes may adapt better to fluctuations in the network structure.

Fig. 4: Communities in a PSO network with an average degree $\bar{k}=8$ and N = 1000 nodes, generated at β = 0.6, T = 0.1.

a The modules found by the Louvain algorithm, indicated by colours. b The communities according to the partitioning studied in this paper, consisting of equally sized angular regions. The number of modules in this case was set to the optimal ${q}_{* }={C}_{1}^{-1/2}$ value.

An interesting remaining question is how does the modularity behave when q is kept at a fixed value while letting the size of the network N tend to infinity? According to Eq. (10), for a fixed q value

$$\mathop{\lim }\limits_{N\to \infty }\bar{Q}(q)=1-\frac{1}{q},$$

(18)

where we used that C₁ approaches 0 when N → ∞. Since the number of communities q is not bounded for infinitely large PSO networks, the above equation already shows that the modularity of PSO networks can get arbitrarily close to 1 in the thermodynamic limit. Note that an analogous formula holds for the modularity of networks that are composed of disjoint sub-graphs having the same number of internal links E/q (including, for instance, a set of disjoint cliques)²⁷. By assuming a fixed value of q, this analogy also entails that as the network size is increased, the communities defined by equally sized angular sectors formally start to behave as if they were cliques that share no links with each other. This again indicates that in general, modularity scores in PSO networks are indeed not so far from the theoretically possible maximum value.

Naturally, instead of working with a fixed q when N → ∞, it is a better idea to consider the communities obtained at the optimal q_*(N) when seeking the maximal modularity. Nevertheless, based on Eqs. (15) and (11), the rate at which $\bar{Q}({q}_{* })$ approaches 1 is β-dependent. For simplicity, we move the details of the calculations into the “Methods” section and summarise the scaling of a few quantities of interest (including $1-\bar{Q}({q}_{* })$) in Table 1. According to the results, the modularity at q_* converges to 1 as fast as ${\left(\frac{\ln N}{N}\right)}^{1/2}$ when $\beta \, < \, \frac{1}{2}$, and still as fast as N^β−1 when $\beta \, > \, \frac{1}{2}$. Surprisingly, the modularity at ${q}_{{{{{{{{\rm{res}}}}}}}}}$ corresponding to the resolution limit also approaches 1 if $\beta \, < \, \frac{3}{4}$; however, always at a slower rate compared to Q(q_*).

Table 1 Asymptotic scaling of the modularity.

Finally, based on the above results one may also ask whether it is possible to set the model parameters in such a way that the modularity does not approach 1 in the thermodynamic limit. By leaving the more rigorous examination of this question to future work, here we conjecture that for large values of the temperature T, the modularity is likely to converge to a non-unit value, perhaps even to zero, in the thermodynamic limit. This hypothesis seems plausible considering the conclusions of the work by Kovács and Palla²⁵, where low values of Q were reported in numerical investigations of PSO networks generated at temperatures close to T = 1. However, unfortunately, this change of the modularity in the thermodynamic limit towards the higher temperatures cannot be confirmed analytically in the current framework, since our calculations are valid only for T < 1/2.

Discussion

We have shown that despite having no built-in community formation mechanism included in the network generation process, the modularity of PSO networks can converge to 1 in the asymptotic limit, and we have also analysed the dependence of the convergence rate on the model parameters. Although modularity scores reaching above Q = 0.3 could be a convincing sign of a strong community structure in practice^27,29, it is worth remarking that a high modularity value alone does not necessarily indicate a true underlying community structure. For instance, it has been shown that under appropriate circumstances even Erdős–Rényi graphs can have high values of Q despite lacking real modules of any kind³⁰. However, this is not the case for hyperbolic networks, where high Q values de facto entail the presence of real communities, which was explicitly confirmed from various points of view²⁵. For example, it can be shown that there is a strong consensus and, as a consequence, reasonably high adjusted mutual information³¹ values between the modules identified by different community finding algorithms, even if these methods do not directly locate the modules based on modularity optimisation²⁵. Moreover, the angular separation index³² (which is a quality measure independent of the modularity) also shows significantly high values²⁵, confirming again the statistical significance of the communities identified in PSO networks. In the present work, we complemented these results by establishing an extended theoretical background and also by providing pieces of analytical evidence that PSO networks are becoming extremely modular in the thermodynamic limit. The possibly maximal modularity is a remarkable feature of hyperbolic networks, given that their overall structure is very similar to that of real systems.

Very recently, closely related results were obtained for the random hyperbolic graph (RHG) model as well³³. According to Chellig et al.³³, the static networks generated by this model exhibit modularity of 1 with probability 1 in the thermodynamic limit at temperature T = 0 for degree decay exponents γ > 2 and any average degree. Taken together, the attainability of extremely large modularity values seems to be a universal feature of hyperbolic network models. The fact that maximally modular networks can be obtained using both the PSO and the RHG models naturally leads to the question of whether the modularity maximisation mechanism is the same in the two approaches. Although the fine details of this behaviour can be different, it seems that the fundamental basis of the effect is the same. In both approaches, by fixing the model parameters we implicitly define a characteristic distance at which the connection probability between nodes drops down close to zero. When increasing the system size to the thermodynamic limit, the size of the disk occupied by the network in the hyperbolic plane becomes very large compared to this distance, hence the vast majority of the links will connect nodes that are very close to each other compared to the size of the entire disk. The results indicate that in this state, it is possible for both models to segment the network into parts in such a way that the fraction of links between the segments becomes negligible compared to the fraction of links inside the segments, resulting in a modularity value approaching 1 in the N → ∞ limit.

Since the above argument is based mainly on the difference between the scale of the typical distance between connected nodes and the scale of the system size, one may ask whether a similar behaviour could occur also in geometric graphs living in Euclidean spaces. In our view, homogeneously distributed nodes and a connection probability that decays as a function of the node-node distance may lead to highly modular networks also in Euclidean spaces. It is plausible that networks generated under the above circumstances can be divided into parts where the links connecting different communities are mainly located on the surface of the modules, whereas the internal connections of the communities can occupy the entire volume of the given module. When increasing the system size to the thermodynamic limit in networks of this type, the fraction of external links can become negligible compared to the fraction of internal links, leading to a high modularity value. Nevertheless, it is very important to note that such Euclidean networks are expected to have homogeneous degree distribution instead of a scale-free one, and are not going to be small-world networks either. In contrast, the hyperbolic networks considered in this paper retain the scale-free degree distribution and the small-world property at any system size.

So far, only a few graph construction mechanisms were reported to generate networks with such an enhanced community structure that the modularity or similar quality measures take their maximal value. Schematic, but at the same time very illustrative examples where Q can approach 1 in the thermodynamic limit for graphs with a topology deliberately optimised for maximal modularity were provided by Brandes et al.³⁴ and by Fortunato and Barthelemy²⁷. Another emblematic example is given by the combination of the triadic closure mechanism with preferential attachment^35,36, where additional triad formation steps are also carried out during the graph generation process to increase the clustering coefficient in networks that eventually become scale-free. Combining these mechanisms in different types of growing network models can lead to significantly high values of the so-called node-based embeddedness³⁷, which, similarly to Q, quantifies how pronounced the communities are. In addition to this, the networks generated in these approaches also display heavy-tailed degree distributions and relatively high values of the clustering coefficient as well, making them more similar to real networks compared to the constructions optimised solely for maximal modularity.

Hyperbolic network models including both the RHG and PSO models are now proven to constitute an equally important family of graph construction mechanisms from the point of view of the maximal modularity. The advantage of these models is that they are capable of simultaneously explaining all the above features in a natural manner, without the need for any exogenous triad formation mechanism during the network growth or graph generation process. The seen universal properties of hyperbolic networks (corresponding to the scale-free degree distribution, the high clustering coefficient and the extremely large modularity) are making them without a doubt ideal candidates for modelling real-world networks.

Methods

Detailed description of the PSO model

In the popularity-similarity optimisation (PSO) model¹⁵ initially the network is empty, and the network nodes are placed one by one on the hyperbolic plane with increasing radial coordinates and uniformly random angular coordinates. The new node always connects to the previously appeared nodes with a linking probability that decreases as a function of the hyperbolic distance. The model works in the native representation of the hyperbolic plane of curvature K < 0, where the hyperbolic plane is represented in the Euclidean plane by a disk of infinite radius. The hyperbolic distance x between two points located at polar coordinates (r, θ) and $({r}^{{\prime} },{\theta }^{{\prime} })$ can be expressed as

$$x=\frac{1}{\zeta }\cdot {{{{{{{\rm{acosh}}}}}}}}(\cosh (\zeta r)\,\cosh (\zeta {r}^{{\prime} })-\sinh (\zeta r)\,\sinh (\zeta {r}^{{\prime} })\,\cos (\Delta \theta ))$$

(19)

from the hyperbolic law of cosines, where $\Delta \theta =\pi -| \pi -| \theta -{\theta }^{{\prime} }| |$ is the angular distance between the examined points and $\zeta =\sqrt{-K}$. At $\Delta \theta =\pi ,x=r+{r}^{{\prime} }$, while for $\Delta \theta =0,x=| r-{r}^{{\prime} }|$, meaning that in this representation, the hyperbolic distance of a point from the disk centre is equal to its radial coordinate r, i.e. its Euclidean distance from the disk centre.

The properties of a PSO network that can be tuned are the total number of nodes N, the expected average degree $\bar{k}$ (via the model parameter m that corresponds to $\bar{k}/2$), the exponent γ ≥ 2 of the tail of the degree distribution that decays as ${{{{{{{\mathcal{P}}}}}}}}(k) \sim {k}^{-\gamma }$ (via the popularity fading parameter β ∈ (0, 1] that controls the speed of the outward drift of the nodes during the network growth), and the average clustering coefficient $\bar{c}$ (via the temperature T ∈ [0, 1) that regulates how sharp the cutoff in the connection probability function is). Interpreting m as the expected number of new connections per step – as in the ${{{{{{{{\rm{Model}}}}}}}}}_{{2}^{{\prime} }}$ variant of the PSO model–, the network growth can be realised using the following rules:

• 1. In the ith step, node i appears with the radial coordinate ${r}_{ii}=\frac{2}{\zeta }\ln i$ and an angular coordinate θ_i sampled from the interval [0, 2π) uniformly at random. (Note that due to this choice of the radial coordinate formula, changing the value of the curvature K = − ζ² of the hyperbolic plane corresponds to a simple rescaling of all the hyperbolic distances. The usual custom is to simply set the value of ζ to 1).

• 2. The radial coordinates of all the previous nodes j < i are increased toward r_ii as r_ji = βr_jj + (1 − β)r_ii. This outward shift of the node positions is usually referred to as ‘popularity fading’, as it reduces the differences in the nodes’ radial attractivity.

• 3. The new node i gets attached to the already existing nodes as follows:

  • a. If T = 0, then node i becomes connected to all nodes j < i at a hyperbolic distance x_ij not larger than

    $${R}_{i}=\left\{\begin{array}{ll}{r}_{ii}-\frac{2}{\zeta }\ln \left(\frac{2}{\pi }\cdot \frac{1-{{{{{{{{\rm{e}}}}}}}}}^{-\frac{\zeta }{2}(1-\beta ){r}_{ii}}}{m(1-\beta )}\right)&{{{{{{{\rm{if}}}}}}}}\,\beta \, < \, 1,\\ {r}_{ii}-\frac{2}{\zeta }\ln \left(\frac{\zeta {r}_{ii}}{\pi \cdot m}\right)\hfill&{{{{{{{\rm{if}}}}}}}}\,\beta =1.\end{array}\right.$$

    (20)

  • b. If T > 0, then node i becomes connected to nodes j < i with a probability depending on the hyperbolic distance x_ij as

    $$p({x}_{ij})=\frac{1}{1+{{{{{{{{\rm{e}}}}}}}}}^{\frac{\zeta }{2T}({x}_{ij}-{R}_{i})}},$$

    (21)

    where the cutoff distance R_i can be written as

    $${R}_{i}=\left\{\begin{array}{ll}{r}_{ii}-\frac{2}{\zeta }\ln \left(\frac{2T}{\sin (T\pi )}\cdot \frac{1-{{{{{{{{\rm{e}}}}}}}}}^{-\frac{\zeta }{2}(1-\beta ){r}_{ii}}}{m(1-\beta )}\right)&{{{{{{{\rm{if}}}}}}}}\,\beta \, < \, 1,\\ {r}_{ii}-\frac{2}{\zeta }\ln \left(\frac{T}{\sin (T\pi )}\cdot \frac{\zeta {r}_{ii}}{m}\right)\hfill &{{{{{{{\rm{if}}}}}}}}\,\beta =1.\end{array}\right.$$

    (22)

Calculation of the expected modularity $\bar{Q}$

In this section, we explain in detail how the expected value of the modularity can be calculated in PSO networks for a uniform partition scheme.

Expected modularity for a uniform partition scheme

Let us rewrite Eq. (4) in the “Results” section as follows:

$$Q=\mathop{\sum }\limits_{c=1}^{q}\mathop{\sum}\limits_{i\in c}\frac{{b}_{i}}{2E}-\mathop{\sum }\limits_{c=1}^{q}{\left(\mathop{\sum}\limits_{i\in c}\frac{{k}_{i}}{2E}\right)}^{2}.$$

(23)

Provided that each node is assigned to a community, the double sum in Eq. (23) can simply be replaced with a single summation running over the whole set of nodes, yielding

$$Q=\mathop{\sum }\limits_{i=1}^{N}\frac{{b}_{i}}{2E}-\mathop{\sum }\limits_{c=1}^{q}{\left(\mathop{\sum}\limits_{i\in c}\frac{{k}_{i}}{2E}\right)}^{2}.$$

(24)

Based on the fact that the angular position of the nodes is distributed uniformly and we identified the communities as equally sized circular sectors of the hyperbolic disk, the sum of the node degrees has to be equal for each community in the thermodynamic N → ∞ limit. This assumption of homogeneous mixing implies that

$$\mathop{\lim }\limits_{N\to \infty }\mathop{\sum}\limits_{i\in {c}_{1}}{k}_{i}=\mathop{\lim }\limits_{N\to \infty }\mathop{\sum}\limits_{i\in {c}_{2}}{k}_{i}=\mathop{\lim }\limits_{N\to \infty }\frac{1}{q}\mathop{\sum }\limits_{i=1}^{N}{k}_{i}$$

(25)

for any community c₁ and c₂, based on which Eq. (24) can be approximated as

$$Q\approx \mathop{\sum }\limits_{i=1}^{N}\frac{{b}_{i}}{2E}-\mathop{\sum }\limits_{c=1}^{q}{\left(\mathop{\sum }\limits_{i = 1}^{N}\frac{{k}_{i}}{2Eq}\right)}^{2}=\mathop{\sum }\limits_{i=1}^{N}\frac{{b}_{i}}{2E}-q{\left(\mathop{\sum }\limits_{i = 1}^{N}\frac{{k}_{i}}{2Eq}\right)}^{2}$$

(26)

$$=\mathop{\sum }\limits_{i=1}^{N}\frac{{b}_{i}}{2E}-\frac{1}{q}.$$

(27)

By taking the expected value of the modularity Q given by Eq. (27) over different PSO networks of the same model parameters, we obtain

$$\bar{Q}\approx \frac{\mathop{\sum }\nolimits_{i = 1}^{N}{\bar{b}}_{i}}{2E}-\frac{1}{q},$$

(28)

which is the same as Eq. (7) in the “Results” section.

In order to provide a closed-form expression for the expected value of the modularity in PSO networks, one needs to compute the expected number of intra-community links ${\bar{b}}_{i}$ for each node i at the end of the network generation process, i.e. at time t = N. Since ${\bar{b}}_{i}$ is a degree-based quantity, its evaluation is similar to that of ${\bar{k}}_{i}$. Thus, in the followings we first revisit the derivation of ${\bar{k}}_{i}$ first proposed by Papadopoulos et al.¹⁵ and then, we turn to discuss in detail how to calculate ${\bar{b}}_{i}$ by applying a similar set of arguments.

Derivation of the expected degree ${\bar{k}}_{s}$ of node s at the end of the network growth

We again emphasize that here we use the variant of the PSO model called ${{{{{{{{\rm{Model}}}}}}}}}_{{2}^{{\prime} }}$ introduced in the Supplementary Information of the article of Papadopoulos et al.¹⁵. According to the results shown therein, during the growth of PSO networks of T > 0, the probability that node t connects to a previously appeared node s can be given by

$$\Pi (s,t)=\frac{1}{\pi }\int\nolimits_{0}^{\pi }\frac{1}{1+{\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st}\approx \frac{2T}{\sin (T\pi )}\frac{1}{X(s,t)},$$

(29)

where

$$\frac{1}{X(s,t)}={e}^{-\frac{\zeta }{2}\cdot ({r}_{st}+{r}_{tt}-{R}_{t})}={s}^{-\beta }{t}^{-(1-\beta )}\frac{\sin (T\pi )}{2T}\frac{m(1-\beta )}{1-{t}^{-(1-\beta )}}.$$

(30)

By using Eq. (30), Π(s, t) in Eq. (29) can equivalently be rephrased as

$$\Pi (s,t)=m\frac{{s}^{-\beta }{t}^{-(1-\beta )}}{{I}_{t}}$$

(31)

with ${I}_{t}=\frac{1-{t}^{-(1-\beta )}}{1-\beta }$. Based on the the form of attraction probability Π(s, t) in Eq. (31), one can determine the expected number of connections that node s establishes by time t, yielding

$${\bar{k}}_{s}(t)=\int\nolimits_{1}^{s}\Pi (i,s){{{{{{{\rm{d}}}}}}}}i+\int\nolimits_{s}^{t}\Pi (s,j){{{{{{{\rm{d}}}}}}}}j\approx m+m\int\nolimits_{s}^{t}\frac{{s}^{-\beta }{j}^{-(1-\beta )}}{{I}_{j}}{{{{{{{\rm{d}}}}}}}}j$$

(32)

$$\approx m+\frac{m}{{I}_{t}\beta }\left({\left(\frac{s}{t}\right)}^{-\beta }-1\right),$$

(33)

where we have exploited that $\int\nolimits_{1}^{s}\Pi (i,s){{{{{{{\rm{d}}}}}}}}i=m$ and I_j ≈ I_t for sufficiently large values of j and t, in accordance with the approximation used by Papadopoulos et al.¹⁶.

Note that as T → 0, the connection probability in Eq. (21) converges to a reversed Heaviside step function, that is,

$$\mathop{\lim }\limits_{T\to 0}p({x}_{st})=\left\{\begin{array}{ll}1&\,{{\mbox{if}}}\,\,\Delta {\theta }_{st}\le \frac{2}{X(s,t)}\\ 0&\,{{\mbox{otherwise}}}\,,\hfill\end{array}\right.$$

(34)

meaning that only nodes with $\Delta {\theta }_{st}\le \frac{2}{X(s,t)}$ can establish connections between one another, but those with a probability of 1. In this case, the probability that node t connects to a previously appeared node s can be given by

$$\Pi (s,t)=\frac{1}{\pi }\int\nolimits_{0}^{2/X(s,t)}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st}=\frac{2}{\pi }\frac{1}{X(s,t)},$$

(35)

which can also be obtained by taking the T → 0 limit in the right-hand side of Eq. (29). Note that however, Π(s, t) in Eq. (31) does not depend on T, therefore letting T → 0 does not influence the value of ${\bar{k}}_{s}(t)$ in Eq. (33) either. Finally, if we are interested in the value of ${\bar{k}}_{s}(t)$ at the end of the network growth, we simply evaluate the formula appearing in Eq. (33) at time t = N, yielding

$${\bar{k}}_{s}(t=N)\equiv {\bar{k}}_{s}\approx m+\frac{m}{{I}_{N}\beta }\left({\left(\frac{s}{N}\right)}^{-\beta }-1\right).$$

(36)

Derivation of the expected internal degree ${\bar{b}}_{s}$ of node s at the end of the network growth

Let us assume that the entire two-dimensional hyperbolic disk is divided into q number of equally sized circular sectors that correspond to communities. Although the angular distance Δθ_st is distributed uniformly for the whole set of nodes, its distribution is no longer uniform within a given circular sector. Instead, given that two nodes s and t fall into the same sector ${{{{{{{{\mathcal{S}}}}}}}}}_{c}\,(c=1,...,q)$ corresponding to the angular interval $\left[\alpha +\frac{2\pi (c-1)}{q},\alpha +\frac{2\pi c}{q}\right)$, the probability density for them to have angular distance Δθ_st can be calculated as follows:

$$\varrho (\Delta {\theta }_{st}| s,t\in {{{{{{{{\mathcal{S}}}}}}}}}_{c})=\frac{q}{\pi }-\frac{1}{2}{\left(\frac{q}{\pi }\right)}^{2}\Delta {\theta }_{st},$$

(37)

where $\Delta {\theta }_{st}\in \left[\alpha +\frac{2\pi (c-1)}{q},\alpha +\frac{2\pi c}{q}\right)$. Note that by means of rotational symmetry and the statistical equivalence of the sectors the α and c parameters above can always be set to α = 0 and c = 1 without any loss of generality. For a detailed derivation of Eq. (37), see section “Distribution of angular distances within a circular sector”.

Since communities are identified as angular sectors on the hyperbolic disk, intra-community links correspond to the connections between nodes located in the same circular sector. Based on this, the probability that node s forms an intra-community link with a new-coming node t given that both nodes are inside community c of width 2π/q can be written as

$${\Pi }_{q}(s,t| s,t\in {{{{{{{{\mathcal{S}}}}}}}}}_{c})=\int\nolimits_{0}^{2\pi /q}\frac{\varrho (\Delta {\theta }_{st}| s,t\in {{{{{{{{\mathcal{S}}}}}}}}}_{c})}{1+{\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st},$$

(38)

where $\varrho (\Delta {\theta }_{st}| s,t\in {{{{{{{{\mathcal{S}}}}}}}}}_{c})$ is given by Eq. (37). However, there are altogether q number of distinct communities; therefore, the total probability that a node pair s, t shares an intra-community link in any community can be written as

$${\Pi }_{q}(s,t)=\mathop{\sum }\limits_{c=1}^{q}{\Pi }_{q}(s,t| s,t\in {{{{{{{{\mathcal{S}}}}}}}}}_{c})P(s,t\in {{{{{{{{\mathcal{S}}}}}}}}}_{c}),$$

(39)

where $P(s,t\in {{{{{{{{\mathcal{S}}}}}}}}}_{c})=1/{q}^{2}$ denotes the probability that both node s and node t fall into the circular sector ${{{{{{{{\mathcal{S}}}}}}}}}_{c}$. Due to the statistical equivalence of the communities, each term in Eq. (39) gives the same contribution, which, along with the substitution of Eq. (38) into Eq. (39), yields

$${\Pi }_{q}(s,t)=\frac{1}{q}\int\nolimits_{0}^{2\pi /q}\frac{\frac{q}{\pi }-\frac{1}{2}{\left(\frac{q}{\pi }\right)}^{2}\Delta {\theta }_{st}}{1+{\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st}$$

(40)

$$ =\frac{1}{q}\int\nolimits_{0}^{2\pi /q}\frac{\frac{q}{\pi }}{1+{\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st}+\frac{1}{q}\int\nolimits_{0}^{2\pi /q}\frac{-\frac{1}{2}{\left(\frac{q}{\pi }\right)}^{2}\Delta {\theta }_{st}}{1+{\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st}\\ := {I}_{1}+{I}_{2}.-35pt$$

(41)

Let us evaluate I₁ and I₂ separately. The first term I₁ turns out to have the same form as Π(s, t) in Eq. (29), that is,

$${I}_{1}= \frac{1}{q}\int\nolimits_{0}^{2\pi /q}\frac{\frac{q}{\pi }}{1+{\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st}=\frac{1}{\pi }\frac{2}{X(s,t)}\int\nolimits_{0}^{\frac{X(s,t)\pi }{q}}\frac{1}{1+{y}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}y\\ \approx \frac{1}{\pi }\frac{2}{X(s,t)}\int\nolimits_{0}^{\infty }\frac{1}{1+{y}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}y=\frac{2T}{\sin (T\pi )}\frac{1}{X(s,t)},$$

(42)

being valid for any T < 1 temperature values. In Eq. (42) we have also taken advantage of the fact that for sufficiently large networks at temperatures T < 1 the main contribution to the integral I₁ comes from the range of small angular distances Δθ_st ≪ 2π/q, and consequently, the upper bound of the integral can safely be extended to infinity. The second term I₂ in Eq. (41) is a bit more complicated to evaluate; however, similar considerations suggest that

$${I}_{2} =-\frac{1}{q}\int\nolimits_{0}^{2\pi /q}\frac{\frac{1}{2}{\left(\frac{q}{\pi }\right)}^{2}\Delta {\theta }_{st}}{1+{\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{1/T}}\,{{{{{{{\rm{d}}}}}}}}\Delta {\theta }_{st}=-{\left(\frac{q}{\pi X(s,t)}\right)}^{2}\int\nolimits_{0}^{{\left(\frac{X(s,t)\pi }{q}\right)}^{2}}\frac{1}{1+{y}^{1/(2T)}}\,{{{{{{{\rm{d}}}}}}}}y\\ \approx -{\left(\frac{q}{\pi X(s,t)}\right)}^{2}\int\nolimits_{0}^{\infty }\frac{1}{1+{y}^{1/(2T)}}\,{{{{{{{\rm{d}}}}}}}}y=-\frac{q}{\pi }\frac{2T}{\sin (2T\pi )}\frac{1}{{X}^{2}(s,t)},$$

(43)

where we have used the change of variables with a new variable defined as $y={\left(\frac{X(s,t)}{2}\Delta {\theta }_{st}\right)}^{2}$. Using Eq. (34), one can show that the T = 0 case is again well-defined. Taking the T → 0 limit in Eqs. (42) and (43) yields

$$\mathop{\lim }\limits_{T\to 0}{I}_{1}=\frac{2}{\pi }\frac{1}{X(s,t)}$$

(44)

and

$$\begin{array}{r}\mathop{\lim }\limits_{T\to 0}{I}_{2}=-\frac{q}{{\pi }^{2}}\frac{1}{{X}^{2}(s,t)},\end{array}$$

(45)

respectively. Nevertheless, it is important to note that the approximation in Eq. (43) is no longer applicable for T ≥ 1/2 values since in such case the corresponding integral becomes divergent.

Finally, combining Eq. (41) with Eqs. (42) and (43) yields

$$\begin{array}{r}{\Pi }_{q}(s,t)={I}_{1}+{I}_{2}\approx \frac{2T}{\sin (T\pi )}\frac{1}{X(s,t)}\left(1-\frac{q}{2\pi \cos (T\pi )}\frac{1}{X(s,t)}\right),\end{array}$$

(46)

which can be rephrased as

$${\Pi }_{q}(s,t)={s}^{-\beta }{t}^{-(1-\beta )}\frac{m}{{I}_{t}}\left(1-q\frac{\tan (T\pi )}{4\pi T}{s}^{-\beta }{t}^{-(1-\beta )}\frac{m}{{I}_{t}}\right)$$

(47)

$$=\Pi (s,t)-q\frac{\tan (T\pi )}{4\pi T}{s}^{-2\beta }{t}^{-2(1-\beta )}\frac{{m}^{2}}{{I}_{t}^{2}}$$

(48)

$$=\Pi (s,t)-q\frac{\tan (T\pi )}{4\pi T}{\Pi }^{2}(s,t),$$

(49)

In the above derivation, we used the formulae of $\frac{1}{X(s,t)}$ and Π(s, t) defined by Eqs. (30) and (31), respectively. Analogously to Eq. (32), the expected number of intra-community links of node s emerged by time t can be calculated as

$${\bar{b}}_{s}(t)=\int\nolimits_{1}^{s}{\Pi }_{q}(i,s){{{{{{{\rm{d}}}}}}}}i+\int\nolimits_{s}^{t}{\Pi }_{q}(s,j){{{{{{{\rm{d}}}}}}}}j.$$

(50)

The first term in Eq. (50) can be simplified to

$$\phantom{a}\phantom{a}\int\nolimits_{1}^{s}{\Pi }_{q}(i,s){{{{{{{\rm{d}}}}}}}}i=\int\nolimits_{1}^{s}\left(\Pi (i,s)-q\frac{\tan (T\pi )}{4T\pi }{\Pi }^{2}(i,s)\right){{{{{{{\rm{d}}}}}}}}i$$

(51)

$$=m-q\frac{\tan (T\pi )}{4T\pi }\int\nolimits_{1}^{s}{i}^{-2\beta }{s}^{-2(1-\beta )}\frac{{m}^{2}}{{I}_{s}^{2}}{{{{{{{\rm{d}}}}}}}}i$$

(52)

$$=m-q\frac{\tan (T\pi )}{4T\pi }\frac{{s}^{-1}-{s}^{-2+2\beta }}{1-2\beta }\frac{{m}^{2}}{{I}_{s}^{2}},$$

(53)

where we used Eq. (49) in the first step, and Eq. (32) together with the definition of $m=\int\nolimits_{1}^{s}\Pi (i,s){{{{{{{\rm{d}}}}}}}}i$ in the second step. As the second term in Eq. (53) is a decreasing function of s, in sufficiently large networks for the majority of the nodes the $\int\nolimits_{1}^{s}{\Pi }_{q}(i,s){{{{{{{\rm{d}}}}}}}}i$ integral is close to m. For the sake of simplicity, in the following, we extend this approximation for all nodes and replace the first term in Eq. (50) by m.

Furthermore, substituting Eq. (49) into the second term of Eq. (50) yields

$${\bar{b}}_{s}(t)\approx m+\int\nolimits_{s}^{t}\Pi (s,i){{{{{{{\rm{d}}}}}}}}i-q{m}^{2}\frac{\tan (T\pi )}{4\pi T}\int\nolimits_{s}^{t}\frac{{s}^{-2\beta }{i}^{2\beta -2}}{{I}_{i}^{2}}{{{{{{{\rm{d}}}}}}}}i$$

(54)

$$={\bar{k}}_{s}(t)-q{m}^{2}\frac{\tan (T\pi )}{4\pi T}\int\nolimits_{s}^{t}\frac{{s}^{-2\beta }{i}^{2\beta -2}}{{I}_{i}^{2}}{{{{{{{\rm{d}}}}}}}}i$$

(55)

$$\approx {\bar{k}}_{s}(t)-q{m}^{2}\frac{\tan (T\pi )}{4\pi T}\frac{{s}^{-2\beta }}{{I}_{t}^{2}}\int\nolimits_{s}^{t}{i}^{2\beta -2}{{{{{{{\rm{d}}}}}}}}i$$

(56)

$$={\bar{k}}_{s}(t)-q{m}^{2}\frac{\tan (T\pi )}{4\pi T}\frac{\left({\left(\frac{s}{t}\right)}^{1-2\beta }-1\right)}{s(2\beta -1){I}_{t}^{2}},$$

(57)

where the same approximation has been utilised as in the case of Eq. (33). In terms of modularity, we are specifically interested in the value of ${\bar{b}}_{s}(t)$ for each node s = 1, . . . , N at the end of the network generation process, i.e. at t = N, which simply reads as

$${\bar{b}}_{s}(t=N)\equiv {\bar{b}}_{s}\approx {\bar{k}}_{s}-q{m}^{2}\frac{\tan (T\pi )}{4\pi T}\frac{\left({\left(\frac{s}{N}\right)}^{1-2\beta }-1\right)}{s(2\beta -1){I}_{N}^{2}}.$$

(58)

Hereinafter, for the sake of notational simplicity, the argument of ${\bar{b}}_{s}(t)$ is always omitted when being evaluated at t = N. As an illustration, in Fig. 5 we show the measured values of ${\bar{b}}_{s}$ in PSO networks as a function of the node index s for different values of the number of communities q in comparison with the analytical prediction given by Eq. (58). According to the results, in the q regime of interest ($q \, \le \, {q}_{{{{{{{{\rm{res}}}}}}}}}$) our approximation works well.

Fig. 5: The expected number of intra-community links ${\bar{b}}_{i}$ in PSO networks as a function of the node index i for different values of the number of communities q.

In all the panels a–d, the solid green curves correspond to the number of intra-community links obtained by averaging over 10 PSO networks generated independently with parameters ζ = 1, N = 10000, m = 2, β = 0.6 and T = 0.1, while the red dashed lines show the analytic prediction for the same model parameters. The number of communities used for creating panel c and panel d at this parameter setting were q_* = 48 and ${q}_{{{{{{{{\rm{res}}}}}}}}}=133$, respectively.

Distribution of angular distances within a circular sector

As it is discussed in the previous section, the angular distance of the nodes is not uniform within a circular sector, but instead follows a linearly decreasing form given by Eq. (37). In the proof of this statement, because of the statistical equivalence of the communities, it is sufficient to consider only one circular sector, namely e.g. the one that corresponds to the angular interval $[\alpha ,\alpha +\frac{2\pi }{q})$. Due to the rotational invariance that is statistically valid for the system, α can be set to 0 in the proof.

First, let us examine the cumulative distribution function ${F}_{\Delta {\theta }_{st}}(\chi )$ of the angular distances inside the chosen angular sector given by the interval $[0,\frac{2\pi }{q})$. By definition, ${F}_{\Delta {\theta }_{st}}(\chi )$ denotes the probability that the value of the angular distance Δθ_st is less than χ, given that nodes s and t both belong to the chosen sector, i.e. ${\theta }_{s}\in [0,\frac{2\pi }{q})$ and ${\theta }_{t}\in [0,\frac{2\pi }{q})$. Using Fig. 6, ${F}_{\Delta {\theta }_{st}}(\chi )$ can be determined in a purely geometric way. The grey shaded strip in Fig. 6 covers the set of points where Δθ_st = π − ∣π − ∣θ_s − θ_t∣∣ = ∣θ_s − θ_t∣ < χ holds, whereas the points of the whole square represent all possible values of the angular coordinates that nodes s and t can have inside the given circular sector. Since θ_s and θ_t are distributed uniformly, ${F}_{\Delta {\theta }_{st}}(\chi )$ can be calculated as the area of the grey strip A_strip divided by the total area of the yellow square A_total in Fig. 6, that is,

$${F}_{\Delta {\theta }_{st}}(\chi )=\frac{{A}_{{{{{{{{\rm{strip}}}}}}}}}(\chi )}{{A}_{{{{{{{{\rm{total}}}}}}}}}(\chi )}=\frac{{\left(\frac{2\pi }{q}\right)}^{2}-{(\frac{2\pi }{q}-\chi )}^{2}}{{\left(\frac{2\pi }{q}\right)}^{2}}.$$

(59)

Now taking the derivative of Eq. (59) with respect to χ, we obtain the corresponding probability density function, yielding

$$\frac{{{{{{{{\rm{d}}}}}}}}}{{{{{{{{\rm{d}}}}}}}}\chi }{F}_{\Delta {\theta }_{st}}(\chi )=2{\left(\frac{q}{2\pi }\right)}^{2}\left(\frac{2\pi }{q}-\chi \right)=\frac{q}{\pi }-\frac{1}{2}{\left(\frac{q}{\pi }\right)}^{2}\chi ,$$

(60)

from which we immediately recover Eq. (37).

Fig. 6: Graphical solution for calculating the distribution of the angular distance between nodes inside a given circular sector.

The yellow region represents all possible values of the angular coordinates θ_s, θ_t of two arbitrary nodes s, t conditioned on that they fall into the same angular sector with a central angle 2π/q. The grey strip shows those combinations of θ_s and θ_t values, where Δθ_st is smaller than a given value of χ.

Expected modularity as a function of q and the introduction of the C ₁ parameter

Let us now turn to the q-dependence of $\bar{Q}$. This can be determined by plugging Eq. (58) into Eq. (28), which yields

$$\bar{Q}(q)\approx \frac{\mathop{\sum }\nolimits_{i = 1}^{N}{\bar{k}}_{i}-\frac{q{m}^{2}}{(2\beta -1){I}_{N}^{2}}\frac{\tan (\pi T)}{4\pi T}\mathop{\sum }\nolimits_{i = 1}^{N}\frac{1}{i}\left({\left(\frac{i}{N}\right)}^{1-2\beta }-1\right)}{2E}-\frac{1}{q}$$

(61)

$$=1-q\frac{{m}^{2}}{2E(2\beta -1){I}_{N}^{2}}\frac{\tan (\pi T)}{4\pi T}\mathop{\sum }\limits_{i=1}^{N}\frac{1}{i}\left({\left(\frac{i}{N}\right)}^{1-2\beta }-1\right)-\frac{1}{q}$$

(62)

$$=1-{C}_{1}q-\frac{1}{q},$$

(63)

where C₁ is defined as

$${C}_{1}\equiv \frac{{m}^{2}}{2E(2\beta -1){I}_{N}^{2}}\frac{\tan (\pi T)}{4\pi T}\mathop{\sum }\limits_{i=1}^{N}\frac{1}{i}\left({\left(\frac{i}{N}\right)}^{1-2\beta }-1\right),$$

(64)

or, using E ≈ mN, as

$${C}_{1}=\frac{m}{2(2\beta -1)N{I}_{N}^{2}}\frac{\tan (\pi T)}{4\pi T}\mathop{\sum }\limits_{i=1}^{N}\frac{1}{i}\left({\left(\frac{i}{N}\right)}^{1-2\beta }-1\right).$$

(65)

The dependence of C ₁ on the system size N

Many key quantities discussed in the “Results” section – including e.g. q_* or ${q}_{{{{{{{{\rm{res}}}}}}}}}$ – are strongly related to the value of C₁. Therefore, it would be more convenient to re-express C₁ in a simplified form. Although it is impossible to analytically evaluate the summation in Eq. (65) for arbitrary values of N, fair approximations can still be done in the large network size limit, i.e. when N ≫ 1. Using an integral approximation with a midpoint rule in Eq. (65), for β ≠ 1 one obtains

$$\mathop{\sum }\limits_{i=1}^{N}{i}^{-2\beta } ={N}^{1-2\beta }\mathop{\sum }\limits_{i=1}^{N}\frac{1}{N}{\left(\frac{i}{N}\right)}^{-2\beta }\approx {N}^{1-2\beta }\left(\int\nolimits_{1/N}^{1}{x}^{-2\beta }{{{{{{{\rm{d}}}}}}}}x+\frac{{N}^{2\beta -1}+1/N}{2}\right)\\ =\frac{{N}^{1-2\beta }-1}{1-2\beta }+\frac{1+{N}^{-2\beta }}{2},$$

(66)

based on which C₁ can be simplified to

$${C}_{1} =\frac{m}{2}\frac{\tan (\pi T)}{4\pi T}\frac{\mathop{\sum }\nolimits_{i = 1}^{N}\frac{1}{i}\left({\left(\frac{i}{N}\right)}^{1-2\beta }-1\right)}{N{I}_{N}^{2}(2\beta -1)}\\ =\frac{m}{2}\frac{\tan (\pi T)}{4\pi T}\frac{{N}^{2\beta -1}\mathop{\sum }\nolimits_{i = 1}^{N}{i}^{-2\beta }-\mathop{\sum }\nolimits_{i = 1}^{N}{i}^{-1}}{N{I}_{N}^{2}(2\beta -1)}\\ \approx \frac{m}{2}\frac{\tan (\pi T)}{4\pi T}\frac{\frac{1}{1-2\beta }+\left(\frac{1}{2}-\frac{1}{1-2\beta }\right){N}^{2\beta -1}-\ln N}{N\frac{2\beta -1}{{(1-\beta )}^{2}}},$$

(67)

where we used that ${I}_{N}=\frac{1-{N}^{-(1-\beta )}}{1-\beta }\approx \frac{1}{1-\beta }$ and $\mathop{\sum }\nolimits_{i = 1}^{N}{i}^{-1}\approx \ln N$ in the thermodynamic limit N → ∞. The validity of this approximation is supported by Fig. 7, where we show the value of C₁ as a function of the number of nodes N according to Eq. (65) and also its approximated form appearing in Eq. (67).

Fig. 7: Comparison between the exact and the approximate values of the parameter C₁ as a function of the system size N for different values of the popularity fading parameter β.

Each panel corresponds to a different value of β, showing the exact values of C₁ with a red dashed line, whereas the approximating form of C₁ is displayed with a green solid line. In all panels a–d, we used ζ = 1, m = 2 and T = 0.1.

It is worth remarking that for different values of the popularity fading parameter β, C₁ in Eq. (67) behaves in a slightly different manner. Further simplifications in the thermodynamic limit suggest that

$${C}_{1}\approx \frac{m\tan (\pi T)}{8\pi T}\cdot \left\{\begin{array}{ll}\frac{{(1-\beta )}^{2}}{1-2\beta }\frac{\ln N}{N},\hfill&\,{{\mbox{if}}}\,\,\beta \, < \, \frac{1}{2},\hfill\\ \frac{{\ln }^{2}N}{N},\hfill&\,{{\mbox{if}}}\,\,\beta =\frac{1}{2},\hfill\\ \frac{2(\beta +1){(1-\beta )}^{2}}{2(2\beta -1)}{N}^{2\beta -2},&\,{{\mbox{if}}}\,\,\frac{1}{2} \, < \, \beta \, < \, 1,\end{array}\right.$$

(68)

where the $\beta =\frac{1}{2}$ case can be verified by applying the L’Hôpital’s rule in Eq. (67). For β equal to 1, I_N in Eq. (65) diverges as $\ln N$, therefore it should be handled as a separate case. A quick calculation reveals that for β = 1, the parameter C₁ decays slower than any power law, more precisely,

$${C}_{1}(\beta =1)\approx \frac{m\tan (\pi T)}{8\pi T}\frac{N\frac{{\pi }^{2}}{6}-\ln N}{N{\ln }^{2}N}\approx \frac{m\tan (\pi T)}{8\pi T}\frac{{\pi }^{2}}{6{\ln }^{2}N},$$

(69)

where we used the fact that $\mathop{\sum }\nolimits_{i = 1}^{N}{i}^{-2}\approx \frac{{\pi }^{2}}{6}$ for large values of N. Although C₁ can display fundamentally different types of scaling with N, it can easily be shown that for any values of the β parameter, C₁ is a decreasing function of N and

$$\mathop{\lim }\limits_{N\to \infty }{C}_{1}=0,$$

(70)

as a result of which further calculations in the thermodynamic limit become considerably easier. Combining Eq. (70) with Eq. (10) suggests that when q is kept at a fixed value while letting N → ∞ expected modularity can be written as

$$\mathop{\lim }\limits_{N\to \infty }\bar{Q}(q)=1-\frac{1}{q},$$

(71)

from which immediately recover Eq. (18) in the “Results” section.

In the the following sections, we derive two key quantities used in the “Results” section, namely the optimal q_* value at which the modularity is maximal and the resolution limit ${q}_{{{{{{{{\rm{res}}}}}}}}}$. Moreover, we are going to discuss in detail how these quantities are related to the parameter C₁.

Optimal number of communities

One can simply compute q_* by setting the derivative of $\bar{Q}(q)$ to zero in Eq. (10), which yields

$${\left.\frac{{{{{{{{\rm{d}}}}}}}}\bar{Q}(q)}{{{{{{{{\rm{d}}}}}}}}q}\right\vert }_{{q}^{* }}={C}_{1}-\frac{1}{{q}_{* }^{2}}=0,$$

(72)

from which we recover that ${q}_{* }={C}_{1}^{-1/2}$ as it is given by Eq. (14). Utilising Eqs. (68) and (69) allows us to express how the optimal number of communities q_* depends on the system size N. Namely, at N → ∞ this can be written as

$${q}_{* }(N)\approx {\left(\frac{8\pi T}{m\tan (\pi T)}\right)}^{\frac{1}{2}}\cdot \left\{\begin{array}{ll}\frac{{(1-2\beta )}^{\frac{1}{2}}}{(1-\beta )}{\left(\frac{N}{\ln N}\right)}^{\frac{1}{2}},&\,{{\mbox{if}}}\,\,\beta \, < \, \frac{1}{2},\hfill\\ \frac{{N}^{\frac{1}{2}}}{\ln N},\hfill&\,{{\mbox{if}}}\,\,\beta =\frac{1}{2},\hfill\\ \frac{{(2\beta -1)}^{\frac{1}{2}}}{{(\beta +1)}^{\frac{1}{2}}(1-\beta )}{N}^{1-\beta },&\,{{\mbox{if}}}\,\,\frac{1}{2} \, < \, \beta \, < \, 1,\\ \frac{{6}^{\frac{1}{2}}}{\pi }\ln N,\hfill&\,{{\mbox{if}}}\,\,\beta =1.\hfill\end{array}\right.$$

(73)

The above results are concisely summarised in the second row of Table 1 in the “Results” section.

Maximum value of the modularity

Once q_* is known, the maximum value of the expected modularity can be obtained by plugging Eq. (14) into Eq. (63), yielding

$$\bar{Q}({q}_{* })=1-{C}_{1}{q}_{* }-\frac{1}{{q}_{* }}=1-\frac{2}{{q}_{* }}=1-2{C}_{1}^{1/2},$$

(74)

which, by means of Eq. (70), goes to 1 in the thermodynamic limit N → ∞. Based on Eqs. (74) and Eq. (68), one can also calculate how quickly the modularity reaches 1 as a function of N. The corresponding results are summarised in the fourth row of Table 1 in the “Results” section.

Resolution limit

The resolution limit can naturally be phrased in the language of q as

$$l\approx \frac{\mathop{\sum }\nolimits_{i = 1}^{N}{\bar{b}}_{i}(q)}{2q} \, > \, {l}_{{{{{{{{\rm{res}}}}}}}}}=\frac{\mathop{\sum }\nolimits_{i = 1}^{N}{\bar{b}}_{i}({q}_{{{{{{{{\rm{res}}}}}}}}})}{2{q}_{{{{{{{{\rm{res}}}}}}}}}}\equiv {(E/2)}^{1/2},$$

(75)

where ${q}_{{{{{{{{\rm{res}}}}}}}}}$ specifies an upper limit on the number of partitions; using values of q larger than ${q}_{{{{{{{{\rm{res}}}}}}}}}$ would result in the communities being certainly unresolvable. By means of Eq. (58), the last part of Eq. (75) can be rewritten as

$$\frac{\mathop{\sum }\nolimits_{i = 1}^{N}{\bar{b}}_{i}({q}_{{{{{{{{\rm{res}}}}}}}}})}{2{q}_{{{{{{{{\rm{res}}}}}}}}}}\approx \frac{\mathop{\sum }\nolimits_{i = 1}^{N}{\bar{k}}_{i}-2E{C}_{1}{q}_{{{{{{{{\rm{res}}}}}}}}}}{2{q}_{{{{{{{{\rm{res}}}}}}}}}}=\frac{2E(1-{C}_{1}{q}_{{{{{{{{\rm{res}}}}}}}}})}{2{q}_{{{{{{{{\rm{res}}}}}}}}}}={(E/2)}^{1/2},$$

(76)

which, after rearrangement, yields

$${q}_{{{{{{{{\rm{res}}}}}}}}}=\frac{{(2E)}^{1/2}}{1+{C}_{1}{(2E)}^{1/2}}=\frac{{(2E)}^{1/2}}{1+\frac{{(2E)}^{1/2}}{{q}_{* }^{2}}}.$$

(77)

The dependence of ${q}_{{{{{{{{\rm{res}}}}}}}}}$ on the system size N is conjointly determined by C₁(N) and E ≈ mN. More precisely, taking the N → ∞ limit in Eq. (77) and additionally using Eqs. (68) and (69) suggest that

$${q}_{{{{{{{{\rm{res}}}}}}}}}(N) \sim \left\{\begin{array}{ll}{N}^{\frac{1}{2}},\hfill&\,{{\mbox{if}}}\,\,\beta \, < \, \frac{3}{4},\hfill\\ {N}^{2-2\beta },\hfill&\,{{\mbox{if}}}\,\,\frac{3}{4}\le \beta < 1.\\ {\ln }^{2}N,\hfill&\,{{\mbox{if}}}\,\,\beta =1.\hfill\end{array}\right.$$

(78)

Modularity at ${q}_{{{{{{{{\rm{res}}}}}}}}}$

In the followings, we discuss the rate at which $\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})$ goes to 1 as a function of the system size N. The value of the modularity at ${q}_{{{{{{{{\rm{res}}}}}}}}}$ can be expressed by plugging Eq. (77) into Eq. (63) yielding

$$\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})=1-\frac{{C}_{1}{(2E)}^{1/2}}{1+{C}_{1}{(2E)}^{1/2}}-\frac{1+{C}_{1}{(2E)}^{1/2}}{{(2E)}^{1/2}}$$

(79)

$$=1-\frac{2E{C}_{1}}{{(2E)}^{1/2}+2E{C}_{1}}-\frac{{(1+{C}_{1}{(2E)}^{1/2})}^{2}}{{(2E)}^{1/2}+2E{C}_{1}}.$$

(80)

Since E ~ N and C₁ is a decreasing function of N, the dominant part of $\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})$ is always given by the first term in Eq. (80). This simplification suggests that

$$1-\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})\approx \frac{{C}_{1}{(2E)}^{1/2}}{1+{C}_{1}{(2E)}^{1/2}},$$

(81)

which, along with the result obtained for C₁ in Eq. (68), leads to

$$1-\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})\approx {C}_{1}{(2E)}^{1/2} \sim \left\{\begin{array}{ll}\frac{\ln N}{{N}^{1/2}},\hfill&\,{{\mbox{if}}}\,\,\beta < \frac{1}{2},\hfill\\ \frac{{\ln }^{2}N}{{N}^{1/2}},\hfill&\,{{\mbox{if}}}\,\,\beta =\frac{1}{2},\hfill\\ {N}^{2\beta -3/2},&\,{{\mbox{if}}}\,\,\frac{1}{2} < \beta < \frac{3}{4},\end{array}\right.$$

(82)

where we exploited the fact that C₁(2E)^1/2 goes to zero as N → ∞ for β < 3/4, and thus, the Taylor-expansion of $\frac{x}{1+x}\approx x$ with x = C₁(2E)^1/2 can be used in Eq. (81). Note, however, that for β ≥ 3/4 values the above approximation does not hold since C₁(2E)^1/2 in Eq. (81) is either divergent or converges to a non-zero value in the thermodynamic limit. More precisely, based on Eqs. (68) and (80) one can show that for β = 3/4

$$1-\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})\approx \frac{{K}_{1}}{1+{K}_{1}}+\frac{1+{K}_{1}}{{(2mN)}^{1/2}}\approx \frac{{K}_{1}}{1+{K}_{1}},$$

(83)

where ${K}_{1}:= \frac{{(2m)}^{1/2}m\tan (\pi T)}{8\pi T}\frac{\left(\frac{3}{4}+1\right){\left(1-\frac{3}{4}\right)}^{2}}{\left(\frac{3}{2}-1\right)}$ is a constant which does not depend on the system size N. For β > 3/4, similar considerations suggest that we can approximate $1-\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})$ as

$$1-\bar{Q}({q}_{{{{{{{{\rm{res}}}}}}}}})\approx \frac{{K}_{2}{N}^{2\beta -3/2}}{1+{K}_{2}{N}^{2\beta -3/2}}\approx \frac{1}{1+{K}_{2}^{-1}{N}^{3/2-2\beta }}\approx 1-{K}_{2}^{-1}{N}^{3/2-2\beta },$$

(84)

where K₂ is again a constant defined as ${K}_{2}:= \frac{{(2m)}^{1/2}m\tan (\pi T)}{8\pi T}\frac{(\beta +1){(1-\beta )}^{2}}{(2\beta -1)}$. In the last step above we have exploited that since K₂N^2β−3/2 → ∞ as N → ∞, therefore the Taylor expansion $\frac{1}{1+x}\approx 1-x$ with $x={K}_{2}^{-1}{N}^{3/2-2\beta }$ can be utilised in Eq. (84). The results presented herein are concisely summarised in Table 1 of the “Results” section.