Introduction

Rashba nanowire-superconductor hybrid systems1,2,3,4,5,6,7 are the front-running platforms for detecting and manipulating Majorana zero modes (MZMs)8,9,10,11,12,13. The quantized zero-bias conductance peak (ZBCP), observed in two terminal setups featuring the normal metal-topological superconductor (N-TS) link, once considered to be a definitive signature of MZMs14,15,16,17,18,19, has become a controversial issue. Quasi-MZMs13,20,21,22,23,24, which are near-zero energy trivial Andreev bound states (ABS) mimic most of the MZM signatures.

As a result, recent efforts25,26,27,28,29,30,31,32 have focused on distinguishing between trivial and topological zero-energy modes. Recent efforts33,34,35,36,37,38, culminating in the topological gap protocol (TGP)39,40, have converged on guidelines that necessitate the measurement of all the elements of the conductance matrix, particularly focusing on non-local transport measurements using three-terminal normal-topological superconductor-normal (N-TS-N) setups to identify the bulk-gap closing and reopening, which separates the trivial and topological regimes. Non-local conductance signatures should thus supplement the local conductance measurements in identifying MZM signatures by detecting non-local correlations, particularly in the presence of disorder.

With the aforementioned on one hand, the basic Rashba wire setup itself has further drawbacks which includes the requirement of large magnetic fields that could potentially destroy superconductivity41,42,43,44 apart from the practicalities of precise magnetic field alignment45. Recently, efforts are being made towards realizing topological superconductivity with zero external magnetic fields by using proximity effects from magnetic insulators (MI)46,47,48,49,50,51,52,53,54,55,56,57,58,59. Recent experimental47 and theoretical works48,49,50,51,52,55,60 featuring this setup indicate that at very low external magnetic fields, or even zero external magnetic fields, a topological phase can emerge.

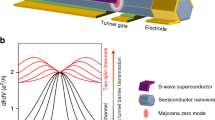
Theoretical studies on the isolated system, schematized in Fig. 1a, thus far have set a preliminary stage by providing an insight on the geometric configurations and regimes of physical parameters which support the emergence of topological phases. However, the experimental basis for probing the formation of MZMs, in connection with the TGP, will entail a detailed analysis of conductance signatures. This necessitates detailed quantum transport calculations to evaluate the‘current flow in a multi-terminal geometry that is schematized in Fig. 1b. The object of this paper is hence to provide an in-depth analysis of the transport signatures of MZMs in these structures, particularly focusing on the local and non-local conductance spectra in both pristine and disordered nanowires.

Fig. 1: Device schematics.
figure 1

a Cross section of Rashba nanowire epitaxially epitaxially coated with a superconductor (SC) and a magnetic-insulator (MI), showing overlapping SC and MI layers. b A 3-D schematic of the device setup with the nanowire connected to two normal contacts via tunnel barriers, and a gate to control chemical potential, μ. c, d Effective 1D models used for computation, treating MI-SC as a stacked bilayer, with the homogeneous and inhomogeneous chemical potential profiles shown below.

Full size image

Using the Keldysh non-equilibrium Green’s function (NEGF) technique, we develop a detailed quantum transport approach that accounts for the complex interplay between the quasiparticle dynamics in the superconductor-magnetic insulator (SC-MI) bilayer structure, and the transport processes through the semiconducting Rashba nanowire. Using this, we provide a detailed analysis of three terminal setups to probe the local and non-local conductance spectra in both the pristine as well as the disordered cases. We uncover the conductance quantization scaling with the bilayer coupling and the signatures of the gap closing followed by the emergence of near-zero energy states, which can be attributed to the zero modes in the clean nanowire. However, in the presence of a smoothly varying disorder potential, trivial Andreev bound states may form with signatures reminiscent of topological zero modes.

Results and discussions

We consider semiconductor nanowires (SM) with Rashba-spin-orbit coupling with epitaxial layers of superconductors (SC) (usually Al/Pb) and magnetic insulators (MI) (usually EuS), as depicted in Fig. 1a. We then consider the device geometry where the MI and SC are in contact with the SM individually and overlap with each other, and connected to metallic leads as depicted in Fig. 1b.

The strength of the coupling of the metallic leads to the nanowire is controlled by the parameter γ, which represents the escape rate of the electrons into the leads. In the broadband limit of treating the contacts, as described in earlier works, this quantity is energy independent and can be used as a parameter. The isolated Rashba nanowire is described by the following Hamiltonian:

$${H}_{SM}={V}_{Z}^{SM}{\hat{\sigma }}_{x}+\left(\frac{{\hslash }^{2}{k}^{2}}{2{m}^{* }}-\mu +{\alpha }_{R}k{\hat{\sigma }}_{y}\right){\hat{\tau }}_{z},$$
(1)

Where \({V}_{Z}^{SM}\) is the Zeeman Hamiltonian in the SM, μ is the electrochemical potential, αR is the strength of the Rashba spin–orbit coupling, m* is the effective mass of the electron and \({\hat{\sigma }}_{i},{\hat{\tau }}_{i}\), are the Pauli matrices in the spin and the particle–hole space, respectively.

As detailed in the Methods section and in Supplementary Note 1, the effects of the SC-MI bilayer are accounted for as a self-energy term in the Green’s function for the nanowire and the effect of the direct coupling of the MI to the nanowire is taken to be an effective Zeeman field in the wire. The strength of the coupling of the SC-MI bilayer to the Rashba nanowire is controlled by the parameter γSC. It comes into play while calculating the self-energy accounting SC-MI bilayer from the Green’s function for the bilayer. We also use the self-consistent value of the superconducting gap, Δ, calculated from the bare superconducting gap Δ0 of the parent superconductor in the presence of the Zeeman field and scattering processes. The process of obtaining this is involved and has been described in Supplementary Note 1. We use Δ0 = 0.23 meV, m* = 0.015me, where me is the electron rest mass, for all our simulations.

In order to model the system to simulate transport measurements, we reduce the hexagonal nanowire to a quasi one-dimensional system52 as shown in Fig. 1c, d. In Fig. 1c, we consider a ‘clean’ nanowire, with a constant chemical potential. We also consider an inhomogeneous potential which is a spatially varying Gaussian potential as illustrated in Fig. 1d. Smoothly varying Gaussian potentials such as the one we have used in our simulations may arise in experimental situations due to charged impurities in the nanowire61,62.

An external Zeeman field is applied which is anti-parallel to the magnetization in the MI. It reduces the Zeeman term in the Hamiltonian of the SC, but increases the Zeeman field in the normal metal. We parameterize the Zeeman fields in the SC and the SM in terms of the field directly induced in the SC due to the MI \(({V}_{0}^{SC})\), and the coupling strengths of the SC and SM nanowire to the external magnetic field, (gSC, gSM) as follows:

$${V}_{Z}^{SC} ={V}_{0}^{SC}+{g}_{SC}{V}_{ext}^{Z}\\ {V}_{Z}^{SM} ={g}_{SM}{V}_{ext}^{Z}.$$
(2)

We use gSC = 2, gSM = − 15 for our calculations, closely following the setup in52, used for equilibrium calculations. A finite Zeeman energy in the semiconductor, either induced by coupling to a magnetic insulator or by an applied magnetic field, is required to enter the topological phase63. Here we have considered only an external Zeeman field, and neglected the direct coupling of the SM to the MI–an assumption which can altered by adjusting the parameterization.

We first present the numerical results for the pristine nanowire, in the absence of an inhomogeneous potential. The low energy density of states (DOS) shown in Fig. 2a, b illustrates the lowest ABS which form a near-zero energy oscillating mode after the topological transition, which is marked by the bulk gap closing and reopening. The bulk gap closing and reopening is more prominent in the longer nanowire than the shorter one, since there are more sub-gap states. As the length of the nanowire increases, the oscillations around zero-energy are exponentially suppressed64,65,66.

Fig. 2: Majorana Zero Modes (MZMs) in the structure.
figure 2

a, b Density of states (DOS) as a function of the energy(E) and the externally applied Zeeman field \({V}_{Z}^{ext}\) of the device region for nanowire (NW) lengths a 2.25 μm, and b 4.5 μm. The low energy DOS shows the gap closing, followed by the emergence of a state near zero energy. The splitting of this low energy state is greater for shorter nanowires than longer nanowires. c, d Local density of states (LDOS) profiles at \({V}_{Z}^{ext}=0.1{\Delta }_{0}\) which clearly show the localization of the zero energy states at the ends of the nanowire, consistent with the appearance of MZMs. The longer (length 4.5 μm) nanowire d shows a greater degree of localization than the shorter (length 2.25 μm) nanowire c. The bare superconducting gap in the parent superconductor Δ0 sets the scale for all energies. The colorbars represent the magnitude of the DOS, LDOS.

Full size image

The local density of states (LDOS) corresponding to these nanowires, as seen in Fig. 2c, d, shows that the zero energy state is well localized at both ends, and more prominently so in the longer nanowire. The LDOS plots also show a greater splitting in energy around the zero energy for the shorter nanowire than the longer nanowire. While on closer inspection, the longer nanowire also shows some splitting, in reasonable experimental measurements we expect to see a single broadened peak. These observations are due to the hybridization of the MZMs when they overlap in finite nanowires, resulting in a splitting of the zero mode67. The hybridization of the MZMs through the nanowire is suppressed with increasing length64,65,66, which is consistent with our observations.

In Fig. 3a, b we plot the differential conductance for clean nanowires of lengths 2.25 μm and 4.5 μm with chemical potential μ = 0.125 meV and find a clear ZBCP in the topological regime, and no peak near zero energy in the topologically trivial regime. The peak is close to the quantized value of \(\frac{{e}^{2}}{h}\) expected from an MZM in an N–S–N setup under symmetric biasing64,65, but is smaller. We attribute this observation to the level broadening due to the composite SC-MI bilayer which effectively acts as an extra contact68 and induces further broadening compared to a two-terminal N–TS–N device69. This is also borne out by the fact that as the coupling to the metallic contacts becomes much stronger than the coupling to the bilayer, the ZBCP asymptotically reaches the quantized value, as shown in Fig. 3c, since the broadening due to the effective MI-SC bilayer becomes negligible in comparison to the broadening induced by the metallic contacts. It should also be noted that the exactness of the quantization would also depend on the external magnetic field because the Majorana overlap energy oscillates with the externally applied magnetic field. As the overlap energy of the MZMs at the ends of the nanowire varies, the peak value of the ZBCP also changes70. This figure clearly elucidates the effect of introducing the bilayer on the actual conductance quantization of MZMs in the setup.

Fig. 3: Scaling of conductance quantization with bilayer coupling.
figure 3

a, b Low bias differential conductance plots for nanowires of length a 2.25 μm, and b 4.5 μm in the topological region (External Zeeman field, \({V}_{Z}^{ext}=0.07{\Delta }_{0}\)) (orange) and trivial region (\({V}_{Z}^{ext}=0.005{\Delta }_{0}\)) (green). The topological regime shows clear conductance peaks absent in the trivial regime, though not quantized. The splitting of the zero bias peak is more pronounced for the shorter nanowire, consistent with Fig. 2. c Shows that as the coupling to the normal contacts, γ, is increased, so that it becomes much larger than the coupling, γSC, between the nanowire and the superconductor-magnetic insulator bilayer, the peak asymptotically reaches the expected quantized value. The bare superconducting gap in the parent superconductor Δ0 sets the scale for all energies. The differential conductance, G is plotted as a function of the bias, V. G is measured in units of e2/h, which is the conductance quantum, e being the electronic charge and h being Planck’s constant.

Full size image

The ZBCP quantization reflects upon the local Andreev reflection process, and can be a diagnostic for MZMs in pristine setups. In disordered setups, as currently encountered in experiments, the current guidelines on the detection of MZMs follows the TGP39,40. The TGP employs a combination of local and non-local conductance measurements on three terminal setups as an effective diagnostic tool for the detection of MZMs. In this protocol, first, the local conductance measurements at the two ends of a disordered setup must individually show a sustained gap closure and ZBCP spanning a large range of applied magnetic fields. Such gap closures will have local variations due to the presence of random uncorrelated impurities at the two ends. In addition, the non-local conductance gap must close and re-open, signaling a topological phase transition. Besides that, at the point at which the non-local conductance gap closes, one must observe a zero magnitude of the conductance along with a flip in the sign of the conductance. From the transport physics angle33,66, this can be attributed to the fact that the non-local conductance magnitude is given by the difference between the direct component and the crossed Andreev component, all of which are described in Supplementary Note 2 and several other references.

We now turn our attention to our simulations on the local and non-local conductances in accordance with the TGP. Following previous analysis61,71 for the disordered setup, we have specifically considered the inhomogenous potential as depicted in Fig. 1d. A smoothly-varying potential barrier can be interpreted as a spatially varying chemical potential. In such a scenario, parts of the nanowire may locally enter the topological regime, resulting in a local pair of near-zero energy modes. This typically happens when the system is tuned close to the topological phase. These quasi-MZMs may mimic many of the characteristic signatures of MZMs, including zero bias peaks in the local conductance at magnetic fields smaller than those at which the topological MZMs appear. However, these near-zero-energy states do not have topological protection and are hence not true MZMs.

Before embarking on the results related to the local and nonlocal transport spectroscopy simulations, we must make a quick remark on the biasing conditions of three terminal setups. In such a setup, voltages can be applied and currents can be measured across either terminals independently. As defined in (6) and explicitly derived in (7) and (8), this tantamounts to enforcing asymmetric biasing at the contacts, (VL = V, VR = 0). As a consequence, the ZBCP is quantized at \(\frac{2{e}^{2}}{h}\), unlike that in Fig. 3, where we had considered a symmetric bias scenario (VL = V/2, VR = − V/2), and hence obtained the ZBCP quantized at \(\frac{{e}^{2}}{h}\)65. The quantized peak is a signature of the MZM and may be attributed to a perfect and coherent Andreev reflection at a semiconductor—topological superconductor (N-TS) interface, typically seen in two-terminal devices69.

Both the local and non-local conductance spectra for the pristine nanowire are shown in Fig. 4, for nanowires of length 2.25 μm (Fig. 4a, b) and 4.5 μm (Fig. 4c, d) which exhibit similar features, that is, the bulk gap closing and reopening followed by the emergence of Majorana oscillations around zero energy. Since the zero modes appear after the closure of the bulk gap, we can conclude that they are not quasi-MZMs, but may indeed be topological MZMs72. We also note that a finite low-bias non-local conductance only emerges after the topological transition. The low bias non-local conductance is rectifying in nature33 and switches sign as the the voltage polarity is reversed. At the turning points, the non-local conductance vanishes.

Fig. 4: Conductance spectra for the clean nanowire.
figure 4

a Local (GLL) and b non-local conductance (GLR) signatures for a nanowire of length 2.25 μm, with a potential profile as shown in Fig. 1c. c Local and d non-local conductance spectra for a nanowire of length 4.5 μm, with a potential profile as shown in Fig. 1c. Both the local and the non-local conductances show the bulk gap closing and reopening, which signals a topological transition, followed by the emergence of a near-zero energy state with a splitting that oscillates as a function of the externally applied magnetic field, \({V}_{Z}^{ext}\). The bare superconducting gap in the parent superconductor Δ0 sets the scale for all energies. GLL, GLR are plotted as a function of the biasing energy e, and the externally applied magnetic field \({V}_{Z}^{ext}\) and are measured in units of e2/h, which is the conductance quantum, e being the electronic charge and h being Planck’s constant. The colorbars represent the magnitude of the DOS, LDOS.

Full size image

In the sub-gap region, there is a correspondence between the non-local conductance and the BCS charges of the bound state at the leads such that the nonlocal conductance is proportional to the BCS charge at a contact73. The charge difference between the even and odd parity ground states is equal to the net charge carried by the BdG fermion state, which can be nonzero when the constituent Majorana wave functions overlap74. The vanishing of the non-local conductance at the turning points is a signature expected from hybridized MZMs, which should be chargeless at turning points. From the plots of local and nonlocal conductance of the pristine nanowire, we can see an oscillation in the energy splitting as the magnetic field is increased. Meanwhile, the magnitude of the nonlocal conductance, which corresponds to the BCS charge, vanishes at the turning points (maxima and minima) of the energy splitting, and is maximum (close to the quantized value) at the points where the energy splitting vanishes75. Therefore, the BCS charge and the energy splitting oscillate out of phase with each other, which is a characteristic signature of MZMs. The local conductance is almost quantized at \(\frac{2{e}^{2}}{h}\) where the Majorana splitting goes to zero. The deviation from the precise quantization value may be attributed to contact broadening, and due to the fact that we have three contacts in our system, as elaborated previously. At the points where the Majorana overlap energy becomes significant, the value of the local conductance drops further.

In the presence of a smoothly-varying potential barrier, the formation of quasi-MZMs is expected33,62,76,77,78,79,80,81,82,83,84,85. They characteristically appear in the topologically trivial regime before the closure of the bulk gap, mimicking many signatures originally considered as ‘smoking gun signatures’ for MZMs including oscillations with the externally applied magnetic field, and with the associated local conductance quantized at values close to \(\frac{2{e}^{2}}{h}\). It is expected that systems which show quasi-MZMs, will also exhibit true MZMs in the topological phase on increasing the external Zeeman field. For such a disordered case, for the longer nanowire, as shown in Fig. 5a, in the DOS, we find signatures characteristic of a quasi-MZM state, followed by a gap reopening signature and the emergence of a potential topological MZM. The local conductance, as shown in Fig. 5b in this case is quite deceptive since we see a premature gap closing and the bulk-gap reopening signature is extremely faint.

Fig. 5: Conductance spectra for the disordered nanowire.
figure 5

a Low Energy density of states (DOS) b local and c non-local conductance spectra for a nanowire of length 4.5 μm, with a potential profile as shown in Fig. 1d. d Low energy DOS, e the local and f the non-local conductance conductance spectra for a nanowire of length 2.25 μm, with a potential profile as shown in Fig. 1d. For the long nanowire, we see premature emergence of a quasi-Majorana Zero Mode before the bulk gap closing and reopening.The bare superconducting gap in the parent superconductor Δ0 sets the scale for all energies. GLL, GLR are plotted as a function of the biasing energy e, and the externally applied magnetic field \({V}_{Z}^{ext}\) and are measured in units of e2/h, which is the conductance quantum, e being the electronic charge and h being Planck’s constant. The colorbars represent the magnitude of the DOS, LDOS.

Full size image

The quasi-MZM and the true MZM regions are quite difficult to distinguish. In the non-local conductance plot shown in Fig. 5c, the bulk-gap reopening is seen more prominently, in closer accord with the gap protocol39. The non-local conductance shows signatures of both the quasi-MZM and the topological MZM states, which can be distinguished by their position with respect to the reopening of the bulk gap76. For the shorter nanowire, as seen in Fig. 5d–f, the local and the non-local conductance spectra both show the gap closing and reopening followed by the emergence of MZMs, which oscillate in energy as the Zeeman field is increased. At the points where the splitting is zero, the local conductance is quantized at values very close to \(\frac{2{e}^{2}}{h}\). We do not find any signatures of quasi-MZM states in this device. An interesting point to note is that the local conductance exhibits signs of negative differential conductance. It is also worth noting that especially for longer nanowires, neither the local nor the non-local conductance alone has the entire information regarding the channel DOS, that arises from its eigenspectrum.

The MZMs are protected by a clear topological gap both for the pristine nanowire and for the nanowire with a smoothly varying background potential. The local conductance fails to probe the bulk states for sufficiently long nanowires. Before one lays claim to having observed topological MZMs, it is necessary to measure the entire conductance matrix to probe a device and investigate whether the zero bias peaks at both the contacts or on both the sides are correlated and emerging after the bulk gap closing and reopening,

To conclude, using the NEGF technique, we developed a detailed quantum transport approach that accounts for the complex interplay between the quasiparticle dynamics in the SC-MI bilayer structure, and the transport processes through the semiconducting Rashba nanowire. We provided a detailed analysis of three terminal setups to probe the local and non-local conductance spectra in both the pristine as well as the disordered limits. We uncovered the conductance quantization scaling with the bilayer coupling and the signatures of the gap closing followed by the emergence of near-zero energy states, which can be attributed to the topological zero modes in the clean nanowire limit. However, in the presence of a smoothly varying potential, trivial Andreev bound states may form with signatures reminiscent of topological zero modes in the form of a premature gap closure in the conductance spectra. Our results therefore provide transport-based analysis of the operating regimes that support the formation of MZMs in these hybrid systems of current interest, while considering experimentally relevant device structures with realistic disordered potentials accounting for shallow tunnel barriers which may be formed inside the hybrid nanowire structure. Having set the stage for understanding device modeling in these emerging structures, the technique can also be easily extended to account for other experimental device designs and also the inclusion of scattering effects64,77 inside the nanowire channel.

Methods

We discretize the Hamiltonian of the system (2) on a 1D lattice with N sites, and write the Green’s function in the Nambu spinor basis78 \({({\psi }_{\uparrow },{\psi }_{\downarrow },-{\psi }_{\uparrow }^{{{{\dagger}}} },{\psi }_{\downarrow }^{{{{\dagger}}} })}^{T}\). The Hamiltonian for the Rashba nanowire and the self-energies corresponding to the metallic contacts and the SC-MI bilayer, are then used obtain the retarded Green’s function for the hybrid device which is used for our transport calculations,

$${G}^{R}={\left[(E+i\eta ){\mathbb{I}}-{H}_{SM}-{\Sigma }_{L}-{\Sigma }_{R}-{\Sigma }^{{\prime} }\right]}^{-1},$$
(3)

where η is an infinitesimal positive damping parameter introduced for numerical stability, and \({\mathbb{I}}\) is the identity matrix of the dimension of the Hamiltonian matrix in Nambu space. In the wide-band approximation64,65,66, the self energies for the metallic contacts, ΣL(R), are written in their eigenbasis and are hence diagonal, as detailed in Supplementary Note 2. We use the Usadel equation, which is derived from a quasi-classical approximation to the Gorkov equations, to find the Green’s function, and hence, the self-energy, \({\Sigma }^{{\prime} }\) for the SC-MI bilayer52. The effect of the proximity of the MI on the SC can be taken into account in the boundary conditions of the Usadel equation. The MI layer induces a uniform Zeeman field \({V}_{Z}^{SC}\) in the diffusive superconductor79. The Usadel equation is then solved with the self-consistent value of Δ to obtain the quasi-classical Green’s function for the bilayer, \(\check{g}\). The gap is induced in the bare Rashba nanowire by considering the proximity effect of the bilayer, which is taken into account using the self energy, \({\Sigma }^{{\prime} }\) which can be obtained from the semi-classical Green’s function, \(\check{g}\). The imaginary part of \({\Sigma }^{{\prime} }\) connects the electron and hole subspaces, thus, inducing a gap in the system.

We also take into account spin-orbit and spin-flip scattering in the SC, by adding a scattering self-energy term in the Usadel equation. The energy scales for the spin-orbit and spin-flip relaxation processes are characterized by Γso, Γsf respectively. We take Γso = Γsf = 0.4Δ0 for our simulations unless stated otherwise. We also use the Usadel Equation to calculate the self-consistent value of the superconducting gap in the presence of an external magnetic field. For this, we solve the Usadel equation self-consistently with the superconducting gap equation along with a thermodynamic constraint as outlined in Supplementary Note 1.

The retarded Green’s function is be used to calculate the spectral function, A(E), the trace of which gives the density of states (times 2π), and the diagonal elements of which gives us the local density of states (times 2π).

$$DOS(E)=\frac{1}{2\pi }Tr[A(E)]=\frac{1}{2\pi }Tr[{G}^{R}(E)-{G}^{A}(E)]$$
(4)

We also use the retarded Green’s function defined above to calculate the transmission coefficients, and hence the conductance matrix for this setup64,65,66,78. As shown in Fig. 1, we apply voltages VL(R) to the left and right contacts and measure terminal currents IL(R). We use the Keldysh non-equilibrium Green’s function formalism to evaluate the terminal currents64,65,66,78. The terminal electronic current at the left contact80 can be derived in the Landauer Büttiker form as:

$${I}_{L}^{(e)}= -\frac{e}{h}\left\{\int\,dE{T}_{A}^{(e)}(E)\left[f\left(E-e{V}_{L}\right)-f\left(E+e{V}_{L}\right)\right]\right.\\ +\int\,dE{T}_{CAR}^{(e)}(E)\left[f\left(E-e{V}_{L}\right)-f\left(E+e{V}_{R}\right)\right]\\ \left.+\int\,dE{T}_{D}^{(e)}(E)\left[f\left(E-e{V}_{L}\right)-f\left(E-e{V}_{R}\right)\right]\right\}+{I}^{{\prime} },$$
(5)

where, \({T}_{D}^{(e)}(E)\), \({T}_{A}^{(e)}(E)\), and \({T}_{CAR}^{(e)}(E)\) represent the energy resolved transmission probabilities for the direct, Andreev and crossed-Andreev processes involving the left and right contacts for the electronic sector of the Nambu space and I’ is the extra current due to the SC-MI bilayer acting as an effective contact, derived in Supplementary Note 1. These transmission probabilities can be calculated from Green’s function of the device and the self-energies of the contacts64,66.

Using the expressions for the terminal currents from above, the conductance matrix [G] can be defined as:

$${{{{{{{\rm{[G]}}}}}}}}=\left(\begin{array}{cc}{G}_{LL}&{G}_{LR}\\ {G}_{RL}&{G}_{RR}\end{array}\right)=\left(\begin{array}{cc}{\left.\frac{\partial {I}_{L}}{\partial {V}_{L}}\right\vert }_{{V}_{R} = 0}&{\left.\frac{\partial {I}_{L}}{\partial {V}_{R}}\right\vert }_{{V}_{L} = 0}\\ {\left.\frac{\partial {I}_{R}}{\partial {V}_{L}}\right\vert }_{{V}_{R} = 0}&{\left.\frac{\partial {I}_{R}}{\partial {V}_{R}}\right\vert }_{{V}_{L} = 0}\end{array}\right),$$
(6)

The diagonal matrix elements represent the local conductance at the left and right contacts, and the off-diagonal components represent the non-local conductance.

The local conductance at the left contact can be derived by taking a partial derivative of the left terminal current (IL), as given in (5), with the left contact voltage (VL), and the right contact voltage (VR) set to zero, and is given by : \({G}_{LL}={\left.\frac{\partial {I}_{L}}{\partial {V}_{L}}\right\vert }_{{V}_{R} = 0}\). Using this, we derive the following expression for the local conductance using the Landauer Büttiker form

$${\left.{G}_{LL}(V)\right\vert }_{T\to 0} \equiv \frac{{e}^{2}}{h}\left[{T}_{A}(E=eV)+{T}_{A}(E=-eV)\right.\\ + \left. {T}_{CAR}(E =eV)+{T}_{D}(E=eV)+{G}_{LL}^{{\prime} }(V)\right],$$
(7)

The term \({G}_{LL}^{{\prime} }(V)\) is due to currents flowing into the SC-MI bilayer66.

The non-local conductance formula can similarly be derived by taking a partial derivative of the left terminal current (IL), as given in (5), over the right terminal voltage (VR), with the left terminal voltage (VL) set to zero, such that, \({G}_{LR}={\left.\frac{\partial {I}_{L}}{\partial {V}_{R}}\right\vert }_{{V}_{L} = 0}\).

$${\left.{G}_{LR}(V)\right\vert }_{T\to 0}\equiv \frac{{e}^{2}}{h}\left[{T}_{CAR}(E=-eV)-{T}_{D}(E=eV)\right].$$
(8)

Using the above, we have analyzed the local and non-local conductances of the device in both the pristine and disordered setups.