Introduction

The future of quantum technologies lies in hybrid systems achieving multitasking potentialities by combining different physical components with complementary functionalities1,2. In particular, devices based on hybrid Josephson junctions (JJs) have opened up new possibilities to engineer noise protected qubits being at the same time easily tunable via electrical ports3. Gate tunable superconducting qubits, so-called gatemons, have been successfully implemented with semiconducting nanowires4,5, InAs JJs6,7,8, 2D materials9, van der Waals heterostructures10 and graphene11,12. Their promising characteristics are reduced dissipative losses, crosstalk and compatibility with high magnetic fields13,14. An exciting perspective is creating fault-tolerant topological qubits based on Majorana zero modes 15,16. A fundamental step towards these achievements has been the realization of high-quality graphene superconductor heterostructures with clean interfaces obtained by encapsulating graphene in hexagonal boron nitride (hBN) with one-dimensional edge contacts to superconducting leads17,18,19. These heterostructures show ballistic transport of Cooper pairs over micron-scale lengths, gate-tunable supercurrents that persist at large parallel magnetic fields 20,21,22, and different features of 2D Andreev physics23,24,25. In addition, the extremely low specific-heat of graphene embedded in hBN allowed the realization of high sensitive graphene Josephson Junction (GJJ) based microwave bolometers enabling circuit quantum electrodynamics applications26,27. Single near-infrared photon detection has also been proven by coupling photons to localized surface plasmons of a GJJ which can be readily integrated into future JJ-based computing architectures as a high-speed, low-power optical interconnects28. GJJ is an excellent platform to realize exotic quantum states, recently long-lived Floquet-Andreev states have been generated by applying continuous microwave light without significant heating29.

The unifying microscopic description of the Josephson effect in these heterostructures results from proximity effect and constructive interference between Andreev processes at the two N/S interfaces leading to coherent electron-hole superpositions, known as Andreev bound states (ABSs). In the short junction regime, the current-phase relation (CPR) resulting from the phase-dependence of the ABSs spectrum and density of states, differs from the sinusoidal CPR of tunnel JJs30,31 showing a skewness intrinsically related to the microscopic characteristics of the junctions as the number of transmitting channels and their transparency, and dependent on gate voltage and temperature32,33. Recently, concomitant measurements of CPR and Andreev bound state spectrum in a highly transmissive InAs JJ6 highlighted the potentialities of hybrid planar JJ as sensors of fundamental phenomena occurring in heterostructures. Tunneling spectroscopy measurements in GJJ revealed the possible presence of microscopic quantum dots weakly coupled to the proximitized graphene, that behave as energy filters in tunneling process12,34. Whether these impurities may influence the supercurrent of GJJ has not been yet established. On the other side it has been predicted that carrier density fluctuations of the graphene channel due carrier traps in the nearby substrate35,36 may induce critical current fluctuations with 1/f spectrum37,38,39. An alternative mechanism, related to variation of the proximity induced gap in the graphene junction fabricated using hBN encapsulation, has been reported40.

In this work, motivated by these observations, we investigate the effect of a dilute ensemble of non-magnetic localized impurities on the equilibrium supercurrent in a ballistic GJJ, employing an analytical approach based on the Dirac-Bogoliubov-de Gennes model41. In particular, we focus on the short channel limit30, where the junction length is much smaller than the coherence length of the superconductors. Impurities are modeled by the Anderson model42, which has been used to study the effect of adatoms on the graphene electron system43,44,45,46,47. Muñoz et al.48 have recently investigated, using a self-consistent tight-binding approach, the influence of ripples49,50 and localized defects, described as Lifshitz impurities51, on an intermediate length GJJ, where multiple ABSs occur at zero temperature. A Lifshitz impurity modifies the on-site energy at its location in the corresponding tight-binding Hamiltonian. In the dilute limit this type of disorder introduces a finite width to the Andreev peaks in the density of states, in agreement with the results obtained for a generic SNS junction with quasiclassical methods52. Contrary to the Lifshitz model, the Anderson model includes the possibility of electron transfer from the host to some energy level that belongs to the adsorbed atom46.

We derive the CPR of the disordered GJJ and demonstrate that dilute impurities are responsible for a peculiar forward skewness effect accompanied by the reduction of the critical current. Both quantities display a characteristic nonmonotonic temperature dependence rooted in the hybridized ABS-impurities energies. These results are complemented by the derivation of supercurrent power spectrum which allows to perform spectroscopy of impurity levels with energies close to the Fermi energy. In the static limit and at very low temperatures, the supercurrent noise displays a linear temperature dependence, resembling thermal noise, with a slope related to energy distribution of the impurity states. These results highlight the potentialities of short GJJ as highly sensitive detectors of microscopic defects spectral characteristics via measurements of the supercurrent and its thermal equilibrium noise.

Results and discussion

Model

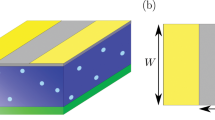
The system considered in this work, schematically shown in Fig. 1, consists of a graphene layer (gray) partially covered by two superconducting electrodes (yellow), and deposited on a substrate (blue). We model the GJJ in the ballistic regime within the Dirac-Bogoliubov-de Gennes (D-BdG) approach, where superconducting metal stripes induce very large doping and superconductivity by proximity effect in the underlying graphene layer 41,53,54,55,56. The D-BdG Hamiltonian reads

$${\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D-BdG}}}}}}}=\mathop{\sum}\limits_{\zeta =\pm }\int {d}^{2}{{{{{\boldsymbol{r}}}}}}{\hat{{{\Psi }}}}_{\zeta }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}}){H}_{{{{{{\rm{D-BdG}}}}}}}{\hat{{{\Psi }}}}_{\zeta }({{{{{\boldsymbol{r}}}}}})\,,$$
(1)

where ζ = ± denotes the sum over the valley indices and

$${H}_{{{{{{\rm{D-BdG}}}}}}}= \,{\tau }_{z}\left[U({{{{{\boldsymbol{r}}}}}}){{\mathbb{1}}}_{\sigma }+\frac{\hslash {v}_{{{{{{\rm{D}}}}}}}}{i}({\partial }_{x}{\sigma }_{x}+{\partial }_{y}{\sigma }_{y})\right]\\ +{\tau }_{x}{{\mathbb{1}}}_{\sigma }{{{{{\rm{Re}}}}}}{{\Delta }}({{{{{\boldsymbol{r}}}}}})-{\tau }_{y}{{\mathbb{1}}}_{\sigma }{{{{{\rm{Im}}}}}}{{\Delta }}({{{{{\boldsymbol{r}}}}}})\,,$$
(2)
$${\hat{{{\Psi }}}}_{+}({{{{{\boldsymbol{r}}}}}})={[{\hat{\psi }}_{A,{{{{{\boldsymbol{K}}}}}},\uparrow }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}}),{\hat{\psi }}_{B,{{{{{\boldsymbol{K}}}}}},\uparrow }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}}),{\hat{\psi }}_{A,{{{{{{\boldsymbol{K}}}}}}}^{\prime},\downarrow }({{{{{\boldsymbol{r}}}}}}),{\hat{\psi }}_{B,{{{{{{\boldsymbol{K}}}}}}}^{\prime},\downarrow }({{{{{\boldsymbol{r}}}}}})]}^{{{\dagger}} }\,,$$
(3)
$${\hat{{{\Psi }}}}_{-}({{{{{\boldsymbol{r}}}}}})={[-{\hat{\psi }}_{B,{{{{{{\boldsymbol{K}}}}}}}^{\prime},\uparrow }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}}),{\hat{\psi }}_{A,{{{{{{\boldsymbol{K}}}}}}}^{\prime},\uparrow }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}}),-{\hat{\psi }}_{B,{{{{{\boldsymbol{K}}}}}},\downarrow }({{{{{\boldsymbol{r}}}}}}),{\hat{\psi }}_{A,{{{{{\boldsymbol{K}}}}}},\downarrow }({{{{{\boldsymbol{r}}}}}})]}^{{{\dagger}} }\,,$$
(4)

vD ~ c/300 is the Fermi velocity in monolayer graphene (c is the speed of light), the identity \({{\mathbb{1}}}_{\sigma }\) and the set of Pauli matrices {σx, σy, σz} act on the (A and B) sublattice subspace. The identity \({{\mathbb{1}}}_{\tau }\) and {τx, τy, τz} act on the electron-hole pair subspace. We approximate the superconductive order parameter and the scalar potential by a step-like profile, i.e.

$${{\Delta }}({{{{{\boldsymbol{r}}}}}})={{\Theta }}(| x| -L/2){{{\Delta }}}_{0}{e}^{i{\phi }_{0}(x)}\,,$$
(5)
$${\phi }_{0}(x)={{\Theta }}(x){\phi }_{{{{{{\rm{R}}}}}}}+{{\Theta }}(-x){\phi }_{{{{{{\rm{L}}}}}}}\,,$$
(6)
$$U({{{{{\boldsymbol{r}}}}}})=-{\mu }_{0}{{\Theta }}(L/2-| x| )-{U}_{0}{{\Theta }}(| x| -L/2)\,,$$
(7)

where Θ(x) is the Heaviside step function, and U0 ≫ ∣μ0∣.

Fig. 1: Schematic of the device.
figure 1

From bottom to top there are a substrate (blue), a monolayer graphene (gray) and two superconducting electrodes (yellow). The uncovered gray region represents the stripe in normal phase and yellow sides are the regions covered by superconductors. Here, L represents the junction channel, Lx is the lateral size of each superconducting electrode, and W is the length of the device along the invariant direction.

Full size image

Andreev bound states

We are interested in the short junction limit W ≪ ξ ~ ℏvD/Δ0, where ξ is the superconducting coherence length. In general, the spectrum of the D-BdG Hamiltonian consists of Andreev bound states (ABSs) and a continuum of eigenstates. The ABSs are subgap eigenstates, ∣E∣ < Δ0, and they are sensitive to the phase difference between the superconductive sides, ϕ = ϕR − ϕL. They are spatially localized in the central normal phase region, while in the superconductive regions an evanescent tail is present. On the other hand, eigenstates corresponding to the continuum spectrum with eigenergies above the gap, ∣E∣ > Δ0, are spatially delocalized along the entire device57,58. In the short junction limit, eigenstates with energies above the gap do not depend on the phase difference ϕ, thus only ABSs carry the Josephson equilibrium supercurrent. In this work, we neglect the continuum, focusing on the low-energy properties of the GJJs. We project the D-BdG Hamiltonian \({\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D-BdG}}}}}}}\) onto the subspace spanned by the ABSs by the projector \({\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}\), defining the Andreev Hamiltonian as \({\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{A}}}}}}}={\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D-BdG}}}}}}}{\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}\). For a given value of the phase difference ϕ, we express the Andreev Hamiltonian as

$${\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{A}}}}}}}=\mathop{\sum}\limits_{\zeta =\pm }\mathop{\sum}\limits_{k}\epsilon (k,\phi ){\hat{{{\Sigma }}}}_{\zeta ,k}^{z}\,,$$
(8)

where \({\hat{{{\Sigma }}}}_{\zeta ,k}^{z}={\hat{\gamma }}_{+,\zeta ,k}^{{{\dagger}} }{\hat{\gamma }}_{+,\zeta ,k}-{\hat{\gamma }}_{-,\zeta ,k}^{{{\dagger}} }{\hat{\gamma }}_{-,\zeta ,k}\), \({\hat{\gamma }}_{j,\zeta ,k}\) represents the fermionic ABS operator labeled by the subband index j = ± which denotes if the eigenenergy is below or above the Fermi level, the valley index ζ = ± , and the y − component of the momentum k, that is a conserved quantity because the GJJ is invariant along the y direction. The ABSs of the subband which lays below (above) the Fermi level are called lower (upper) ABSs. Each pair of valley index ζ and momentum k identifies a two-level system with energy splitting 2ϵ(k, ϕ), independent of the valley index and given by

$$\epsilon (k,\phi )={{{\Delta }}}_{0}\sqrt{1-\tau (k){\sin }^{2}(\phi /2)}\,,$$
(9)

where \(\tau (k)=({k}_{{{{{{\rm{F}}}}}}}^{2}-{k}^{2})/[{k}_{{{{{{\rm{F}}}}}}}^{2}-{k}^{2}{\cos }^{2}(L\sqrt{{k}_{{{{{{\rm{F}}}}}}}^{2}-{k}^{2}})]\) is the normal state transmission probability, and kF = μ0/(ℏvD) is the Fermi wavenumber41. Within the subspace spanned by the ABSs, we express the Andreev current operator as

$${\hat{I}}_{{{{{{\rm{A}}}}}}}= -\frac{e{{{\Delta }}}_{0}^{2}}{\hslash }\mathop{\sum}\limits_{\zeta =\pm }\mathop{\sum}\limits_{k}\frac{\tau (k)}{\epsilon (k,\phi )}\sin (\phi /2)[\cos (\phi /2){\hat{{{\Sigma }}}}_{\zeta ,k}^{z}\\ -\sqrt{1-\tau (k)}\sin (\phi /2){\hat{{{\Sigma }}}}_{\zeta ,k}^{x}]\,,$$
(10)

where the operators \({\hat{{{\Sigma }}}}_{\zeta ,k}^{z}\) and \({\hat{{{\Sigma }}}}_{\zeta ,k}^{x}={\hat{\gamma }}_{+,\zeta ,k}^{{{\dagger}} }{\hat{\gamma }}_{-,\zeta ,k}+{\hat{\gamma }}_{-,\zeta ,k}^{{{\dagger}} }{\hat{\gamma }}_{+,\zeta ,k}\) are respectively diagonal and off-diagonal in the subband index j. The diagonal term is related to the supercurrents sustained by the respective ABSs, while the off-diagonal term is mainly responsible for current fuctuations59. We note that the supercurrent is suppressed in case of total reflection τ(k) → 0, and the off-diagonal matrix elements of \({\hat{I}}_{{{{{{\rm{A}}}}}}}\) become negligible for total transmission τ(k) → 1. (See Supplementary Note 1 for the wavefunctions solving the stationary D-BdG equation for the subgap ABSs and derivation of \({\hat{I}}_{{{{{{\rm{A}}}}}}}\))

Dilute impurities

We model the dilute ensemble of impurities by the Anderson model42, which has been conveniently applied to describe the effect of disorder in other graphene based devices43,44,45,46. To start with, we consider ND identical impurities, which respect the time reversal symmetry

$${\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D}}}}}}}=\mathop{\sum }\limits_{d=1}^{{N}_{{{{{{\rm{D}}}}}}}}{\hat{{{\Phi }}}}_{d}^{{{\dagger}} }{\epsilon }_{0}{\tau }_{z}{\hat{{{\Phi }}}}_{d}\,,$$
(11)

where \({\hat{{{\Phi }}}}_{d}={[{\hat{c}}_{d,\uparrow }^{{{\dagger}} },{\hat{c}}_{d,\downarrow }]}^{{{\dagger}} }\). The electron tunneling between Andreev states and impurities states is expressed by a potential \({\hat{{{{{{\mathcal{V}}}}}}}}_{{{{{{\rm{D}}}}}}}=\hat{{{{{{\mathcal{V}}}}}}}+{\hat{{{{{{\mathcal{V}}}}}}}}^{{{\dagger}} }\) of the following general form (see Supplementary Note 2)

$$\hat{{{{{{\mathcal{V}}}}}}}=\mathop{\sum }\limits_{d=1}^{{N}_{{{{{{\rm{D}}}}}}}}\mathop{\sum}\limits_{\zeta =\pm }\int {d}^{2}{{{{{\boldsymbol{r}}}}}}{\hat{{{\Phi }}}}_{d}^{{{\dagger}} }{V}_{d,\zeta }({{{{{\boldsymbol{r}}}}}}){\hat{{{\Psi }}}}_{\zeta }({{{{{\boldsymbol{r}}}}}})\,,$$
(12)

and

$${V}_{d,+}({{{{{\boldsymbol{r}}}}}})=\left[\begin{array}{cccc}{v}_{A,d}({{{{{\boldsymbol{r}}}}}})&{v}_{B,d}({{{{{\boldsymbol{r}}}}}})&0&0\\ 0&0&-{v}_{A,d}^{* }({{{{{\boldsymbol{r}}}}}})&-{v}_{B,d}^{* }({{{{{\boldsymbol{r}}}}}})\end{array}\right]\,,$$
(13)
$${V}_{d,-}({{{{{\boldsymbol{r}}}}}})=\left[\begin{array}{cccc}-{v}_{B,d}^{* }({{{{{\boldsymbol{r}}}}}})&{v}_{A,d}^{* }({{{{{\boldsymbol{r}}}}}})&0&0\\ 0&0&{v}_{B,d}({{{{{\boldsymbol{r}}}}}})&-{v}_{A,d}({{{{{\boldsymbol{r}}}}}})\end{array}\right]\,.$$
(14)

The complete Hamiltonian of ABSs and impurities can be written in compact form by the following block decomposition

$${\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{tot}}}}}}}=\left[\begin{array}{cc}{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{A}}}}}}}&{\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}{\hat{{{{{{\mathcal{V}}}}}}}}^{{{\dagger}} }\\ \hat{{{{{{\mathcal{V}}}}}}}{\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}&{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D}}}}}}}\end{array}\right]\,.$$
(15)

We emphasize that the diagonal blocks \({\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{A}}}}}}}\) and \({\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D}}}}}}}\) act onto two different subspaces, the ABSs and impurities subspaces respectively. The off-diagonal blocks connect the two subspaces. The effect of disorder enters in the Green’s function

$${\hat{{{{{{\mathcal{G}}}}}}}}_{{{{{{\rm{tot}}}}}}}({{\Omega }})={({{\Omega }}-{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{tot}}}}}}})}^{-1}\,.$$
(16)

By exploiting the block decomposition of the total Hamiltonian in Eq. (15), it is easy to express the block of the ABS’s Green’s function as follows

$$\hat{{{{{{\mathcal{G}}}}}}}({{\Omega }})={\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}{\hat{{{{{{\mathcal{G}}}}}}}}_{{{{{{\rm{tot}}}}}}}({{\Omega }}){\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}={[{{\Omega }}-{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{eff}}}}}}}]}^{-1}\,,$$
(17)

where the effective Hamiltonian including the disordered ensemble of impurities reads

$${\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{eff}}}}}}}={\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{A}}}}}}}+{\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}{\hat{{{{{{\mathcal{V}}}}}}}}^{{{\dagger}} }{({{\Omega }}-{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D}}}}}}})}^{-1}\hat{{{{{{\mathcal{V}}}}}}}{\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}\,,$$
(18)

and

$${\hat{{{{{{\mathcal{V}}}}}}}}^{{{\dagger}} }{({{\Omega }}-{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D}}}}}}})}^{-1}\hat{{{{{{\mathcal{V}}}}}}}= \int {d}^{2}{{{{{\boldsymbol{r}}}}}}\int {d}^{2}{{{{{{\boldsymbol{r}}}}}}}^{\prime}\mathop{\sum}\limits_{\zeta ,{\zeta }^{\prime}}\mathop{\sum }\limits_{d=1}^{{N}_{{{{{{\rm{D}}}}}}}}{\hat{{{\Psi }}}}_{\zeta }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}}){V}_{d,\zeta }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}})\\ \left(\frac{{{\Omega }}}{{{{\Omega }}}^{2}-{\epsilon }_{0}^{2}}{{\mathbb{1}}}_{\tau }+\frac{{\epsilon }_{0}}{{{{\Omega }}}^{2}-{\epsilon }_{0}^{2}}{\tau }_{z}\right){V}_{d,{\zeta }^{\prime}}({{{{{{\boldsymbol{r}}}}}}}^{\prime}){\hat{{{\Psi }}}}_{{\zeta }^{\prime}}({{{{{{\boldsymbol{r}}}}}}}^{\prime})\,,$$
(19)

for details see Supplementary Note 3.

Starting from a tight-binding description, and assuming that a generic impurity placed at rd in correspondence of a carbon site, acts on the electron system in graphene at atomic scale60, the matrix elements of the short-range interaction potential, which appear in Eqs. (13)-(14), read

$${v}_{\alpha ,d}({{{{{\boldsymbol{r}}}}}})={t}_{0}\sqrt{{A}_{c}}[{m}_{d}{\delta }_{\alpha ,A}+(1-{m}_{d}){\delta }_{\alpha ,B}]{e}^{-i\frac{2\pi }{3}{n}_{d}}\delta ({{{{{\boldsymbol{r}}}}}}-{{{{{{\boldsymbol{r}}}}}}}_{d})\,,$$
(20)

where t0 is a tunneling amplitude, md (nd) is an index taking the values {0, 1} ({ − 1, 0, 1}), and \({A}_{{{{{{\rm{c}}}}}}}=3\sqrt{3}{a}^{2}/2\) is the area of a unit cell61. The md index is related to the presence of the A/B sublattices, while nd index is a consequence of the hexagonal symmetry of the lattice (technical details on the microscopic treatment of the impurities are in Supplementary Note 2). We assume a random distribution of the impurities positions rd, and of the indices (md, nd), this justifies the approximation of homogeneity \({\sum }_{d}\approx [{N}_{D}/(12{L}_{x}W)]{\sum }_{{m}_{d}}{\sum }_{{n}_{d}}\int {d}^{2}{{{{{{\boldsymbol{r}}}}}}}_{d}\), which gives

$${\hat{{{{{{\mathcal{V}}}}}}}}^{{{\dagger}} }{({{\Omega }}-{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D}}}}}}})}^{-1}\hat{{{{{{\mathcal{V}}}}}}}= \frac{{n}_{{{{{{\rm{D}}}}}}}{t}_{0}^{2}}{2}\mathop{\sum}\limits_{\zeta =\pm }\int {d}^{2}{{{{{\boldsymbol{r}}}}}}{\hat{{{\Psi }}}}_{\zeta }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}})\\ \left(\frac{{{\Omega }}}{{{{\Omega }}}^{2}-{\epsilon }_{0}^{2}}{{\mathbb{1}}}_{\tau }+\frac{{\epsilon }_{0}}{{{{\Omega }}}^{2}-{\epsilon }_{0}^{2}}{\tau }_{z}\right){\hat{{{\Psi }}}}_{\zeta }({{{{{\boldsymbol{r}}}}}})\,,$$
(21)

where nD = ND/N, and N = 2WLx/Ac. By projecting this effective potential, Eq. (21), onto the subspace spanned by the ABSs we obtain

$${\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}{\hat{{{{{{\mathcal{V}}}}}}}}^{{{\dagger}} }{({{\Omega }}-{\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{D}}}}}}})}^{-1}\hat{{{{{{\mathcal{V}}}}}}}{\hat{{{{{{\mathcal{P}}}}}}}}_{{{{{{\rm{A}}}}}}}=\frac{{n}_{{{{{{\rm{D}}}}}}}{t}_{0}^{2}{{\Omega }}}{2({{{\Omega }}}^{2}-{\epsilon }_{0}^{2})}\mathop{\sum}\limits_{\zeta =\pm }\mathop{\sum}\limits_{k}{\hat{{{\Sigma }}}}_{\zeta ,k}^{0}\,,$$
(22)

where \({\hat{{{\Sigma }}}}_{\zeta ,k}^{0}={\hat{\gamma }}_{+,\zeta ,k}^{{{\dagger}} }{\hat{\gamma }}_{+,\zeta ,k}+{\hat{\gamma }}_{-,\zeta ,k}^{{{\dagger}} }{\hat{\gamma }}_{-,\zeta ,k}\). Note that, if Anderson impurities are replaced with defects described by localized electrostatic δ-potentials51, within the homogeneity approximation, one finds a potential of the form \(\propto {\sum }_{\zeta = \pm }\int {d}^{2}{{{{{\boldsymbol{r}}}}}}{\hat{{{\Psi }}}}_{\zeta }^{{{\dagger}} }({{{{{\boldsymbol{r}}}}}}){\tau }_{z}{\hat{{{\Psi }}}}_{\zeta }({{{{{\boldsymbol{r}}}}}})\). Projecting this potential onto the subspace spanned by the ABSs, one obtains that these defects have no effect on the ABSs.

If, instead of identical Anderson impurities, we consider a set of impurities with a distribution of energies ρimp(ϵ) = ∑l(ND,l/Nimp)δ(ϵ − ϵl), where Nimp = ∑lND,l is the total number of impurities, the effective Andreev Hamiltonian takes the form

$${\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{eff}}}}}}}={\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{A}}}}}}}+\frac{{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}u({{\Omega }})}{2}\mathop{\sum}\limits_{\zeta =\pm }\mathop{\sum}\limits_{k}{\hat{{{\Sigma }}}}_{\zeta ,k}^{0}\,,$$
(23)

where u(Ω) = Ω∫dϵρimp(ϵ)/(Ω2 − ϵ2), and nimp = Nimp/N. Here, for simplicity the tunneling amplitude t0 between ABSs and all types of impurities is approximated by a constant, independent of the type of impurity. We emphasize that, due to the symmetries of the Hamiltonian, each pair of ABSs hybridizes independently with impurities states and the short-range interaction does not induce mixing of the upper and lower ABSs. In the following sections we will investigate how the spectral features of the entangled system enter the equilibrium supercurrent and its fluctuations.

Equilibrium supercurrent

The equilibrium supercurrent sustained by the GJJ in the short junction regime in the presence of a dilute distribution of impurities takes the following form

$$I(\phi )=\left\langle {\hat{I}}_{{{{{{\rm{A}}}}}}}\right\rangle =-\frac{4e}{\hslash }\int \frac{d{{\Omega }}}{2\pi }\mathop{\sum}\limits_{j=\pm }\mathop{\sum}\limits_{k}j\frac{\partial \epsilon (k,\phi )}{\partial \phi }{n}_{F}({{\Omega }})A(\,j,k,{{\Omega }})\,,$$
(24)

where \({n}_{F}({{\Omega }})={\{1+\exp [{{\Omega }}/({k}_{{{{{{\rm{B}}}}}}}T)]\}}^{-1}\), and

$$A(\,j,k,{{\Omega }}) =-2{{{{{{{\rm{Im}}}}}}}}\left\langle j,\zeta ,k| {\hat{{{{{{{{\mathcal{G}}}}}}}}}}_{{{{{{{{\rm{tot}}}}}}}}}({{\Omega }}+i{0}^{+})| j,\zeta ,k\right\rangle \\ =-2{{{{{{{\rm{Im}}}}}}}}\left\langle j,\zeta ,k| \hat{{{{{{{{\mathcal{G}}}}}}}}}({{\Omega }}+i{0}^{+})| j,\zeta ,k\right\rangle \\ =-2{{{{{{{\rm{Im}}}}}}}}{[{{\Omega }}+i{0}^{+}-j\epsilon (k,\phi )-{n}_{{{{{{{{\rm{imp}}}}}}}}}{t}_{0}^{2}u({{\Omega }}+i{0}^{+})]}^{-1}$$
(25)

is the spectral function, the last term accounts for coupling to the impurities. In the following, we will consider a Lorentzian distribution of their energies \({\rho }_{{{{{{\rm{imp}}}}}}}(\epsilon )=(\gamma /\pi )/[{(\epsilon -{\epsilon }_{0})}^{2}+{\gamma }^{2}]\), which gives \(u({{\Omega }})=({{\Omega }}+i\gamma )/[{({{\Omega }}+i\gamma )}^{2}-{\epsilon }_{0}^{2}]\). There is no dependence on the valley index ζ which introduces a degeneracy factor 2 (details of the equilibrium Green’s functions formalism are given in Supplementary Note 4). In the CPR, the subband index j in front of ABSs eigenenergies ∂ϵ(k, ϕ)/∂ϕ is responsible for the opposite directions of the supercurrent carried by the two ABSs of each pair, for any value of the y-component of the wavevector. For sake of simplicity, in the following discussion we set the central energy of the impurities at the Fermi energy, i.e. ϵ0 = 0. Under this condition the spectral function reads

$$A(\,j,k,{{\Omega }})= -2{{{{{\rm{Im}}}}}}{\left[{{\Omega }}+i{0}^{+}-j\varepsilon (k,\phi )-\frac{{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}}{{{\Omega }}+i\gamma }\right]}^{-1}\\ = -2{{{{{\rm{Im}}}}}}\left[\frac{1}{{{\Omega }}-{{{\Omega }}}_{+,j}(k,\phi )}\frac{{{{\Omega }}}_{+,j}(k,\phi )+i\gamma }{{{{\Omega }}}_{+,j}(k,\phi )-{{{\Omega }}}_{-,j}(k,\phi )}+\frac{1}{{{\Omega }}-{{{\Omega }}}_{-,j}(k,\phi )}\right.\\ \times \left.\frac{{{{\Omega }}}_{-,j}(k,\phi )+i\gamma }{{{{\Omega }}}_{-,j}(k,\phi )-{{{\Omega }}}_{+,j}(k,\phi )}\right]\,,$$
(26)

which has two complex poles

$${{{\Omega }}}_{\lambda ,j}(k,\phi )=\frac{j\epsilon (k,\phi )-i\gamma }{2}+\lambda \sqrt{{\left(\frac{j\epsilon (k,\phi )+i\gamma }{2}\right)}^{2}+\frac{{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}}{2}}\,,$$
(27)

with λ = ± . Symmetry properties and dependence of these complex energies on the system’s physical parameters influence fundamentally the CPR. Here we discuss these properties in detail. Since the system is electron-hole symmetric, the poles in Eq. (27) have the following properties \({{{{{\rm{Re}}}}}}{{{\Omega }}}_{\lambda ,j}(k,\phi )=-{{{{{\rm{Re}}}}}}{{{\Omega }}}_{-\lambda ,-j}(k,\phi )\), and \({{{{{\rm{sgn}}}}}}[{{{{{\rm{Re}}}}}}{{{\Omega }}}_{\lambda ,j}(k,\phi )]=\lambda \). In addition, Ωλ,j(k, ϕ) are even function of k, since the k dependence originates from the transmission probability τ(k), see Eqs. (27) and (9). The dependence on the impurities parameters, in the dilute regime \({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}^{2}\ll 1\), is as follows. The two poles \({{{{{\rm{Re}}}}}}{{{\Omega }}}_{-,-}(k,\phi )\) and \({{{{{\rm{Re}}}}}}{{{\Omega }}}_{+,+}(k,\phi )\) are close to energies − ϵ(k, ϕ) and + ϵ(k, ϕ) of the ABS of the clean GJJ, for any value of the doping level μ0. Instead, \({{{{{\rm{Re}}}}}}{{{\Omega }}}_{+,-}(k,\phi )\) and \({{{{{\rm{Re}}}}}}{{{\Omega }}}_{-,+}(k,\phi )\) are close to the central energy ϵ0 of the impurities energy distribution which we have fixed at the Fermi energy. The width of the impurities energies distribution, γ > 0, determines the finite lifetime of the resonances at \({{{{{\rm{Re}}}}}}{{{\Omega }}}_{\lambda ,j}(k,\phi )\). For any γ, the hybridization between the ABSs and the impurity states is stronger in correspondence of the component k such that τ(k) ~ 1. Indeed, in proximity of the total transmission, the dispersion relation ϵ(k, ϕ) moves close to the Fermi energy, where the distribution ρimp(ϵ) is centered. In the limiting case γ → ∞, for given j and k, the spectral function tends to a single Dirac delta function at the ABSs energies, i.e. A( j, k, Ω) → − 2πδ(Ω − jϵ(k, ϕ)), corresponding to the clean GJJ. Figure 2a sketches a couple of subgap levels ± ϵ(k, ϕ) for a generic y-component of the wavevector k and superconductive phase difference ϕ, in the clean limit (γ → ∞). Gray (black) level represents the lower (upper) ABSs, gray (black) horizontal arrow indicates the direction of the corresponding supercurrent contributions. The Fermi-Dirac distribution on the left-hand side of Fig. 2a evidences that at low temperatures, kBT ≪ Δ0, only the lower ABS is occupied thus only its supercurrent contribution is active. In the opposite limit γ → 0+, the poles in Eq. (27) reduce to the exact eigenenergies of the total Hamiltonian \({\hat{{{{{{\mathcal{H}}}}}}}}_{{{{{{\rm{tot}}}}}}}\), namely \({{{\Omega }}}_{\lambda ,j}(k,\phi )\to j\epsilon (k,\phi )/2+\lambda \sqrt{\epsilon {(k,\phi )}^{2}/4+{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/2}\). The poles labeled by λ = − (λ = + ) lay energetically below (above) the Fermi energy. For given j and k, the spectral function becomes a weighted sum of two Dirac delta functions centered at those eigenenergies, A( j, k, Ω) → − 2π∑λ=±δ(Ω − Ωλ,j(k, ϕ))Ωλ,j(k, ϕ)/[Ωλ,j(k, ϕ) − Ω−λ,j(k, ϕ)]. Figure 2b shows the four subgap levels for γ → 0+, for a generic y-component of the wavevector k and superconductive phase difference ϕ. Here, the states associated with the gray (black) levels Ωλ,− (Ωλ,+) labeled by the subband index j = − ( j = + ) have a finite overlap on the lower (upper) and zero overlap on the upper (lower) ABSs of the clean GJJ, and they carry a supercurrent contribution ∝ − ∂ϵ(k, ϕ)/∂ϕ ( ∝ ∂ϵ(k, ϕ)/∂ϕ). By comparing the Fermi-Dirac distribution at low temperature, kBT ≪ Δ0, with the structure of levels, one sees that the occupied states are those labeled by (λ = − , j = − ) and (λ = − , j = + ). They have finite overlap with the lower and upper ABS respectively. Therefore, they carry supercurrent contributions in opposite directions. In other words, the presence of impurities activates the supercurrent contribution of the upper ABS also at zero temperature, reducing the total supercurrent contribution for each k. This compensating effect on the supercurrent is largest when the hybridization is maximal, namely for k such that τ(k) ~ 1. Figure 3a, b show the CPR at zero temperature, obtained by using Eq. (24), with \({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}=0.1\), for different values of γ, at zero doping, μ0 = 0 (Fig. 3a) and at the finite doping level μ0 = 5ℏvD/L (Fig. 3b). In both cases we observe that in the clean limit (γ → ∞) the CPR shows the largest skewness and critical current. For finite values of γ, the hybridization between the ABSs and the impurities sets in. As a consequence, both skewness and critical current reduce. This effect can explained by observing that the modes mainly affected by the presence of disorder are the high transparent ones, τ(k) ~ 1. These modes are also the ones largely responsible for skewness of the clean GJJ giving a supercurrent contribution \(\propto \partial \epsilon (k,\phi )/\partial \phi \sim {{{\Delta }}}_{0}\sin (\phi /2)\), whereas modes with low transparency imply the standard sinusoidal dependence \(\propto \sin (\phi )\). The phase difference where the supercurrent is maximal \({\phi }_{\max }\), depends on γ and on the doping level μ0. In particular, we denote with ϕ* the value in the clean limit \({\phi }^{* }={\lim }_{\gamma \to \infty }{\phi }_{\max }\). The effect of the impurities energy distribution, γ, on the maximal supercurrent is illustrated in Fig. 3c, d where we plot the supercurrent evaluated at ϕ = ϕ*, for two different values of the doping. In both cases we observe a monotonic increase of the supercurrent with increasing γ, the supercurrent is minimal for the Dirac delta energy distribution, i.e. γ → 0+.

Fig. 2: Scheme of the subgap levels for a generic y-component of the wavevector k, and superconductive phase difference ϕ.
figure 2

a The clean limit (γ → ∞), where the effect of the impurities vanishes. Gray (black) level represent the lower (upper) Andreev bound state (ABS), the gray (black) horizontal arrow sketches the direction of the supercurrent contribution ∝ − ∂ϵ(k, ϕ)/∂ϕ ( ∝ ∂ϵ(k, ϕ)/∂ϕ), and the red vertical dashed arrow denotes the possible transition. On the left side, there is the Fermi-Dirac distribution at low temperature, kBT ≪ Δ0, which shows that lower (upper) ABS is occupied (empty). b The limit γ → 0+. Gray (black) levels Ωλ,− (Ωλ,+) are associated to states which have a finite overlap on the lower (upper) ABSs of the clean graphene Josephson Junction (GJJ), and zero overlap on the upper (lower) ABSs of the clean GJJ. The colored vertical arrows represent the possible transitions between two subgap levels, arrows represented with the same color correspond to the same transition energy. On the left side, there is the Fermi-Dirac distribution at low temperature, by comparing this with the vertical transitions, one can infer that the transitions between ABSs labeled with opposite j indices and identical λ indices (green dashed lines) are suppressed by the Pauli blocking.

Full size image
Fig. 3: Current-phase relation at zero temperature.
figure 3

Here, the impurity density is set at \({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}^{2}=0.1\). Panels a and b show the supercurrent as a function of the phase ϕ in units of \({I}_{{{{{{\rm{c}}}}}}}^{* }=e{{{\Delta }}}_{0}W/(\hslash L)\), and the Fermi energy is set at μ0 = 0 and μ0 = 5ħvD/L, respectively. In both panels one has γ → 0+ (black dashed lines) γ = 10−2Δ0 (yellow solid lines), γ = 10−1Δ0 (red solid lines), γ = Δ0 (green solid lines), γ = 10Δ0 (blue solid lines), γ → ∞ (cyan dashed lines, i.e. the clean limit). The dotted gray vertical line denotes ϕ*, which is the superconductive phase difference such that \(I({\phi }^{* })=\mathop{\max }\limits_{\phi }I(\phi )\) in the clean GJJ, in particular ϕ* = 0.63π for μ0 = 0, and ϕ* = 0.68π for μ0 = 5ħvD/L. Panels c and d show supercurrent I(ϕ*) (red solid line), at zero temperature, as a function of γ, and the Fermi energy is set at μ0 = 0 and μ0 = 5ħvD/L, respectively. In panels c and d, the horizontal lines refer to two limiting cases: I(ϕ*), at zero temperature, in the clean limit (horizontal cyan dashed line) and in the presence of single-energy impurities (horizontal black dashed line), i.e. γ → 0+.

Full size image

According to the D-BdG theory, the critical current in short ballistic GJJ decreases monotonically with temperature41. Whereas this qualitative trend has been observed in recent experiments, smaller values of the critical current than one at zero temperature accompanied by unexplained irregularities have also been reported22,32,33,62. Similar discrepancies have been observed also for the temperature dependence of the skewness33. Here, we discuss the temperature dependence of the critical current and skewness resulting from the hybridization of ABSs with impurities which provide an alternative mechanism for the reported deviations. Figure 4 shows the critical current, panels a) and b), and the skewness defined as \(S=2{\phi }_{\max }/\pi -1\), panels c) and d), as a function of temperature (solid lines), compared with the respective values at zero temperature (horizontal dashed lines). Figure 4a, c refer to the undoped case, while Fig. 4b, d refer to the doped case with μ0 = 5ℏvD/L. The temperature dependencies in the clean limit, γ → ∞, derive form the thermal population of pairs of ABSs carrying opposite supercurrents inducing a monotonic decrease of the critical current with temperature (cyan lines). Moreover, for any given phase difference ϕ, thermal activation of the upper Andreev levels is mainly effective for wavevector components k corresponding to large transmission τ(k), since the corresponding energies ϵ(k, ϕ) are closer to the Fermi energy. These modes are also responsible for the forward skewness of the CPR. Therefore, in the clean limit, S diminishes with increasing temperature, as shown in Fig. 4c and d) (cyan lines). Instead the presence of single-energy impurities (black lines), i.e. γ → 0+, both the critical current and skewness display a nonmonotonic temperature dependence. This behavior can be understood considering the thermal population of hybridized Andreev-impurities energies sketched in Fig. 2b. For small temperatures \({k}_{{{{{{\rm{B}}}}}}}T\lesssim {n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}\) the only levels above the Fermi energy which become populated are levels (λ = + , j = − ). They carry a supercurrent in the same direction of the dominant contribution due to the lowest hybridized level (λ = − , j = − ), while it is opposite to the contribution of the level (λ = − , j = + ). In other words, the thermal activation of supercurrent contributions of the hybridized levels (λ = + , j = − ) suppresses the effect of the disorder and induces an increase both of the critical current and the forward-skewness. For larger temperatures, such that \({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0} < {k}_{{{{{{\rm{B}}}}}}}T < {{{\Delta }}}_{0}\), for each k, the supercurrent contributions of the levels (λ = − , j = + ) and (λ = + , j = − ) are comparable and cancel each other. On the other side the population of the topmost level (λ = + , j = + ) becomes significant and contributes with a supercurrent summing up to the one due to the hybridized ground state. As a consequence, the thermal trend becomes one observed in the clean limit (cyan lines). At these range of temperatures, critical current and skewness are decreasing. Finally, the red line in Fig. 4 shows the temperature dependence of the critical current and the skewness in the presence of a finite width γ = Δ0/10, which are qualitatively similar to the case with a single-energy (cyan lines), but the finite width \(\gamma \sim {n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}\), makes the increasing dependencies of the temperature less visible. Thus hybridization between ABSs and impurities originates smaller critical current and skewness than the clean limit expectation based on the BdG theory, but nonmonotonic temperature dependence.

Fig. 4: Critical current and skewness S as a function temperature.
figure 4

a, b The critical current, in units of \({I}_{{{{{{\rm{c}}}}}}}^{* }\), and the Fermi energy is set at μ0 = 0 and μ0 = 5ħvD/L, respectively. Panels c and d show the skewness, and the Fermi energy is set at μ0 = 0 and μ0 = 5ħvD/L, respectively. For both quantities, the temperature dependence is displayed in solid line, and compared with the respective value at zero temperature (horizontal dashed line). In all panels, one has γ → 0+ (black lines), γ = 10−1Δ0 (red lines), γ → ∞ (cyan lines), the temperature dependence of the order parameter Δ0 is neglected, and the impurity density is set at \({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}^{2}=0.1\).

Full size image

Supercurrent noise

A convenient quantity to identify spectral features of the hybridized system is the supercurrent noise spectrum. As a difference with the CPR, which reflects the overall effect of the hybridized system, the supercurrent noise spectrum directly probes the possible absorption/emission frequencies because of the fluctuation-dissipation theorem 63. In particular, for ω > 0, \({{{{{\mathcal{S}}}}}}(\omega )\) gives the absorption spectrum. Therefore, the supercurrent power spectrum can be used for a spectroscopic analysis of the source of disorder. For fixed phase difference ϕ, the equilibrium supercurrent fluctuations are expressed by noise power spectral density

$${{{{{\mathcal{S}}}}}}(\omega )=\int\nolimits_{-\infty }^{\infty }dt{e}^{i\omega t}[\langle {\hat{I}}_{A}(t){\hat{I}}_{A}(0)\rangle -\langle {\hat{I}}_{A}(t)\rangle \langle {\hat{I}}_{A}(0)\rangle ]\,,$$
(28)

where 〈 ⋯  〉 denotes the thermal equilibrium average of the entire system and the Andreev current operator \({\hat{I}}_{A}\) defined in Eq. (10). After algebraic manipulations (shown in detail in Supplementary Note 4), we obtain

$${{{{{\mathcal{S}}}}}}(\omega )= \ \hslash \mathop{\sum}\limits_{j=\pm ,{j}^{\prime}=\pm }\mathop{\sum}\limits_{\zeta =\pm }\mathop{\sum}\limits_{k}\int \frac{d{{\Omega }}}{2\pi }{n}_{F}({{\Omega }})[1-{n}_{F}({{\Omega }}+\hslash \omega )]| \left\langle j,\zeta ,k| {\hat{I}}_{{{{{{\rm{A}}}}}}}| {j}^{\prime},\zeta ,k\right\rangle {| }^{2}\\ \times A(\,j,k,{{\Omega }})A(\,{j}^{\prime},k,{{\Omega }}+\hslash \omega )\,,$$
(29)

where the spectral function is given by Eq. (25). Figure 5a, b show \({{{{{\mathcal{S}}}}}}(\omega )\) evaluated at ϕ = ϕ* for zero and finite doping and different widths γ of the impurities energy distribution, at T = 10−2Δ0/kB. In the clean limit, spectral features are present only in the frequency domain \(2{{{\Delta }}}_{0}| \cos ({\phi }^{* }/2)| \le \hslash \omega \le 2{{{\Delta }}}_{0}\) (gray-shaded region). The first qualitative feature of the presence of the dilute impurities is the appearance of additional spectral features at smaller frequencies (white region).

Fig. 5: Supercurrent power spectrum.
figure 5

Panels (a) and (b) show \({{{{{\mathcal{S}}}}}}(\omega )\), in units of \(e{I}_{{{{{{\rm{c}}}}}}}^{* }\) at ϕ = ϕ*, as a function of frequency ω, and the Fermi energy is set at μ0 = 0 and μ0 = 5ħvD/L, respectively. In both panels a and b, one has T = 10−2Δ0/kB, \({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}^{2}=0.1\), γ = 0+ (black lines) γ = 10−2Δ0 (yellow lines), γ = 10−1Δ0 (red lines), γ = Δ0 (green lines), γ = 10Δ0 (blue lines), and γ = ∞ (cyan lines). The shaded region is the frequency domain where the supercurrent power spectrum is non-zero in a clean GJJ. Panels c and d show the static supercurrent power spectrum \({{{{{\mathcal{S}}}}}}(0)\), in units of \(e{I}_{{{{{{\rm{c}}}}}}}^{* }\) at ϕ = ϕ*, as a function of temperature, in a log-log scale, and the Fermi energy is set at μ0 = 0 and μ0 = 5ħvD/L, respectively. In both panels c and d, one has γ = 10−2Δ0 (yellow circles), γ = 10−1Δ0 (red circles), γ = Δ0 (green circles), γ = 10Δ0 (blue circles), each colored solid line represents the corresponding low-temperature linear behavior by Eq. (30). The temperature dependence of the order parameter Δ0 is neglected, and the impurity density is set at \({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/{{{\Delta }}}_{0}^{2}=0.1\).

Full size image

The supercurrent power spectrum can be explained in terms of the transitions indicated in the scheme of Fig. 2b. For a generic y-component of the wavevector k, there are four possible energies indicated by the colored dashed vertical arrows. The transition with largest energy (red dashed arrow) links the levels labeled by (λ = − , j = − ) and (λ = + , j = + ), the transition energy lays in the interval Δ0 < ℏω < 2Δ0. The two levels involved collapse respectively to the lower and upper Andreev level by turning off the interaction, t0 → 0. The transitions at intermediate energies, i.e. ℏω ≲ Δ0, can be classified in two types, the first one is (λ = − , j) → (λ = + , j) (blue dashed) and the second one (λ, j = − ) → (λ, j = + ) (green dashed). The latter class of transitions (green dashed) are strongly suppressed by the Pauli blocking. Finally, there is a class of very low energy transitions, ℏω ≪ Δ0, (orange dashed) between the levels (λ = + , j = − ) and (λ = − , j = + ). By turning off the interaction these two states have no overlap with the ABSs, so they do not contribute to the supercurrent.

In order to understand the origin of the main features of the supercurrent power spectrum, we first focus on the case with γ → 0+. Here, for any generic ϕ, the supercurrent power spectrum shows several square root divergences, each singularity occurs at an energy ℏω that corresponds to an extremum of the energy difference between the two subgap levels involved in the transition \({{{\Omega }}}_{\lambda ,j}(k,\phi )-{{{\Omega }}}_{{\lambda }^{\prime},{j}^{\prime}}(k,\phi )\). Since ∂Ωλ,j(k, ϕ)/∂k = (∂Ωλ,j(k, ϕ)/∂τ(k))(∂τ(k)/∂k), the extrema of \({{{\Omega }}}_{\lambda ,j}(k,\phi )-{{{\Omega }}}_{{\lambda }^{\prime},{j}^{\prime}}(k,\phi )\) occur at the wavenumber k where also the transmission probability τ(k) is extreme. In fact τ(k) is a bounded even function (0 ≤ τ(k) ≤ 1), which takes its maximum value τ(k) = 1 (total transmission), for k = 0 (Klein tunneling) and for \(k=\pm \sqrt{{k}_{{{{{{\rm{F}}}}}}}^{2}-{(\pi n)}^{2}/{L}^{2}}\) (stationary wave condition). The number of wavevector component k which fulfills the stationary wave condition is 2Int(kFL/π), and it depends on the doping level μ0. In correspondence of the values of k which give total transmission the energy differences are equal to \({{{\Omega }}}_{\lambda ,j}(0,\phi )-{{{\Omega }}}_{{\lambda }^{\prime},{j}^{\prime}}(0,\phi )\). In between the 2Int(kFL/π) + 1 values of k where τ(k) = 1, the transmission probability τ(k) takes 2Int(kFL/π) local minima for k values solving the transcendental equation \({k}_{{{{{{\rm{F}}}}}}}^{2}\sin (L\sqrt{{k}_{{{{{{\rm{F}}}}}}}^{2}-{k}^{2}})=L{k}^{2}\sqrt{{k}_{{{{{{\rm{F}}}}}}}^{2}-{k}^{2}}\cos (L\sqrt{{k}_{{{{{{\rm{F}}}}}}}^{2}-{k}^{2}})\), such that ∣k∣ < kF. By analyzing the supercurrent power spectrum \({{{{{\mathcal{S}}}}}}(\omega )\), we see that if the two subgap levels involved (λ, j) and \(({\lambda }^{\prime},{j}^{\prime})\) are such that \({j}^{\prime}=j\) then square root divergences may appear in correspondence of both a global maximum and a local minimum of the transmission probability. Thus, there are Int(kFL/π) square root divergences associated with the minima and a further square root divergence associated with total transmission. On the other hand, if the two subgap levels involved are (λ, j) and \(({\lambda }^{\prime},{j}^{\prime})\) such that \({j}^{\prime}=-j\) then the square root divergences appear in correspondence only of a local minimum of the transmission probability, since the matrix element \(\left\langle j,\zeta ,k| {\hat{I}}_{{{{{{\rm{A}}}}}}}| -j,\zeta ,k\right\rangle \) vanishes for k such that τ(k) = 1, independently of the valley index ζ. Thus, for \({j}^{\prime}=-j\) there are Int(kFL/π) square root divergences. At a finite γ > 0, the exact levels described above are replaced by resonances with a finite lifetime, see Eq. (27). The square root divergences become resonances and the supercurrent power spectrum is a regular function of the frequency. For γ → ∞, the levels (λ = − , j = − ) and (λ = + , j = + ) collapse to the Andreev levels of the clean GJJ that have an infinite lifetime, whereas the levels (λ = − , j = + ) and (λ = + , j = − ) become ill-defined resonances with a vanishing lifetime. For γ ≫ Δ0, the supercurrent power spectrum tends to the profile of a clean GJJ (see cyan lines in Fig. 5a,b), where there is no signal in the low-frequency domain ℏω ≲ Δ0 (see white regions in Fig. 5a, b). In Fig. 5a, which refers to the undoped case, one sees that for γ → 0+ (black line) the supercurrent power spectrum shows a single square root divergence placed at the intermediate energy \(\hslash \omega =\sqrt{{{{\Delta }}}_{0}^{2}{\cos }^{2}({\phi }^{* })+2{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}}\approx 0.71{{{\Delta }}}_{0}\), while in the clean limit γ → ∞ (cyan line) the supercurrent power spectrum is a smooth function. The case of finite doping is shown in Fig. 5b, where μ0 = 5ℏvD/L. In the limiting case γ → 0+ (black line) the supercurrent power spectrum shows four square root divergences. In particular, there is a divergence in the shaded region \(\hslash \omega =\epsilon (\bar{k},{\phi }^{* })+\sqrt{\epsilon {(\bar{k},{\phi }^{* })}^{2}+2{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}}\approx 1.43{{{\Delta }}}_{0}\) (where the value \(\bar{k}\approx 2.9/L\) solves the transcendental equation shown above), there are two divergences in the intermediate energies, i.e. \(\hslash \omega =\sqrt{\epsilon {(\bar{k},{\phi }^{* })}^{2}+2{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}}\approx 0.78{{{\Delta }}}_{0}\) and \(\hslash \omega =\sqrt{{{{\Delta }}}_{0}^{2}{\cos }^{2}({\phi }^{* })+2{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}}\approx 0.71{{{\Delta }}}_{0}\), and a further square root divergence appears at low energy \(\hslash \omega =-\epsilon (\bar{k},{\phi }^{* })+\sqrt{\epsilon {(\bar{k},{\phi }^{* })}^{2}+2{n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}}\approx 0.14{{{\Delta }}}_{0}\). In the clean limit γ → ∞ (cyan line), only the square root divergence in shaded region holds, and it is red-shifted at \(\hslash \omega =2\epsilon (\bar{k},{\phi }^{* })\approx 1.29{{{\Delta }}}_{0}\).

We note that, because of disorder, the zero frequency current noise reduces to the linear thermal noise behavior for sufficiently small temperatures. The slope of the linear dependence can be related to the impurity energy distribution. Indeed, the limit kBT ≪ γ, Δ0, one has

$${{{{{\mathcal{S}}}}}}(0) = \,\hslash \mathop{\sum}\limits_{j=\pm ,{j}^{\prime}=\pm }\mathop{\sum}\limits_{\zeta =\pm }\mathop{\sum}\limits_{k}\int \frac{d{{\Omega }}}{2\pi }\frac{1}{4{\cosh }^{2}(\frac{{{\Omega }}}{2{k}_{{{{{{\rm{B}}}}}}}T})}| \left\langle j,\zeta ,k| {\hat{I}}_{{{{{{\rm{A}}}}}}}| {j}^{\prime},\zeta ,k\right\rangle {| }^{2}\\ \times A(j,k,{{\Omega }})A({j}^{\prime},k,{{\Omega }})\\ \approx \left[\frac{\hslash }{2\pi }\mathop{\sum}\limits_{j=\pm ,{j}^{\prime}=\pm }\mathop{\sum}\limits_{\zeta =\pm }\mathop{\sum}\limits_{k}| \left\langle j,\zeta ,k| {\hat{I}}_{{{{{{\rm{A}}}}}}}| {j}^{\prime},\zeta ,k\right\rangle {| }^{2}A(j,k,0)A({j}^{\prime},k,0)\right]{k}_{{{{{{\rm{B}}}}}}}T\\ = \,{\sin }^{2}(\phi /2)\left\{\frac{8\pi {e}^{2}{{{\Delta }}}_{0}^{2}}{\hslash }\mathop{\sum}\limits_{k}B{\left[\frac{\tau (k)}{\pi }\frac{({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2})/(2\gamma )}{{\epsilon }^{2}(k,\phi )+{({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2})}^{2}/{(2\gamma )}^{2}}\right]}^{2}\right\}{k}_{{{{{{\rm{B}}}}}}}T\,,$$
(30)

where we have approximated \(1/[4{\cosh }^{2}(\frac{{{\Omega }}}{2{k}_{{{{{{\rm{B}}}}}}}T})]\to {k}_{{{{{{\rm{B}}}}}}}T\delta ({{\Omega }})\). We have assumed that any spectral function A( j, k, Ω) is smooth, thus it can be approximated as \(A(\,j,k,0)=({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2}/\gamma )/[{\epsilon }^{2}(k,\phi )+{({n}_{{{{{{\rm{imp}}}}}}}{t}_{0}^{2})}^{2}/{(2\gamma )}^{2}]\). Note that the slope of the linear temperature behavior depends on the width γ, in particular it vanishes in both limits γ → 0+ and γ → ∞. The dependence on γ of \({{{{{\mathcal{S}}}}}}(0)\) is shown in Fig. 5c, d for zero and finite doping, respectively.

Conclusion

In this work we have investigated the modifications of the Andreev spectrum in a short ballistic GJJ due to the hybridization with a dilute set of non-magnetic impurities homogeneously distributed below the entire device. The ABSs are described by a D-BdG model. Within this formalism, we considered a set of impurities described by the Anderson model, and with a Lorentzian distribution of energies about the Fermi energy with a width γ. We remark that our analytic formalism can be readily applied also to other distributions of impurity energy levels. Here, we have obtained that, both with undoped and doped normal region, for any value of the energy width γ, the dilute ensemble of impurities causes a reduction of the critical current and, more prominently, of the skewness the current-phase relation. In an impurity-free GJJ the current phase relation is skewed by very high transmittance channels30,41. Here, we found that exactly these ABSs, labeled by k such that τ(k) ~ 1, are mainly hybridized with the impurity levels. This phenomenon leads to a reduction of the supercurrent contributions that induce the skewness of the CPR. Moreover, we found that thermal excitations can inhibit this mechanism due to the population of higher energy hybridized ABS-impurity states carrying opposite supercurrent. This determines a counterintuitive increase of both the critical current and the skewness around a range of low temperatures, such that \({k}_{{{{{{\rm{B}}}}}}}T \sim {t}_{0}^{2}{n}_{{{{{{\rm{imp}}}}}}}/{{{\Delta }}}_{0}\). Within our formalism, we have also derived the power spectrum of the supercurrent both with undoped and doped normal region. This quantity turns out to be a powerful spectroscopic tool of the hybridized spectrum. In particular, for an impurity-free GJJ, we find a low-frequency domain, \(0\le \omega \, < \,2{{{\Delta }}}_{0}| \cos (\phi /2)| /\hslash \), where the power spectrum of the supercurrent is vanishing, and it is tunable by the superconductive phase difference ϕ. Because of the hybridization of the ABSs with impurity levels, resonances appear in the low-frequency region whose position and number have been predicted. Moreover, we have connected all the peaks of the power spectrum to features of the transmittance probability τ(k). Finally, we have seen that at very low temperatures (kBT ≪ Δ0, γ), the power spectrum of the supercurrent displays a linear dependence on the temperature, with a slope related to the spectral weight at the Fermi level, which vanishes both for γ → 0+ and γ → ∞. These results highlight the extraordinary potentialities of the supercurrent in a GJJ and its equilibrium noise as probes of impurities accidentally present even in clean van der Waals heterostructures. Future work will be devoted to study the effect of Anderson impurities on GJJ in the long and intermediate junction limits, by taking into account the Andreev continuum which cannot be disregarded.

Methods

The integration above has been performed with Python numerical routines, in particular we have used the free and open-source library Scipy64.