Main

A variety of important physical phenomena require a non-perturbative understanding of quantum field theory. This includes solitonic waves, but also several deeply quantum mechanical phenomena like the confinement of quarks in quantum chromodynamics. While many non-perturbative problems are notably hard to compute, some are within reach and yield accurate predictions. Among the most striking non-perturbative predictions of quantum field theory is the instability of an electric field under the creation of particle–antiparticle pairs. The Schwinger effect (SE) states that pairs are created, out of a false vacuum with an electric field, to minimize energy. It is a simple yet non-trivial and non-perturbative prediction of quantum electrodynamics1,2,3,4. The pair-creation rate w per unit d-dimensional volume writes as the n-th order perturbation development \(w(E)\propto {\sum }_{n\ge 1}{\left(\frac{E}{n}\right)}^{\frac{d+1}{2}}{e}^{-\pi \frac{n{E}_{{\mathrm{S}}}}{E}}\) (see prefactors in ref. 4 and Supplementary Discussion Section I), where E is the electric field and \({E}_{\mathrm{S}}={{{\Delta }}}_{\mathrm{S}}^{2}/e\hslash c=1.32\ 1{0}^{18}\ {{{\rm{V{m}}}^{-1}}}\) (with e the elementary charge, c the speed of light and ℏ the reduced Planck constant), called the Schwinger field, corresponds to the electron-mass energy ΔS = mc2 = 511 keV, 2ΔS being the threshold energy needed to create an electron–positron pair at a characteristic length-scale given by the Compton length λC = hc/ΔS. Large efforts have been devoted to produce such extremely strong electric fields in the laboratory to check this prediction explicitly5. Unfortunately, the attempts to observe the SE in the last decades have not yet met with success.

With the advent of graphene, a novel playground for the study of relativistic effects has been opened in the completely different framework of condensed matter physics6,7,8,9,10,11. In such a mesoscopic variant, electron–positron pairs are substituted by electron–hole pairs, speed of light c by the Fermi velocity vF ≃ 106 m s−1, and the rest energy by a bandgap (Interpretation of the Schwinger voltage). While graphene is intrinsically gapless, we show below that an effective gap is provided for one-dimensional (1D) transport. Our experiments point out that this effective energy scale ΔS is less than 0.2 eV, in which case the Schwinger fields \({E}_{\mathrm{S}}={{{\Delta }}}_{\mathrm{S}}^{2}/e\hslash {v}_{\mathrm{F}}\lesssim 6.1{0}^{7}\ {{{\rm{V{m}}}^{-1}}}\) are experimentally accessible, while remaining smaller than breakdown fields of the embedding hexagonal boron nitride (hBN) dielectric12. Neutral single-layer graphene, considered in refs. 8,9,10, corresponds to the gapless two-dimensional (2D) limit where ES = 0 so that the 2D Schwinger rate reduces to a superlinear \(J\propto {E}^{\frac{3}{2}}\) current density–field relation. This power law is indeed observed in single-layer graphene13, but alternatively interpreted in terms of Zener tunnelling. More recently, the same dependence has been reported in twisted bilayer graphene heterostructures, where the SE develops on top of a saturation current14, with a sign reversal of the Hall effect as an additional signature. Our experiment is motivated by the study of transport in bottom-gated (gate voltage Vg) single-layer graphene field-effect transistors, where pair creation is subject to a finite breakdown field at large doping. Most saliently, our experiment investigates the large bias regime where a giant Klein collimation establishes a quasi-1D transport characterized by a transport gap, and where the SE is accurately fitted by the 1D pair-creation rate with a finite Schwinger bandgap ΔS. It develops over a ballistic junction of length Λ < 1 μm set by the gate dielectric thickness (Interpretation of the Schwinger voltage), which builds up at current saturation. This saturation is due to a large drain-source voltage V that reduces the drain-gate voltage V − Vg, inducing a suppression of the electronic density nd at the drain below the channel density. The latter is given by the density at the source ns (and the chemical potential at the source μs), itself set by the gate voltage Vg. This so-called pinchoff generates a peak effect with a large local electric field prone to the ignition of Schwinger-pair creation, which shows up as the breakdown of the giant Klein collimation. As this situation differs from the canonical vacuum breakdown, we distinctively call it the Klein-Schwinger effect (KSE).

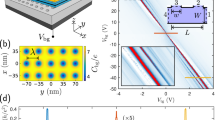
Let us detail theoretical prediction for the mesoscopic 1D SE, as sketched in Fig. 1a. Pair creation is monitored by the current generated across the junction upon dissociation in the large electric field. Starting from the 1D Schwinger rate in equation (1), and taking into account the factor 2 for pair dissociation, as well as spin and valley degeneracies gs and gv, the pair current IS and differential conductance GS can be written as:

$${w}_{1d}=\frac{2e}{h}E\mathop{\sum }\limits_{n=1}^{\infty }\frac{{e}^{-n\pi \frac{{E}_{\mathrm{S}}}{E}}}{n}=\frac{2e}{h}E\ln \left(\frac{1}{1-{e}^{-\pi \frac{{E}_{\mathrm{S}}}{E}}}\right)$$
(1)
$${I}_{\mathrm{S}}=4V\ln \left(\frac{1}{1-{e}^{-\pi \frac{{V}_{\mathrm{S}}}{V}}}\right)\times {g}_{\mathrm{s}}{g}_{\mathrm{v}}\frac{{e}^{2}}{h}\qquad {{{\rm{with}}}}\qquad {V}_{\mathrm{S}}={{\Lambda }}{E}_{\mathrm{S}}={{\Lambda }}\frac{{{{\Delta }}}_{\mathrm{S}}^{2}}{e\hslash {v}_{\mathrm{F}}}$$
(2)
$${G}_{\mathrm{S}}=4\left[\frac{\pi \frac{{V}_{\mathrm{S}}}{V}}{{e}^{\pi \frac{{V}_{\mathrm{S}}}{V}}-1}+\ln \left(\frac{1}{1-{e}^{-\pi \frac{{V}_{\mathrm{S}}}{V}}}\right)\right]\times {g}_{\mathrm{s}}{g}_{\mathrm{v}}\frac{{e}^{2}}{h}$$
(3)
$$\approx 1.20\left(\frac{V}{0.62{V}_{\mathrm{S}}}-1\right)\times {g}_{\mathrm{s}}{g}_{\mathrm{v}}\frac{{e}^{2}}{h}\qquad \qquad ({V}_{\mathrm{C}}=0.62{V}_{\mathrm{S}}\lesssim V\lesssim 2{V}_{\mathrm{S}})$$
(4)

where V is the total bias and VS the Schwinger voltage, product of the Schwinger field \({E}_{\mathrm{S}}=\frac{{{{\Delta }}}_{\mathrm{S}}^{2}}{e\hslash {v}_{\mathrm{F}}}\) by the length Λ of the pair-creation domain. The differential conductance (equation 3) possesses an inflection point at V = 1.22 VS, supporting an affine approximation given by equation (4) and characterized by a critical voltage VC = 0.62 VS and a zero-bias extrapolate − G0 stemming from a quantized pair conductance \({G}_{0}/{g}_{\mathrm{s}}{g}_{\mathrm{v}}=2\times 0.60\ \frac{{e}^{2}}{h}\) (per spin and valley), with the prefactor 2 as a tag for pair dissociation. The Schwinger conductance (equation 3) is plotted in Fig. 1b for 1D graphene, where gs = gv = 2 (solid red line), including the affine approximation (dotted black line for equation (4)) with G0 = 0.186 mS. Also shown in the figure is the conductance \({G}_{\mathrm{S}}^{* }=4{g}_{\mathrm{s}}{g}_{\mathrm{v}}\frac{{e}^{2}}{h}\left(1+\pi \frac{{V}_{\mathrm{S}}}{V}\right){e}^{-\pi \frac{{V}_{\mathrm{S}}}{V}}\) (dash-dotted blue line) calculated with the Schwinger rate (equation 1) truncated to its first n = 1 term; the truncated variant deviates from the full Schwinger conductance for V/VS ≳ 1.5 and GS ≳ 0.2 mS. Comparison of massive 1D and 2D Schwinger conductances, as well as that of three-dimensional Schwinger and the non-relativistic Fowler–Nordheim mechanism, are contrasted as discussed in Supplementary Discussion Section I.

Fig. 1: Mesoscopic SE for massive 1D Dirac fermions.
figure 1

a, Sketch of the 1D SE across a graphene junction of length Λ and gap ΔS, defining a Schwinger field \({E}_{\mathrm{S}}={{{\Delta }}}_{\mathrm{S}}^{2}/e\hslash {v}_{\mathrm{F}}\) and a junction Schwinger voltage VS = ESΛ. It leads to the proliferation of electron–hole pairs at a rate w1dΛ, with w1d given by equation (1) and a pair current given by equation (2). b, The differential conductance GS = ∂IS/∂V given by equation (3) for gs = gv = 2 (red line). It is well approximated by the affine approximation (equation 4), \({G}_{\mathrm{S}}=1.20\left(\frac{V}{{V}_{\mathrm{C}}}-1\right)\times \frac{4{e}^{2}}{h}\), with VC = 0.62 VS (black dashed line). The truncated (first-order perturbation) Schwinger conductance (blue dash-dotted line), \({G}_{\mathrm{S}}^{* }=4{g}_{\mathrm{s}}{g}_{\mathrm{v}}\frac{{e}^{2}}{h}\left(1+\pi \frac{{V}_{\mathrm{S}}}{V}\right){e}^{-\pi \frac{{V}_{\mathrm{S}}}{V}}\) (main text), substantially deviates from the full series (equation 3).

Full size image

Measurements are performed at room temperature in a series of six hBN-encapsulated single-layer graphene transistors deposited on local backgates, made of graphite for devices GrS1–3 and gold for devices AuS1–3, and equipped with high-transparency edge contacts (Methods and Supplementary Table I). As explained below (Klein collimation junction), high mobilities μ ≳ 10 m2 V−1 s−1, large dimensions (L, W) ≳ 10 μm, high doping ns and small-gate dielectric thicknesses thBN ≲ 100 nm, are key ingredients for observing the SE. High mobility provides current saturation at low bias Vsat < Vg, whereas high doping and long channels are needed to reject the Zener channel instability at a large bias VZ > Vg. The SE is visible in the bias window [Vsat, VZ] where Klein collimation is effective, at a Schwinger voltage VS ≈ Vg controlled by the channel doping ns and dielectric thickness thBN. Data reported below refer mostly to the representative GrS3 sample, leaving the full sample series description for Supplementary Discussion Section IV.

Klein collimation junction

Prior to discussing the SE in the next section, it is worth understanding the electric field profile it stems from, and the current saturation mechanism. We show in Fig. 2a the high-bias current-voltage (I-V) characteristics of sample GrS3 (Fig. 2 caption), which exhibit prominent current saturation plateaus centred at the I(V = Vg) pinchoff line (dashed black line). The highlighted Vg = 3 V trace (thick turquoise line) illustrates the three main transport regimes: (1) the diffusive Drude regime for V ≲ Vsat, (2) the Klein collimation saturation regime for Vsat ≲ V ≲ VZ and (3) the Zener regime for V ≳ VZ. As discussed in previous works15,16, the Zener effect corresponds to a field-induced bulk interband Klein tunnelling and is characterized by a doping- and bias-independent Zener channel conductivity (σZ ≈ 1 mS). It is subject to Pauli blockade leading up to a finite threshold voltage VZ = LEZ with a critical Zener field \({E}_{\mathrm{Z}}\propto {\mu }_{\mathrm{s}}^{2}\propto {n}_{\mathrm{s}}\) (ref. 16). Consequently the Zener voltage VZ ∝ LVg of long transistors is rejected well above Vg. This important feature characterizes our device series (Supplementary Discussion Section IV), which differs from conventional devices17,18 where lower mobility and shorter channel lengths substitute saturation plateaus by a crossover between the Drude and Zener ohmic regimes.

Fig. 2: Room temperature ballistic pinchoff in sample GrS3 of dimensions L × W × thBN = 15 × 10 × 0.042 μm, mobility μ = 12m2 V−1 s−1 (gate capacitance Cg = 0.67 mFm−2) and contact resistance Rc = 120 Ω.
figure 2

a, Set of current–voltage characteristics after subtraction of contact voltage drop, including the representative Vg = 3 V trace (thick turquoise line). The pinchoff regime V = Vg is indicated by the dashed black line. b, Differential conductance scaling \(G\left[\frac{V}{{V}_{\mathrm{g}}}\right]\) illustrating the steep decay of saturation conductance below pinchoff, and the sharp onset of Zener conductance at twice the pinchoff voltage. Inset is an artist’s view of the supposed carrier density distribution, characterized by a sharp drop over a collimation length Λ at the drain side. c, Semilog representation of conductance showing the exponential decay at current saturation, \(G=G(0){e}^{-\frac{V}{{V}_{\mathrm{sat}}}}\) (dotted blue line), with a doping-dependent saturation voltage Vsat ≃ 3 μs/e (dashed line in the inset). d, High-frequency (1–10 GHz) current noise measured in sample GrS2 at T = 10 K as a function of current. The sharp drop at pinchoff maps the vanishing of the thermal noise contribution SI = 4G(I)kBTe, where Te is the hot-electron temperature, according to the differential conductance dip at saturation. The residual noise (dashed blue line) is attributed to shot noise SI = 2eIF obeying the Fano factor \(F\simeq 0.04/\sqrt{1+{({I}_{\mathrm{sat}}/0.006)}^{2}}\). e, Huge low-frequency (0.1–1 MHz) current noise peak at the onset of the Zener instability.

Source data

Full size image

In Supplementary Discussion Section VI we compare the pinchoff-induced exponential current saturation observed in the present Vg = Constant biasing mode, with the current obtained in the pinchoff-free drain-doping-compensated mode15. We also provide a simple 1D model of the electrostatic potential distribution in the channel to estimate the respective channel and collimation junction voltage drops in the pinchoff regime, thereby establishing the existence of a Klein collimation junction. Klein collimation is the semimetal variant of the pinchoff junction of metal oxide semiconductor field-effect transistors19. The exponential saturation is reminiscent of the collimation effect of gate-defined long p–n junctions20, characterized by a transmission \(T({k}_{y}) \approx \exp (-\pi \hslash {v}_{\mathrm{F}}{k}_{y}^{2}/e{E}_{x})\), where \({k}_{y}={k}_{\mathrm{F}}\sin \theta\) is the transverse projection of the Fermi wave vector, θ is the angle of incidence and Ex = 2μs/Λ is the built-in in-plane electric field20,21,22. This p–n junction model, where electrons with a finite transverse momentum acquire a 1D massive Dirac fermion character with a gap 2ℏvFky, provides a natural framework for the bias-induced giant Klein collimation reported here. In contrast to the p–n junction case, Klein collimation entails large Ex ≃ V/Λ and \(\hslash {v}_{\mathrm{F}}{k}_{y}=eV\sin {\theta }_{\mathrm{sat}}\), leading to an exponentially vanishing transmission \(T(V) \approx \exp (-\pi V\frac{e{{\Lambda }}}{\hslash {v}_{\mathrm{F}}}{\sin }^{2}{\theta }_{\mathrm{sat}})\). This giant Klein collimation effect turns an incident 2D electron gas into a 1D transmitted beam, leading to an emergent 1D transport regime of relativistic electrons at a velocity vF.

Current saturation is best characterized by the differential conductance G = ∂I/∂V, whose scaling properties as a function of V/Vg are shown in Fig. 2b. The high-bias Zener regime corresponds to a doping-independent step-like increase to the Zener conductance GZ ≃ 1.5 mS at VZ ≃ 1.8 Vg. The saturation regime of interest in this work is characterized by a vanishing conductance in the [Vsat, VZ] window. Figure 2c is a semilog plot showing the exponential decay of the saturation conductance above the saturation voltage Vsat. It is exemplified by the dashed blue-line fit of the representative Vg = 3 V data. This exponential decay is observed over a broad doping range, and characterized by a doping-dependent saturation voltage Vsat according to the fitting law \(G=G(0){e}^{-V/{V}_{\mathrm{sat}}}\). The inset shows the Fermi energy dependence of Vsat, which obeys a linear law Vsat ≃ 3μs/e, implying that tunnelling-conductance suppression at pinchoff, \(G({V}_{\mathrm{g}}\propto {\mu }_{\mathrm{s}}^{2})\propto {e}^{-{\mu }_{\mathrm{s}}/{\mathrm{Constant}}}\), increases with doping. This property is consistently observed in the full sample series (Supplementary Table 1) where eVsat/μs = 2.5–5. In the above p–n junction model, the saturation voltage \({V}_{\mathrm{sat}}=\hslash {v}_{\mathrm{F}}/\pi e{{\Lambda }}{\sin }^{2}{\theta }_{\mathrm{sat}}\) is related to the collimation angle θsat.

An additional signature of the existence of a Klein junction is found in the transistor shot noise in Fig. 2d. Shot noise \({S}_{\mathrm{I}}=2eI{{{\mathcal{F}}}}\), where \({{{\mathcal{F}}}}\lesssim 1\) is the Fano factor, is deduced from the microwave current noise SI, which adds to the thermal noise SI = 4G(I)kBTe, where kB is the Boltzmann constant and Te is the electronic temperature. Here we take advantage of the conductance suppression at saturation, with G(I ≃ Isat) → 0 corresponding to the noise dips at the saturation current Isat in Fig. 2d, to extract the junction Fano factor \({{{\mathcal{F}}}}({I}_{\mathrm{sat}})\lesssim 0.04\) (Supplementary Discussion Section III). The presence of a shot noise, and the tiny value of the Fano factor, are strong indications of the presence of a ballistic junction23. Finally, the Zener threshold is reached upon increasing further the bias voltage; it entails an upheaval of the electric field distribution, as the electric field, initially confined over Λ in the Klein collimation regime, penetrates the full channel length L in the ohmic Zener regime. A signature of this collective instability of Klein collimation can be seen in the huge low-frequency current noise observed over the [VZ, 1.5 VZ] range in Fig. 2e.

The exponential current saturation, the presence of shot noise and the Zener electric field instability are three independent signatures of the giant Klein collimation effect and its collective instability towards a bulk Zener effect. The Klein collimation and its associated high-field region will act as a seed for the SE demonstrated below.

Evidence of a universal 1D Schwinger conductance

To highlight the small Schwinger-pair contribution in transport, we magnify in Fig. 3a the conductance-scaling plot of Fig. 2b. We focus first on the Vg = 3 V data (turquoise circles), for which the exponential tails of the Klein collimation (dotted blue line) and Zener (dotted green line) contributions are fully suppressed in a bias window [1.1 Vg, 1.7 Vg]. In this window, the measured conductance is solely governed by the Schwinger contribution, as evidenced by the fit of Vg = 3 V data with equation (3) taking VS = 1.4 Vg (thick turquoise line). The SE is also visible at lower doping, albeit partially obscured by a residual Klein tunnelling contribution. To extract the Schwinger contribution at arbitrary doping, we rely on the de-embedding of the Klein tunnelling contribution using a three-parameter fit \(G={G}_{\mathrm{S}}(V/{V}_{\mathrm{S}})+G(0){e}^{-V/{V}_{\mathrm{sat}}}\) performed in the relevant range [Vsat, VZ]. The resulting pair conductance GS is displayed in Fig. 3b. It highlights the sharp transition (dotted black line) separating the Schwinger and Zener regimes, and reveals the Schwinger conductance fan-like scaling predicted by the affine approximation (equation 4) for a doping-dependent VS. Remarkably, the linear zero-bias extrapolate is a constant G0 ≃ 0.18 ± 0.02 mS, which is very close to the universal quantization \({G}_{0}=1.20\frac{4{e}^{2}}{h}=0.186\ {{{\rm{mS}}}}\) for the 1D SE in graphene. The same procedure has been applied to the full sample series in Supplementary Figs. 6 and 7, which shows similar scaling with consistent values of G0. This observation of a robust conductance quantization, in quantitative agreement with 1D Schwinger theory, is a parameter-free demonstration of the relevance of 1D SE, and of its ubiquity in high-mobility graphene transistors, which constitutes the main finding of our work.

Fig. 3: KSE in long ballistic transistors.
figure 3

a, Blow-up of GrS3 conductance in Fig. 2b. The fully developed gap at large doping (dashed blue and green lines of the Vg = 3 V data) unveils the Schwinger-pair contribution (thick turquoise line) corresponding to VS ≃ 1.4 Vg. Inset: Artist’s view of the Klein-Schwinger mechanism. At lower doping, where the Schwinger contribution is embedded in a finite Klein contribution, the pair contribution is extracted from the single-particle tunnelling contribution by a three-parameter fit of conductance data according to the law \(G(V)={G}_{\mathrm{S}}(V/{V}_{\mathrm{S}})+G(0){e}^{-V/{V}_{\mathrm{sat}}}\). b, The pair contribution \(G(V)-G(0){e}^{-V/{V}_{\mathrm{sat}}}\) (same colour code as in a), reveals the affine approximation scaling of the Schwinger conductance (equation 4) with G0 ≃ 0.18 ± 0.02 mS and \({V}_{\mathrm{S}}=0.7{V}_{\mathrm{g}}+0.15{V}_{\mathrm{g}}^{2}\). The Zener regime is signalled by a sharp increase of pair conductance above the Schwinger–Zener boundary (dotted black line) set by GS(V = VZ = 1.9 Vg). c, Linear increase of the VS/Vg(ns) ratio with doping observed in the full transistor series (Supplementary Fig. 7) where Schwinger-pair conductance scaling is reported with consistent values of G0. The slope increases with dielectric thickness (main text). The VS/Vg ratio is minimized in sample AuS2 (L × W × thBN = 10.5 × 15 × 0.035 μm) and maximized in sample AuS3 (L × W × thBN = 11.1 × 11.4 × 0.090 μm). d, Broad-range (V/VS ≲ 4) Schwinger conductance at low doping in AuS2 where VS/Vg ≃ 0.5 showing the quantitative agreement with equation (3) (solid lines) that deviates from the affine approximation (equation 4) (dotted lines), and from the truncated approximation \({G}_{\mathrm{S}}^{* }\) (dash-dotted lines).

Source data

Full size image

Interpretation of the Schwinger voltage

Going one step further, we analyse the dependence of the Schwinger voltage VS(ns, thBN) on doping ns and hBN thickness thBN, extracted from theoretical fits of pair-conductance data with (equation 3). We assume that VS(ns, thBN) = ES(ns)Λ(ns, thBN) with \({E}_{\mathrm{S}}={{{\Delta }}}_{\mathrm{S}}^{2}({n}_{\mathrm{s}})/e\hslash {v}_{\mathrm{F}}\) for a Schwinger gap ΔS set by a collimation gap 2ℏvFkS at finite transverse momentum kS. In high-energy physics, the Schwinger threshold for electron–positron creation in a vacuum (the absence of any other particles before pair creation) is set by a true spectral gap 2mc2. In condensed matter, the threshold for electron–hole creation can also be associated to a Pauli blocking effect related to the presence of other electrons filling graphene bands before pair creation. For the KSE, we assume heuristically that this threshold energy is set by 2ℏvFks, where ks is a typical transverse momentum for the fully populated Klein transmitted electrons. In the absence of a fully fledged theory, and for the purpose of estimating the Klein collimation length Λ(ns, thBN), we use the Ansatz ΔS ≃ μs.

We plot in Fig. 3c the ratio VS/Vg(ns) for the full device series. We observe a linear doping dependence with a slope that increases with gate dielectric thickness thBN = 25–90 nm. As detailed in the Supplementary Discussion Section V, these dependencies can be explained by Λ(ns, thBN), according to the law \(\frac{{{\Lambda }}}{{t}_{\mathrm{hBN}}}\frac{{{{\Delta }}}_{\mathrm{S}}^{2}}{{\mu }_{\mathrm{s}}^{2}}=4{\alpha }_{\mathrm{g}}\frac{{V}_{\mathrm{S}}}{{V}_{\mathrm{g}}}\), where \({\alpha }_{\mathrm{g}}=\frac{{e}^{2}}{4\pi {\epsilon }_{\mathrm{hBN}}{\varepsilon }_{0}\hslash {v}_{\mathrm{F}}}=0.70\) (with ϵhBN = 3.1 at high field12) is the graphene fine structure constant. Assuming that ΔS ≃ μs, we can cast the measured \(\frac{{V}_{\mathrm{S}}}{{V}_{\mathrm{g}}}({t}_{\mathrm{hBN}},{n}_{\mathrm{s}})\) into the thBN power expansion \({{\Lambda }}\simeq a{t}_{\mathrm{hBN}}+\xi {n}_{\mathrm{s}}{t}_{\mathrm{hBN}}^{2}\), where a = 1–2 is a geometrical factor depending on the details of the contact gate arrangements, and ξ ≃ 4 nm is a microscopic interaction length (ξ is the typical interaction radius per electron (for \({n}_{\mathrm{s}}{t}_{\mathrm{hBN}}^{2}=1\)) fitting in a junction length Λ ≈ thBN), quantifying the doping-induced dilation of the junction length. This Coulomb repulsion effect enhances VS, favouring the visibility of the KSE at large doping (GrS3 data in Fig. 3c), up to the limit where its onset exceeds VZ so that the SE becomes masked by the Zener instability (AuS3 data in Fig. 3c). The latter case prevails in thick-hBN samples, giving rise to extremely flat current saturation plateaus (Supplementary Fig. 4f). Conversely, the small VS/Vg ≃ 0.5 ratio of thin-hBN samples (AuS2 data in Fig. 3c), allows for investigating conductance over an extended bias range V/VS ≲ 4. The doping and hBN-thickness dependencies of the ratio VS/Vg, which contrast with the constant VZ/Vg, support our interpretation of the SE as the intrinsic breakdown mechanism of Klein collimation, rather than a precursor of the extrinsic (length-dependent) collective Zener instability.

We conclude our experimental report by analysing the extended Schwinger conductance regime in the AuS2 data, which are plotted in Fig. 3d. The accessible experimental range of Schwinger conductance (GS ≲ 0.6 mS) exceeds the validity domain (GS ≲ 0.2 mS) of the affine approximation (4), unveiling the sublinearities involved in equation (3) (solid lines). Experimental data are in excellent agreement with the full non-perturbative 1D Schwinger prediction, substantially deviating from the affine approximation (dotted lines), and strongly deviating from the truncated-rate 1D Schwinger conductance \({G}_{\mathrm{S}}^{* }\) (dash-dotted lines). This observation constitutes complementary evidence of the relevance of the Schwinger theory3.

The demonstration of the SE in an effective field theoretical 1 + 1D system is, to our knowledge, the first of its kind and a confirmation of a crucial prediction of quantum electrodynamic field theory. It fulfils the promise of using graphene to emulate quantum electrodynamics24, specifically here in its strong field sector. The use of condensed matter analogues has already proven fruitful in cosmology25, in particular with the observation of vortex formation in neutron-irradiated superfluid He-3 as an analogue of cosmological defect formation26, or that of the analogue of black hole Hawking radiation27, as well as in the understanding of energy renormalization via Lorentz boosts28.

Our experiment shows the ability of giant Klein collimation to generate large local electric fields. This opens a way for exploration of the SE in different systems, like the massive Dirac fermions in bilayer graphene11, or the massless fermions in three-dimensional Weyl or Dirac semimetals29. In this respect, theoretical challenges remain concerning the modelling of strongly out-of-equilibrium collimation and the emergence of the Schwinger gap. Our experiment also shows that prominent current saturations, with large saturation velocities, can be obtained in gapless graphene. On the application side, the understanding of the Klein-Schwinger mechanism turns out to be the key for the optimization of large voltage gain A = ∂V/∂Vg = Gm/G (with Gm the transconductance, see Supplementary Fig. 2) in high-mobility graphene transistors, which is tunable from A ≈ 10 in thin-hBN AuS2 to A ≈ 100 in thick-hBN AuS3 according to the VS/Vg ratio (Supplementary Table 1). Our work thus describes the implementation of a fully relativistic Klein-Schwinger field-effect transistor showing large saturation currents and voltage gain.

Finally, one may attempt to go deeper in the condensed matter analogy of quantum electrodynamics by investigating other manifestations of the SE, like the full counting statistics of pair creation, or the vacuum polarization3 that is a precursor of pair creation. This raises the question of the dynamics of Schwinger-pair creation, which is an open field that can be investigated by dynamical transport and electromagnetic radiation spectroscopy.

Methods

Fabrication of ballistic graphene transistors

The hexagonal boron nitride encapsulated graphene heterostructures are fabricated with the standard pick-up and stamping technique, using a polydimethylsiloxane/ polypropylenecarbonate stamp30. The gate is first fabricated on a high-resistivity Si substrate covered by 285 nm SiO2. The gate electrode is either a thin exfoliated graphite flake (thickness ≲ 15 nm) or a prepatterned gold pad (thickness 70 nm) designed by laser lithography and Cr/Au metallization. Deposition of the heterostructure on the backgate is followed by acetone cleaning of the stamp residues, Raman spatial mapping and atomic force microscopy characterization of the stack. Graphene edge contacts are then defined by means of laser lithography and reactive ion etching, securing low contact resistance ≲ 1 kΩ μm. Finally, metallic contacts to the graphene channel are designed with a Cr/Au Joule evaporation that also embeds the transistor in a coplanar waveguide geometry suited for cryogenic probe station microwave and noise characterization. The large transistor dimensions L, W ≳ 10 μm secure moderate channel electric field E ≈ V/L ≲ 106 V m−1 up to the metal oxide semiconductor field-effect transistor pinchoff at V = Vg, while their high mobility μ ≳ 6 m2 V−1 s−1 at room temperature, and μ ≳ 35 m2 V−1 s−1 at 10 K, secures ballistic transport in the channel.

Radio-frequency transport and noise measurement

Characterization of the ballistic graphene transistors is performed in a cryogenic probe station adapted to radio-frequency measurements up to 67 GHz. The d.c. measurements are performed using a Keithley 2612 voltage source to apply gate and bias. Noise measurements are enabled by the use of a Tektronix DPO71604C ultrafast oscilloscope for measurements up to 16 GHz. The high-frequency signal coming from the device is amplified by a CITCRYO1-12D Caltech low noise amplifier in the 1–10 GHz band, whose noise and gain have been calibrated against the thermal noise of a 50 Ω calibration resistance measured at various temperatures between 10 K and 300 K in the probe station. For low-frequency noise measurements in the 0.1–1 MHz band, an NF Corporation amplifier (SA-220F5) is used.