Electron acceleration from transparent targets irradiated by ultra-intense helical laser beams

Abstract

The concept of electron acceleration by a laser beam in vacuum is attractive due to its seeming simplicity, but its implementation has been elusive, as it requires efficient electron injection into the beam and a mechanism for counteracting transverse expulsion. Electron injection during laser reflection off a plasma mirror is a promising mechanism, but it is sensitive to the plasma density gradient that is hard to control. We get around this sensitivity by utilizing volumetric injection that takes place when a helical laser beam traverses a low-density target. The electron retention is achieved by choosing the helicity, such that the transverse field profiles are hollow while the longitudinal fields are peaked on central axis. We demonstrate using three-dimensional simulations that a 3 PW helical laser can generate a 50 pC low-divergence electron beam with a maximum energy of 1.5 GeV. The unique features of the beam are short acceleration distance (∼100 μm), compact transverse size, high areal density, and electron bunching (∼100 as bunch duration).

Introduction

The interest in helical light structures was triggered by a groundbreaking study showing that they carry orbital angular momentum¹. There has been an ongoing effort to utilize this property for various applications². In recent years, the attention has shifted towards higher intensity laser pulses with helical wave fronts. The shift in interest can be credited to the realization that the helical wave front structures can be achieved by reflecting a conventional high-intensity laser beam off a helical step-like mirror^3,4,5,6. Given the high conversion efficiency afforded by these mirrors, there is potential for these beams to be created on the latest generation of extreme-intensity (~10²³ W cm⁻²) laser facilities^7,8.

High-intensity helical beams represent drivers with features that are qualitatively different from those of conventional laser beams. Manifestations of these features include the generation of large magnetic fields inside a plasma^9,10,11, production of helical electron beams in laser-wakefield accelerators^12,13, and improved laser-driven ion acceleration¹⁴. The helicity or the wave front twist introduces an extra ‘control knob’ for adjusting the field topology. For example, the radial profile of the transverse electric and magnetic field can be made hollow by twisting their wave fronts. For a properly chosen twist, the helical laser beams can have strong longitudinal electric and magnetic fields that peak on the axis where there are essentially no strong transverse fields. Such a unique field structure offers an exciting possibility of generating collimated beams of ultra-relativistic electrons via direct acceleration of electrons by the longitudinal laser electric field.

The idea of using intense laser pulses to directly accelerate electrons in a vacuum to ultra-relativistic energies^15,16 is as old as the capability to generate such pulses. However, successful experimental implementation of the concept has been elusive, as it requires a method for efficient electron injection into the laser beam and a mechanism for counteracting transverse electron expulsion that is typical for conventional laser beams. It has recently been shown that no expulsion occurs if, rather than using a conventional laser beam, one uses a helical laser beam with dominant longitudinal electric and magnetic fields in the near-axis region¹⁷. In this case, the electrons obtain their energy from the longitudinal electric field. The longitudinal magnetic field is essential for electron retention. Radially polarized laser beams can also have a dominant on-axis longitudinal electric field^18,19, but they have no on-axis magnetic field. As a result, electron acceleration by these beams is rather sensitive to perturbative effects¹⁹.

In search of a solution to the electron injection problem, multiple approaches have been examined and laser reflection off a plasma mirror has emerged as the preferred method^17,18,19. However, this method is sensitive to the gradient of the plasma density. Achieving a necessary steep density gradient at high laser intensities is extremely difficult. It is also challenging to reliably measure the electron density profile all the way to the reflection point since the reflection at relativistic intensities occurs inside a classically opaque region. Another difficulty arises due to the constraint that experiments at ultra-high intensities must be performed using oblique incidence. It has been shown experimentally for radially polarized beams that the laser reflection in the case of oblique incidence negatively impacts electron injection and their subsequent acceleration¹⁹.

In this paper, we consider a qualitatively different approach, offered by the recent progress in target fabrication, where the injection takes place during volumetric interaction between the laser and a solid target. It is now possible to produce inorganic foam targets (e.g., SiO₂ foam targets^20,21 with the pore size of just a few nm) whose electron density, after the target is fully ionized and homogenized, is close to the classical cutoff density for an optical laser. For a laser with an 800 nm wavelength, the cutoff density (also often referred to as the critical density) is n_c ≈ 1.7 × 10²¹ cm⁻³. This value is much higher than the electron density in an expanding gas jet and much lower than the density in a solid metal target. The advantage of near-critical targets, as those made of inorganic foams²², is that they become transparent when irradiated by a high-intensity laser, so they can transmit the laser pulse and enable a volumetric interaction of the pulse with a dense electron population. In the context of the electron acceleration problem, the benefit of the volumetric interaction compared to the reflection is that the electron injection takes place at an electron density that is known relatively well. Additionally, the density is set by the target fabrication process rather than by the laser prepulse, so it is possible to choose the desired density²¹.

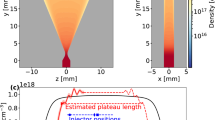
Using three-dimensional particle-in-cell (3D PIC) simulations we show that both the electron injection and the electron retention problems can be successfully solved by employing a ~10-μm-thick near-critical target irradiated by a helical laser beam. We consider a 3 PW, 29 fs laser beam focused to a 3 μm spot, but our results are rather generic and not specific to these exact parameters. The electrons are “injected” into the laser beam while it is being transmitted by the near-critical target. We find that a proper choice of the target electron density n_e is important for preserving the topology of the laser beam. At $\max ({n}_{{{{{{{{\rm{e}}}}}}}}})=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$, the considered laser beam retains its structure without generating high-amplitude higher-order radial modes whose presence is detrimental to the generation of an ultra-relativistic collimated electron beam. The simulation for the optimal regime shows that, upon exiting the target, the laser beam carries dense bunches of electrons, which solves the injection problem. As shown in Fig. 1a, b, the bunches remain close to the axis of the laser beam due to the hollow profiles of the transverse fields, which solves the retention problem. The electrons are accelerated by the longitudinal electric field that has a peak on the axis. The electron energies seen in Fig. 1c reach 1.5 GeV, which is similar to the maximum energy achieved using a plasma mirror and a 6 PW laser pulse¹⁷. The divergence of the beam, whose charge is about 50 pC, is less than 3^∘. Such a low divergence is the advantage of the acceleration by the longitudinal, rather than the transverse, electric field. The presented electron injection and acceleration mechanisms are qualitatively different from those employed by more established schemes that can achieve similar electron energy and charge, e.g., laser wakefield acceleration^23,24. The differences lead to several unique features that include short acceleration distance (~100 μm); high areal density (~10¹⁶ cm⁻²); the compact transverse size of the beam (≲1 μm); and bunching of energetic electrons, with the bunches being ~100 as in duration.

Fig. 1: Electron acceleration by a helical beam transmitted through a relativistically transparent target and the vacuum field structure of the beam.

a Longitudinal electric field E_x (red/blue) and electron density n_e (green) shortly after a circularly-polarized helical beam (l = −1, σ = 1, and p = 0) passes through a near-critical target with $\max ({n}_{{{{{{{{\rm{e}}}}}}}}})=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ (prior to the arrival of the laser). The red/blue colors correspond to E_x ≷ 0 and the contours show ∣e∣E_x/m_ecω = ±1, 2, 4, 6, 8 in decreasing opacity. The green color shows n_e between 0.025n_c (transparent green) and 0.05n_c (fully opaque green). b Trajectories of four energetic electrons that are located within the central-most bunch at t = 398.3 fs. The dashed vertical lines mark the initial target boundary. Color-coded is the kinetic energy ε_k = (γ − 1)m_ec². c Time evolution of the energy distribution for forward-moving electrons (p_x > 10m_ec) that are close to the central axis of the laser beam. The specific selection criterion is ∣y∣ < 1 μm, ∣z∣ < 1 μm, and x > 0 within the moving window used in the simulation. The time t = 0 is the time when the peak of the laser envelope passes through x = 0 in the absence of the target. d–h Vacuum (in the absence of the target) field structure of the circularly-polarized laser beam at t = −1.7 fs. The vertical dashed line in (d) and (e) indicates where the planes shown in these panels intersect. The same dashed line is shown in (g) and (h). d, g Transverse, E_z, and longitudinal, E_x, an electric field in the (x, y)-plane at z = 0. e, h Transverse, E_z, and longitudinal, E_x, electric field in the (z, y)-plane at x marked by the dashed line in (d) and (g). f Line-outs of the transverse and longitudinally electric fields along the dashed line are shown in (d) and (e) for the transverse field and in (g) and (h) for the longitudinal field. The subscript s denotes z for the solid blue curve and x for the dot-dashed orange curve. The thin vertical dashed lines mark the boundaries of the region where the longitudinal field dominates.

Results

We consider a setup where a thin (~10 μm) near-critical target is irradiated by an ultra-high-intensity laser beam and becomes very transparent due to the effect of the relativistically induced transparency. The purpose of the target is to “inject” electrons into the transmitted laser beam for their subsequent acceleration in a vacuum. In our setup, the majority of the energy gain occurs during the vacuum propagation of the transmitted laser. In order to make this process effective, one must use a beam structure that can accelerate electrons without the transverse expulsion that is typical for conventional laser beams whose transverse fields peak on the central axis. Here we focus specifically on helical beams and, in the next two subsections, we identify the most suitable helical mode and make analytical predictions for the electron energy gain. The desired mode can be created (even at a high intensity) from a conventional laser beam using recently developed techniques involving reflective optics. However, the considered target must preserve the helicity of the beam during its transmission without generating high-amplitude higher-order radial modes. Our 3D PIC simulations for different target densities explore the changes induced during the beam transmission. We use these results to identify the optimal regime. This section concludes by considering a case of oblique incidence for the optimal density aimed to show that the considered setup can be used in those laser systems that do not permit experiments at normal incidence.

Vacuum field structure of a helical laser beam

As shown in Fig. 1a, we consider a laser beam propagating in the positive direction along the x-axis. In the case of a beam with helical wave fronts, it is convenient to represent the spatial structure of each field component as a superposition of Laguerre-Gaussian modes. The modes describing vacuum propagation are well-known, so we provide the corresponding expressions without derivation. The purpose is to identify the key features and set the stage for the discussion of electron acceleration.

The polarization of a laser beam determines the orientation of its fields, whereas the helicity or twist index l determines the topology of the wave fronts. We illustrate the difference by considering a linearly-polarized beam with wavelength λ₀ and beam width w₀ that has E_y and E_x electric field components and B_z and B_x magnetic field components. It is convenient to use cylindrical coordinates (x, r, ϕ) to describe the spatial structure of each component, where r is the distance and ϕ is the polar angle in the (y, z) plane. The transverse electric field E_y of a mode with a twist index l and radial index p is given by

$${E}_{y}(\widetilde{x},\widetilde{r},\phi ;t)={E}_{0}{\psi }_{p,l}g(\xi )\exp (i\xi ),$$

(1)

$${\psi }_{p,l}\equiv {C}_{p,l}f{(\widetilde{x})}^{| l| +1+2p}{(1+{\widetilde{x}}^{2})}^{p}{L}_{p}^{| l| }\left(\frac{2{\widetilde{r}}^{2}}{1+{\widetilde{x}}^{2}}\right){\left(\sqrt{2}\widetilde{r}\right)}^{| l| }\exp \left[-{\widetilde{r}}^{2}f(\widetilde{x})+il\phi \right],$$

(2)

$$f(\widetilde{x})\equiv \frac{1-i\widetilde{x}}{1+{\widetilde{x}}^{2}},$$

(3)

$$\xi \equiv 2\widetilde{x}/{\theta }_{{{{{{{{\rm{d}}}}}}}}}^{2}-\omega t,$$

(4)

where E₀ is a constant that sets the field amplitude, C_p,l is a normalization coefficient, g(ξ) is the temporal envelope, ${L}_{p}^{| l| }$ is the generalized Laguerre polynomial. Additionally, we introduced the beam divergence angle θ_d = w₀/x_R, the Rayleigh length ${x}_{{{{{{{{\rm{R}}}}}}}}}=\pi {w}_{0}^{2}/{\lambda }_{0}$, and the laser frequency ω = 2πc/λ₀. The tilde indicates the following normalization:

$$\widetilde{x}\equiv x/{x}_{{{{{{{{\rm{R}}}}}}}}},$$

(5)

$$\widetilde{r}\equiv r/{w}_{0}.$$

(6)

We set ${C}_{l,p}=\sqrt{2p!/\pi (p+| l| )!}$, so that $\int\nolimits_{0}^{2\pi }d\phi \int\nolimits_{0}^{\infty }{\psi }_{p,l}{\psi }_{p,l}^{* }\widetilde{r}d\widetilde{r}=1$. The transverse magnetic field is simply B_z = E_y. It follows from Eqs. (1) and (2) that, even though the polarization of the modes with different l is the same, the surface of the constant phase changes its shape with the change of l. Specifically, it becomes helical for l ≠ 0, whereas the l = 0 case corresponds to a conventional laser beam whose wave fronts have no twist.

The helicity profoundly alters the radial dependence of the laser fields. For simplicity, we examine the field structure in the vicinity of the focal plane ($\widetilde{x}=0$). The transverse fields of a conventional beam (l = 0) peak on the central axis. In contrast to that, E_y and B_z of a helical beam vanish on the central axis, with ${E}_{y}={B}_{z}\propto {\widetilde{r}}^{| l| }$ at $\widetilde{r}\ll 1$. It follows from Eqs. (1) and (4) that for l ≠ 0 the surface of constant phase for the transverse electric and magnetic fields is a helix. The sign of l determines the direction of the twist and the value of ∣l∣ determines the number of full rotations/twists per wavelength: Δx/λ₀ = − lΔϕ/2π.

The changes in the topology of the transverse fields lead to similarly profound changes in the topology of the longitudinal electric and magnetic fields. The changes result from the fact that the electric and magnetic fields must be divergence-free, with (∇ ⋅ E) = 0 and (∇ ⋅ B) = 0. We are particularly interested in the field structure close to the axis where E_y and B_z vanish for helical beams. It follows from (∇ ⋅ E) = 0 that for the considered linearly-polarized wave we have

$${E}_{x}=\frac{i{\theta }_{{{{{{{{\rm{d}}}}}}}}}}{2}\left[\sin \phi \frac{\partial }{\partial \widetilde{r}}+\frac{\cos \phi }{\widetilde{r}}\frac{\partial }{\partial \phi }\right]{E}_{y}.$$

(7)

For a helical beam (i.e., l ≠ 0), we have $\partial {E}_{y}/\partial \widetilde{r}\approx | l| {E}_{y}/\widetilde{r}$ close to the central axis. We take this into account to find from Eq. (7) that at $\widetilde{r}\ll 1$ the longitudinal electric field is approximately given by

$${E}_{x}^{\pm }\approx \frac{i{\theta }_{{{{{{{{\rm{d}}}}}}}}}}{2}\frac{| l| }{\widetilde{r}}{e}^{\mp i\phi }{E}_{y}\propto {\widetilde{r}}^{| l| -1},$$

(8)

where the superscript on the left-hand side represents the sign of l. The longitudinal magnetic field B_x has the same radial dependence. The modes with ∣l∣ = 1 are evidently unique because their longitudinal fields peak on the central axis. The longitudinal fields of these modes dominate in the near-axis region, so these modes are well-suited for longitudinal electron acceleration.

These results can be generalized to the case of a circularly-polarized laser beam. We construct such a beam out of two linearly-polarized beams with a phase offset. Its transverse electric field is set by the relation E_z = iσE_y, where E_y is given by Eq. (1). Here σ = 1 corresponds to a right-circularly-polarized wave and σ = −1 corresponds to a left-circularly-polarized wave. Only for ∣l∣ = 1 the longitudinal rather than transverse fields peak on axis, but the two circular polarizations (right and left) are not equivalent. In the case of σ = −l, the longitudinal fields reach their highest amplitude at $\widetilde{r}\to 0$. On the other hand, in the case of σ = l, the longitudinal fields vanishes on the central axis. Figure 1 compares the topology of the transverse and longitudinal electric fields in the circularly-polarized beam with σ = −l and l = −1. Figure 1d, e show that the transverse field for this beam indeed vanishes on the central axis. In the near-axis region, the longitudinal electric field dominates, as seen in Fig. 1f. The structure of the longitudinal field is shown in Fig. 1g, h.

Close to the axis, E_x and B_x are axis-symmetric for both linearly and circularly-polarized pulses. The linearly-polarized beam loses this symmetry away from the axis. In contrast to that, the fields of the circularly-polarized beam with σ = −l retain their symmetry [e.g., see Fig. 1h]. Motivated by this observation, we focus in the remainder of this paper on the more symmetric circularly-polarized beam with σ = −l= 1. Its longitudinal electric field is

$${E}_{x}=\left\{\begin{array}{l}i{\theta }_{{{{{{{{\rm{d}}}}}}}}}{E}_{y}{e}^{i\phi }\left[| l| /\widetilde{r}-\widetilde{r}f-{L}_{p-1}^{| l| +1}/(1+{\widetilde{x}}^{2}){L}_{p}^{| l| }\right]\,{{\mbox{for}}}\,p\ge 1,\\ i{\theta }_{{{{{{{{\rm{d}}}}}}}}}{E}_{y}{e}^{i\phi }\left[| l| /\widetilde{r}-\widetilde{r}f\right]\,{{\mbox{for}}}\,p=0.\end{array}\right.$$

(9)

The longitudinal magnetic field has the same radial dependence, but it has an additional phase shift: B_x = iE_x.

We have intentionally retained higher mode numbers corresponding to p ≥ 1 in our analysis. Even if the irradiating laser beam contains only a single radial mode (e.g., p = 0), the transmitted beam is likely to consist of various modes with different amplitudes (this assertion is later confirmed via mode decomposition). The mode coupling during laser propagation through the thin targets occurs due to laser focusing by the plasma. By definition, the radial mode number p changes the radial field structure of E_x away from the axis. However, the on-axis field changes with p as well. In order to clearly identify the corresponding changes, we take the limit of $\widetilde{r}\to 0$ in Eq. (9). Note that the expressions in square brackets reduce to $| l| /\widetilde{r}$ for p ≥ 1 and for p = 0. We then have

$${E}_{x}(\widetilde{r}=0)=\frac{ig(\xi ){E}_{\parallel }^{\max }}{1+{\widetilde{x}}^{2}}\exp \left[i\xi -i2(1+p)\,\tan^{-1}(\widetilde{x})\right],$$

(10)

where

$${E}_{\parallel }^{\max }=2\sqrt{\frac{p+1}{\pi }}{\theta }_{d}{E}_{0}=\frac{2}{\pi }\sqrt{\frac{p+1}{\pi }}\frac{{\lambda }_{0}}{{w}_{0}}{E}_{0}$$

(11)

is the peak value of the longitudinal electric field.

The explicit dependence of the phase of the on-axis field on the mode number via the (1 + p) multiplier deserves particular attention. We define the phase velocity as v_ph = dx/dt for the constant phase given by the expression in the square brackets in Eq. (10). We take the derivative of this expression with respect to t and assume that θ_d is small to find the following approximate expression for the relative superluminosity:

$$\frac{{v}_{{{{{{{{\rm{ph}}}}}}}}}-c}{c}\approx \frac{(p+1){\theta }_{{{{{{{{\rm{d}}}}}}}}}^{2}}{1+{\widetilde{x}}^{2}}\ll 1.$$

(12)

The key feature here is that the relative degree of superluminosity is given by Eq. (12) increases with the radial mode number. Even though the phase velocity is very close to the speed of light, the explicit dependence on p can have a significant impact on the dynamics of ultra-relativistic electrons with c − v_x ≪ v_ph − c.

Estimates for electron acceleration by the longitudinal electric field of a helical beam

In order to obtain analytical scalings for the energy and momentum gain, we consider an electron that is moving along the central axis of a circularly-polarized helical beam with σ = −l = 1. The transverse fields of this beam vanish on the axis, so such a simple model is a reasonable approximation for the dynamics of electrons that start their motion close to the axis. Even though most of the energy gained by electrons in our setup takes place in a vacuum, we anticipate that the electrons undergo some initial acceleration while moving with the laser through the target. We mimic this by assuming that electron starts its vacuum acceleration with an initial relativistic longitudinal momentum p_x = p₀ ≳ m_ec.

Under our assumptions, the change in electron momentum results from the electron interaction with ${E}_{x}(\widetilde{r}=0)$ whose explicit expression is given by Eq. (10):

$${{\Delta }}{p}_{x}={p}_{x}(t)-{p}_{0}=-\int\nolimits_{{t}_{0}}^{t}| e| {E}_{x}(\widetilde{r}=0)dt^{\prime} ,$$

(13)

where t₀ is the time when the electrons starts its vacuum acceleration with the initial momentum p₀. In order to compute this integral, one needs to know how the phase of E_x evolves along the electron trajectory. Even though a general dependence is complicated, a simplified expression can be derived for a regime where c − v_x ≪ v_ph − c. We find from Eq. (12) that the condition c − v_x ≈ v_ph − c is equivalent to

$$\gamma \approx {\gamma }_{* }\equiv \sqrt{1+{\widetilde{x}}^{2}}/2(p+1){\theta }_{{{{{{{{\rm{d}}}}}}}}}$$

(14)

for a forward-moving electron with $\gamma =1/\sqrt{1-{v}_{x}^{2}/{c}^{2}}$. The irradiating laser beam in the simulation whose results are shown in Fig. 1 has w₀ = 3 μm, λ₀ = 0.8 μm, and p = 0. This means that the requirement c − v_x ≪ v_ph − c is satisfied after the electron γ-factor (at $\widetilde{x}\;\lesssim\; 1$) exceeds ${\gamma }_{* }\approx {12}$. This is not a particularly constraining condition, considering that the peak value of γ exceeds 3000. The condition eventually breaks down at large $\widetilde{x}$ as v_ph decreases and approaches c, with the corresponding value of $\widetilde{x}$ increasing with γ. In the considered example, this occurs at a very large distance of $\widetilde{x}\approx 17$ even for a relatively modest γ ≈ 100. At such a large distance, the laser amplitude is very low due to the beam divergence, so no energy gain takes place and the breakdown of the considered condition is inconsequential.

In the regime where c − v_x ≪ v_ph − c, the change in phase is predominantly determined by the superluminosity of the wave fronts. We can thus set x = x₀ + c(t − t₀) and eliminate the explicit time dependence of the phase. For simplicity, we consider an electron that undergoes its acceleration in a region close to the peak of the field envelope, so that g(ξ) ≈ 1. The resulting expression for the longitudinal on-axis electric field is

$$\frac{| e| {E}_{x}}{{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega }=\sqrt{\frac{p+1}{\pi }}\frac{2{a}_{0}{\theta }_{d}}{1+{\widetilde{x}}^{2}}\sin \left({{{\Phi }}}_{0}+2(p+1)\left[{\tan }^{-1}(\widetilde{{x}_{0}})-{\tan }^{-1}(\widetilde{x})\right]\right),$$

(15)

where

$${a}_{0}\equiv \frac{| e| {E}_{0}}{{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega }$$

(16)

and e and m_e are the electron charge and mass. We have introduced Φ₀, which is the phase of E_x at $\widetilde{x}={\widetilde{x}}_{0}$ at t = t₀, to explicitly take into account the initial conditions. In our analysis, Φ₀ is an input parameter that can be interpreted as the ‘injection phase’ at the start of the vacuum acceleration. In order to calculate the integral in Eq. (14) we change the integration variable from $t^{\prime}$ to $\widetilde{x}^{\prime}$ by taking into account that $d\widetilde{x}^{\prime} /dt^{\prime} \approx c/{x}_{R}$. The resulting expression for the change of momentum is

$$\frac{{{\Delta }}{p}_{x}}{{m}_{{{{{{{{\rm{e}}}}}}}}}c}=\, \frac{2{a}_{0}}{{\theta }_{d}\sqrt{\pi (p+1)}}\left(\cos {{{\Phi }}}_{0}-\cos \left[{{{\Phi }}}_{0}+2(p+1){\tan }^{-1}({\widetilde{x}}_{0})\right.\right.\\ \left.\left.-2(p+1){\tan }^{-1}(\widetilde{x})\right]\right).$$

(17)

Based on the obtained expression, there are two distinct regimes of electron acceleration: acceleration by modes with an even radial index p and acceleration by modes with an odd radial index p. In order to make the difference more evident, we consider the terminal change in momentum. The corresponding expression is obtained by taking the limit of $\widetilde{x}\to \infty$. We further simplify the expression by assuming that ${\widetilde{x}}_{0}\ll 1$, so that ${\tan }^{-1}({\widetilde{x}}_{0})\approx {\widetilde{x}}_{0}$. In the case of an even p value, we obtain

$$\frac{{({{\Delta }}{p}_{x})}^{{{{{{{{\rm{term}}}}}}}}}}{{m}_{{{{{{{{\rm{e}}}}}}}}}c}=\frac{4{a}_{0}\cos \left[(p+1){\widetilde{x}}_{0}\right]}{{\theta }_{d}\sqrt{\pi (p+1)}}\cos \left[{{{\Phi }}}_{0}+(p+1){\widetilde{x}}_{0}\right].$$

(18)

In the case of an odd p value, we obtain

$$\frac{{({{\Delta }}{p}_{x})}^{{{{{{{{\rm{term}}}}}}}}}}{{m}_{{{{{{{{\rm{e}}}}}}}}}c}=\frac{4{a}_{0}\sin \left[(p+1){\widetilde{x}}_{0}\right]}{{\theta }_{d}\sqrt{\pi (p+1)}}\sin \left[{{{\Phi }}}_{0}+(p+1){\widetilde{x}}_{0}\right].$$

(19)

The difference in the prefactor that is independent of the injections phase Φ₀ means that the momentum gain for odd values of p can be significantly suppressed if $(p+1){\widetilde{x}}_{0}\ll 1$. The p = 1 mode is the one that is most impacted for ${\widetilde{x}}_{0}\ll 1$.

The qualitative difference in acceleration between different p values can be understood by examining the terminal phase slip. According to (17), the phase slip is ${{\Delta }}{{\Phi }}=2(p+1)[{\tan }^{-1}({\widetilde{x}}_{0})-{\tan }^{-1}(\widetilde{x})]$. For an electron that starts its acceleration at ${\widetilde{x}}_{0}\approx 0$, the phase slip at $\widetilde{x}\to \infty$ is ΔΦ = − π(p + 1). The dependence on p here is a result of the dependence of v_ph on p [see Eq. (12)]. The key point is that the electron is slipping with respect to E_x faster at higher p. Since ΔΦ = − π for p = 0, then a properly injected electron can remain in the accelerating phase of the beam almost the entire time. In contrast to that, we have ΔΦ = −2π for p = 1. The electron then experiences not only acceleration but also deceleration by E_x. The deceleration leads to the reduction of ${({{\Delta }}{p}_{x})}^{{{{{{{{\rm{term}}}}}}}}}$ given by Eq. (19). At p = 2, ΔΦ = −3π and the electron can experience the accelerating phase twice. As a result, the momentum gain increases compared to the case with p = 1. However, it is reduced compared to the p = 0 case because the acceleration alternates with deceleration.

The key conclusion from our results is that, for given a₀ and θ_d, the biggest momentum increase and thus the biggest energy gain should be expected for a mode with p = 0. Excitation of the modes with higher p values during the beam propagation through the target is likely to be detrimental. The plasma can also focus the beam, reducing w₀. The size of the focal spot w₀ however has no impact on the terminal momentum gain at fixed power¹⁷. At fixed power, a₀ scales as 1/w₀. On the other hand, the divergence angle θ_d also scales as 1/w₀. As a consequence, the ratio of a₀/θ_d that enters the expressions for ${({{\Delta }}{p}_{x})}^{{{{{{{{\rm{term}}}}}}}}}$ remains unaffected by changes in w₀, provided that the beam power remains the same.

3D PIC simulation results

In order to perform a self-consistent analysis of the electron acceleration in the considered setup, we have performed a 3D PIC simulation with a moving window where a uniform plasma slab is irradiated by a normally incident 3 PW, 29.4  fs helical laser beam that is focused to a 3 μm spot to achieve a₀ ≈ 89. Detailed simulation and target parameters are provided in the Methods section. The incident beam is chosen to be circularly-polarized with l = −1, σ = 1, and p = 0 because this mode has been identified as the optimal mode for the vacuum acceleration of electrons. The laser focal plane (in the absence of the target) is located at x = 0 μm. The target is 12 μm-thick with a central plane located at x = 0 μm. The target is uniform in the central region that is 8 μm-thick. There are 2 μm density ramps on both sides to mimic target pre-expansion that likely takes place in experiments with ultra-high intensity due to the presence of a prepulse. The electron density in the target is subcritical, ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$, so the target is transparent to the laser pulse.

Figure 1a shows the topology of the longitudinal laser electric field E_x and electron density in the beam transmitted by the target at t = 88.3 fs. The time t = 0 fs is defined as the time when the peak of the laser envelope passes through x = 0 in the absence of the target. In the incident beam, E_x peaks on the axis of the beam, since l = −1 and σ = 1. The target evidently preserves this key feature, with E_x remaining peaked on the axis of the transmitted beam. The surface plot of the electron density past the initial surface of the target (x > 6 μm) confirms that the laser propagation through the transparent target serves as an effective mechanism for electron injection. The peak electron density in the transmitted beam exceeds 10% of the initial electron density in the target. There are two key features that are evident from the plot of n_e: the electrons are confined in the transverse direction and they are bunched longitudinally with a period roughly equal to λ₀. The confinement results from a combination of vanishing transverse electric and magnetic fields near the central axis and a peaked longitudinal magnetic field on the central axis. The electron bunching is a manifestation of the electron acceleration by the longitudinal laser electric field. Similar bunching can be observed for test electrons that are initially uniformly distributed along one wavelength by integrating electron equations of motion with E_x given by Eq. (15).

Figure 1b, c show several representative electron trajectories and the time evolution of the electron spectrum for all injected electrons. Rather than moving only along the x-axis, the electrons in Fig. 1b move at an angle of θ ≈ 3.3 × 10⁻³ to the central axis during the acceleration process. In this case, the longitudinal velocity is determined mainly by the angle θ and not by the difference between v and c, so that $(c-{v}_{x})/c\approx 1-\cos \theta \approx {\theta }^{2}/2$. On the other hand, the laser divergence angle is at least θ_d = 8.5 × 10⁻² (the transmitted beam is narrower, which means its divergence angle is greater than this value). It follows from Eq. (12) that, for $\widetilde{x}\;\lesssim\; 1$ and p = 0, we have $({v}_{{{{{{{{\rm{ph}}}}}}}}}-c)/c\;\lesssim\; {\theta }_{{{{{{{{\rm{d}}}}}}}}}^{2}/2$. We then conclude that c − v_x ≪ v_ph − c for the considered particle trajectories. Therefore, the change in phase during the acceleration is predominantly determined by the superluminosity of the wave fronts and the expressions derived for the electron momentum gain are applicable to these trajectories in Fig. 1b.

In order to estimate the maximum possible momentum gain, we assume that the transmitted beam is only a p = 0 mode. We have already shown that the beam narrowing or widening is inconsequential in terms of the momentum gain, so we take the original values of θ_d = 8.5 × 10⁻² and a₀ = 88.6. It follows from Eq. (18) that

$${({{\Delta }}{p}_{x})}^{{{{{{{{\rm{term}}}}}}}}}\approx 2.35\times 1{0}^{3}{m}_{{{{{{{{\rm{e}}}}}}}}}c\cos \left({\widetilde{x}}_{0}\right)\cos \left({{{\Phi }}}_{0}+{\widetilde{x}}_{0}\right)\le 2.35\times 1{0}^{3}{m}_{{{{{{{{\rm{e}}}}}}}}}c.$$

(20)

This corresponds to a maximum energy gain of 1.2 GeV during the acceleration in vacuum by the longitudinal electric field of the helical beam with p = 0. The electrons that start at the rear side of the target, e.g. x₀ = 5 μm, can achieve an energy gain very close to this value because the target is relatively thin compared to the Rayleigh length x_R. Indeed, we have $\cos \left({\widetilde{x}}_{0}\right)\cos \left({{{\Phi }}}_{0}+{\widetilde{x}}_{0}\right)\approx 0.99$ for Φ₀ ≈ −0.047π and ${\widetilde{x}}_{0}={x}_{0}/{x}_{{{{{{{{\rm{R}}}}}}}}}\approx 0.14$, where x₀ = 5 μm and x_R ≈ 35 μm.

According to the time evolution of the electron spectrum shown in Fig. 1c, the maximum terminal electron energy in the 3D PIC simulation is however about 25% or 300 MeV higher than what is predicted by Eq. (20). We have performed particle tracking that shows that the electrons leaving the target have appreciable energy, with a peak kinetic energy of ~300 MeV at x ≈ 5 μm. Using this value as an initial condition, we can then reconcile the result of the PIC simulation with the prediction given by Eq. (20). Specifically, ${\varepsilon }_{{{{{{{{\rm{k}}}}}}}}}^{{{{{{{{\rm{term}}}}}}}}}=({\gamma }^{{{{{{{{\rm{term}}}}}}}}}-1){m}_{{{{{{{{\rm{e}}}}}}}}}{c}^{2}\approx {p}_{x}^{{{{{{{{\rm{term}}}}}}}}}c={p}_{0}c+{({{\Delta }}{p}_{x})}^{{{{{{{{\rm{term}}}}}}}}}c\approx 1.5$ GeV, where p₀ is the initial momentum corresponding to ε_k = 300 MeV and ${({{\Delta }}{p}_{x})}^{{{{{{{{\rm{term}}}}}}}}}$ is the contribution from the vacuum acceleration for Φ₀ ≈ −0.047π and x₀ = 5 μm. The conclusion then is that the acceleration within the target, which is likely to differ from that in a vacuum due to the presence of the plasma electric and magnetic fields, provides an additional mechanism for the energy gain in the considered setup.

Target density scan

We have performed two additional 3D PIC simulations to examine the impact of the target density on the discussed electron acceleration process. In both simulations, the electron density in the target is higher than the electron density in the original simulation (${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$). These two densities are ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ and ${n}_{\max }={n}_{{{{{{{{\rm{c}}}}}}}}}$. The results of the two additional runs are shown in Fig. 2, where we also show the results of the original simulation to facilitate the comparison between different target densities.

Fig. 2: Target density scan for a circularly-polarized helical beam.

a–c Electron density n_e normalized to the critical density n_c for three different target densities (${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$, 1.0n_c, and 0.5n_c), shortly after laser pulse transmission (t = 48.3 fs). d–f Normalized amplitude of the longitudinal electric field, ∣e∣∣E_x∣/m_ecω, for the same three target densities also at t = 48.3 fs. g–i Density of accelerated electrons for the same three target densities at t = 248.3 fs. j–l Time evolution of the energy distribution for forward-moving electrons selected using the same criterion as that used for Fig. 1c, with ε_k = (γ − 1)m_ec². In panels (a–i), the quantities are shown in the (x, y)-plane at z = 0. Panels (a), (d), (g), and (j) correspond to a target with ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$; panels (b), (e), (h), and (k) correspond to a target with ${n}_{\max }={n}_{{{{{{{{\rm{c}}}}}}}}}$; panels (c), (f), (i), and (l) correspond to a target with ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$.

Figure 2a–f show the electron density and the topology of the longitudinal electric field shortly after the laser pulse transmission in all three simulations (t = 48.3 fs). We find from Fig. 2a–c that the divergence of the electron “beam” generated by the laser pulse outside of the target (x > 6 μm) reduces as we reduce the target density. The fact that the electrons in Fig. 2c have traveled further along the x-axis than in Fig. 2a is a result of a higher group velocity in the lower density target. We also observe noticeable changes to the structure of the longitudinal electric field E_x in the transmitted laser beam. As we reduce the target density, we find that the radial dependence in Fig. 2d–f changes, which suggests that higher radial modes (the original beam is a p = 0 mode) are generated during the laser beam transmission by the target.

Figure 2g–i show the electron density profiles at t = 248.3 fs for all three targets. By this point in time, the electrons shown in the plots have experienced significant acceleration. We find that the already discussed increased divergence at higher target density at t = 48.3 fs translates into the higher divergence of the accelerated electrons at t = 248.3 fs. In the case of the target with an initial density of n_e = 0.5n_c, the accelerated electrons remain within roughly 1 μm distance of the central axis, shown with the vertical dashed lines in Fig. 2i. In the case of the target with ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$, there are electrons that are at least 6 μm away from the central axis, which means that the divergence angle for the electrons at this density is roughly six times higher than that in the simulation with ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$.

The target density increase also impacts the energy gain by the electrons during their vacuum acceleration by the transmitted laser beam. Figure 2j –l show the time evolution of the energy spectra for the electrons that remain close to the central axis (∣y∣ < 1 μm and ∣z∣ < 1 μm). As we increase the target density from ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ to ${n}_{\max }=1.0{n}_{{{{{{{{\rm{c}}}}}}}}}$, the energy gain remains relatively unchanged. However, a further increase from ${n}_{\max }=1.0{n}_{{{{{{{{\rm{c}}}}}}}}}$ to ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ causes a visible reduction. We conjecture that the difference in the energy gain is, in part, caused by the excitation of higher-order radial modes, as these modes are less effective in terms of electron acceleration.

In order to find the changes in the structure of the transmitted beam in each simulation, we perform a mode decomposition detailed in the Methods. We perform our analysis for a snapshot of the magnetic field B_z at t = 88.3 fs. In general, it is not possible to recover the mode structure from a single snapshot due to insufficient information regarding the propagation of the field. However, the inherent ambiguity can be resolved in our case by taking into account that there are no reflected modes behind the target. This information is not automatically encoded in the real field values outputted by the PIC code. We use the Hilbert transform to convert the real field B_z provided by the PIC code into a complex field ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$, where the imaginary part is such that the field represents a beam propagating in the positive direction along the x-axis.

The field is given by the following mode decomposition:

$$\frac{| e| {B}_{z}^{{{{{{{{\rm{H}}}}}}}}}(\widetilde{x},\widetilde{r},\phi ;t)}{{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega }=\mathop{\sum }\limits_{p=0}^{\infty }\left[\mathop{\sum }\limits_{l=-\infty }^{\infty }{b}_{p,l}(\xi ){\psi }_{p,l}(\widetilde{x},\widetilde{r},\phi )\exp (i\xi )\right].$$

(21)

We find the complex amplitudes b_p,l(ξ) by performing a double integral

$${b}_{p,l}(\xi )=\int\nolimits_{0}^{2\pi }d\phi \left[\int\nolimits_{0}^{\infty }\frac{| e| {B}_{z}^{{{{{{{{\rm{H}}}}}}}}}}{{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega }{\psi }_{p,l}^{* }(\widetilde{x},\widetilde{r},\phi )\exp (-i\xi )\widetilde{r}d\widetilde{r}\right].$$

(22)

The transverse coordinate is normalized to ${w}_{0}^{\prime}$ rather than to w₀ that is associated with the irradiating beam. We determine the value of ${w}_{0}^{\prime}$ by minimizing the number of modes with considerable amplitude in the decomposition, as detailed in the Methods. To understand the need for minimization, consider the original beam. It is represented by a single-mode with l = −1 and p = 0 if ${w}_{0}^{\prime}={w}_{0}$. On the other hand, it is represented by multiple modes if ${w}_{0}^{\prime}\ne {w}_{0}$. The amplitudes of the additional modes increase with the increase of the mismatch in the transverse scale, $| {w}_{0}^{\prime}-{w}_{0}|$. The two representations are equivalent, but the decomposition that contains only a single mode is much easier to use when considering electron acceleration.

Figure 3 shows $| {B}_{z}^{{{{{{{{\rm{H}}}}}}}}}|$ of the transmitted beam in the simulations with ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ and ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ at t = 88.3 fs [see Fig. 3a, d]. The discussed minimization procedure yields ${w}_{0}^{\prime}/{w}_{0}\approx 0.8$ for ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ and ${w}_{0}^{\prime}/{w}_{0}\approx 0.9$ for ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$. Additional details are provided in Methods. In both simulations, the modes with l = −1 and p = 0, which are the l and p values of the original beam, dominate the decomposition. The corresponding field profiles for these modes in the (x, y) plane are shown in Fig. 3b, e, where we use the following notation: $| e| {B}_{p,l}/{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega ={b}_{p,l}(\xi ){\psi }_{p,l}(\widetilde{x},\widetilde{r},\phi )\exp (i\xi )$. We find that $\max | {b}_{0,-1}| \approx 92.43$ for ${n}_{\max }=2.5$, whereas $\max | {b}_{0,-1}| \approx 94.37$ for ${n}_{\max }=0.5$. For comparison, $\max | {b}_{0,-1}| \approx 88.6$ in the original beam. The amplitude increase is a result of the beam narrowing that occurs during the propagation inside the target. In both cases, the amplitudes of the modes with l ≠ −1 are negligible.

Fig. 3: Mode structure of the laser beam at higher and lower target densities.

a Amplitude of the complex field ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ determined by the Hilbert transform from a snapshot of B_z at t = 88.3 fs in the 3D PIC simulation for a target with ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$. b The amplitude of the dominant mode with l = −1 and p = 0 obtained by mode decomposition of ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ in (a). c The amplitude of a generated mode with l = −1 and p = 2 obtained by mode decomposition of ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ in (a). d Amplitude of the complex field ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ determined by the Hilbert transform from a snapshot of B_z at t = 88.3 fs in the 3D PIC simulation for a target with ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$. e The amplitude of the dominant mode with l = −1 and p = 0 obtained by mode decomposition of ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ in (d). f The amplitude of a generated mode with l = −1 and p = 2 obtained by mode decomposition of ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ in (d).

The narrowing of the beam inside the plasma generates modes with higher radial numbers. In both cases, the generated mode with the biggest amplitude is the p = 2 mode (see Methods for a plot of mode amplitudes). However, the mode amplitude increases with the increase of the target density. We find that $\max | {b}_{2,-1}| \approx 30.68$ for ${n}_{\max }=2.5$, whereas $\max | {b}_{2,-1}| \approx 16.51$ for ${n}_{\max }=0.5$. The structure of the modes with p = 2 and l = −1 is shown in Fig. 3c,  f. The mode decomposition indicates that there is a phase shift with respect to the dominant mode, with Δξ ≈ −2.73 for ${n}_{\max }=2.5$ and Δξ ≈ −2.40 for ${n}_{\max }=0.5$ close to the peak of the envelope. The phase shift varies only gradually along each transmitted beam compared to the oscillations associated with λ₀, so we can treat it as being constant for our estimates.

The described changes in the structure of the transmitted beams impact the acceleration of electrons in vacuum. Our primary focus is on the relative differences between the simulations with ${n}_{\max }=2.5$ and ${n}_{\max }=0.5$. We use Eq. (18) to find that for the acceleration by the main mode, i.e., the mode with p = 0 and l = −1,

$$\frac{{({{\Delta }}{p}_{x})}_{{n}_{\max } = 2.5}^{{{{{{{{\rm{term}}}}}}}}}}{{({{\Delta }}{p}_{x})}_{{n}_{\max } = 0.5}^{{{{{{{{\rm{term}}}}}}}}}}={\left[| {b}_{0,-1}| {w}_{0}^{\prime}\right]}_{{n}_{\max } = 2.5}\bigg/{\left[| {b}_{0,-1}| {w}_{0}^{\prime}\right]}_{{n}_{\max } = 0.5}\approx 0.87,$$

(23)

where we took into account that the amplitude of the transverse electric field is equal to the amplitude of the magnetic field and that ${\theta }_{d}\propto 1/{w}_{0}^{\prime}$. The estimate assumes that the acceleration starts close to the focal plane and that the electrons are injected into the most favorable phase, which is Φ₀ = 0. The conclusion from Eq. (23) is that there is less power associated with the dominant mode at higher density, which contributes to the reduction in energy gain.

The impact of the p = 2 mode can also be assessed using Eq. (18). The analysis that we used to derive Eq. (18) neglects changes to the electron velocity during the acceleration. Therefore, the contributions from the modes with p = 2 and p = 0 can be added up while taking into account their phase shift. For the sake of simplicity, we again assume that the acceleration starts close to the focal plane and that the electrons are injected into the p = 0 mode with Φ₀ = 0. Using the parameters provided earlier for the p = 2 mode in both simulations, we find that

$$\frac{{({{\Delta }}{p}_{x})}_{{n}_{\max } = 2.5}^{{{{{{{{\rm{term}}}}}}}}}}{{({{\Delta }}{p}_{x})}_{{n}_{\max } = 0.5}^{{{{{{{{\rm{term}}}}}}}}}}= {\left[| {b}_{0,-1}| {w}_{0}^{\prime}+\frac{1}{\sqrt{3}}| {b}_{2,-1}| \cos ({{\Delta }}\xi ){w}_{0}^{\prime}\right]}_{{n}_{\max } = 2.5}\\ \bigg/{\left[| {b}_{0,-1}| {w}_{0}^{\prime}+\frac{1}{\sqrt{3}}| {b}_{2,-1}| \cos ({{\Delta }}\xi ){w}_{0}^{\prime}\right]}_{{n}_{\max } = 0.5}\approx 0.78.$$

(24)

The difference between the two cases has further increased with the inclusion of the p = 2 mode that is generated while the beam passes through the target. At ${n}_{\max }=2.5$, the amplitude of this mode is almost two times higher than at ${n}_{\max }=0.5$. This mode is decelerating the electron due to its phase shift, which explains why the difference between the two cases has increased.

Our analysis neglects higher-order harmonics generated during the considered laser-plasma interaction. The amplitude of the second harmonic in our simulations is roughly two orders of magnitude smaller than the amplitude of the main mode. We have performed two additional simulations with a higher spatial resolution (see the Methods section for details): one for the target with n_e = 2.5n_c and one for the target with n_e = 0.5n_c. In these simulations, the amplitude of the second harmonic is three orders of magnitude smaller than the amplitude of the main mode, which means that the amplitude of the second harmonic is lower than in the original simulations. We can therefore conclude that the harmonics generated in our setup are too weak to significantly influence electron acceleration. The mode decomposition shows higher radial modes with amplitudes that are ~30% of the zeroth mode, far larger than the contributions of the second harmonic. This is the reason why our focus is on the impact of the higher-order radial modes.

Our estimates explain the trend observed in the simulations and, more importantly, clarify the negative impact of higher radial modes on electron acceleration. Another feature of the modes with the high p values is that their transverse fields peak much closer to the axis than for the mode with p = 0. For example, the field in Fig. 3c peaks close to the vertical dashed line, whereas the field in Fig. 3b peaks at a distance from the central axis that is about three times greater. The same is the case for the transverse electric field. The transverse fields of the higher p modes close to the central axis deteriorate electron confinement and increase the rate of the phase slip by adding transverse momentum. These aspects are likely to further reduce the energy gain in the higher density case where the modes with p ≥ 2 have a much higher amplitude (see Methods).

Optimal regime at normal and oblique incidence

We now consider just the lowest density case, ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$, that delivers the best performance with the goal of providing additional details regarding the electron acceleration.

Figure 4 shows the case of normal incidence, where panel a shows the electron density during the laser beam transmission and panels b through e show various characteristics of the accelerated electrons much later in time. During the laser beam transmission, it produces a ring-like channel inside the target, with a narrow mostly straight compressed region at the center, as seen in Fig. 4a. The electrons injected into the laser pulse are accelerated in the positive direction along the x-axis. Figure 4e shows the number density n_e in the (x, y)-plane at t = 238.3 fs and demonstrates that the electrons remain tightly grouped in bunches close to the laser axis. Figure 4b shows the corresponding areal density obtained by integrating n_e of the entire electron beam along x. The areal density is concentrated in the region where the longitudinal laser electric field dominates. The average divergence angle for the electrons with r < 1 μm is 47 mrad or 2.7^∘. The electron energy distribution as a function of the longitudinal coordinate x and divergence angle θ_⊥ is shown in Fig. 4d, c, respectively. The profile of the maximum kinetic energy in Fig. 4d is similar to the envelope of the laser pulse, though the higher energy electrons (ε_k ≳ 1 GeV) can be seen to be grouped in bunches with a length of ≲0.2 μm, which is equivalent to a temporal bunch length of ≲0.6 fs. The peaks correspond to the oscillations of the longitudinal laser electric field.

Fig. 4: Optimal regime of electron acceleration at normal incidence and comparison with a plane-polarized Gaussian beam.

a–e Electron data from a simulation where a target with ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ is irradiated by the helical beam. f–h Electron data from a simulation where the same target is irradiated by a plane-polarized Gaussian beam that has the same peak power of 3 PW. a, f Electron density n_e normalized to the critical density n_c during laser pulse transmission. b, g Areal density at t = 238.3 fs calculated by integrating n_e along x. e Density of electrons accelerated by the helical beam at t = 238.3 fs. The vertical dashed lines mark the region shown in (b). c, h Electron energy distribution at t = 398.3 fs for different divergence angles ${\theta }_{\perp }={\tan }^{-1}\left({p}_{x}/\sqrt{{p}_{y}^{2}+{p}_{z}^{2}}\right)$. The distribution in (c) is calculated for ∣y, z∣≤5 μm, whereas the distribution in (h) is calculated for ∣y, z∣≤14 μm. d Electron energy distribution along the x-axis at t = 398.3 fs for the case with the helical beam, where ε_k is the kinetic energy. Only the electrons with ∣y, z∣≤5 μm are shown. i Electron spectra (t = 398.3 fs), where the red curve shows electrons with ∣y, z∣≤5 μm in the simulation with the helical beam and the black curve shows electrons with ∣y, z∣≤14 μm in the simulation with the Gaussian beam.

In order to emphasize the advantages of using the helical beam to inject and accelerate electrons, we have repeated the simulation discussed here using a plane-polarized Gaussian beam that has the same energy, peak power, and temporal envelope. Figure 4f shows a snapshot of the electron density while the Gaussian beam is traversing the target. In contrast to Fig. 4a for the helical beam, no dense population of electrons is being injected in the near-axis region. Instead, the electrons appear to be strongly divergent even at this early stage. This aspect, together with fundamental differences in the field topology, leads to a strongly divergent and very diffuse electron population at later times. The areal density of laser-accelerated electrons in Fig. 4g shows that the electron profile is more reminiscent of a result associated with a point source rather than with a beam.

The electron energy spectra are compared between the two runs by using all of the electrons generated by the Gaussian beam. In the case of the helical beam, we select only the electrons in the near-axis region. This is done by limiting the transverse dimensions to ∣y, z∣ < 5 μm at t ≈ 398 fs. The Gaussian laser beam produces so few electrons in the same region, marked with a dashed square in Fig. 4g, that a direct comparison would discard most of the laser-accelerated electrons. This is the reason why the plots in Fig. 4h, i that corresponds to the Gaussian beam include all of the electrons in the simulation box. Our box is a square that is 28 μm wide, so the corresponding selection criterion is ∣y, z∣ < 14 μm. It is evident from the electron spectra in Fig. 4i that the cut-off energy for the Gaussian beam is roughly 1.7 lower than that for the helical beam. Moreover, the energetic electrons generated by the Gaussian beam have a much wider angular distribution, as seen in Fig. 4h. Another way to interpret the result is by pointing out that the energetic collimated part (ε_k > 800 MeV; θ_⊥ < 80 mrad) from Fig. 4c is missing in Fig. 4h.

It is also worth noting that even though both beams have the same peak power (3 PW), the helical beam has a lower peak electric field. Indeed, due to both the circular polarization and the intrinsically hollow beam profile, the peak electric field in the helical beam, $| e| {E}_{\max }/{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega \simeq 42$, is roughly two times lower than the peak electric field in the plane-polarized Gaussian beam, $| e| {E}_{\max }/{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega \simeq 88$. Despite this, the helical beam produces electrons with peak energy close to twice that of the Gaussian beam. This underlines the fact that our findings are a manifestation of qualitative differences in physics between the two types of laser beams.

Firing a laser pulse at normal incidence to a target surface, even one that has low reflectivity is not a procedure that is regularly performed in high-intensity high-power laser systems and so it is necessary to examine the electron acceleration mechanism for a case of oblique incidence. An incidence angle of 15^∘ (to the normal direction to the target surface) is often sufficient to eliminate the danger of reflection. At the same time, this angle is sufficiently small not to fundamentally alter the interaction discussed in the manuscript. In order to implement this regime, we rotate the target rather than the irradiating laser beam, so that the laser axis is at 15^∘ to target normally. The simulation parameters are provided in the Methods section.

Figure 5 shows the results for the oblique incidence case. The electron density during the laser pulse transmission by the target is shown in Fig. 5a. The shape of the channel is asymmetric, which translates into changes in the radial position of the accelerated electrons and their density compared to the case of normal incidence. Specifically, the density of the accelerated electron population is lower by a factor of ~7. However, the average divergence angle of the electrons close to the axis remains relatively unchanged. It is 50 mrad or 2.9^∘ for the electrons within 1 μm of the central axis. The electron energy distribution as a function of the divergence angle θ_⊥ is shown in Fig. 5b.

Fig. 5: Optimal regime of electron acceleration at oblique incidence.

a Electron density n_e normalized to the critical density n_c at t = 26.6 fs for a target with an initial maximum electron density ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$. b Electron energy distribution at t = 386.6 fs for different divergence angles ${\theta }_{\perp }={\tan }^{-1}\left({p}_{x}/\sqrt{{p}_{y}^{2}+{p}_{z}^{2}}\right)$. Only those electrons that have ∣y∣≤5 μm and ∣z∣≤5 μm are shown in this plot. c Electron energy spectra for the normal and oblique cases at the end of each simulation (t = t_end). The spectra are for the electrons that are closer than 1 μm to the axis of the laser beam. Here t_end = 398.3 fs for the case of normal incidence and t_end = 386.6 fs for the case of oblique incidence.

Figure 5c compares the electron energy spectra for the normal and oblique cases at the end of the simulation. Here we select only those electrons that are closer than 1 μm to the laser propagation axis in order to examine the spectrum of the collimated part of the electron population. Below 800 MeV, the two spectra are similar. The spectrum for the oblique incidence case has a slightly steeper slope and, as a result, a somewhat lower number of energetic electrons. Above 800 MeV, the spectrum for the oblique case appears to be under-resolved, which precludes us from using it to make a reliable comparison. The likely cause is the reduction in electron density. One would need to increase the number of macro-particles per cell by an order of magnitude in order to better resolve the energetic tail above 1 GeV. We can conclude based on the provided results that the investigated mechanism is sufficiently robust and that it can be used at oblique incidence without a significant increase in the divergence of the electron beam.

Discussion

We have shown that the injection and retention problems of the electron vacuum acceleration can be successfully solved by employing a thin near-critical target and a high-intensity helical laser beam with a helical index l = −1 and a radial index p = 0. The injection takes place while the laser pulse goes through the target. In contrast to a conventional beam, the retention is provided by the field of the beam itself, because the transverse fields vanish on the central axis while the longitudinal fields, including the magnetic field, peak on axis. The electrons are first accelerated inside the target and then behind the target in the vacuum by the longitudinal electric field of the transmitted pulse. Our simulations predict an electron beam with a peak energy of 1.5 GeV for a 3 PW laser. The divergence of the beam, whose charge is about 50 pC, is less than 3^∘. The following unique features distinguish our mechanism from other more mature approaches (e.g., laser wakefield acceleration): short acceleration distance (~100 μm); high areal density (~10¹⁶ cm⁻²); compact transverse size (~1 μm) of the beam; and bunching of energetic electrons, with the bunches being ~100 as in duration.

From an experimental point of view, the extremely short acceleration distance is a significant advantage. It opens up the possibility of performing experiments with energetic electron beams using very compact setups. Laser wakefield acceleration experiments with high-power lasers require parabolic mirrors of long focal length, typically 10s of meters, and gas targets of 10s of centimeters, whereas the setup proposed in this manuscript can be achieved with parabolic mirrors of short focal length, typically below 2 m, and very small targets. This is an important aspect because high-power laser facilities would need to have large space for very long focusing optics and such space may not be always available. Therefore, having the possibility of performing particle acceleration over short acceleration distances can be beneficial for a wide number of facilities. The resulting electron beam can be used to create a compact collider for quantum electrodynamics-based experiments²⁵ and applied research (e.g., generation of highly energetic photons via inverse scattering and electron-positron beam generation).

There are also advantages to our setup when compared to a more commonly used setup for vacuum electron acceleration where the laser is reflected off a plasma mirror. In our setup, the interaction of the laser with the target is volumetric, which eliminates the sensitivity to the surface density gradient. The terminal energy gain is more efficient. Our simulations predict peak energy of 1.5 GeV for a 3 PW beam, which is comparable to the prediction for a 6 PW laser that is reflected off a plasma mirror¹⁷. However, our simulations also show that the laser-target interaction can become detrimental if it leads to the excitation of higher-order radial modes. This consideration imposes an upper limit on the target density. For the considered laser parameters, we determined that the electron density of the ~10 μm target should remain at or below the critical density.

The parameters selected for this study are such that both the laser and target specifications are within reach of the existing laser systems and target fabrication facilities. The production of helical laser beams has already been demonstrated³, whereas the laser pulse intensity and duration are similar to those of the Extreme Light Infrastructure-Nuclear Physics (ELI-NP) laser facility^7,8. The capability to generate circularly-polarized beams is also already available at ELI-NP and was successfully demonstrated in recent experimental campaigns. This method is based on commercially available large aperture mica plates. The production of foams at densities as low as 2 mg cm⁻³is almost routine at this point^20,21. The considered thickness can potentially be achieved by employing a concave structured foam within a small opening (of the order of an mm) on a thin sheet. One advantage of inorganic foams such as SiO₂ is that they combine particularly fine pore structures (typically a few nm) with extremely low densities (as low as 2 mg cm⁻³)^20,21,26. This allows for some reduction in the complexity when considering high-power high-intensity laser pulses. Specifically, the pore collapse time^27,28 is likely to occur during laser prepulse due to the fine pore structure.

Methods

Particle-in-cell simulations

Table 1 provides detailed parameters for the simulations with normal incidence presented in the manuscript. Simulations were carried out using the fully relativistic PIC code Smilei^29,30. All our simulations are 3D-3V.

Table 1 3D PIC simulation parameters for cases with normal laser incidence.

The x-axis is aligned with the axis of the irradiating laser beam that propagates in the positive direction. The beam is launched at the boundary (x = −8 μm) of the simulation box by specifying the transverse magnetic field. The beam is focused (in the absence of the target) at x = 0 μm. The wavelength λ₀ and the divergence angle θ_d are given in Table 1. The corresponding Rayleigh length is ${x}_{R}={\lambda }_{0}/\pi {\theta }_{{{{{{{{\rm{d}}}}}}}}}^{2}\approx 35.33\,\mu {{{{{{{\rm{m}}}}}}}}$ and the corresponding beam width is w₀ = λ₀/πθ_d = 3 μm. The envelope of the pulse is Gaussian, with a pulse duration of 29.4 fs (full width at half maximum for the intensity). We limit the total duration of the envelope to 150 fs (the envelope is truncated and set to zero 75 fs before and after the peak of the envelope). The laser beam is circularly-polarized with l = −1, p = 0, and σ = 1. It is created by two linearly-polarized beams (l = −1, p = 0) with a phase offset. We use a moving window in our simulation, which reduces the size of the computational domain needed to simulate the electron acceleration for ~400 fs. The window moves with the speed of light along the x-axis. The window starts moving after the beam has been fully in injected into the box. The start time is t = 28.3 fs, with t = 0 fs being the time when the peak of the envelope reaches x = 0 μm.

The target is initialized as a fully ionized silicon dioxide plasma slab. The electron density profile along the x-axis is

$${n}_{{{{{{{{\rm{e}}}}}}}}}=\left\{\begin{array}{ll}{n}_{\max }\exp [(| x| -{{\Delta }}{x}_{1})/{{\Delta }}{x}_{2}] &{{{{{{{\rm{for}}}}}}}}\,4\,\mu {{{{{{{\rm{m}}}}}}}} < | x| < 6\,\mu {{{{{{{\rm{m}}}}}}}};\\ {n}_{\max } &{{{{{{{\rm{for}}}}}}}}\,| x| \le 4\,\mu {{{{{{{\rm{m}}}}}}}},\end{array}\right.$$

(25)

where Δx₁ = 4 μm and Δx₂ = 0.5 μm, so that the central plane is located at x = 0 μm. The electron density is independent of y and z. The three values for ${n}_{\max }$ used in our simulations are listed in Table 1. In each case, the densities of oxygen and silicon ions are chosen as specified in Table 1 to ensure that the target is quasineutral.

In order to examine the generation of high harmonics, we have performed two simulations with a higher spatial resolution than that listed in Table 1. The new resolution is increased to 40 cells/micron in the x-direction and to 27.4 cells/micron in both y and z directions. These simulations have a larger box size of 36.8 μm × 28 μm × 28 μm. They are run without using the moving window.

One additional simulation is performed for a case of oblique incidence. In this simulation, the target is tilted such that the front surface normal is at 15^∘ to the x-axis. One of the initial domain boundaries is moved by 3 μm from x = −8 μm to x = −11.5 μm and the width of the simulation box along x is increased to 31.5 μm to keep the original spatial resolution. All other parameters remain the same.

We compare our results for the optimal regime at normal incidence with those for a linearly-polarized Gaussian pulse. The comparison is performed using the simulation setup for a target with n_e = 0.5n_c where the original beam is replaced by a linearly-polarized Gaussian beam that has the same energy, peak power, and temporal envelope. The transverse electric field of this beam is directed along the y-axis, whereas its magnetic field is directed along the z-axis. The normalized peak amplitude is a₀ = 88.6.

Mode decomposition

A snapshot of an electric or magnetic field generated by the 3D PIC code can be presented as a superposition of the ${\psi }_{p,l}(\widetilde{x},\widetilde{r},\phi )$ modes with different twist indices l and radial indices p. In the transmitted beam, all of the modes propagate in the positive direction along the x-axis, which means that their complex field has the $\exp (i\xi )=\exp (ikx-i\omega t)$ multiplier, where k = 2π/λ₀ is the amplitude of the wave vector. However, this information is not automatically encoded in the real field values provided by the code. To illustrate the ambiguity, consider a real electric field with a longitudinal profile given by ${E}_{0}\cos (kx)$ at t = 0. This field can be the real part of ${E}_{0}\exp (ikx-\omega t)$ or the real part of ${E}_{0}\exp (-ikx-i\omega t)$, which corresponds to a mode propagating in the negative direction along the x-axis. This field can even be the field of two counter-propagating modes, with the complex field given by $0.5{E}_{0}\exp (ikx-i\omega t)+0.5{E}_{0}\exp (-ikx-i\omega t)$.

The ambiguity can be removed by recovering the missing information using the Hilbert transform along x. The Hilbert transform converts the real field provided by the PIC code into a complex field, where the imaginary part is such that the field represents a beam propagating in the positive direction along the x-axis. We denote the field obtained via the Hilbert transform using the superscript H. For example, the Hilbert transform converts the real longitudinal field (at time t)

$${E}_{x}(\widetilde{x})=-\frac{g[\xi (t)]{E}_{\parallel }^{\max }}{1+{\widetilde{x}}^{2}}\sin \left[\xi (t)-2(1+p){\tan }^{-1}(\widetilde{x})\right]$$

(26)

into ${E}_{x}^{{{{{{{{\rm{H}}}}}}}}}(\widetilde{x})$, with ${{{{{{{\rm{Re}}}}}}}}\left[{E}_{x}^{{{{{{{{\rm{H}}}}}}}}}(\widetilde{x})\right]={E}_{x}(\widetilde{x})$ and

$${{{{{{{\rm{Im}}}}}}}}[{E}_{x}(\widetilde{x})]=\frac{g[\xi (t)]{E}_{\parallel }^{\max }}{1+{\widetilde{x}}^{2}}\cos \left[\xi (t)-2(1+p){\tan }^{-1}(\widetilde{x})\right].$$

(27)

The resulting complex field ${E}_{x}^{{{{{{{{\rm{H}}}}}}}}}$ is a snapshot of the field of a forward propagating mode given by Eq. (10).

The fields obtained via the Hilbert transform can be presented as the following superposition:

$$\frac{| e| {B}_{z}^{{{{{{{{\rm{H}}}}}}}}}(\widetilde{x},\widetilde{r},\phi ;t)}{{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega }=\left[\mathop{\sum }\limits_{p=0}^{\infty }\left[\mathop{\sum }\limits_{l=-\infty }^{\infty }{b}_{p,l}(\xi ){\psi }_{p,l}(\widetilde{x},\widetilde{r},\phi )\exp (i\xi )\right]\right],$$

(28)

where, without any loss of generality, we used the z-component of the magnetic field to provide an explicit expression. Here b_p,l(ξ) is a dimensionless complex amplitude that has both real and imaginary parts. If ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}(\widetilde{x},\widetilde{r},\phi )$ is known at time t, then one can recover all complex amplitudes by performing a double integral,

$${b}_{p,l}(\xi )=\int\nolimits_{0}^{2\pi }d\phi \left[\int\nolimits_{0}^{\infty }\frac{| e| {B}_{z}^{{{{{{{{\rm{H}}}}}}}}}}{{m}_{{{{{{{{\rm{e}}}}}}}}}c\omega }{\psi }_{p,l}^{* }(\widetilde{x},\widetilde{r},\phi )\exp (-i\xi )\widetilde{r}d\widetilde{r}\right],$$

(29)

for all possible combinations of l and p. The meaning of b_p,l can be readily understood when considering a simple signal ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}(\widetilde{x},\widetilde{r},\phi )={B}_{0}{\psi }_{p^{\prime} ,l^{\prime} }g(\xi )\exp (i\xi )$. This signal consists of an amplitude of B₀, a single Laguerre-Gaussian mode ${\psi }_{p^{\prime} ,l^{\prime} }$, an envelope g(ξ), and an oscillating term $\exp (i\xi )$. In this simple case the resulting decomposition, when trying all values of p and l, from Eq. (29) will give a single nonzero amplitude of ${b}_{p^{\prime} ,l^{\prime} }(\xi )\equiv {B}_{0}g(\xi )$, where g(ξ) is the temporal envelope of the original signal. The right-hand side of Eq. (29) is calculated for ξ at time t, so the result is a function of $\widetilde{x}$. In order to find the corresponding dependence on ξ, we take into account that $\xi =2\widetilde{x}/{\theta }_{{{{{{{{\rm{d}}}}}}}}}^{2}-\omega t$ at a given time t. We have benchmarked this method using a 3D PIC simulation (without a target) for a helical circularly-polarized beam with p = 0, l = −1, and σ = −1. Following our procedure, we have recovered b_0,−1(ξ) from a single snapshot of the real field ${B}_{z}(\widetilde{x},\widetilde{r},\phi )$ outputted by the PIC code.

The representation given by Eq. (28) is unique for a given w₀. The value of w₀ sets a characteristic transverse scale. A single helical mode with a beam width w_b is represented by a single term if w₀ = w_b. On the other hand, if w₀ ≠ w_b, then, in general, it is represented by multiple terms. The number of terms with an appreciable amplitude can be adjusted by adjusting w₀. We use this approach when post-processing the transmitted beam whose w_b is not known to minimize the number of terms in the mode decomposition. Specifically, we minimize the sum

$$M\equiv \left[\mathop{\sum }\limits_{p=0}^{\infty }\left[\mathop{\sum }\limits_{l=-\infty }^{\infty }\int\nolimits_{-\infty }^{\infty }| {b}_{p,l}(\xi )| d\xi \right]\right]/\left[\int\nolimits_{-\infty }^{\infty }| {b}_{0,-1}(\xi )| d\xi \right]-1$$

(30)

by varying the width that we denote as ${w}_{0}^{\prime}$ to distinguish it from the width of the original beam w₀. This approach assumes that the mode with l = −1 and p = 0 is the dominant mode in the transmitted beam, which is indeed the case for all our simulations. It is worth noting that M = 0 at ${w}_{0}^{\prime}={w}_{0}$ for the irradiating beam because it can be represented by a single mode with l = −1 and p = 0.

Figure 6 shows the mode decomposition for two simulations discussed in the main text: a simulation with ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ and a simulation with ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$. The values of the sum defined by Eq. (30) for different ${w}_{0}^{\prime}$ are shown in Fig. 6. We find that M reaches its local minimum at ${w}_{0}^{\prime}/{w}_{0}=0.8$ for ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ and at ${w}_{0}^{\prime}/{w}_{0}=0.9$ for ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$. In both cases, the modes with l = −1 dominate. The plots of 〈b_p,−1〉 for these optimal values of ${w}_{0}^{\prime}$ are shown in Fig. 6a, b, d.

Fig. 6: Mode decomposition.

a Amplitudes of different radial modes for ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ in Fig. 3a obtained via Eq. ((29)). b Amplitudes of different radial modes for ${B}_{z}^{{{{{{{{\rm{H}}}}}}}}}$ in Fig. 3d obtained via Eq. (29). c The sum of mode amplitudes is defined by Eq. (30) as a function of ${w}_{0}^{\prime}$ that sets the characteristic transverse scale in the mode decomposition. The crosses mark the values that are used in (a) and (b) to compute the mode amplitudes. The solid and dashed curves correspond to the targets with ${n}_{\max }=2.5{n}_{{{{{{{{\rm{c}}}}}}}}}$ and ${n}_{\max }=0.5{n}_{{{{{{{{\rm{c}}}}}}}}}$, respectively. d Mode amplitudes at the axial location marked with a dashed line in (a) and (b).