Coupled electronic and magnetic excitations in the cuprates and their role in the superconducting transition

Abstract

The formation of Cooper pairs, a bound state of two electrons of opposite spin and momenta by exchange of a phonon, is a defining feature of conventional superconductivity. In the cuprate high temperature superconductors, even though the superconducting state also consists of Cooper pairs, the pairing mechanism remains intensely debated. Here, we investigate superconducting pairing in the Bi₂Sr₂CaCu₂O_8+δ (Bi2212) cuprate by employing spectral functions obtained from angle-resolved photoemission as input to the Bethe-Salpeter equation. Assuming Cooper pairing is driven by spin fluctuations, we construct the spin-fluctuation-mediated pairing interaction and use it to compute the eigenfunctions and eigenvalues of the Bethe-Salpeter equation for multiple Bi2212 samples. The leading d-wave eigenvalue increases as the temperature is decreased toward T_c, reaching a value of approximately 1 at the T_c corresponding to each doping value. This suggests that spin fluctuations can approximately account for T_c and mediate pairing in the cuprate superconductors.

Introduction

Superconductivity in the cuprates emerges following quantum melting of the antiferromagnetic Mott insulating state of the parent compound, either via electron or hole doping. It has been proposed that the spin fluctuations resulting from the melted Mott state act as the “glue” leading to Cooper pairing in high-temperature superconductors^1,2. In support of this proposal, neutron scattering experiments on the YBa₂C₃O_6.95 cuprate superconductors demonstrate that the change in magnetic exchange energy between the superconducting and normal states can provide sufficient superconducting condensation energy³. Moreover, it has been shown that the interaction of electrons with spin fluctuations can account for several anomalies in charge, spin, and optical response measurements in the cuprates². An outstanding question is whether the spin-fluctuation-mediated pairing interaction is strong enough to yield the high transition temperatures observed in these materials.

While several studies have attempted to answer this important question by using a combination of theoretical approaches and various experimentally measured electronic and spin excitation spectra, the results have been inconclusive. Using the electron spectral functions from angle-resolved photoemission spectroscopy (ARPES) experiments in near-optimally doped Bi2212 and solving a generalized gap equation, Mishra et al.⁴ did not obtain a superconducting transition at any temperature. In contrast, Dahm et al.⁵, using the spin excitation spectrum measured via inelastic neutron scattering experiments (INS) in YBa₂C₃O_6.6 and computing the electron spectral function theoretically rather than utilizing experimental ARPES data, obtained a superconducting transition temperature of about 150 K. In a subsequent theoretical study, Maier et al.⁶ ascribed the failure of Mishra et al. to find any superconducting transition to the fact that the experimental ARPES data were taken at a temperature of 140 K, well above the critical temperature of T_c= 90 K. Taken together, these studies suggest that, in order to reliably determine whether the spin-fermion interaction can be the source of the unconventional superconducting state in the cuprate superconductors, three requirements need to be satisfied: (i) experimental ARPES data need to be taken above, but near T_c, (ii) the effective superconducting pairing vertex needs to be computed from these ARPES data, and (iii) the solution of the gap equation, using the ARPES data and the derived pairing vertex as input, should reproduce the transition temperature of the material.

Here, we use experimental ARPES excitation spectra from Bi2212 near and above T_c to construct the spin-fluctuation-mediated pairing interaction and solve the gap equation. Following previous work^4,5,6,7, we employ the Bethe-Salpeter equation for a generalized order parameter $\varPhi ({{{\bf{k}}}},{\omega }_{n},T)$:

$$\lambda \left(T\right)\varPhi (T)=\hat{O}\left(T\right)\varPhi (T)$$

(1)

The transition to superconductivity takes place when the eigenvalue λ reaches λ(T_c) = 1. The operator $\hat{O}\left(T\right)$ is given by (we solve the equation in Matsubara frequency space):

$$\hat{O}\left(T\right)\varPhi \left({{{\bf{k}}}},{\omega }_{n},T\right)= -\frac{T}{N}\mathop{\sum}\limits_{{{{{\bf{k}}}}}^{\prime},{\varOmega }_{n}}V\left({{{\bf{k}}}}-{{{{\bf{k}}}}}^{\prime},i{\omega }_{n}-i{\varOmega }_{n},T\right)\\ G\left({{{{\bf{k}}}}}^{\prime},i{\varOmega }_{n},T\right)G\left({{{{\boldsymbol{-}}}}{{{\bf{k}}}}}^{\prime} ,-i{\varOmega }_{n},T\right)\varPhi \left({{{{\bf{k}}}}}^{\prime},{\varOmega }_{n},T\right)$$

(2)

where G is the electron’s Green’s function and V the effective electron–electron pairing interaction. Equations (1) and (2) are quite universal in that the specific mechanism leading to the emergence of superconductivity is reflected only in the form of V, as noted previously by Mishra et al. For the three samples considered (see “Results—Bethe-Salpeter Equation”), we find solutions to this equation which approximately reproduce their observed T_c values.

Results and discussion

Spectral function

The required quantities for the Bethe-Salpeter equation can be obtained, within certain approximations, from the electron spectral function $A({{{\bf{k}}}},\omega )$ obtained from the ARPES signal $I\left({{{\bf{k}}}},\omega \right)={I}_{0}f\left(\omega \right)A\left({{{\bf{k}}}},\omega \right)+B\left(\omega \right)$, where I₀ is the matrix element, $f(\omega )$ the Fermi function, and $B(\omega )$ the inelastic background signal. To extract the spectral function, we first subtract the background signal, while simultaneously normalizing out the matrix element I₀⁸. We then note that, although ARPES only measures the occupied states, the cuprates exhibit particle-hole mixing below⁹ and slightly above¹⁰ T_c. Therefore, the symmetrized spectral function $A({{{\bf{k}}}},\omega )=I({{{\bf{k}}}},\omega )+I(-{{{\bf{k}}}}+2{{{{\bf{k}}}}}_{{{{\bf{F}}}}},-\omega )$ also yields the unoccupied part, for k values close to the Fermi momentum k_F. The validity of this assumption in this work is justified by (i) the approximate insensitivity of the pairing interaction constructed from ARPES data to particle-hole asymmetry put in by hand⁸ and (ii) the robustness of the Bethe-Salpeter eigenvalues (see “Results—Bethe-Salpeter Equation”) against the stronger assumption $A({{{\bf{k}}}},\omega )=A({{{\bf{k}}}},-\omega )$. Finally, the spectral function is normalized to unit area within the binding energies probed in our experiments. (For more details, see “Methods—Data analysis” and Supplementary Note 2) The Green’s functions in the Matsubara representation then follow from the relation

$$G\left({{{\bf{k}}}},{\omega }_{n},T\right)=\int {{{\rm{d}}}}\omega \frac{A({{{\bf{k}}}},\omega ,T)}{i{\omega }_{n}-\omega }$$

(3)

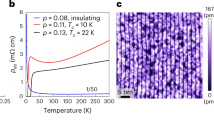
We analyze ARPES data for three Bi2212 samples: two thin films, one underdoped with T_c= 67 K (UD67), the other optimally doped with T_c= 80 K (OP80), and a single crystal, optimally doped with T_c= 91 K (OP91). (The data for the thin films have been presented elsewhere¹¹.) Representative data are shown in Fig. 1. Figure 1a shows the experimentally determined phase diagram for our samples¹², with the circles, diamonds, and squares indicating the spectra used in this work. In Fig. 1b, we plot the spectral function in the Y-quadrant of the Brillouin zone, with a tight-binding fit to the Fermi surface¹³ appearing as a continuous yellow line. The measured spectra for the UD67 sample along the high symmetry directions, highlighted by the coloured dots in panel b, are shown in Fig. 1c.

Fig. 1: Extent and resolution of angle-resolved photoemission spectroscopy (ARPES) data employed in the calculation of the pairing interaction V and the Green’s function G.

a Phase diagram of Bi2212. Black circles correspond to the UD67 sample, red diamonds to OP80, and blue squares to OP91. There are two superconducting domes, one dashed for the thin films and one solid for the single crystal, with a higher optimal T_c. b Raw Fermi Surface (after interpolation and reflection about symmetry axes) for the UD67 sample at 20 K. The thin yellow line is a tight-binding fit to the Bi2212 dispersion¹³ and is used here as a guide to the eye. c Energy Distribution Curves corresponding to (b) along the path indicated by the coloured dots. Throughout this article, we take a = 1 for the lattice constant.

Spin susceptibility

For pairing induced by spin fluctuations, we consider the pairing vertex¹⁴

$$V\left({{{\bf{q}}}},i{\omega }_{m}\right)=\frac{3}{2}{U}^{2}\chi \left({{{\bf{q}}}},i{\omega }_{m}\right)$$

(4)

where χ is the spin susceptibility and U is an effective spin-fermion coupling energy. The spectral function allows us to calculate the (real frequency) spin fluctuation propagator in the random phase approximation (RPA) ¹⁵:

$$\chi \left({{{\bf{q}}}},\omega \right)=\frac{{\chi }_{0}({{{\bf{q}}}},\omega )}{1-{U}_{q}{\chi }_{0}\left({{{\bf{q}}}},\omega \right)}$$

(5)

where χ₀ is the bare susceptibility,

$${\chi }_{0}\left({{{\bf{q}}}},\varOmega \right)=\frac{1}{N}\mathop{\sum}\limits_{{{{\bf{k}}}}}{\int }_{-{{\infty }}}^{{{\infty }}}{{{\rm{d}}}}\omega {{{\rm{d}}}}\nu A\left({{{\bf{k}}}},\omega \right)A({{{\bf{k}}}}+{{{\bf{q}}}},\nu )\frac{f\left(\nu \right)-f(\omega )}{\varOmega +\nu -\omega +i\delta }$$

(6)

and the coupling U_q is assumed to have a super-exchange momentum dependence ^13,16,17,18:

$${U}_{q}=-\frac{{U}_{0}}{2}({{\cos }}{q}_{x}+{{\cos }}{q}_{y})$$

(7)

(see Supplementary Note 4). Here, U₀ reflects the strength of the antiferromagnetic interaction in the particle-hole channel. As such, it is in general distinct from the spin-fermion coupling U¹⁹. However, our estimates of U₀ and U (see Supplementary Note 5) indicate that these two energies differ by <11%, and we will therefore take them to be equal for simplicity. Since U₀ is a high energy scale not provided by the RPA nor the low-energy formalism adopted here, its value was chosen so as to reproduce the salient features of the spin susceptibility measured in INS experiments. In particular, in the superconducting state, the cuprates exhibit a sharp resonance in their spin excitation spectra at the commensurate wave-vector ${{{\bf{Q}}}}=({{\pi }},{{\pi }}).$^20,21 The energy of this resonance throughout the phase diagram of the cuprate YBa₂Cu₃O_6+x has been extensively reported; however, due to technical limitations, such information is lacking for underdoped Bi2212. For this reason, we used the empirical relation^21,22,23

$${E}_{{{{\rm{R}}}}}=5.4{k}_{{{{\rm{B}}}}}{T}_{{{{\rm{c}}}}}$$

(8)

to fix the resonance energies for the three samples (${E}_{{{{\rm{R}}}}}^{67}=32$ meV, ${E}_{{{{\rm{R}}}}}^{80}=37$ meV, and ${E}_{{{{\rm{R}}}}}^{91}=41$ meV). We then adjusted U₀ such that ${{{\rm{Im}}}}\chi ({{{\bf{Q}}}},\varOmega )$ exhibited resonance peaks at the energies given by Eq. (8). As the temperature increases, INS data suggest that the resonance broadens and decreases in intensity, but disperses weakly with temperature, even above T_c^24,25,26. This observation, which is consistent with the reported near-constancy of the ARPES antinodal gap in the temperature range considered here¹¹, justifies the use of Eq. (8) even above T_c. Near T_c, the values of U₀ extracted from this procedure are ~730 meV for UD67, ~650 meV for OP80 and ~580 meV for OP91 (see Supplementary Note 3 for a discussion of the contribution from the anomalous Green’s function and Supplementary Note 6 for the effects of varying E_R).

Figure 2 shows the calculated spin susceptibilities (${{{\rm{Im}}}}\chi$) for the two Bi2212 films (additional results for the single crystal can be found in Supplementary Note 1). Here, we include results well below T_c to compare with the more extensive INS data in this regime. The commensurate peak intensity decreases with increasing temperature and doping (Fig. 2a, b), as seen in INS experiments on YBa₂Cu₃O_6+x^24,27. Also, the resonance peak widths deep in the superconducting state are ~15–20 meV (blue curves in Fig. 2a, b), in agreement with INS data from optimally doped Bi2212²⁰. In addition to the resonance, our calculations also reproduce the ubiquitous “upward branch” ($\omega > {E}_{{{{\rm{R}}}}}$), observed in all cuprate families, but not the “lower branch”, which is material-specific^5,28 (Fig. 2c, d). The energy-momentum integral of ${{{\rm{Im}}}}\chi ({{{\bf{q}}}},\varOmega )$ (multiplied by the matrix element $2{\mu }_{{{{\rm{B}}}}}^{2}$¹³) gives a total fluctuating moment of $\left\langle {m}^{2}\right\rangle \sim 0.43{\mu }_{{{{\rm{B}}}}}^{2}$ for the UD67 sample and $\left\langle {m}^{2}\right\rangle \sim 0.39{\mu }_{{{{\rm{B}}}}}^{2}$ for OP80, both varying weakly with temperature. Moreover, for the UD67 sample at 20 K, the total spectral weight taken up by the resonance (integrated over all momenta and from 0 to 70 meV) is about $0.16{\mu }_{{{{\rm{B}}}}}^{2}$, whereas the remaining spectral weight (up to 200 meV), $\sim 0.27{\mu }_{{{{\rm{B}}}}}^{2}$. These values compare reasonably well with the corresponding figures for YBa₂Cu₃O_6.6 (with a similar T_c)²⁹. While the use of weak-coupling approaches like the RPA may be called into question in the strongly correlated cuprates, the above results suggest that this approximation can semi-quantitatively account for the spin susceptibility probed in INS experiments (as has been reported before^4,8), which is a necessary ingredient in the calculation of the Bethe-Salpeter eigenvalues.

Fig. 2: Temperature and doping dependence of the inelastic spin response in Bi2212 calculated from angle-resolved photoemission spectroscopy (ARPES) data.

a, b Calculated spin susceptibility for both thin films (UD67 and OP80, respectively) as a function of energy at the commensurate wave vector $({{{\rm{\pi }}}},{{{\rm{\pi }}}})$ for various temperatures. c, d Dispersion of magnetic excitations along the diagonal direction at 20 K or UD67 and OP80 samples, respectively. Pink symbols in (d) represent inelastic neutron scattering (INS) measurements only above the resonance energy from optimally doped Bi2212 at 10 K (adapted from Xu et al.²⁶). Colour bars in (c) and (d) are in units of (states/eV/formula unit) and dashed lines indicate the resonance energies.

Bethe-Salpeter equation

With the experimentally derived values of U₀ and the functions $G({{{\bf{k}}}},{\omega }_{n})$ and ${{{\rm{Im}}}}\chi ({{{\bf{q}}}},\varOmega )$, Eq. (1) can be solved after obtaining the Matsubara frequency representation for the spin response function:

$$\chi \left({{{\bf{q}}}},{\omega }_{m}\right)=-\frac{1}{{{\pi }}}\int {{{\rm{d}}}}\varOmega \frac{{{{\rm{Im}}}}\chi \left({{{\bf{q}}}},\varOmega \right)}{i{\omega }_{m}-\varOmega }$$

(9)

For the linearized Bethe-Salpeter equation, we considered only data sets near and above T_c, and solved for the leading eigenvalue and eigenvector $\varPhi ({{{\bf{k}}}},{\omega }_{n},T)$ using the power method³⁰ (see “Methods—Numerical analysis”). Figure 3a, b shows the momentum dependence of the eigenvector at ${\omega }_{n=0}$ along the direction $({{\pi }},0)\to (0,{{\pi }})$ for both thin films close to T_c. (Results for the OP91 crystal are presented in Supplementary Note 1) The eigenvector changes sign and closely follows a ${{\cos }}(\theta )$ dependence, exhibiting a d-wave character.

Fig. 3: Solution of the Bethe-Salpeter equation and symmetry properties of the order parameter near the superconducting critical temperature T_c.

a Momentum dependence along the $({{{\rm{\pi }}}},0)\to (0,{{{\rm{\pi }}}})$ direction (as shown in the inset of (b)) of the eigenfunction $\varPhi$ for the UD67 sample at T = 62 K (blue) and T = 80 K (red). b Same as (a) but for the OP80 sample at T = 70 K (purple) and T = 90 K (green). The black, dashed line in (a) and (b) is the d-wave function $\frac{1}{2}({{\cos }}{k}_{x}-{{\cos }}{k}_{y})$ along the path ${k}_{y}={{\pi }}-{k}_{x}$. c Matsubara energy dependence of the eigenfunction $\varPhi$ at $(\pi ,0)$ for the UD67 sample at the temperatures indicated in (a). d Same as (c) but for the OP80 sample. e Comparison of angle-resolved photoemission spectroscopy (ARPES) gaps (${\Delta }_{0}$, grey triangles) for UD67 at 20 K with the calculated $\varPhi ({{{\bf{k}}}},{k}_{{{{\rm{B}}}}}T)$ at 62 K (blue line) along the Fermi surface shown in (f). g Same as (e), but the ARPES gap values correspond to the OP80 sample at 20 K and the pairing eigenfunction was calculated from the OP80 data at 70 K (purple line). In (e), (g) the pairing eigenfunctions were re-scaled to match the ARPES gaps at $\theta =0^\circ$ and the gap values were adapted from Kanigel et al.¹¹. The curve colours are consistent throughout each column of panels.

For the same data sets, Fig. 3c, d show the (Matsubara) energy dependence of the normalized eigenvector at $({{\pi }},0)$. The eigenvector is even in frequency, with a characteristic energy scale of the order of 250 meV. Following the Hubbard model calculations of Maier et al.⁷, where this characteristic energy is $\sim 2J$, we extract values for the in-plane exchange energy $J\sim 125$ meV, in agreement with estimates obtained from INS for La_2−xSr_xCuO₄ and YBa₂Cu₃O_6+x³¹. The energy dependence of $\varPhi$ implies a retardation in time of the pairing interaction ${\left(2J\right)}^{-1}\sim 10$ fs, as has been observed in ultrafast optical spectroscopy measurements³². Finally, the calculated $\varPhi$ allows us to recover the superconducting gaps measured in ARPES along the Fermi surface, as shown in Fig. 3e for the UD67 film, where $\varPhi$ was calculated from the data at 62 K and the ARPES gap values were obtained from the same film at 20 K. Figure 3f shows the Bi22212 Fermi surface indicating the angle plotted in Fig. 3e. Similarly, the pairing eigenfunction calculated from superconducting state (${{{\rm{T}}}}=70\,{{{\rm{K}}}}$) data from the OP80 film and the ARPES gaps from the same film at 20 K show remarkable agreement, as shown in Fig. 3g.

Figure 4 summarizes our results for the leading eigenvalues at temperatures slightly below and above T_c, for both thin films and the single crystal. Note the temperature dependence of the eigenvalues (Fig. 4a–c); for the three samples, the eigenvalues increase as T is lowered toward T_c, as observed in some Hubbard model calculations^6,7,33. This temperature dependence is a direct consequence of using temperature-dependent, experimental spectral functions. Our main result is that, to the accuracy of the present calculation (see Supplementary Note 6), the eigenvalues are essentially equal to unity near T_c.

Fig. 4: Temperature dependence of leading Bethe-Salpeter eigenvalues for three Bi2212 samples.

a–b Leading eigenvalues for the two thin films UD67 and OP80. c Leading eigenvalue for the single crystal OP91. The dashed lines indicate the critical temperatures for the three samples. The error bars are dominated by the uncertainty in the coupling energy U₀, coming from the finite resolution of inelastic neutron scattering (INS) measurements and possible deviations of the $({{{\rm{\pi }}}},{{{\rm{\pi }}}})$ peak energy from the value given by Eq. (8) (see Supplementary Note 6).

It is worth noting that the temperature extracted from the condition $\lambda \left(T\right)=1$ in this work is not the temperature scale associated with incoherent pair formation (${T}_{{{{\rm{pair}}}}}$) reported recently³⁴. Indeed, we solve the Bethe-Salpeter equation in momentum space, which implicitly assumes the existence of a phase-coherent, long-range superconducting order parameter (as the Greens functions and the pairing interaction that enter Eq. (2) are coherent). As such, the temperature at which the eigenvalue of Eq. (1) reaches 1 must be identified with T_c.

Conclusions

Our results show that the magnetically mediated pairing interaction, constructed from ARPES data within the RPA, is strong enough to mediate high-temperature, d-wave superconductivity in the cuprates at optimal and sub-optimal doping. We note that the emergence of superconductivity in the underdoped sample (UD67) arises from the increased strength of the pairing interaction which compensates for the loss of low-energy electronic states in the pseudogap region. This result is consistent with the notion that antiferromagnetic correlations promote high-T_c superconductivity in a dry Fermi sea ⁶.

Methods

Experimental

Bi2212 thin films were epitaxially grown by radio frequency magnetron sputtering³⁵ up to a thickness of about 2000 Å. The resistivity curves for these films showed transition widths of about 10 K for the OP80 film (optimally doped) and 15 K for the UD67 film (underdoped)³⁶. These were measured with 22 eV photons at the U1 undulator beamline at the Synchrotron Radiation Center in Madison, Wisconsin. The spectra were collected with a Scienta R2002 spectrometer, with an energy resolution of 15 meV. The films were mounted with the Cu–O bond parallel to the photon polarization and cleaved in situ at a pressure below $2\times {10}^{-11}$ Torr. The optimally doped single crystal was grown by the travelling solvent, floating zone technique. ARPES measurements for this sample were performed at the University of Illinois at Chicago, using the unpolarized He-I line (21.2 eV) from a Helium discharge lamp. Photoelectrons were analyzed with a Scienta R4000 spectrometer, the energy resolution of the system was set at 25 meV, and the sample was measured at a pressure below our measurement limit of $2\times {10}^{-11}$ Torr. Throughout all the experiments, antinodal spectra were repeatedly measured and compared with the corresponding spectra collected at the beginning of each run. These measurements showed no signs of surface contamination or doping (see Supplementary Note 2).

Data analysis

Starting from the raw ARPES data, we first subtract the contribution due to second order light. In the second step, an EDC far away from the Fermi momentum ${{{{\bf{k}}}}}_{{{{\bf{F}}}}}$ in the “unoccupied” side is used as an energy-dependent background. This background is subtracted from the EDCs at each momentum point after normalizing it to each EDC at a certain binding energy ${\omega }_{0}$ (640 meV for the thin films and 510  meV for the single crystal). The reason why we can subtract the same background EDC throughout the Brillouin Zone is that this spectrum is roughly momentum-independent, as we reported elsewhere³⁷. We also checked that changing ${\omega }_{0}$ within an energy window of 140 meV does not significantly alter the end results. Subsequently, we divide the spectra by a resolution-broadened Fermi function to get an effective ${{{\rm{Im}}}}G({{{\bf{k}}}},\omega )$. Afterwards, we determine the unoccupied part of ${{{\rm{Im}}}}G({{{\bf{k}}}},\omega )$ by adopting particle-hole symmetry with respect to the Fermi surface: ${{{\rm{Im}}}}G({{{\bf{k}}}}+{{{{\bf{k}}}}}_{{{{\bf{F}}}}},\omega )={{{\rm{Im}}}}\,G({{{{\bf{k}}}}}_{{{{\bf{F}}}}}-{{{\bf{k}}}},-\omega )$ where k is normal to the Fermi surface.

We then normalize the derived ${{{\rm{Im}}}}G({{{\bf{k}}}},\omega )$ so that the integral of the spectral function $A({{{\bf{k}}}},\omega )=-1/{{\pi }}\,{{{\rm{Im}}}}G({{{\bf{k}}}},\omega )$ is equal to unity over the energy range $[-{\omega }_{0},{\omega }_{0}]$. Even though the above-described steps cannot be claimed to be exact, they collectively minimize the effect of dipole matrix elements. Finally, we interpolate the data on to a rectangular grid and apply reflections appropriate to the symmetries of the CuO₂ planes to obtain the spectral function across most of the BZ. (See Supplementary Note 2 for more details.)

In previous work^38,39 we have used the above data normalization procedure to conduct an autocorrelation analysis of ARPES data and compare quantitatively with Fourier transformed STS (FT-STS) data, with excellent agreement. In addition, our current analysis provides estimates for the spin-fermion coupling constant ${U}_{0}$ and the time scale for the pairing interaction in cuprate HTSCs, which are consistent with reported values in the literature³². This agreement with experiments provides confidence in our methodology for extracting $A({{{\bf{k}}}},\omega )$ from ARPES data.

Numerical analysis

The method employed in solving the eigenvalue problem in Eqs. (1) and (2) followed very closely that of Monthoux³⁰. In assessing whether a hypothetical pairing interaction is strong enough to mediate superconductivity at a given temperature, it is sufficient to focus on the largest eigenvalue of $\hat{O}$. To this end, we used the power method, which is an iterative procedure to calculate the maximum eigenvalue of an operator. There are several equivalent ways of carrying out this procedure; in this work, the implementation goes as follows. We start with a guess for the eigenfunction $\varPhi$, which is a generalized gap function reflecting the momentum and energy dependence of the pairing interaction. Motivated by the well-established d-wave form of this interaction, we take ${\varPhi }_{0}({{{\bf{k}}}},{\omega }_{n})={{\cos }}\,{k}_{x}-{{\cos }}\,{k}_{y}$ as our starting guess.

With this guess, we perform the first iteration ${F}_{1}=\hat{O}{\varPhi }_{0}$ and factor out the largest entry in ${F}_{1}$, so that ${F}_{1}={\lambda }_{1}{\varPhi }_{1}$, where ${\lambda }_{1}={{\max }}({F}_{1})$ and ${\varPhi }_{1}={F}_{1}{/\lambda }_{1}$. We then use ${\varPhi }_{1}$ as input to the second iteration ${F}_{2}={\hat{O}\varPhi }_{1}$ to obtain ${\lambda }_{2}={{\max }}({F}_{2})$ and ${\varPhi }_{2}={F}_{2}/{\lambda }_{2}$, as before. The above process is repeated until the iteration (N) is reached where the difference ${\lambda }_{N}-{\lambda }_{N-1}$ is negligible. At this point, the function ${\varPhi }_{N}$ is the normalized eigenfunction of $\hat{O}$ corresponding to the largest eigenvalue ${\lambda }_{N}$.

Since Eq. (2) is essentially a convolution equation, the operations $\hat{O}{\varPhi }_{j}$ were performed using Fourier techniques for increased computational speed. The numerical efficiency afforded by the convolution structure of the Bethe-Salpeter equation was our main reason for studying the pairing problem in Matsubara frequencies.

From the Lehmann representation of the Green’s function, it can be seen that $P({{{\bf{k}}}},{\omega }_{n})=G({{{\bf{k}}}},{\omega }_{n})G(-{{{\bf{k}}}},-{\omega }_{n})$ is even in Matsubara frequency, real, and positive. For the Matsubara spin response, the property ${{{\rm{Im}}}}\chi ({{{\bf{q}}}},-\varOmega )=-{{{\rm{Im}}}}\chi ({{{\bf{q}}}},\varOmega )$ implies that $\chi ({{{\bf{q}}}},{\omega }_{m})$ is also even in ${\omega }_{m}$, real and positive. These properties are not only useful as consistency checks of the numerical procedure, but also enable us to use the power method, which breaks down when the eigenvalues are complex.