Observation of a transition to a localized ultrasonic phase in soft matter

Abstract

Anderson localization arises from the interference of multiple scattering paths in a disordered medium, and applies to both quantum and classical waves. Soft matter provides a unique potential platform to observe localization of non-interacting classical waves because of the order of magnitude difference in speed between fast and slow waves in conjunction with the possibility to achieve strong scattering over broad frequency bands while minimizing dissipation. Here, we provide long sought evidence of a localized phase spanning up to 246 kHz for fast (sound) waves in a soft elastic medium doped with resonant encapsulated microbubbles. We find the transition into the localized phase is accompanied by an anomalous decrease of the mean free path, which provides an experimental signature of the phase transition. At the transition, the decrease in the mean free path with changing frequency (i.e., disorder strength) follows a power law with a critical exponent near unity. Within the localized phase the mean free path is in the range 0.4–1.0 times the wavelength, the transmitted intensity at late times is well-described by the self-consistent localization theory, and the localization length decreases with increasing microbubble volume fraction. Our work sets the foundation for broadband control of localization and the associated phase transition in soft matter, and affords a comparison of theory to experiment.

Introduction

For strongly disordered three-dimensional (3D) systems the Anderson transition has been expected to separate phases comprised of extended and localized states^1,2,3,4,5,6. Early theoretical studies based on either scaling arguments derived from perturbative expansions³ or on renormalization group in 2 + ε dimensions^7,8 predicted a mobility edge in 3D (the energy at which the transition from localized to extended behavior occurs). The theoretical predictions are based on analyses of single particle wavefunctions of disordered systems and are thus applicable to both quantum mechanical (single particle) and classical waves. However, predictive capabilities in 3D are still incomplete with the most powerful theoretical tool available, the supersymmetric sigma model⁹, unable to make predictions at the mobility edge⁶. Experimental comparisons with theory are (and have been) inevitably incomplete, but have begun to help develop a more sound understanding of the phase transition associated with the localized phase.

Experiments seeking to observe single-particle quantum effects induced by disorder are complicated by a number of physical phenomena. Obtaining comparisons between theory and experiment in the electronic case, for which the theory was originally intended, is greatly complicated by the Coulomb interaction between electrons^{6,10,11,12,13,14}, and substantial modifications of the theory are needed to compare with experiment. As a result, researchers have shifted their focus to systems enabling the study of non-interacting, single-particle wavefunctions.

Studies on the expansion dynamics of atomic matter waves in a disordered potential defined by a laser speckle field circumvent the issues associated with interparticle interactions and have led to the observation of localization effects in 3D^15,16,17. However, results of these matter wave experiments are complicated by certain experimental factors including the range of energy states that exist within the expanding wavepacket (diffusive and localized states), the long experimental timescales required, and subtleties in the random distributions (including anisotropic correlations within the disordered potentials and the nature of the quasi-periodic potential). These experimental complications have led to significant differences between measured values of the mobility edge and numerical predictions¹⁸, and these differences are still not well understood. In addition, no matter wave experiment has thus far demonstrated an energy distribution narrow enough to determine the phase transition’s critical exponents or multifractal behavior^17,18. Studies on dynamical wave localization where the wavefunction is exponentially attenuated in momentum space show promise for determining the phase transition’s critical exponents¹⁹; however, these experiments are not a real space realization of the Anderson localization of wave energy by disorder and do not address the question of Anderson localization in systems with topological disorder.

It was long expected that studying classical waves would provide a straightforward path to observe localization effects in non-interacting systems and a means for comparing experiment directly to theory. Further, experiments aimed at studying classical wave propagation through a disordered medium can circumvent the challenges associated with a Bose–Einstein condensate expansion measurement owing to the long times over which energy can be measured and the possibility of separating diffusive from localized effects in frequency domain, which could lead to measurable localization effects that are not skewed by the presence of delocalized states as in the case for matter waves. In the classical case, instead of a single mobility edge (as in the electronic case) there is expected to be a second, low-frequency mobility edge driven by Rayleigh scattering, which is a phenomenon that does not occur in quantum systems; the difference results from the different boundary conditions, which lead to the different scattering phenomena at low energies and frequencies²⁰. Thus, one expects in the classical case to observe a disorder-driven band of localized states at intermediate frequencies, separated from extended states at low and high frequencies by two mobility edges^8,20,21,22. Experimental observation of such a localized phase, however, has proven to be elusive.

The difficulty in observing a localized phase for a classical wave system in 3D is due in large part to the difficulty in achieving strong enough scattering with small dissipation. In studies on light scattering, observation of a phase transition has been difficult with several early claims of light localization^23,24 being disputed²⁵. In parallel studies, investigators have examined resonant mesoglass systems and have observed localization effects in narrow frequency bands near resonance^26,27,28. This is indeed a significant finding, but it is not the observation of a broad frequency band of localized states that one may fairly interpret as a localized phase, as originally envisioned.

We report here observations of a broadband localized phase spanning up to 246 kHz for sound transmission through a suspending gel (a Bingham fluid) doped with compliant encapsulated microbubbles (EMBs)^29,30,31. A key difference between this system and those systems searching for light localization is in the type of resonant scatterer (monopole scattering in this work versus dipole scattering in the case of light), which give rise to different near-field couplings that can affect localization³². A key advantage of this system is the broad, continuous resonance frequency bandwidth for the EMB dopants spanning 100 s kHz (afforded by the soft matter disparate wave speeds resulting in the compressional wavelength being much larger than the EMB equilibrium diameter), which provides a tunable disorder strength and allows unprecedented access to the predicted localized phase and the corresponding phase transition. The transition into the localized phase occurs at a critical density ρ_C = 2.2 × 10⁹ scatterers/m³ = 0.09k³ where k is the effective wave number, and is accompanied by a strong anomalous decrease in the measured scattering mean free path l_S, which provides an experimental signature of the phase transition. At the phase transition, the decrease in l_S with changing frequency (i.e., disorder strength) follows a power law with a critical exponent γ = 1.08 ± 0.05. Within the localized phase the maximum ratio of the mean free path to the wavelength, l_S/λ, equals unity and this ratio reaches values as low as l_S/λ = 0.4, which is expected for localization based upon early work by Ioffe and Regel³³. Within the localized phase, the time-dependent transmitted intensity shows late-time deviations from diffusion, which cannot be explained by absorption and are in agreement with self-consistent theory (SCT) predictions; the nature of the soft medium results in negligible coupling between longitudinal and transverse waves³⁴, which is a key advantage ensuring the slow transverse waves do not skew our late-time analysis. Fitting the localized phase transmitted intensity to the SCT allows us to extract the localization length ξ, which is found to be more than a factor of five smaller than the sample thickness at an EMB volume fraction ϕ = 2.7%. At higher frequencies an observed change in slope of the frequency-dependent phase angle results in a factor 2.5 reduction in phase velocity and a discontinuous rise in l_S/λ, which corresponds to a second higher-frequency mobility edge and provides experimental evidence of a finite frequency range for the localized phase.

Results

EMB-doped soft matter

Our samples consist of an EMB-doped gel encased within a polymer shell (see Materials and Fabrication in Methods); the gel and polymer shell are soft since G < < B where G and B are the shear and bulk moduli, respectively (see Supplementary Note 1), and the materials exhibit low mechanical loss (tan(δ) < 0.03) within the targeted frequency range (see Supplementary Note 2). A sample is shown in Fig. 1a and the side-view cross section in Fig. 1b; the thickness of the doped gel L_G = 10 mm while the thickness of the undoped polymer (Uralite) shell L_U = 4 mm. The 4 mm-thick polymer shell is acoustically impedance-matched to water with negligible attenuation and reflection in the frequency range of interest and provides structural support for the doped gel. Optical images of the gel doped with EMBs to a volume fraction ϕ = 1.2 ± 0.9% are shown in Fig. 1c,d, Fig. 1e shows an EMB schematic, and Fig. 1f shows an EMB image obtained with scanning electron microscopy (SEM). The effect of the nanoscale shell on sound velocities in soft materials was previously reported³⁵; also, see EMB characterization with SEM in Methods and Supplementary Fig. 5. We note the EMBs remain fixed in position within the gel with no observable time-dependent drift.

Fig. 1: Soft gel doped with encapsulated microbubbles.

a A Uralite shell encases encapsulated microbubble (EMB)-doped gel (Carbopol ETD 2050, 0.2 wt %). The center ports are sealed input/output through which the gel was injected. The corner tabs are for suspension and weighting. b Cross-sectional side view showing material thicknesses: L_G and L_U for the doped gel and Uralite layers, respectively. c, d Optical images of the gel (on a glass slide) doped to a volume fraction ϕ = 1.2 ± 0.9%. The scale bar in (c) is 300 μm. The scale bar in (d) is 125 μm. The exaggerated shell thickness and bright spot in the EMB center are the result of light focusing. e EMB schematic. The enclosed gas (blue) is a mixture of isobutane and isopentane. The shell (gray) is primarily polyacrylonitrile (PAN). The shell thickness is of order 100 nm. f Scanning electron microscopy image of an EMB. The scale bar is 8 μm. g EMB diameter D distribution determined via optical microscopy. A total of 238 diameters were measured to obtain the distribution. h Predicted EMB resonance frequency f_O versus D. The purple region corresponds to those diameters within the distribution in (g). The green region corresponds to the experimental frequency range. i Predicted EMB scattering cross section σ(f) (normalized to the shell outer radius) versus frequency f for D = 90 μm accounting for acoustic radiation damping. Inset: damping coefficient β as a function of f for damping from acoustic radiation, EMB shell viscosity, and thermal effects.

Figure 1g shows the EMB diameter D distribution; the average diameter falls within the 60–95 μm range (with approximately half the EMB diameters larger than this average value), and the largest (smallest) measured diameters fall in the 130–140 μm (1–10 μm) range. Figure 1h shows the predicted EMB resonance frequency f_O versus D, and indicates a large range of EMB resonance frequencies coincide with the experimental frequency range (see Supplementary Note 3). Figure 1i shows the predicted normalized EMB scattering cross section, which indicates a peak σ(f) upon resonance. Here, σ(f) is determined from the same EMB model as f_O and accounts for acoustic radiation damping; the Fig. 1i inset shows acoustic radiation damping dominates the damping coefficient in the f_O range of interest (400–800 kHz). For the undoped gel we find the longitudinal phase velocity v_L = 1498 m/s and at f = 700 kHz λ = 2140 μm, which is a factor of 24 larger than D. Thus, the EMB is driven into resonant radial oscillations though λ is over an order of magnitude larger than the equilibrium diameter³⁶.

Localization phase transitions in EMB-doped gel

Normal incidence measurements are carried out in water (see In-water measurements in Methods). The sound level SL = 20log₁₀(P_t/P_ref), attenuation coefficient α, and scattering mean free path l_S frequency spectra are obtained from the coherent part of the transmitted wavepacket, which is accessible by time-windowing the data; P_t/P_ref is the amplitude transmission coefficient where P_t and P_ref are the transmitted and water reference pressure amplitudes, respectively, l_S is determined from the normalized intensity $I/I_{{{{{{{\mathrm{O}}}}}}}} = e^{-\left( {L_{{{{{{{\mathrm{G}}}}}}}}/l_{{{{{{{\mathrm{S}}}}}}}}} \right)}$ and l_S = (2α)⁻¹; recall, L_G is the doped gel thickness.

We point out that in our experiments, we have experimental access to the real-space transmitted and reflected pressures in response to an incident, nearly plane wave, and therefore to the Green’s function $G\left( {x,t;x_{{{{{{{\mathrm{O}}}}}}}},t_{{{{{{{\mathrm{O}}}}}}}}} \right)$. From this quantity we can, in a model-independent manner, evaluate both the average Green’s function $\langle G( {x,\;t;\;x_{{{{{{{\mathrm{O}}}}}}}},\;t_{{{{{{{\mathrm{O}}}}}}}}} )\rangle$ (the coherent field) and correlation functions of the general form $\left\langle G\left( {x,\;t;\;x_{{{{{{{\mathrm{O}}}}}}}},\;t_{{{{{{{\mathrm{O}}}}}}}}} \right)G\left( {x^{\prime} ,t^{\prime} ;x_{{{{{{{\mathrm{O}}}}}}}},t_{{{{{{{\mathrm{O}}}}}}}}} \right)\right\rangle$. The latter quantity, related to energy transport, has been the main focus of localization investigations since Anderson’s original work¹, as the coherent field vanishes exponentially at late times or large distances. The coherent field does, however, enable a measurement of the mean free path via the Fourier transform $\left| \left\langle{G\left( {x,\;\omega ;\;x_{{{{{{{\mathrm{O}}}}}}}},\;\omega } \right)} \right\rangle\right| = G_{{{{{{{\mathrm{O}}}}}}}}e^{ - \left| {x - x_{{{{{{{\mathrm{O}}}}}}}}} \right|/2l_{{{{{{{\mathrm{S}}}}}}}}}$ where ω is the angular frequency, which is valid away from the near field (note that $\left| \left\langle{G(x,\;\omega ;\;x_{{{{{{{\mathrm{O}}}}}}}},\;\omega )} \right\rangle\right|^2 = \left| {G_{{{{{{{\mathrm{O}}}}}}}}} \right|^2e^{ - \left| {x - x_{{{{{{{\mathrm{O}}}}}}}}} \right|/l_{{{{{{{\mathrm{S}}}}}}}}}$, which is equivalent to the expression provided for the normalized intensity). This relationship is common across all existing theoretical models of localization phenomena^3,7,9,37, and describes the scattering of energy from the coherent field by all physical mechanisms.

As seen in Fig. 2a, we observe significant reductions in SL upon EMB doping beginning near the anticipated minimum f_O ~ 360 kHz. The lowest SL corresponds to ϕ = 2.7% at f = 742 kHz where the intensity transmission coefficient decreases eight orders of magnitude with respect to the water reference (accounting for a small impedance mismatch between the doped gel and water). The Fig. 2a doped gel data shows a clear transition in governing physics from the low-frequency regime where the transmission is governed by composite material properties resulting in thickness modes to higher frequencies where EMB oscillations drive the observed SL. With increasing frequency the number of resonant EMB diameters per wavelength (i.e., the disorder strength) increases, which partially explains the observed SL spectra at higher frequencies.

Fig. 2: Sound transmission through encapsulated microbubble-doped gel.

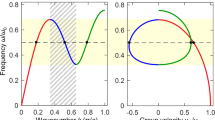
a Sound level SL (referenced to a water measurement) versus frequency f for an undoped sample (open black circles), and three doped samples with encapsulated microbubble (EMB) volume fractions ϕ = 1.2% (solid green triangles), ϕ = 2.7 ± 0.5% (open blue squares), and ϕ = 9.9 ± 1.8% (solid gray diamonds). Several low-f thickness modes are indicated. The shaded yellow region highlights the anticipated EMB resonance frequency range. A correction factor is applied to the data to account for the finite sample thickness: −0.64 dB for the undoped sample and −0.36 dB for the doped samples. b Attenuation coefficient α versus f for the undoped sample and two doped samples from (a). Dashed lines and arrows indicate the frequency ranges for the two localized phases, which are bounded by mobility edges (identified by attenuation peaks). c Ratio of the scattering mean free path l_S to the wavelength λ versus f for the two doped samples in (b). The x-axis frequency range spans the anticipated range of EMB resonance frequencies. The black arrows indicate the mobility edges (corresponding to the indicated α peaks in b) d, α (left vertical axis) and change in the phase angle Δθ (right vertical axis) versus f for ϕ = 2.7%. Note, the α spectrum in (d) is the same spectrum shown in (b). The black arrows indicate the mobility edges.

Figure 2b shows α versus f where attenuation resonances with amplitudes exceeding 200 Np/m (unexplained by thickness modes) are observable above 400 kHz. The conclusion of anomalous attenuation at these frequencies is supported by reflection measurements (see Supplementary Fig. 7) where no resonant reflection is observed for f  > 400 kHz for any ϕ. Based upon the Fig. 2 data, as well as our diffusion and localization analysis (discussed later), we have determined several of these attenuation resonances to be mobility edges and they are indicated in Fig. 2b by dashed lines and arrows. The peaks shift toward lower frequency with increasing ϕ indicating a critical density for the phase transition. For the strongest lower-frequency mobility edge (ϕ = 1.2%, f = 527 kHz), based upon the peak width, the EMB diameter distribution, and total density ρ_tot ~ 5.6 × 10¹⁰ EMBs/m³ we estimate the critical density ρ_C ~ 2.2 × 10⁹ EMBs/m³ = 0.09k³. This ρ_C is a factor of 2.2 larger than the minimum critical density ρ_C ~ 1.0 × 10⁹ scatterers/m³ estimated with the criterion l_S/λ ≤ 1 from the early work of Ioffe and Regel:³³ see Supplementary Note 4. The value of ρ_C found here is also in close agreement with the results of numerical calculations both for a system of resonant point scatterers (ρ_C = 0.08k³)³⁸ and for light scattering by cold atoms (ρ_C = 0.1k³)³⁹.

Figure 2c shows l_S/λ versus f for the same dopant concentrations presented in Fig. 2b, and the mobility edges, corresponding to those frequencies at which l_S/λ shows a sharp anomalous decay, are indicated by arrows. From the ϕ = 1.2% dataset it is clear the transition to the localized phase, identified by the minimum at f = 527 kHz, occurs when l_S/λ falls below unity. The data for ϕ = 2.7% further shows that even if the criterion l_S/λ ≤ 1 is satisfied the phase transition does not occur until ρ = ρ_C, which indicates both criteria must be met before the system transitions to a localized phase. Across samples, we find that within the localized phase l_S/λ never exceeds 1.0 and can be as low as 0.4. Further, for ϕ = 2.7% and at f = 526 kHz (center of the phase) l_S = 1.0 mm (l_S/λ = 0.65), which is a factor ~ 9.2 larger than the equilibrium diameter for the EMB with that resonance frequency.

Also shown in Fig. 2c is a discontinuity in l_S/λ at f = 618 kHz for ϕ = 2.7%. The discontinuity occurs at the same frequency as an attenuation peak (the higher-frequency mobility edge) as seen in Fig. 2d where α is plotted along with the phase change Δθ (from which we determine v_L). For f < 618 kHz waves are localized while for f > 618 kHz l_S/λ saturates to values around 1.4. Also, for f > 618 kHz v_L is lowered by a factor of 2.5 and this slowing suggests a transition to a different transport regime; we suspect this higher frequency regime above the second mobility edge is primarily governed by the wave’s small spatial extent at those frequencies²⁰ and by the EMB enclosed gas because gaseous isobutane and pentane have wave speeds ~200 m/s^40,41, which is comparable to the measured v_L = 334 m/s in this higher-frequency regime, and also because even at these higher frequencies the EMB frequency-dependent concentration is still near the maximum in the D distribution shown in Fig. 1g. Nevertheless, the l_S/λ discontinuity provides experimental evidence of a finite frequency range for the localized phase in agreement with predictions for scalar wave localization^8,20,21,22; the phase occurs for frequencies between the indicated attenuation peaks in Fig. 2b and the corresponding l_S/λ minima in Fig. 2c. Following the same procedure used to determine ρ_C, we estimate the scatterer density ρ ~ 0.05k³ at f = 773 kHz for ϕ = 1.2%, which suggests the higher-frequency transition to extended states might also occur because ρ does not increase as f³.

The mean free path is not expected to contain an indication of Anderson localization as the interference responsible for this phenomena appears only in the higher-order averages $\langle GG \ldots\rangle$; this well-known expectation is again true across all existing theoretical models^3,7,9,37,42. From first principles with no weak-coupling approximations, field-theoretic methods applied to a random, Gaussian distributed  collection of point scatterers demonstrate that the spontaneous symmetry breaking leading to diffusive behavior, and a breakdown of perturbative expansions, does not occur in the calculation of the mean Green’s function^7,9. Thus, the renormalized diffusion responsible for Anderson localization is not accessible in the measurement of the mean Green’s function, and hence not in the mean free path. While we have found this to be the case in the localized phase, we nevertheless have observed strong anomalies in the mean free path at the mobility edges separating localized and extended states (with the mobility edge identification supported by late-time analysis of the higher-order Green’s functions, as discussed later). We believe this observation of the anomalous behavior for the mean free path, which serves as a clear experimental signature of the mobility edge, is associated with the notion that our system contains a macroscopic number of internal degrees of freedom (resonances). The presence of such resonances generally leads to a slowing of the diffusive energy velocity in the perturbative models^43,44,45,46 and has only been briefly considered in a field-theoretic context⁴⁷; however, these works do not examine potential effects associated with a near vanishing mean free path at the mobility edge. An explanation of this phenomena will require additional theoretical work.

We point out the lowest kl_S values occur for frequencies associated with the distribution of EMB f_O (see Supplementary Fig. 8). At the low-frequency mobility edge kl_S = 3.2 ± 0.1 and kl_S = 3.6 ± 0.1 for ϕ = 1.2% and 2.7%, respectively, while between the mobility edges and in the localized phase the minimum kl_S = 2.4 ± 0.1 and kl_S = 2.9 ± 0.1 for ϕ = 1.2% and 2.7%, respectively. The kl_S values found here are comparable to values found for sound localization in mesoglasses^26,27,28.

Figure 3 shows l_S versus f near the mobility edge at f = 527 kHz for ϕ = 1.2%. Clearly, l_S decreases rapidly in the vicinity of the critical frequency f_C at which the phase transition occurs, and we find this rapid decrease in l_S obeys the power law $l_{{{{{{{\mathrm{S}}}}}}}} = a\left| {f - f_{{{{{{{\mathrm{C}}}}}}}}} \right|^\gamma + b$ with the critical exponent γ = 1.08 ± 0.05 (an additional power law fit to the mobility edge at f = 773 kHz shown in Fig. 2c for ϕ = 1.2% yielded γ = 1.01 ± 0.11). The divergence of a scaling parameter is a key property of the Anderson transition: scaling arguments derived from perturbative expansions predict such a power law behavior for the rapid decrease of the conductivity at the Anderson transition in disordered electronic system³, while numerical calculations predict such a behavior for the divergence of the correlation and localization lengths at the transition^48,49, and dynamical localization measurements with matter waves find a power law behavior for the scaling parameter on both sides of the transition¹⁸. However, we point out the critical exponent found here applies to the mean free path in a weakly dissipative medium, which distinguishes the exponent from those determined through numerical calculations for the correlation and localization lengths^48,49 in non-dissipative systems. The value γ = 1.08 found here should thus be interpreted as a measure of the l_S renormalization critical exponent and not as a claim of a measured correlation length critical exponent.

Fig. 3: Scattering mean free path critical exponent.

Scattering mean free path l_S versus frequency f for an encapsulated microbubble volume fraction ϕ = 1.2% at the 527 kHz mobility edge. Note, the data shown here is the same dataset shown in Fig. 2c. The error bars represent the statistical uncertainty, and are determined through knowledge of the uncertainties in the measured sound level (±3 dB) and the measured doped gel thickness (±0.01 mm). The solid red line is a fit to the power law shown in the graph’s legend with R² = 0.995, which yields the critical exponent γ = 1.08 ± 0.05.

Wave propagation at the mobility edge

At late-times, diffusion sets in unless the system has passed through a localization transition^50,51. To study late-time behavior of the transmitted energy we use a narrow impulse with Δt < 10 μs. Figure 4a shows P versus t for ϕ = 1.2% across multiple speckles (see In-water measurements in Methods). We find the coherent field (260 μs < t  < 268 μs) is speckle independent. However, a strong incoherent field is observed for t  > 269 μs, which varies across speckles and shows temporal fluctuations that vary on a time scale corresponding to the input wavepacket. The temporal fluctuations are highlighted in Fig. 4b where we have time-windowed the data to remove the coherent field. Such fluctuations are the result of wave interference along multiple scattering paths^52,53,54.

Fig. 4: Diffusion and localization fluctuations in encapsulated microbubble-doped gel.

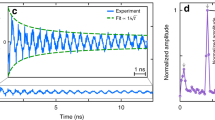
a Pressure P versus time t for an encapsulated microbubble volume fraction ϕ = 1.2% measured in different speckles. The incident wavepacket is based on a Gaussian first derivative, which provides a narrow impulse. The coherent pressure field is observable for 260 μs < t  < 268 μs, and is followed by the incoherent field. Inset: measured frequency spectrum of the incident wavepacket. b Incoherent pressure field after time-windowing the data shown in (a). c Normalized transmitted intensity peak envelope I/I_O versus t for ϕ = 1.2% after digitally filtering the data in (b) to include the 400–550 kHz range. Here, I/I_O is found from averaging over 11 different speckle measurements. Normalization is done so the input pulse peak is unity. The dashed red line is a linear fit to the data. d I/I_O versus t for ϕ = 2.7% and for the 340–465 kHz range. Here, I/I_O is found from averaging over 11 different speckle measurements. The dashed red line is the result of a linear fit to the data similar to that shown in (c). The solid blue line is a fit to the self-consistent theory (SCT) of localization. Note, the time range in (a, b) is the experiment time while in (c, d) the time range has been shifted so the maximum in I/I_O for the incoherent field occurs shortly after t = 0s.

Figure 4c shows I/I_O for ϕ = 1.2% after digitally filtering the Fig. 4b data to include the 400–550 kHz frequency range; note the frequency range was chosen to target the lower range of EMB resonance frequencies up to the high-frequency side of the f = 527 kHz l_S/λ minimum in Fig. 2c (i.e., the low-f mobility edge). Here, I/I_O is averaged over 11 speckles where I = P_t²(2ρ_Gv_L)⁻¹ is computed for each speckle based upon P_t, the doped gel density ρ_G, and v_L. Classically, I/I_O decays according to the exponential law $I/I_{{{{{{{\mathrm{O}}}}}}}} = e^{ - t/\tau _{{{{{{{\mathrm{D}}}}}}}}}$ where τ_D⁻¹ is the lowest eigenvalue of the diffusion operator $- D\nabla ^2$ ⁵⁵, and the Fig. 4c data shows excellent agreement to an exponential model. From the linear fit shown in Fig. 4c we obtain a characteristic diffusion time τ_D = 8.9 ± 0.5 μs, which yields a diffusion coefficient $D^ \ast = L_{{{{{{{\mathrm{G}}}}}}}}^2\left( {\tau _{{{{{{{\mathrm{D}}}}}}}}{\uppi}^2} \right)^{ - 1}$ = 1.14 ± 0.07 m²/s. The values found here for τ_D and D* yield a diffusion length $l_{{{{{{{\mathrm{D}}}}}}}} = \left( {D^ \ast \tau _{{{{{{{\mathrm{D}}}}}}}}} \right)^{1/2}$ = 3 mm, which is more than a factor of 3 smaller than L_G. Diffusion occurs in our samples in this frequency range (400–550 kHz) because while the doped gel is a strongly scattering medium, the l_S/λ and ρ_C criteria for localization are not satisfied. We expect our analysis to be weakly dependent on internal reflections since the ratio of the penetration depth z_O to the doped gel thickness z_O/L_G = K can be more than an order of magnitude less than unity where $K = 2l_{{{{{{{\mathrm{S}}}}}}}}\left( {1 + R} \right)/3L_{{{{{{{\mathrm{G}}}}}}}}\left( {1 - R} \right)$ and the internal reflectivity R is estimated by averaging over the reflected sound level within the 50–800 kHz range (see Supplementary Fig. 7). Furthermore, we do not expect absorption to skew our late-time diffusion (or localization) analysis as the characteristic absorption time τ_a found from fitting the ϕ = 1.2% data within the localized phase to the localization SCT is significantly higher than τ_D = 8.9 μs and also because a value τ_a ≤ 10 μs is not consistent with the experimental data at late times across the full range of ϕ studied here (see the discussion on absorption in the next section).

With increasing ϕ, we find noticeable late-time deviations from diffusion for frequencies near and at the mobility edge as evident by the ϕ = 2.7% dataset in Fig. 4d. Here, the frequency range was again chosen to target the lower range of EMB resonance frequencies up to the high-frequency side of the f = 445 kHz l_S/λ minimum in Fig. 2c. The Fig. 4d data indicates the onset of a time-dependent reduction of the diffusion coefficient. A fit of the Fig. 4d data to the phenomenological SCT of localization⁵⁰ where at late times in the Anderson localized regime the average transmission coefficient is given by T(t) ~e^−ηt/t^p+1. Here, η = (D_B/ξ²)exp(−L_G/ξ), D_B is the bare diffusion coefficient, and ξ is the localization length. The restriction 0.5 ≤ p ≤ 1.0 yields ξ = 9.62 mm and D_B comparable to D*. The value of ξ found here is a factor of 5 larger than the lowest value found for the localized phase. That ξ is found to be nearly equal to L_G in this frequency range agrees with a statistical interpretation of localization: a range of localization lengths exist in the sample and even though ξ diverges at the mobility edge the finite sample dimensions restrict the measurement of closed loops of wave transport to length scales less than the sample thickness (as pointed out in Ref. ²⁴.). In addition, the SCT fit shown in Fig. 4d accounts for absorption and yields τ_a ~ 2τ_D, which represents a marked decrease in τ_a at the mobility edge with respect to that found for the localized phase. This reduction in τ_a at the mobility edge is consistent with a renormalization group theory in 2 + ε dimensions⁸, which predicts an anomalous rise in attenuation (absorption) of the incoherent field due to fluctuations in the wave diffusivity as the mobility edge associated with the Anderson transition is approached from the conducting side. Therefore, we attribute the value of τ_a found here to the change in the fundamental nature of wave propagation as the system approaches the mobility edge. That the late-time behavior observed in Fig. 4d accompanies an anomalous rise in attenuation (consistent with Ref. ⁸.) and yields ξ ~ L_G suggests the deviation from diffusion shown in Fig. 4d is primarily due to fluctuations in wave diffusivity and represents the onset of a localized phase.

Intensity transmission in the localized phase

We next consider the late-time behavior for frequencies between the l_S/λ minima identified as mobility edges in Fig. 2c. Further, we present late-time data for an additional sample with ϕ = 1.0 ± 0.6% (the α spectrum for this sample is provided in Supplementary Fig. 9). Similar to the late-time behavior observed in Fig. 4d, the data presented in Fig. 5 also shows late-time deviations from diffusion, which is a hallmark of localization. Each of the Fig. 5 datasets are well-fitted by the SCT, and from these SCT fittings we find ξ at least a factor of four times smaller in the localized phase than near the mobility edge and also comparable to λ indicating waves are localized to a length scale comparable to the wavelength; for ϕ = 2.7% and at f = 490 kHz ξ/λ = 1.1 and we find the ratio ξ/λ depends on both ϕ and f. As evident from the Fig. 5 data, we find stronger late-time deviations from diffusion with increasing ϕ, which is accompanied by a reduction in ξ to a length scale a factor of 5.2 smaller than the doped gel thickness. Within the localized phase z_O ~ 9.0 × 10⁻⁴ m for ϕ = 1.2%, which suggests wave localization occurs in the doped gel beyond a small penetration depth. The SCT fittings shown in Fig. 5 account for absorption and yield absorption times τ_a ≥ 100 μs and absorption lengths l_a ≥ 62 mm, which suggests negligible absorption within the localized phase.

Fig. 5: Localization in encapsulated microbubble-doped gel.

Normalized transmitted intensity peak envelope I/I_O versus time t found from averaging over 11 different speckle measurements for three separate encapsulated microbubble (EMB) volume fractions: ϕ = 1.0% in (a), ϕ = 1.2% in (b), and ϕ = 2.7% in (c). The frequency ranges were chosen to target those frequencies between the mobility edges identified in Fig. 2c and Supplementary Fig. 9, and the incoherent wave data is digitally filtered to target a specific range. Solid blue lines are fits to the self-consistent theory (SCT) of localization. The bare diffusion coefficient D_B, the localization length ξ, and the absorption time τ_a serve as free-fitting parameters for the SCT fitting and the parameters for each ϕ are specified. Dashed red lines correspond to setting τ_a = 10 μs in the SCT fit while keeping all other parameters fixed at the values specified for each ϕ.

Also shown in Fig. 5 are SCT predictions for when τ_a ~ τ_D: the dashed red lines correspond to setting τ_a = 10 μs with all other parameters kept as specified for each ϕ. If τ_a = 10 μs then the SCT cannot account for the observed late-time deviations from linearity shown in Fig. 5. This provides supporting evidence that τ_a is indeed >10 μs, that the values of τ_D shown in Fig. 4c&d are not due to absorption, and that absorption does not skew the observation of localization effects. We find that for τ_a > 2τ_D the change in ξ determined from the SCT fittings to the data is less than the experiment’s spatial resolution.

We find a significant increase in D_B with respect to D* in the diffusive regime, which is consistent with observations of sound localization in mesoglasses²⁷ and further theoretical work is needed to address the large values of D_B obtained from these fits. Interestingly, values for D_B found here vary at most 13% across samples from 33.35 to 38.70 m²/s. Though one might expect a decrease in D_B with increasing ϕ since $D_{{{{{{{\mathrm{B}}}}}}}} = \left( {1/3} \right)v_{{{{{{{\mathrm{E}}}}}}}}l_{{{{{{{\mathrm{S}}}}}}}} = \left( {1/3} \right)v_{{{{{{{\mathrm{E}}}}}}}}\left( {\rho \sigma } \right)^{ - 1}$ where v_E is the energy velocity, differences in the average l_S across samples (both at the mobility edge and in the localized phase) are less than the experiment spatial resolution, which might suggest negligible changes are expected for D_B within the range of ϕ studied here (assuming a constant v_E). Additional estimates for l_S within the different regimes (i.e., at the mobility edge and in the localized phase) based upon $\left( {\rho \sigma } \right)^{-1}$, the known diameter distribution, and σ predicted with EMB theory²⁹ confirm the expected constant D_B across the measured ϕ range. We point out the value of v_E found here is only a factor 1.25 larger than the value found in Ref. ²⁷.

Discussion

From the data analysis accompanying Fig. 4 and 5 it is clear the l_S/λ minimum at f  = 527 kHz in Fig. 2c for ϕ = 1.2% separates the frequency ranges associated with diffusion and localization, which supports the conclusions that the minimum occurs at the mobility edge and the localized phase extends over the specified frequency range. We find comparable widths for each mobility edge attenuation peak shown in Fig. 2b (Δf  ~ 40–50 kHz), which further suggests a common origin. Our data also indicates a localization transition originating from the localized phase is also accompanied by an anomalous reduction  of the mean free path, and that the observed attenuation resonances and l_S/λ minima provide an experimental signature of the mobility edge. We further point out for ϕ = 9.9 ± 1.8% the broad minimum in SL versus f in Fig. 2a centered upon 636 kHz and spanning 613–782 kHz corresponds to a mobility edge with ρ_C ~ 0.09k³. This demonstrates a significant mobility edge variation with increasing disorder (in agreement with Ref. ¹⁷.). The mobility edge shift to lower frequencies observed in Fig. 2b suggests the ϕ = 9.9% SL minimum at 350 kHz might also a mobility edge, and further work is required to shed light on the results in the high-ϕ limit.

It is interesting that localization effects are observed despite the values for kl_S being greater than 1 (true for our work and also prior studies). Theoretical works predicting a critical density for scalar wave localization within a system of resonant point scatterers³⁸ have suggested that in such a system the Ioffe-Regel criterion kl_S ~ 1 is only valid qualitatively and cannot be used as a quantitative condition for Anderson localization in three-dimensions; this has been attributed primarily to the coherent wavepacket being strongly affected by the effective medium’s spatial dispersion, which prevents the definition of the mean free path and effective wave number in the conventional way. That the critical density found here is in agreement with that predicted for a system of resonant point scatterers suggests a non-negligible contribution from the medium’s spatial dispersion on the coherent wavepacket.

We also point out that in prior work on sound localization in mesoglasses²⁸ stronger localized behavior was found near a minimum in the amplitude transmission coefficient with mobility edges on either side of the minimum (determined via SCT fittings). This, however, is quite different from our results in that we find stronger localized behavior away from the l_S/λ minima identified as mobility edges as opposed to near the minima: for example, the frequency range shown in Fig. 5b begins at a frequency more than 70 kHz higher than the minimum in l_S/λ. In addition, we find evidence of strong attenuation of the incoherent wave at the mobility edge due to fluctuations in the wave diffusivity, and this result is absent in the mesoglass literature. The discrepancies could most likely be due to the differences in the unique systems themselves for here the frequency-dependent disorder strength is generated through variations in EMB resonance frequencies and topological disorder while for the case of the mesoglass samples the disorder is generated by variations in the weak couplings between brazed aluminum beads.

In summary, our work demonstrates broadband control of sound localization and phase transitions in soft matter. Localized phases as broad as 246 kHz are observed, which are separated from extended states by mobility edges. The phase transition is found to be accompanied by a strong anomalous decrease of the mean free path at the mobility edge. We determine the critical density needed for the localized phase and find evidence of an extended-state transport regime at the highest frequencies used in our experiments and above the critical frequency at which the system transitions out of the localized phase. We anticipate our work will enable further investigations in soft and condensed matter physics, and will aid in the realization of materials governed by the physics of Anderson localization impacting broad areas of technological importance including materials with tunable acoustic and elastic properties, high-frequency thermoelectric heat transport, and phonon excitation and suppression, to name a few.

Methods

Materials and fabrication

The soft suspending gel (Carbopol ETD 2050) is obtained from the Lubrizol corporation. The pre-expanded EMBs (043 DET 80 d20) are obtained from Expancel (part of the Technical Solutions Group within Nouryon). The Uralite 3140 polymer is acquired from Ellsworth Adhesives.

Uralite 3140 is a two-component, low viscosity elastomer. Prior to combining parts A and B, the thicker Part A is degassed for several minutes to remove undesired trapped air. Subsequently, Part A is combined with Part B and then the entire mixture is again degassed for several minutes. Following degassing, the mixture is transferred to a pressure vessel that is connected to the mold into which the mixture is injected. Following a 24 h partial cure, the Uralite is baked at 82 °C for 4 h to hasten the curing time. Once the 4 mm-thick Uralite shell is fully cured the top is trimmed and a cap is glued in place using Uralite as the glue. All subsequent caps (those covering the gel injection ports) and suspension/weighting tabs are glued onto the shell with a water-resistant glue.

Preparation of the gel is done by slowly adding the Carbopol ETD 2050 powder (0.2 wt %) to agitated water. Mixing is continued for several minutes to ensure consistency, and a neutralizer is added so that the final gel is pH neutral. The entire mixture is then degassed to remove any undesired trapped air. During degassing, the break occurs after ~1.5 min for the undoped material while multiple breaks are observed with increasing EMB concentration. The total degassing time is about 1 h. Following degassing, the gel is mechanically injected into the Uralite shell. For those samples requiring EMBs, the EMBs are added to the gel following the gel preparation and prior to degassing. Finally, the EMB/gel mix is then degassed prior to mechanical injection into the Uralite shell.

Sample thickness was measured using Starrett calipers with a resolution of 1.0 × 10⁻⁵ m. Sample mass is measured on a scale with a resolution of either 5.0 × 10⁻⁴ kg or 1.0 × 10⁻⁵ kg. Volume of gel-based material is measured using a graduated cylinder with a line width of ~5 × 10⁻⁴ m. From these measurements, the sample density and EMB volume fraction are determined; note that for the samples discussed in the main text, the target volume fractions were ϕ = 0.5%, ϕ = 2.0%, and ϕ  = 10%.

EMB characterization with scanning electron microscopy

Scanning electron microscopy (SEM) is used to confirm EMB surface uniformity as well as to quantify the EMB shell thickness. Figure 1f of the main text shows an SEM image of an EMB following fabrication of a Uralite-doped sample and subsequent exposure of the EMB by cutting into the doped polymer with scissors. The image in Fig. 1f shows an EMB with no significant surface abnormalities or deviations from a spherical geometry. Also, Supplementary Fig. 5 shows an SEM image of an intentionally deflated EMB, which allows for a measurement of the shell thickness. A thickness measurement is made where the deflated shell maintains contact with the remaining polymer cavity. Multiple measurements of the shell thickness within the highlighted region of Supplementary Fig. 5 gave a value ~350–580 nm with an average of ~437 nm (note, the way the EMB has collapsed suggests the true EMB thickness is half the measured thickness, or ~219 nm).

In-water measurements

Measurements are carried out using a 0.5 MHz piston-faced immersion transducer and a Reson TC 4035 hydrophone from Teledyne Marine. The experiments utilize a Krohn-Hite 5920 arbitrary waveform generator. Prior to the output waveform reaching the source, the waveform is filtered with an Ithaco 4302 dual 24 dB/octave filter and then amplified using an E&L 240 L RF power amplifier. The hydrophone signal is amplified using an Ithaco 1201 low-noise preamplifier before being digitized for data collecting and processing. For all datasets presented 1000 measurements are collected, averaged together, and a background subtraction is used to eliminate any y-axis offset. The sample temperature was monitored throughout the duration of the experiments and was T ~ 296–298 K. Samples are held in place underwater using fishing line with weights to hold the sample stationary. Appropriate correction factors are applied to the data, which account for the finite sample thickness as well as the measurement range.

Supplementary Fig. 6 shows the transmitted pressure P versus time t for the water reference (no sample), an undoped sample, and for ϕ = 1.2% (the maximum pressure decreases over an order of magnitude upon doping). The wavepacket shown in Supplementary Fig. 6 for the water reference (No Sample dataset) was used to collect the data presented in Fig. 2 of the main text. The data shown in Supplementary Fig. 6 indicates the undoped sample group velocity is equal to that of water. Further, at f = 700 kHz we determine the attenuation coefficient α = 15 Np/m for the undoped sample, which is a factor of 59 smaller than the maximum α measured for ϕ = 1.2% (881 Np/m) and indicates minimal attenuation due to the soft materials.

For measuring within independent speckles, the sample was translated within the plane perpendicular to the central axis from the source transducer to the hydrophone. We use displacements larger than the wavelength of sound in water at 500 kHz, namely λ ~ 3 mm. The sample was displaced such that the source-hydrophone central axis traced a circle counterclockwise about the sample center. Furthermore, the aerial dimensions of the hydrophone sensor are smaller than the speckle coherence area (~λ²), which ensures measurements within independent speckles.