Abstract
Microscopic physical laws are time-symmetric, hence, a priori there exists no preferential temporal direction. However, the second law of thermodynamics allows one to associate the “forward” temporal direction to a positive variation of the total entropy produced in a thermodynamic process, and a negative variation with its “time-reversal” counterpart. This definition of a temporal axis is normally considered to apply in both classical and quantum contexts. Yet, quantum physics admits also superpositions between forward and time-reversal processes, whereby the thermodynamic arrow of time becomes quantum-mechanically undefined. In this work, we demonstrate that a definite thermodynamic time’s arrow can be restored by a quantum measurement of entropy production, which effectively projects such superpositions onto the forward (time-reversal) time-direction when large positive (negative) values are measured. Finally, for small values (of the order of plus or minus one), the amplitudes of forward and time-reversal processes can interfere, giving rise to entropy-production distributions featuring a more or less reversible process than either of the two components individually, or any classical mixture thereof.
Similar content being viewed by others
Introduction
In spite of it being seemingly straightforward, physics is still nowadays seeking to provide a comprehensive understanding of the apparent passage of time1. The concept of time flow is intimately related to the observation of a change in physical systems. However, the recognition that, at their most fundamental level, physical systems generally obey time-reversible laws led to the realisation that systems’ evolutions do not intrinsically differentiate between forward and backward time directions. Attempts to uphold with physical arguments the evidence of the time flow are being made on multiple fronts, mainly on the basis of empirical observations: we see that entropy in the universe increases (thermodynamic time’s arrow), that the universe expands (cosmological time’s arrow), that causes always precede their effects (causal time’s arrow). Likewise, there have been several proposals as to the explanation of the time’s arrow in a quantum-mechanical contexts2,3,4,5,6. The peculiarity of the quantum framework is that it enables processes to be placed in quantum superposition. Applied to the notion of thermodynamic time’s arrow, this implies that quantum mechanics can allow the superposition of thermodynamic processes (namely, dynamic processes wherein a system of interest exchanges either heat, work, or both with other systems, the environment and/or external agents) producing opposite variations in the entropy. This raises the question of how a well-defined thermodynamic arrow of time can be established in the quantum framework when such superpositions are in place. To address this question, in this work we show that a measurement of the entropy production has a decisive role in restoring a definite thermodynamic time’s arrow, and we investigate interference effects in such superpositions. Our investigations bear a conceptual similarity to the field of indefinite quantum causality, wherein the order of operations is placed in a quantum superposition7,8,9. Note, however, that there is a crucial difference between these two types of studies. In indefinite quantum causality, operations are performed in the same temporal direction (here referred to as “forward”) in each amplitude of the superposition. In contrast, in the present case, we analyse superpositions of thermodynamic processes with opposing thermodynamic arrows of time.
In thermodynamics, the time’s arrow is introduced by the second law of thermodynamics, according to which the total entropy of the universe can only either increase or remain constant. Consequently, one might think that observations of entropy changes are all we need to distinguish the past from the future: an overall increase in entropy shall be identified with the direction of time “forward”, while an overall decrease in entropy with its “time-reversal” counterpart. Yet, for a microscopic system, fluctuations blur the direction of the time’s arrow, and the time flow is only defined on average. More specifically, in this regime, the time’s arrow cannot be inferred, as both positive and negative entropy changes can be observed with comparable probability in a single experimental run. As a consequence, for such systems, the two opposite time’s arrows become classically indistinguishable. The extension of this indistinguishability to the quantum domain gives rise to quantum superpositions between opposite time’s arrows, whose investigation is the focus of the present work.
In what follows, we will explore how a definite time’s arrow arises in quantum superpositions between “forward” and “time-reversal” processes (i.e., thermodynamic processes whose quenches are related by time-inversion symmetry). In particular, we will show that quantum measurements of the dissipative work Wdiss (or, equivalently, entropy production ΔStot) can restore the time directionality of the process. The dissipative work Wdiss = W − ΔF is the amount of work W invested in a thermodynamic transformation between equilibrium states having a free energy difference ΔF, which cannot be recovered by reversing the process. Furthermore, the relation between the dissipative work and the entropy production (or total entropy) ΔStot in the process is established through the relation: ΔStot = β Wdiss, where \(\beta ={({k}_{B}T)}^{-1}\) is the inverse temperature, with kB being the Boltzmann constant and T the temperature of the bath10,11,12. We will then show that, when the measured dissipative work equals βWdiss ≫ 1, the superposition is effectively projected onto the forward process, whereas when βWdiss ≪ −1, it is effectively projected onto the time-reversal one, hence recovering a definite thermodynamic arrow of time (albeit, in each individual execution of the experiment, the outcome “forward" or “time reversal" is random). Conversely, when β∣Wdiss∣ is of the order of one, the forward and the time-reversal thermodynamic processes can quantum mechanically interfere under certain conditions, resulting in a work probability distribution describing work fluctuations that have no classical counterpart. More precisely, in the case of interference, the probabilities take on values that cannot be obtained by any classical (convex) mixture of the forward and the time-reversal processes.
Results
Superposition of forward and time-reversal dynamics
We start by defining the framework used to characterise thermodynamic processes and work fluctuations. First, we will introduce all the necessary elements to formally construct a state representing the quantum superposition of a thermodynamic process evolving in the forward temporal direction, and one evolving in the opposite (time-reversal) direction. Then, we will discuss how to characterise work and entropy-production fluctuations in such superposition states using an extended two-point-measurement (TPM) scheme, and we illustrate how the outcomes achieved through processes with well-defined time directions can be recovered inside our framework.
We consider a thermodynamic system S being, in both forward and time-reversal processes, initially in equilibrium with a thermal reservoir at inverse temperature β. The process occurring in the forward direction will be realised by a quench U(t, 0) induced by the time-dependent Hamiltonian \(H\left(\lambda (t)\right)\) executing a controlled protocol Λ ≡ {λ (t); 0 ≤ t ≤ τ} in the time-frame t ∈ [0, τ], followed by a final thermalisation in contact with the reservoir at β. Here, \(U({t}_{1},{t}_{2})=\vec{{{{{{{{\bf{T}}}}}}}}}\exp \left[-\frac{i}{\hslash }\int\nolimits_{{t}_{1}}^{{t}_{2}}d\nu \ H\left(\lambda (\nu )\right)\right]\), where \(\vec{{{{{{{{\bf{T}}}}}}}}}\) is the so-called “time-ordering” operator resulting from the Dyson decomposition. Its time-reversal twin will be described by a quench \(\tilde{U}(\tau -t,0)\) associated to the implementation of the operational time-reversal protocol \(\tilde{{{\Lambda }}}\equiv \{\lambda (\tau -t);0\le t\le \tau \}\), where in both cases λ is a control parameter, and again the quench is followed by a final thermalisation step. The micro-reversibility principle for non-autonomous systems establishes a strong relation between forward and time-reversal quenches lying at the core of fluctuation theorems13,14:
where Θ denotes the (anti-unitary) time-reversal operator acting on the system’s Hilbert space, which flips the sign of observables with odd parity under time-reversal. This operator verifies the relations \({{\Theta }}\ \ {\Bbb{1}}i=-{\Bbb{1}}i\ {{\Theta }}\), and \({{\Theta }}\ {{{\Theta }}}^{{{{\dagger}}} }={{{\Theta }}}^{{{{\dagger}}} }\ {{\Theta }}={\mathbb{1}}\).
In order to describe superpositions of forward and time-reversal processes, the initial equilibrium states of the system S can be purified by including some environmental degrees of freedom E with a generic Hamiltonian HE in the description. These purifications are not unique, and they can be represented by joint states of the system and the environment of the form
where \({E}_{k}^{(0)}\) and \({E}_{k}^{(\tau )}\) are the eigenvalues of the Hamiltonian at times t = {0, τ}, i.e., H[λ(0)] and H[λ(τ)], whereas \({|{E}_{k}^{(0)}\rangle }_{{{{{{{\mathrm{S}}}}}}}}\) and \({|{E}_{k}^{(\tau )}\rangle }_{{{{{{{\mathrm{S}}}}}}}}\) are the corresponding eigenvectors (for the sake of brevity, we will henceforth omit the subscript S in the system’s energy eigenvectors). Furthermore, \({|{\varepsilon }_{k}^{(0)}\rangle}_{{{{{{{\mathrm{E}}}}}}}}\), \({|{\varepsilon }_{k}^{(\tau )}\rangle }_{{{{{{{\mathrm{E}}}}}}}}\) represent the corresponding sets of states of the environmental degree of freedom, which can always be chosen as sets of orthogonal states. Notice that the environment may possess further degrees of freedom that are not entangled with the system under consideration, and which we will thus not explicitly account for.
The state \({|{\psi }_{0}\rangle }_{{{{{{{\mathrm{S,E}}}}}}}}\) above corresponds to the initial state of the process evolving in the forward direction as defined by Λ, whereas \({|{\tilde{\psi }}_{0}\rangle }_{{{{{{{\mathrm{S,E}}}}}}}}\) is the initial state of the time-reversed process as defined by \(\tilde{{{\Lambda }}}\). Notice that, by tracing out the environmental degrees of freedom, we recover the corresponding Gibbs thermal states for the system \({\rho }_{0}^{\,{{{{{{\mathrm{th}}}}}}}\,}\equiv {{{{{{{{\rm{Tr}}}}}}}}}_{{{{{{{\mathrm{E}}}}}}}}(|{\psi }_{0}\rangle {\langle {\psi }_{0}|}_{{{{{{{\mathrm{S,E}}}}}}}})={e}^{-\beta H[\lambda (0)]}/{Z}_{0}\) and \({\tilde{\rho }}_{0}^{\,{{{{{{\mathrm{th}}}}}}}\,}\equiv {{{{{{{{\rm{Tr}}}}}}}}}_{{{{{{{\mathrm{E}}}}}}}}(|{\tilde{\psi }}_{0}\rangle {\langle {\tilde{\psi }}_{0}|}_{{{{{{{\mathrm{S,E}}}}}}}})= {{\Theta }}\ {e}^{-\beta H[\lambda (\tau )]}{{{\Theta }}}^{{{{\dagger}}} }/{Z}_{\tau }\), being \({Z}_{0}={{{{{{{\rm{Tr}}}}}}}}\left({e}^{-\beta H[\lambda (0)]}\right)\), and \({Z}_{\tau }={{{{{{{\rm{Tr}}}}}}}}\left({e}^{-\beta H[\lambda (\tau )]}\right)\) the partition functions.
Moreover, we introduce an auxiliary system A whose two orthogonal states \(\{{\left|0\right\rangle }_{A},{\left|1\right\rangle }_{A}\}\) govern the evolution of the process in the two temporal directions. This is a quantum analogue of the coin tossed to decide classically which process to run (forward or time reversal). With this in place, the global Hamiltonian of the system, the environment, and the auxiliary qubit reads \({{{{{{{\mathcal{H}}}}}}}}(t)\equiv \left(\left|0\right\rangle {\left\langle 0\right|}_{{{{{{{\mathrm{A}}}}}}}}\otimes H[\lambda (t)]+\left|1\right\rangle {\left\langle 1\right|}_{{{{{{{\mathrm{A}}}}}}}}\otimes {{\Theta }}H[\lambda (\tau -t)]{{{\Theta }}}^{{{{\dagger}}} }\right)\otimes {{\Bbb{1}}}_{{{{{{{\mathrm{E}}}}}}}}+{{\Bbb{1}}}_{{{{{{{\mathrm{S,A}}}}}}}}\otimes {H}_{{{{{{{\mathrm{E}}}}}}}}\). We then entangle each orthogonal auxiliary state to one of the initial states in Eq. (2). The overall initial state of thermodynamic system, environment and auxiliary system reads therefore:
with arbitrary coefficients \({\alpha }_{0},{\alpha }_{1}\in {\Bbb{C}}\), ∣α0∣2 + ∣α1∣2 = 1. If, subsequently, in each branch of the superposition in Eq. (3) the forward and time-reversal quenches are respectively applied, the evolved state at some arbitrary instant of time t ∈ [0, τ] is given by \({|{{\Psi }}(t)\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}={\alpha }_{0}\kern-1pt\ [U(t,0)\otimes \kern-1pt{{\Bbb{1}}}_{{{{{{{\mathrm{E,A}}}}}}}}]{|{\psi }_{0}\rangle }_{{{{{{{\mathrm{S,E}}}}}}}}\kern-1pt\otimes\! {|0\rangle }_{{{{{{{\mathrm{A}}}}}}}}\kern-1pt+\kern-1pt{\alpha }_{1}| [\tilde{U}(t,0)\kern-1pt\otimes {{\Bbb{1}}}_{{{{{{{\mathrm{E,A}}}}}}}}]{|{\tilde{\psi }}_{0}\rangle }_{{{{{{{\mathrm{S,E}}}}}}}}\kern-1pt\otimes\kern-1pt {|1\rangle }\kern-0.7pt_{{{{{{{\mathrm{A}}}}}}}}\kern-0.9pt.\) In this expression, the first and the second amplitudes correspond to the forward and the time-reversal processes, respectively. Furthermore, we assume that the system does not interact with the environment during the timescale of the quenches (however, after the quench, the system thermalises through the interaction with the thermal reservoir). This is verified whenever the quenches are implemented in a fast timescale as compared to the characteristic relaxation time of the system in interaction with the environment15, or when the system is artificially disconnected from the environment during the quench implementation and reconnected after it. Furthermore, we will consider the quenches U(t, 0) and \(\tilde{U}(t,0)\) in the superposition to be implemented by some external (classical) control. As we discuss in the Supplementary Note 116,17,18,19,20, this limit is adequate in our setup, and it corresponds to the case in which the control mechanism acts approximately as an ideal reservoir of energy and coherence21,22,23,24, as is the case, for instance, with lasers or radiofrequency pulses.
Taking a gas enclosed in a vessel as a pictorial example, the aforementioned state can be constructed by entangling the position of the piston with a further auxiliary quantum system, thereby establishing a quantum superposition of the following two processes: (i) a process wherein the gas particles are initially in thermal equilibrium confined in one half of the vessel by a piston, and the piston is pulled outwards, and (ii) the reverse process, in which the piston is pushed towards the gas, starting from an initial state where the gas occupies the entire vessel in thermal equilibrium.
Extended two-point measurement scheme
We will now measure the work of the system undergoing the above-mentioned superposition of forward and time-reversal dynamics. In order to implement such a measurement, we formally construct a procedure described by a set of measurement operators forming a completely positive and trace-preserving (CPTP) map. In this regard, we will refer to a standard TPM procedure to measure work in quantum thermodynamic processes13. Implementations of the TPM in quantum setups25,26,27,28,29, as well as suitable extensions30,31,32,33, have recently received increasing attention. Our procedure can be seen as a generalisation of the TPM scheme to situations where different thermodynamic processes are allowed to be superposed, and can consequently interfere.
In the TPM scheme, work is defined as the energy difference between the initial and final states of the system, which are measured through ideal projective measurements of the system Hamiltonian implemented before and after the thermodynamic process associated with the protocol Λ34,35. This measurement scheme can be performed, individually, both for the forward and the time-reversal processes, enabling the construction of the work probability distributions P(W) and \(\tilde{P}(W)\), respectively.
As far as the forward process is concerned, the probability to observe a transition \(\left|{E}_{n}^{(0)}\right\rangle \to \left|{E}_{m}^{(\tau )}\right\rangle\) is given by \({p}_{n,m}={p}_{m| n}\ {p}_{n}^{(0)}\), where \({p}_{n}^{(0)}={e}^{-\beta {E}_{n}^{(0)}}/{Z}_{0}\) is the probability of observing the energy \({E}_{n}^{(0)}\) at t = 0, and \({p}_{m| n}={\left|\langle {E}_{m}^{(\tau )}| U(\tau ,0)| {E}_{n}^{(0)}\rangle \right|}^{2}\) is the conditional probability of measuring \({E}_{m}^{(\tau )}\) at t = τ after having measured \({E}_{n}^{(0)}\) at the beginning of the process. Similarly, for the time-reversal process one has \({\tilde{p}}_{m,n}={\tilde{p}}_{n| m}\ {\tilde{p}}_{m}^{(0)}\), where \({\tilde{p}}_{m}^{(0)}={e}^{-\beta {E}_{m}^{(\tau )}}/{Z}_{\tau }\) is the probability to obtain the energy \({E}_{m}^{(\tau )}\) at the beginning of the time-reversal process, and \({\tilde{p}}_{n| m}={\left|\langle {E}_{n}^{(0)}| {{{\Theta }}}^{{{{\dagger}}} }\tilde{U}(\tau ,0){{\Theta }}| {E}_{m}^{(\tau )}\rangle \right|}^{2}\) is the corresponding conditional probability for observing the inverse transition \({{\Theta }}\left|{E}_{m}^{(\tau )}\right\rangle \to {{\Theta }}\left|{E}_{n}^{(0)}\right\rangle\) given that one obtained \({E}_{m}^{(\tau )}\) in the first measurement. The micro-reversibility principle in Eq. (1) relates the conditional probabilities in the forward and time-reversal processes as \({\tilde{p}}_{n| m}={p}_{m| n}\)13,14.
The TPM scheme allows one to compute the stochastic work invested by the external driver in a single realisation of the protocol Λ, \({W}_{n,m}\equiv {E}_{m}^{(\tau )}-{E}_{n}^{(0)}\), associated to the outcomes of initial and final energy measurements. Its probability distribution reads:
Analogously, the probability distribution associated to the work invested in the time-reversal protocol, \({\tilde{W}}_{n,m}={E}_{n}^{(0)}-{E}_{m}^{(\tau )}= -{W}_{n,m}\), is given by:
Hereafter, we consider an extension of the TPM scheme in which we include energy measurements at t = 0 and t = τ in both branches of the superposition between a forward and a time-reversal processes, as illustrated in Fig. 1. More precisely, starting with the initial state in Eq. (3), and conditionally on the auxiliary state, we consider the application of the projectors \(\left|{E}_{n}^{(0)}\right\rangle \left\langle {E}_{n}^{(0)}\right|\) and \({{\Theta }}\left|{E}_{m}^{(\tau )}\right\rangle \left\langle {E}_{m}^{(\tau )}\right|{{{\Theta }}}^{{{{\dagger}}} }\) to the initial states \({\left|{\psi }_{0}\right\rangle }_{{{{{{{\mathrm{S,E}}}}}}}}\) and \({\left|{\tilde{\psi }}_{0}\right\rangle }_{{{{{{{\mathrm{S,E}}}}}}}}\), respectively. Subsequently, the unitary quenches U(τ, 0) and \(\tilde{U}(\tau ,0)\) are implemented in each branch, after which the projectors \(\left|{E}_{m}^{(\tau )}\right\rangle \left\langle {E}_{m}^{(\tau )}\right|\) and \({{\Theta }}\left|{E}_{n}^{(0)}\right\rangle \left\langle {E}_{n}^{(0)}\right|{{{\Theta }}}^{{{{\dagger}}} }\) are respectively applied. Consequently, given the outcomes \({E}_{n}^{(0)}\) and \({E}_{m}^{(\tau )}\), a work Wn,m is invested in the forward-dynamics branch by applying the protocol Λ, whereas the work invested in its time-reversal counterpart \(\tilde{{{\Lambda }}}\) is \({\tilde{W}}_{n,m}=-{W}_{n,m}\) (i.e., the same amount of work as in the forward dynamics is here extracted).
A thermodynamic system S and its environment are coupled to an auxiliary system A in a suitable entangled state. Depending on the state of the auxiliary system, \({\left|0\right\rangle }_{{{\mbox{A}}}}\) or \({\left|1\right\rangle }_{{{\mbox{A}}}}\), when the state of the environment is traced out, the system S is initially prepared in a thermal state of the initial or final Hamiltonians, H(0) and H(τ), respectively. This is then sent through a thermodynamic quench U(t, 0) or its time reversal \(\tilde{U}(t,0)\) in the time-frame t ∈ [0, τ]. Before and after each quench, the system’s energy is measured. The measurement outcomes \({E}_{n}^{(0)}\) and \({E}_{m}^{(\tau )}\) are found when the auxiliary system is in \({\left|0\right\rangle }_{{{\mbox{A}}}}\), whereas the outcomes \({E}_{m}^{(0)}\) and \({E}_{n}^{(\tau )}\) are obtained when the auxiliary system is in \({\left|1\right\rangle }_{{{\mbox{A}}}}\). After these measurements, the system may eventually undergo a second thermalisation with the environment. Note that the first (second) measurement when the auxiliary system is in \({\left|0\right\rangle }_{{{\mbox{A}}}}\), and the second (first) measurement when it is in \({\left|1\right\rangle }_{{{\mbox{A}}}}\) are physically one and the same measurement. A possible implementation of this scheme is reported in Fig. 2.
The operator representing the application of the scheme through which the work Wn,m is obtained can be written as:
The set of operators {Mn,m} forms a CPTP map, \({{{{{{{\mathcal{E}}}}}}}}(\rho )\equiv {\sum }_{n,m}{M}_{n,m}\rho {M}_{n,m}^{{{{\dagger}}} }\), acting on the composite system S, E, A and fulfilling \({\sum }_{n,m}{M}_{n,m}^{{{{\dagger}}} }{M}_{n,m}={{\Bbb{1}}}_{{{{{{{\mathrm{S,E,A}}}}}}}}\). The map \({{{{{{{\mathcal{E}}}}}}}}\) describes the average effect of the measurement scheme on an arbitrary initial state of the composite system ρ, while the operations \({{{{{{{{\mathcal{E}}}}}}}}}_{n,m}(\rho )\equiv {M}_{n,m}\rho {M}_{n,m}^{{{{\dagger}}} }\) provide the probability \({{{{{{{\mathcal{P}}}}}}}}(W)\equiv {\sum }_{n,m}{{{{{{\mathrm{Tr}}}}}}}\,[{{{{{{{{\mathcal{E}}}}}}}}}_{n,m}(\rho )]\delta (W-{W}_{n,m})\) to measure the work W.
It is important to stress that the operations \({{{{{{{{\mathcal{E}}}}}}}}}_{W}\) preserve the coherence between the forward and time-reversal thermodynamic processes. Indeed, performing a standard quantum measurement on the process would destroy the coherence, as it would reveal the time at which the measurement has been performed, and, from this, also whether the outcome Em was observed before (in the forward process) or after the outcome En (in the time-reversal process). In other words, such a measurement would reveal the time direction, and it would be equivalent to the measurement of the auxiliary qubit in the basis \(\{{\left|0\right\rangle }_{A},{\left|1\right\rangle }_{A}\}\). However, there exist also measurement schemes in which the result is encoded in an auxiliary system through its entanglement with the measured system, and the result is then read-only at the end of the whole evolution, thereby preserving its coherence. (Such a measurement scheme was recently used to measure the system undergoing superposition of causal orders36) In such a scheme, the system on which the thermodynamic quenches act and the auxiliary system can be encoded on two different degrees of freedom of the same quantum system. If the auxiliary degree of freedom is of sufficient dimension, it is possible to encode the results of each measurement taking place within the process in a state of this system. More precisely, suppose that the auxiliary system has two additional registers \(A^{\prime}\) which can store the results of the two energy measurements. When the auxiliary system is in the \({\left|0\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\) (\({\left|1\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\)) state, the thermodynamic system is subject to an unitary \({{{{{{{{\mathcal{U}}}}}}}}}_{1}\) (\({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{1}\)) that couples the energy of the system to the first (second) register of the auxiliary system. This results in an overall unitary that entangles the thermodynamic system with the auxiliary system:
where
for any basis state \({\left|x,y\right\rangle }_{A^{\prime} }\) of the two registers. Here, the symbol ⊕ means the sum modulo the total number of different energy values. Subsequently, the thermodynamic system is subject to a quench, followed by another entangling unitary
with
which now couples the energy of the thermodynamic system after the quench in the second (first) register when the auxiliary system is in the state \({\left|0\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\) (\({\left|1\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\)). If the two registers are initially prepared in the state \({\left|0,0\right\rangle }_{A^{\prime} }\), their final state \({\left|n,m\right\rangle }_{A^{\prime} }\) will encode both energy values. The coherence of the overall state has to be maintained until the end of the entire thermodynamic process when the auxiliary system is measured in the basis \(\{({\left|0\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\pm {\left|1\right\rangle }_{A})/\sqrt{2}\}\) to erase any information as to whether the system has gone through the “forward” or “time-reversal” process (which might be encoded, for instance, in the temporal or directional mode of the auxiliary system). A sketch of a possible experimental realisation of the extended TPM scheme is shown in Fig. 2 in the case of two measurements outcomes for \({E}_{n}^{(0)}\), \({E}_{m}^{(\tau )}\). For simplicity, in this study we consider only two states of the auxiliary system (Fig. 1). Nevertheless, all the conclusions drawn herein can be extended to the case of more than two states.
A beam splitter (BS) creates a quantum superposition of the auxiliary state in \({|0\rangle }_{{{{\mathrm A}}}}\), \({|1\rangle }_{{{{\mathrm A}}}}\) as represented by the upper (solid) and lower (dashed) paths in the left part of the figure, over which the initial state in Eq. (3) is prepared. Unitary operators \({{{{{{{{\mathcal{U}}}}}}}}}_{1,2}\) and \({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{1,2}\) couple the system with two additional internal registers \(A^{\prime}\), initially prepared in the state \({\left|0,0\right\rangle }_{A^{\prime} }\) (for simplicity, unitaries \({{{{{{{{\mathcal{U}}}}}}}}}_{1,2}\) and \({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{1,2}\) are here imagined to produce binary results). Encoding pairs of system energy eigenstates (n, m) onto the registers \(A^{\prime}\) leads to further subdivisions into different paths (middle part of the figure), which are recombined and measured only at the final stage of the interferometer. The unitaries \({{{{{{{{\mathcal{U}}}}}}}}}_{1,2}\) and \({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{1,2}\) and the final measurement replace the initial and final projective measurements of \({E}_{n}^{(0)}\) and \({E}_{m}^{(\tau )}\) in the TPM scheme in Fig. 1. When the auxiliary system is in the state \({|0\rangle }_{{{{{{{\mathrm{A}}}}}}}}\) (\({|1\rangle }_{{{{{{{\mathrm{A}}}}}}}}\)), the thermodynamic system is first subjected to a unitary \({{{{{{{{\mathcal{U}}}}}}}}}_{1}\) (\({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{1}\)), then to the thermodynamic process U(τ, 0) [\(\tilde{U}(\tau ,0)\)] within the time interval [0, τ], and finally to a second unitary \({{{{{{{{\mathcal{U}}}}}}}}}_{2}\) (\({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{2}\)), see solid (dashed) paths in the figure. Unitary \({{{{{{{{\mathcal{U}}}}}}}}}_{1}\) encodes the energy of the eigenstates \(\left|{E}_{n}^{(0)}\right\rangle\) of the thermodynamic system into the first register \({\left|n,0\right\rangle }_{A^{\prime} }\) (n = 0, 1) of the auxiliary system, while unitary \({{{{{{{{\mathcal{U}}}}}}}}}_{2}\) encodes the energy of the eigenstates \(\left|{E}_{m}^{(\tau )}\right\rangle\) into the states \({\left|n,m\right\rangle }_{A^{\prime} }\) (m = 0, 1) of the second register. The four possible outcomes are indicated as four solid paths (bottom part of the figure), each labelled as \({|0\rangle }_{{{{{{{\mathrm{A}}}}}}}}{|n,m\rangle }_{A^{\prime} }\). Similarly, the unitaries \({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{1}\) and \({\tilde{{{{{{{{\mathcal{U}}}}}}}}}}_{2}\) encode the energies of the thermodynamic system before and after the quench in the second and the first register respectively, when the auxiliary system is in \({\left|1\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\) (four dashed paths labelled as \({\left|1\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}{\left|m,n\right\rangle }_{A^{\prime} }\) in the top part of the figure). This enables to maintain the coherence of the auxiliary system’s states until the end of the interferometer. There, the states \({\left|0\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}{\left|n,m\right\rangle }_{A^{\prime} }\) and \(\left|1\right\rangle {\left|m,n\right\rangle }_{A^{\prime} }\) are interfered pairwise through further BSs, and measured. The results of the final measurements over the system A in the diagonal basis \(\{{\left|\pm \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\}\) are indicated by the symbols \({E}_{n,m}^{\pm }\).
In order to evaluate the work probability distribution in the extended TMP scheme, it is also crucial to take into account the mutual phases between the conditional probabilities. We thus write, in general
and we notice that
from which we get \({{{\Phi }}}_{n,m}={\tilde{{{\Phi }}}}_{m,n}\), since \({\tilde{p}}_{n| m}={p}_{m| n}\).
We now consider the concatenation of the operation Mn,m with a projection of the auxiliary qubit onto an arbitrary state \({\left|\xi \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\). By applying this sequence of operations to the initial state in Eq. (3), we derive the (unnormalized) state of the composite system associated to the work outcome Wn,m and projection of the auxiliary qubit onto \({\left|\xi \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\):
where we identified the two branches of the superposition corresponding to the forward \((|{{{\Xi }}}_{0}^{\xi }\rangle )\) and the time-reversal dynamics \((|{{{\Xi }}}_{1}^{\xi }\rangle )\). They read, respectively:
where, in the second equation, we made use of \({\tilde{p}}_{n,m}={p}_{n,m}\ {e}^{-\beta ({W}_{n,m}-{{\Delta }}F)}\) (see the Supplementary Note 2), and of the relation between the forward and time-reversal phases \({\tilde{{{\Phi }}}}_{m,n}={{{\Phi }}}_{n,m}\). The final thermalisation step, which effectively leads to the irreversible dissipation of work Wdiss, occurs only after the projection onto the auxiliary qubit, and is thus not included within the (extended) TPM scheme.
The joint probability of measuring the work W and projecting the auxiliary state onto \({\left|\xi \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\) is given by \({{{{{{{\mathcal{P}}}}}}}}(\xi ,W)={\sum }_{n,m}{||{|{{{\Psi }}}_{n,m}^{\xi }\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}||}^{2}\delta (W-{W}_{n,m})\). Furthermore, from the joint probabilities \({{{{{{{\mathcal{P}}}}}}}}(\xi ,W)\), one can obtain the conditional ones \({{{{{{{{\mathcal{P}}}}}}}}}_{\xi }(W):= {{{{{{{\mathcal{P}}}}}}}}(W| \xi )={{{{{{{\mathcal{P}}}}}}}}(\xi ,W)/{{{{{{{\mathcal{P}}}}}}}}(\xi )\), which we will hereafter refer to as “post-selected work probability distributions”, and where \({{{{{{{\mathcal{P}}}}}}}}(\xi )=\int dW\ {{{{{{{\mathcal{P}}}}}}}}(\xi ,W)\). By introducing the notation \({q}_{0}^{\xi }=| {\alpha }_{0}{| }^{2}{| \langle \xi | 0\rangle | }^{2}/{{{{{{{\mathcal{P}}}}}}}}(\xi )\) and \({q}_{1}^{\xi }= | {\alpha }_{1}{| }^{2}{| \langle \xi | 1\rangle | }^{2}/{{{{{{{\mathcal{P}}}}}}}}(\xi )\), we can rewrite \({{{{{{{{\mathcal{P}}}}}}}}}_{\xi }(W)\) as:
where we identified the probability distributions for the work in the forward process P(W), and in the time-reversal one \(\tilde{P}(-W)\) as given in Eqs. (4)–(5), respectively. From this, we obtain the interference term:
The functional dependence of \({{{{{{{{\mathcal{P}}}}}}}}}_{\xi }(W)\) on W consists of two parts: (i) an “incoherent” part, reflecting the fact that each work value W obtained in the scheme is compatible with running the process in one or the other temporal direction with a given probability (i.e., investing the work W when running the protocol Λ, and extracting the same amount of work − W when executing its time-reversal counterpart \(\tilde{{{\Lambda }}}\)), and (ii) a “coherent” part, which is a genuinely quantum feature arising from the superposition of the two temporal directions of the quench.
In the case \(| {\alpha }_{0}| =| {\alpha }_{1}| =1/\sqrt{2}\), the forward state \(|{{{\Xi }}}_{0}^{\xi }\rangle\) and the time-reversal one \(|{{{\Xi }}}_{1}^{\xi }\rangle\) in Eq. (15) have the same amplitudes in the superposition. Nevertheless, as in the standard scenario of well-defined temporal directions, one may use the properties of the work probability distribution \({{{{{{{{\mathcal{P}}}}}}}}}_{\xi }(W)\) together with Bayesian reasoning to infer the time’s arrow of the thermodynamic process. As we will see shortly, in some cases, the thermodynamic time’s arrow can be determined even in a single realisation of the process, which effectively projects the state \({|{{{\Psi }}}_{n,m}^{\xi }\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}\) onto either its forward or its time-reversal component.
Effective projection onto a definite time’s arrow
In the following, we demonstrate that measuring work values such that W − ΔF ≫ β−1, or W − ΔF ≪ − β−1, in single realisations of the extended TPM scheme effectively results in projecting the state \({|{{{\Psi }}}_{m,n}^{\xi }\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}\) in Eq. (14) onto either the forward or the time-reversal components in Eq. (15) (i.e., \(|{{{\Xi }}}_{0}^{\xi }\rangle\) or \(|{{{\Xi }}}_{1}^{\xi }\rangle\), respectively). In order to show this, we consider the probabilities for the superposition state \({|{{{\Psi }}}_{n,m}^{\xi }\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}\) to be found in either \(| | |{{{\Xi }}}_{0}^{\xi }\rangle | {| }^{2}\) or \(| | |{{{\Xi }}}_{1}^{\xi }\rangle | {| }^{2}\), respectively. In particular, we notice that the term \(| | |{{{\Xi }}}_{1}^{\xi }\rangle | {| }^{2}\) is upper bounded by
where we used the fact that ∣α1∣2∣〈ξ∣1〉∣2 ⩽ 1, and ∑n,m pn,m = 1. Consequently, in the limit βWdiss ≫ 1, we have \(| | |{{{\Xi }}}_{1}^{\xi }\rangle | {| }^{2}\approx 0\), and hence \(| | |{{{\Xi }}}_{0}^{\xi }\rangle | {| }^{2}\approx 1\), that is, \({|{{{\Psi }}}_{n,m}^{\xi }\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}\simeq |{{{\Xi }}}_{0}^{\xi }\rangle\). Indeed, applying the detailed fluctuation theorem in Eq. (21) to Eq. (16), we obtain:
where we made use of the fact that \({I}_{\xi }(W)\propto {e}^{-\beta {W}_{{{{{{{\mathrm{diss}}}}}}}}/2}\). Therefore, we obtained that, whenever one performs a measurement of the work in the extended TPM scheme and observes W − ΔF ≫ β−1 (or, equivalently, ΔS = βWdiss ≫ 1), the state of the system is projected onto the forward component of the quantum superposition without measuring the auxiliary qubit (similarly to what one would obtain, had one projected the joint state \({\left|{{\Psi }}(t)\right\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}\) through a projective measurement \(\left|0\right\rangle {\left\langle 0\right|}_{{{{{{{\mathrm{A}}}}}}}}\) on the auxiliary system, and subsequently observed the work value W). The probability to observe this work value in the extended TPM scheme is given by Eq. (19).
Analogously, whenever the result of the extended TPM scheme is such that W − ΔF ≪ − β−1 (or, equivalently, ΔS = βWdiss ≪ − 1), one can neglect the term \(| | |{{{\Xi }}}_{0}^{\xi }\rangle | {| }^{2}\le {e}^{\beta {W}_{{{{{{{{\rm{diss}}}}}}}}}}\), and thus obtain the projection \({|{{{\Psi }}}_{W}^{\xi }\rangle }_{{{{{{{\mathrm{S,E}}}}}}}}\simeq |{{{\Xi }}}_{1}^{\xi }\rangle\). In this case, we correspondingly achieve:
Hence, here the joint state is projected onto the time-reversal component of the quantum superposition (as if a projective measurement \(\left|1\right\rangle {\left\langle 1\right|}_{{{{{{{\mathrm{A}}}}}}}}\) on the auxiliary system was performed, followed by the observation of the work value W). Similarly to the previous case, Eq. (20) provides the probability to get such an outcome in an estimation of the work.
Interference effects in the work distribution
In the previous section, we observed that, for individual runs of the process’ superposition, whenever the observed entropy production is of the order ∣ΔS∣ ≫ 1 (or, equivalently, ∣W − ΔF∣ ≫ β−1), the system is effectively projected onto a state with a definite thermodynamic time’s arrow. Conversely, if the measured entropy production is ∣ΔS∣ ≲ 1 (or equivalently ∣W − ΔF∣ ≲ β−1), the superposition state Eq. (14) resulting from the application of the extended TPM scheme lacks a definite time’s arrow, exhibiting interference effects.
A closer examination of the term Iξ(W) highlights the fact that the second source of loss of interference effects in the extended TPM scheme lies in the presence of environmental decoherence, manifested in a negligible overlap between the environmental degrees of freedom, i.e., \(\left\langle {\varepsilon }_{n}^{(0)}| {\varepsilon }_{m}^{(\tau )}\right\rangle \sim 0\) for all n, m. This is the case in all instances where the environment is large and uncontrollable, thus leading the states \(\left|{\varepsilon }_{n}^{(0)}\right\rangle\) and \(\left|{\varepsilon }_{m}^{(\tau )}\right\rangle\) to have scarcely any significant overlap. However, for small environments or purposely-engineered environments, such effects can be avoided. For instance, one way to implement this scheme would be keeping a sufficiently small path separation in the interferometer in Fig. 2, such that the particle can be assumed to interact with the same environmental degree of freedom regardless of the path it takes. In this specific case, \(\left\langle {\varepsilon }_{n}^{(0)}| {\varepsilon }_{m}^{(\tau )}\right\rangle ={\delta }_{n,m}\).
As an illustrative example, we study the effect of interference in the work distribution in the case of a spin-\(\frac{1}{2}\) system, as illustrated in Fig. 3. In particular, in the forward quench, the spin system is subjected to a magnetic field whose direction is rotating within the x − z plane at constant angular velocity Ω around the y axis (ω being the spin’s natural frequency) \(H({{\Omega }}t)=\frac{\hslash \omega }{2}\left[{\Bbb{1}}+\cos \left({{\Omega }}t\right)\ {\sigma }_{z}+\sin \left({{\Omega }}t\right)\ {\sigma }_{x}\right]\). In the extended TPM scheme, we superpose the forward quench and its time-reversal twin, and we project the auxiliary system onto the diagonal basis \(\left\{{\left|\pm \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}=({\left|0\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\pm {\left|1\right\rangle }_{A})/\sqrt{2}\right\}\). This leads to the work probability distributions \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\), which illustrates the role played by the interference term. In the limit of a rapid quench (ω ≪ Ω) (and hence of a large degree of irreversibility), the distributions are presented in Fig. 4 (yellow and blue bars), together with the one corresponding to a classical mixture of the forward and time-reversal processes (turquoise bars), where here \(P(W)=\tilde{P}(-W)\). While the classical mixture displays large fluctuations in the work probability distributions, the contribution of the interference term in \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\) can sharpen [\({{{{{{{{\mathcal{P}}}}}}}}}_{+}(W)\)] or flatten [\({{{{{{{{\mathcal{P}}}}}}}}}_{-}(W)\)] the coherent work distribution, effectively increasing or decreasing the degree of reversibility, respectively. Specifically, the probability that the process will occur in a reversible fashion (i.e., that W = 0) is higher for P+(W = 0) [lower for P−(W = 0)] than for a classical mixture (see the “Case study: a spin-\(\frac{1}{2}\) system” subsection in “Methods”). In this example, reversibility and adiabaticity coincide, being both reached for slow modulations. In the post-selected case, we can obtain a probability distribution \({{{{{{{{\mathcal{P}}}}}}}}}_{+}(W)\) corresponding to that of a slower realisation of the quench. In this sense, through our protocol, one can achieve a net “speed-up” of the realisation of an adiabatic quench.
A spin-\(\frac{1}{2}\) particle in the thermal state of the initial Hamiltonian is measured in its eigenbasis \(\{\left|{z}_{\pm }\right\rangle \}\) at time t = 0. After the action of the quench described by the time-dependent Hamiltonian in Eq. (25), it is measured in the eigenbasis \(\{\left|{x}_{\pm }\right\rangle \}\) of the final Hamiltonian at time t = τ. Depending on the measured states at the two times, the thermodynamic quench causes an energy change ΔE = 0, ± ℏω, with ω being the spin’s natural frequency, and ℏ the reduced Planck constant.
Discussion
Viewed in isolation, a thermodynamic system coupled to a reservoir undergoes a dynamic which is generally non-unitary, even though the joint state of the system and the environment evolves in a unitary, reversible fashion. Depending on whether this dynamics favours events involving a positive or a negative change in the total entropy, it is possible to establish the temporal direction of the quench to which the system has been subjected to, that is, the time’s arrow is aligned along the direction where the total entropy increases. (Notice that, under our sign convention, this means that the time’s arrow matches a positive entropy change in the case of the forward process, and a negative entropy change for the time-reversal process.) However, it can be expected that, under some circumstances, the joint state of the system and the environment may as well evolve in an arbitrary superposition of the two, whereby the direction of evolution is controlled by a further quantum system. We note that this superposition of thermodynamic processes does evolve according to an external dynamical time (e.g., the time as shown by the laboratory clock). However, from a quantum-mechanical perspective, there is a priori no preferential thermodynamic time’s arrow (i.e., the forward protocol Λ and the time-reversal one \(\tilde{{{\Lambda }}}\) occur in a quantum superposition), and this peculiarity is what this work has explored. In particular, the core questions behind this work are (i) how a definite (thermodynamic) arrow of time can emerge in such a picture, and (ii) what the signature of quantum interference among the forward-in-time and backward-in-time thermodynamic processes is.
We showed that the coherence between the two temporal directions is effectively lost when the entropy production in the process is measured: the observation of a large increase (decrease) of dissipative work effectively projects the system in the forward (time-reversal) temporal direction. It is conceivable to imagine that such a projection could also result from the interaction of the system with the environment, which decoheres the system in a well-defined thermodynamic time’s arrow. Furthermore, when considering the total-entropy production in our process, one could consider adding the contribution arising from the irreversibility of the measurement itself. In Supplementary Note 3, we clarify that the entropy production linked to such a measurement, however, does not contribute to the definition of the orientation of the time’s axis associated to the quantum superposition of forward and time-reversal processes.
Finally, for small values of the observed dissipative work (of the order of β−1), the system and the auxiliary state may display interference effects. This aspect bears important implications, insofar as, by measuring the state of the control, the system can exhibit a work (entropy-production) distribution which is classically impossible with the protocols at hand. This feature can be best observed when both the forward and the time-reversal processes are, to a high degree, irreversible (i.e., the probability of zero entropy production is low). In this case, indeed, the quantum superposition between the two irreversible processes can result in a dynamics that is no longer such (i.e., the above probability can be significantly increased due to constructive interference). Formally, this means that when the distribution of the work \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\) is affected by interference effects, this can result in a probability distribution radically different from any classic mixture of \({{{{{{{\mathcal{P}}}}}}}}(W)\) and \(\tilde{{{{{{{{\mathcal{P}}}}}}}}}(-W)\). As a consequence, \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\) does not generally satisfy the fluctuation theorem (21). This is not extremely surprising given that the process generating \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\) does not verify the requirements needed for the work fluctuation theorems. In particular, the initial state in Eq. (3) is not a thermal state neither of the system alone, nor of the system together with the control, and the work performed is defined differently in the two quenches of the superposition. Nevertheless, this violation has a crucial implication: it entails that the distribution \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\) cannot be generated by any thermodynamic process starting in equilibrium with the environment, and being subsequently driven out of it by means of any given protocol Λ. Consequently, our procedure provides a recipe to generate thermodynamic processes with a work probability distribution that cannot be reproduced within the standard framework of fluctuation theorems.
Methods
Fluctuation theorems and the thermodynamic time’s arrow
The link between work fluctuations and the thermodynamic time’s arrow can be illustrated in terms of a “guessing the time directionality game” which was introduced by Jarzynski37. There, the author supposes to record the motion of a non-equilibrium thermodynamic process, and then to toss a coin. Depending on the outcome of the coin, he either plays the movie in the order in which it took place, or in the time-reversal one. In order to determine in which order the movie is being shown, the optimal guessing strategy for a macroscopic system follows from the second law of thermodynamics: if 〈W〉 > ΔF, the movie proceeds in the correct order, while if 〈W〉 < ΔF, the movie is being run backwards. Here, 〈W〉 is the average work performed on the system by the external driving mechanism, and ΔF the difference in free energies of the thermodynamic states at the beginning and at the end of the movie. Conversely, for a microscopic system, the optimal guessing strategy exploits the so-called “fluctuation theorems”13,38,39,40, together with Bayesian probabilistic reasoning41,42. We review this study briefly in Supplementary Note 4.
In one of its most famous versions43,44,45,46, the fluctuation theorem describes the fluctuations of the dissipative work Wdiss associated to the observation of a particular value of W in a single realisation of a non-equilibrium driving protocol (i.e., a single shot of the movie):
where P(+W) represents the probability that a work W is invested along the forward thermodynamic evolution, whereas \(\tilde{P}(-W)\) is the probability linked to recovering the same amount of work along the time-reversal evolution, both of which start in equilibrium with a thermal bath. From this equation, it follows that both the probability of total-entropy-decreasing events (βWdiss < 0) in the forward evolution, and that of total-entropy-increasing ones (βWdiss > 0) using the time-reversal dynamics vanish exponentially with the size of the total-entropy variation:
for any ξ ≥ 0, and where the second inequality (22b) arises from the fact that, in the time-reversal process, the dissipative work equals − Wdiss. In other words, large reductions in the total entropy are unlikely in the forward evolution, while events leading to a large entropy production are unlikely in the time-reversal one. (Notice that the sign of the entropy change is defined to match that of the dissipative work in the forward process.) On the other hand, it is evidenced that, when βWdiss is of the order of one, it is inherently impossible to tell in which of the two orders the process has occurred. In this region, the directionality of time flow cannot be inferred, and the time’s arrow is, so to say, blurred. A clear temporal directionality is then reestablished for β∣Wdiss∣ ≫ 1.
We remark that, here, “forward” and “time-reversal” are interchangeable labels since each process represents the time-inverted version of the other. Moreover, it is worth noticing that considerations on time-inversion only take on relevance in the absence of complete time-symmetry, as this latter may lead to ΔStot equal to zero in every single realisation. In order to exhibit time-asymmetry, in the present study the two conjugated processes are assumed to start from equilibrium states, a standard procedure in the derivation of fluctuations theorems13,39. This introduces a final (implicit) thermalisation step which enables irreversibility to emerge11,47,48.
Case study: a spin-\(\frac{1}{2}\) system
In this section, we detail on the interference effects between forward and time-reversal thermodynamic evolution of a spin-\(\frac{1}{2}\) system. To this end, we further develop the general expression of Eq. (16). Specifically, we project the auxiliary system onto the diagonal basis \({\left|\xi \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}=\left\{{\left|\pm \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}=({\left|0\right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\pm {\left|1\right\rangle }_{A})/\sqrt{2}\right\}\). This leads to the joint state of the system and the environment \({|{{{\Psi }}}_{n,m}^{\pm }\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}\equiv ({{\Bbb{1}}}_{{{{{{{\mathrm{S,E}}}}}}}}\otimes |\pm \rangle {\langle \pm |}_{A})\circ {M}_{n,m}{|{{{\Psi }}}_{0}\rangle }_{{{{{{{\mathrm{S,E,A}}}}}}}}\).
The corresponding post-selected work probability distribution, conditioned on the projection of the auxiliary system onto \({\left|\pm \right\rangle }_{{{{{{{\mathrm{A}}}}}}}}\), reads:
where the interference term I±(W) is given by Eq. (17) with \({\langle 0| \pm \rangle }_{{{{{{{\mathrm{A}}}}}}}}=1/\sqrt{2}\) and \({\langle \pm | 1\rangle }_{{{{{{{\mathrm{A}}}}}}}}=\pm 1/\sqrt{2}\). We recall that the states \({{\Theta }}\left|{E}_{n}^{(0)}\right\rangle\) in the above expressions are the eigenstates of the Hamiltonian \({{\Theta }}H[\lambda (0)]{{{\Theta }}}^{{{{\dagger}}} }=H[\tilde{\lambda }(0)]\). Moreover, we notice that the distribution \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\) in Eq. (23) differs by the term I±(W) ≠ 0 from what one would have obtained by applying the extended TPM scheme to a (classical) convex mixture \(| {\alpha }_{0}{| }^{2}\ \left|0\right\rangle {\left\langle 0\right|}_{{{{{{{\mathrm{A}}}}}}}}\otimes {\rho }_{0}^{{{{{{{\mathrm{th}}}}}}}\,}+| {\alpha }_{1}{| }^{2}\ \left|1\right\rangle {\left\langle 1\right|}_{{{{{{{\mathrm{A}}}}}}}}\otimes {\tilde{\rho }}_{0}^{\,{{{{{{\mathrm{th}}}}}}}\,}\) of the initial states.
For the outcome W = 0, the interference term in Eq. (17) can be simplified when ΔF = 0, and the sets of eigenvalues of the initial and final Hamiltonians coincide, i.e., \({E}_{n}^{(0)}={E}_{n}^{(\tau )}\). In that case:
As a result, it emerges that the interference effects can increase (decrease) the probability of observing the work value W = 0. This yields to a work probability distribution \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\) analogous to the one potentially generated by a more reversible (irreversible) process than the forward and time-reversal processes themselves, or any classical mixture therefrom. We remark that the interference term I±(W) may show non-zero values for W ≠ 0 in general, as we will see below.
We conclude by evaluating Eq. (23) in the concrete example of a spin-\(\frac{1}{2}\) system introduced in the “Interference effects in the work distribution” subsection in the Results. We consider a spin system with natural frequency ω in a magnetic field \(\overrightarrow{\lambda }(t)\) whose direction is rotating within the x − z plane at a constant angular velocity around the y axis:
where \(\overrightarrow{\lambda }\left(t\right)=\left({\lambda }_{0}\ \sin \left({{\Omega }}t\right),0,{\lambda }_{0}\ \cos \left({{\Omega }}t\right)\right)\) and λ0 = 1 is the dimensionless magnetic field, and where the protocol reads \({{\Lambda }}=\{\overrightarrow{\lambda }(t)\,;\,0\le t\le \pi /(2{{\Omega }})\}\). We notice that \({{\Theta }}H\left[\overrightarrow{\lambda }(t)\right]{{{\Theta }}}^{{{{\dagger}}} }=H[-\overrightarrow{\lambda }(t)]\), implying that the time-reversal of the control parameter corresponds to a flip of the magnetic field. At the initial and final times of the protocol, the Hamiltonian is diagonal in the \(\left\{\left|{z}_{\pm }\right\rangle \right\}\) and \(\left\{\left|{x}_{\pm }\right\rangle \right\}\) bases, respectively. Therefore, \(\left|{E}_{n}^{(0)}\right\rangle =\{{\left|{z}_{\pm }\right\rangle }_{{{{{{{\mathrm{S}}}}}}}}\}\), with corresponding eigenvalues \({E}_{n}^{(0)}=\{0,\hslash \omega \}\), and \(\left|{E}_{m}^{(\tau )}\right\rangle =\{{\left|{x}_{\pm }\right\rangle }_{{{{{{{\mathrm{S}}}}}}}}=\frac{1}{\sqrt{2}}\left({\left|{z}_{-}\right\rangle }_{{{{{{{\mathrm{S}}}}}}}}\pm {\left|{z}_{+}\right\rangle }_{S}\right)\}\), with eigenvalues \({E}_{m}^{(\tau )}=\{0,\hslash \omega \}\) (we shifted the lower energy level by ℏω/2 to avoid negative energy eigenvalues). As a result, \({F}_{0}={F}_{\tau }=-{{{{{{{\rm{log}}}}}}}}\left(1+{e}^{-\beta \hslash \omega }\right)\) and Wn,m = {ℏω, 0, − ℏω}.
In the frame rotating around the y axis at frequency Ω, the Hamiltonian becomes time-independent, and the unitary governing the evolution can be obtained straightforwardly. Turning back to the Schrödinger picture, the applied unitary U(t, 0) reads:
This is used below to compute the work distribution.
Effect of interference on reversibility
In this subsection, we will represent the environment as a spin-\(\frac{1}{2}\) system which is left unaffected during the quench. For instance, we can assume that the purification of the thermal states in Eq. (2a)–2b read
Furthermore, we will assume to begin the protocol in the state in Eq. (3) with \({\alpha }_{0}=1/\sqrt{2}\), \({\alpha }_{1}={e}^{-i\varphi }/\sqrt{2}\), with φ being a controllable phase between the forward and the time-reversal processes.
Next, we compute \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W)\):
where we used the fact that \(\langle {E}_{n}^{(\tau )}| {{\Theta }}| {E}_{n}^{(0)}\rangle =-1/\sqrt{2}\) for all n, whereas \({\langle {\varepsilon }_{n}^{(0)}| {\varepsilon }_{n}^{(\tau )}\rangle }_{{{{{{{\mathrm{E}}}}}}}}=1\), and where the marginal probability of the auxiliary system reads \({{{{{{{\mathcal{P}}}}}}}}(\pm )=\frac{1}{2}\pm \frac{1}{2\sqrt{2}}\left[\ {p}_{0,0}\ \cos \left(2{{{\Phi }}}_{0,0}+\varphi \right)+{p}_{1,1}\ \cos \left(2{{{\Phi }}}_{1,1}+\varphi \right)\right]\), with \({p}_{0,0}=\frac{{\left|\langle {x}_{-}| U(\tau ,0)| {z}_{-}\rangle \right|}^{2}}{1+{e}^{-\beta \hslash \omega }}\), \({e}^{i{{{\Phi }}}_{0,0}}=\frac{\langle {x}_{-}| \ U(\tau ,0)| {z}_{-}\rangle }{\sqrt{\left|\langle {x}_{-}| \ U(\tau ,0)| {z}_{-}\rangle \right|}}\), and \({p}_{1,1}=\frac{{\left|\langle {x}_{+}| U(\tau ,0)| {z}_{+}\rangle \right|}^{2}}{1+{e}^{-\beta \hslash \omega }}\ {e}^{-\beta \hslash \omega }\), \({e}^{i{{{\Phi }}}_{1,1}}=\frac{\langle {x}_{+}| \ U(\tau ,0)| {z}_{+}\rangle }{\sqrt{\left|\langle {x}_{+}| \ U(\tau ,0)| {z}_{+}\rangle \right|}}\). (To evaluate \({\langle {E}_{n}^{(\tau )}| {{\Theta }}| {E}_{n}^{(0)}\rangle }_{{{{{{{\mathrm{S}}}}}}}}\), we made use of the fact that the time-reversal operator Θ for a spin-\(\frac{1}{2}\) system acts as Θ = iσyK, where K is the complex conjugation operator. Thus, \({{\Theta }}|{z}_{\pm }\rangle =\mp |{z}_{\mp }\rangle\)). From this result, we deduce that it is possible to observe interference between thermodynamic processes occurring in the forward and time-reversal temporal directions. Following the same procedure for the cases W = ± ℏω, we get
which do not feature interference. In the last expressions, \({p}_{0,1}=\frac{{\left|\langle {x}_{+}| U(\tau ,0)| {z}_{-}\rangle \right|}^{2}}{1+{e}^{-\beta \hslash \omega }}\), \({e}^{i{{{\Phi }}}_{0,1}}=\frac{\langle {x}_{+}| \ U(\tau ,0)| {z}_{-}\rangle }{\sqrt{\left|\langle {x}_{+}| \ U(\tau ,0)| {z}_{-}\rangle \right|}}\), and \({p}_{1,0}=\frac{{\left|\langle {x}_{-}| U(\tau ,0)| {z}_{+}\rangle \right|}^{2}}{1+{e}^{-\beta \hslash \omega }}\ {e}^{-\beta \hslash \omega }\), \({e}^{i{{{\Phi }}}_{1,0}}=\frac{\langle {x}_{-}| \ U(\tau ,0)| {z}_{+}\rangle }{\sqrt{\left|\langle {x}_{-}| \ U(\tau ,0)| {z}_{+}\rangle \right|}}\). We illustrate the probability distribution in Eq. (28)–(29) in Fig. 4.
Interference terms for varying ±ℏ ω
In the previous case study, we represented the environment as a spin-\(\frac{1}{2}\) system which is left unmodified by the thermodynamic quench. This caused the cancellation of all interference terms in \({{{{{{{{\mathcal{P}}}}}}}}}_{\pm }(W=\pm \hslash\! \omega )\). In this subsection, on the contrary, we suppose that the environment undergoes a spin-flip during the quench:
This change results in \({\langle {\varepsilon }_{n}^{(0)}| {\varepsilon }_{m}^{(\tau )}\rangle }_{{{{{{{\mathrm{E}}}}}}}}=0\), for n = m. For the sake of simplicity, below we will also set φ = π. The three probabilities discussed in the previous section become therefore:
where the marginal probability of the auxiliary system is now \({{{{{{{\mathcal{P}}}}}}}}(\pm )=\frac{1}{2}\pm \frac{1}{2\sqrt{2}}\left[{p}_{0,1}\ {e}^{-\frac{\beta \hslash \omega }{2}}\cos (2{{{\Phi }}}_{0,1})-{p}_{1,0}\ {e}^{\frac{\beta \hslash \omega }{2}}\cos (2{{{\Phi }}}_{1,0})\right]\), and where p0,0, Φ0,0, p1,1, and Φ1,1 are the same as in case study “Effect of interference on reversibility”.
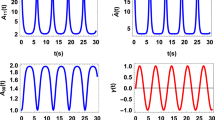
In Fig. 5, we show the work probability distributions for varying ℏω. For work values ℏω smaller than, or of the order of β−1, we observe strong interference effect, as shown by the difference between \({{{{{{{{\mathcal{P}}}}}}}}}_{+}(W=\hslash \omega )\) and \({{{{{{{{\mathcal{P}}}}}}}}}_{-}(W=\hslash \omega )\). For work values ℏω ≫ β−1, this difference vanishes, and the probability \({{{{{{{\mathcal{P}}}}}}}}(W=\hslash \omega ):= {{{{{{{{\mathcal{P}}}}}}}}}_{+}(W=\hslash \omega )+{{{{{{{{\mathcal{P}}}}}}}}}_{-}(W=\hslash \omega )\) to obtain the work value ℏω tends to the probability p0,1 of first projecting the auxiliary system onto the forward direction, and then obtaining the work value ℏω. This trend shows that the observation of large work values effectively projects the system into a well-defined temporal direction.
For values of ℏω smaller or of the order of β−1 = kBT = 1/2 (kB = ℏ = 1), the work probabilities \({{{{{{{{\mathcal{P}}}}}}}}}_{+}(W=\hslash \omega )\) and \({{{{{{{{\mathcal{P}}}}}}}}}_{-}(W=\hslash \omega )\) (see Eq. (31); turquoise and purple curves) strongly depend on the interference terms. For values ℏω ≫ β−1, \({{{{{{{{\mathcal{P}}}}}}}}}_{+}(W=\hslash \omega )\,+\,\)\({{{{{{{{\mathcal{P}}}}}}}}}_{-}(W=\hslash \omega )\) (green curve) tends to the value p0,1 (yellow curve), which is obtained by projecting the process to the forward direction and obtaining the work difference ℏω. This illustrates that observing large work values ℏω ≫ β−1 (ℏω ≪ − β−1) effectively projects the process onto the forward (time-reversal) direction.
Data availability
All data needed to evaluate the conclusions of the paper are present in the paper and/or the Supplementary Information. Additional data related to this paper will be made available from the authors upon reasonable request.
References
Halliwell, J. J., Pérez-Mercader, J. & Zurek, W. H. Physical Origins of Time Asymmetry Paperback (The University Press, 1996).
Maccone, L. Quantum solution to the arrow-of-time dilemma. Phys. Rev. Lett. 103, 080401 (2009).
Jennings, D. & Rudolph, T. Comment on “quantum solution to the arrow-of-time dilemma”. Phys. Rev. Lett. 104, 148901 (2010).
Jennings, D. & Rudolph, T. Entanglement and the thermodynamic arrow of time. Phys. Rev. E 81, 061130 (2010).
Mlodinow, L. & Brun, T. A. Relation between the psychological and thermodynamic arrows of time. Phys. Rev. E 89, 052102 (2014).
Erker, P. et al. Autonomous quantum clocks: does thermodynamics limit our ability to measure time? Phys. Rev. X 7, 031022 (2017).
Chiribella, G. Perfect discrimination of no-signalling channels via quantum superposition of causal structures. Phys. Rev. A 86, 040301 (2012).
Chiribella, G., D’Ariano, G. M., Perinotti, P. & Valiron, B. Quantum computations without definite causal structure. Phys. Rev. A 88, 022318 (2013).
Oreshkov, O., Costa, F. & Brukner, Č. Quantum correlations with no causal order. Nat. Commun. 3, 1092 (2012).
Kawai, R., Parrondo, J. M. R. & den Broeck, C. V. Dissipation: the phase-space perspective. Phys. Rev. Lett. 98, 080602 (2007).
Parrondo, J. M. R., den Broeck, C. V. & Kawai, R. Entropy production and the arrow of time. N. J. Phys. 11, 073008 (2009).
Batalhão, T. B. et al. Irreversibility and the arrow of time in a quenched quantum system. Phys. Rev. Lett. 115, 190601 (2015).
Campisi, M., Hänggi, P. & Talkner, P. Colloquium: quantum fluctuation relations: foundations and applications. Rev. Mod. Phys. 83, 771–791 (2011).
Andrieux, D. & Gaspard, P. Quantum work relations and response theory. Phys. Rev. Lett. 100, 230404 (2008).
Dorner, R., Goold, J., Cormick, C., Paternostro, M. & Vedral, V. Emergent thermodynamics in a quenched quantum many-body system. Phys. Rev. Lett. 109, 160601 (2012).
Eddington, A. S. The Nature of the Physical World (The University Press, 1928).
Hofmann, A. et al. Heat dissipation and fluctuations in a driven quantum dot. Phys. status solidi (b) 254, 1600546 (2017).
Dakić, B. & Brukner, Č. The classical limit of a physical theory and the dimensionality of space. In Quantum Theory: Informational Foundations and Foils. Fundamental Theories of Physics (eds Chiribella, G. & Spekkens, R.) Vol. 181 (Springer, 2016).
Vaccaro, J. A., Croke, S. & Barnett, S. M. Is coherence catalytic? J. Phys. A: Math. Theor. 51, 414008 (2018).
Sagawa, T. Second law-like inequalitites with quantum relative entropy: an introduction. In Lectures on quantum computing, thermodynamics and statistical physics. Kinki University Series on Quantum Computing, (ed. Nakahara, M.) Vol. 8 (World Scientific, New Jersey, 2013).
Åberg, J. Catalytic coherence. Phys. Rev. Lett. 113, 150402 (2014).
Malabarba, A. S. L., Short, A. J. & Kammerlander, P. Clock-driven quantum thermal engines. N. J. Phys. 17, 045027 (2015).
Korzekwa, K., Lostaglio, M., Oppenheim, J. & Jennings, D. The extraction of work from quantum coherence. N. J. Phys. 18, 023045 (2016).
Bartlett, S. D., Rudolph, T. & Spekkens, R. W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 79, 555–609 (2007).
Dorner, R. et al. Extracting quantum work statistics and fluctuation theorems by single-qubit interferometry. Phys. Rev. Lett. 110, 230601 (2013).
Mazzola, L., De Chiara, G. & Paternostro, M. Measuring the characteristic function of the work distribution. Phys. Rev. Lett. 110, 230602 (2013).
Batalhão, T. B. et al. Experimental reconstruction of work distribution and study of fluctuation relations in a closed quantum system. Phys. Rev. Lett. 113, 140601 (2014).
Roncaglia, A. J., Cerisola, F. & Paz, J. P. Work measurement as a generalized quantum measurement. Phys. Rev. Lett. 113, 250601 (2014).
Chiara, G. D., Roncaglia, A. J. & Paz, J. P. Measuring work and heat in ultracold quantum gases. N. J. Phys. 17, 035004 (2015).
Perarnau-Llobet, M., Bäumer, E., Hovhannisyan, K. V., Huber, M. & Acin, A. No-go theorem for the characterization of work fluctuations in coherent quantum systems. Phys. Rev. Lett. 118, 070601 (2017).
Åberg, J. Fully quantum fluctuation theorems. Phys. Rev. X 8, 011019 (2018).
Debarba, T., Manzano, G., Guryanova, Y., Huber, M. & Friis, N. Work estimation and work fluctuations in the presence of non-ideal measurements. N. J. Phys. 21, 113002 (2019).
Mohammady, M. H. & Romito, A. Conditional work statistics of quantum measurements. Quantum 3, 175 (2019).
Talkner, P., Lutz, E. & Hänggi, P. Fluctuation theorems: work is not an observable. Phys. Rev. E 75, 050102 (2007).
Talkner, P. & Hänggi, P. Aspects of quantum work. Phys. Rev. E 93, 022131 (2016).
Rubino, G. et al. Experimental verification of an indefinite causal order. Sci. Adv. 3, e1602589 (2017).
Jarzynski, C. Equalities and inequalities: Irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter Phys. 2, 329–351 (2011).
Evans, D. J. & Searles, D. J. The fluctuation theorem. Adv. Phys. 51, 1529–1585 (2002).
Esposito, M., Harbola, U. & Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 81, 1665–1702 (2009).
Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 75, 126001 (2012).
Shirts, M. R., Bair, E., Hooker, G. & Pande, V. S. Equilibrium free energies from nonequilibrium measurements using maximum-likelihood methods. Phys. Rev. Lett. 91, 140601 (2003).
P., M., Ritort, F., Bustamante, C., Karplus, M. & Crooks, G. Equilibrium free energies from nonequilibrium measurements using maximum-likelihood methods. J. Chem. Phys. 129, 024102 (2008).
Bochkov, G. N. & Kuzovlev, I. E. General theory of thermal fluctuations in nonlinear systems. Zh . Eksperimentalnoi i Teoreticheskoi Fiz. 72, 238–247 (1977).
Bochkov, G. & Kuzovlev, Y. Nonlinear fluctuation-dissipation relations and stochastic models in nonequilibrium thermodynamics: I. generalized fluctuation-dissipation theorem. Phys. A: Stat. Mech. Appl. 106, 443–479 (1981).
Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 78, 2690–2693 (1997).
Crooks, G. E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 60, 2721–2726 (1999).
Manzano, G., Horowitz, J. M. & Parrondo, J. M. R. Quantum fluctuation theorems for arbitrary environments: adiabatic and nonadiabatic entropy production. Phys. Rev. X 8, 031037 (2018).
Landi, G. T. & Paternostro, M. Irreversible entropy production: From classical to quantum. Rev. Mod. Phys. 93, 035008 (2021).
Acknowledgements
The authors wish to thank P. Skrzypczyk for useful comments on the draft, as well as the organisers of the conference “New Directions in Quantum Information”, (Nordita, Stockholm (Sweden); April 1-26 2019) for providing a stimulating platform for the discussion which originated this result. G.R. acknowledges financial support from the Royal Society through the Newton International Fellowship No. NIF\R1\202512. G.M. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 801110 and the Austrian Federal Ministry of Education, Science and Research (BMBWF). Č.B. acknowledges financial support from the Austrian Science Fund (FWF) through BeyondC (F7103-N48), the project no. I-2906, from the European Commission via Testing the Large-Scale Limit of Quantum Mechanics (TEQ) (No. 766900) project, from Foundational Questions Institute (FQXi) and from the John Templeton Foundation through grant 61466, The Quantum Information Structure of Spacetime (qiss.fr).
Author information
Authors and Affiliations
Contributions
G.R., G.M. and Č.B. contributed to all aspects of the research, with the leading input of G.R.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks Peter Talkner and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rubino, G., Manzano, G. & Brukner, Č. Quantum superposition of thermodynamic evolutions with opposing time’s arrows. Commun Phys 4, 251 (2021). https://doi.org/10.1038/s42005-021-00759-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00759-1
This article is cited by
-
Quantum Supertime
Russian Physics Journal (2023)
-
Quantum operations with indefinite time direction
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.