Quantum operations with indefinite time direction

Abstract

The fundamental dynamics of quantum particles is neutral with respect to the arrow of time. And yet, our experiments are not: we observe quantum systems evolving from the past to the future, but not the other way round. A fundamental question is whether it is possible, at least in principle, to conceive a broader set of operations that probe quantum processes in the backward direction, from the future to the past, or more generally, in a combination of the forward and backward directions. Here we introduce a mathematical framework for operations that are not constrained to a definite time direction. More generally, we introduce a set of multipartite operations that include indefinite time direction as well as indefinite causal order, providing a framework for potential extensions of quantum theory.

Introduction

The experience of time flowing in a definite direction, from the past to the future, is deeply rooted in our thinking. At the microscopic level, however, the laws of Nature seem to be indifferent to the distinction between past and future. Both in classical and quantum mechanics, the fundamental equations of motion are reversible, and changing the sign of the time coordinate (possibly together with the sign of some other parameters) still yields a valid dynamics. For example, the CPT theorem in quantum field theory^1,2 implies that an evolution backwards in time is indistinguishable from an evolution forward in time in which the charge and parity of all particles have been inverted. An asymmetry between past and future emerges in thermodynamics, where the second law postulates an increase of entropy in the forward time direction. But even the time-asymmetry of thermodynamics can be reduced to time-symmetric laws at the microscopic level³, e.g. by postulating a low entropy initial state⁴.

While the microscopic world is time-symmetric, the way in which we interact with it is not. As a matter of fact, we operate only in the forward time direction: in ordinary experiments, we initialise physicals system at a given moment, let them evolve forward in time, and perform measurements at a later moment. Still, the asymmetry in the structure of our experiments does not feature in the dynamical laws themselves. This fact suggests that, rather than being fundamental, time asymmetry may be specific to the way in which ordinary agents, such as ourselves, interact with other physical systems^5,6,7,8.

An intriguing possibility is that, at least in principle, some other type of agent could perform experiments in the opposite direction, by initialising the state of physical systems in the future, and by observing their evolution backward in time. This possibility is implicit in a variety of frameworks wherein pre-selected and postselected quantum states are treated on the same footing^{9,10,11,12,13,14,15,16,17,18,19}. Building on these frameworks, one can even conceive agents with the ability to deterministically pre-select certain systems and to deterministically post-select others, thus observing physical processes in an arbitrary combination of the forward and backward direction. Such agents may or may not exist in reality, but can serve as a useful fiction to shed light on the operational significance of the constraint of a fixed time direction, by contrasting the information-theoretic capabilities associated to alternative ways to operate in time.

Here we establish a mathematical framework for operations that use quantum devices in arbitrary combinations of the forward and backward direction. We first characterise the processes that could in principle be accessed in both directions. Then, we construct a set of operations that act on these processes without being constrained to a definite time direction. As an example, we introduce an operation, called the quantum time flip, that uses processes in a coherent superposition of the forward and backward directions, and we demonstrate its advantage in an information-theoretic task. Our work initiates the exploration of quantum operations with indefinite time direction, and provides a rigorous framework for analysing their information-theoretic power. The framework also allows for multipartite operations with both indefinite time direction and indefinite causal order^20,21,22, raising the open question whether these operations may be physically accessible in new regimes, such as quantum gravity, or whether they are prevented by some yet-to-be-discovered mechanism.

Results

Bidirectional devices and their characterisation

We start by identifying the set of quantum devices that are in principle compatible with two alternative modes of operation: either in the forward time direction, or in the backward time direction.

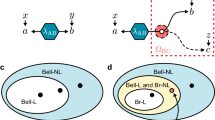
Consider a process that takes place between two times t₁ and t₂ ≥ t₁, corresponding to two events, such as the entry in and exit from a Stern-Gerlach apparatus, respectively. Ordinary agents can interact with the process in the forward time direction: they can deterministically pre-select state of an incoming system S₁ at time t₁, and later measure an outgoing system S₂ at time t₂. The overall input-output transformation from time t₁ to time t₂ is described by a quantum channel ${{{{{{{\mathcal{C}}}}}}}}$, that is, a trace-preserving, completely positive (CPTP) map transforming density matrices of system S₁ into density matrices of system S₂²³. Now, imagine a hypothetical agent that operates in the opposite time direction, by deterministically post-selecting the system at time t₂ and performing measurements at time t₁, as illustrated in Fig. 1. For such a backward-facing agent, the role of the input and output systems is exchanged, and the two systems at times t₁ and t₂ may even appear to be different from S₁ and S₂, e.g. they may have opposite charge and opposite parity. In the following we denote the systems observed by the backward-facing agent as ${S}_{1}^{* }$ and ${S}_{2}^{* }$, and we assume that they have the same dimensions of S₁ and S₂, respectively. If the overall input-output transformation observed by the backward-facing agent is still described by a valid quantum channel (CPTP map), we call the process bidirectional.

Fig. 1: Bidirectional devices.

A bidirectional device is in principle compatible with two alternative modes of operation. In the forward mode (a), an agent prepares an input system at time t₁ and obtains an output system at time t₂ ≥ t₁. In the backward mode (b), a hypothetical agent could prepare an input at time t₂ and obtain an output at time t₁. These two modes of using the device correspond to two different input-output transformations ${{{{{{{\mathcal{C}}}}}}}}$ and ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$, respectively.

To determine whether a given process is bidirectional, one has to specify a map Θ, converting the channel ${{{{{{{\mathcal{C}}}}}}}}$ observed by the forward-facing agent into the corresponding channel ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$ observed by the backward-facing agent. We call the map Θ an input-output inversion. The set of bidirectional processes is then defined as the set of all quantum channels ${{{{{{{\mathcal{C}}}}}}}}$ with the property that ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$ is a quantum channel. In the following, the set of bidirectional channels will be denoted by B(S₁ → S₂).

We now characterise all the possible input-output inversions satisfying four natural requirements. Specifically, we require that the map Θ be

• 1. order-reversing: ${{\Theta }}({{{{{{{\mathcal{D}}}}}}}}\,{{{{{{{\mathcal{C}}}}}}}})={{\Theta }}({{{{{{{\mathcal{C}}}}}}}})\,{{\Theta }}({{{{{{{\mathcal{D}}}}}}}})$ for every ${{{{{{{\mathcal{C}}}}}}}}\in {\mathsf{B}}({S}_{1}\to {S}_{2})$ and ${{{{{{{\mathcal{D}}}}}}}}\in {\mathsf{B}}({S}_{2}\to {S}_{3})$,

• 2. identity-preserving: ${{\Theta }}({{{{{{{{\mathcal{I}}}}}}}}}_{S})={{{{{{{{\mathcal{I}}}}}}}}}_{{S}^{* }}$, where ${{{{{{{{\mathcal{I}}}}}}}}}_{S}$ (S_*) is the identity channel on system S (S^*).

• 3. distinctness-preserving: if ${{{{{{{\mathcal{C}}}}}}}}\,\ne\, {{{{{{{\mathcal{D}}}}}}}}$, then ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})\,\ne\, {{\Theta }}({{{{{{{\mathcal{D}}}}}}}})$,

• 4. compatible with random mixtures: ${{\Theta }}(p\,{{{{{{{\mathcal{C}}}}}}}}+(1-p)\,{{{{{{{\mathcal{D}}}}}}}})$$\,=\,p\,{{\Theta }}({{{{{{{\mathcal{C}}}}}}}})+(1-p)\,{{\Theta }}({{{{{{{\mathcal{D}}}}}}}})$ for every pair of channels ${{{{{{{\mathcal{C}}}}}}}}$ and ${{{{{{{\mathcal{D}}}}}}}}$ in B(S₁ → S₂), and for every probability p ∈ [0, 1].

Requirement 1, illustrated in Fig. 2, is the most fundamental: for every sequence of processes, the order in which a backward-facing agent sees the processes should be the opposite of the order in which a forward-facing agent sees them. Requirement 2 is also quite fundamental: if the forward-facing agent does not see any change in the system, then also the backward-facing agent should not see any change. Requirement 3 is a weak form of symmetry: processes that appear distinct to a forward-facing agent should appear distinct also to a backward-facing agent. A stronger requirement would have been to require that applying Θ twice brings every process back to itself. This condition is stronger than our Requirement 3, because it implies not only that Θ must be invertible, but also that Θ is its own inverse. Finally, Requirement 4 is that if a process has probability p to be ${{{{{{{\mathcal{C}}}}}}}}$ and probability 1 − p to be ${{{{{{{\mathcal{D}}}}}}}}$ for the forward-facing agent, then the process has probability p to be ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$ and probability 1 − p to be ${{\Theta }}({{{{{{{\mathcal{D}}}}}}}})$ for the backward-facing agent.

Fig. 2: The order-reversing condition.

If a system experiences a sequence of processes ${{{{{{{{\mathcal{C}}}}}}}}}_{1},\ldots ,{{{{{{{{\mathcal{C}}}}}}}}}_{N}$ in the forward-time representation (in blue), then the system should experience the opposite sequence ${{\Theta }}({{{{{{{{\mathcal{C}}}}}}}}}_{N}),\ldots ,{{\Theta }}({{{{{{{{\mathcal{C}}}}}}}}}_{1})$ in the backward-time representation (in red).

Our notion of input-output inversion is closely related with the notion of time-reversal in quantum mechanics^24,25 and in quantum thermodynamics²⁶. It is worth stressing, however, that input-output inversion is more general than time-reversal, because it can include combinations of time-reversal with other symmetries, such as charge conjugation and parity inversion (see Supplementary Note 1 for more discussion). Moreover, the input-output inversion can also describe situations that do not involve time-reversal, including, for example, the use of optical devices where the roles of the input and output modes is exchanged, as discussed later in the paper.

In the following, we will focus on the scenario where the systems S₁ and S₂ have the same dimension. We will assume that all unitary dynamics are bidirectional, that is, that the set B(S₁ → S₂) contains all possible unitary channels. For unitary channels, Requirements 1-3 completely determine the action of the input-output inversion. Specifically, we show that the input-output inversion of the unitary channel associated to a unitary operator U must either be unitarily equivalent to the adjoint U^†, or to the transpose U^T (Supplementary Note 1).

For general quantum channels, we show that the set of bidirectional processes coincides with the set of bistochastic channels^27,28, that is, channels ${{{{{{{\mathcal{C}}}}}}}}$ with a Kraus representation ${{{{{{{\mathcal{C}}}}}}}}(\rho )={\sum }_{i}{C}_{i}\rho {C}_{i}^{{{{\dagger}}} }$ satisfying both conditions ${\sum }_{i}{C}_{i}^{{{{\dagger}}} }{C}_{i}={I}_{{S}_{1}}$ and ${\sum }_{i}{C}_{i}{C}_{i}^{{{{\dagger}}} }={I}_{{S}_{2}}$ (see Methods). Also in this case we find that, up to unitary equivalence, there exist only two possible choices of input-output inversion: the adjoint ${{{{{{{{\mathcal{C}}}}}}}}}^{{{{\dagger}}} }$, defined by ${{{{{{{{\mathcal{C}}}}}}}}}^{{{{\dagger}}} }(\rho ):= {\sum }_{i}{C}_{i}^{{{{\dagger}}} }\rho {C}_{i}$, and the transpose ${{{{{{{{\mathcal{C}}}}}}}}}^{T}$, defined by ${{{{{{{{\mathcal{C}}}}}}}}}^{T}(\rho )={\sum }_{i}{C}_{i}^{T}\rho {\overline{C}}_{i}$, with ${\overline{C}}_{i}:={({C}_{i}^{T})}^{{{{\dagger}}} }$.

For two-dimensional quantum systems the adjoint and transpose are unitarily equivalent, and therefore the input-output inversion is essentially unique. For higher dimensional systems, however, the adjoint and the transpose exhibit a fundamental difference: unlike the transpose, the adjoint does not generally produce quantum channels (CPTP maps) when applied locally to bipartite quantum processes (see Methods). Technically, the difference is that the adjoint is not a completely positive map on quantum channels.

Quantum operations with indefinite time direction

The standard operational framework of quantum theory describes sequences of operations performed in the forward time directions. We now define a more general type of operations, which employ quantum devices in arbitrary combinations of the forward and backward direction. Our approach is based on the framework of quantum supermaps^22,29,30,31, a mathematical framework to describe candidate operations that could in principle be performed on a given set of quantum devices. In general, a quantum supermap from an input set of quantum channels B to an output set of quantum channels ${\mathsf{B}}^{\prime}$ is a map that preserves convex combinations, and can act locally on the dynamics of composite systems, transforming any extension of a channel in B into an extension of a channel in ${\mathsf{B}}^{\prime}$²².

The possible operations on bidirectional devices correspond to quantum supermaps transforming bistochastic channels into ordinary channels (CPTP maps). Some of these supermaps employ the devices in the forward direction: they are of the form ${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{fwd}}}}}}}}}({{{{{{{\mathcal{C}}}}}}}})={{{{{{{\mathcal{B}}}}}}}}({{{{{{{\mathcal{C}}}}}}}}\otimes {{{{{{{{\mathcal{I}}}}}}}}}_{{{{{{{{\rm{aux}}}}}}}}}){{{{{{{\mathcal{A}}}}}}}}$, where ${{{{{{{\mathcal{C}}}}}}}}$ is the bistochastic channel describing the device of interest, and ${{{{{{{\mathcal{A}}}}}}}}$ and ${{{{{{{\mathcal{B}}}}}}}}$ are two fixed channels, possibly involving an auxiliary system aux²⁹. Other supermaps could be realised by using the device is the backward direction: they are of the form ${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{bwd}}}}}}}}}({{{{{{{\mathcal{C}}}}}}}})={{{{{{{\mathcal{B}}}}}}}}^{\prime} ({{\Theta }}({{{{{{{\mathcal{C}}}}}}}})\otimes {{{{{{{{\mathcal{I}}}}}}}}}_{{{{{{{{{\rm{aux}}}}}}}}}^{\prime}}){{{{{{{\mathcal{A}}}}}}}}^{\prime}$, where ${{{{{{{\mathcal{A}}}}}}}}^{\prime}$ and ${{{{{{{\mathcal{B}}}}}}}}^{\prime}$ are two fixed channels and Θ is (unitarily equivalent to) the transpose.

A complete characterization of the possible supermaps acting on bistochastic channels is provided in Methods. As we will see in the following, the set of these supermaps contains operations that are neither of the forward type nor of the backward type, nor of any random mixture of these two types. We call these transformations quantum operations with indefinite time direction. These operations are the analogue for the time direction of the operations with indefinite causal order^20,21,22, also known as causally inseparable operations^21,32,33.

In Methods, we also extend our construction from operations on a single bistochastic channel to more general multipartite operations, described by quantum supermaps ${{{{{{{\mathcal{S}}}}}}}}$ that transform a list of bistochastic channels $({{{{{{{{\mathcal{C}}}}}}}}}_{1},{{{{{{{{\mathcal{C}}}}}}}}}_{2},\ldots ,{{{{{{{{\mathcal{C}}}}}}}}}_{N})$ into an ordinary channel ${{{{{{{\mathcal{S}}}}}}}}({{{{{{{{\mathcal{C}}}}}}}}}_{1},{{{{{{{{\mathcal{C}}}}}}}}}_{2},\ldots ,{{{{{{{{\mathcal{C}}}}}}}}}_{N})$. This general type of supermaps can exhibit both indefinite time direction and indefinite causal order, and provide a broad framework for potential extensions of quantum theory.

The quantum time flip

We now introduce a concrete example of an operation with indefinite time direction, called the quantum time flip. This operation is an analogue of the quantum SWITCH^20,22, previously introduced in the study of indefinite causal order. The quantum time flip takes in input a bidirectional device, and produces as output a controlled channel^{10,34,35,36,37}, which acts as ${{{{{{{\mathcal{C}}}}}}}}$ if a control qubit is initialised in the state $\left|0\right\rangle$, and as ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$ if the control qubit is initialised in the state $\left|1\right\rangle$.

The construction of the quantum time flip is as follows. For a fixed set of Kraus operators C = {C_i}, we consider the controlled channel ${{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\bf{C}}}}}}}}}$ of the form ${{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\bf{C}}}}}}}}}(\rho )={\sum }_{i}{F}_{i}\rho {F}_{i}^{{{{\dagger}}} }$, with

$${F}_{i}:= {C}_{i}\otimes \left|0\right\rangle \langle 0| +\theta ({C}_{i})\otimes | 1\rangle \left\langle 1\right|,$$

(1)

where the map θ : C_i ↦ θ(C_i) is either unitarily equivalent to the adjoint or to the transpose. In passing, we observe that the channel ${{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\bf{C}}}}}}}}}$ is itself bistochastic, and therefore it also admits an input-output inversion.

We observe that (i) ${{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\bf{C}}}}}}}}}$ is a valid quantum channel (CPTP map) if and only if the input channel ${{{{{{{\mathcal{C}}}}}}}}$ is bistochastic, and (ii) the definition of ${{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\bf{C}}}}}}}}}$ is independent of the Kraus representation if and only if the map θ is unitarily equivalent to the transpose (Supplementary Note 2). When (and only when) these two conditions are satisfied, the map ${{{{{{{\mathcal{F}}}}}}}}:{{{{{{{\mathcal{C}}}}}}}}\to {{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\bf{C}}}}}}}}}$ satisfies all the requirements of a valid quantum supermap. We call this supermap the quantum time flip and we write the controlled channel as ${{{{{{{\mathcal{F}}}}}}}}({{{{{{{\mathcal{C}}}}}}}})$.

The quantum time flip is an example of an operation with indefinite time direction: it is impossible to decompose it as a random mixture ${{{{{{{\mathcal{F}}}}}}}}=p\,{{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{fwd}}}}}}}}}+(1-p)\,{{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{bwd}}}}}}}}}$ where p is a probability, and ${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{fwd}}}}}}}}}$ (${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{bwd}}}}}}}}}$) is a forward (backward) supermap. In Supplementary Note 3 we show that, if such decomposition existed, then there would exist an ordinary quantum circuit that transforms a completely unknown unitary gate U into its transpose U^T, a task that is known to be impossible^38,39. We also show that the quantum time flip cannot be realised in a definite time direction even if one has access to two copies of the original channel ${{{{{{{\mathcal{C}}}}}}}}$. It is worth noting that this stronger no-go result holds even if the two copies of the channel ${{{{{{{\mathcal{C}}}}}}}}$ are combined in an indefinite order: as long as all copies of the channel are used in the same time direction, there is no way to reproduce the action of the quantum time flip.

Realisation of the quantum time flip through teleportation

We have seen that the quantum time flip cannot be perfectly realised by any quantum circuit with a definite time direction. This no-go result concerns perfect realisations, which reproduce the quantum time flip with unit probability and without error. On the other hand, the quantum time flip can be realised with non-unit probability in an ordinary quantum circuit, using quantum teleportation⁴⁰.

The setup is depicted in Fig. 3. An unknown bistochastic channel ${{{{{{{\mathcal{C}}}}}}}}$ is applied on one side of a maximally entangled state, say the canonical Bell state $|{{\Phi }}\rangle =\mathop{\sum }\nolimits_{i = 1}^{d}|i\rangle \otimes |i\rangle /\sqrt{d}$, and the resulting state is used as a resource for quantum teleportation. The transpose is realized by swapping the two copies of the system: for example, when the channel ${{{{{{{\mathcal{C}}}}}}}}$ is unitary, the application of the channel to the Bell state $\left|{{\Phi }}\right\rangle$ yields another maximally entangled state $\left|{{{\Phi }}}_{U}\right\rangle := (I\otimes U)\left|{{\Phi }}\right\rangle$, where U is a unitary matrix, and swapping the two entangled systems produces the state $|{{{\Phi }}}_{{U}^{T}}\rangle$, where the unitary U is replaced by its transpose U^T. Coherent control of the choice between the forward channel ${{{{{{{\mathcal{C}}}}}}}}$ and the backward channel ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$ is then realized by adding control to the swap. Finally, a Bell measurement is performed and the outcome corresponding to the projection on the state $\left|{{\Phi }}\right\rangle$ is post-selected. When this outcome occurs, the circuit reproduces the quantum time-flipped channel ${{{{{{{\mathcal{F}}}}}}}}({{{{{{{\mathcal{C}}}}}}}})$, as shown in the following.

Fig. 3: Probabilistic realisation of the quantum time flip.

An unknown channel ${{{{{{{\mathcal{C}}}}}}}}$ is applied locally on a maximally entangled state Φ, which then undergoes a controlled SWAP operation and is used as a resource for quantum teleportation. The probabilistic realisation of the quantum time flip is heralded by a specific value of the outcome m of the Bell measurement in the teleportation protocol.

Let us denote by ${|\phi\rangle }_{S}$ the initial state of the target system and by ${|\psi\rangle }_{C}=\alpha \,{\left|0\right\rangle }_{C}+\beta \,{\left|1\right\rangle }_{C}$ the initial state of the control qubit. Then, the joint state of all systems after the controlled swap is $\alpha \,{|\phi\rangle }_{S}\otimes |{{{\Phi }}}_{U}\rangle \otimes |0\rangle +\beta \,{|\phi \rangle }_{S}\otimes |{{{\Phi }}}_{{U}^{T}}\rangle \otimes |1\rangle$. When the Bell measurement is performed, the target system and the control collapse to one of the states $\alpha \,U{U}_{m}{|\phi\rangle }_{S}\otimes {|0\rangle }_{C}+\beta \,{U}^{T}{U}_{m}{|\phi\rangle }_{S}\otimes {|1\rangle }_{C}$, where m ∈ {1, …, d²} is the measurement outcome and ${\{{U}_{m}\}}_{m = 1}^{{d}^{2}}$ are the unitaries associated to the Bell measurement. For the outcome corresponding to the state $\left|{{\Phi }}\right\rangle$, one obtains the overall state transformation ${|\phi\rangle }_{S}\otimes {|\psi\rangle }_{C}\mapsto \alpha \,U{|\phi\rangle }_{S}\otimes {|0\rangle }_{C}+\beta \,{U}^{T}{|\phi\rangle }_{S}\otimes {|1\rangle }_{C}$, corresponding to the time-flipped channel ${{{{{{{\mathcal{F}}}}}}}}({{{{{{{\mathcal{C}}}}}}}})$. More generally, each outcome of the Bell measurement gives rise to a conditional transformation that uses the gate U in an indefinite time direction. This fact is not in contradiction with the definite time direction of the overall setup in Fig. 3: averaging over all outcomes of the Bell measurement yields an overall operation that uses the gate U in a well-defined direction (the forward one).

In the teleportation setup, the quantum time flip is realised probabilistically. However, in principle the quantum time flip could also be implemented deterministically and without error by some agent who is not constrained to operate in a well-defined time direction. For example, Fig. 3 shows that an agent with the ability to deterministically pre-select a Bell state, and to deterministically post-select the outcome of a Bell measurement would be able to deterministically achieve the quantum time flip. Note that not all circuits built from deterministic pre-selections and deterministic postselections are compatible with quantum theory. In this respect, the framework of quantum operations with indefinite time direction provides a candidate criterion for determining which postselected circuits can be allowed and which ones should be forbidden.

An information-theoretic advantage

We now introduce a game where the quantum time flip offers an advantage over arbitrary setups with definite time direction. The structure of the game is similar to that of another game, previously introduced by one of us to highlight the advantages of the quantum SWITCH⁴¹. However, the variant introduced here exhibits a fundamental difference: in this variant of the game, the quantum time flip offers a perfect win, but no perfect win can be achieved by the quantum SWITCH, nor by any of the processes with indefinite causal order considered so far in the literature.

The game involves a referee, who challenges a player to discover a property of two black boxes. The referee promises that the two black boxes implement two unitary gates U and V satisfying either the condition UV^T = U^TV, or the condition UV^T = − U^TV. The goal of the player is to discover which of these two alternatives holds.

A player with access to the quantum time flip can win the game with certainty. The winning strategy is to apply the quantum time flip to both gates, exchanging the roles of $\left|0\right\rangle$ and $\left|1\right\rangle$ in the control for gate V. In this strategy, one time flip generates the gate ${S}_{U}=U\otimes |0\rangle \langle 0|+{U}^{T}\otimes |1\rangle \langle 1|$, while the other generates the gate ${S}_{V}={V}^{T}\otimes |0\rangle \langle 0|+V\otimes |1\rangle \langle 1|$. The strategy is to prepare the target and control systems in the product state $|\psi\rangle \otimes|+\rangle$, where $|\psi\rangle$ is arbitrary, and $\left|\pm \right\rangle := (\left|0\right\rangle \pm \left|1\right\rangle )/\sqrt{2}$. Then, the target and control are sent first through the gate S_V and then through the gate S_U, obtaining the state

$${S}_{U}{S}_{V}(|\psi\rangle \otimes |+\rangle )=\, \left[\frac{U{V}^{T}+{U}^{T}V}{2}|\psi\rangle\right]\otimes \left|+\right\rangle \\ +\left[\frac{U{V}^{T}-{U}^{T}V}{2}|\psi\rangle \right]\otimes \left|-\right\rangle .$$

(2)

If U and V satisfy the condition UV^T = U^TV, then the second term in the sum vanishes, and the control qubit ends up in the state $\left|+\right\rangle$. Instead, if U and V satisfy the condition UV^T = − U^TV, then the first term vanishes, and the control qubit ends up in the state $\left|-\right\rangle$. Hence, the player can measure the control qubit in the basis $\{\left|+\right\rangle ,\left|-\right\rangle \}$, and figure out exactly which condition is satisfied.

Overall, the transformation of the gate pair (U, V) into the controlled-gate S_US_V is an example of a bipartite supermap with indefinite time direction, of the type discussed in Methods. A player that implements this supermap can in principle win the game with certainty.

The situation is different for players who can only probe the two unknown gates in a definite time direction. In Supplementary Note 4 we show that every such player will have a probability of at least 11% to lose the game. This limitation applies not only to strategies that use the two gates U and V in a fixed order, but also to all strategies where the relative order of U and V is indefinite.

Photonic realisation of the superposition of a process and its input-output inverse

A coherent superposition of a unitary process and its input-output inverse can be realised with polarisation qubits, using the interferometric setup illustrated in Fig. 4. In this setup, a beamsplitter puts the photon in a coherent superposition of two paths, which lead to an unknown polarisation rotator from two opposite spatial directions, respectively. Along one path, the passage through the polarisation rotator induces an unknown unitary gate U. Along the other path, the role of the input and output modes is exchanged and the passage through the same rotator induces the unitary gate GU^TG^†, where G is a fixed unitary gate depending on the choice of basis used for representing polarisation states (in the standard representation of the Poincaré sphere, G is the Pauli matrix $Z=\left|0\right\rangle \langle 0| -| 1\rangle \left\langle 1\right|$). By undoing the unitary gate G, one can then obtain a quantum process with coherent control over the gates U and U^T, as described by Eq. (1).

Fig. 4: Photonic realisation of the superposition of a process and its input-output inverse.

Using a beamsplitter, a single photon is coherently routed along two paths, one (in blue) traversing an unknown waveplate from top to bottom, and the other (in red) traversing it from bottom to top. Along one path, the photon polarisation experiences a unitary gate U, while on the other path it experiences the transpose gate U^T, up to a change of basis G that is undone by placing suitable polarisation rotations before and after the waveplate. a The two paths are finally recombined in order to allow for an interferometric measurement on the control qubit. b By concatenating two setups with the above structure, one can probe two unitary gates U and V in a superposition of time directions, implementing the winning strategy in Eq. (2).

Note that the above realisation is not in contradiction with our no-go result on the realisation of the quantum time flip in a quantum circuit with a fixed time direction. The no-go result implies that it is impossible to build the controlled unitary gate $U\otimes \left|0\right\rangle \langle 0| +{U}^{T}\otimes | 1\rangle \left\langle 1\right|$ starting from an unknown and uncontrolled gate U as the initial resource. However, it does not rule out the existence of a device that directly implements the controlled gate $U\otimes \left|0\right\rangle \langle 0| +{U}^{T}\otimes | 1\rangle \left\langle 1\right|$ in the first place. Such devices do exist in nature, as shown above, and the unitary U appearing in them can be either known or unknown. A similar situation arises in the implementation of other controlled gates, which cannot be constructed from their uncontrolled version^38,42,43,44, but can be directly realised in various experimental setups^45,46.

Discussion

In this work we established a framework for quantum operations with indefinite time direction. This class of operations is broader than the set of operations considered so far in the literature, and in the multipartite case it includes all known operations with definite and indefinite causal order. Quantum operations with both indefinite time direction and indefinite causal order provide a framework for describing the interactions of an agent with the fundamentally time-symmetric dynamics of quantum theory, and for composing local processes into more complex structures. This higher order framework is expected to contribute to the study of quantum gravity scenarios, as envisaged by Hardy¹³. Such applications, however, are beyond the scope of the present paper and remain as a direction for future research.

The characterization of the bidirectional quantum channels provided in this paper also reveals an interesting connection with thermodynamics. We showed that the set of bidirectional quantum processes coincides with the set of bistochastic channels. On the other hand, bistochastic channels can also be characterised as the set of entropy non-decreasing processes: any entropy non-decreasing process must transform the maximally mixed state into itself, and therefore be bistochastic; vice-versa, every bistochastic channel is entropy non-decreasing⁴⁷. Putting everything together, we conclude that the processes admitting an input-output inversion are exactly those that are compatible with the non-decrease of entropy both in the forward and in the backward time direction. This conclusion is worth noting, because no entropic consideration was included in the derivation of our results. A promising direction for future research is to further investigate the role of input-output inversion in the search of axiomatic principles for quantum thermodynamics^48,49.

Finally, another interesting direction is to explore generalisations of quantum thermodynamics to the scenario where agents are not constrained to operate in a definite time direction. A first step in this direction has been recently taken by Rubino, Manzano, and Brukner⁵⁰, who explored thermal machines using a coherent superpositions of forward and backward processes. Their notion of backward process is different from ours, in that it is defined in terms of the joint unitary evolution of the system and an environment, rather than the dynamics of the system alone. An interesting direction of future research is to explore the thermodynamic power of the operations introduced in our work, taking advantage of recent insights on quantum thermodynamics with indefinite causal order^51,52,53.

Methods

Characterisation of the input-output inversions of bistochastic channels

The foundation of our framework is the characterisation of the bidirectional quantum devices. The logic of our argument is the following: first, we observe that the input-output inversion must be linear in its argument (Supplementary Note 5). Hence, the action of the map Θ on the unitary channels uniquely determines the action of the map Θ on every channel in the linear space generated by the unitary channels. This linear space is characterised by the following theorem from²⁸, for which we provide a new, constructive proof in Supplementary Note 6.

Theorem 1

The linear span of the set of unitary channels coincides with the linear span of the set of bistochastic channels.

Theorem 1 implies that the action of the map Θ on of bistochastic channels is uniquely determined by the action of the map Θ on unitary channels. For unitary channels, we have seen that there are only two possible choices: either the action of Θ on the bistochastic channels is unitarily equivalent to the adjoint, or it is unitarily equivalent to the transpose. In either case, ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$ is a valid quantum channel (CPTP map) for every bistochastic channel ${{{{{{{\mathcal{C}}}}}}}}$. Hence, all bistochastic channels are bidirectional.

Characterisation of the bidirectional channels

We now show that the set of bidirectional channels coincides with the set of bistochastic channels. The key of the argument is the following result:

Theorem 2

If a channel ${{{{{{{\mathcal{C}}}}}}}}$ admits an input-output inversion satisfying Requirements 1, 2, and 4, then its input-output inversion ${{\Theta }}({{{{{{{\mathcal{C}}}}}}}})$ is a bistochastic channel.

The proof is provided in Supplementary Note 7. Theorem 2, combined with Requirement 3 (the input-output inversion maps distinct channels into distinct channels), implies that only bistochastic channels can admit an input-output inverse. Indeed, if a non-bistochastic channel had an input-output inversion, then the input-output inverse would coincide with the input-output inversion of a bistochastic channel, in contradiction with Requirement 3.

In Supplementary Note 8 we show that, even if Requirement 3 is dropped, defining a non-trivial input-output inversion satisfying requirements 1, 2, and 4 is impossible for every system of dimension d > 2. For d = 2, instead, a map Θ satisfying conditions (1), (2), and (4) can be defined on all channels, but it maps all channels into bistochastic channels, in agreement with Theorem 2.

Summarising, the set of bidirectional channels is the set of bistochastic channels, and the input-output inversion is either equivalent to the adjoint or to the transpose. The adjoint and the transpose exhibit a fundamental difference when applied locally to bipartite processes. Suppose that a composite system S ⊗ E undergoes a joint evolution with the property that the reduced evolution of system S is bistochastic for every initial state of system E. Then, one may want to apply the input-output inversion only on the S-part of the evolution, while leaving the E-part unchanged. In Supplementary Note 9 we show that, when the dimension of system S is larger than two, the local application of the input-output inversion generates valid quantum evolutions (CPTP maps) if and only if the input-output inversion is described by the transpose.

Characterisation of the operations on bistochastic channels

A basic way to interact with a bidirectional quantum device is described by a particular type of quantum supermap²² that transforms bistochastic channels into ordinary channels (CPTP maps).

Hereafter, we will denote by $L({{{{{{{\mathcal{H}}}}}}}},{{{{{{{\mathcal{K}}}}}}}})$ the set of linear operators on a generic Hilbert space ${{{{{{{\mathcal{H}}}}}}}}$ to another generic Hilbert space ${{{{{{{\mathcal{K}}}}}}}}$, and we will use the shorthand notation $L({{{{{{{\mathcal{H}}}}}}}}):=L({{{{{{{\mathcal{H}}}}}}}},{{{{{{{\mathcal{H}}}}}}}})$. Also, we will denote by Map(S_i, S_o) the set of linear maps from $L({{{{{{{{\mathcal{H}}}}}}}}}_{{S}_{{{{{{{{\rm{i}}}}}}}}}})$ to $L({{{{{{{{\mathcal{H}}}}}}}}}_{{S}_{{{{{{{{\rm{o}}}}}}}}}})$, by Chan(S_i, S_o) ⊂ Map(S_i, S_o) the set of all quantum channels (CPTP maps), and by BiChan(S_i, S_o) the subset of all bistochastic channels. The set of density matrices of system S will be denoted as St(S).

A quantum supermap transforming bistochastic channels in BiChan(A_i, A_o) into channels Chan(B_i, B_o) is a linear map ${{{{{{{\mathcal{S}}}}}}}}:{\mathsf{Map}}({A}_{{{{{{{{\rm{i}}}}}}}}}\,,\,{A}_{{{{{{{{\rm{o}}}}}}}}})\to {\mathsf{Map}}({B}_{{{{{{{{\rm{i}}}}}}}}},{B}_{{{{{{{{\rm{o}}}}}}}}})$. The map ${{{{{{{\mathcal{S}}}}}}}}$ is required to produce valid channels even when acting locally on part of bipartite processes. Explicitly, the requirement is that $({{{{{{{\mathcal{S}}}}}}}}\otimes {{{{{{{{\mathcal{I}}}}}}}}}_{{E}_{{{{{{{{\rm{i}}}}}}}}}{E}_{{{{{{{{\rm{o}}}}}}}}}})\,({{{{{{{\mathcal{C}}}}}}}})$ must be a valid quantum channel in Chan(B_iE_i ,  B_oE_o) for every ${{{{{{{\mathcal{C}}}}}}}}\in {\mathsf{Chan}}({A}_{{{{{{{{\rm{i}}}}}}}}}{E}_{{{{{{{{\rm{i}}}}}}}}}\,,\,{A}_{{{{{{{{\rm{o}}}}}}}}}{E}_{{{{{{{{\rm{o}}}}}}}}})$ satisfying the condition that the reduced channel ${{{{{{{{\mathcal{C}}}}}}}}}_{\sigma }:\rho \mapsto {{{{{{{{\rm{Tr}}}}}}}}}_{{E}_{{{{{{{{\rm{o}}}}}}}}}}[{{{{{{{\mathcal{C}}}}}}}}(\rho \otimes \sigma )]$ is in BiChan(A_i, A_o) for every density matrix σ ∈ St(E_i)²².

A convenient way to represent quantum supermaps is to use the Choi representation⁵⁴. A generic linear map ${{{{{{{\mathcal{M}}}}}}}}:L({{{{{{{{\mathcal{H}}}}}}}}}_{{S}_{{{{{{{{\rm{i}}}}}}}}}})\to L({{{{{{{{\mathcal{H}}}}}}}}}_{{S}_{{{{{{{{\rm{o}}}}}}}}}})$ is in one-to-one correspondence with its Choi operator ${{{{{{{\rm{Choi}}}}}}}}({{{{{{{\mathcal{M}}}}}}}})\in L({{{{{{{{\mathcal{H}}}}}}}}}_{{S}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{S}_{{{{{{{{\rm{i}}}}}}}}}})$, defined by ${{{{{{{\rm{Choi}}}}}}}}({{{{{{{\mathcal{M}}}}}}}}):={\sum }_{m,n}{{{{{{{\mathcal{M}}}}}}}}(\left|m\right\rangle \left\langle n\right|)\otimes \left|m\right\rangle \left\langle n\right|$, where $\{\left|n\right\rangle \}$ is a fixed orthonormal basis. For a bistochastic channel ${{{{{{{\mathcal{C}}}}}}}}\in {\mathsf{BiChan}}({A}_{{{{{{{{\rm{i}}}}}}}}},{A}_{{{{{{{{\rm{o}}}}}}}}})$ with A_i ≃ A_o, the Choi operator C satisfies the conditions

$${{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}[C]={I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}\quad {{{{{{{\rm{and}}}}}}}}\quad {{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}[C]={I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}.$$

(3)

Equivalently, the operator C can be decomposed as

$$C=\frac{{I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}}{d}+T,$$

(4)

where d is the dimension of systems A_i and A_o, and T is an operator such that

$${{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}[T]=0\quad {{{{{{{\rm{and}}}}}}}}\quad {{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}[T]=0.$$

(5)

and ∥T∥≤1/d.

Now, every supermap ${{{{{{{\mathcal{S}}}}}}}}:{\mathsf{Map}}({A}_{{{{{{{{\rm{i}}}}}}}}}\,,\,{A}_{{{{{{{{\rm{o}}}}}}}}})\to {\mathsf{Map}}({B}_{{{{{{{{\rm{i}}}}}}}}},{B}_{{{{{{{{\rm{o}}}}}}}}})$ is itself a linear map, and, as such, it can be represented by Choi operator $S\in L({{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}})$. The operator S is completely specified by the relation

$${\mathsf{Choi}}({{{{{{{\mathcal{S}}}}}}}}({{{{{{{\mathcal{M}}}}}}}}))={{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[{({I}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {\mathsf{Choi}}{({{{{{{{\mathcal{M}}}}}}}})}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}})}^{T}\,S] \,, \qquad \forall {{{{{{{\mathcal{M}}}}}}}}\in {\mathsf{Map}}({A}_{{{{{{{{\rm{i}}}}}}}}},{A}_{{{{{{{{\rm{o}}}}}}}}}),$$

(6)

where ${{{{{{{\mathcal{M}}}}}}}}$ is an arbitrary map in Map(A_i ,  A_o), and T denotes the transpose with respect to the basis $\{\left|n\right\rangle \}$. This relation can be used, for example, to compute the Choi operator of the quantum time flip. In the case of the quantum time flip, the systems A_i and A_o have the same dimension, and the systems B_i and B_o are of the bipartite form B_i = B_itB_ic and A_i = A_itA_ic, where B_it (B_ot) is a target system, of the same dimension as A_i and A_o, and B_ic (B_oc) is a two-dimensional control system. Using this notation, we can express the Choi operator of the quantum time flip as

$$F=\left|V\right\rangle \left\langle V\right|,$$

(7)

with

$$\left|V\right\rangle :=\, {\left.\left|I\right\rangle \right\rangle }_{{B}_{{{{{{{{\rm{ot}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {\left.\left|I\right\rangle \right\rangle }_{{B}_{{{{{{{{\rm{it}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {\left|0\right\rangle }_{{B}_{{{{{{{{\rm{oc}}}}}}}}}}\otimes {\left|0\right\rangle }_{{B}_{{{{{{{{\rm{ic}}}}}}}}}}\\ +{\left.\left|I\right\rangle \right\rangle }_{{B}_{{{{{{{{\rm{ot}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {\left.\left|I\right\rangle \right\rangle }_{{B}_{{{{{{{{\rm{it}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {\left|1\right\rangle }_{{B}_{{{{{{{{\rm{oc}}}}}}}}}}\otimes {\left|1\right\rangle }_{{B}_{{{{{{{{\rm{ic}}}}}}}}}},$$

(8)

and $\left.\left|I\right\rangle \right\rangle :={\sum }_{m}\,\left|m\right\rangle \otimes \left|m\right\rangle$. (Here the vector $\left|V\right\rangle$ belongs to the Hilbert space ${{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{ot}}}}}}}}}{B}_{{{{{{{{\rm{oc}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{it}}}}}}}}}{B}_{{{{{{{{\rm{ic}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}$, and it is understood that the Hilbert spaces in the r.h.s. have to be reordered consistently according to the systems’ labels).

In the Choi representation, the requirement that ${{{{{{{\mathcal{S}}}}}}}}$ be applicable locally on part of a larger process is equivalent to the requirement that the operator S be positive semidefinite^22,29. The requirement that ${{{{{{{\mathcal{S}}}}}}}}$ transforms any bistochastic channel into a CPTP map is equivalent to the condition

$${{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[{({I}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {C}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}})}^{T}\,S]={I}_{{B}_{{{{{{{{\rm{i}}}}}}}}}},$$

(9)

where C is an arbitrary Choi operators of a bistochastic channel ${{{{{{{\mathcal{C}}}}}}}}\in {\mathsf{Bi}}{\mathsf{Chan}}({A}_{{{{{{{{\rm{i}}}}}}}}},{A}_{{{{{{{{\rm{o}}}}}}}}})$.

The normalisation condition (9) can be put in a more explicit form by decomposing the operator S into orthogonal components, in a similar way as it was done in²¹ for the characterisation of the operations with definite time direction.

Choosing T = 0 in Eq. (4) and inserting the operator $C={I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}/d$ into Eq. (9), we obtain

$$\frac{{{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]}{d}={I}_{{B}_{{{{{{{{\rm{i}}}}}}}}}}.$$

(10)

Choosing an arbitrary T, instead, we obtain

$${{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[({I}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {T}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}})S]=0.$$

(11)

The combination of conditions (10) and (11) is equivalent to the original condition (9).

We will now cast condition (11) in a more explicit form. Condition (11) is equivalent to the requirement that S be orthogonal (with respect to the Hilbert-Schmidt product) to all operators of the form ${I}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {J}_{{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {T}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}$, where ${J}_{{B}_{{{{{{{{\rm{i}}}}}}}}}}$ is an arbitrary operator on ${{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{i}}}}}}}}}}$ and ${T}_{{A}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}}$ is an arbitrary operator satisfying Eq. (5). This condition implies that S can be decomposed into the sum of four mutually orthogonal operators, namely

$$S=\, {G}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {I}_{{{{{{{{\rm{{A}}}}}}}_{{{{{{{{\rm{o}}}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}+{K}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}+{L}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}} +{W}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}},$$

(12)

where ${G}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}$ is an arbitrary operator on ${{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{i}}}}}}}}}}$, and the remaining operators on the right hand side satisfy the relations

$${{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}[{K}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}}] = \, 0\\ {{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}[{L}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}] = \, 0\\ {{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}[{W}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}] = \, 0\\ {{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}[{W}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}] = \, 0\\ {{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}[{W}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}] = \, 0.$$

(13)

(The operator ${L}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}$ in Eq. (12) is understood as acting on ${{{{{{{{\mathcal{H}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {{{{{{{{\mathcal{B}}}}}}}}}_{{{{{{{{\rm{i}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}$, with an implicit reordering of the Hilbert spaces according to the systems’ labels. In the following, this implicit reordering will be used).

We now express the first three operators in the right-hand side of Eq. (12) in terms of the partial traces of S. Explicitly, we have

$${G}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}} = \, \frac{{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]}{{d}^{2}}\\ {K}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}} = \, \frac{{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]}{d}-{G}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}\\ {L}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}} = \, \frac{{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}[S]}{d}-{G}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}.$$

(14)

Inserting the above relations into Eq. (12), we obtain

$$S = {{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}}{d}+{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}}{d}-{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}}{d}\otimes \frac{{I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}}{d}+{W}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}},$$

(15)

or equivalently,

$$S-{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}}{d}-{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}}{d} +{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}}{d}\otimes \frac{{I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}}{d} = {W}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}.$$

(16)

In other words, the left-hand side of the equation should be an operator that satisfies the last three conditions of Eq. (13). The first two conditions are automatically guaranteed by the form of the right-hand side of Eq. (16), while the third condition reads

$${{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}[S]={{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}}{d}+{{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}}{d}-{{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{o}}}}}}}}}{A}_{{{{{{{{\rm{i}}}}}}}}}}[S]\otimes \frac{{I}_{{A}_{{{{{{{{\rm{o}}}}}}}}}}}{d}\otimes \frac{{I}_{{A}_{{{{{{{{\rm{i}}}}}}}}}}}{d}.$$

(17)

Summarising, we have shown that the normalisation of the supermap ${{{{{{{\mathcal{S}}}}}}}}$ is expressed by the two conditions (10) and (17).

As an example, one can easily verify that the Choi operator of the quantum time flip, provided in Eq. (7) satisfies conditions (10) and (17). In fact, the quantum time flip satisfies these conditions even when the roles of B_i and B_o are exchanged. This additional property expresses the fact that the quantum time flip supermap transforms bistochastic channels into bistochastic channels.

Multipartite quantum operations on bistochastic channels

Multipartite operations with indefinite time direction can also be described as quantum supermaps on the set of N-partite no-signalling bistochastic channels, that is, the set of N-partite quantum channels of the form

$${{{{{{{\mathcal{N}}}}}}}}=\mathop{\sum}\limits_{j}\,{c}_{j}\,{{{{{{{{\mathcal{A}}}}}}}}}_{1,j}\otimes {{{{{{{{\mathcal{A}}}}}}}}}_{2,j}\otimes \cdots \otimes {{{{{{{{\mathcal{A}}}}}}}}}_{N,j}.$$

(18)

where each c_j is a real coefficient, each ${{{{{{{{\mathcal{A}}}}}}}}}_{i,j}$ is a bistochastic channel. We denote the set of channels of this form as BiNoSig(A_1i, A_1o ∣ A_2i, A_2o ∣  ⋯  ∣A_Ni, A_No) where A_ni (A_no) is the input (output) of channel ${{{{{{{{\mathcal{A}}}}}}}}}_{n,j}$, for every possible n and every possible j.

A quantum supermap on no-signalling bistochastic channels is then defined as a linear map ${{{{{{{\mathcal{S}}}}}}}}:{\mathsf{Map}}({A}_{1{{{{{{{\rm{i}}}}}}}}}{A}_{2{{{{{{{\rm{i}}}}}}}}}\cdots {A}_{N{{{{{{{\rm{i}}}}}}}}}\,,\,{A}_{1{{{{{{{\rm{o}}}}}}}}}{A}_{2{{{{{{{\rm{o}}}}}}}}}\cdots {A}_{N{{{{{{{\rm{o}}}}}}}}})\to {\mathsf{Map}}({B}_{{{{{{{{\rm{i}}}}}}}}},{B}_{{{{{{{{\rm{o}}}}}}}}})$, where B_i (B_o) is the input (output) of the channel produced by ${{{{{{{\mathcal{S}}}}}}}}$. The map ${{{{{{{\mathcal{S}}}}}}}}$ is required to transform no-signalling bistochastic channels into CPTP maps even when acting locally on part of a composite process. Explicitly, this means that the map $({{{{{{{\mathcal{S}}}}}}}}\otimes {{{{{{{{\mathcal{I}}}}}}}}}_{{E}_{{{{{{{{\rm{i}}}}}}}}}{E}_{{{{{{{{\rm{o}}}}}}}}}})\,({{{{{{{\mathcal{N}}}}}}}})$ must be a valid quantum channel in Chan(B_i, B_o) for every ${{{{{{{\mathcal{N}}}}}}}}\in {\mathsf{Chan}}({A}_{1{{{{{{{\rm{i}}}}}}}}} \,{A}_{2{{{{{{{\rm{i}}}}}}}}} \,\cdots \, {A}_{N{{{{{{{\rm{i}}}}}}}}} \, {E}_{{{{{{{{\rm{i}}}}}}}}} , \, {A}_{1{{{{{{{\rm{o}}}}}}}}}\, {A}_{2{{{{{{{\rm{o}}}}}}}}}\, \cdots \, {A}_{N{{{{{{{\rm{o}}}}}}}}} {E}_{{{{{{{{\rm{o}}}}}}}}} )$ satisfying the condition that the reduced channel ${{{{{{{{\mathcal{N}}}}}}}}}_{\sigma }:\rho \,\mapsto\, {{{{{{{{\rm{Tr}}}}}}}}}_{{E}_{{{{{{{{\rm{o}}}}}}}}}}[{{{{{{{\mathcal{N}}}}}}}}(\rho \otimes \sigma )]$ belongs to BiNoSig(A_1i, A_1o ∣ A_2i, A_2o ∣  ⋯  ∣A_Ni, A_No) for every density matrix σ ∈ St(E_i).

Quantum supermaps on bistochastic no-signalling channels describe the most general way in which N bidirectional quantum processes can be combined into a single channel. In general, this combination can be incompatible with a definite direction of time, and, at the same time, incompatible with a definite ordering of the N channels.

Here we provide three examples of bipartite supermaps. To specify each supermap, we specify its action on the set of product channels, which by definition are a spanning set of the set of bipartite bistochastic no-signalling channels. The first supermap, ${{{{{{{{\mathcal{S}}}}}}}}}_{1}$, is defined as

$${{{{{{{{\mathcal{S}}}}}}}}}_{1}({{{{{{{{\mathcal{A}}}}}}}}}_{1}\otimes {{{{{{{{\mathcal{A}}}}}}}}}_{2})(\rho ) : = \, \mathop{\sum}\limits_{m,n}{S}_{1mn}\rho {S}_{1mn}^{{{{\dagger}}} }\\ {S}_{1mn} : = \, {A}_{1m}{A}_{2n}^{T}\otimes \left|0\right\rangle \langle 0| +{A}_{1m}^{T}{A}_{2n}\otimes | 1\rangle \left\langle 1\right|,$$

(19)

where {A_1m} and {A_2,n} are Kraus operators of channels ${{{{{{{{\mathcal{A}}}}}}}}}_{1}$ and ${{{{{{{{\mathcal{A}}}}}}}}}_{2}$, respectively. This supermap can be generated by applying two independent quantum time flips to channels ${{{{{{{{\mathcal{A}}}}}}}}}_{1}$ and ${{{{{{{{\mathcal{A}}}}}}}}}_{2}$, respectively: indeed, one has ${{{{{{{{\mathcal{S}}}}}}}}}_{1}({{{{{{{{\mathcal{A}}}}}}}}}_{1}\otimes {{{{{{{{\mathcal{A}}}}}}}}}_{2})={{{{{{{\mathcal{F}}}}}}}}({{{{{{{{\mathcal{A}}}}}}}}}_{1})\circ {{{{{{{\mathcal{F}}}}}}}}^{\prime} ({{{{{{{{\mathcal{A}}}}}}}}}_{2})$, where ${{{{{{{\mathcal{F}}}}}}}}^{\prime}$ is the variant of the quantum time flip in which the roles of the control states $\left|0\right\rangle$ and $\left|1\right\rangle$ are exchanged.

The supermap ${{{{{{{{\mathcal{S}}}}}}}}}_{1}$ describes the winning strategy in Eq. (2). This strategy cannot be realized by using the two channels ${{{{{{{{\mathcal{A}}}}}}}}}_{1}$ and ${{{{{{{{\mathcal{A}}}}}}}}}_{2}$ in a definite time direction, but is compatible with a definite causal order: the channel ${{{{{{{{\mathcal{A}}}}}}}}}_{1}$ (${{{{{{{{\mathcal{A}}}}}}}}}_{1}^{T}$) always acts after channel ${{{{{{{{\mathcal{A}}}}}}}}}_{2}^{T}$ (${{{{{{{{\mathcal{A}}}}}}}}}_{2}$).

The second supermap, ${{{{{{{{\mathcal{S}}}}}}}}}_{2}$, is the quantum SWITCH ^20,22, defined as

$${{{{{{{{\mathcal{S}}}}}}}}}_{2}({{{{{{{{\mathcal{A}}}}}}}}}_{1}\otimes {{{{{{{{\mathcal{A}}}}}}}}}_{2})(\rho ) := \, \mathop{\sum}\limits_{m,n}{S}_{2mn}\rho {S}_{2mn}^{{{{\dagger}}} }\\ {S}_{2mn} : = \, {A}_{1m}{A}_{2n}\otimes \left|0\right\rangle \langle 0| +{A}_{2n}{A}_{1m}\otimes | 1\rangle \left\langle 1\right|.$$

(20)

Note that here the quantum SWITCH is restricted to act on the set of bistochastic no-signalling channels. Interestingly, however, this definition determines the action of the quantum SWITCH on arbitrary channels (and on arbitrary linear maps as well): the reason is that the set of bistochastic no-signalling channels includes the set of all products of unitary channels, and it is known that the quantum SWITCH is uniquely determined by its action on such channels⁵⁵. In the quantum SWITCH, the order of the channels ${{{{{{{{\mathcal{A}}}}}}}}}_{1}$ and ${{{{{{{{\mathcal{A}}}}}}}}}_{2}$ is indefinite, but each channel is used in the forward time direction.

Finally, our third example is a supermap ${{{{{{{{\mathcal{S}}}}}}}}}_{3}$ arising from the combination of the quantum time flip with the quantum SWITCH. It is defined as follows:

$${{{{{{{{\mathcal{S}}}}}}}}}_{3}({{{{{{{{\mathcal{A}}}}}}}}}_{1}\otimes {{{{{{{{\mathcal{A}}}}}}}}}_{2})(\rho ) : = \, \mathop{\sum}\limits_{m,n}{S}_{3mn}\rho {S}_{3mn}^{{{{\dagger}}} }\\ {S}_{3mn} : = \, {A}_{1m}{A}_{2n}\otimes \left|0\right\rangle \langle 0| +{A}_{2n}^{T}{A}_{1m}^{T}\otimes | 1\rangle \left\langle 1\right|.$$

(21)

This supermap describes a coherent superposition of the process ${{{{{{{{\mathcal{A}}}}}}}}}_{1}\circ {{{{{{{{\mathcal{A}}}}}}}}}_{2}$ and its input-output inverse ${{\Theta }}({{{{{{{{\mathcal{A}}}}}}}}}_{1}\circ {{{{{{{{\mathcal{A}}}}}}}}}_{2})={{{{{{{{\mathcal{A}}}}}}}}}_{2}^{T}\circ {{{{{{{{\mathcal{A}}}}}}}}}_{1}^{T}$. Such supermap is incompatible with both a definite time direction and with a definite causal order.

Choi representation of multipartite operations

An equivalent way to represent quantum supermaps on bistochastic no-signalling channels is to use the Choi representation. When this is done, one obtains a generalisation of the notion of process matrix²¹, originally used for supermaps that combine processes in an indefinite order while using each process in a definite time direction.

Since ${{{{{{{\mathcal{S}}}}}}}}$ is a linear map, it has a Choi operator S ∈ L(B_oB_iA_1oA_1iA_2oA_2i   ⋯  A_NoA_Ni), uniquely determined by the relation

$${\mathsf{Choi}}({{{{{{{\mathcal{S}}}}}}}}({{{{{{{\mathcal{M}}}}}}}})) = {{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{1{{{{{{{\rm{o}}}}}}}}}{A}_{1{{{{{{{\rm{i}}}}}}}}}{A}_{2{{{{{{{\rm{o}}}}}}}}}{A}_{2{{{{{{{\rm{i}}}}}}}}}\cdots {A}_{N{{{{{{{\rm{o}}}}}}}}}{A}_{N{{{{{{{\rm{i}}}}}}}}}}[{({I}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes {\mathsf{Choi}}({{{{{{{\mathcal{M}}}}}}}}))}^{T}\,S],$$

(22)

where ${{{{{{{\mathcal{M}}}}}}}}$ is an arbitrary map in Map(A_1iA_2i ⋯ A_Ni ,  A_1oA_2o ⋯ A_No).

As in the N = 1 case, the requirement that ${{{{{{{\mathcal{S}}}}}}}}$ be applicable locally on part of a larger process is equivalent to the requirement that the operator S be positive semidefinite. The requirement that ${{{{{{{\mathcal{S}}}}}}}}$ transforms any bistochastic no-signalling channel into a CPTP map is equivalent to the condition

$${{{{{{{{\rm{Tr}}}}}}}}}_{{B}_{{{{{{{{\rm{o}}}}}}}}}}{{{{{{{{\rm{Tr}}}}}}}}}_{{A}_{1{{{{{{{\rm{o}}}}}}}}}{A}_{1{{{{{{{\rm{i}}}}}}}}}{A}_{2{{{{{{{\rm{o}}}}}}}}}{A}_{2{{{{{{{\rm{i}}}}}}}}}\cdots {A}_{N{{{{{{{\rm{o}}}}}}}}}{A}_{N{{{{{{{\rm{i}}}}}}}}}}[{({I}_{{B}_{{{{{{{{\rm{o}}}}}}}}}{B}_{{{{{{{{\rm{i}}}}}}}}}}\otimes N)}^{T}\,S]={I}_{{B}_{{{{{{{{\rm{i}}}}}}}}}},$$

(23)

where N is the Choi operator of an arbitrary bistochastic no-signalling channel in BiNoSig(A_1i, A_1o ∣  A_2i, A_2o ∣  ⋯  ∣A_Ni, A_No). A more explicit characterization can be obtained using an orthogonal decomposition of the operator S as illustrated earlier in the N = 1 case.