Introduction

Magnetic metals support both collective spin-wave (Fig. 1a) and quasiparticle (Stoner) (Fig. 1b, c) spin-flip excitations1,2,3,4,5,6,7. In three-dimensional (3D) metallic ferromagnets like iron8,9 and nickel10, the quasiparticle bands are broad and spin waves are well-defined only at long wavelengths, disappearing when they enter the Stoner continuum at intermediate spin-wave momenta (Fig. 1c)11,12,13. In 2D metallic kagome lattice materials (Fig. 1d–g), destructive interference of electronic hopping pathways around the kagome bracket can produce nearly localized electrons, and thus electronic bands that are flat in momentum space (Fig. 1h–j)14,15,16,17,18. When combined with spin-orbit coupling and magnetic order, the geometric frustration induced flat bands provide an ideal platform for novel topological phases19,20,21, ferromagnetism22, and superconductivity23,24. Although flat bands below the Fermi level have recently been identified in the antiferromagnetic (AF) kagome metal FeSn25, paramagnetic kagome metal CoSn26,27, as well as in other materials28,29,30, their influence on spin-wave and Stoner excitations is unknown.

Fig. 1: Schematic diagrams of spin waves, Stoner continuum, lattice and magnetic structures of FeSn and its reciprocal space notations.
figure 1

a Collective spin waves in a local moment Heisenberg model. b, c Schematic illustrations of Stoner excitations. This excitation corresponds to a transition from occupied states in a spin-up band to unoccupied states in a spin-down band. The numbered arrows in (b) indicate the possible scattering processes, corresponding to the numbered points in (c), the energy spectrum of the single particle electron-hole pair excitations. d Crystal and magnetic structures of FeSn. e Top view of the kagome lattice, where J1, J2, and Jc are the dominant magnetic interactions used in the Heisenberg model to fit spin waves of FeSn. f, g 3D and 2D Brillouin zone of FeSn, respectively. The high symmetry points are specified and the green-colored hexagon marks the integration area in reciprocal space to obtain the total magnetic scattering within one Brillouin zone. h, i, j Schematic illustrations of destructive quantum interferences induced electronic confinement and flat band in kagome lattice. Electron hoppings outside the purple-colored hexagon will be prohibited due to the antiphase of flat band eigenstates at the neighboring sublattices, resulting in the perfect electron localization and flat electronic band in reciprocal space.

Full size image

In general, spin-flip excitations in a magnet can be interpreted in terms of either a quantum spin model1,2 with local moments on each atomic site (Fig. 1a), or a Stoner3,4,5,6,13 itinerant electron model. In insulating ferromagnets such as EuO, magnetic excitations can be fully described by a Heisenberg Hamiltonian31 with spins on Eu lattice sites. In ferromagnetic (FM) metals, magnetic order breaks the degeneracy of the electronic bands, splitting spin-up majority and spin-down minority electrons (Fig. 1b)6. For 3D metallic FM Fe and Ni, the low-energy spin waves are strongly damped when they enter a broad Stoner continuum of band-electron spin-flips that extends over several eV in energy (Fig. 1c)8,9,10,11,12. For a paramagnetic metal, there is no splitting of the degenerate electronic bands, although a continuum of electron-hole pair (Stoner continuum) excitations can still occur if the system has electron and hole pockets below and above the Fermi level. In strongly correlated materials like copper and iron-based superconductors, the subtle balance between electron kinetic energy and short-range interactions can lead to debates concerning whether magnetism has a localized or itinerant origin32,33.

In some 2D crystals, electrons can be confined in real space to form flat bands, for example through geometric lattice frustration19,20,21. The flat bands of magic-angle twisted bilayer graphene23 provide one example of this route toward strong electronic correlation24. The kagome lattice depicted in Fig. 1h, in which the simplest nearest neighbor electronic hopping model predicts destructive phase interference (Fig. 1i) leading to real-space electron localization and a flat electronic band (Fig. 1j)20, provides a second. Recently, a spin-polarized flat electronic band has been identified in the AF kagome metal FeSn at an energy \(E = 230 \pm\)50 meV below the Fermi level by angle-resolved photoemission spectroscopy (ARPES) experiments25. FeSn is a A-type AF with antiferromagnetically coupled FM planes34, which we will view as 2D ferromagnets. Neutrons should in principle detect the electron-hole-pair Stoner excitations from the majority-spin flat band below the Fermi level to minority-spin bands near or above the Fermi level (Fig. 1b)6,13. Since neutron scattering measures electron-hole-pair excitations, having a flat spin-up electronic band below the Fermi level is a necessary, but not a sufficient condition to observe a flat Stoner continuum band. Instead, such a dispersionless narrow energy spin excitation band also requires a flat spin-down electronic band above (or near) the Fermi level13. Unfortunately, ARPES measurements cannot provide any information concerning such an electronic band above the Fermi level, although density functional theory (DFT) calculations suggest its presence25. For comparison, although ARPES measurements have also identified flat band at an energy \(E = 270 \pm\)50 meV below the Fermi level in CoSn26,27, one would not expect to observe a flat Stoner continuum band due to degenerate electronic bands nature of the system35.

In this paper, we report inelastic neutron scattering (INS) studies of spin excitations in 2D metallic kagome lattice antiferromagnetic FeSn34 and paramagnetic CoSn35. For FeSn, our measurements reveal well-defined spin waves extending well above 140 meV. However, there is no evidence for a narrow band Stoner continuum expected from the band structure calculation. For CoSn, there are correlated paramagnetic scatterings centered around Γ point extending to ~90 meV. We also observe two dispersion-less bands of excitations at ~170 meV and ~360 meV in FeSn and CoSn, due mostly to hydrocarbon scattering of the CYTOP-M (a trademarked fluoropolymer) commonly used to glue the samples to aluminum holder36. Therefore, our results established the evolution of spin excitations in FeSn and CoSn, and revealed that the observed flat electronic band below the Fermi level does not induce a narrow band Stoner continuum. In addition, we identified anomalous flat modes arising mostly from the CYTOP-M phonon scattering. A reanalysis of the high spin excitation data on iron pnictide samples glued using CYTOP-M confirmed the presence of ~170 meV flat mode that has been overlooked over the years37.

Results

Neutron scattering on FeSn

We have carried out INS experiments to study spin waves and search for anomalous Stoner excitations in AF kagome metallic FeSn34 and paramagnetic CoSn35. The structure of FeSn consists of 2D kagome nets of Fe separated by layers of Sn, and exhibits AF order below \(T_N \approx 365\) K with in-plane FM moments in each layer stacked antiferromagnetically along the c-axis (Fig. 1d)34. Since each unit cell contains three Fe atoms (Fig. 1e), we expect one acoustic and two optical spin-wave branches in a local moment Heisenberg Hamiltonian34,38,39. Figure 1f, g show the reciprocal spaces corresponding to the crystal structures of FeSn depicted in Fig. 1d, e, respectively. CoSn has the same crystal structure as that of FeSn but is paramagnetic at all temperatures35.

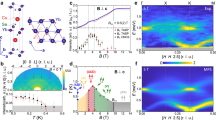
Figure 2a illustrates low-energy spin excitations observed in FeSn along the high symmetry directions in the (H,K) plane depicted in Fig. 1g. We see a nearly isotropic spin-wave mode stemming from the Γ point at the FM zone center that moves towards the zone boundary with increasing energy. Along the [H,0,0] direction towards the M point, the acoustic mode reaches the zone boundary at around 90 meV. Figure 2b shows an image of the wave vector transfer (Q) and energy (E) dependence of spin excitations around the M point. The data confirm that the acoustic spin waves reach around 90 meV at the M point, and reveal an optical spin-wave mode that is visible at energies between 115 and 140 meV, and is characterized by out-of-phase oscillations amongst the three Fe sublattice spins. The evolution of the in-plane Q-dependence of acoustic spin waves with increasing energy is summarized in Fig. 2e, revealing spin wave rings around the Γ point that enlarge with increasing energy. Unlike the in-plane FM spin waves stemming from the Γ point, which have excitation energies exceeding 140 meV (Fig. 2a, e), the spin waves along the c-axis stem from the AF ordering wave vectors \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,0.5 + L)\) with (L = 0, 1) and reach the zone boundary around \(E \approx 20\) meV (Fig. 2g), reflecting relatively weak coupling between ferromagnetic kagome planes. We also observe an easy-axis anisotropy gap \({\Delta}_a \approx 2\) meV due to single-ion magnetic anisotropy (Fig. 2i, j)34.

Fig. 2: Low-energy spin waves of FeSn and fit to a Heisenberg Hamiltonian.
figure 2

a Neutron scattering function \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) at 5 K along the high symmetric line Γ-M-K-Γ through the Brillouin zone. The Data below and above \(E = 55\) meV were collected with incident neutron energy \(E_i = 100\) and 250 meV, respectively. b, c Measured \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) at 5 K along the high symmetric line Γ-M-Γ. The orange box shows the integration range along the [H,0] direction for the energy cut on the right-hand side. d Calculated \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) along the Γ-M-K-Γ direction using a Heisenberg model. e Constant-energy cuts within the (H,K) plane at energies \(E = 10 \pm 2,25 \pm 4,45 \pm 5,80 \pm 10\) meV. f Constant-energy cuts of the fitted \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) in the Heisenberg model. g Measured \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) along the [0,0,L] direction. Dashed lines are from the Heisenberg model fit. h Calculated \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) along the [0,0,L] direction. i, j Images and cuts of magnetic excitations near the antiferromagnetic (AF) zone center \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,0.5)\). In the present study, the color bars represent the vanadium standard normalized absolute magnetic excitation intensity in the units of mbarn meV−1 per formula unit, unless otherwise specified. The calculated spin wave intensity in (c,e,g) is in absolute units assuming \(S = 1\) in the SpinW+Horace program50. The error bars in h represent statistical errors of 1 standard deviation.

Full size image

To understand these observations, we start with a local moment Heisenberg Hamiltonian \(H = \mathop {\sum }\nolimits_{i \ne j} J_{ij}{{{{{{{\boldsymbol{S}}}}}}}}_i \cdot {{{{{{{\boldsymbol{S}}}}}}}}_j + \mathop {\sum }\nolimits_i A({{{{{{{\boldsymbol{S}}}}}}}}_i^x)^2\), where \(J_{ij}\) is magnetic exchange coupling of the spin \({{{{{{{\boldsymbol{S}}}}}}}}_i\) and \({{{{{{{\boldsymbol{S}}}}}}}}_j\), the exchange coupling J consists of J1 (in-plane nearest neighbor), J2 (in-plane next-nearest neighbor), and Jc (out-of-plane nearest neighbor) (Fig. 1d, e)34. The magnetic anisotropy is represented by the second term parameterized by A. Since spin waves have FM in-plane dispersion [Fig. 2a, e] and AF out-of-plane dispersion (Fig. 2g, i), we assume J1, J2 < 0 and Jc > 0. Assuming an in-plane spin easy-axis along the [3.72,1,0] (x) direction40,41, we define A ( < 0) to be the single-ion anisotropy. Figure 2d, f, h shows the outcome of our least-square fit to the spin-wave excitations of FeSn in Fig. 2a, e, g, respectively. The solid lines in Fig. 2c and in Fig. 2g are spin wave dispersions determined from the Heisenberg Hamiltonian with J1 = −20.7 ± 3.5 meV, J2 = −5.1 ± 1.3 meV, Jc = 9.5 ± 0.2 meV, A = −0.052 ± 0.002 meV, and Fe spin \(S = 1\). The experimental in-plane FM exchange couplings obtained from this fit are smaller than theoretical predictions, while the the c-axis exchange coupling is larger by a factor of two34.

To determine whether or not the magnetic excitations of FeSn can be understood within a Heisenberg Hamiltonian with \(S = 1\)34, we consider the energy dependence of the local dynamic susceptibility \(\chi ^{\prime\prime} (E)\) (Fig. 3i), obtained by integrating the imaginary part of the generalized dynamic spin susceptibility \(\chi ^{\prime\prime} ({{{{{{{\boldsymbol{Q}}}}}}}},E)\) over the first Brillouin zone (the green shaded region in Fig. 1g) at different energies42 using \(\chi ^{\prime\prime} ({{{{{{{\mathbf{Q}}}}}}}},E) = \left[ {1 - {{{{{{{\mathrm{exp}}}}}}}}\left( { - \frac{E}{{k_BT}}} \right)} \right]S({{{{{{{\boldsymbol{Q}}}}}}}},E)\), where \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) is the measured magnetic scattering in absolute units, \(E\) is the neutron energy transfer, and \(k_B\) is the Boltzmann’s constant. Since the static ordered moment per Fe is \(M \approx 1.85\;\mu _B\) at 100 K34, the total magnetic moment \(M_o\) of FeSn satisfies \(M_0^2 = M^2 + m^2 \approx 5.5\;\mu _B^2\) per Fe, where the local fluctuating moment \(m^2 \approx 2\;\mu _B^2\) is obtained by integrating \(\chi ^{\prime\prime} (E)\) at energies below 150 meV. In the local moment Heisenberg Hamiltonian with \(S = 1,\) the total moment sum rule implies that \(M_0^2 = g^2S(S + 1)\), where \(g \approx 2\)is the Lande \(g\)-factor, requiring a fluctuating moment contribution of \(g^2S = 4\;\mu _B^2\) per Fe, which is a factor of 2 larger than the measured \(m^2 \approx 2\;\mu _B^2\) per Fe. The solid and dashed lines in Fig. 3i are the calculated \(\chi ^{\prime\prime} (E)\) in absolute units assuming \(S = 1\), and 0.5, respectively. These unusual fluctuation properties suggest that electronic itineracy plays a role in the observed static ordered moment of FeSn34.

Fig. 3: Dispersionless excitations from FeSn+CYTOP-M.
figure 3

a, b Measured \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) of FeSn at 5 K along the [H,H] and [H,0] directions, respectively. Data were collected with incident neutron energy of \(E_i = 250\) meV. The dispersionless excitation is peaked at around \(E = 173\) meV with the full width at half maximum (FWHM) of 24 meV. The instrument energy resolution at \(E = 173\) meV is about 11 meV. c Energy cuts at the selected wave vectors within the first Brillouin zone. The scattering seems to decrease in intensity with increasing \({{{{{{{\boldsymbol{Q}}}}}}}}\). d, e Calculated \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) using the Heisenberg model with the same parameters as those in Fig. 2. Red dashed lines are corresponding spin wave dispersions, showing one acoustic and two optical spin waves. Vertical white dashed lines indicate the first Brillouin zone boundaries. f Constant energy cut of the calculated \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) within the (H,K) plane at \(E = 170 \pm 5\) meV from Heisenberg model. The dashed lines are the Brillouin zone boundaries of the 2D reciprocal lattice. g, h Measured \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) along the [H,H] direction with incident neutron energy of \(E_i = 300\) meV and corresponding energy cut on the right-hand side, whose \({{{{{{{\boldsymbol{Q}}}}}}}}\)-integration range over H and K directions is indicated by the red box in f. i Energy-dependent local dynamic susceptibility \(\chi ^{\prime\prime} (E)\) of FeSn, obtained by \({{{{{{{\boldsymbol{Q}}}}}}}}\)-integration of \(\chi^{\prime\prime} ({{{{{{{\boldsymbol{Q}}}}}}}},E)\) in the green box of 1 (g) and from \(1 \le L \le 2\). The blue solid and dashed lines are the calculated \(\chi^{\prime\prime} (E)\) using identical \({{{{{{{\boldsymbol{Q}}}}}}}}\)-integration from the Heisenberg model assuming \(S = 1\) and \(0.5\), respectively. The statistical errors in (i) do not include the 30% accuracy induced by the vanadium standard normalization. The horizontal and vertical error bars in (c) and (i) represent \({{{{{{{\boldsymbol{Q}}}}}}}}(E)\) integration range and statistical errors of 1 standard deviation, respectively. CYTOP-M is a trademarked fluoropolymer.

Full size image

In addition to clear spin wave excitations that disappear above ~140 meV in FeSn (Figs. 2 and 3i), we also discovered an anomalous Q-independent excitation continuum centered at E = 173 ± 1 meV with an energy width of about 24 meV. Figure 3a, b shows 2D Q-E space images measured along the in-plane [H,0] and [H,H] directions over a broader energy regime. Energy cuts at different wave vectors within the first Brillouin zone reveal similar results, indicating that the mode is indeed Q-independent (Fig. 3c). Figure 3c reveals that the intensity of the mode decreases with increasing Q. Figure 3d, e shows the 2D Q-E space images along the in-plane [H,0] and [H,H] directions, calculated using the Heisenberg Hamiltonian magnetic exchange parameters from the fit in Fig. 2. Although the energy of the expected second optical spin waves is similar to that of the flat mode, the experimental in-plane Q-dependence in Fig. 3a, b, c, g, h differs qualitatively from the theoretical Heisenberg Hamiltonian fits in Fig. 3d, e, f. For example, the optical spin waves from a Heisenberg Hamiltonian should have no magnetic scattering intensity within the first Brillouin zone (Fig. 3f), in clear contrast with the experimental data (Fig. 3g). We remark that flat spin wave flat bands can occur in kagome lattice ferromagnets with Dzyaloshinskii–Moriya (DM) interactions38, but these have an entirely different origin39.

Neutron scattering on CoSn

If the flat band observed in Fig. 3a, b arises from a flat spin-down electronic band above (or near) the Fermi level (Fig. 1b), there should not be a flat band in paramagnetic CoSn due to the absence of spin polarized flat electronic bands. Surprisingly, excitation spectra in CoSn again show a flat mode at ~170 meV (Fig. 4a), suggesting that the modes in both compounds do not have a magnetic origin. Since our FeSn and CoSn samples are glued on the aluminum plates by CYTOP-M which is an amorphous fluoropolymer but contains one hydrogen to facilitate bonding to metal surface36,43, the hydrogenated amorphous carbon films formed between sample and aluminum plates should have C–H bending and stretching vibrational modes occurring around 150–180 meV and 350–380 meV, respectively44,45. Indeed, a scan with incident neutron beam energy of 500 mV reveals the presence of a flat mode around 350–380 meV (Fig. 4b), thus confirming the nonmagnetic nature of the flat modes at 170 meV and 360 meV in FeSn and CoSn.

Fig. 4: Measurements of excitations in CoSn+CYTOP-M.
figure 4

a Measured \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) of CoSn with Ei = 300 meV at 5 K along the [H,0] direction. b Powder-averaged spectrum of CoSn with Ei = 550 meV at 5 K. c, d Comparison between low-momentum-transfer 1.7 ≤ Q ≤ 2.3 Å−1 and high-momentum-transfer 7.7 ≤ Q ≤ 8.3 Å-1 energy dependence of measured \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) for CoSn c and FeSn d, respectively. e, f Momentum dependence of \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) along the [H,0] direction at E = 70 ± 15 meV for CoSn e and FeSn f, respectively. CYTOP-M is a trademarked fluoropolymer.

Full size image

To compare the paramagnetic scattering in CoSn and spin waves in FeSn, we first determine the energy scales of the phonon scattering. The blue and red data points in Fig. 4c and d show energy dependence of the scattering at Q = 7.7–8.3 Å−1 and 1.7–2.3 Å−1, respectively. At large Q, the scattering is dominated by phonons and shows a cut off above 50 meV for both samples. Figure 4e and f compare wave vector dependence of the scattering above the phonon cut off, which reveal broad paramagnetic scattering centered around the Γ point in CoSn and clear spin waves in FeSn. These results suggest that the energy scale of the paramagnetic scattering in CoSn is comparable to spin waves of FeSn.

Neutron scattering on CYTOP-M

Although our measurements in CoSn conclusively identified the flat modes at 170 meV arises from C-H bending vibrational modes, these results cannot establish conclusively that the mode in Fig. 3a arises entirely from CYTOP-M and there is still the possibility that the 170 meV flat mode in FeSn has a magnetic component. To test these possibilities, we deposited liquid CYTOP-M on aluminum plates but without sample (~0.34 grams), and baked the assembly in an evacuated furnace at temperatures similar to how FeSn samples were prepared. The experimental outcome at 5 K reveals a clear flat mode at 170 meV, thus establishing that solidified CYTOP-M gives rise to the scattering (Fig. 5a, b). The presence of a flat mode at 360 meV in Fig. 5c confirms that the scattering at 170 meV arises from the C–H bending mode44,45. Figure 5d shows the scattering from liquid CYTOP-M at room temperature, where the 170 meV C–H bending mode in solidified CYTOP-M moves to 150 meV.

Fig. 5: Measurements of excitations in solidified/liquid CYTOP-M and clean FeSn.
figure 5

a–c Inelastic neutron scattering intensity from baked CYTOP-M on aluminum plates at 5 K with Ei = 300 a, b and 550 c meV. d Inelastic neutron scattering intensity from liquid CYTOP-M at room temperature with Ei = 300 meV. e, f Energy dependence of measured \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) of clean FeSn for momentum transfer 4 ≤ Q ≤ 7 Å-1 e and 7 ≤ Q ≤ 10 Å-1 f at 5 K. Because measurements in FeSn with (Fig. 3a, b) and without (Fig. 5e, f) CYTOP-M were normalized to absolute units, we find that the integrated intensity ratio of the 170 meV mode with and without CYTOP-M is \((18.4 \pm 0.3)/(1.3 \pm 0.2)\), thus confirming that majority of the signal at 170 meV is due to CYTOP-M (a trademarked fluoropolymer).

Full size image

Neutron scattering on clean FeSn

To further test if pure FeSn without CYTOP-M can also be contaminated by hydrocarbons, we prepared fresh single crystals of FeSn and carried out measurements at 5 K using unaligned single crystals on SEQUOIA. We again find weak and broad excitations at 170 meV and 360 meV, respectively, suggesting the presence of additional hydrocarbon contamination. By shifting the incident beam neutron away from the sample, the hydrocarbon contamination is still present with the similar intensity ratio between 170 meV and 360 meV modes (Table 1). These results suggest that the 170 meV scattering can only come from C-H bending mode and does not have a magnetic component. Our careful infrared absorption spectrum analysis on the thermal shielding suggests the presence of hydrocarbon contamination, probably silicone oil accidentally contaminating the vacuum system at SEQUOIA. Therefore, we conclude that the observed scattering at 170 meV in FeSn arises mostly from solid CYTOP-M with small additional contamination from hydrocarbons on thermal shielding.

Table 1 Comparison of the integrated intensity of the two C-H modes between FeSn sample position and shifted slits position.
Full size table

Discussion

To account for electronic itineracy, we calculate the electronic structure of FeSn in the paramagnetic and AF ordered states using a combination of DFT and dynamical mean field theory (DFT+DMFT)46. In the paramagnetic state, the mass enhancements of the Fe 3d electrons near the Fermi level are about 1.8 for the \(d_{z^2}\)orbital, 2.4 for \(d_{x^2 - y^2}\) and \(d_{xy}\) orbitals, and around 4 for the \(d_{xz}\) and \(d_{yz}\) orbitals [Fig. 6a]. Since these values are similar to the values in iron arsenide superconductors, we conclude that FeSn is a Hund’s metal47 with intermediate strength correlations. Figure 6b shows the DFT+DMFT electronic structures, with the dominant Fe d orbitals highlighted, in the paramagnetic state. To calculate the spin polarized magnetically ordered state, we assume FM exchange couplings along both the in-plane and c-axis directions because of the small c-axis AF exchange coupling [Fig. 2f] and the simplicity of the electronic band structure in a ferromagnet. We find that the mass enhancements of the Fe 3d electrons near the Fermi level are reduced substantially to around 1.5 for all Fe 3d orbitals in the minority spin channel, about 1.7 for the \(d_{z^2}\) and \(d_{xy}\) orbitals, and 2.4 for the \(d_{x^2 - y^2}\), \(d_{xz}\) and \(d_{yz}\) orbitals in the majority spin channel. Figure 6c, d respectively show the calculated spin-up and spin-down electronic structure of FeSn in the FM ordered state. In addition to confirming the spin-up flat electronic band around 230 meV below the Fermi level seen in ARPES experiments25, we obtain a flat minority spin electronic band around 170 meV above the Fermi level.

Fig. 6: Electronic structures of FeSn from the DFT + DMFT calculations.
figure 6

a Wave functions of the Fe five d orbitals. b–d Orbital-resolved band structures of FeSn in the paramagnetic, spin up, and spin down magnetically ordered state, respectively. Green color is the contribution from the \(d_{xz}\) and \(d_{yz}\) orbitals. Red, blue, and black colors represent \(d_{x^2 - y^2}\), \(d_{xy}\), and \(d_{z^2}\) orbitals, respectively.

Full size image

Based on ARPES measurement and DMFT calculation, we would expect the presence of a flat band Stoner continuum arising from quasiparticle excitations between the spin-up majority and spin-down minority electrons. Our failure to observe such a mode means that such a mode, if present, must be much weaker than spin waves in FeSn. From our absolute intensity measurements of spin waves in FeSn, we find that a local moment Heisenberg model with S = 1 cannot account for the integrated spin wave intensity, suggesting the important role played by itinerant electrons in these materials.

Although CYTOP-M has been used by neutron scattering community as a glue to mount small samples for over 20 years, its characteristics at high energies have not been reported36. This is mostly because the difficulty in carrying inelastic neutron scattering at energies above 100 meV in traditional reactor sources. The development of neutron time-of-flight technology allows measurements at energies well above 200 meV. We have checked again high-energy spin waves of iron pnictide discussed in previous work37,42, and found that for samples glued with CYTOP-M, there is a weak Q dependence at 170 meV. Fortunately, since magnetic scattering from iron pnictide samples is much stronger and centered around a specific Q, the conclusions of these work are not affected. In any case, our identification of the flat C-H bending and stretching vibrational modes should help future neutron scatterers to separate these scattering from genuine magnetic signal, particularly in situations where weak and broad magnetic scattering is expected.

Methods

Sample synthesis, structural and composition characterizations

Single crystals of FeSn and CoSn were grown by the self-flux method. The high-purity Fe (Co) and Sn were put into corundum crucibles and sealed into quartz tubes with a ratio of Fe (Co): Sn = 2: 98. The tube was heated to 1273 K and held there for 12 h, then cooled to 823 K (873 K) at a rate of 3 (2) K/h. The flux was removed by centrifugation. And shiny crystals with typical size about 2 × 2 × 5 mm3 can be obtained. The single crystal X-ray diffraction (XRD) pattern of FeSn was performed using a Bruker D8 X-ray diffractometer with Cu Kα radiation (λ = 0.15418 nm) at room temperature (Fig. S1).

The elemental analysis was performed using energy-dispersive X-ray (EDX) spectroscopy analysis in a FEI Nano 450 scanning electron microscope (SEM). In order to determine composition of FeSn accurately, we carefully polished FeSn surface using sandpaper and carried out EDX measurements on five FeSn crystals (Fig. S2). The average stoichiometry of each crystal was determined by examination of multiple points (5 positions). As shown in Table S1, the atomic ratio of Fe:Sn is close to 1:1.

To further determine the crystalline quality and stoichiometry of the samples used in neutron scattering experiments, we took X-ray single-crystal diffraction experiments on two pieces of these samples at the Rigaku XtaLAB PRO diffractometer housed at Spallation Neutron Source at Oak Ridge National Laboratory (ORNL). The measured crystals were carefully suspended in Paratone oil and mounted on a plastic loop attached to a copper pin/goniometer (Fig. S3). The single-crystal X-ray diffraction data were collected with molybdenum Kα radiation (λ = 0.71073 Å). More than 2800 diffraction Bragg peaks were collected and refined using Rietveld analysis (Table S2). We find no evidence of superlattice peaks indicating possible Fe vacancy order (Fig. S3). The refinement results indicate less than 1.5% possible Fe vacancy (Fig. S4), suggesting that the single crystals are essentially fully stoichiometric.

To determine whether the AF phase transition in our sample is consistent with earlier work34, we carried out temperature and field dependence of the magnetization measurement. Figure S5 reveals an AF phase transition around 377 K under a magnetic field of 0.5 and 14 T (Figs. S5a and b). Magnetic field dependences of the magnetization for both field directions at various temperatures (Fig. S5c and d) are also in agreement with earlier work34.

Neutron scattering experiments

INS measurements on FeSn were carried out using the MAPS time-of-flight chopper spectrometer at the ISIS Neutron and Muon Source, Rutherford Appleton Laboratory, UK48. INS measurements on CoSn and FeSn are also performed using the SEQUOIA spectrometer at Spallation Neutron Source, Oak Ridge National Laboratory49. Fifty pieces of single crystals of FeSn with the total mass of 0.97 g were co-aligned on one single piece of aluminum plate and mounted inside a He displex. Figure S6 shows that the mosaic of aligned single crystals is about 6 degrees. The crystal structure of FeSn is hexagonal with space group P6/mmm with lattice parameters \(a = b = 5.529{\AA}\), and \(c = 4.4481{\AA}\)34. The lattice parameters of CoSn are \(a = b = 5.528{\AA}\), and \(c = 4.26{\AA}\)35. We define the momentum transfer Q in 3D reciprocal space in \({\AA}^{ - 1}\) as \({{{{{{{\boldsymbol{Q}}}}}}}} = H{{{{{{{\boldsymbol{a}}}}}}}}^\ast + K{{{{{{{\boldsymbol{b}}}}}}}}^\ast + L{{{{{{{\boldsymbol{c}}}}}}}}^\ast\), where H, K, and L are Miller indices and \({{{{{{{\boldsymbol{a}}}}}}}}^\ast = 2\pi ({{{{{{{\boldsymbol{b}}}}}}}} \times {{{{{{{\boldsymbol{c}}}}}}}})/[{{{{{{{\boldsymbol{a}}}}}}}} \cdot \left( {{{{{{{{\boldsymbol{b}}}}}}}} \times {{{{{{{\boldsymbol{c}}}}}}}}} \right)]\), \({{{{{{{\boldsymbol{b}}}}}}}}^\ast = 2\pi ({{{{{{{\boldsymbol{c}}}}}}}} \times {{{{{{{\boldsymbol{a}}}}}}}})/[{{{{{{{\boldsymbol{a}}}}}}}} \cdot \left( {{{{{{{{\boldsymbol{b}}}}}}}} \times {{{{{{{\boldsymbol{c}}}}}}}}} \right)]\), \({{{{{{{\boldsymbol{c}}}}}}}}^\ast = 2\pi ({{{{{{{\boldsymbol{a}}}}}}}} \times {{{{{{{\boldsymbol{b}}}}}}}})/[{{{{{{{\boldsymbol{a}}}}}}}} \cdot \left( {{{{{{{{\boldsymbol{b}}}}}}}} \times {{{{{{{\boldsymbol{c}}}}}}}}} \right)]\) with \({{{{{{{\boldsymbol{a}}}}}}}} = a{{{\hat{\boldsymbol x}}}}\), \({{{{{{{\boldsymbol{b}}}}}}}} = a(\cos 120\;{{{\hat{\boldsymbol x}}}} + \sin 120\;{{{\hat{\boldsymbol y}}}})\), \({{{{{{{\boldsymbol{c}}}}}}}} = c{{{\hat{\boldsymbol z}}}}\) (Fig. 1d, e). The horizontal scattering plane is [H,0,L] and INS data were collected with incident neutron energies set to \(E_i = 300,250,150,100,30,\) and 15 meV in Horace mode and the temperature is set at 5 K. The neutron scattering data is normalized to absolute units using a vanadium standard, which has an accuracy of approximately 30%42.

Heisenberg model fitting to spin waves of FeSn

We use the Heisenberg model and least-square method to fit spin waves of FeSn (Figs. S7-S9). The software package used was SpinW and Horace50. The Heisenberg Hamiltonian is \(H = \mathop {\sum }\nolimits_{i \ne j} J_{ij}{{{{{{{\boldsymbol{S}}}}}}}}_i \cdot {{{{{{{\boldsymbol{S}}}}}}}}_j + \mathop {\sum }\nolimits_i A({{{{{{{\boldsymbol{S}}}}}}}}_i^x)^2\) as discussed in the main text. Note in our Heisenberg Hamiltonian fit to spin wave data, we only used dispersion relations from experiments, and assumed \(S = 1\), which is close to the 1.86 \(\mu _B\) per Fe ordered moment34. The overall intensity from SpinW fit, when considered in absolute units, is considerably higher than the experiment (Fig. 2h). This suggests that Heisenberg Hamiltonian overestimates the spin wave intensity contribution from the ordered moment. We first determine the interlayer coupling Jc. Using linear spin wave theory, we find that the spin-wave band top along the c axis direction to have energy \(E_{Ltop} = 2|J_c|\) when anisotropy A is not too large. A constant-Q cut at the zone boundary wave vector \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,1.75)\) shows ELtop = 19.0 ± 0.3 meV (Fig. 2f), therefore yielding Jc = 9.5 ± 0.2 meV.

To estimate A, we note that the spin gap of \({\Delta}_a \approx 2\) meV at the AF wave vector \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,0.5)\) (Fig. 2h). Several types of anisotropy are considered as shown in Fig. S7, and we choose the dipole-like anisotropy because it is the only one that can create a gap in the neutron spectrum. Assuming Jc = 9.5 meV, we find \({\Delta}_a = 8.761\sqrt {\left| A \right|}\). The calculated anisotropic parameter is A = 0.052 ± 0.002 meV. The presence of A will cause the ELtop to shift by 0.1 meV, and therefore can be safely ignored in fits of the in-plane magnetic exchange couplings.

To fit the in-plane exchanges J1 and J2, we use constant-E cuts along the [H,0] and [H,H] directions made for spin wave energies of 15–80 meV. Gaussian fits are used to extract the spin-wave peak position. We iterate over [J1, J2], calculate every dispersion, and calculate the square error between calculation and experiment of each [J1, J2] configuration (Fig. S7). To narrow down the range of J1 and J2, we fit part of the optical spin wave modes at the M point (Fig. S8). A constant-Q cut integrating between [H, H] = (−0.1, 0.1), [H, 0] = [0.4, 0.6], and L = [−1, 3] is used as fitting data (Fig. 2c, e, g). Least-square error mode is used to get the best fit, giving J1 = −20.7 ± 3.5 meV and J2 = −5.1 ± 1.3 meV, which concludes the Heisenberg model fitting of the data.

Note that the error bars of these parameters are estimated as follows: First, calculate the least square error using best-fit parameter J0 and denote it as R0; then determine the parameter J0’ when the square error values give 2R0, and the error bar is given by ΔJ = |J0’ - J0|. This error range gives 68% confidence interval, meaning that if the residual of the fit has a Gaussian distribution, the calculation generated by range [J0 - ΔJ, J0 + ΔJ] can cover 68% (i.e., 1σ in Gaussian distribution) of the data points.

DFT+DMFT calculations

The electronic structures and spin dynamics of FeSn in the paramagnetic and magnetically ordered states are computed using DFT+DMFT method46. The density functional theory part is based on the full-potential linear augmented plane wave method implemented in Wien2K51. The Perdew–Burke–Ernzerhof generalized gradient approximation is used for the exchange correlation functional52. DFT+DMFT was implemented on top of Wien2K and was described in detail before53. In the DFT+DMFT calculations, the electronic charge was computed self-consistently on DFT+DMFT density matrix. The quantum impurity problem was solved by the continuous time quantum Monte Carlo (CTQMC) method54,55 with a Hubbard U = 4.0 eV and Hund’s rule coupling J = 0.7 eV in both the paramagnetic state and the magnetically ordered state. Bethe-Salpeter equation is used to compute the dynamic spin susceptibility where the bare susceptibility is computed using the converged DFT+DMFT Green’s function while the two-particle vertex is directly sampled using CTQMC method after achieving full self-consistency of DFT+DMFT density matrix56. For the magnetically ordered state, the averaged Green’s function of the spin up and spin down channels is used to compute the bare susceptibility. In the paramagnetic state, an electronic flat band of dominating \(d_{xz}\) and \(d_{yz}\) orbital characters locates a few meV above the Fermi level (Fig. 6b). In the magnetic state, the spin exchange interaction leads to about 400 meV splitting of this electronic flat band where the spin-up flat band is pushed down to about −230 meV (Fig. 6c) whereas the spin-down flat band is pushed up to ~170 meV (Fig. 6d). The experimental crystal structure (space group P6/mmm, No. 191) of FeSn with lattice constants \(a = b = 5.297{\AA}\) and \(c = 4.481{\AA}\) is used in the calculations. Figure S10 shows orbital-resolved band structures of FeSn in the paramagnetic, spin up, and spin down magnetically ordered state. We also note that the possible ~1.2% iron deficiency in FeSn obtained from X-ray refinement (Table S2) is not expected to modify the band structure.

The infrared absorption measurements

To determine if the thermal heat shielding of SEQUOIA experiments has organic coating, we cut a small piece of the shielding right after the experiment and carried out the infrared absorption spectrum measurement. The spectrum in Fig. S11 shows clear evidence of an organic coating on the foil exposed to the contaminant. The modes at 1072, 1038, and 960 cm−1 in the fingerprint region of the spectrum point unambiguously at Si–O–Si stretches (siloxane groups). The strong peak at 1128 cm−1 can also be assigned to Si--R (R = aryl) stretches. The very strong, sharp mode at 1240 cm−1 is characteristic of a symmetric deformation mode of CH3 in Si–CH3 bonds. The expected frequency range is 1240–1290 cm−1. Electropositive metals attached to Si tend to move this peak to higher frequencies, whereas for siloxanes, the band occurs at the lower end. The mode at 1462 cm−1 is either a scissoring -CH2 mode or, more likely, the asymmetric deformation mode of -CH3. The presence of C–H bonds is confirmed by the existence of a strong absorption band with three clear, relatively sharp modes just below 3000 cm−1 (symmetric and antisymmetric C-H stretches). This information points at the contaminant being a polysiloxane material, probably a silicone oil accidentally contaminating the vacuum system at SEQUOIA. The origin of this contaminant is uncertain: lubricant or electrical insulating material around power or signal cables. The very intense mode at 1728 cm−1 is undoubtedly a carbonyl stretching mode. It may be part of a pendant group on the polysiloxane backbone (e.g., a carbinol group used to modify the hydrophobic/hydrophilic of the oil). No further attempt was made at solving the precise molecular structure of the polymeric material.