Resistivity saturation in Kondo insulators

Abstract

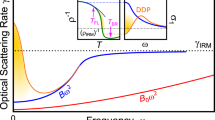
Resistivities of heavy-fermion insulators typically saturate below a characteristic temperature T*. For some, metallic surface states, potentially from a non-trivial bulk topology, are a likely source of residual conduction. Here, we establish an alternative mechanism: at low temperature, in addition to the charge gap, the scattering rate turns into a relevant energy scale, invalidating the semi-classical Boltzmann picture. Then, finite lifetimes of intrinsic carriers drive residual conduction, impose the existence of a crossover T*, and control—now on par with the gap—the quantum regime emerging below it. Assisted by realistic many-body simulations, we showcase the mechanism for the Kondo insulator Ce₃Bi₄Pt₃, for which residual conduction is a bulk property, and elucidate how its saturation regime evolves under external pressure and varying disorder. Deriving a phenomenological formula for the quantum regime, we also unriddle the ill-understood bulk conductivity of SmB₆—demonstrating a wide applicability of our mechanism in correlated narrow-gap semiconductors.

Introduction

In Kondo insulators¹ the formation of bound-states between quasi-localized f-states and conduction electrons leads to the opening of a narrow hybridization gap at the Fermi level. When this hybridization is coherent, the resistivity exhibits an activation-type behavior. This semiconductor-like regime has as upper bound the Kondo lattice temperature, above which the local f-moments break free, inducing an insulator-to-metal crossover. This Kondo effect has been exhaustively studied over the last decades^2,3,4. A more recent focus is the experimental observation of a lower bound to the semiconductor comportment, see Fig. 1 for the example of Ce₃Bi₄Pt₃^5,6,7: below an inflection temperature T* the resistivity levels off from exponential rise and enters a saturation regime—indicative of residual conduction. Possible explanations include exhaustion regimes (where extrinsic impurities pin the chemical potential), off-stoichiometry and impurity-band conduction^8,9, as well as, metallic surface states short-circuiting the gapped bulk. The latter can be an inevitable consequence of the non-trivial insulating bulk found in topological Kondo insulators¹⁰.

Fig. 1: Resistivity saturation in Ce₃Bi₄Pt₃.

Below an inflection temperature T* (indicated by small arrows), experimental resistivities ρ(T)^5,6,7 deviate from activation-like behavior (T > T*) and enter a regime of resistivity saturation (T < T*). Pressure and disorder affect the resistivity differently: under pressure (black and shades of red; from Cooley et al.⁵) the crossover temperature T* (labeled with colored triangles and reported in the inset) grows significantly and the saturation value ρ(T → 0) decreases. Radiation-induced disorder (black and blue to green; from Wakeham et al.⁶) only suppresses ρ(T → 0), while T* (labeled with colored circles and reported in the inset) remains constant. Also shown are results at ambient pressure from Katoh et al.⁵⁷ (dashed black line). Differences between black curves (solid and dashed) demonstrate a strong sample dependence. Inset: dependence of T* on pressure (upper x axis; red-shaded triangles⁵, gray diamonds from Campbell et al.⁷) and disorder (measured in displacements per atom (DPA); lower x axis; blue to green open circles⁶).

Here, we develop an alternative mechanism in which residual conduction derives from finite lifetimes of intrinsic carriers of the (3D) bulk. We show that realistic many-body simulations, supplemented by a simple treatment for the disorder, capture the puzzling resistivity in the (non-topological) Kondo insulator Ce₃Bi₄Pt₃. We then distill essential ingredients from a reductionist model, establish a microscopic understanding, and provide a phenomenological form of the resistivity with which experiments can be readily analyzed. Our theory is applicable to other correlated narrow-gap semiconductors⁴: for mixed-valence SmB₆, we demonstrate that surface conduction coexists with our mechanism for a residual bulk conductivity—providing a definitive interpretation of recent experiments¹¹.

Results

The Kondo insulator Ce₃Bi₄Pt₃

Cubic intermetallic Ce₃Bi₄Pt₃ is a prototypical Kondo insulator^2,4,12: spectroscopic^13,14 and susceptibility¹² measurements (also in high magnetic field^15,16) are consistent with the Kondo scenario^17,18. While a topological bulk state has been envisaged¹⁹, experiments argue against surface-dominated transport⁶. Further constraints for a theory of resistivity saturation in Ce₃Bi₄Pt₃ come from, see Fig. 1: (i) pressure-dependent measurements that show a substantial increase in the crossover temperature T*, accompanied by a decrease of the saturation value ρ(T → 0)^5,7; (ii) radiation-damaged samples in which residual conduction is successively suppressed, while T* is unaffected⁶. In the following, we develop a microscopic theory encompassing these diverse experimental findings.

Many-body simulations vs. experiment

Using realistic many-body techniques, we simulate the bulk response of Ce₃Bi₄Pt₃ under pressure. In addition to renormalizations from electronic correlations—effective masses m* and scattering rates Γ(T)—we mimic the effect of disorder²⁰ with an added scattering term Γ_imp. The resulting resistivities ρ(T) are shown in Fig. 2 for varying (a) disorder and (b) pressure P. In all cases, we identify an inflection point T* below which a saturation regime emerges: at ambient pressure, see Fig. 2a, a growing disorder (Γ_imp) causes T* to only marginally increase. The saturation value ρ(T → 0), however, is notably suppressed as lifetimes shorten—congruent with experiments (Fig. 1). Applying pressure, see Fig. 2b, boosts T* significantly, until it saturates between 20 and 30 GPa. The extracted T*, reported in Fig. 3a, is in qualitative agreement with the experiment (Fig. 1 inset). Also, the saturation limit ρ(T → 0) depends strongly on pressure. In experiments, the trend in ρ(T → 0) varies, however, significantly between samples⁵ and setups^5,7. We, therefore, follow Campbell et al.⁷ and reduce systematic errors by plotting in Fig. 3b the ratio ρ_base/ρ_RT of the simulated resistivity at the lowest (base) temperature (T = 1 K) and at room temperature (RT: T = 290 K). In agreement with an experimental ratio at similar temperatures⁷, we see an increase from P = 0 up to P ~ 3–5 GPa—the system becomes more insulating. For higher pressures, however, the ratio decreases again—mirroring the pressure-driven crossover to a bad insulator (cf. ρ(T) in Fig. 2b). The simulations thus contain the necessary ingredients to account for the observed resistivity saturation in Ce₃Bi₄Pt₃, including its dependence on disorder and pressure. Next, we characterize the saturation regime in more detail and elucidate its origin using a microscopic model.

Fig. 2: Simulated resistivity of Ce₃Bi₄Pt₃.

Shown are results for the resistivity ρ(T) a at ambient pressure (P = 0) for varying impurity scattering Γ_imp (shades blue to green) and b at different pressures P (shades of red) for fixed impurity scattering Γ_imp = 5 meV. Filled circles in ρ(T) indicate simulation temperatures; results shown by open circles have been obtained by extrapolating the many-body scattering rate Γ(T) with a quadratic fit. Vertical arrows indicate inflection points T* in ρ(T). The simulations mirror the experimental trends: T* varies significantly with pressure, but depends only weakly on disorder. While transport simulations include the full self-energy Σ(ω), it is instructive to quantify electron-electron scattering: we display the square root of ${{\Gamma }}=-{\left\langle {{{{{{{\rm{Im}}}}}}}}{{\Sigma }}(\omega = 0)\right\rangle }_{J = 5/2}$, the simulated many-body scattering rate at the Fermi level (averaged over Ce-4fJ = 5/2 components); black and red-shaded lines are linear fits to Γ^1/2 of simulated points, suggesting that for all pressures: Γ = γT²; γ decreases notably under compression, indicative of weakening correlation effects. Horizontal lines (shades of blue and green in a; dotted line in b) indicate the additional impurity-scattering rate Γ_imp. The total rate is the sum: Γ_total = Γ + Γ_imp.

Fig. 3: Crossover temperature T* and resistivity ratio.

a Inflection temperatures T* as a function of pressure for different impurity scatterings Γ_imp (lines shaded blue to green). At low pressures, T* slightly depends on Γ_imp; above P = 5GPa, the onset of saturation is insensitive to the magnitude of impurity scattering. b Ratio of the resistivity at base temperature, ρ_base, and at room temperature (RT), ρ_RT, for different impurity scatterings Γ_imp (lines shaded blue to green), compared to experiment (circles; from ref. ⁷). In the simulation (experiment⁷) the base and room temperatures were 1 and 290 K (2 and 300 K), respectively. The overall trend of the resistivity ratio with pressure is independent of the strength of impurity scattering. We find the best quantitative agreement with the experiment for Γ_imp ~ 7.5meV.

Microscopic theory

We consider a half-filled two-band (n = 1, 2) model with hopping t on the cubic lattice separated by a non-interacting gap Δ₀: ${\epsilon }_{{{{{{{{\bf{k}}}}}}}}n}^{0}={(-1)}^{n}[2t{\sum }_{i = 1,3}\cos ({k}_{i})+(6t+{{{\Delta }}}_{0}/2)]$. We endow these dispersions with (i) a constant lifetime τ = ℏ/(2Γ₀) and (ii) a quasi-particle weight or mass enhancement Z = m/m* ≤ 1. The latter renormalizes the dispersion, ${\epsilon }_{{{{{{{{\bf{k}}}}}}}}n}=Z{\epsilon }_{{{{{{{{\bf{k}}}}}}}}n}^{0}$, yields the interacting gap Δ = ZΔ₀, and dresses the scattering rate Γ = ZΓ₀. In the absence of particle-hole interactions, we can compute the linear-response conductivity of the model exactly (see “Method” section):

$$\sigma (T)=\frac{2\pi {e}^{2}\hslash }{V}\frac{{Z}^{2}}{4{\pi }^{3}}\frac{\beta }{{{\Gamma }}}\mathop{\sum}\limits_{{{{{{{{\bf{k}}}}}}}}n}{v}_{{{{{{{{\bf{k}}}}}}}}n}^{2}\left({{{{{{{\rm{Re}}}}}}}}{{{\Psi }}}^{\prime}(z)-\frac{\beta {{\Gamma }}}{2\pi }{{{{{{{\rm{Re}}}}}}}}{{{\Psi }}}^{^{\prime\prime} }(z)\right)$$

(1)

with the inverse temperature $\beta ={({k}_{{{{{{\mathrm{B}}}}}}}T)}^{-1}$, the unit-cell volume V, (derivatives of) the digamma function Ψ(z) evaluated at $z=\frac{1}{2}+\frac{\beta }{2\pi }\left({{\Gamma }}+i{\epsilon }_{{{{{{{{\bf{k}}}}}}}}n}\right)$, and the Fermi velocities ${v}_{{{{{{{{\bf{k}}}}}}}}n}=1/\hslash \partial {\epsilon }_{{{{{{{{\bf{k}}}}}}}}n}^{0}/\partial {{{{{{{\bf{k}}}}}}}}$ in the Peierls approximation. The above formula is rich in physics: in the coherent limit Γ → 0, Eq. (1) simplifies to the well-known Boltzmann expression in the constant relaxation-time approximation²¹

$$\sigma (T)\mathop{=}\limits^{{{\Gamma }}\to 0}\frac{{e}^{2}\hslash }{V}\frac{{Z}^{2}}{{{\Gamma }}}\mathop{\sum}\limits_{{{{{{{{\bf{k}}}}}}}}n}{v}_{{{{{{{{\bf{k}}}}}}}}n}^{2}{\left(-\partial f/\partial \omega \right)}_{\omega = {\epsilon }_{{{{{{{{\bf{k}}}}}}}}n}},$$

(2)

with the Fermi function f—albeit with a renormalization Z² commonly not included. In this semi-classical regime, the conductivity is simply proportional to the lifetime τ = ℏ/(2Γ). Then, for k_BT ≪ Δ, the resistivity has an activated form $\rho (T)\propto \exp ({{\Delta }}/(2{k}_{B}T))$ that diverges for T → 0. In fact, here, Δ is the only relevant energy scale: as epitomized by Arrhenius-plot analyses, Δ single-handedly accounts for the archetypal ρ(T) of semiconductors in the Boltzmann regime. There, resistance can be approximately described through electrons with sharply defined one-particle states (a band-structure ϵ_kn) that undergo collisions at a rate Γ, causing the charge current to decay on a timescale ℏ/(2Γ). For sizable Γ, however, the broadening of the one-particle spectrum itself can no longer be neglected (Supplementary Note 1), spilling incoherent weight into the gap that contributes to conduction. This phenomenon is clearly beyond thermal activation across the gap. Still, Eq. (1) can be seen to retain an effective one-particle description (sharply defined dispersions), with many-body (lifetime) effects accounted for by a modified (Ψ-based) fermionic distribution function. To characterize the transport signatures of Γ > 0, we compute the resistivity ρ(T) = 1/σ(T) according to Eq. (1), see Fig. 4. Akin to Ce₃Bi₄Pt₃, we see the emergence of a crossover temperature T* below which ρ(T) tends towards saturation. Since this phenomenon defies the semi-classical (Boltzmann) picture, we will label its domain the quantum regime. In conventional semiconductors, deviations from activated behavior typically occur when an extrinsic in-gap density pins the chemical potential. In the current scenario, impurity states influence conduction merely by limiting the lifetime of intrinsic carriers. Importantly, already minute scattering rates (mediated by impurities or other defects or couplings) lead to strong signatures at observable temperatures: in Fig. 4b, c, we indicate, respectively, the saturation limit ρ(T → 0) and the characteristic temperature T* for the resistivities of the panel (a). In the relevant Γ ≪ Δ regime, T* changes more rapidly with Δ, whereas ρ(T → 0) is more sensitive to changes in Γ—as observed in experiments and simulations for Ce₃Bi₄Pt₃ (see above).

Fig. 4: Prototypical resistivity in correlated narrow-gap semiconductors.

For a minimal two-band model, the figure shows: a The resistivity (lines) as a function of temperature for different gaps Δ and scattering rates Γ (both measured in eV). Closed symbols indicate the saturation limit ρ(T → 0); open symbols mark the inflection point T*—the lower (upper) bound of the semi-classical (quantum) regime. The semi-classical Boltzmann conductivity, Eq. (2), is shown as a dashed black line. b The saturation limit ρ(T → 0) (colored map; on a log-scale) as a function of Δ and Γ; black lines are iso-curves for indicated values; colored symbols mark the choices of Δ and Γ from a. c Crossover temperature T* of the quantum regime. The data shows that T* (ρ(T → 0)) is dominantly controlled by Δ (Γ). Calculated for a three-dimensional half-filled two-band model with bare dispersions ${\epsilon }_{{{{{{{{\bf{k}}}}}}}}n}^{0}={(-1)}^{n}[2t{\sum }_{i = 1,3}\cos ({k}_{i})+(6t+{{{\Delta }}}_{0}/2)]$ (n = 1, 2), with hopping t = 0.25 eV, a quasi-particle weight Z = 1, and a lattice constant a = 1 Å.

We can give more precise analytical insight: at low temperatures, the minimum (maximum) of conduction (valence) states dominates transport. For this leading contribution to Eq. (1), we neglect band-dispersions and consider two levels (2L) ϵ_n = (−1)ⁿΔ/2 (n = 1, 2) separated by a gap Δ. Then, with z = 1/2 + β/(2π)(Γ + iΔ/2),

$${\sigma }_{2{{{{{\rm{L}}}}}}}(T)\propto \frac{\beta }{{{\Gamma }}}\left[{{{{{{{\rm{Re}}}}}}}}{{{\Psi }}}^{\prime}(z)-\frac{\beta {{\Gamma }}}{2\pi }{{{{{{{\rm{Re}}}}}}}}{{{\Psi }}}^{^{\prime\prime} }(z)\right].$$

(3)

This phenomenological quantum conductivity depends on two energy scales: Δ and Γ, and is very useful for analyzing experimental data, as shown below. A low-temperature expansion of Eq. (3) to second-order yields

$${\sigma }_{2{{{{{\rm{L}}}}}}}(T)\propto \frac{{{{\Gamma }}}^{2}}{{({{{\Delta }}}^{2}+4{{{\Gamma }}}^{2})}^{2}}\left(1+\frac{8{\pi }^{2}}{3}\frac{5{{{\Delta }}}^{2}-4{{{\Gamma }}}^{2}}{{({{{\Delta }}}^{2}+4{{{\Gamma }}}^{2})}^{2}}\ {({k}_{{{{{{\mathrm{B}}}}}}}T)}^{2}\right)$$

(4)

resulting—for finite Γ—in the residual conductivity

$${\sigma }_{2{{{{{\rm{L}}}}}}}(T=0)\propto \frac{{{{\Gamma }}}^{2}}{{({{{\Delta }}}^{2}+4{{{\Gamma }}}^{2})}^{2}}.$$

(5)

Unlike conduction by surface states in topological insulators, the quantum-regime conductivity depends on the bulk values Δ and Γ. Therefore, as a paramount distinction, residual conduction can be manipulated by pressure, while topological surface conduction is oblivious to it²². A direct consequence of Eq. (5) is the existence of a temperature T* below which ρ(T) must depart from Boltzmann behavior. Using Eq. (4), we can crudely estimate the dependencies of T* via ∂²ρ(T)/∂T² = 0 (Supplementary Fig. S1):

$${k}_{{{{{{\mathrm{B}}}}}}}{T}^{* }=\frac{1}{\sqrt{10}\pi }\left(\frac{{{\Delta }}}{2}+\frac{11}{5}\frac{{{{\Gamma }}}^{2}}{{{\Delta }}}+{{{{{{{\mathcal{O}}}}}}}}({{{\Gamma }}}^{4})\right)$$

(6)

For Γ ≪ Δ, T* is essentially controlled by Δ—consistent with our numerical results and available experiments.

The take-away message is this: If Γ/Δ is not vanishingly small, the lifetime of intrinsic charge carriers manifests as a relevant energy scale. It introduces a coherence temperature T*, delimits the applicability of Boltzmann theory from below, and leads to an algebraic saturation regime with residual conduction.

The quantum regime in experiments

Returning to Ce₃Bi₄Pt₃, we anatomize the experimental conductivity vis-à-vis the characteristic temperature profile of the quantum regime established above. With the phenomenological conductivity, Eq. (3), we fit in Fig. 5 the data of (a) Cooley et al.⁵ and (b) Wakeham et al.⁶ and find near-perfect agreement: our Ansatz accurately reproduces the experimental temperature dependence for varying pressure and disorder.

Fig. 5: Analysis of the quantum regime in Ce₃Bi₄Pt₃.

We fit the conductivity σ(T) = 1/ρ(T) from a Cooley et al.⁵ (colored lines correspond to pressures indicated in the inset) and b Wakeham et al.⁶ (colored lines indicate the degree of disorder quantified in displacements per atom (DPA)) with the phenomenological quantum conductivity Eq. (3) (dashed lines). The agreement is excellent: from a finite residual value for T → 0, the conductivity grows algebraically (see the quantum regime formula: Eq. (4)) up to the crossover temperature T* (circles). Above, higher powers in T become relevant as σ(T) enters the exponential (semi-classical) regime. For pressures P > 4 GPa and very low T, the experimental conductivity deviates from the quantum regime and instead matches 3D variable-range hopping (VRH) characteristics, $\propto \exp [{(T/{T}_{0})}^{1/4}]$⁵. The fit parameters Δ and Γ are given in the insets.

We analyze trends in the fit parameters: as shown in the inset of Fig. 5a, we extract a gap Δ ~ 7.5meV at P = 0, which is largely enhanced for P > 0; also Γ increases with P. We extract smaller Γs and Δs for Wakeham et al.’s sample, see inset of Fig. 5b, owing to the overall smaller conductivity. Consistent with the degree of radiation damage, Γ increases with growing displacements per atom (DPA). The extracted Δ is congruent with activation-law fits above T*⁶ and increases only marginally under radiation. Note in Fig. 5a, for pressures P > 4GPa and very low temperatures, deviations from the quantum regime occur. There, as shown in ref. ⁵, σ(T) matches 3D variable-range hopping (VRH) characteristics, $\propto \exp [{(T/{T}_{0})}^{1/4}]$.

In Fig. 6, we perform a similar analysis for the bulk conductivity of the mixed-valence insulator SmB₆¹¹, finding again excellent agreement. These results will be reviewed in the “Discussion” section.

Fig. 6: Bulk conductivity of SmB₆.

Low-T transport in SmB₆ is dominated by surface contributions^11,38,39,40. With an inverted resistance setup, Eo et al.¹¹ eliminated the latter and extracted the bulk conductivity, reproduced here for two samples, in order of growing off-stoichiometry: S3, S4. Crucially, bulk conduction still saturates below T* (inflection points in ρ(T), circles). We fit the experiment using the phenomenological quantum conductivity Eq. (3). The excellent agreement suggests that the bulk resistivity in SmB₆ is lifetime-limited. Gaps Δ are fixed to indicated values obtained in ref. ¹¹ from activation laws, $\exp ({{\Delta }}/(2{k}_{{{{{{\mathrm{B}}}}}}}T))$, above 3 K. We extract a scattering rate Γ that increases by more than two-fold for an off-stoichiometry that almost doubles from S3 to S4¹¹. For cleaner samples S1 and S2, experimental noise is large and T* moves outside the measured temperature window, see Supplementary Fig. S3. From all samples combined, we extract: T* ∝ Γ^1/8.

Intermezzo: Ce₃Bi₄Pt₃ at high pressures

Next, we briefly turn to Ce₃Bi₄Pt₃ at high pressures, where Campbell et al.⁷ found an insulator-to-metal crossover, cf. Fig. 3b. Indeed pressure-induced metallic phases are rather common for correlated semiconductors, e.g., for SmB₆^23,24, CeRhSb²⁵, and FeSi²⁶. We consider three candidate mechanisms: changes in (1) correlation effects, (2) the valence, (3) structural aspects. (1) Our many-body calculations reveal that pressure reduces electronic correlations: effective masses shrink from m*/m ~ 10 at P = 0 (see also ref. ¹⁸) to a mere ~ 2 at P = 40 GPa. Also, electron–electron scattering becomes less prevalent: the rate Γ is—for all pressures—of the form γT² (Fig. 2), with γ significantly decreasing with pressure. Reduced many-body renormalizations amplify the pressure enhancement of the non-interacting hybridization (see point (3), below), leading to larger gaps. In the absence of other factors, this is the canonical behavior of Kondo insulators. (2) Changes in the f-valency drive metal-insulator transitions, e.g., in rare-earth monochalcogenides²⁷. In Ce₃Bi₄Pt₃, congruent with experiment^5,7, pressure decreases (increases) the simulated 4f-occupation n_f (valence 4 − n_f) from n_f = 1.05 (P = 0) to 0.96 (P = 40GPa)—while temperature has little influence²⁸. 4f ⁰ (J = 0) admixtures augment with P—accounting for the larger valence. Yet, also 4f ² (and 4f ¹ with J = 7/2) contributions grow—increasing the mixed-valence character. Still, the probability of finding the system in a 4f ¹-state with J = 5/2 merely decreases quantitatively from 80% (P = 0) to ~55% (P = 40GPa)—excluding a dominantly valence-driven metallization. (3) Instead, we unravel the non-monotonic transport to originate from two counter-acting structural trends within the confines of spacegroup $I\bar{4}3d$: globally, pressure shrinks the lattice, enhancing hybridization gaps. While the atomic coordinates of Ce and Pt are dictated by symmetry, the local Bi position (u, u, u) may vary. Minimizing total energies, we find u = 0.088 at P = 0—in agreement with the experimental u = 0.086²⁹—and predict a much larger u = 0.097 at P = 40GPa (Supplementary Fig. S2). This seemingly minute modification drastically changes inter-atomic hybridizations: instead of a monotonic increase (realized for u = const), a critical pressure emerges above which the gap decreases. Hence, Ce₃Bi₄Pt₃ exhibits a peculiar high-pressure behavior, not canonical for Kondo insulators in general.

Discussion

The above results strongly suggest that electronic scattering is the microscopic driver of the resistivity saturation in Ce₃Bi₄Pt₃. Our mechanism is relevant also for other Kondo insulators. Indeed, iso-structural Ce₃Sb₄Pt₃ displays a ρ(T)³⁰ consistent with our understanding: different growth techniques (varying amounts of disorder) lead to largely different ρ(T → 0) while T* changes little³⁰. Ce₃Bi₄Pd₃, has recently been characterized as a semi-metal³¹ or a Kondo insulator³². That the gap is next to non-existing^31,32 has been ascribed to spin–orbit³¹ or Kondo³³ coupling effects. Here, we conjecture that under compression a resistivity plateau develops in Ce₃Bi₄Pd₃. Future transport and susceptibility measurements could then elucidate whether pressurized Ce₃Bi₄Pd₃ mimics Ce₃Bi₄(Pd_1−xPt_x)₃ for small x—(dis)favouring the (spin–orbit) Kondo scenario. Saturation tendencies have also been found in the Kondo insulators CeFe₂Al₁₀³⁴ and pressurized CeRu₄Sn₆^35,36,37. However, Kondo physics is not a prerequisite for our mechanism. What makes these systems natural hosts for the quantum regime are their small gaps ${{\Delta }} \sim {{{{{{{\mathcal{O}}}}}}}}(\lesssim\, 50\ {{{{{{{\rm{meV}}}}}}}})$. Correlation effects also drive narrow gaps in SmB₆^11,38,39,40, YbB₁₂⁴¹, U₃Sb₄Pt₃⁴², or FeSb₂⁴³, all of which exhibit saturation regimes, while rather belonging to the class of intermediate-valence insulators or d-electron intermetallics⁴.

Yet, how can we ascertain that the presented microscopic scenario is at work in any such compound? Salient signatures of the quantum regime provide guidance: T* correlates with the bulk gap and the residual conductivity increases with shrinking lifetimes. In U₃Sb₄Pt₃, the gap is unaffected by pressure, and—consistently—so is T*⁴². In mixed-valence SmB₆, however, the activation gap shrinks under pressure, while T* is hardly affected^23,24, and added disorder at first increases the resistivity⁶. Also in CeRu₄Sn₆ single crystals, pressure significantly increases activation energies, while T* remains inert³⁷. These observations are incompatible with our scenario and suggest a different origin to dominate residual conduction. Incidentally, for the latter two compounds conducting surface states of proposedly topological character^44,45 have been evidenced^6,11. Note, however, that more disordered, polycrystalline samples of CeRu₄Sn₆ exhibit an additional inflection point in ρ(T), which—consistent with our theory—moves up under compression⁴⁶. Also for SmB₆, the situation is more complex: using a special measurement setup, Eo et al.¹¹ were able to disentangle surface and bulk contributions to conduction. Crucially, the isolated bulk conductivity still exhibits a saturation regime—whose temperature profile defies all previous scenarios^11,47. As we demonstrate in Fig. 6, the phenomenological quantum conductivity Eq. (3) delivers an accurate description of the experimental data—providing strong evidence that the bulk resistivity in SmB₆ is lifetime-limited. Noteworthy, our theory shares its key ingredient with the scenario of Shen and Fu⁴⁸ that suggests finite lifetimes of Landau levels to account for quantum oscillations, e.g., in SmB₆^49,50.

In conclusion, we pinpoint finite lifetimes of intrinsic bulk carriers as a driver for residual conduction in semiconductors. Using a simple phenomenology, we demonstrated the characteristic temperature profile associated with this scenario to accurately match the saturation regimes in several materials. Possible microscopic sources for a finite scattering amplitude at low-T are impurities, other forms of disorder, and zero-point fluctuations. Indeed, the resistivity of no semiconductor in practice diverges for T → 0. In the absence of other factors (or, see SmB₆, in combination with), signatures of the presented physics can therefore be expected to be ubiquitous in correlated narrow-gap semiconductors.

Methods

Realistic many-body electronic structure

We simulate Ce₃Bi₄Pt₃ at finite pressures using lattice constants from experimental fits to the third-order Birch–Murnaghan equation-of-state⁷. While the Wyckoff site 12a (12b) uniquely defines the placement of Ce (Pt) atoms, we relax the internal positions of Bi in density-functional theory (DFT) as implemented in WIEN2k⁵¹ using the PBE functional. Band-structure results are summarized in Supplementary Fig. S2. Realistic dynamical mean-field theory (DFT+DMFT) calculations⁵² are performed with the code of Haule et al.⁵³, including charge self-consistency, spin–orbit coupling, and using a continuous-time quantum Monte Carlo solver. Rotationally invariant interactions for the Ce-4f shell were parametrized by a Hubbard U = 5.5eV and Hund’s J = 0.68eV (see also Supplementary Note 2) in conjunction with the nominal double-counting scheme⁵³; Ce-4f hybridizations were allowed in an energy window of ±10 eV around the Fermi level. At ambient pressure, this setup yielded excellent results for spectral and optical properties¹⁸ (see also ref. ⁵⁴). For illustrative purposes, we extract from the self-energy Σ(ω) a scattering rate Γ by averaging over the total angular momentum J = 5/2 components that dominate spectral weight near the Fermi level: ${{\Gamma }}=-{\left\langle {{{{{{{\rm{Im}}}}}}}}{{\Sigma }}(\omega = 0)\right\rangle }_{J = 5/2}$. Finding that always Γ(T) ∝ T², we quadratically extrapolate the minima in ${{{{{{{\rm{Im}}}}}}}}{{\Sigma }}(\omega )$ toward zero for temperatures beyond the reach of quantum Monte Carlo simulations, assuming that the frequency-dependence and the real-part do not change. Besides renormalizations from electronic correlations, we mimic the effect of disorder²⁰ with an additive, temperature-independent Γ_imp, typical for impurity scattering. In all cases, the crossover temperature T* occurs in a regime in which scattering is largely dominated by Γ_imp. Since we are interested in the system’s properties around and below T*, uncertainties in the extrapolation of Γ(T) are negligible.

Transport properties

Methodology

Resistivities for Ce₃Bi₄Pt₃ (Figs. 2 and 3) are simulated in linear-response theory using the full self-energy Σ(ω) as described in ref. ⁵⁵. High-precision transport calculations that evaluate Eq. (1) for a two-band model (Fig. 4) are performed using LINRETRACE⁵⁶. The realistic conductivities require a sizable additional scattering rate Γ_imp (broadening) for numerical stability. Comparing the resistivities in Figs. 1 and 2, we see that simulated absolute values are on par with data from Katoh et al.⁵⁷. Experiments with better residual-resistance ratios^5,6,7, have higher resistivities—suggesting that the broadening necessary in the simulations is too large for quantitatively mimicking high-quality samples. For simplicity, Γ_imp was only included in the transport simulations, not the DMFT. In Supplementary Fig. S4, we show that this leads to a small underestimation of ${{{{{{{\rm{Im}}}}}}}}{{\Sigma }}$ at low pressures. LINRETRACE⁵⁶, instead, yields numerically exact results for arbitrary scattering rates.

Expression of the conductivity

The derivation of the central Eq. (1) (outlined in Supplementary Note 1) uses contour integration techniques for the usual Kubo linear response for intra-band optical transitions with a static scattering rate⁵⁸, neglecting—in the DMFT spirit⁵²—particle-hole couplings. This omission of vertex corrections is deliberate: we demonstrate that already the one-loop approximation possesses an intricate (and hitherto unknown) structure that qualitatively describes the resistivity saturation. We can motivate that, here, vertex corrections do not change the qualitative picture: impurity corrections to the current vertex of intrinsic carriers via ladder diagrams mainly reduce the decay rate Γ in the response function’s prefactor by filtering out forward scattering⁵⁹, i.e., they do not change the essential physics. Corrections from crossed diagrams can be important, e.g., in doped semiconductors where they may lead to metal-to-insulator transitions via localization. Here, instead, we are concerned with metallic signatures in an a priori insulating host. Deviations from activated behavior could still be provided by extrinsic in-gap states: (a) through pinning of the chemical potential in an exhaustion regime, or in-gap states could themselves conduct, leading to (b) effectively smaller gap energies (gapped in-gap states), or (c) corrections from metallic but (weakly) localized in-gap states. Mechanisms (a,b) would lead to a resuming activated behavior at lower T, which is not observed in Ce₃Bi₄Pt₃. Route (c) as well as anti-localization effects would have characteristic signatures in the magnetoresistance, but are absent in Ce₃Bi₄Pt₃^7,60. Further, Kondo-hole conduction^8,9, owing to Ce-off-stoichiometry, produces metallic slopes, dρ/dT > 0, not seen here. Our scenario thus provides a new interpretation to controversial in-gap states in Kondo insulators: we argue that they may derive from intrinsic valence and conduction states. The latter’s finite (disorder-limited) lifetime causes incoherent weight to spill into the gap. For lifetime effects on quasi-particle transport in correlated metals, see, e.g., refs. ^61,62.

Fermi velocities

Standard Peierls velocities in the band-basis only account for intra-band transitions (to incorporate inter-band transitions, see ref. ⁶³). For a discussion of intra- and inter-orbital transitions in the realistic simulations, that use full (intra+inter) dipolar transition elements, see Supplementary Fig. S5.

Data analysis

Crossover temperatures T* are extracted from the simulations of ρ(T) at discrete temperature points using derivatives of a cubic spline interpolation. Experimental curves are fitted with the approximative formula, Eq. (3), which neglects the momentum dependence of excitations. As illustrated in Supplementary Fig. S6, this assumption generally leads to an overestimation of, both, Δ and Γ. Bare scattering rates Γ₀ (in analogy to Γ_imp in Fig. 2), are obtained by multiplying Γ with the mass enhancement m*/m = 1/Z. Because m*/m decreases with P (see text), the pressure-driven increase in Γ₀ is smaller than for Γ.