Introduction

Correlated adatoms expand upon the plethora of remarkable properties already existent in two-dimensional (2D) metallic surfaces. Stemming from the competition of localization and itinerant characters, such properties include: hybridization, superlattice self formation1,2,3,4,5,6 and long range interactions7,8,9,10. Moreover, due to the comparatively low coordination between adatoms and substrate, single atom magnets in the form of Pt/Ho11,12,13 have been debated and magnetic hysteresis of Er trimers on Cu have been observed14. These phenomena have attracted a wide academic interest, but also offer pathways towards industrial applications, for example as candidates for future atomic scale memory storage15,16,17.

While the limits of Mott18,19,20 superlattice and Kondo impurity behaviour are well documented, little is known about the transition between the densely packed (Mott) and the diluted (Kondo) limits of superlattice systems. Furthermore, although physical cases of 3d transition adatom2,21,22,23 and rare-earth adatom24,25,26 self-organization have been reported and justified with tight-binding models and kinetic Monte Carlo simulations1,3,27,28,29, the quantum mechanism responsible for the formation of the superlattice, and the adatom-substrate requirements for self-formation are so far elusive.

To paint a picture of the phenomena observed in this work, an overview of impurity lattice physics is due: a single Kondo adatom within a material does not conserve momentum when scattering electrons. However, in this work, we discuss lattices whose unit cell contains Kondo impurities: Kondo lattices. Due to translational symmetries, Kondo scattering within such lattices conserve momentum, leading to coherent scattering and a decrease in resistivity below the Kondo temperature30,31. Interpreting requirements for constructing Kondo lattices will be essential in further understanding of correlated low-temperature research. Friedel oscillations32 are another form of impurity-impurity communication. They describe electronic screening of an impurity and charge distribution on lattice sites. Different mechanisms have been proposed as the mediator for self-assembly. One such mechanism, which theorises how Friedel oscillations from two adatoms interact was proposed by Hyldgaard and Persson33. Lastly, Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions34,35,36 provide a mechanism for spin-spin coupling between f and/or d band electrons.

2D systems promote surface electron states. These states are formed with lower electron densities in comparison to the bulk electron states observed in three-dimensional systems. Therefore, electrons become localized under the effects of impurities, and the system becomes devoid of conduction band electrons. Since there is no scattering of conduction band electrons, this leads to an atomic limit behaviour at the lattice impurities. Moreover, substrate electrons are further localized by the impurity induced potential. Under these circumstances, a spin–spin interaction can occur between the impurities electrons and electrons localized near the impurities, forming singlet/triplet bound states. Lastly, due to the periodic structure of both the lattice and the impurity ionic potential, localization can occur around both the adatoms and on the substrate. Localization on substrate sites might be expected when inter-adatom distances become sufficiently large, and the conduction band of the substrate sufficiently high, permitting localization effects and realizing a charge density wave concomitant with a pseudogap formation. These effects have so far not been investigated, due to the complexity of the problem, which involves dealing with large unit-cells and the presence of strong correlations in the f-shell of the adatoms. Typically, such systems are beyond the reach of density functional theory, and even more so, from many body perturbative techniques like GW and its extensions.

In this work, we use a combination of dynamical mean field theory (DMFT) and tight binding calculations for a triangular lattice substrate, techniques which have been utilised on previous works concerning other superstructures19,37,38. We present our investigations into the generic properties of single orbital correlated adatom structure upon a triangular metallic substrate. This model is a canonical model for the description of a 4f1 orbital hybridized to a Ag(111) substrate. We systematically investigate the phase diagram as a function of correlation strength, substrate electronic density and adatom inter-distances, and outline the different phases obtained. We study the strength of correlations, quantified by the quasi-particle weight factor (Z), and examine the electron localization at the adatom and its impact on the correlated energy bands and Fermi surfaces.

We report a sharp Mott to Kondo transition as adatom spacing varies from a tightly packed solid to a diluted solid. We also report the stabilization of a charge density wave competing with Kondo physics at large inter-adatom distances. For any given superlattices, large mass renormalization are obtained at low and high-density regimes, corresponding to the limit of a weakly hybridized impurity, and the limit of a screened impurity respectively. These two phases are separated by the formation of a tightly bound triplet between the adatom and the substrate that exhibits a weak mass renormalization. In our view, the experimental realization of the Ce/Ag(111) superlattice falls in the latter regime, and our result shed light on the lack of evidence for Kondo physics as previously observed by spin-polarized scanning tunneling microscopy. Our work predicts that Kondo Lattices are obtained at intermediate adatom distances (5–9 substrate lattice sizes, L).

Results

Strength of correlations and emergent quasi-particles in the superlattice

First, we report the systematic study of the superlattice correlation strength, as function of the substrate electronic density and adatom distances, obtained by paramagnetic DMFT calculations (permitting fluctuating moments and correlations across adatoms, but not for long-range magnetic order). Correlation strength is measured by the adatom quasi-particle weight factor Z, obtained with the low energy imaginary component of Matsubara self-energy Σ(iωn), reported in Fig. 1a. The results outlined below correspond to Hubbard repulsion U/t = 6, where t is the tunnelling amplitudes across the substrate, typically t = 0.75 eV for the case of the Ag/Ce superlattice (we discuss results for this Coulomb repulsion thereafter, extended the calculations to other values of the Coulomb repulsion, see Supplementary Fig. 1).

Fig. 1
figure 1

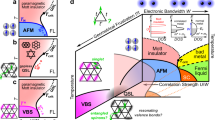
Phase diagram. a Colour map of the quasi-particle weight Z for U/t = 6 and different lattice sizes L. Z is a measure of the strength of the electronic correlations induced by U, where the colour map indicates Z = 0 (blue) and Z = 1 (red). We identified three regions of interest in the phase diagram: for nf = 0.3, nf = 0.5 and nf = 0.7. Each region is analyzed and split into phases (M - Mott, KI - Kondo impurity, AL - atomic limit, TBS - triplet bound state, KL - Kondo lattice and CDW - charge density wave). We report further in the text observables that characterize these phases. b Colour map of the substrate conduction band (CB) electronic density different substrate sizes L (blue for nCB = 0 and red for nCB = 1). The substrate's electronic states are empty in the lower right corner of the phase diagram, which indicates that in this region the adatom is decoupled from the substrate. c–e Total system density of states at nf = 0.7, 0.5, 0.3 respectively. Each set of data is renormalized with the supercell size and shifted with respect to the chemical potential. This was done to allow for comparison between datasets

Full size image

We report a phase diagram in terms of the adatom electronic occupation nf (all occupation refer to the single spin component only, as the calculations are paramagnetic). Although in our calculations we systematically change the chemical potential, we report the phase diagram in terms of the adatom occupancy. The total occupation is indeed a monotonic function of the adatom density at any finite temperature. We find two dominant regimes where correlation effects are large, at two nearly horizontal minima near the single spin adatom (f band) electron density nf = 0.3 and 0.7, separated by a weakly correlated regime at half-filled adatom nf = 0.5 across all values of U (see also Supplementary Figs. 1 and 2).

We report the electronic density of the substrate in Fig. 1b (blue denotes an empty substrate, and red the band insulating limit).

The energy resolved spectral weight ρ(ω), obtained respectively at adatom density nf = 0.7 (see Fig. 1c), at half-filled adatom density nf = 0.5 (see Fig. 1d, which also is concomitant with a filling of two electron in total per unit-cell, meaning there is one electron in the substrate), and at low density nf = 0.3 (see Fig. 1e).

In Fig. 2a, b, we report the spectral function A(k, ω) resolved in real frequencies ω and momentum k obtained for the same density. Note that, as the band structure is trivially folded due to the unit-cell construction of the periodic superlattice, we reconstruct the unfolded band structure of the original unit-cell of the substrate, which allows for comparison across different superlattices.

Fig. 2
figure 2

Spectral weight. Ak,ω, indicated with red (high) and blue/black (low) resolved in momentum and energy for U/t = 6 and nf = 0.3 for a L = 5 and b L = 10. The adatom f state is strongly hybridized to the conduction band for intermediate lattice sizes (L = 5), but we observe a dehybridization of the adatom f state and conduction band at larger size L = 10. For the latter, the adatom is in the atomic limit (AL), as the conduction band remains weakly populated, as proposed in the discussion

Full size image

The Mott to Kondo crossover in the diluted solid

To investigate the correlated regions of the phase diagram (Fig. 1a), a polynomial regression was preformed on the adatom self-energy to obtain the electron scattering rate and the Kondo temperature (TK) in the two correlated phases obtained at respectively nf = 0.3 (Fig. 3a) and nf = 0.7 (Fig. 3b). In both phases, we obtain a significant mass renormalization, concomitant with a large magnetic moment (see Supplementary Fig. 3), a required but not sufficient condition to obtain Kondo physics.

Fig. 3
figure 3

Quasi-particle weight. Z across a range of lattice sizes L for U/t = 6 at adatom electron density a nf ~ 0.3 and b nf ~ 0.7. Scattering rate Γ and Kondo temperature TK (as obtained by the formalism detailed in the Method section), both in units of Kelvin, in c nf ~ 0.3 and d nf ~ 0.7. At low density (nf ~ 0.3), we observe a sharp first-order transition between non-Fermi liquid NFL and Fermi liquid FL for L = 4 (see the sharp onset of TK at L = 4, concomitant with a reduction of the effective mass m*). FL properties are eventually suppressed in the diluted limit (L > 12), as the atomic limit is obtained with the absence of electronic states in the substrate (see Discussion hereafter). For large density (nf ~ 0.7) we observe a similar NFL/FL transition at L = 6

Full size image

The Kondo temperature TK, extracted from the low frequency hybridization (see Method section) was used here as a marker of the formation of a Kondo singlet. Note that TK as extracted in this approximation provides the right trend, but is known to overestimate TK. We obtain (see Fig. 3c, d) that a crossover occurs for both regions as the adatom distances reaches L = 3–4 for nf = 0.3 and L = 5–6 for nf = 0.7, respectively.

The calculation of the Kondo temperature has been validated by the measurement of the static local magnetic susceptibility χ(ω = 0) of the adatom, obtained from calculations carried out at different temperatures, this is presented in Fig. 4.

Fig. 4
figure 4

Local magnetic susceptibility. χ(ω = 0) of the adatom for L = 6 and nf = 0.7, as a function of inverse temperature β. At high temperature (T > TC), the susceptibility is proportional to 1/T, indicating that the system is above the Curie temperature, whereas at low temperature (T < TK), the susceptibility is temperature independent, showing that the system has entered into the Kondo regime

Full size image

Weakly correlated triplet bound state

Finally, we investigated the region of the phase diagram that divides the two correlated regions obtained in the phase diagram (obtained at nf = 0.3 and nf = 0.7, respectively). At nf = 0.5, which corresponds to the case of a half-filled f level, we obtain the weakest mass renormalization and a regime of nearly free electrons (NFE) (see Fig. 1a). In Fig. 5, we report the integrated occupation over the supercell (both adatom and substrate). In particular, we find that the half-filled adatom f shell is obtained with a concomitant total charge of 2 electrons, and hence an occupation of a single electron per unit-cell on the substrate. The real space average charge (not shown) also reveals that the electron pair is localized in the unit cell around the adatom. This can be rationalized in a simple toy model, where 2 electrons are forming a bound state between the adatom and the three substrate neighbours (see Fig. 5). This toy model can be used as an approximation to capture the physics of the superlattice locally.

Fig. 5
figure 5

Adatom electron occupation. Number of electrons within the supercell Ntot as a function of nf for U = 6. Across all lattice size L, the graph follows the same linear increase from an empty system to (nf = 0.5, Ntot = 1). We conclude that (taking both spins into account) when the adatom is singly occupied, the conduction band must also be singly occupied, allowing singlet/ triplet states between the adatom and substrate to form

Full size image

Mott localization driven by adatom interactions mediated by the substrate

We also extended our calculations to larger and smaller values of the correlation U. Whilst most results remain identical, we note that for the strong coupling regime (U/t = 10), the systems undergoes a charge localization for L = 9 for nf = 0.7, followed by the formation of a pseudogap and the suppression of the Kondo resonance (see Supplementary Fig. 4). The localization is directly observed in the real space electronic density (compare Fig. 6a, b with Fig. 6c). Albeit observed in all calculations that electrons localized naturally around the adatoms, due to the attractive ionic potential, the localization induced by the Coulomb repulsion in this particular regime of parameters happens in-between the adatoms.

Fig. 6
figure 6

Charge density wave. Real space electronic density nCB of the substrate conduction band for the strongly coupled regime and nf ~ 0.7 for a L = 3, b L = 7 and c L = 9. Black (white) colours indicate large (small) electronic density. For L = 3, we observe localized states around the adatom (the adatom, not shown, is located at the centre of the black circles). As L increases, we observe a delocalization, which is concomitant with Kondo physics (see Discussion hereafter). For the limit of diluted solids, corresponding to L = 9 and larger, we observe the formation of a charge density wave (CDW), where localized states develop in between adatoms. The CDW is concomitant with the formation of a pseudogap (see Discussion hereafter)

Full size image

Discussion

In Fig. 1a, low nf, we obtain here that the quasi-particle state is localized at the adatom. As nf increases, however, Z also increases, reaching a maximum when the adatom is exactly half-filled. Although we might naively expect that the reduction of the mass renormalization is associated with a delocalization of the charge, we observe that the electron remain tightly bound to the adatom location. In our view, this is associated with the creation of a two-electron tightly bound triplet state between the adatom and the substrate (see Fig. 5). Finally, at densities larger than two-electron per unit-cell, we obtain another localization process near nf = 0.7 with a concomitant increase of the mass renormalization.

Moving onto Fig. 1b. As expected, at low occupation of the adatom, the substrate is empty, and we obtain the limit of an impurity in vacuum (atomic limit, AL). This limit is not physical and provides a lower bound on the adatom occupation for a given superlattice structure. Additionally, at small adatom distances L, we observe a rapid filling of the substrate upon increasing the adatom occupation, an effect related to the Coulomb repulsion U at the adatom site, that prevents an occupation of more than one electron and induces a charge transfer to the substrate.

At high electron density nf = 0.7 (see Fig. 1c), we observe the emergence of a resonance, that starts to develop at L = 5, and becomes resonant at L = 7, and ultimately vanishes at L = 10. We associate this feature to the presence of a screened Kondo singlet (see discussion thereafter). We note that at the same density, we observe at large adatom distances L > 9 the formation of a charge density wave, where electron on the substrate localize half-way in-between adatoms, with the opening of a pseudogap in the spectral density (see Supplementary Figs. 1 and 4). This phase is denoted as CDW in the phase diagram.

The spectral feature of the weakly correlated region at nf = 0.5 (see Fig. 1d) exhibits a large degree of hybridization between the adatom and substrate. We associate this state to a Triplet Bound State (TBS) formation.

The low density regime exhibits (see Fig. 1e) sharp features that corresponds to the localized states at the adatom. We obtain a transition from a broad feature, reminiscent the correlated metal, to a narrow spectral feature at the Fermi level obtained at adatom distances L > 4. This is fingerprint of a localized electron at the adatom location, which we denote at a Kondo impurity (KI). Ultimately, the KI localized quasi-particle states converges to the atomic limit (AL) at large adatom separation.

In Fig. 2, we observe that the adatom are strongly hybridized to the substrate for nf = 0.3, L = 5 (Fig. 2a), as shown by the fluctuations induced in the substrate bands by the adatom, but dehybridize at larger adatom distance L = 10 (Fig. 2b), a fingerprint that the atomic limit has been reached (AL).

Regarding Fig. 3c, for the limit of the Kondo impurity (nf = 0.3), the system enters into the Kondo regime abruptly via an abrupt transition (see Supplementary Fig. 2) between a non Fermi liquid at short adatom distances to a Fermi liquid at intermediate adatom distances (a linear behaviour of the self-energy as a function of the Matsubara frequency is obtained in the self-energy, a signature of a Fermi liquid, see Supplementary Fig. 2).

For nf = 0.7 (Fig. 3d), the crossover is continuous and, unlike the abrupt change obtained between the NFL to FL regime obtained at nf = 0.3, an increase in the mass renormalization occurs simultaneously with the large increase of TK at nf = 0.7.

In Fig. 4, we observe that the system manifests true Kondo behaviour in the large density regime nf = 0.7, for temperatures lower than T = 0.007 × t, which corresponds to ≈ 60° K (the tunneling amplitude for the silver substrate is t = 0.75  eV). We, therefore, identify the region of the phase diagram L > 5 and nf = 0.7 as a Kondo lattice (KL): a lattice of independent screened magnetic moments. At large temperature T > 0.02 × t, we recover the usual Curie Weiss law, which describes a fluctuation moment.

Moreover, in the low density limit (nf = 0.3), we find that the local susceptibility remains small at all temperatures with weak temperature dependence (χ ~ 0.02), as expected for a system which exhibits a large degree of localization due to correlation effects. We also note that a larger Coulomb repulsion U/t = 10 opens a gap and suppresses the resonance obtained in this regime (see Supplementary Fig. 4), gaping in turn the fluctuations associated with the magnetic moment by Mott physics. Due to the low occupation of the conduction band, we consider the region L > 3 and nf = 0.3 as a system of Kondo impurities (KI).

The solution of the 2 electron model in Fig. 5 gives a bound triplet ground state for any realistic values of the screened Coulomb interaction U (U < 11 eV). For U > 11 eV, we obtain a singlet ground state. It is worth noting that this limit was obtained by renormalizing the hopping parameters between the substrate atoms to recover the bandwidth of the conduction band, as those have been integrated out in this simple picture (without this renormalization, the U separating the singlet from the triplet is larger). We, therefore, conclude that for this region of the phase diagram, we obtain triplet bound electron pairs localized around the adatoms. Note that the triplet can be seen as an uncorrelated state, as the Pauli principle excludes the double occupations. In our view, this phenomena explains the nearly free electron regime, separating the correlated phases at low and high nf.

Lastly, regarding the Coulombic localization effects in Fig. 6. In our view, this effect is driven by the two-body potential induced by the interference energies between Friedel oscillations. This two-body adatom interaction, mediated by surface state electrons, is an oscillating function of the adatom distance (similarly to the RKKY interaction), and is parametrized by the electronic mass. In the free electron model, its oscillations are involving distances larger than 11 lattice spacings, and therefore does not play a role in our calculations for L < 11. Furthermore, this interaction is also suppressed when the states at the Fermi level are absent (as it is the case in the low density regime nf = 0.3 at large U/t = 10 that opens a gap).

However, at large density nf = 0.7, the adatom mediated interaction is modified by the large mass renormalization induced by the local Hubbard U term, and produces an attractive potential in-between the adatoms.

We emphasize that this CDW is fundamentally different from Friedel oscillations (FO), where the amplitude decreases as distance from impurity increases. Secondly, as discovered by Chatterjee et al.39. the amplitude of FO decreases as U increases, in contradiction to our observation in the Kondo superlattice. Furthermore, the charge localization, in our measurements, is obtained in the large U limit (U/t = 10), and is concomitant with a renormalization of the electronic mass (see Supplementary Fig. 1). We associate hence the CDW to a charge ordering induced by the narrowing of the conduction band induced by correlation. The electronic localization is associated with the opening of a pseudogap.

Methods

In this paper, we have used the following computational setup in order to model the deposition of Ce adatoms on Ag substrate: the Ag substrate was modelled by a 2D triangular lattice of Ag 5s orbitals, while the Ce adatom 4f orbital was represented by an additional site connected with its three nearest neighbour Ag atoms. The heavy deposited Ce adatom hybridize with the substrate, and also induce an attractive ionic potential on the three neighbours of the substrate.

In this work, we use the dynamical mean-field theory (DMFT) approximation. Heavy f-materials have been extensively studied by DMFT, which captures well both the itinerant and localized behaviour of the electrons in f-materials40,41,42,43,44. In the DMFT formalism, the adatom (Ce) sites with the on-site U are treated as strongly correlated orbitals, while the conduction band of the substrate (Ag sites) are considered as uncorrelated. More formally, the Hamiltonian of the system considered here reads in real-space as:

$$\begin{array}{*{20}{l}} H \hfill & = \hfill & { - t\mathop {\sum}\limits_{\left\langle \mathrm{i,j} \right\rangle ,\sigma } {c_{\mathrm{i}\sigma }^\dagger c_{{\mathrm{j}}\sigma }} + \mathop {\sum}\limits_{\sigma ,k} {\varepsilon _{{\mathrm{imp}}}} f_{\sigma ,k}^\dagger f_{\sigma ,k} + \mathop {\sum}\limits_{\mathrm{i},\sigma } {V_{\mathrm{i}}} c_{\mathrm{i}\sigma }^\dagger c_{{\mathrm{i}}\sigma }} \hfill \\ {} \hfill & {} \hfill & {\hskip-6.6pt} { + \mathop {\sum}\limits_{\left\langle {\mathrm{i},k} \right\rangle ,\sigma } {(V_{{\mathrm{if}}}c_{{\mathrm{i}}\sigma }^\dagger f_{\sigma ,k} + \text{h.c.})} + U\mathop {\sum}\limits_{\sigma ,k} {n_{{\mathrm{f}} \uparrow ,k}} n_{{\mathrm{f}} \downarrow ,k} + \mu N_{{\mathrm{tot}}},} \hfill \end{array}$$
(1)

where t is the inter-substrate hopping (in our calculation t is the energy scale, for the case of a Ag(111) substrate, t = 0.75 eV), εimp is the adatom energy level, U the adatom Hubbard repulsion, μ the chemical potential and h.c. denotes Hermitian conjugate. \(c_{{\mathrm{i}}\sigma }^{(\dagger )}\) and \(f_{{\mathrm{i}}\sigma }^{(\dagger )}\) are the Fermionic annihilation (creation) operators of the site i, spin σ, surface state and the adatom respectively. Vi describes the on-site potential asserted upon the substrate by the adatom (as described in ref. 1). And lastly, the adatom/substrate hopping parameter \(V_{{\mathrm{if}}} = V_{{\mathrm{fi}}}^ \ast = t_{{\mathrm{Ad}}}\) is assumed finite for three of the substrate sites, otherwise it is zero. This assumption can be justified through consideration of the triangular substrate1,4. The schematic view of our computational setup is shown in Fig. 7.

Fig. 7
figure 7

Cartoon picture of the dynamical mean field theory setup. The model includes the conduction band of the substrate (depicted by the blue circles) and the concomitant Hamiltonian parameters. The correlated adatom (red circle) sits in between three sites of the substrate (blue circles)

Full size image

In analogy with DFT+DMFT, the calculation requires convergence with respect to the number of k-points in the Brillouin zone of substrate lattice. Calculations carried out in this work were computationally intensive, convergence in some cases required 100 × 100 sixfold reduced k-points (triangular substrate symmetry). Without any simplifications, calculations of each k-point scales as nfreqN3, for number of sites N and number of Green’s function frequency points \(n_{{\mathrm{freq}}} = {\cal{O}}(1000)\). For the largest lattice size considered, L = 15, of the order of 1000*2253 calculations was needed to invert the Hamiltonian to calculate the Green’s function for a single DMFT iteration.

In DMFT, we have employed an exact diagonalization (ED) solver improved by using the cluster perturbation theory (CPT). The ED solver45,46,47 uses a finite discretization approximation of hybridization Δ(iωn) function, which induces finite discretization errors48. As the size of the basis used to represent the Hamiltonian scales exponentially with the number of bath energies in the system, solving the eigenvalue problem is not computationally achievable if the number of bath orbitals is typically larger than 15. ED-CPT49 bypasses this problem by utilizing a small number of bath systems and incorporating additional bath sites in order to mimic the effect of coupling to an infinite bath, which was used in our work to check that no remaining systematic error due to the bath discretization was obtained in our calculations. Finally, we have used Lichtenstein’s double counting scheme50.

Sherman-Morrison

Calculation of the full lattice Green’s function G(k) involves a matrix inversion at each k-point and ω. In the case of large supercell sizes this becomes a bottleneck of the formalism. An optimization is possible here due to the fact that the matrix to be inverted contains a large number of empty entries. This is due to the properties of the supercell: the self-energy is non-zero only at the adatom, and the hybridization between the adatom and the substrate occurs only on three sites of the substrate. Therefore, to reduce the computational load, the Sherman-Morrison algorithm51 was implemented to update the full Green’s function G(k) from the substrate Green’s function G0(k):

$$G_0^{ - 1}(k) = \left[ {\begin{array}{*{20}{c}} {i\omega - V_{\mathrm{i}}} & { - t} & { - t} & 0 & \ldots \\ { - t} & {i\omega - V_{\mathrm{i}}} & { - t} & { - t} & \ldots \\ { - t} & { - t} & {i\omega - V_{\mathrm{i}}} & { - t} & \ldots \\ 0 & { - t} & { - t} & {i\omega } & \ldots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{array}} \right],$$
(2)
(3)

Here Vif, εf, t, and Vi are defined in (1), iωn is the n's Matsubara frequency, while the substrate sites are ordered in such a way that the three sites connected to the adatom are listed first.

G0 is obtained via matrix products for all nfreq (N2 operations), G is then updated from G0. Since only three substrate sites hybridizes with the adatom, the updating process scales linearly with N.

Kondo physics

In order to extract the Kondo physics fingerprints from our DMFT results, we have calculated the scattering rate Γ and Kondo temperature TK.

In order to estimate Γ, we performed the polynomial regression with the following low frequency, low-temperature expansion of Σ′′(iωn) in the Kondo regime52:

$$\Sigma ^{{\prime}{\prime}}(i\omega _{\mathrm{n}}) = a + \left( {1 - \frac{1}{Z}} \right)\omega _{\mathrm{n}} - \frac{1}{{2Z^{2}{{\Delta ^{{\prime}{\prime}}}}(i\omega _{\mathrm{n}})}}\omega _{\mathrm{n}}^{2}.$$
(4)

Γ is obtained from the above parameters a and Z as follows:

$$\Gamma = - \frac{a}{Z}.$$
(5)

We used53 the following definition of the Kondo temperature TK after Hewson’s renormalized perturbation theory54 of the Anderson impurity model (AIM):

$$T_{\mathrm{K}} = - \frac{{\pi Z}}{4}{\mathrm{\Delta }}^{\prime\prime} (i\omega _{\mathrm{n}})|_{\omega _{\mathrm{n}} \to 0}$$
(6)

where Δ′′ is the imaginary part of the resonant level scattering width as defined in ref. 54.

Triplet bound state toy model

Here we briefly outline the simple toy model used to analyze the regime of the phase diagram, where we have two electrons per unit-cell. As we observed in the superlattice calculations that the electronic states are localized around the adatoms, we solve the isolated plaquette of three substrate atoms connected to the adatom site. This Hamiltonian includes a local Coulomb repulsion U on the adatom site, an hybridization between the adatom and the three substrate atoms, and hopping across the substrate atoms. The impurity energy and hybridization are the same as the one treated in the full DMFT calculations, whereas the hopping across the substrate elements is renormalized to account for the bandwidth of the full calculation. Upon diagonalizing this Hamiltonian and finding the ground state, we then evaluate the expectation value of the spin correlator K operator between the adatom and one of the substrate atom, which identifies a singlet (triplet) ground state if K < 0 (K > 0). We identify the first-order transition between the triplet state at small U and the singlet state at large U (see Supplementary Fig. 5). Interestingly, we find that the critical U to obtain a singlet state is larger than all realistic U considered in our calculation. This suggests that in the limit of low occupation, pairs of electrons will form a triplet state for realistic values of the Coulomb repulsion.

This triplet state is indeed a multiplet that also includes the polarized contribution with two electrons of same spin, and exhibit a lower degree of correlation. Indeed, in the \(S_{{\mathrm{tot}}}^{\mathrm{z}} = \pm 1\) sectors, there are no contributions from the Coulomb energy, as observed in the phase diagram near the nf = 0.5 region, where the mass renormalization is weak. We attribute hence this region of the phase diagram to a triplet bound state.