Abstract
Noether’s calculus of invariant variations yields exact identities from functional symmetries. The standard application to an action integral allows to identify conservation laws. Here we rather consider generating functionals, such as the free energy and the power functional, for equilibrium and driven many-body systems. Translational and rotational symmetry operations yield mechanical laws. These global identities express vanishing of total internal and total external forces and torques. We show that functional differentiation then leads to hierarchies of local sum rules that interrelate density correlators as well as static and time direct correlation functions, including memory. For anisotropic particles, orbital and spin motion become systematically coupled. The theory allows us to shed new light on the spatio-temporal coupling of correlations in complex systems. As applications we consider active Brownian particles, where the theory clarifies the role of interfacial forces in motility-induced phase separation. For active sedimentation, the center-of-mass motion is constrained by an internal Noether sum rule.
Similar content being viewed by others
Introduction
Emmy Noether’s 1918 Theorems for Invariant Variation Problems1,2, as applied to action functionals both in particle-based and field-theoretic contexts, form a staple of our fundamental description of nature. The formulation of energy conservation in general relativity had been the then open and vexing problem, that triggered Hilbert and Klein to draw Noether into their circle, and she ultimately solved the problem3. Her deep insights into the relationship of the emergence and validity of conservation laws with the underlying local and global symmetries of the system has been exploited for over a century.
While Noether’s work has been motivated by the then ongoing developments in general relativity, being a mathematician, she has formulated her theory in a much broader setting than given by the specific structure of the action as a space-time integral over a Lagrangian density, as formulated by Hilbert in 1916 for Einstein’s field equations. Her work rather applies to functionals of a much more general nature, with only mild assumptions of analyticity and careful treatment of boundary conditions of integration domains.
In Statistical Physics, the use of Noether’s theorems is significantly more scarce, as opposed to both classical mechanics and high energy physics. Notable exceptions include the square-gradient treatment of the free gas–liquid interface, cf. Rowlinson and Widom’s enlightening description4 of van der Waals’ prototypical solution5. In a striking analogy, the square gradient contribution to the free energy is mapped onto kinetic energy of an effective particle that traverses in time between two potential energy maxima of equal height. Exploiting energy conservation in the effective system yields a first integral, which constitutes a nontrivial identity in the statistical problem. This reasoning has been generalized to the delicate problem of the three-phase contact line that occurs at a triple point of a fluid mixture6,7. While these treatments strongly rely on the square-gradient approximation, Boiteux and Kerins also developed a method that they refer to as variation under extension, which permitted them to treat more general cases8.
Evans has derived a number of exact sum rules for inhomogeneous fluids in his pivotal treatment of the field9. While not spelling out any connection to Noether’s work, he carefully examines the effects of spatial displacements on distribution functions. This shifting enables him, as well as Lovett et al.10 and Wertheim11 in earlier work, to identify systematically the effects that result from the displacement and formulate these as highly nontrivial interrelations (“sum rules”) between correlation functions. This approach was subsequently generalized to higher than two-body direct12 and density13 correlation functions and the relationship to integral equation theory was addressed14,15. Considering also rotations Tarazona and Evans16 have addressed the case of anisotropic particles, where their sum rules correct earlier results by Gubbins17. The exploitation of the fundamental spatial symmetries9,10,11,12,13,14,15,16 appears to be intimately related to Noether’s thinking. This is no coincidence, as Evans’ classical density functional approach (DFT) is variational as is the general problem that she addresses.
DFT constitutes a powerful modern framework for the description of a broad range of interfacial, adsorption, solvation, and phase phenomenology in complex systems9,18,19,20. Examples of recent pivotal applications include the treatments of hydrophobicity21,22,23,24,25,26,27 and of drying23,24,26, electrolytes near surfaces28, dense fluid structuring as revealed in atomic force microscopy29, thermal resistance of liquid–vapor interfaces30, and layered freezing in confined colloids31. Xu and Rice31 have used the sum rules of Lovett et al.10 and Wertheim11 (LMBW) to carry out a bifurcation analysis of the confined fluid state. The sum rules were instrumental for investigating a range of topics, such as precursors to freezing32, nonideal33 and cluster crystals34, liquid crystal deformations35, and –prominently– interfaces of liquids36,37,38,39,40. A range of further techniques besides DFT was used in this context, including integral equation theory32,36,39, mode-coupling theory41, and Mori-Zwanzig equations33,35.
Much of very current attention in Statistical Physics is devoted to nonequilibrium and active systems that are driven in a controlled way out of equilibrium, such as e.g. active Brownian particles42,43,44 and magnetically controlled topological transport of colloids45,46,47. The power functional (variational) theory48 (PFT) offers to obtain a unifying perspective on nonequilibrium problems such as the above. In PFT the (time-dependent) density distribution is complemented by the (time-dependent) current distribution as a further variational field. A rigorous extremal principle determines the motion of the system, on the one-body level of correlation functions. The concept enabled to obtain a fundamental understanding and quantitative description of a significant array of nonequilibrium phenomena, such as the identification of superadiabatic forces49, the treatment of active Brownian particles50,51,52,53, of viscous54, structural55,56 and flow forces56. Crucially, the DFT remains relevant for the description of nonequilibrium situations, via the adiabatic construction48,49, which captures those parts of the dynamics that functionally depend on the density distribution alone, and do so instantaneously. Both equilibrium DFT and nonequilibrium PFT provide formally exact variational descriptions of their respective realm of Statistical Physics. While action integrals feature in neither formulation, the relevant functionals do fall into the general class of functionals that Noether considered in her work.
Here we apply Noether’s theorem to Statistical Physics. We first introduce the basic concepts via treating spatial translations for both the partition sum and for the free energy density functional. Considering the symmetries of the partition sum does not require to engage with density functional concepts; the elementary definition suffices. We demonstrate that this approach is consistent with the earlier work in equilibrium9,10,11,12,13,14,15,16, and that it enables one to go, with relative ease, beyond the sum rules that these authors formulated. In nonequilibrium, we apply the same symmetry operations to the time-dependent case and obtain novel exact and nontrivial identities that apply for driven and active fluids. The three different types of time-dependent shifting are illustrated in Fig. 1. The resulting sum rules are different from the nonequilibrium Ornstein–Zernike (NOZ) relations57,58, but they possess an equally fundamental status. We also consider the more general case of anisotropic interparticle interactions and treat rotational invariance both in and out of equilibrium. To illustrate the theory we apply it to both passive and active phase coexistence as well as to active sedimentation under gravity.
The system is spatially displaced by ϵ = const at all times (green dashed), analogously to the operation in equilibrium. The system is dynamically displaced by \({{{{{\boldsymbol{\epsilon }}}}}}(t^{\prime} )\), such that the spatial displacement vanishes at the boundaries of the considered time interval, ϵ(0) = ϵ(t) = 0 (cyan solid). The system is displaced instantaneously only at the latest time t, such that the differential displacement is \(\dot{{{{{{\boldsymbol{\epsilon }}}}}}}dt\) (purple dotted).
Results and discussion
Adiabatic state
We start with an initial illustration of Noether’s concept as applied to the grand potential Ω. We consider spatial translations of the position coordinate r at fixed chemical potential μ and fixed temperature T. The system is under the influence of a one-body external potential Vext(r), cf. Fig. 2a. We take Vext(r) to also describe container walls, such that there is no need for the system volume as a further thermodynamic variable. For the moment we only examine systems completely bounded by external walls. Systems with open boundaries are considered below. Clearly the value of the grand potential Ω is independent of the global location of a system. Hence spatial shifting by a (global) displacement vector ϵ leaves the value of Ω invariant. To exploit this symmetry in a variational setting, note that the value of Ω depends on the function Vext(r), hence Vext(r) → Ω constitutes a functional map, at given μ and T. Here the grand potential is defined by its elementary Statistical Mechanics form \({{\Omega }}[{V}_{{{{{{\rm{ext}}}}}}}]=-{k}_{{{{{\rm{B}}}}}}T{{{{{\mathrm{ln}}}}}}\,{{\Xi }}\), with the grand partition sum Ξ depending functionally via the Boltzmann factor on Vext(r). The spatial displacement amounts to the operation Vext(r) → Vext(r + ϵ), cf. Fig. 2b. For small ϵ we can Taylor expand to linear order: Vext(r + ϵ) = Vext(r) + δVext(r), where δVext(r) = ϵ ⋅ ∇ Vext(r) indicates the local change of the external potential that is induced by the shift. As Ω[Vext] is invariant under the shift (which can be shown by translating all particle coordinates in Ξ accordingly), we have
Here the second equality constitutes a functional Taylor expansion in δVext(r) to linear order, and δΩ[Vext]/δVext(r) indicates the functional derivative of Ω[Vext] with respect to its argument, evaluated here at the unshifted function Vext(r), i.e. ϵ = 0. It is a straightforward elementary exercise9,18 to show via explicit calculation that δΩ[Vext]/δVext(r) = ρ(r), where \(\rho ({{{{{\bf{r}}}}}})={\langle {\sum }_{i}\delta ({{{{{\bf{r}}}}}}-{{{{{{\bf{r}}}}}}}_{i})\rangle }_{{{{{{\rm{eq}}}}}}}\) is the microscopically resolved one-body density profile. Here ri indicates the position of particle i = 1…N, with N being the total number of particles, δ(⋅) indicates the Dirac distribution, and the average is over the equilibrium distribution at fixed μ and T; the sum runs over all particles i = 1…N.
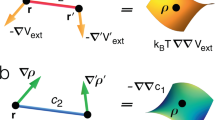
a In the presence of external potential Vext(r), the system develops an inhomogeneous density profile ρ(r), where r denotes the position coordinate. b Shifting the external potential by a displacement vector −ϵ (green arrow) induces a local change in external potential δVext(r) (black arrow) between the original (solid line) and the shifted external potential (dashed line); the grand potential is invariant, δΩ = 0. c The displaced density profile (dashed line) implies a local change δρ(r) (black arrow) in comparison to the initial density profile (solid line), which leaves the intrinsic free energy unchanged, δF = 0.
Comparing the left and right hand sides of (1) and noticing that ϵ is arbitrary, we conclude
where we have defined the total external force \({{{{{{\bf{F}}}}}}}_{{{{{{\rm{ext}}}}}}}^{{{{{{\rm{tot}}}}}}}\) using the one-body fields ρ(r) and Vext(r). It is straightforward to show the equivalence with the more elementary form \({{{{{{\bf{F}}}}}}}_{{{{{{\rm{ext}}}}}}}^{{{{{{\rm{tot}}}}}}}=-{\langle {\sum }_{i}{\nabla }_{i}{V}_{{{{{{\rm{ext}}}}}}}({{{{{{\bf{r}}}}}}}_{i})\rangle }_{{{{{{\rm{eq}}}}}}}\), where ∇i indicates the derivative with respect to ri. Clearly, (2) expresses the vanishing of the total external force (consider e.g. the gravitational weight of an equilibrium colloidal sediment being balanced by the force that the lower container wall exerts on the particles).
Equation (2) was previously obtained by Baus13. Here we have identified it as a Noether sum rule for the case of spatial displacement of Ω[Vext]. We can generate local sum rules by observing that (2) holds for any form of Vext(r) and that hence Vext(r) → ρ(r) constitutes a functional map (defined by the grand canonical average \({\langle \hat{\rho }({{{{{\bf{r}}}}}})\rangle }_{{{{{{\rm{eq}}}}}}}\), which features Vext(r) in the equilibrium many-body probability distribution). We hence functionally differentiate (2) by \({V}_{{{{{{\rm{ext}}}}}}}({{{{{\bf{r}}}}}}^{\prime} )\), where \({{{{{\bf{r}}}}}}^{\prime}\) is a new position variable. The first and the nth functional derivatives yield, respectively, the identities
where β = 1/(kBT), with kB indicating the Boltzmann constant, \({H}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )=-\delta \rho ({{{{{\bf{r}}}}}})/\delta \beta {V}_{{{{{{\rm{ext}}}}}}}({{{{{\bf{r}}}}}}^{\prime} )\) is the two-body correlation function of density fluctuations, and Hn = δHn−1/δβVext(rn) is its n-body version9,18. Here position arguments have been omitted for clarity: Hn ≡ Hn(r1…rn), and ∇α indicates the derivative with respect to rα. The variable names r and \({{{{{\bf{r}}}}}}^{\prime}\) have been interchanged in (3) and \(\nabla ^{\prime}\) indicates the derivative with respect to \({{{{{\bf{r}}}}}}^{\prime}\). The derivation of (3) and (4) requires spatial integration by parts. Recall that boundary terms vanish as we only consider systems with impenetrable bounding walls.
The sum rule (3) has been obtained by LMBW10,11 and by Evans9 on the basis of shifting considerations. The present formulation based on Noether’s more general perspective allows to reproduce (3) with great ease and to generalize to the hierarchy (4), as previously obtained by Baus13. Equation (3) has the interpretation of the density gradient ∇ ρ(r) being stabilized by the action of the external force field, −∇ Vext(r). The effect is mediated by \(\beta {H}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )\), where the correlation of the density fluctuations is due to the coupled nature of the interparticle interactions. Equation (4) is the multi-body generalization of this mechanism. Via multiplying (3) by Vext(r), integrating over r, and using (2), and iteratively repeating this process for all orders, one obtains a multi-body analog of the vanishing external force (2):
for α = 1…n.
We turn to intrinsic contributions. As Noether’s theorem poses no restriction on the type of physical functional, we consider the intrinsic Helmholtz free energy F[ρ] as a functional of the density profile as its natural argument. Here a functional Legendre transform9,18 yields F[ρ] = Ω[Vext] − ∫dr(Vext(r) − μ)ρ(r). Crucially, F[ρ] is independent of Vext(r), and its excess (over ideal gas) contribution Fexc[ρ] is specific to the form of the interparticle interaction potential u(rN); here we use the shorthand r1…rN ≡ rN. The full intrinsic free energy functional consists of a sum of ideal gas and excess contributions, i.e. \(F[\rho ]={k}_{{{{{\rm{B}}}}}}T\int d{{{{{\bf{r}}}}}}\rho ({{{{{\bf{r}}}}}})[{{{{{\mathrm{ln}}}}}}\,(\rho ({{{{{\bf{r}}}}}}){{{\Lambda }}}^{D})-1]+{F}_{{{{{{\rm{exc}}}}}}}[\rho ]\), where Λ is the (irrelevant) thermal de Broglie wavelength and D is the dimensionality of space.
As u(rN) is globally translationally invariant, Fexc[ρ] will not change its value when evaluated at a spatially displaced density, ρ(r + ϵ) = ρ(r) + δρ(r), where δρ(r) = ϵ ⋅ ∇ ρ(r), cf. Fig. 2(c). Hence in analogy to (1), we obtain Fexc[ρ] = Fexc[ρ + δρ] = Fexc[ρ] + ∫dr(δFexc[ρ]/δρ(r))ϵ ⋅ ∇ ρ(r). Again ϵ is arbitrary. As boundary terms vanish in the considered systems, integration by parts yields
where the first equality expresses the total internal force \({{{{{{\bf{F}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}=-{\langle {\sum }_{i}{\nabla }_{i}u({{{{{{\bf{r}}}}}}}^{N})\rangle }_{{{{{{\rm{eq}}}}}}}\) in DFT language. Hence (6) expresses the fact that the total internal force vanishes in equilibrium; the more general time-dependent case is treated below. The functional derivatives of Fexc[ρ] constitute direct correlation functions9,18,59, with the lowest order being the one-body direct correlation function c1(r) = − δβFexc[ρ]/δρ(r). The equilibrium ("adiabatic”) force field is simply fad(r) = kBT ∇ c1(r). This one-body force field arises from the interparticle forces that all other particles exert on the particle that resides at position r.
From the global internal Noether sum rule (6), we can obtain local sum rules by observing that (6) holds for all ρ(r) and hence that its functional derivative with respect to ρ(r) vanishes identically, i.e.,
where \({c}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )\) is the (inhomogeneous) two-body direct correlation function of liquid state theory18; cn ≡ cn(r1…rn) is the n-body direct correlation function, defined recursively via cn+1 = δcn/δρ(rn+1). As identified by LMBW10,11 and Evans9, (7) expresses the conversion of the density gradient, via the two-body direct correlations, to the locally resolved intrinsic force field; recall that fad(r) = kBT ∇ c1(r). Via the Noether formalism the corresponding hierarchy (8) is obtained straightforwardly from repeated functional differentiation12,13,14 with respect to ρ(r). Note that similar to the structure of (4), only consecutive terms of order n and n + 1 are directly coupled in (8). A multi-body version of (6) is obtained by multiplying (7) with ρ(r), integrating over r, exploiting (6), and iterating for all orders. The result is:
for α = 1…n. In the case α = n = 1 we recover (6).
The global sum rule (6) of vanishing total internal force can be straightforwardly obtained by more elementary analysis. We exploit translation invariance in this non-functional setting: u(rN) ≡ u(r1 + ϵ…rN + ϵ). Then the derivative with respect to ϵ vanishes, 0 = ∂u(r1 + ϵ…rN + ϵ)/∂ϵ = ∑i∇iu(rN). The latter expression follows from the chain rule and constitutes the total internal force (up to a minus sign), which hence vanishes for each microstate rN. The connection to (the many-body version of) Newton’s third law actio equals reactio becomes apparent in the rewritten form − ∇αu(rN) = ∑i≠α∇iu(rN), for α = 1…N. The thermal equilibrium average is then trivial and on average \({{{{{{\bf{F}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}=0\). This argument is very general and it remains true if the average is taken over a nonequilibrium many-body distribution function. The total internal force in such a general situation is
where the average is taken over the nonequilibrium many-body probability distribution at time t. We have hence proven that the total internal force vanishes for all times t. In addition, the particles can possess additional degrees of freedom ωi, i = 1…N, as is the case for the orientation vectors of active Brownian particles, to which we return after first laying out the setup in nonequilibrium.
Nonequilibrium states
To be specific, we consider overdamped Brownian motion, at constant temperature T and with no hydrodynamic interactions present18, as described by the Smoluchowski (Fokker–Planck) equation. The microscopically resolved local internal force field is fint(r, t) = − 〈∑iδ(r − ri)∇iu(rN)〉/ρ(r, t), where the average is over the nonequilibrium distribution (which evolves in time according to the Smoluchowski equation) at time t. The total internal force is then the spatial integral \({{{{{{\bf{F}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}=\int d{{{{{\bf{r}}}}}}\rho ({{{{{\bf{r}}}}}},t){{{{{{\bf{f}}}}}}}_{{{{{{\rm{int}}}}}}}({{{{{\bf{r}}}}}},t)\). Applying Noether’s theorem to the nonequilibrium case requires to have a variational description, as is provided by PFT48. Here the variational fields are the time-dependent density profile ρ(r, t) and the time-dependence one-body current J(r, t) = 〈∑iδ(r − ri)vi〉, where vi(rN, t) is the configurational velocity of particle i. The microscopically resolved average velocity profile is v(r, t) = J(r, t)/ρ(r, t). PFT ascertains the splitting \({{{{{{\bf{f}}}}}}}_{{{{{{\rm{int}}}}}}}({{{{{\bf{r}}}}}},t)={{{{{{\bf{f}}}}}}}_{{{{{{\rm{ad}}}}}}}({{{{{\bf{r}}}}}},t)+{{{{{{\bf{f}}}}}}}_{\sup }({{{{{\bf{r}}}}}},t)\), where the adiabatic force field is that in a corresponding equilibrium (“adiabatic”) system with identical instantaneous density profile, fad(r, t) = − ∇ δFexc[ρ]/δρ(r, t) and \({{{{{{\bf{f}}}}}}}_{\sup }({{{{{\bf{r}}}}}},t)\) is the superadiabatic internal force field, obtained as \({{{{{{\bf{f}}}}}}}_{\sup }({{{{{\bf{r}}}}}},t)=-\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\), where \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]\) is the superadiabatic excess free power functional48.
Crucially, fad(r, t) is a density functional, independent of the flow in the system, while \({{{{{{\bf{f}}}}}}}_{\sup }({{{{{\bf{r}}}}}},t)\) is a kinematic functional, i.e. with dependence on both ρ(r, t) and J(r, t), including memory, i.e. dependence on the value of the fields at times < t. As the local force fields split into adiabatic and superadiabatic contributions, so do the total forces: \({{{{{{\bf{F}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}=\int d{{{{{\bf{r}}}}}}\rho {{{{{{\bf{f}}}}}}}_{{{{{{\rm{int}}}}}}}=\int d{{{{{\bf{r}}}}}}\rho {{{{{{\bf{f}}}}}}}_{{{{{{\rm{ad}}}}}}}+\int d{{{{{\bf{r}}}}}}\rho {{{{{{\bf{f}}}}}}}_{\sup }\equiv {{{{{{\bf{F}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}+{{{{{{\bf{F}}}}}}}_{\sup }^{{{{{{\rm{tot}}}}}}}\). We have seen above that \({{{{{{\bf{F}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}={{{{{{\bf{F}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}=0\). Hence also
While the above reasoning required to rely on the many-body level, the same result (11) can be straightforwardly obtained in a pure Noetherian way, by considering an instantaneous shift of coordinates at time t, i.e. \({{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\to {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)-\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\rho ({{{{{\bf{r}}}}}},t)\), cf. Fig. 3a (Fig. 3 gives an overview of the three different types of shifting). Here \(\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\) is the corresponding instantaneous change in velocity with \({{{{{\bf{v}}}}}}({{{{{\bf{r}}}}}},t)\to {{{{{\bf{v}}}}}}({{{{{\bf{r}}}}}},t)-\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\), as obtained by dividing the current by the density profile. Due to the overdamped nature of the Smoluchowski dynamics, the internal interactions are unaffected and the shift constitutes a symmetry operation for the generator of the superadiabatic forces, \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]\). Hence the instantaneous current perturbation \(\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)=-\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\rho ({{{{{\bf{r}}}}}},t)\) that is generated by the invariance transformation leads to \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]={P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}+\delta {{{{{\bf{J}}}}}}]={P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]-\int d{{{{{\bf{r}}}}}}(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t))\cdot \dot{{{{{{\boldsymbol{\epsilon }}}}}}}\rho ({{{{{\bf{r}}}}}},t)\). As \(\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\) is arbitrary, we obtain (11). Treating the dynamical adiabatic contribution \(\dot{F}[\rho ]=\int d{{{{{\bf{r}}}}}}{{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\cdot \nabla \delta {F}_{{{{{{\rm{exc}}}}}}}[\rho ]/\delta \rho ({{{{{\bf{r}}}}}},t)\) in the same way, we re-obtain (6). As Noether’s theorem is converse, it allows for alternative reasoning: the invariance of \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]\) to the instantaneous shift of the current (or analogously of the velocity) can hence be derived from (11) by simply reversing the above chain of arguments.
All transformations affect both the density profile ρ(r, t) (blue) and the current profile J(r, t) (yellow), while the superadiabatic excess power functional is invariant, \(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}=0\). Here t indicates the time and r is the position coordinate. a An instantaneous spatial shift by \(\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\) at time t induces a current change \(\delta {{{{{\bf{J}}}}}}=-\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\rho\). b A static shift by ϵ = const is applied at all times t. c A time-dependent shift \({{{{{\boldsymbol{\epsilon }}}}}}(t^{\prime} )\) is applied between initial time 0 and final time t of the considered time interval.
We can generate nonequilibrium sum rules by differentiating the Noether identity (11) with respect to J(r, t), which yields
where \({{\mathsf{M}}}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} ,t)=-\beta {\delta }^{2}{P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,t)\) is the tensorial two-body equal-time direct correlation function57,58. Its n-body version is obtained from Mn+1(r1…rn+1, t) = δMn(r1…rn, t)/δJ(rn+1, t), and it satisfies the hierarchy
as obtained by differentiating (12) repeatedly with respect to the current.
Open boundaries
All our considerations have been based on applying the symmetry operation to the entire system confined by external walls. The effects of these system walls are modeled by a suitable form of Vext(r). The position integrals formally run over all space, with the cutoff provided by hard (or steeply rising) external wall potentials. In many practical and relevant situations, it is more useful to consider a system with open boundaries. Alternatively one can consider only a subvolume V of the entire system, and restrict the accounting of force contributions to those particles that reside inside of V at a given time. In doing so, one needs to take account of boundary effects60, as the boundaries of V are open, such that interparticle forces can be transmitted, and flow can occur.
In case that there are no net boundary contributions, all previous derived sum rules still hold. This includes e.g. an effectively one-dimensional system in planar geometry that evolves to the same bulk state at the left and right boundaries or if the boundary conditions are periodic. In both cases left and right boundary terms are equal up to a minus sign and hence cancel each other. This example can be generalized straightforwardly to more complex geometries.
For nonvanishing net boundary terms additional contributions arise in the above sum rules. These contributions occur if the system develops different (bulk) states, e.g. for x → ±∞ as is relevant for bulk phase separation (see the section below). We demonstrate that such cases can be systematically treated in the current framework, by exemplary considering the total internal force. Then boundary force contributions arise due to an imbalance of “outside” particles that exert forces on “inside” particles. The outside particles are per definition excluded from the accounting of the total internal force exerted by all particles inside of V. The sum of all interactions between inside particles vanishes due to the global internal Noether sum rule (10). For simplicity we restrict ourselves to systems that interact via short-ranged pairwise central forces, where Fij indicates the force on particle i exerted by particle j. So only forces exerted from an inside to an outside particle contribute. The total internal force that acts on V is hence \({{{{{{\bf{F}}}}}}}_{{{{{\rm{int}}}}}}^{{{{{\rm{tot}}}}}\,}=\langle \mathop{\sum }\nolimits_{ij}^{\prime}{{{{{{\bf{F}}}}}}}_{ij}\rangle\), where the restricted sum (prime) runs only over those i ∈ V and \(j\in \bar{V}\), where \(\bar{V}\) indicates the complement of V. The total internal force between particles inside of V, i.e. i ∈ V and j ∈ V, vanishes due to (10). We then rewrite \({{{{{{\bf{F}}}}}}}_{{{{{\rm{int}}}}}}^{{{{{\rm{tot}}}}}\,}\) via inserting the identity ∫drδ(r) = 1 twice into the average. Then the restrictions of the sums can be transferred to restrictions on the spatial integration domains. As a result the total internal force acting on V can be expressed via correlation functions as
where ϕ(r) indicates the interparticle pair potential as a function of interparticle distance r. In order to obtain the form (15) we have identified the many-body definition of the radial distribution function \(g({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )=\left\langle \right.{\sum }_{i,j\ne i}\delta ({{{{{\bf{r}}}}}}-{{{{{{\bf{r}}}}}}}_{i})\delta ({{{{{\bf{r}}}}}}^{\prime} -{{{{{{\bf{r}}}}}}}_{j})\rangle /(\rho ({{{{{\bf{r}}}}}})\rho ({{{{{\bf{r}}}}}}^{\prime} ))\). Recall that the pair distribution function g and the density-density correlation function H2, as used in (3)–(5), are related via \({H}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )=(g({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )-1)\rho ({{{{{\bf{r}}}}}})\rho ({{{{{\bf{r}}}}}}^{\prime} )+\delta ({{{{{\bf{r}}}}}}-{{{{{\bf{r}}}}}}^{\prime} )\rho ({{{{{\bf{r}}}}}})\). Equation (15) still holds for non-conservative interparticle forces, when \(-\nabla \phi (| {{{{{\bf{r}}}}}}-{{{{{\bf{r}}}}}}^{\prime} | )\) is replaced by the (nongradient) interparticle force field. We demonstrate in the following section the practical relevance of these considerations.
Phase coexistence
We turn to situations of phase coexistence. As we demonstrate, considering a large, but finite subvolume V of the entire system is useful but it also requires to take boundary terms into account. Here we take V to be cuboidal and to contain the free (planar) interface between two coexisting phases, see Fig. 4a for a graphical illustration. The volume boundaries parallel to the interface are taken to be seated deep inside either bulk phase. The internal force contributions on those faces of V that “cut through” the interface, i.e. have a normal that is perpendicular to the interface normal, vanish by symmetry. It remains to evaluate (15) over each of the two faces in the respective bulk region. Therefore the position dependences simplify to ρ(r) = ρb = const, where ρb indicates the bulk number density, and the inhomogeneous pair distribution function simplifies as \(g({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )=g(| {{{{{\bf{r}}}}}}-{{{{{\bf{r}}}}}}^{\prime} | )\). Furthermore only force contributions colinear with e, the outer interface normal of the considered bulk phase b, contribute. For a single face in bulk phase b, it is straightforward to show that the result is the virial pressure multiplied by the interface area A, i.e. the force \(A{p}_{{{{{\rm{int}}}}}\,}^{b}{{{{{\bf{e}}}}}}\), where the internal interaction pressure \({p}_{{{{{\rm{int}}}}}\,}^{b}\) in phase b is e.g. given via the Clausius virial18, \({p}_{{{{{\rm{int}}}}}\,}^{b}=-\frac{\pi }{2}{\rho }_{b}^{2}\int\limits_{0}^{{r}_{0}}dr\ {r}^{2}g(r)\frac{d\phi }{dr}\) in two spatial dimensions (the argument remains general). The constant r0 denotes the range of the interparticle interactions.
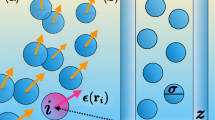
a Illustration of the geometry of phase separation of passive or active particles. Shown are the gaseous ρg and liquid ρl plateau values of the density profile (indicated by the color gradient) and the direction vector e normal to the interface. The total system volume \(V+\bar{V}\) consists of the subvolume V and its complement \(\bar{V}\). b Illustration of an active Brownian particle (blue disc) with position ri and orientation ωi undergoing translational and rotational diffusion. The self propulsion along ωi creates directed motion as indicated by the trajectory (magenta line). c Schematics of motility-induced phase separation into active gas (left) and active liquid phases (right). The arrows indicate the orientations ωi of the active particles. The interface is polarized.
The total force density balance for equilibrium phase separation contains thermal diffusion and the internal force density, which cancel each other,
Integration over the volume V yields the total force which is proportional to the pressure. Hence the total internal force \({{{{{{\bf{F}}}}}}}_{{{{{\rm{int}}}}}}^{{{{{\rm{tot}}}}}\,}={\int}_{V}d{{{{{\bf{r}}}}}}\ \rho {{{{{{\bf{f}}}}}}}_{{{{{\rm{int}}}}}}\) on V, cf. (15), amounts to the pressure difference \(({p}_{{{{{{\rm{int}}}}}}}^{g}-{p}_{{{{{{\rm{int}}}}}}}^{l})A{{{{{\bf{e}}}}}}\), where e is the (unit vector) normal of the interface, pointing from, say, the gas (index g) to the liquid phase (index l). The total diffusive force is \(({p}_{{{{{{\rm{id}}}}}}}^{g}-{p}_{{{{{{\rm{id}}}}}}}^{l})A{{{{{\bf{e}}}}}}\) with the pressure of the ideal gas pid = kBTρ, evaluated at the gas (ρg) and liquid bulk density (ρl). As there are no external forces (Vext ≡ 0) then requesting the volume V to be forcefree amounts to \({p}_{{{{{{\rm{tot}}}}}}}^{g}={p}_{{{{{{\rm{tot}}}}}}}^{l}\), where the total pressure is the sum ptot = pid + pint. Hence the boundary consideration yields the mechanical equilibrium condition of equality of pressure in the coexisting phases.
We conclude that the internal interactions that occur across the free interface do not influence the (bulk) balance of the pressure at phase coexistence, as the net effect of these interactions vanishes. At the heart of this argument lies Noether’s theorem for invariance against spatial displacements.
Anisotropic particles
We turn to anisotropic interparticle interactions, where ωi, ϖi are two perpendicular unit vectors that describes the particle orientation in space. Such systems are described by an interparticle interaction potential u(rN, ωN, ϖN), which is assumed a priori to be invariant under spatial translations. Similarly one-body fields in general depend on position r and orientations ω and ϖ of the particles, e.g. Vext(r, ω, ϖ) for the external field. The fully resolved one-body density distribution is ρ(r, ω, ϖ, t) = 〈∑iδ(r − ri)δ(ω − ωi)δ(ϖ − ϖi)〉.
It is straightforward to ascertain that all the above (force) sum rules for translation remain valid, as the orientations are unaffected by translations, upon trivially generalizing from position-only to position-orientation integration, ∫dr → ∫drdωdϖ etc.
In the following for simplicity of notation we first consider uniaxial particles. Uniaxial particles depend only on one single orientation ωi, as the particles are rotationally invariant around this vector. Hence the ϖ-dependence of both the one- and many-body quantities vanish and the total integral simplifies to ∫drdω.
Motility-induced phase separation
We use active Brownian particles as an example for uniaxial particles. For simplicity we consider spherical particles (discs) in two dimensions. The particles repel each other and they undergo self-propelled motion along their orientation vector ω. Hence an additional one-body force γsω acts on each swimmer, with γ the friction constant and s the speed of free swimming. This self-propulsion creates characteristic trajectories (see Fig. 4b for a schematic) which are also affected by thermal diffusion (omitted in the schematic) of the particle position ri and orientation ωi. Experimental realizations of active Brownian particles include e.g. Janus colloids driven by photon nudging61,62,63,64,65. If the density is high enough, motility-induced phase separation (MIPS) into an active gas and active liquid phase occurs for high enough values of the swim speed s, cf. Fig. 4c.
The force density balance (see e.g. the work of Hermann et al.52) of such a system in steady state (no time dependence) is
The (negative) frictional force density on the left hand side is balanced with the ideal gas contribution (first term), the interparticle interactions (second term), the self-propulsion (third term) and the external contribution (fourth term) on the right hand side. As in case of the equilibrium phase separation we integrate (17) over the volume V (see Fig. 4(a) for an illustration) and over all orientations ω. In the following we discuss each term separately. For simplicity we assume planar geometry of the system and we assume a vanishing external force, fext(r, ω) = 0. Here, the interaction contribution pintAe is obtained as above in equilibrium via (15), but the virial is averaged over the nonequilibrium steady state many-body probability distribution. The integral over the current ∫drdωJ is assumed to vanish in steady state.
The total swim force that acts on V contributes to the total force. In the considered situation, the swim force is entirely due to the polarization Mtot = ∫drdω ωρ of the free interface in MIPS. Particles at the interface tend to align against the dense phase43 if they interact purely repulsively (cf. Fig. 4(c)), and they align against the dilute phase if interparticle attraction is present44. No such spontaneous polarization occurs in bulk. The interface polarization is a state function of the coexisting phases53 as verified both experimentally66 and numerically67. The total swim force that acts on V is \(({p}_{{{{{{\rm{swim}}}}}}}^{g}-{p}_{{{{{{\rm{swim}}}}}}}^{l})A{{{{{\bf{e}}}}}}\), where \({p}_{{{{{{\rm{swim}}}}}}}^{b}=\gamma s{J}_{b}/(2{D}_{{{{{{\rm{rot}}}}}}})\), with Jb the bulk current in the forward direction ω and Drot indicating the rotational diffusion constant. Apart from the ideal term no further forces act, cf. the force density balance (17). The integral over the ideal term is similar to the total equilibrium ideal contribution, \(({p}_{{{{{\rm{id}}}}}}^{g}-{p}_{{{{{\rm{id}}}}}}^{l})A{{{{{\bf{e}}}}}}\). Combination of all results from integration yields the total force balance.
As the negative integral over the force density defines the nonequilibrium pressure, the volume V being force free amounts to \({p}_{{{{{{\rm{tot}}}}}}}^{g}={p}_{{{{{{\rm{tot}}}}}}}^{l}\), where \({p}_{{{{{{\rm{tot}}}}}}}={p}_{{{{{{\rm{id}}}}}}}+{p}_{{{{{{\rm{int}}}}}}}+{p}_{{{{{{\rm{swim}}}}}}}\). Hermann et al.52 demonstrate the splitting of pint into adiabatic and superadiabatic contributions and present results for the phase diagram based on approximate forms for the interparticle interaction contributions. The pressure, especially its swim contribution is defined in various different ways in the literature68,69,70,71,72,73.
We conclude that the internal interactions that occur across the free interface do not influence the (bulk) balance of the pressure at phase coexistence, as the net effect of these interactions vanishes. In essence this argument follows from Noether’s theorem for invariance against spatial displacements.
Active sedimentation
Sedimentation under the influence of gravity is a ubiquitous phenomenon in soft matter that has attracted considerable interest, e.g. for colloidal mixtures74,75,76,77 and for active systems78,79,80,81. As sedimentation is a force driven phenomenon the Noether sum rules apply directly, as we show in the following.
We assume that the system is translationally invariant in the x-direction and that an impenetrable wall at z = 0 acts as a lower boundary of the system82 (cf. Fig. 5). We assume the wall-particle interaction potential to be short-ranged. Its precise form is irrelevant for the following considerations. The force density balance for such a system is (17) with the external force field chosen as
where m denotes the mass of a particle, g is the gravitational acceleration and ez indicates the unit vector in z-direction. Hence the external force field fext consists of gravity and the wall contribution fwall.
The active particles with orientation ω (black arrows) are confined by a lower wall and periodic boundary conditions on the sides (dashed lines). The total force that the swimming particles exert on the bottom wall (left scale pan) is equal to their weight (right scale pan) in steady states of the system.
To proceed we integrate the force density balance over all positions r in the volume V and over all orientations ω. The total integral of the density distribution (per radiant) ∫drdωρ, as appears in the gravitational term, gives the total number of particles N. The integral over the total current ∫drdω J is proportional to the center of mass velocity \({{{{{{\bf{v}}}}}}}_{{{{{\rm{cm}}}}}}(t)=\int d{{{{{\bf{r}}}}}}d{{{{{\boldsymbol{\omega }}}}}}\ \rho {{{{{\bf{v}}}}}}/\int d{{{{{\bf{r}}}}}}d{{{{{\boldsymbol{\omega }}}}}}\ \rho =\frac{1}{N}\int d{{{{{\bf{r}}}}}}d{{{{{\boldsymbol{\omega }}}}}}\ {{{{{\bf{J}}}}}}\). Here vcm(t) is a global quantity and hence it is independent of both position and orientation. We first only consider steady states, so the center of mass velocity vcm(t) = 0 and hence the total current vanishes. The total thermal diffusion term vanishes because ∫dr ∇ ρ = ∂V dS ρ = 0 as there is no contribution of ρ from the boundaries ∂V of the integration volume V. At the upper and lower boundary the density is zero as it vanishes in the wall and also for z → ∞. The left and the right boundary contributions cancel each other as the density is independent of x due to translational invariance. The total internal interaction force density vanishes, \({{{{{{\bf{F}}}}}}}_{{{{{\rm{int}}}}}}^{{{{{\rm{tot}}}}}\,}=\int d{{{{{\bf{r}}}}}}d{{{{{\boldsymbol{\omega }}}}}}\ \rho {{{{{{\bf{f}}}}}}}_{{{{{\rm{int}}}}}}=0\), using the global internal Noether sum rule (10). The integrated swim force density is proportional to the total polarization Mtot = ∫drdω ωρ. This quantity vanishes, Mtot = 0, as there is no net flux through the boundaries in steady state (see Eq. (10) by Hermann et al.53). Combination of all integrals yields the relation
Hence the z-component of the total force on the wall \({F}_{{{{{\rm{wall}}}}}}^{{{{{\rm{tot}}}}}\,}\) is equal to the total gravitational force acting on all particles (see Fig. 5 for a graphical representation). Equation (19) of course also holds for passive colloids (s = 0).
Keeping the translational invariance in the x-direction, we next turn to time-dependent systems. Therefore all one-body field in (17) additionally depend on the time t. Integration of the force density balance (17) gives identical results for the thermal diffusion, the internal force density and for the gravitational contribution as in the above case of steady state. Even for the time-dependent dynamics these integrals are independent of time t. The total wall force density is given as \({{{{{{\bf{F}}}}}}}_{{{{{\rm{wall}}}}}}^{{{{{\rm{tot}}}}}}={F}_{{{{{\rm{wall}}}}}}^{{{{{\rm{tot}}}}}\,}{{{{{{\bf{e}}}}}}}_{z}\) and it only acts along the unit vector in the z-direction ez, due to the symmetry of the system. The integral of the self-propulsion term is still proportional to the total polarization. However, the total polarization does not vanish in general but decays exponentially (see Eq. (21) by Hermann et al.53),
where Mtot(0) indicates the initial polarization at time t = 0 and the time constant 1/Drot is the inverse rotational diffusion constant. Similarly, integration of the current still gives the (time-dependent) center of mass velocity vcm(t).
Insertion of these results into the spatial and orientational integration of (17) leads to the total friction force
which is hence a direct consequence of the Noether sum rule (10). We find that the x-component of the center of mass velocity decays simultaneously with the total polarization, cf. the first term on the right hand side of (21). The z-component of vcm(t) depends on Mtot(t) and additionally on the time-dependent total force exerted by the wall and the total graviational force. Hence measuring the total force on the wall (i.e. by weighing, cf. Fig. 5) and knowledge of the total initial polarization and the total particle number allows one to determine the center of mass velocity. Note that in the limit of long times, t → ∞, the total polarization vanishes and this system evolves to a steady state. Hence the center of mass velocity vanishes and (19) is recovered. As we have demonstrated both statements (19) and (21) ultimately follow from the global Noether identity (10).
Rotational invariance
We return to the general case and initially consider spatial rotations in systems of spheres, i.e. systems where u(rN) depends solely on (relative) particle positions, and where it is invariant under global rotation of all rN around the origin. We parameterize the rotation by a vector n. The direction of n indicates the rotation axis and the modulus ∣n∣ is the angle of rotation. To lowest nonvanishing order, the rotation amounts to r → r + n × r. One-body functions change accordingly: the external potential undergoes Vext(r) → Vext(r) + δVext(r), with δVext(r) = (n × r) ⋅ ∇ Vext(r) and the density profile ρ(r) → ρ(r) + δρ(r) with δρ(r) = (n × r) ⋅ ∇ ρ(r). Much of the reasoning of the above case of spatial displacement can be applied readily: Ω[Vext] is invariant under the rotation, and δΩ = ∫dr(δΩ/δVext(r))δVext(r) = ∫drρ(r)(n × r) ⋅ ∇ Vext(r) = 0. As the rotation vector n is arbitrary, we can conclude that the total external torque \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{ext}}}}}}}^{{{{{{\rm{tot}}}}}}}\) vanishes in equilibrium13,
As this holds true for any form of the applied Vext(r), we can differentiate with respect to \({V}_{{{{{{\rm{ext}}}}}}}({{{{{\bf{r}}}}}}^{\prime} )\), and obtain13
The excess free energy density functional Fexc[ρ] can be treated accordingly. It is invariant under rotation, as its sole dependence is on u(rN), which by assumption is rotationally invariant. Analogous to this reasoning, we obtain the result that the total interparticle adiabatic torque \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}\) vanishes,
Differentiation with respect to the independent field ρ(r) once and n times yields the respective identities13,14:
The multi-body versions of the theorems of vanishing total external (22) and adiabatic internal (25) torques are, respectively,
and
for α = 1…n. These identities are respectively derived from (23) by multiplying with Vext(r), integrating over r and exploiting (22), and from (26) by multiplying with ρ(r), integrating over r and exploiting (25), and iteratively repeating for each order n.
On the many-body level, it is straightforward to see that the total internal torque − ∑i(ri × ∇iu(rN)) = 0. Hence, as this identity holds for each microstate, its general, nonequilibrium average vanishes, \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}=0\). The force field splitting \({{{{{{\bf{f}}}}}}}_{{{{{{\rm{int}}}}}}}={{{{{{\bf{f}}}}}}}_{{{{{{\rm{ad}}}}}}}+{{{{{{\bf{f}}}}}}}_{\sup }\) induces corresponding additive structure for the internal total torque: \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}={{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}+{{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{\sup }^{{{{{{\rm{tot}}}}}}}\), with the total superadiabatic (internal) torque \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{\sup }^{{{{{{\rm{tot}}}}}}}=\int d{{{{{\bf{r}}}}}}\rho ({{{{{\bf{r}}}}}})[{{{{{\bf{r}}}}}}\times {{{{{{\bf{f}}}}}}}_{\sup }({{{{{\bf{r}}}}}},t)]\). As \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}={{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}=0\), we conclude \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{\sup }^{{{{{{\rm{tot}}}}}}}=0\), ∀ t.
To apply Noether’s theorem to the power functional, we consider an instantaneous rotation, with infinitesimal angular velocity \(\dot{{{{{{\bf{n}}}}}}}\) at time t. The effect is a change in current J → J + δJ with \(\delta {{{{{\bf{J}}}}}}=(\dot{{{{{{\bf{n}}}}}}}\times {{{{{\bf{r}}}}}})\rho ({{{{{\bf{r}}}}}})\). Correspondingly, the velocity field acquires an instantaneous global rotational contribution, according to \({{{{{\bf{v}}}}}}({{{{{\bf{r}}}}}},t)\to {{{{{\bf{v}}}}}}({{{{{\bf{r}}}}}},t)+\dot{{{{{{\bf{n}}}}}}}\times {{{{{\bf{r}}}}}}\). The superadiabatic excess power functional is invariant under this operation and hence \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]={P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}+\delta {{{{{\bf{J}}}}}}]={P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]+{\!\!}\int d{{{{{\bf{r}}}}}}(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t))\cdot (\dot{{{{{{\bf{n}}}}}}}\times {{{{{\bf{r}}}}}})\rho ({{{{{\bf{r}}}}}},t)\). As \(\dot{{{{{{\bf{n}}}}}}}\) is arbitrary, we can conclude
as is consistent with the result of the above many-body derivation. As (30) holds for any (trial) J(r, t), the derivative of (30) with respect to J(r, t) vanishes. Hence
where the cross product with a tensor is defined via contraction with the Levi-Civita tensor. At nth order we obtain
This identity and (31) express the vanishing of the total superadiabatic torque, when resolved on the n-body level of (time direct) correlation functions.
Orbital and spin coupling
The case of rotational symmetry of uniaxial particles is clearly more complex, as both particle coordinates and particle orientations are affected by a global (“rigid”) operation on the entire system, i.e. both positions and orientations are rotated consistently. Noether’s theorem ensures though that this operation is indeed the fundamental one, and that the physically expected coupling of orbital and spinning effects will naturally and systematically emerge. Here we use (common) terminology for referring to spin as orientation vector rotation (i.e. particle rotation around its center), as opposed to orbital rotation (of position vector) around the origin of position space. Hence all the above considered torques that already occur in systems of spheres are of orbital nature. These of course remain relevant for anisotropic particles, but the nontrivial orientational behavior of the latter will generate additional spin torques. The global rotation consists of an orbital part, r → r + n × r, and a spin part, ω → ω + n × ω; see Fig. 6 for a graphical representation.
For anisotropic systems the external field naturally acquires dependence on position r and orientation ω, i.e. Vext(r, ω), where −∇ Vext(r, ω) is the external force field as before, and −ω × ∇ωVext(r, ω) is the external torque field, where ∇ω is the derivative with respect to ω in orientation space. Hence the induced change of external potential is δVext(r, ω) = (n × r) ⋅ ∇ Vext + (n × ω) ⋅ ∇ωVext. This change leaves the grand potential Ω[Vext] invariant, hence δΩ = ∫drdω(δΩ/δVext(r, ω))n ⋅ (r × ∇ Vext + ω × ∇ωVext) = 0, from which we identify the rotational Noether theorem for the total external torque of anisotropic particles:
Differentiation with respect to Vext(r, ω) yields
where we have used \(V_{{{{{{\rm{ext}}}}}}}^{\prime} ={V}_{{{{{{\rm{ext}}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,{{{{{\boldsymbol{\omega }}}}}}^{\prime} )\) as a shorthand, \({H}_{2}({{{{{\bf{r}}}}}},{{{{{\boldsymbol{\omega }}}}}},{{{{{\bf{r}}}}}}^{\prime} ,{{{{{\boldsymbol{\omega }}}}}}^{\prime} )=-\delta \rho ({{{{{\bf{r}}}}}},{{{{{\boldsymbol{\omega }}}}}})/\delta \beta {V}_{{{{{{\rm{ext}}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,{{{{{\boldsymbol{\omega }}}}}}^{\prime} )\) is the density-density correlation function, and its n-body version Hn = Hn(r1, ω1…rn, ωn) with Hn+1 = δHn/δβVext(rn+1, ωn+1); in (35) the prime refers to the n + 1th degrees of freedom. On all levels of n-body correlation functions, the spin and orbital torques remain coupled.
Turning to internal torques, the change of density upon global rotation is δρ(r, ω) = n ⋅ (r × ∇ ρ + ω × ∇ωρ) and the net effect on the excess free energy is δFexc = ∫drdω(δFexc[ρ]/δρ(r, ω))n ⋅ (r × ∇ ρ + ω × ∇ωρ) = 0. We hence obtain
where the adiabatic spin torque field is τad(r, ω) =− ω × ∇ωδFexc[ρ]/δρ(r, ω). From differentiation with respect to ρ(r, ω) we obtain
where \(\rho ^{\prime} =\rho ({{{{{\bf{r}}}}}}^{\prime} ,{{{{{\boldsymbol{\omega }}}}}}^{\prime} )\). Multi-body versions of (33) and (36) read as
and
Here we have used the shorthand notation 1 ≡ r1, ω1 etc., and the derivation is analogous to the above rotational case of spherical particles.
The two-body sum rules (34) and (37) are identical to those obtained by Tarazona and Evans16 using rotational invariance arguments applied directly to correlation functions. Our methodology not only allows to naturally re-derive their results, but also to identify the full gamut of adiabatic rotatational sum rules, from the global statements (33) and (36) to the infinite hierarchies (35) and (38) (we use notational convention different from Tarazona and Evans16: our ∇ω is (only) a partial derivative with respect to ω, i.e. ∇ω ≡ ∂/∂ω, whereas their ∇ω ≡ ω × ∂/∂ω. The modulus is fixed, ∣ω∣ = 1, in both versions. Tarazona and Evans16 notate H2 as G in their (18) and (19)).
Again for each microstate \({\sum }_{i}({{{{{{\bf{r}}}}}}}_{i}\times {\nabla }_{i}u+{{{{{{\boldsymbol{\omega }}}}}}}_{i}\times {\nabla }_{i}^{\omega }u)=0\) and hence on average \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}=0\). From the splitting \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{int}}}}}}}^{{{{{{\rm{tot}}}}}}}={{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{{{{{{\rm{ad}}}}}}}^{{{{{{\rm{tot}}}}}}}+{{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{\sup }^{{{{{{\rm{tot}}}}}}}\), we conclude \({{{{{{\boldsymbol{{{{{{\mathcal{T}}}}}}}}}}}}}_{\sup }^{{{{{{\rm{tot}}}}}}}=0\). From rotational invariance of \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}},{{{{{{\bf{J}}}}}}}^{\omega }]\), where Jω(r, ω, t) is the rotational current50, against an instantaneous angular “kick” \(\delta {{{{{\bf{J}}}}}}=(\dot{{{{{{\bf{n}}}}}}}\times {{{{{\bf{r}}}}}})\rho\) and \(\delta {{{{{{\bf{J}}}}}}}^{\omega }=(\dot{{{{{{\bf{n}}}}}}}\times {{{{{\boldsymbol{\omega }}}}}})\rho\), we find
Local sum rules can be obtained straightforwardly by building derivatives with respect to J(r, ω, t) and Jω(r, ω, t). The result is:
Here the tensorial equal-time direct correlation functions are defined as \({{\mathsf{M}}}_{n,m}=-\beta {\delta }^{n+m}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}(1)\ldots \delta {{{{{\bf{J}}}}}}(n)\delta {{{{{{\bf{J}}}}}}}^{\omega }(n+1)\ldots {{{{{{\bf{J}}}}}}}^{\omega }(n+m)\), where the roman numerals refer to position, orientation and time t (no index), e.g. 1 ≡ r1, ω1, t. We have assumed that all functional derivatives commute.
So far we have restricted ourselves to uniaxial particles. The derived rotational sum rules can be analogously determined for general anisotropic particles with an additional orientation vector ϖ. This can be done by simply replacing ω × ∇ω → ω × ∇ω + ϖ × ∇ϖ, \({{{{{\boldsymbol{\omega }}}}}}\times {\partial }/{\partial {{{{{{\bf{J}}}}}}}^{\omega }}\to {{{{{\boldsymbol{\omega }}}}}}\times {\partial }/{\partial {{{{{{\bf{J}}}}}}}^{\omega }}+{{{{{\boldsymbol{\varpi }}}}}}\times {\partial }/{\partial {{{{{{\bf{J}}}}}}}^{\varpi }}\) and ∫drdω → ∫drdωdϖ in (33)–(42). This replacement also affects the adiabatic spin torque field τad and all one-body field depend additionally to r and ω on the orientation ϖ. For anisotropic particles there exists a more general version of (42) by exchange of Mn,m → Mn,m,l, where l denotes the number of functional derivations with respect to the rotational current Jϖ. The indices n and m belong to the number of functional derivatives with respect to J and Jω as before.
Memory invariance
In the above treatment of nonequilibrium situations we have exploited invariance against an instantaneous transformation applied to the system. As we have shown, the corresponding Noether identities carry imminent physical meaning. These sum rules hold for the nonequilibrium effects that arise from the interparticle interaction, i.e. they constrain superadiabatic forces and torques, as obtained from translation and rotation, respectively. Here we exploit that the corresponding nonequilibrium functional generator \({P}_{t}^{{{{{{\rm{exc}}}}}}}\) carries further invariances, once one allows the transformation to act also on the history of the system. As we demonstrate in the following, the resulting identities constitute exact constraints on the memory structure that are induced by the coupled interparticle interactions. Recall that a reduced one-body description of a many-body system is generically non-Markovian (i.e. nonlocal in time)83. The study of memory kernels, often carried out in the framework of generalized Langevin equations, is a topic of significant current research activity84,85,86,87,88,89,90,91.
Our approach differs from these efforts in that no a priori generic form of a reduced equation of motion is assumed. Rather our considerations are formally exact and interrelate (and hence constrain) time correlation functions, which are generated from the central nonequilibrium object \({P}_{t}^{{{{{{\rm{exc}}}}}}}\) via functional differentiation. Very little is known about the memory structure of superadiabatic forces, with exceptions being the NOZ framework57,58 and the demonstration of the relevance of memory for the observed viscoelasticity of hard sphere liquids92. Both the Ornstein–Zernike (OZ) and NOZ relations are different from the Noether identities. The former relations are a direct consequence of the generality of the variational principle. Per se, neither the OZ nor the NOZ relations reflect the Noether symmetries.
Recalling the illustrated overview of the different types of shifting in Fig. 1, in the following we treat two further types of invariance transformations: One is the static transformation. This operation is formally analogous to the above equilibrium treatment of the adiabatic state, but it is here carried out in the same way at all times. This static transformation contrasts (and complements) the instantaneous transformation used above for the time-dependent case. The corresponding changes to density and current are graphically illustrated in Fig. 3b. The second invariance operation is that of memory shifting, where the transformation parameter is taken to be time-dependent, cf. Fig. 3c for a graphical representation. For simplicity we restrict ourselves to cases where at both ends of the considered time interval, no shifting occurs (i.e. such that the transformation is the identity at the limiting times).
The static spatial shift consists of \(\rho ({{{{{\bf{r}}}}}},t^{\prime} )\to \rho ({{{{{\bf{r}}}}}}+{{{{{\boldsymbol{\epsilon }}}}}},t^{\prime} )\) and \({{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t^{\prime} )\to {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}}+{{{{{\boldsymbol{\epsilon }}}}}},t^{\prime} )\), where the time argument \(t^{\prime}\) is arbitrary, and ϵ = const characterizes magnitude and direction of the translation, see the illustration in Fig. 3b. Hence the time derivative \(\dot{{{{{{\boldsymbol{\epsilon }}}}}}}=0\) such that the current does not acquire any displacement contribution, as also \(-\dot{{{{{{\boldsymbol{\epsilon }}}}}}}\rho =0\) at all times. The spatial shift applies to all times \(t^{\prime}\) considered, and we can restrict ourselves to \(0\le t^{\prime} \le t\). Hence the changes in kinematic fields are to first order given by \(\delta \rho ({{{{{\bf{r}}}}}},t^{\prime} )={{{{{\boldsymbol{\epsilon }}}}}}\cdot \nabla \rho ({{{{{\bf{r}}}}}},t^{\prime} )\) and \(\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t^{\prime} )={{{{{\boldsymbol{\epsilon }}}}}}\cdot \nabla {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t^{\prime} )\). As \({P}_{t}^{{{{{{\rm{exc}}}}}}}\) originates solely from the interparticle interaction potential, the invariance of u(rN) against the global displacement at all times induces invariance of \({P}_{t}^{{{{{{\rm{exc}}}}}}}\). Hence \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]={P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho +\delta \rho ,{{{{{\bf{J}}}}}}+\delta {{{{{\bf{J}}}}}}]={P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]+\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}\). Here \(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}\) indicates the change in superadiabatic free power and due to the invariance \(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}=0\). On the other hand we can express \(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}\) via the functional Taylor expansion. To linear order the result consists of two integrals. One integral comes from the time-slice functional derivative at fixed (end) time t and is given by \(\int d{{{{{\bf{r}}}}}}[(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta \rho )\delta \rho +(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}})\cdot \delta {{{{{\bf{J}}}}}}]\). The second integral is from a functional derivative at (variable) time \(t^{\prime}\), given by \(\int\nolimits_{0}^{t}dt^{\prime} \int d{{{{{\bf{r}}}}}}^{\prime} [(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta \rho ^{\prime} )\delta \rho ^{\prime} +(\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}^{\prime} )\cdot \delta {{{{{\bf{J}}}}}}^{\prime} ]\), where the prime indicates dependence on arguments \({{{{{\bf{r}}}}}}^{\prime}\) and \(t^{\prime}\). We then exploit that the displacement ϵ of the static shift (which parametrizes the changes in density and in current) is arbitrary. The result is a global nonequilibrium Noether theorem, given by
where we have used the relationship of the superadiabatic force field to its generator, \({{{{{{\bf{f}}}}}}}_{\sup }({{{{{\bf{r}}}}}},t)=-\delta {P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho ,{{{{{\bf{J}}}}}}]/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\), the primed symbol \(\nabla ^{\prime}\) indicates the derivative with respect to \({{{{{\bf{r}}}}}}^{\prime}\), and the superscript T denotes the matrix transpose (in index notation the k-component of the vector a ⋅ ∇ bT is \({\sum }_{k^{\prime} }{a}_{k^{\prime} }{\nabla }_{k}{b}_{k^{\prime} }\)).
Equation (43) constitutes a global identity that links density, current, and superadiabatic force field in a nontrivial spatial and temporal form. As the central variation principle48 allows to vary J(r, t) freely, (43) remains true upon building the functional derivative with respect to J(r, t). The result is a local identity
where two-body time direct correlation functions occur in vectorial form: \({{{{{{\bf{m}}}}}}}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} ,t)=-\beta {\delta }^{2}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\delta \rho ({{{{{\bf{r}}}}}}^{\prime} ,t)\), \({{{{{{\bf{m}}}}}}}_{2}({{{{{\bf{r}}}}}},t,{{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )=-\beta {\delta }^{2}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\delta \rho ({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )\), as well as in tensorial form: \({{\mathsf{M}}}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} ,t)=-\beta {\delta }^{2}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,t)\), \({{\mathsf{M}}}_{2}({{{{{\bf{r}}}}}},t,{{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )=-\beta {\delta }^{2}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}},t)\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )\). Here we have made the (common) assumption that the second derivatives can be interchanged.
Repeated differentiation of (44) with respect to J(r, t) generates a hierarchy,
where the n-body equal-time direct correlation functions of rank n are \({{\mathsf{M}}}_{n}({{{{{{\bf{r}}}}}}}^{n},t)=-\beta {\delta }^{n}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{1},t)\ldots \delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{n},t)\) and \({{{{{{\bf{m}}}}}}}_{n}({{{{{{\bf{r}}}}}}}^{n},t)=-\beta {\delta }^{n}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{1},t)\ldots \delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{n-1},t)\delta \rho ({{{{{{\bf{r}}}}}}}_{n},t)\), where we have used the shorthand rn = r1…rn. Furthermore at unequal times we have: \({{\mathsf{M}}}_{n}({{{{{{\bf{r}}}}}}}^{n-1},t,{{{{{{\bf{r}}}}}}}_{n},t^{\prime} )=-\beta {\delta }^{n}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{1},t)\ldots \delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{n-1},t)\delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{n},t^{\prime} )\) as a rank n tensor, and also a rank n − 1 tensor \({{{{{{\bf{m}}}}}}}_{n}({{{{{{\bf{r}}}}}}}^{n-1},t,{{{{{{\bf{r}}}}}}}_{n},t^{\prime} )=-\beta {\delta }^{n}{P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{1},t)\ldots \delta {{{{{\bf{J}}}}}}({{{{{{\bf{r}}}}}}}_{n-1},t)\delta \rho ({{{{{{\bf{r}}}}}}}_{n},t^{\prime} )\).
In the second case, we consider a more general invariance transformation that is obtained by letting the transformation parameter be time-dependent. In this case of time-dependent shifting, we prescribe a displacement vector \({{{{{\boldsymbol{\epsilon }}}}}}(t^{\prime} )\) for times \(0\le t^{\prime} \le t\), i.e. between the initial time, throughout the past and up to the "current” time t. We restrict ourselves to vanishing shift at the boundaries of the considered time interval, i.e. ϵ(0) = ϵ(t) = 0. Due to the overdamped character of the dynamics, its interparticle contributions are unaffected by this transformation, and hence \({P}_{t}^{{{{{{\rm{exc}}}}}}}\) is invariant. The induced changes that the density and the current acquire arise from shifting their position argument, but the current also acquires an additive shifting current contribution. The latter contribution is analogous to the (sole) effect that is present in the instantaneous shifting, but here applicable at all times (in the considered time interval).
Hence the time-dependent shifting, as illustrated in Fig. 3c, induces the following changes to the density and the current: \(\delta \rho ({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )={{{{{\boldsymbol{\epsilon }}}}}}(t^{\prime} )\cdot \nabla ^{\prime} \rho ({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )\) and \(\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )={{{{{\boldsymbol{\epsilon }}}}}}(t^{\prime} )\cdot \nabla {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )-\dot{{{{{{\boldsymbol{\epsilon }}}}}}}(t^{\prime} )\rho ({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )\), where \(\dot{{{{{{\boldsymbol{\epsilon }}}}}}}(t^{\prime} )=d{{{{{\boldsymbol{\epsilon }}}}}}(t^{\prime} )/dt^{\prime}\). Next we can regard \({P}_{t}^{{{{{{\rm{exc}}}}}}}[\rho +\delta \rho ,{{{{{\bf{J}}}}}}+\delta {{{{{\bf{J}}}}}}]\) as a functional of \({{{{{\boldsymbol{\epsilon }}}}}}(t^{\prime} )\) and \(\dot{{{{{{\boldsymbol{\epsilon }}}}}}}(t^{\prime} )\). Its invariance amounts to stationarity, i.e. vanishing first functional derivative, with respect to the displacement. This problem, in particular for the present case of fixed boundary values, amounts to one of the most basic problems in the calculus of variations. It is realized, e.g., in the determination of catenary curves and indeed, in Hamilton’s principle of classical mechanics. Exploiting the corresponding Euler–Lagrange equation leads to
where the one-body time direct correlation functions are \({{{{{{\bf{m}}}}}}}_{1}^{\prime}({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} ,t)=-\beta \delta {P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta {{{{{\bf{J}}}}}}({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )\) and \({m}_{1}^{\prime}({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} ,t)=-\beta \delta {P}_{t}^{{{{{{\rm{exc}}}}}}}/\delta \rho ({{{{{\bf{r}}}}}}^{\prime} ,t^{\prime} )\). Differentiation with respect to J(r, t) yields again a local memory identity.
Conclusions
We have demonstrated that Noether’s theorem for exploiting symmetry in a variational context has profound implications for Statistical Physics. Known sum rules can be derived with ease and powerfully generalized to full infinite hierarchies, to the rotational case, and to time-dependence in nonequilibrium. Recall the selected applications31,32,33,34,35,36,37,38,39,40,41 of the equilibrium sum rules, as we have laid out in the introduction. For the time-dependent case, we envisage similar insights from using the newly formulated nonequilibrium sum rules in investigations of e.g., the dynamics of freezing, of liquid crystal flow, and of driven fluid interfaces. On the conceptual level, Noether’s theorem assigns a clear meaning and physical interpretation to all resulting identities, as being generated from an invariance property of an underlying functional generator. Although the symmetry operation that we considered are simplistic, and only their lowest order in a power series expansion needs to be taken into account, a significantly complex body of sum rules naturally emerges. Hence the application of Noether’s theorem is significantly deeper than mere exploiting of symmetries of arguments of correlation functions, i.e. that the direct correlation function \({c}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )\) in bulk fluids depends solely on \(| {{{{{\bf{r}}}}}}-{{{{{\bf{r}}}}}}^{\prime} |\). Rather, as governed by functional calculus, coupling of different levels of correlation functions occurs.
The Noether sum rules are different from the variational principle, as embodied in the Euler–Lagrange equation. On the formal level, the difference is that the Euler–Lagrange equation (both of DFT and of PFT) is a formally closed equation on the one-body level. In contrast, the Noether rules couple n- and (n + 1)-body correlation functions, hence they are of genuine hierarchical nature. They also describe different physics, as the Euler–Lagrange equation expresses a chemical potential equilibrium in DFT and the local force balance relationship in PFT. In contrast, the Noether identities stem from the symmetry properties of the respective underlying physical system.
The standard DFT approximations, ranging from simple local, square-gradient, and mean-field functional to more sophisticated weighted-density-schemes including fundamental measure theory satisfy the internal force relationships. This can be seen straightforwardly by observing that these functionals do satisfy global translation invariance (the value of the free energy is independent of the choice of coordinate origin). All higher-order Noether identities are then automatically satisfied, as these inherit the correct symmetry properties from the generating (excess free energy) functional. Our formalism hence provides a concrete reason, over mere empirical experience, why the practitioners’ choices for approximate functionals are sound. The situation for more complex DFT schemes could potentially be different though. As soon as, say, self-consistency of some form is imposed, or coupling to auxiliary field comes into play, it is easy to imagine that the Noether identities help in restricting choices in the construction of such approximation schemes.
The sum rules imposed by the three types of dynamical displacements are satisfied within the velocity gradient form of the power functional54,56. It is straightforward to see that the functional is independent of the coordinate origin (static shifting). For the cases of dynamical shifting, the invariance of the functional stems from invariance of the velocity field against shifting. For both instantaneous and memory shifting, the velocity gradient remains invariant under the displacement.
We envisage that the higher than two-body Noether identities can facilitate the construction of advanced liquid state/density functional approximations. Such work should surely be highly challenging. In the context of fundamental measure theory (see e.g. the work by Roth20 for an enlightening review) it is worth recalling that in Rosenfeld’s original 1989 paper93, he calculated the three-body direct correlation function from his then newly proposed functional. The result for the corresponding three-body pair correlations compared favorably against simulation data. Furthermore, the recent insights into two-body correlations in inhomogeneous liquids94 and crystals95 demonstrates that working with higher-body correlation functions is feasible.
In future work it would be very beneficial to bring together the Noether identities with the nonequilibrium Ornstein–Zernike relations57,58, in order to aid construction of new dynamical approximations. One could exploit the rotational invariance of the superadiabatic excess power functional \({P}_{t}^{{{{{{\rm{exc}}}}}}}\) to gain deeper insights in its memory structure and also generalize the translational memory relations (43)–(46) to anisotropic particles. It would be highly interesting to apply (49) to the recently obtained direct correlation function of the hard sphere crystal. This would allow to investigate whether Triezenberg and Zwanzig’s concept that they originally developed for the free gas–liquid interface applies to the also self-sustained density inhomogeneity in a solid. Furthermore, addressing further cases of self motility42,43,44, including active freezing96,97, as well as further types of time evolution, such as molecular dynamics or quantum mechanics should be interesting. This is feasible, as the Noether considerations are not restricted to overdamped classical systems, as (formal) power functional generators exist for quantum98 and classical Hamiltonian99 many-body systems. On the methodological side, besides power functional theory, our framework could be complemented by e.g. mode-coupling theory and Mori-Zwanzig techniques100, as well as approaches beyond that101. Given that the equilibrium force sum rules are crucial in the description of crystal33,34 and liquid crystal35 excitations, the study of such systems under drive is a further exciting prospect.
Methods
Relationship to classical results
We give an overview of how the Noether sum rules relate to previously known results. The famous LMBW-equation was derived independently by Lovett et al.10 and by Wertheim11 and reads
We can conclude that (47) is a combination of the local internal Noether sum rule (7) for translational symmetry and the equilibrium Euler–Lagrange equation \({c}_{1}({{{{{\bf{r}}}}}})={{{{{\mathrm{ln}}}}}}\,\rho ({{{{{\bf{r}}}}}})+\beta \nabla {V}_{{{{{\rm{ext}}}}}}({{{{{\bf{r}}}}}})-\beta \mu\), where μ indicates the chemical potential. LMBW also derived a lesser known external relation, which is equivalent to (47) and reads
We find that (48) contains the local external Noether sum rule (3) along with the relation \({H}_{2}({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )=(g({{{{{\bf{r}}}}}},{{{{{\bf{r}}}}}}^{\prime} )-1)\rho ({{{{{\bf{r}}}}}})\rho ^{\prime} ({{{{{\bf{r}}}}}}^{\prime} )+\rho ({{{{{\bf{r}}}}}})\delta ({{{{{\bf{r}}}}}}-{{{{{\bf{r}}}}}}^{\prime} )\)18.
The Triezenberg–Zwanzig equation102 holds for vanishing external potential Vext(r) = 0 and is given by
Originally (49) was derived for the free liquid–vapor interface in a parallel geometry. We find that the relation consists of the local internal Noether sum rule (7) and the equilibrium Euler–Lagrange equation. The LMBW equation (48) reduces to the Triezenberg–Zwanzig equation (49) for cases of Vext(r) = 0.
Another related equation is the first member of the Yvon–Born–Green (YBG) hierarchy103,104,
where ϕ(r) denotes the interparticle pair potential as before. Although (50) has a similar structure as the LMBW equation, it is not based on symmetry or Noether arguments but arises from integration out of degrees of freedom. If one would like to include the translational symmetry one can simply replace the left hand side of (50) with the right hand side of the LMBW equation (47), which leads to
Some of the here derived sum rules are rederivations of known relations. We reiterate the relationships. In his overview Baus13 showed that in equilibrium the total external (2) and internal (6) force vanish and derived the corresponding local hierarchies (3), (4) and (7), (8). Similar sum rules13 hold for the external (22) and internal (25) total torques and their corresponding hierarchies (23), (24) and (26), (27). Tarazona and Evans16 generalized these equations for uniaxial particles and derived the first order of the external (34) and internal (37) hierarchies due to rotations.
To the best of our knowledge the hierarchies of global Noether sum rules, such as (5), (9), (28), and (29), have not been determined previously. Furthermore the global external (33) and internal (36) Noether sum rules for uniaxial colloids and their corresponding hierarchies (35) and (38) (with exception of the first order) are reported here for the first time. As the considerations in the literature focused on equilibrium, all our nonequilibrium relations, as e.g. (11)–(13) and especially the ones including memory (43)–(46) have not been found before.
Data availability
Data sharing is not applicable to this study as no datasets were generated or analyzed during the current study.
References
Noether, E. Invariante Variationsprobleme. Nachr. d. König. Gesellsch. d. Wiss. zu Göttingen, Math.-Phys. Klasse 235 (1918). English translation by Tavel, M. A. Invariant variation problems. Transp. Theo. Stat. Phys. 1, 186 (1971); for a version in modern typesetting see: Wang, F.Y. arXiv:physics/0503066v3 (2018).
Neuenschwander, D. E. Emmy Noether’s Wonderful Theorem (Johns Hopkins University Press, 2011). For a description of many insightful and pedagogical examples and applications..
Byers, N. E. Noether’s discovery of the deep connection between symmetries and conservation laws. Preprint at https://arxiv.org/abs/physics/9807044 (1998).
Rowlison, J. S. & Widom, B. Molecular theory of capillarity (Dover, New York, 2002).
van der Waals, J. D. The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density. Z. Phys. Chem. 13, 657 (1894); English translation by J. S. Rowlinson. J. Stat. Phys. 20, 197 (1979).
Kerins, J. & Boiteux, M. Applications of noether’s theorem to inhomogeneous fluids. Phys. A 117, 575 (1983).
Bukman, D. J. Torque balance at a line of contact. Phys. A 319, 151 (2003).
Boiteux, M. & Kerins, J. Thermodynamic properties of inhomogeneous fluids. Phys. A 121, 399 (1983).
Evans, R. The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids. Adv. Phys. 28, 143 (1979).
Lovett, R. A., Mou, C. Y. & Buff, F. P. The structure of the liquid-vapor interface. J. Chem. Phys. 65, 570 (1976).
Wertheim, M. S. Correlations in the liquid-vapor interface. J. Chem. Phys. 65, 2377 (1976).
Kayser, R. F. & Raveché, H. J. Emergence of periodic density patterns. Phys. Rev. B 22, 424 (1980).
Baus, M. Broken symmetry and invariance properties of classical fluids. Mol. Phys. 51, 211 (1984).
Lovett, R. & Buff, F. P. Examples of the construction of integral equations in equilibrium statistical mechanics from invariance principles. Physica A 172, 147 (1991).
Baus, M. & Lovett, R. A direct derivation of the profile equations of Buff-Lovett-Mou-Wertheim from the Born-Green-Yvon equations for a non-uniform equilibrium fluid. Physica A 181, 329 (1992).
Tarazona, P. & Evans, R. On the validity of certain integro-differential equations for the density-orientation profile of molecular fluid interfaces. Chem. Phys. Lett. 97, 279 (1983).
Gubbins, K. E. Structure of nonuniform molecular fluids – integrodifferential equations for the density-orientation profile. Chem. Phys. Lett. 76, 329 (1980).
Hansen, J. P. & McDonald, I. R. Theory of Simple Liquids, 4th ed. (Academic Press, London, 2013).
Evans, R., Oettel, M., Roth, R. & Kahl, G. New developments in classical density functional theory. J. Phys.: Condens. Matter 28, 240401 (2016).
Roth, R. Fundamental measure theory for hard-sphere mixtures: a review. J. Phys. Condens. Matt. 22, 063102 (2010).
Levesque, M., Vuilleumier, R. & Borgis, D. Scalar fundamental measure theory for hard spheres in three dimensions: Application to hydrophobic solvation. J. Chem. Phys. 137, 034115 (2012).
Jeanmairet, G., Levesque, M. & Borgis, D. Molecular density functional theory of water describing hydrophobicity at short and long length scales. J. Chem. Phys. 139, 154101 (2013).
Evans, R. & Wilding, N. B. Quantifying density fluctuations in water at a hydrophobic surface: evidence for critical drying. Phys. Rev. Lett. 115, 016103 (2015).
Evans, R., Stewart, M. C. & Wilding, N. B. A unified description of hydrophilic and superhydrophobic surfaces in terms of the wetting and drying transitions of liquids. Proc. Nat. Acad. Sci. 116, 23901 (2019).
Remsing, R. C. Commentary: playing the long game wins the cohesion-adhesion rivalry. Proc. Nat. Acad. Sci. 116, 23874 (2019).
Evans, R., Stewart, M. C. & Wilding, N. B. Critical drying of liquids. Phys. Rev. Lett. 117, 176102 (2016).
Chacko, B., Evans, R. & Archer, A. J. Solvent fluctuations around solvophobic, solvophilic, and patchy nanostructures and the accompanying solvent mediated interactions. J. Chem. Phys. 146, 124703 (2017).
Martin-Jimenez, D., Chacón, E., Tarazona, P. & Garcia, R. Atomically resolved three-dimensional structures of electrolyte aqueous solutions near a solid surface. Nat. Comms. 7, 12164 (2016).
Hernández-Muñoz, J., Chacón, E. & Tarazona, P. Density functional analysis of atomic force microscopy in a dense fluid. J. Chem. Phys. 151, 034701 (2019).
Muscatello, J., Chacón, E., Tarazona, P. & Bresme, F. Deconstructing temperature gradients across fluid interfaces: the structural origin of the thermal resistance of liquid-vapor interfaces. Phys. Rev. Lett. 119, 045901 (2017).
Xu, X. & Rice, S. A. A density functional theory of one- and two-layer freezing in a confined colloid system. Proc. R. Soc. A 464, 65 (2008).
Brader, J. M. Structural precursor to freezing: an integral equation study. J. Chem. Phys. 128, 104503 (2008).
Walz, C. & Fuchs, M. Displacement field and elastic constants in nonideal crystals. Phys. Rev. B 81, 134110 (2010).
Häring, J. M., Walz, C., Szamel, G. & Fuchs, M. Coarse-grained density and compressibility of nonideal crystals: General theory and an application to cluster crystals. Phys. Rev. B 92, 184103 (2015).
Häring, J. M. Microscopically founded elasticity theory for defect-rich systems of anisotropic particles. Ph.D. Thesis, Universität Konstanz (2020).
Bryk, P., Henderson, D. & Sokolowski, S. A fluid in contact with a semipermeable surface: second-order integral equation approach. J. Chem. Phys. 107, 3333 (1997).
Henderson, J. R. & van Swol, F. On the interface between a fluid and a planar wall. Mol. Phys. 51, 991 (1984).
Tejero, C. F. & Baus, M. Viscoelastic surface waves and the surface structure of liquids. Mol. Phys. 54, 1307 (1985).
Iatsevitch, S. & Forstmann, F. Density profiles at liquid-vapor and liquid-liquid interfaces: an integral equation study. J. Chem. Phys. 107, 6925 (1997).
Kasch, M. & Forstmann, F. An orientational instability and the liquid-vapor interface of a dipolar hard sphere fluid. J. Chem. Phys. 99, 3037 (1993).
Mandal, S., Lang, S., Botan, V. & Franosch, T. Nonergodicity parameters of confined hard-sphere glasses. Soft. Matter. 13, 6167 (2017).
Farage, T. F. F., Krinninger, P. & Brader, J. M. Effective interactions in active Brownian suspensions. Phys. Rev. E 91, 042310 (2015).
Paliwal, S., Rodenburg, J., van Roij, R. & Dijkstra, M. Chemical potential in active systems: predicting phase equilibrium from bulk equations of state? New J. Phys. 20, 015003 (2018).
Paliwal, S., Prymidis, V., Filion, L. & Dijkstra, M. Non-equilibrium surface tension of the vapour-liquid interface of active Lennard- Jones particles. J. Chem. Phys. 147, 084902 (2017).
Loehr, J., Loenne, M., Ernst, A., de las Heras, D. & Fischer, T. M. Topological protection of multiparticle dissipative transport. Nat. Commun. 7, 11745 (2016).
Loehr, J. et al. Colloidal topological insulators. Comms. Phys. 1, 4 (2018).
Rossi, A. M. E. B. et al. Hard topological versus soft geometrical magnetic particle transport. Soft Matter 15, 8543 (2019).
Schmidt, M. & Brader, J. M. Power functional theory for Brownian dynamics. J. Chem. Phys. 138, 214101 (2013).
Fortini, A., de las Heras, D., Brader, J. M. & Schmidt, M. Superadiabatic forces in Brownian many-body dynamics. Phys. Rev. Lett. 113, 167801 (2014).
Krinninger, P., Schmidt, M. & Brader, J. M. Nonequilibrium phase behaviour from minimization of free power dissipation. Phys. Rev. Lett. 117, 208003 (2016).
Hermann, S., de las Heras, D. & Schmidt, M. Non-negative interfacial tension in phase-separated active Brownian particles. Phys. Rev. Lett. 123, 268002 (2019).
Hermann, S., Krinninger, P., de las Heras, D. & Schmidt, M. Phase coexistence of active Brownian particles. Phys. Rev. E 100, 052604 (2019).
Hermann, S. & Schmidt, M. Active interface polarization as a state function. Phys. Rev. Research 2, 022003(R) (2020).
de las Heras, D. & Schmidt, M. Velocity gradient power functional for Brownian dynamics. Phys. Rev. Lett. 120, 028001 (2018).
Stuhlmüller, N. C. X., Eckert, T., de las Heras, D. & Schmidt, M. Structural nonequilibrium forces in driven colloidal systems. Phys. Rev. Lett. 121, 098002 (2018).
de las Heras, D. & Schmidt, M. Flow and structure in nonequilibrium Brownian many-body systems. Phys. Rev. Lett. 125, 018001 (2020).
Brader, J. M. & Schmidt, M. Nonequilibrium Ornstein-Zernike relation for Brownian many-body dynamics. J. Chem. Phys. 139, 104108 (2013).
Brader, J. M. & Schmidt, M. Dynamic correlations in Brownian many-body systems. J. Chem. Phys. 140, 034104 (2014).
Ornstein, L. S. & Zernike F. The influence of accidental deviations of density on the equation of state. Proc. Acad. Sci. Amsterdam 17, 793 (1914); this article is reprinted in Frisch, H. & Lebowitz, J. L. The Equilibrium Theory of Classical Fluids (Benjamin, New York, 1964).
Requardt, M. & Wagner, H. J. (Infinite) Boundary corrections for the LMBW-Equations and the TZ-Formula of surface tension in the presence of spontaneous symmetry breaking. Phys. A 154, 183 (1988).
Khadka, U., Holubec, V., Yang, H. & Cichos, F. Active particles bound by information flows. Nat. Commun. 9, 3864 (2018).
Selmke, M., Khadka, U., Bregulla, A. P., Cichos, F. & Yang, H. Theory for controlling individual self-propelled micro-swimmers by photon nudging I: directed transport. Phys. Chem. Chem. Phys. 20, 10502 (2018).
Selmke, M., Khadka, U., Bregulla, A. P., Cichos, F. & Yang, H. Theory for controlling individual self-propelled micro-swimmers by photon nudging II: confinement. Phys. Chem. Chem. Phys. 20, 10521 (2018).
Bregulla, A. P., Yang, H. & Cichos, F. Stochastic localization of microswimmers by photon nudging. ACS Nano 8, 6542 (2014).
Qian, B., Montiel, D., Bregulla, A., Cichos, F. & Yang, H. Harnessing thermal fluctuations for purposeful activities: the manipulation of single micro-swimmers by adaptive photon nudging. Chem. Sci. 4, 1420 (2013).
Söker, N. A., Auschra, S., Holubec, V., Kroy, K. & Cichos, F. How Activity Landscapes Polarize Microswimmers without Alignment Forces. Phys. Rev. Lett. 126, 228001 (2021).
Auschra, S., Holubec, V., Söker, N. A., Cichos, F. & Kroy, K. Polarization-density patterns of active particles in motility gradients. Phys. Rev. E 103, 062601 (2021).
Speck, T. & Jack, R. L. Ideal bulk pressure of active Brownian particles. Phys. Rev. E 93, 062605 (2016).
Takatori, S. C., Yan, W. & Brady, J. F. Swim pressure: stress generation in active matter. Phys. Rev. Lett. 113, 028103 (2014).
Yang, X., Manning, M. L. & Marchetti, M. C. Aggregation and segregation of confined active particles. Soft. Matter. 10, 6477 (2014).
Winkler, R. G., Wysocki, A. & Gompper, G. Virial pressure in systems of spherical active Brownian particles. Soft. Matter. 11, 6680 (2015).
Solon, A. P. et al. Pressure and phase equilibria in interacting active Brownian spheres. Phys. Rev. Lett. 114, 198301 (2015).
Paliwal, S., Rodenburg, J., van Roij, R. & Dijkstra, M. Chemical potential in active systems: predicting phase equilibrium from bulk equations of state? New J. Phys. 20, 015003 (2018).
de las Heras, D. et al. Floating nematic phase in colloidal platelet-sphere mixtures. Sci. Rep. 2, 789 (2012).
de las Heras, D. & Schmidt, M. The phase stacking diagram of colloidal mixtures under gravity. Soft Matter 9, 98636 (2013).
de las Heras, D. & Schmidt, M. Sedimentation stacking diagram of binary colloidal mixtures and bulk phases in the plane of chemical potentials. J. Phys.: Condens. Matter 27, 194115 (2015).
Geigenfeind, T. & de las Heras, D. The role of sample height in the stacking diagram of colloidal mixtures under gravity. J. Phys.: Condens. Matter 29, 064006 (2017).
Enculescu, M. & Stark, H. Active colloidal suspensions exhibit polar order under gravity. Phys. Rev. Lett. 107, 058301 (2011).
Hermann, S. & Schmidt, M. Active ideal sedimentation: exact two-dimensional steady states. Soft Matter 14, 1614 (2018).
Vachier, J. & Mazza, M. G. Dynamics of sedimenting active Brownian particles. Eur. Phys. J. E 42, 11 (2019).
Solon, A. P., Cates, M. E. & Tailleur, J. Active Brownian particles and run-and-tumble particles: A comparative study. Eur. Phys. J. Spec. Top. 224, 1231 (2015).
Lee, C. F. Active particles under confinement: aggregation at the wall and gradient formation inside a channel. New J. Phys. 15, 055007 (2013).
Zwanzig, R. Nonequilibrium statistical mechanics (Oxford University Press, 2001).
Lesnicki, D., Vuilleumier, R., Carof, A. & Rotenberg, B. Molecular hydrodynamics from memory kernels. Phys. Rev. Lett. 116, 147804 (2016).
Lesnicki, D. & Vuilleumier, R. Microscopic flow around a diffusing particle. J. Chem. Phys. 147, 094502 (2017).
Jung, G. & Schmid, F. Computing bulk and shear viscosities from simulations of fluids with dissipative and stochastic interactions. J. Chem. Phys. 144, 204104 (2016).
Jung, G., Hanke, M. & Schmid, F. Iterative reconstruction of memory kernels. J. Chem. Theo. Comput. 13, 2481 (2017).
Jung, G., Hanke, M. & Schmid, F. Generalized Langevin dynamics: construction and numerical integration of non-Markovian particle-based models. Soft Matter 14, 9368 (2018).
Yeomans-Reyna, L. & Medina-Noyola, M. Overdamped van Hove function of colloidal suspensions. Phys. Rev. E 62, 3382 (2000).
Chávez-Rojo, M. A. & Medina-Noyola, M. Van Hove function of colloidal mixtures: Exact results. Physica A 366, 55 (2006).
Lázaro-Lázaro, E. et al. Self-consistent generalized Langevin equation theory of the dynamics of multicomponent atomic liquids. J. Chem. Phys. 146, 184506 (2017).
Treffenstädt, L. L. & Schmidt, M. Memory-induced motion reversal in Brownian liquids. Soft Matter 16, 1518 (2020).
Rosenfeld, Y. Free-energy model for the inhomogeneous hard-sphere fluid mixture and density-functional theory of freezing. Phys. Rev. Lett. 63, 9 (1989).
Tschopp, S. M. & Brader, J. M. Fundamental measure theory of inhomogeneous two-body correlation functions. Phys. Rev. E 103, 042103 (2021).
Lin, S.-C., Oettel, M., Häring, J. M., Haussmann, R., Fuchs, M., & Kahl, G. Direct correlation function of a crystalline solid. Phys. Rev. Lett. (to appear). Preprint at https://arxiv.org/abs/2104.11558 (2021).
Turci, F. & Wilding, N. B. Phase separation and multibody effects in three-dimensional active Brownian particles. Phys. Rev. Lett. 126, 038002 (2021).
Omar, A. K., Klymko, K., GrandPre, T. & Geissler, P. L. Phase diagram of active Brownian spheres: crystallization and the metastability of motility-induced phase separation. Phys. Rev. Lett. 126, 188002 (2021).
Schmidt, M. Quantum power functional theory for many-body dynamics. J. Chem. Phys. 143, 174108 (2015).
Schmidt, M. Power functional theory for Newtonian many-body dynamics. J. Chem. Phys. 148, 044502 (2018).
Janssen, L. M. C. Mode-coupling theory of the glass transition: A primer. Front. Phys. 6, 97 (2018).
Vogel, F. & Fuchs, M. Stress correlation function and linear response of Brownian particles. Eur. Phys. J. E 43, 70 (2020).
Triezenberg, D. G. & Zwanzig, R. Fluctuation theory of surface tension. Phys. Rev. Lett. 28, 1183 (1972).
Yvon, J. Actualités Scientifiques et Industrielles (Hermann & Cie., 1935).
Born, M. & Green, H. S. A general kinetic theory of liquids I. The molecular distribution functions. Proc. R. Soc. London, Ser. A 188, 10 (1946).
Acknowledgements
This work is supported by the German Research Foundation (DFG) via project number 436306241. Open Access funding is provided by project DEAL. We would like to thank Matthias Fuchs, Johannes Häring, Bob Evans, Pedro Tarazona, Daniel de las Heras, Matthias Krüger, Jim Lutsko, Hartmut Löwen, and Thomas Fischer for useful discussions and comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
S.H. and M.S. have jointly carried out the work and written the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks Benjamin Goddard, Gyula Toth and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hermann, S., Schmidt, M. Noether’s theorem in statistical mechanics. Commun Phys 4, 176 (2021). https://doi.org/10.1038/s42005-021-00669-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00669-2
This article is cited by
-
Hyperforce balance via thermal Noether invariance of any observable
Communications Physics (2024)
-
A symmetry analysis methodology for general energy conversion systems
Communications Engineering (2023)
-
Variance of fluctuations from Noether invariance
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.