Hyperforce balance via thermal Noether invariance of any observable

Abstract

Noether invariance in statistical mechanics provides fundamental connections between the symmetries of a physical system and its conservation laws and sum rules. The latter are exact identities that involve statistically averaged forces and force correlations and they are derived from statistical mechanical functionals. However, the implications for more general observables and order parameters are unclear. Here, we demonstrate that thermally averaged classical phase space functions are associated with exact hyperforce sum rules that follow from translational Noether invariance. Both global and locally resolved identities hold and they relate the mean gradient of a phase-space function to its negative mean product with the total force. Similar to Hirschfelder’s hypervirial theorem, the hyperforce sum rules apply to arbitrary observables in equilibrium. Exact hierarchies of higher-order sum rules follow iteratively. As applications we investigate via computer simulations the emerging one-body force fluctuation profiles in confined liquids. These local correlators quantify spatially inhomogeneous self-organization and their measurement allows for the development of stringent convergence tests and enhanced sampling schemes in complex systems.

Introduction

The task of predicting thermal averages of phase space functions lies at the center of attention in Statistical Mechanics. Prominent examples include correlation functions and order parameters, but also global quantities such as internal and external energies, entropy, and much more are considered^1,2. Significant progress has been reported for problem-specific order parameters that are tailored to capture intricate correlation effects. Recent examples that address the spatial ordering behavior of dense liquids include beyond-two-body correlation functions, as advocated by Kob and coworkers^3,4 and by Janssen and her coworkers⁵.

In contrast to such freedom of choice, the variables within classical density functional theory^2,6,7 seem to be a priori uniquely determined by the existence of a generating free energy functional and the associated structure of pairs of conjugate variables, which in particular are the external one-body potential energy V_ext(r) and the density profile ρ(r). However, there are recent extensions to density functional theory to systematically include the local compressibility^8,9,10, which forms a well-accessible order parameter for local particle number fluctuations. Technically, the local compressibility constitutes either a parametric derivative of the equilibrium density profile with respect to the chemical potential or, analogously, the covariance of the local density and the global particle number. A generalization from such chemical particle number fluctuation to thermal fluctuations has been recently performed^11,12. Working in the grand ensemble, where the particle number fluctuates, is thereby crucial to not impose artificial constraints on the system.

Besides the standard thermodynamical thinking in terms of thermal and chemical equilibrium, there is much recent progress from the force point of view. Highly efficient force sampling techniques allow to obtain reliable results within many-body simulations that outperform more straightforward counting methods^{13,14,15,16,17,18,19}. Forces are also at the core of power functional theory²⁰ as a systematic approach to formulate coupled many-body dynamics on the one-body level of dynamical correlation functions.

To be specific, in the thermal equilibrium of a spatially inhomogeneous system, the sum of all mean forces necessarily vanishes at each position r. This is expressed by the following exact sum rule:

$${{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})-\rho ({{{{{{{\bf{r}}}}}}}})\nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})={k}_{B}T\nabla \rho ({{{{{{{\bf{r}}}}}}}}).$$

(1)

Here, F_int(r) is the localized force density that acts at position r due to the interparticle interactions with all surrounding particles, ∇ denotes the derivative with respect to r such that − ∇V_ext(r) is the external force field, k_B indicates the Boltzmann constant, and T is the absolute temperature.

The sum of the interparticle and external force densities on the left-hand side of Eq. (1) balances the thermal diffusive contribution on its right-hand side. This is a classical result due to Yvon, Born, and Green (YBG)¹, where for particles that mutually interact only via a pair potential, the interparticle force density F_int(r) is expressed as an integral over the two-body density multiplied by the pair force¹. Higher-order versions of Eq. (1) form a hierarchy. That the first YBG equation (1) has practical consequences for carrying out sampling tasks in simulations is only a quite recent insight. Loosely speaking, force sampling^13,14,15 amounts to obtaining simulation data for the left-hand side of Eq. (1) and then in a post-processing step dividing by k_BT and building the inverse operation of the spatial derivative on the right-hand side via suitable integration in position. This method yields results for the density profile ρ(r) which feature a significant reduction of statistical noise^{13,14,15,16,17,18,19}.

Exploiting Noether’s Theorem^21,22 in statistical mechanics has been performed in a variety of ways^{23,24,25,26,27,28,29,30}. Considering the invariance of statistical mechanical functionals leads very naturally to the notion of statistically averaged forces when spatial displacement is imposed on the system; mean torques emerge when invariance against rotations is addressed^31,32. In previous work, we have shown that the statistical Noether concept also applies quantum mechanically³³ and that it gives access to global force fluctutations³⁴. Generalizing to local invariance^33,35 that is resolved in spatial position facilitated fresh insights into the correlation structure of the liquid state³⁶. Considering the first order in the displacement field yields the thermal equilibrium force balance relationship according to the YBG equation (1)^33,35. At second-order hitherto unknown two-body force-gradient and force-force correlators emerge and these, together with the standard pair correlation function, are constrained by exact Noether identities³⁶.

This situation of theory development leaves open the question of whether more general observables that serve as important order parameters and quantifiers of spatial structure will also be affected by the statistical Noether invariance, as one could glean from the generality of the thermal invariance concept. Here we demonstrate that any statistical observable $\hat{A}$ is intrinsically associated with a corresponding hierarchy of exact identities that emerges from its statistical shifting invariance properties. We validate the corresponding exact local and global sum rules for a range of relevant observables via many-body simulations of a confined Lennard-Jones fluid. The results clarify a very intimate link of global and locally resolved correlators and they suggest a very general statistical mechanical structure.

Our framework can be viewed as a generalization of the YBG equation (1) to systematically include the dependence on a further given observable $\hat{A}$. The equilibrium force balance (1) itself is recovered for the trivial case $\hat{A}=1$. Such generalization is not uncommon in Statistical Mechanics. The relationship of our theory and the YBG force balance equation is akin Hirschfelder’s hypervirial theorem³⁷ as a generalization of the standard virial theorem¹ to also invoke an additional dependence on a given phase space function $\hat{A}$. Our theory can hence be viewed as a hyperforce balance relationship, and we derive global and local variants below, see Eqs. (4) and (10). We further show that the local version simplifies further to Eq. (11) and more explicitly to Eq. (12) in case of $\hat{A}$ being independent of momenta. As a specific example, our methodology not only allows to sample density gradients, as is possible in force sampling schemes^{13,14,15,16,17,18,19}, but also to sample force density gradients. The general method complements existing counting and force-sampling techniques and it gives much inspiration for rigorous statistical mechanical theories based on exact identities. As we lay out, the degree of numerical accuracy to which the Noether sum rules are satisfied can serve as an estimator for sufficient equilibration of slowly converging systems.

Methods

Statistical mechanics

We consider general thermal many-body systems of particles with identical mass m, coordinates r₁, …, r_N ≡ r^N, and momenta p₁, …, p_N ≡ p^N, where N denotes the number of particles. The Hamiltonian is of the standard form $H={\sum }_{i}{{{{{{{{\bf{p}}}}}}}}}_{i}^{2}/(2m)+u({{{{{{{{\bf{r}}}}}}}}}^{N})+{\sum }_{i}{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})$, where the sums i = 1, …, N run over all particles, u(r^N) is the interparticle interaction potential, and V_ext(r) is an external potential that depends on position r. Thermal equilibrium is characterized by a statistical equilibrium ensemble with grand canonical probability distribution Ψ_eq = Ξ⁻¹e^{−β(H−μN)}, where β = 1/(k_BT) and μ indicates the chemical potential. The normalization factor of Ψ_eq is the partition sum $\Xi ={{{{{{{\rm{Tr}}}}}}}}\,{{{{{{{{\rm{e}}}}}}}}}^{-\beta (H-\mu N)}$, where the classical trace is defined as ${{{{{{{\rm{Tr}}}}}}}}\,\cdot =\mathop{\sum }\nolimits_{N = 0}^{\infty }{(N!{h}^{3N})}^{-1}\int\,d{{{{{{{{\bf{r}}}}}}}}}^{N}\int\,d{{{{{{{{\bf{p}}}}}}}}}^{N}\cdot$, with h indicating Planck’s constant. The thermal equilibrium average A of a given phase space function $\hat{A}$ is then obtained as $A=\langle \hat{A}\rangle \equiv {{{{{{{\rm{Tr}}}}}}}}\,{\Psi }_{{{{{{{{\rm{eq}}}}}}}}}\hat{A}$, where we have suppressed the dependence of $\hat{A}$ on the phase space variables r^N and p^N in the notation, i.e., in full notation we have $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$ as well as potentially further parametric dependence such as on a generic position variable r.

Global shifting invariance

To develop the Noether invariance theory, we first consider a global coordinate displacement ${{{{{{{{\bf{r}}}}}}}}}_{i}\to {{{{{{{{\bf{r}}}}}}}}}_{i}+{{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0}\equiv {\tilde{{{{{{{{\bf{r}}}}}}}}}}_{i}$, where the shifting vector ϵ₀ = const is independent of position and acts on all particles in the same way³¹. The tilde indicates the new coordinates. Expressing H as well as the corresponding distribution function Ψ_eq in the new coordinates makes averages become formally dependent on the shifting parameter, i.e., A(ϵ₀). However, the coordinate change can also be viewed as a mere re-parameterization of the phase space integral which induces no change to its value such that A(ϵ₀) = A, with the right-hand side denoting $\langle \hat{A}\rangle$ in the original representation. Partially differentiating both sides of the equation yields:

$$\frac{\partial A({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0})}{\partial {{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0}}=\frac{\partial }{\partial {{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0}}{{{{{{{\rm{Tr}}}}}}}}\,{\Psi }_{{{{{{{{\rm{eq}}}}}}}}}({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0})\hat{A}({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0})=0,$$

(2)

where the second equality arises trivially from ∂A/∂ϵ₀ = 0, as there is no dependence on ϵ₀.

Carrying out the derivative is straightforward upon using the Boltzmann form of the equilibrium distribution function and noting that the partition sum is independent of ϵ₀. Explicitly we have ∂Ψ_eq(ϵ₀)/∂ϵ₀ = − βΨ_eq(ϵ₀)∂H(ϵ₀)/∂ϵ₀. Using the product rule of differentiation and evaluating at vanishing displacement ϵ₀ = 0 then leads from Eq. (2) to

$$-\beta \left\langle {\left.\frac{\partial H({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0})}{\partial {{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0}}\right| }_{{{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0} = 0}\hat{A}\right\rangle +\left\langle {\left.\frac{\partial \hat{A}({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0})}{\partial {{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0}}\right| }_{{{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0} = 0}\right\rangle =0.$$

(3)

Observing that here $\partial /\partial {{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0}{| }_{{{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0} = 0}\equiv {\sum }_{i}{\nabla }_{i}$ allows to make the derivatives more explicit with ∇_i indicating the partial derivative with respect to r_i. In the first term in Eq. (3) we have $-\partial H({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0})/\partial {{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0}{| }_{{{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{0} = 0}=-{\sum }_{i}{\nabla }_{i}{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})\equiv {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}$, which defines the global external force operator ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}$. Here the global interparticle force due to the mutual interactions between all particles in the system vanishes, ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}^{0}=-{\sum }_{i}{\nabla }_{i}u({{{{{{{{\bf{r}}}}}}}}}^{N})\equiv 0$, as is due to Newton’s third law or, analogously, to the translational invariance of u(r^N) against global displacement³¹.

Re-ordering the two terms in Eq. (3) gives the following global hyperforce identity that holds for any given observable $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$:

$$\beta \left\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{A}\right\rangle =-\left\langle \mathop{\sum}\limits_{i}{\nabla }_{i}\hat{A}\right\rangle .$$

(4)

Here $\hat{A}=\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$ can feature additional parametric dependence, such as on a generic position argument r. The sum rule (4) relates the correlation of $\hat{A}$ with the external force operator (left-hand side) to the mean negative global coordinate derivative of $\hat{A}$ (right-hand side); here we use the term correlation to imply the average of the product of two observables. As announced in the introduction, Eq. (4) is similar to Hirschfelder’s hypervirial theorem³⁷ in the inclusion of the phase space function $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$ and our hyperforce terminology parallels his use of the term hypervirial.

While Noether invariance enabled us to obtain the global hyperforce identity Eq. (4) constructively, one can verify its validity a posteriori by integration by parts in phase space on the right-hand side. The derivatives ∇_i then act on the probability distribution and exploiting again the Boltzmann form leads to $\hat{A}{\sum }_{i}{\nabla }_{i}{\Psi }_{{{{{{{{\rm{eq}}}}}}}}}=-\beta {\Psi }_{{{{{{{{\rm{eq}}}}}}}}}\hat{A}{\sum }_{i}{\nabla }_{i}H={\Psi }_{{{{{{{{\rm{eq}}}}}}}}}\beta {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{A}$, which gives the left-hand side of Eq. (4) upon building the trace. Alternatively one can start with the Yvon theorem¹, $\beta \langle \hat{A}{\nabla }_{i}H\rangle =\langle {\nabla }_{i}\hat{A}\rangle$, which itself also follows from partial phase space integration¹. Summing the Yvon theorem over all particles i and noting that ∑_i∇_iu(r^N) ≡ 0 gives Eq. (4). A similar derivation can also be based on the hypervirial theorem³⁷.

Local shifting invariance

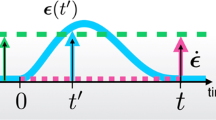
Before presenting explicit applications of Eq. (4) to specific forms of $\hat{A}$, we first generalize to the fully position-resolved case. In a generalization of the uniform coordinate displacement used for global shifting in the previous subsection, we consider the following local transformation on phase space, as parameterized by a three-dimensional vector field ϵ(r)^33,35:

$${{{{{{{{\bf{r}}}}}}}}}_{i}\to {{{{{{{{\bf{r}}}}}}}}}_{i}+{{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i}),$$

(5)

$${{{{{{{{\bf{p}}}}}}}}}_{i}\to {[{\mathbb{1}}+{\nabla }_{i}{{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})]}^{-1}\cdot {{{{{{{{\bf{p}}}}}}}}}_{i}.$$

(6)

The gradient ∇_i ϵ(r_i) is a 3 × 3 matrix, ${\mathbb{1}}$ denotes the 3 × 3 identity matrix, and the superscript −1 indicates matrix inversion. Figure 1a depicts an illustration of the spatial transformation (5). The momentum transformation (6) has the following Taylor expansion to the lowest order in the displacement field: ${{{{{{{{\bf{p}}}}}}}}}_{i}\to [{\mathbb{1}}-{\nabla }_{i}{{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})]\cdot {{{{{{{{\bf{p}}}}}}}}}_{i}$.

Fig. 1: Illustrations of the relevant geometries.

a The shifting field (orange arrows) displaces the coordinates r_i of all particles i by a vector ϵ(r_i); the specific particle i is highlighted in red and all particles are identical. A corresponding change in momenta, see Eq. (6), compensates for the spatial distortion such that the differential phase space volume element (integration measure) remains unchanged. b Planar geometry of the confined Lennard-Jones fluid between two smooth parallel soft attractive Lennard-Jones walls; σ is the particle size, z measures the distance across the planar pore, and L is the distance between the two walls.

The joint transformation (5) and (6) is canonical^33,35,38 and it hence preserves the phase space volume element, $d{{{{{{{{\bf{r}}}}}}}}}_{i}d{{{{{{{{\bf{p}}}}}}}}}_{i}=d{\tilde{{{{{{{{\bf{r}}}}}}}}}}_{i}d{\tilde{{{{{{{{\bf{p}}}}}}}}}}_{i}$, where the tilde indicates the transformed variables [right-hand sides of Eqs. (5) and (6)]. The Hamiltonian also remains unchanged (up to expressing the original via the new variables). Hence the partition sum Ξ is an invariant under the joint transformation (5) and (6)^33,35,36. Together with the invariance of the integration measure, the setup implies that any average $A=\langle \hat{A}\rangle ={{{{{{{\rm{Tr}}}}}}}}\,{\Psi }_{{{{{{{{\rm{eq}}}}}}}}}\hat{A}$ is an invariant. This property holds despite the explicit occurrence of the shifting field ϵ(r) in the integrand, and hence A[ϵ] = A, where the left-hand side carries the apparent dependence on the shifting field and the right-hand side is the average expressed in the original variables where ϵ(r) is absent. We use the standard notation to express dependence on a function (so-called functional dependence) by bracketed arguments.

From the local Noether invariance, we can conclude from functionally differentiating the equation A[ϵ] = A with respect to the shifting field that

$$\frac{\delta A[{{{{{{{\boldsymbol{\epsilon }}}}}}}}]}{\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}})}=0.$$

(7)

The right-hand side of Eq. (7) vanishes trivially due to the average A being independent of ϵ(r) in the original representation and hence δA/δϵ(r) = 0. Carrying out the functional derivative on the left-hand side of Eq. (7) requires to functionally differentiate the equilibrium distribution, δΨ_eq[ϵ]/δϵ(r) = − βΨ_eq[ϵ]δH[ϵ]/δϵ(r), as follows from the chain rule. This allows to rewrite Eq. (7) upon using the product rule and re-ordering the resulting two terms as

$$-\beta \left\langle {\left.\frac{\delta H[{{{{{{{\boldsymbol{\epsilon }}}}}}}}]}{\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}})}\right| }_{{{{{{{{\boldsymbol{\epsilon }}}}}}}} = 0}\hat{A}\right\rangle =-\left\langle {\left.\frac{\delta \hat{A}[{{{{{{{\boldsymbol{\epsilon }}}}}}}}]}{\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}})}\right| }_{{{{{{{{\boldsymbol{\epsilon }}}}}}}} = 0}\right\rangle ,$$

(8)

where we have evaluated both sides at vanishing shifting field, ϵ(r) = 0.

Differentiating the transformed Hamiltonian with respect to the shifting field gives $-\delta H[{{{{{{{\boldsymbol{\epsilon }}}}}}}}]/\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}}){| }_{{{{{{{{\boldsymbol{\epsilon }}}}}}}} = 0}=\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$^33,35, where the position-resolved total force operator comprises the following three terms:

$$\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=\nabla \cdot \hat{{{{{{{{\boldsymbol{\tau }}}}}}}}}({{{{{{{\bf{r}}}}}}}})+{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})-\hat{\rho }({{{{{{{\bf{r}}}}}}}})\nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}}).$$

(9)

The right-hand side of Eq. (9) features the one-body kinematic stress operator $\hat{{{{{{{{\boldsymbol{\tau }}}}}}}}}({{{{{{{\bf{r}}}}}}}})=-{\sum }_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i}){{{{{{{{\bf{p}}}}}}}}}_{i}{{{{{{{{\bf{p}}}}}}}}}_{i}/m$²⁰, the one-body interparticle force density operator ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=-{\sum }_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i}){\nabla }_{i}u({{{{{{{{\bf{r}}}}}}}}}^{N})$²⁰, the standard form of the density operator $\hat{\rho }({{{{{{{\bf{r}}}}}}}})={\sum }_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})$^1,2,20, and the external force field − ∇V_ext(r). (The force density operator $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ defined in (9) also arises as the time derivative of the one-body current operator²⁰. In equilibrium the kinematic term in (9) reduces to a diffusive contribution: $\nabla \cdot \langle \hat{{{{{{{{\boldsymbol{\tau }}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle =-{k}_{B}T\nabla \rho ({{{{{{{\bf{r}}}}}}}})$; we refer the Reader to Schmidt²⁰ for details). Equation (8) can then be written upon carrying out the functional derivatives and using Eq. (9) (on the left-hand side) together with the chain rule (on the right-hand side), as the following hyperforce sum rule that holds for a given form of $\hat{A}=\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$:

$$\beta \left\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{A}\right\rangle = -\left\langle \mathop{\sum}\limits_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i}){\nabla }_{i}\hat{A}\right\rangle \\ -\nabla \cdot \left\langle \mathop{\sum}\limits_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})\frac{\partial \hat{A}}{\partial {{{{{{{{\bf{p}}}}}}}}}_{i}}{{{{{{{{\bf{p}}}}}}}}}_{i}\right\rangle ,$$

(10)

where $\hat{A}$ can again feature additional parametric dependencies, such as on r.

For cases where the observable under consideration is independent of the momenta, i.e., $\hat{A}\equiv \hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})$, the second term on the right-hand side of Eq. (10) vanishes and we obtain the coordinate-based local hyperforce sum rule:

$$\beta \left\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})\right\rangle =-\left\langle \mathop{\sum}\limits_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i}){\nabla }_{i}\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})\right\rangle .$$

(11)

Equation (11) can be viewed as a generalization of the framework developed by Coles et al.¹⁷, where they consider observables of the specific form $\hat{A}={\sum }_{i}{a}_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})$, where a_i is a unique property of particle i only, such as, e.g., its charge or, when taking orientational degrees of freedom into account, its polarization¹⁷.

As a consistency check, from integrating the locally resolved sum rules (10) and (11) over position r, i.e., applying ∫ dr to both sides of these equations, and observing that ∫ drδ(r − r_i) = 1, one retrieves the global Noether identity (4). Here the global external force is the only remaining nontrivial global force contribution, ${\hat{{{{{{{{\bf{F}}}}}}}}}}^{0}\equiv \int\,d{{{{{{{\bf{r}}}}}}}}\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})={\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}$, as the global interparticle force vanishes due to Newton’s third law³¹ and there is also no global diffusive effect due to vanishing boundary terms. Hence Eq. (4) continues to hold upon replacing ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}$ by the global total force operator ${\hat{{{{{{{{\bf{F}}}}}}}}}}^{0}$.

As a further remark, by splitting off the kinetic term in Eq. (11), its left-hand side can be re-written as $\beta \langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})\rangle =\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{U}({{{{{{{\bf{r}}}}}}}})\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})\rangle -\nabla \langle \hat{\rho }({{{{{{{\bf{r}}}}}}}})\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})\rangle$, with the potential force density operator being given as the sum of interparticle and external contributions: ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{U}({{{{{{{\bf{r}}}}}}}})={\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})-\hat{\rho }({{{{{{{\bf{r}}}}}}}})\nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$.

In summary, the local force decomposition into ideal, interparticle, and external contributions in Eq. (11) allows to obtain the following more explicit form, which holds, as we recall, provided that $\hat{A}=\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})$ is independent of the momenta:

$$ \beta \left\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{A}\right\rangle -\beta \left\langle \hat{\rho }({{{{{{{\bf{r}}}}}}}})\hat{A}\right\rangle \nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\\ \qquad=\nabla \left\langle \hat{\rho }({{{{{{{\bf{r}}}}}}}})\hat{A}\right\rangle -\left\langle \mathop{\sum}\limits_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i}){\nabla }_{i}\hat{A}\right\rangle .$$

(12)

For a given explicit form of $\hat{A}$, such as in the concrete examples discussed below, the sum rule (12) connects the three irreducible correlators $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{A}\rangle$, $\langle \hat{\rho }({{{{{{{\bf{r}}}}}}}})\hat{A}\rangle$, and $\langle {\sum }_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i}){\nabla }_{i}\hat{A}\rangle$ in a formally exact and nontrivial way with each other. Setting $\hat{A}=1$ recovers the YBG equation (which we take to imply thermal averages being taken), as then the last term in Eq. (12) vanishes and the remaining terms constitute Eq. (1). Paralleling the naming convention of the hypervirial theorem, which generalizes the standard virial theorem to include a further observable, Eq. (12) attains the status of a hyper-YBG equation or hyperforce balance relationship. Concrete applications thereof are shown below in the Results section.

The correlators on the left-hand sides of the sum rules (4), (10), and (11) also constitute covariances. We recall that the covariance of two observables $\hat{A}$ and $\hat{B}$, as defined via ${{{{{{{\rm{cov}}}}}}}}(\hat{A},\hat{B})=\langle \hat{A}\hat{B}\rangle -\langle \hat{A}\rangle \langle \hat{B}\rangle$ measures the correlation of the fluctuations of the two observables around their respective mean. In the present case the mean force vanishes both globally, $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\rangle =0$, and locally, $\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle =0$. Hence we can formally subtract the vanishing averages and re-express $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{A}\rangle ={{{{{{{\rm{cov}}}}}}}}({\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0},\hat{A})$ as well as $\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{A}\rangle ={{{{{{{\rm{cov}}}}}}}}(\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}),\hat{A})$. Besides the conceptual difference between correlation and covariance, in practical sampling schemes it can be beneficial to work with covariances rather than correlations to reduce statistical noise, as we will demonstrate further below.

That Eq. (11) holds can again be verified a posteriori by phase space coordinate integration by parts on the right-hand side. Due to the product rule two contributions result, one from the Boltzmann factor: ∑_iδ(r − r_i)∇_iΨ_eq = − βΨ_eq∑_iδ(r − r_i)∇_iH, and one from the Dirac distribution: ${\Psi }_{{{{{{{{\rm{eq}}}}}}}}}{\sum }_{i}{\nabla }_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})=-{\Psi }_{{{{{{{{\rm{eq}}}}}}}}}\nabla \hat{\rho }({{{{{{{\bf{r}}}}}}}})$. Together with the factor $\hat{A}$ their combination yields the left-hand side of Eq. (11) upon identifying $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ via Eq. (9). The more general Eq. (10) follows analogously upon integrating by parts also with respect to the momenta.

Results

Global shifting applications

We turn to applications and hence consider concrete examples for the general phase space function $\hat{A}$, which has remained so far unspecified in the above generic hyperforce framework. We start with investigating the global invariance (4), which as we demonstrate constitutes a powerful device both if $\hat{A}$ is a global object or if it is locally resolved via dependence on a position. We first consider the seemingly trivial case $\hat{A}=1$, for which of course 〈1〉 = 1 due to the correct normalization of Ψ_eq. The right-hand side of Eq. (4) vanishes and we obtain ${{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\equiv \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\rangle =0$, i.e., the vanishing of the mean external force in equilibrium³¹. This is intuitively expected, as can be seen by contradiction as follows. If the mean external force did not vanish, then the system would start to move on average³² and hence it would not be in equilibrium.

Adressing the global external force and hence setting $\hat{A}={\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}$ in Eq. (4) leads upon simplifying the right-hand side via $\langle {\sum }_{i}{\nabla }_{i}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\rangle =-\langle {\sum }_{i}{\nabla }_{i}{\nabla }_{i}{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})\rangle$ to the recently formulated global force-variance relationship $\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\rangle =\int\,d{{{{{{{\bf{r}}}}}}}}\rho ({{{{{{{\bf{r}}}}}}}})\nabla \nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$³⁴. Here the auto-correlation of the global external force (left-hand side) equals up to a factor β the mean external potential energy curvature (right-hand side).

By iteratively replacing $\hat{A}$ with the composite ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{A}$ in Eq. (4), one can systematically generate higher-order sum rules, starting with $\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{A}\rangle =-\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\sum }_{i}{\nabla }_{i}\hat{A}\rangle -\langle \hat{A}{\sum }_{i}{\nabla }_{i}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\rangle$, where the first term on the right-hand side allows repeated application of Eq. (4) and the second term can be written via the external potential curvature. The result is the following global second-order hyperforce sum rule:

$${\beta }^{2}\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{A}\rangle =\left\langle \mathop{\sum}\limits_{ij}{\nabla }_{i}{\nabla }_{j}\hat{A}\right\rangle +\left\langle \hat{A}\mathop{\sum}\limits_{i}{\nabla }_{i}{\nabla }_{i}\beta {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})\right\rangle ,$$

(13)

where $\hat{A}=\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$. The second term on the right hand of Eq. (13) side can alternatively be written as an integral over a correlation function as follows: $\beta \int\,d{{{{{{{\bf{r}}}}}}}}\langle \hat{A}\hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle \nabla \nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$, where $\langle \hat{A}\hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle$ is the correlation of $\hat{A}$ and the local density operator. Alternatively to the present route via Eq. (4), the sum rule (13) can equivalently be derived from second-order invariance of $\langle \hat{A}\rangle$ against global shifting and hence calculating ∂²A(ϵ₀)/∂ϵ₀∂ϵ₀ = 0.

Addressing locally resolved correlation functions on the basis of Eq. (4) allows to access a higher degree of spatial resolution. We first consider the case $\hat{A}=\hat{\rho }({{{{{{{\bf{r}}}}}}}})$, which leads upon re-writing the right-hand side of Eq. (4) via $-{\sum }_{i}{\nabla }_{i}\hat{\rho }({{{{{{{\bf{r}}}}}}}})=-{\sum }_{i}{\nabla }_{i}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})={\sum }_{i}\nabla \delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})=\nabla \hat{\rho }({{{{{{{\bf{r}}}}}}}})$ to the following identity:

$$\beta \left\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{\rho }({{{{{{{\bf{r}}}}}}}})\right\rangle =\nabla \rho ({{{{{{{\bf{r}}}}}}}}),$$

(14)

where we recall that on the right-hand side $\rho ({{{{{{{\bf{r}}}}}}}})=\langle \hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle$ is the averaged density profile. Hence building the correlation of the density operator with the global external force acts to spatially differentiate the density profile. We recall that the density gradient ∇ρ(r), as it occurs on the right-hand side of Eq. (14), follows alternatively from the YBG equation (1), which upon multiplication by β attains the form ∇ρ(r) = βF_int(r) + βF_ext(r), where the external force density is simply given as F_ext(r) = − ρ(r) ∇V_ext(r).

It is interesting to note that Eq. (14), when written in covariance form as $\beta {{{{{{{\rm{cov}}}}}}}}({\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0},\hat{\rho }({{{{{{{\bf{r}}}}}}}}))=\nabla \rho ({{{{{{{\bf{r}}}}}}}})$, mirrors closely the structure of the thermodynamic identity $\beta {{{{{{{\rm{cov}}}}}}}}(N,\hat{\rho }({{{{{{{\bf{r}}}}}}}}))=\partial \rho ({{{{{{{\bf{r}}}}}}}})/\partial \mu \equiv {\chi }_{\mu }({{{{{{{\bf{r}}}}}}}})$ with the local compressibility χ_μ(r)^8,9,10. Here rather than the spatial gradient, the thermodynamic parametric derivative with respect to chemical potential occurs. Equation (14) can also be viewed as the so-called inverse Lovett-Mou-Buff-Wertheim (LMBW) relation $\beta \int\,d{{{{{{{{\bf{r}}}}}}}}}^{{\prime} }{H}_{2}({{{{{{{\bf{r}}}}}}}},{{{{{{{{\bf{r}}}}}}}}}^{{\prime} }){\nabla }^{{\prime} }{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })=\nabla \rho ({{{{{{{\bf{r}}}}}}}})$^39,40, as is obtainable from global translational invariance³¹. Having explicit results for the density covariance ${H}_{2}({{{{{{{\bf{r}}}}}}}},{{{{{{{{\bf{r}}}}}}}}}^{{\prime} })={{{{{{{\rm{cov}}}}}}}}(\hat{\rho }({{{{{{{\bf{r}}}}}}}}),\hat{\rho }({{{{{{{{\bf{r}}}}}}}}}^{{\prime} }))$ is however not required in the much more straightforward form (14). Furthermore, by summing only over particle pairs with unequal indices we obtain the distinct identity ${\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle }_{{{{{{{{\rm{d}}}}}}}}ist}={{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$, which again relates seemingly very different physical objects identically to each other. The derivation is straightforward by starting from Eq. (14), subtracting the self contribution which is the YBG equation (1) in the form − βρ(r) ∇V_ext(r) = − βF_int(r) + ∇ρ(r), and dividing the result by β.

To validate the Noether invariance theory and to investigate its implications for the use of force sampling methods, we turn to many-body simulations and consider the Lennrd-Jones (LJ) fluid as a representative microscopic model. The LJ pair potential ϕ(r) between two particles separated by a distance r has the familiar form ϕ(r) = 4ϵ[(σ/r)¹² − (σ/r)⁶] with the energy scale ϵ and particle size σ both being constants.

As our above statistical mechanical derivations continue to hold canonically, we sample both via adaptive Brownian dynamics (BD)⁴¹ with a fixed number of particles, but also using Monte Carlo simulations in the grand canonical ensemble. Spatial inhomogeneity is induced by confining the system between two planar, parallel LJ walls. Each wall is represented by an external potential contribution V_wall(z) that we choose to be identical to the LJ interparticle potential ϕ(r), but instead of the radial distance r evaluated as a function of the distance z perpendicular to the wall, V_wall(z) = 4ϵ[(σ/z)¹² − (σ/z)⁶]. The joint potential of both walls is then V_ext(z) = V_wall(z) + V_wall(L − z), with L indicating the separation distance between the two walls. The specific choice of 12-6-wall potential is made for convenience only and it differs from the physically motivated 9-3-form (see e.g., Evans et al.⁹).

The system is periodic in the two directions perpendicular to the z-direction across the slit; a sketch is shown in Fig. 1b. The wall separation distance is chosen as L = 10σ, with σ denoting the LJ particle size, and the lateral box length is also set to 10σ. The LJ potential is cut and shifted with a cutoff distance of 2.5σ. The reduced temperature is k_BT/ϵ = 2 with ϵ denoting the LJ energy scale. We use N = 200 particles. Sampling is started after 10⁸ time steps that are used for equilibration. The subsequent sampling runlength is 3 × 10⁸ time steps which corresponds to ~ 2000τ_B, where τ_B = γσ²/ϵ denotes the Brownian timescale with γ being the friction constant. All results that we show for correlators are obtained from evaluation as covariances. Subtracting the residual contribution from the product of the two mean values helps to remove artifacts that occur due to finite sampling.

The density profile of the confined LJ fluid, resolved as a function of the scaled position z/σ across the planar slit, is shown in Fig. 2a. The shape of the spatial density variation features structured packing effects that appear adjacent to each wall and that become damped towards the middle of the pore. Turning to the density gradient, we present simulation results for both sides of Eq. (14) in Fig. 2b. Equation (14) in the specific planar geometry reduces to $\beta \langle \hat{F}_{{{{{{{{\rm{ext}}}}}}}}}^{0,z}{\sum }_{i}\, \delta (z-{z}_{i})/{L}^{2}\rangle =\partial \rho (z)/\partial z$, where δ(z − z_i) is a one-dimensional Dirac distribution, z_i is the component of the vector r_i across the pore, L² is the lateral system area, and the global external force has only a nonvanishing z-component given by $\hat{F}_{{{{{{{{\rm{ext}}}}}}}}}^{0,z}=-{\sum }_{i}\partial {V}_{{{{{{{{\rm{ext}}}}}}}}}({z}_{i})/\partial {z}_{i}$. The density profile is sampled as ρ(z) = 〈∑_i δ(z − z_i)/L²〉. The comparison of the a priori very different data sets shown in Fig. 2b indicates excellent agreement. That the correlation of the density operator with the global external force operator indeed gives the gradient of the density profile, cf. Eq. (14), is surely not only at first glance very counter-intuitive.

Fig. 2: Illustration of the sum rules (14), (15), and (16).

The simulation results were obtained from adaptive BD sampling of the LJ fluid confined between two parallel planar LJ walls. The profiles are shown as a function of scaled distance z/σ across the planar slit. a The density profile ρ(r) of the confined system is shown as a reference. b Comparison of the correlator $\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle$ and the density gradient ∇ρ(r), see Eq. (14); the zoomed inset demonstrates the respective noise levels and it also shows the scaled force density sum βF_U(r) = βF_int(r) + βF_ext(r) which equals ∇ρ(r) due to the local force balance. c Comparison of ${\beta }^{2}\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ and β ∇F_int(r), see Eq. (15). The former route carries less statisical noise and hence can serve as a starting point for a force sampling scheme. d Comparison of ${\beta }^{2}\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ and the local external potential curvature density βρ(r) ∇∇V_ext(r), see Eq. (16).

We next consider the one-body interparticle force density operator $\hat{A}={\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$, for which Eq. (4) yields

$$\beta \left\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\right\rangle =\nabla {{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}}).$$

(15)

Equation (15) gives access to the gradient of the internal force density (right-hand side) via sampling the correlation of the local internal force density with the global external force (left-hand side). This relationship could be used in a force sampling scheme^{13,14,15,16,17,18,19}, where one obtains data for the force correlations and via spatial integration obtains the interparticle force density, which we demonstrate below. We first present simulation results to illustrate the validity of Eq. (15) in Fig. 2c. The results for $\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ carry much less statistical noise, as the need for building the numerical derivative ∇F_int(r) is avoided. However, this is no panacea, as accurately sampling the correlation of the interparticle force density with the global external force also poses challenges to the overall equilibration of the system.

Addressing the total force density operator $\hat{A}=\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ requires to complement the above-considered interparticle force density ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ with the ideal and external contributions. These two latter terms constitute mere variants of the density operator identity (14). First there is the external force density operator $\hat{A}={\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=-\hat{\rho }({{{{{{{\bf{r}}}}}}}})\nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ which yields $\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle =-[\nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})]\nabla \rho ({{{{{{{\bf{r}}}}}}}})$, as ∇V_ext(r) can be taken out of the phase space average on the left-hand side of Eq. (14). Secondly, the diffusive force density, $\hat{A}=-{k}_{B}T\nabla \hat{\rho }({{{{{{{\bf{r}}}}}}}})$, leads trivially to the gradient of Eq. (14).

Collecting all three terms (ideal, interparticle, and external) allows us to obtain for the choice $\hat{A}=\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ a mixed global-local Noether identity:

$$\beta \left\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\right\rangle =\rho ({{{{{{{\bf{r}}}}}}}})\nabla \nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}}).$$

(16)

We present simulation results that validate the sum rule (16) in Fig. 2d. We have checked that via spatial integration these results also validate the global variance identity $\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\rangle =\int\,d{{{{{{{\bf{r}}}}}}}}\rho ({{{{{{{\bf{r}}}}}}}})\nabla \nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$³⁴, which follows from Eq. (13) with operator $\hat{A}=1$. For the presently considered system, the global force-force correlation on the left-hand side is only marginally (0.4%) smaller than the global mean potential curvature on the right-hand side.

Local shifting applications

We turn to the application of the locally resolved hyperforce sum rules (10) and (11). We recall from the Methods section that the seemingly trivial case $\hat{A}=1$ reduces the local hyperforce identity (11) to the locally resolved force balance relationship ${{{{{{{\bf{F}}}}}}}}({{{{{{{\bf{r}}}}}}}})=\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle =0$. The definition of the total force operator (9) and carrying out the average gives the more explicit form − k_BT ∇ρ(r) + F_int(r) − ρ(r) ∇V_ext(r) = 0, i.e., the first member (1) of the Yvon-Born-Green hierarchy¹. Typically this identity is derived from multiplying the equilibrium probability distribution function Ψ_eq by the gradient of the interaction potential and integrating over the degrees of freedom of N − 1 particles. We emphasize that arguably the simplest possible application of Eq. (11) yields such a central result of liquid state theory with very little effort. From the Noetherian point of view the result was also obtained from applying the locally resolved transformation (5) and (6) to the free energy^33,35. At the heart of these Noetherian derivations lies the invariance of the Hamiltonian, of the phase space integration measure, and hence of the partition sum.

We next consider setting $\hat{A}={\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}$ in Eq. (10). This constitutes a valuable consistency check with the above global shifting of $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ that led to Eq. (16) and which we can identically reproduce here. Arguably even more fundamentally the sum rule (16) can be obtained by considering mixed local-global shifting invariance at second order, i.e., building the mixed derivative ∂(δΩ/δϵ(r))/∂ϵ₀ = 0, where the grand potential $\Omega =-{k}_{B}T\ln \Xi$ is subject to the combined displacement r_i → r_i + ϵ₀ + ϵ(r_i). Furthermore increasing the spatial resolution and hence selecting $\hat{A}=\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ in Eq. (10) yields the recent Noether-constrained two-body force-correlation theory, which is discussed in detail by Sammüller et al.³⁶. The theory that is presented therein can hence be viewed as the special case of pure force-dependence within the hyperforce framework.

Reverting back to developing the general theory, here we generalize to higher orders by iteratively replacing $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$ by $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$ in Eq. (8). This leads to the following second-order hyperforce sum rule:

$${\beta }^{2}\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })\hat{A}\rangle =\beta \left\langle \hat{A}\frac{{\delta }^{2}H[{{{{{{{\boldsymbol{\epsilon }}}}}}}}]}{\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}})\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })}\right\rangle +\left\langle \frac{{\delta }^{2}\hat{A}[{{{{{{{\boldsymbol{\epsilon }}}}}}}}]}{\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}})\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })}\right\rangle ,$$

(17)

where evaluation of the right-hand side at ϵ(r) = 0 is suppressed in the notation and ${\delta }^{2}H[{{{{{{{\boldsymbol{\epsilon }}}}}}}}]/\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}})\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })$ is discussed by Sammüller et al.³⁶. In case of no dependence of $\hat{A}$ on momenta, i.e., $\hat{A}=\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})$, the second term on the right-hand side of Eq. (17) can be made more explicit as

$$\left\langle \frac{{\delta }^{2}\hat{A}([{{{{{{{\boldsymbol{\epsilon }}}}}}}}],{{{{{{{{\bf{r}}}}}}}}}^{N})}{\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{\bf{r}}}}}}}})\delta {{{{{{{\boldsymbol{\epsilon }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })}\right\rangle =\left\langle \mathop{\sum}\limits_{ij}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})\delta ({{{{{{{{\bf{r}}}}}}}}}^{{\prime} }-{{{{{{{{\bf{r}}}}}}}}}_{j}){\nabla }_{i}{\nabla }_{j}\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})\right\rangle .$$

(18)

We proceed beyond forces by turning to energies with the aim of exploiting their thermal Noether invariance against shifting. We consider both the global external potential energy $\hat{A}={\sum }_{i}{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})$ as well as the global interparticle energy $\hat{A}=u({{{{{{{{\bf{r}}}}}}}}}^{N})$. Applying Eq. (11) yields in these two cases respectively the following sum rules:

$$\beta \left\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}){\sum }_{i}{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})\right\rangle =-\rho ({{{{{{{\bf{r}}}}}}}})\nabla {V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}}),$$

(19)

$$\beta \left\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})u({{{{{{{{\bf{r}}}}}}}}}^{N})\right\rangle ={{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}}).$$

(20)

Simulation results that demonstrate the validity of Eqs. (19) and (20) are shown in Fig. 3a, b, respectively. Here we have increased the overall density by reducing the lateral box size to 5σ and we sample N = 128 particles over time periods of 2000τ (data shown in Fig. 3a, b) and of 8000τ (data shown in Fig. 3c).

Fig. 3: Demonstration of Noether sum rules (19), (20), and (21).

These identities are respectively based on the global external and interparticle energies and on the center of mass. Shown are results from adaptive BD simulations for the LJ fluid between parallel LJ walls as a function of the scaled distance z/σ. a Comparison of ${\beta }^{2}\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}){\sum }_{i}{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})\rangle$ and βF_ext(r) = − βρ(r) ∇V_ext(r), see Eq. (19). b Comparison of ${\beta }^{2}\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})u({{{{{{{{\bf{r}}}}}}}}}^{N})\rangle$ and βF_int(r), see Eq. (20). c Comparison of $-\beta \langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}){\sum }_{i}{{{{{{{{\bf{r}}}}}}}}}_{i}\rangle$ and ρ(r), see Eq. (21).

The potential energy identities (19) and (20) can be supplemented by considering the kinetic energy, $\hat{A}={\sum }_{i}{{{{{{{{\bf{p}}}}}}}}}_{i}^{2}/(2m)$, which leads upon using Eq. (10) to the identity $\beta \langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}){\sum }_{i}{{{{{{{{\bf{p}}}}}}}}}_{i}^{2}/(2m)\rangle =-{k}_{B}T\nabla \rho ({{{{{{{\bf{r}}}}}}}})$. Treating then the entire Hamiltonian, $\hat{A}=H$, follows from adding up all three energy contributions. The result is the compact identity: $\beta \langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})H\rangle ={{{{{{{\bf{F}}}}}}}}({{{{{{{\bf{r}}}}}}}})=0$. This possibly unexpected behavior also holds for the global entropy. We choose the entropy operator $\hat{A}=\hat{S}\equiv -{k}_{B}\ln {\Psi }_{{{{{{{{\rm{eq}}}}}}}}}$ and obtain from Eq. (10) ${k}_{B}^{-1}\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\hat{S}\rangle ={{{{{{{\bf{F}}}}}}}}({{{{{{{\bf{r}}}}}}}})=0$, i.e., the correlation (as well as the covariance) of the entropy operator with the local force density vanishes. This behavior is very different from the nontrivial fluctuation profile that is obtained from the covariance of the density operator with the global entropy^11,12.

As a final case, we consider the center of mass ∑_ir_i/N as a purely mechanical entity. We multiply by N, such that $\hat{A}={\sum }_{i}{{{{{{{{\bf{r}}}}}}}}}_{i}$ and obtain from Eq. (11) upon multiplication by − 1 the result

$$-\beta \left\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\mathop{\sum}\limits_{i}{{{{{{{{\bf{r}}}}}}}}}_{i}\right\rangle =\rho ({{{{{{{\bf{r}}}}}}}}){\mathbb{1}}.$$

(21)

Integrating Eq. (21) over position yields a simple relationship between the correlator of the global external force and the center of mass: $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\sum }_{i}{{{{{{{{\bf{r}}}}}}}}}_{i}\rangle /\bar{N}=-{k}_{B}T{\mathbb{1}}$, where the mean number of particles is $\bar{N}=\int\,d{{{{{{{\bf{r}}}}}}}}\rho ({{{{{{{\bf{r}}}}}}}})\equiv \langle N\rangle$. Except for an additional sum over all particles, this global relationship is akin to the equipartition theorem. We present simulation results for both sides of the locally resolved Eq. (21) in Fig. 3c. The accurate agreement of the respective profiles confirms that the identity (21) indeed offers a rather unusual route to gain access to the density profile.

Hyperforce sampling and equilibration testing

Besides the unexpected insights into the general correlation structure of equilibrium many-body systems that the thermal Noether invariance delivers, our results are useful for the careful assessment and construction of computer sampling schemes. Force sampling^{13,14,15,16,17,18,19} in perhaps its most intuitive form¹⁵ rests on spatial integration of the YBG equation (1) such that the density profile is obtained via ρ(r) = ρ₀ + β∇⁻¹ ⋅ [F_int(r) − ρ(r) ∇V_ext(r)], where ρ₀ = const is an integration constant and ∇⁻¹ is an inverse ∇ operator. The data input on the right-hand side is obtained via sampling ${{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ and either $\rho ({{{{{{{\bf{r}}}}}}}})=\langle \hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle$ or F_ext(r) = − 〈∑_i δ(r − r_i)∇_iV_ext(r_i)〉. The averages denote those that are being carried out in the simulation. In the present planar geometry ∇⁻¹ reduces to carrying out a simple position integral, which we make explicit below.

Summarizing, we can compare the results from four different routes: i) counting of particle occurrences in a position-resolved histogram, which constitutes the standard method, ii) force sampling¹⁵ according to Eq. (1), iii) hyperforce sampling according to the global external force correlation in Eq. (14) with spatial integration post-processing, and iv) center-of-mass-based hyperforce sampling according to Eq. (21). These routes are respectively given by the following explicit expressions:

$$\rho (z)=\langle \hat{\rho} (z)\rangle ,$$

(22)

$$\rho (z)={\rho }_{0}+\beta \int\nolimits_{0}^{z}d{z}^{{\prime} }\left\langle \hat{{F}}_{U}({z}^{{\prime} })\right\rangle ,$$

(23)

$$\rho (z)={\rho }_{0}+\beta \int\nolimits_{0}^{z}d{z}^{{\prime} }\left\langle {\hat{F}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{\rho }({z}^{{\prime} })\right\rangle ,$$

(24)

$$\rho (z)=-\beta \left\langle \hat{F}(z)\mathop{\sum}\limits_{i}{z}_{i}\right\rangle .$$

(25)

Here we choose the integration constant as ρ₀ = ρ(0) = 0 due to the divergent wall potential at z = 0. The averages on the above right-hand sides denote the actual simulation data, all vectors have been projected onto the z-direction across the pore, and z_i denotes the z-component of the particle position r_i. In more detail, the operators on the right-hand sides of Eqs. (22) and (23) are explicitly given as $\hat{\rho} (z)={\sum }_{i}\delta (z-{z}_{i})/{L}^{2}$ and ${\hat{F}}_{U}(z)={\sum }_{i}{f}_{i,z}^{{{{{{{{\rm{int}}}}}}}}}\delta (z-{z}_{i})/{L}^{2}-\hat{\rho} (z)\partial {V}_{{{{{{{{\rm{ext}}}}}}}}}(z)/\partial z$, where we recall that L² is the lateral system size and the z-component of the interparticle force on particle i is ${f}_{i,z}^{{{{{{{{\rm{int}}}}}}}}}=-\partial u({{{{{{{{\bf{r}}}}}}}}}^{N})/\partial {z}_{i}$. Furthermore the operators on the right-hand sides of Eqs. (24) and (25) are ${\hat{F}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}=-{\sum }_{i}\partial {V}_{{{{{{{{\rm{ext}}}}}}}}}({z}_{i})/\partial {z}_{i}$, and $\beta \hat{F}(z)=\beta {\hat{F}}_{U}(z)\,-\partial \hat{\rho} (z)/\partial z$.

Results for the density profile from the four routes (22)–(25) are shown in Fig. 4. The simulation parameters are identical as before [Fig. 2]. We display the four different statistical estimators for the density profile, as obtained after increasing runlength of (a) 10⁵, (b) 10⁶, (c) 10⁷, and (d) 3 × 10⁸ simulation steps. We recall that as demonstrated above both in the numerical examples as well as in the formal statistical mechanical derivations, the results from all routes are formally identical. In practice, pronounced differences can be observed and these are due to the simulation averages being mere approximations for the true statistical mechanical equilibrium.

Fig. 4: Comparison of standard counting against force sampling.

We show results from four different routes towards the density profile ρ(r) as obtained after a 10⁵, b 10⁶, c 10⁷, d 3 × 10⁸ simulation steps. Shown is data from the standard counting method according to Eq. (22) (orange lines), from force sampling F_U(r) according to Eq. (23) (green dash-dotted lines), from global external force correlation sampling of $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle$ according to Eq. (24) (blue solid lines), and from center-of-mass correlation sampling of $\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}){\sum }_{i}{{{{{{{{\bf{r}}}}}}}}}_{i}\rangle$ according to Eq. (25) (red symbols). Results from the latter route are only displayed from the longest run [panel d] and they still display considerable scatter, whereas the results from the remaining three methods already agree very satisfactorily.

For example the routes (23) and (24) yield less statistical noise due to the spatial integration, but they however can instead accumulate systematic deviations. The expected differences between the four methods are also consistently demonstrated by the fact that the results from the different routes mutually agree better for increasing runlengths. Nevertheless, in particular, the routes (24) and (25) that involve global quantities are very sensitive to the choice of runlength and they can hence serve as indicators of the overall quality of the sampling routine, even when quantities beyond the density profile are the very aim of the simulation. Having such tools for quality control can be particularly useful when investigating capillary and wetting phenomena^{42,43,44,45,46} where surface phase transitions pose significant challenges for reliable prediction.

The Noetherian hyperforce framework allows us to easily go beyond the density profile and we wish to address the interparticle force density as a target, rather than the mere source that it played in contributing to Eq. (23) above for the force sampling. As a demonstration we use and contrast different estimators for the interparticle force density profile F_int(r). The traditional counting method of filling a position-resolved histogram forms the baseline and Eq. (15) provides an alternative. These methods are respectively given by

$${F}_{{{{{{{{\rm{int}}}}}}}}}(z)=\langle {\hat{F}}_{{{{{{{{\rm{int}}}}}}}}}(z)\rangle ,$$

(26)

$${F}_{{{{{{{{\rm{int}}}}}}}}}(z)=\beta \int\nolimits_{0}^{z}d{z}^{{\prime} }\left\langle {\hat{{F}}_{{{{{{{{\rm{ext}}}}}}}}}}^{\!\!\!\!0}{\hat{F}}_{{{{{{{{\rm{int}}}}}}}}}({z}^{{\prime} })\right\rangle .$$

(27)

Figure 5 presents both canonical averages obtained via adaptive BD⁴¹ as well as grand canonical Monte Carlo data. The chemical potential is chosen as μ/ϵ = 1 and the resulting average number of particles is 〈N〉 = 136.5. In the corresponding adaptive BD simulation runs we have set N = 136, which remains sharply fixed in the course of time. The agreement between both sets of results confirms the expectation of independence of the sum rule validity on the choice of ensemble. This is based on the fact that the theoretical derivations continue to hold with fixed N, as we have also explicitly verified. Hence the mechanical effects that the Noether invariance against spatial displacement captures are oblivious to the presence of global particle number fluctuations. We recall that the latter are precisely captured and quantified by the local compressibility^8,9,10.

Fig. 5: Comparison of different statistical estimators for the interparticle one-body force density profile according to Eq. (15).

The results are obtained from the standard counting histogram method, ${{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ (orange lines), and from hyperforce sampling and spatial integration of $\nabla {{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=\beta \langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ (blue lines) with data for the right-hand side forming the basis. These methods are explicitly spelled out in Eqs. (26) and (27). The results stem from sampling 10⁵ strongly correlated microstates at every simulation step (a, b) compared to better-decorrelated configurations obtained from also 10⁵ configurations, with the samples being taken only every 1000th simulation step (c, d). Results are shown from grand canonical Monte Carlo simulations (a, c) and from adaptive BD simulations (b, d). The results from sampling are symmetrized with respect to mirroring at the center of the pore, i.e., via building the arithmetic mean [F_int(z) − F_int(L − z)]/2, as is common practice in force sampling schemes.

The comparison of lower and higher quality statistical data, as obtained from sampling every step (see Fig. 5a, b) or only every 1000th step (see Fig. 5c, d) demonstrates that the force correlation method is a sensitive measure of the degree of sampling quality.

Conclusions

In conclusion, we have developed a statistical mechanical hyperforce framework in generalization of the YBG equilibrium force balance relationship (1). Our theory is based on previously developed global^31,32,34 and local^33,35 shifting transformations on phase space. These variable transformations leave the thermal physics invariant despite an apparent dependence on the transformation parameter. The parameter is a three-dimensional globally constant vector in case of global symmetry, which applies to the entirety of the system, and a position-dependent three-dimensional vector field for the locally resolved case. Treating the corresponding phase space transformations according to Noether’s invariant variational calculus²¹ allows us to systematically generate exact identities.

Here we have generalized this Noetherian concept to the equilibrium average of an arbitrary given phase space function $\hat{A}$. The resulting Noether identities couple in a specific manner the forces, which the underlying Hamiltonian generates, to the observable $\hat{A}$ and its gradient with respect to the phase space variables. In the position-resolved case, we obtain localized correlation functions, with the Dirac distribution generating microscopically sharp, but statistically coarse-grained and hence well-accessible correlators. In detail, we have presented the global hyperforce sum rule (4) that applies to any given phase space function $\hat{A}$. The local versions comprise Eqs. (10) and Eq. (11), where the latter version applies to momentum-independent observables. Decomposing the total force operator into its ideal, interparticle, and external contributions leads to Eq. (12), which generalizes the equilibrium force density balance (1). An overview of these general identities is shown in Fig. 6a.

Fig. 6: Overview of theoretical results.

a Hyperforce sum rules that relate a given observable with the forces that act in the system. The global sum rules (4) and (13) couple the global external force operator ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}$ at first and second order with an observable $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$. The local sum rules (10), (11), and (12) contain the localized force density operator $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ and its interparticle contribution ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ and they apply for full phase space-dependence $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$ (upper bubble) or coordinate-only dependence $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N})$ (lower bubble). In the latter case alternative forms involve the total local force density $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ or the splitting (1) into its three constituent contributions. b Sum rules that result from specific observable choices. Global examples set $\hat{A}({{{{{{{{\bf{r}}}}}}}}}^{N},{{{{{{{{\bf{p}}}}}}}}}^{N})$ as the density operator $\hat{\rho }({{{{{{{\bf{r}}}}}}}})$, the interparticle force density operator ${\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$, and the total local force density operator $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$, as corresponds to the sum rules (14), (15), and (16), respectively. The local examples include the total external potential energy ∑_iV_ext(r_i), the interparticle energy u(r^N), and the sum of all particle coordinates ∑_ir_i, corresponding to the sum rules (19), (20), and (21), respectively.

For a variety of relevant concrete choices of the form of $\hat{A}$, we have demonstrated explicitly their validity via carrying out many-body simulations. This includes forces, energies, and entirely mechanical quantities such as the center of mass; see Fig. 6b for a summary of specific examples. We have shown that the sampling quality and equilibration properties depend significantly on the type of underlying sum rule. We argue that this behavior forms a valuable asset for the systematic assessment of simulation quality.

Our hyperforce identities complement the virial¹, hypervirial³⁷, equipartition¹ and Yvon¹ theorems. Despite certain formal similarities, we emphasize that the underlying phase space invariance is more fundamental than derivations based on ad hoc partial integration. Furthermore, the considered invariance operations naturally lead to correlations with either global or locally resolved forces, which are both simple to interpret and straightforward to acquire in simulations.

We have shown how the global hyperforce identity (4) can alternatively be obtained from the Yvon theorem¹. Hence, as anticipated in the discussion by Rotenberg¹³, the Yvon theorem can indeed be a relevant tool for force sampling. However, the general localized Noether sum rule (10) reaches beyond the Yvon theorem in terms of the momentum effects that are included. We have shown that the derivation of the momentum-independent sum rule (11) based on the Yvon theorem requires to apply the ad hoc localized choice $\hat{A}\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}_{i})$ and summing over i. As a second step, treating the ideal contribution explicitly allows to identify the sequence of emerging terms as the one-body force operator $\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})$ at any position. Conversely, the Yvon theorem can be derived as a limit case from Noether invariance upon shifting only one given particle i according to r_i → r_i + ϵ₀, and keeping unchanged all other particles coordinates r_j with j ≠ i.

Besides the theoretical connections that the Noether hyperforce sum rules establish, they can serve to carry out tests in theoretical and simulation approaches, with possible fruitful connections to the mapped-averaging force sampling framework¹⁶. The hyperforce sum rules can also provide a starting point, together with the existing body of equilibrium sum rules^{42,43,44,45,46}, for the construction of new inhomogeneous liquid state approximations. We have exemplified the use of sum rules in providing gauges for the equilibration quality of simulation data and we are confident in their future beneficial use in machine-learning approaches such as the recent neural functional theory^47,48.

In the context of the use of machine-learning in Statistical Mechanics^{47,48,49,50,51,52,53,54} sum rules were shown to provide tests for the successful construction of neural functionals both in^47,48 and out of equilibrium⁴⁹. These sum rules amount to specific force properties, such as the vanishing of the global interparticle force⁴⁹ and the interrelation of different orders of direct correlation functions^47,48. The present much more general hyperforce framework can form much inspiration for such approaches as well as for the recent force-based density functional theory^35,55, which was compared⁵⁵ to standard fundamental measure theory⁵⁶.

Furthermore, investigating hyperforce correlations in ionic systems, recent work^57,58,59 addresses both concentration and charge fluctuation behavior, as are also relevant in confined systems⁶⁰, appears to be very promising. This also holds true for further interfacial physics^{42,43,44,45,46} and potentially for the higher-order correlation functions^3,4,5.

In our theoretical derivations we have relied on the grand canonical ensemble, with fixed chemical potential μ and fluctuating number of particles N. Carrying out formal manipulations in this way is often more straightforward than working with fixed N, as is appropriate for a canonical treatment. (Temperature is constant in both ensembles.) A prominent example is to obtain the density profile as a functional derivative ρ(r) = δΩ/δV_ext(r) where crucially μ is kept fixed, rather than N, upon building the functional derivative. This prototypical example demonstrates the elegance of working grand canonically, and one could expect that a similar situation applies to the thermal Noether invariance. This, however, is not the case. Rather the phase space shifting transformation, whether global by a constant ϵ₀ or locally resolved in position via a three-dimensional vector field ϵ(r), is an entirely mechanical operation that applies equally well canonically. The shifting invariance gives a powerful new route to correlation functions and their sum rules, an alternative to the traditional method of integrating over degrees of freedom, as pioneered by Yvon⁶¹ and Born and Green⁶².

A detailed account of global shifting in the canonical ensemble is provided by Hermann and Schmidt³². The resulting Noether force identities are analogous in form to the results from a grand canonical treatment³¹, with the sole (and trivial) difference of the definition of the respective ensemble averages. Here we find that the analogous situation holds for the hyperforce identities. As they originate from phase space transformations only, they are insensitive to the ensemble differences between the canonical and the grand ensemble. This theoretical fact is corroborated by our computer simulation results, where we have explicitly compared grand canonical Monte Carlo data and canonical results, with the latter obtained via sampling under adaptive BD time evolution⁴¹.

We have used overdamped Brownian time evolution as a means to sample in thermal equilibrium. We find the adaptive Brownian dynamics time stepping algorithm⁴¹ to be a convenient choice for our present purposes. The principle validity of the hyperforce sum rules is nevertheless independent thereof and we expect careful use of either the simpler Euler-Maruyama method^41,63 or indeed Molecular Dynamics⁶³ to yield identical results. In our BD simulations, we have sampled all correlation functions at equal time as is the appropriate limit in equilibrium time evolution to recover static thermal ensemble averages. We refer to Hermann and Schmidt³¹ for the exploitation of the Noether invariance in nonequilibrium dynamics.

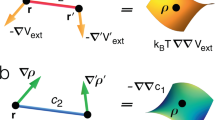
As a final note, we return to classical density functional theory and its prowess in the description and incorporation of the fundamental force correlators that emerge from the hyperforce concept. We recall that classical density functional theory is based on a formally exact variational principle which amounts to solving the following Euler-Lagrange equation:

$${k}_{B}T{c}_{1}({{{{{{{\bf{r}}}}}}}},[\rho ])-{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{\bf{r}}}}}}}})={k}_{B}T\ln \rho ({{{{{{{\bf{r}}}}}}}})-\mu .$$

(28)

Here c₁(r, [ρ]) is the one-body direct correlation function of inhomogeneous liquid state theory. This is expressed as a density functional via c₁(r, [ρ]) = − βδF_exc[ρ]/δρ(r), where F_exc[ρ] is the intrinsic excess Helmholtz free energy functional, which contains the interparticle interactions, and δ/δρ(r) denotes the functional derivative with respect to the density profile. Solving Eq. (28) for given T, μ, and V_ext(r) yields results for the equilibrium density profile ρ(r), which is hence the central variable of density functional theory.

A multitude of connections with the current invariance theory emerge naturally. From the density profile, using the hyperforce identities one can obtain results for $\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}){\sum }_{i}{{{{{{{{\bf{r}}}}}}}}}_{i}\rangle$ via Eq. (21), for $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ via Eq. (16), for $\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}}){\sum }_{i}{V}_{{{{{{{{\rm{ext}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{i})\rangle$ via Eq. (19), and upon building the gradient of the density profile for $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}\hat{\rho }({{{{{{{\bf{r}}}}}}}})\rangle$ via Eq. (14).

We can make further progress by noting that within density functional theory the interparticle force density is given by F_int(r) = k_BTρ(r) ∇c₁(r), where we have suppressed the functional dependence on the density profile in the notation. That this relationship holds can be seen from building the gradient of Eq. (28) whereby − ∇μ vanishes as the chemical potential is constant, multiplying by ρ(r), and comparing term-wise with the force density balance relationship (1).

Having obtained F_int(r) in this (density functional) way gives access to $\langle \hat{{{{{{{{\bf{F}}}}}}}}}({{{{{{{\bf{r}}}}}}}})u({{{{{{{{\bf{r}}}}}}}}}^{N})\rangle$ via Eq. (20). Building the gradient of the interparticle force density via the product rule yields ∇F_int(r) = k_BT[ ∇ρ(r)] ∇c₁(r) + k_BTρ(r) ∇∇c₁(r). Again in principle, the right-hand side is straightforward to evaluate in a typical numerical density functional study as data for both ρ(r) and c₁(r) is accessible. As a result, the correlator $\langle {\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{ext}}}}}}}}}^{0}{\hat{{{{{{{{\bf{F}}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}({{{{{{{\bf{r}}}}}}}})\rangle$ is available via the hyperforce sum rule (15).

Hence standard results that are obtained within the density functional framework allow to access a wealth of nontrivial force correlation structures. This additional information is not redundant. We compare with Evans and his coworkers’ local compressibility χ_μ(r) = ∂ρ(r)/∂μ, where similar to the present force setup, one obtains χ_μ(r) from processing the density profile. In practice then analyzing χ_μ(r) can shed significantly more light on the physics than what is apparent from the density profile alone, as has been demonstrated in a range of insightful studies on drying at substrates and the important phenomenon of hydrophobicity^8,9,10.