Introduction

Non-Hermitian systems which possess gain/loss or non-reciprocal hopping terms, have attracted great attention due to their fantastic resonant characteristics1,2. For example, the spectral degeneracy is always along with the reduction of eigenstates, which is the so-called exceptional point (EP)3,4,5,6,7, distinctive from the Dirac point or Weyl point in Hermitian systems. The intersection of non-Hermitian physics and topology can also lead to novel phenomenon, such as the non-Hermitian skin effect that all the delocalized eigenstates become localized at the boundary or the corner when the periodical boundary condition (PBC) changes to the open boundary condition (OBC)8,9,10,11,12, resulting in the breakdown of bulk-boundary correspondence13. These properties, realized in diverse systems such as mechanical metamaterials14, quantum walk systems15, photonic systems7,16, acoustic systems17, and electrical circuits18,19,20,21,22,23, have created opportunities to achieve significant enhancement of the sensitivity for sensors24,or perfect absorption of the input wave25.

To investigate the spectral degeneracy characteristic in the higher dimension, recent works have extended the exceptional point to exceptional ring (ER)26,27,28,29,30 or exceptional surface (ES)31,32, theoretically. In addition, when combining the non-Hermitian systems with topological behaviors, the topological invariants defined in Hermitian systems cannot predict the existence of the boundary modes any more33. Several methods have been proposed to solve this issue10,33,34,35,36,37, but the limitation manifests as the particular precondition that point gap or line gap should exist under PBC38.

In this study, we utilized an uncomplicated two-dimensional (2D) non-reciprocal hopping model, and extended the spectral degeneracy characteristic into exceptional elliptical rings and exceptional hyperbolic lines. We show how to design the exceptional rings, the topological boundary modes and the bulk-boundary correspondence, by the protection of time-reversal symmetry and pseudo-Hermitian symmetry. We found that the selection of the primitive cell influences the appearance of boundary modes, which is the so-called gauge-dependent topological behaviors, and can be predicted by the well defined topological invariant successfully even for the condition that no gap exists under PBC. Attentively, the skin effect and the breakdown of bulk-boundary correspondence cannot occur in our model due to the pseudo-Hermitian symmetry38,39,40, verified by the transfer-matrix method10 as well. Furthermore, to extend the theoretical model in a practical system easily, we designed a 2D non-reciprocal hopping topolectrical circuit lattice, and confirmed the spectral degeneracy characteristic and topological behaviors through circuit simulation, which even can be compared to other platforms such as photonics, acoustics, mechanics and meta-surface.

Results and discussion

Non-reciprocity and spectral degeneracy

Compared with on-site gain/loss systems, systems with non-reciprocal hopping terms provide more freedom on the flexible realization of different types of spectral degeneracy in 2D non-Hermitian systems. For simplicity and without loss of generality, we started with a 2 × 2 tight-binding model described by H(k) = d0σ0 + dxσx + dyσy + dzσz in the momentum space, where d0 = ε0, dz = 0, and

$$ {d}_{x}={t}_{0}+\mathop{\sum}\limits_{\alpha =x,y}{t}_{1\alpha }\cos {k}_{\alpha }+{\rm{i}}\mathop{\sum}\limits_{\alpha =x,y}{\gamma }_{1\alpha }\sin {k}_{\alpha },\\ {d}_{y}={\rm{i}}{\gamma }_{0}+\mathop{\sum}\limits_{\alpha =x,y}{t}_{2\alpha }\sin {k}_{\alpha }+{\rm{i}}\mathop{\sum}\limits_{\alpha =x,y}{\gamma }_{2\alpha }\cos {k}_{\alpha }.$$
(1)

σx,y,z are Pauli matrices for the spin degree of freedom, and σ0 represents the identity matrix. According to the real-space Hamiltonian described in Supplementary Note 1, ε0 represents the on-site energy, t1α/2α represents the reciprocal part of the hopping terms, while γ0, γ1α/2α represent the non-reciprocity of intra-cell interaction and inter-cell interaction between the nearest cells, respectively.

The existence of exceptional ring relies on a sufficient condition that t2α = 0 and γ1α = 0, as proved in Supplementary Note 2, thus the resulted Hamiltonian is protected by time-reversal symmetry and pseudo-Hermitian symmetry, as follows,

$$ {\mathcal{T}}{H}^{* }({\boldsymbol{k}}){{\mathcal{T}}}^{-1} =H(-{\boldsymbol{k}}),\,{\mathcal{T}}{{\mathcal{T}}}^{* }=\pm 1,\\ \eta H({\boldsymbol{k}}){\eta }^{-1} ={H}^{\dagger }({\boldsymbol{k}}),$$
(2)

where \({\mathcal{T}}\) is a unitary operator, and η is a Hermitian invertible operator41, which is system-specific in the non-Hermitian context (see Supplementary Note 3). These two symmetries restrict that, if \({\Psi }_{+}={({\Psi }_{A},{\Psi }_{B})}^{{\rm{T}}}\) is an eigenvector of the Hamiltonian with energy ε0 + ε1, then \({\Psi }_{-}={({\Psi }_{A},-{\Psi }_{B})}^{{\rm{T}}}\) or \({(-{\Psi }_{A},{\Psi }_{B})}^{{\rm{T}}}\) is an eigenvector with energy ε0 − ε1 (\({\varepsilon }_{1}\in {\mathbb{R}}\) or \({\rm{i}}{\mathbb{R}}\)). Therefore, spectral degeneracy characteristic occur with coalescent eigenvalues E± = ε0 and coalescent eigenstates Ψ± = (1, 0)T or (0, 1)T, if and only if

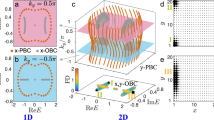
$$({t}_{1x}\pm {\gamma }_{2x})\cos {k}_{x}+({t}_{1y}\pm {\gamma }_{2y})\cos {k}_{y}=-({t}_{0}\pm {\gamma }_{0}).$$
(3)

The solutions to Eq. (3) give various spectral degeneracy behaviors, i.e., hyperbolic lines or elliptical rings, relying on whether the coefficients of \(\cos {k}_{x}\) and \(\cos {k}_{y}\) have opposite signs. For example, as shown in Fig. 1a, two exceptional rings cross with each other, while as shown in Fig. 1b, a pair of exceptional hyperbolic lines intersect with an exceptional ring.

Fig. 1: The real and imaginary parts of the energy spectra under periodical boundary condition.
figure 1

The blue and purple parts represent the eigenvalues E+ and E− respectively, where \({E}_{\pm }={\varepsilon }_{0}\pm \sqrt{{{d}_{x}}^{2}+{{d}_{y}}^{2}}\), and the red lines denote the spectral degeneracy that E+ = E− = ε0. For simplicity and without loss of generality, the on-site energy ε0 is set as zero, and the hopping parameters are set as t1x = t1y = t1. a, b The energy spectra defined by \({E}_{\pm }=\pm \sqrt{{({t}_{0}+{t}_{1}\cos {k}_{x}+{t}_{1}\cos {k}_{y})}^{2}-{({\gamma }_{0}+{\gamma }_{2x}\cos {k}_{x})}^{2}}\) with hopping parameters t0/t1 = 1, γ0/t1 = 0.2, γ2x/t1 = 0.4 in (a), and t0/t1 = 1, γ0/t1 = 0.6, γ2x/t1 = 1.2 in (b), which can exhibit exceptional rings and hyperbolic lines respectively. c–f The energy spectra defined by \({E}_{\pm }=\pm \sqrt{{({t}_{0}+{t}_{1}\cos {k}_{x}+{t}_{1}\cos {k}_{y})}^{2}-{{\gamma }_{0}}^{2}}\). The parameter space is classified into phase I-IV by the distinct forms of the exceptional rings. c Phase I with t0/t1 = 1.85, γ0/t1 = 0.25. d Phase II with t0/t1 = 1.2, γ0/t1 = 2.5. e Phase III with t0/t1 = 0.5, γ0/t1 = 0.75. f Phase IV with t0/t1 = 0.75, γ0/t1 = 0.5.

Full size image

For the purpose to reveal the interesting physics of spectral degeneracy, we simplified the model by only considering the non-reciprocity of the intra-cell interaction and assumed that t1x = t1y = t1. The resulted Hamiltonian can be written as,

$$H({k}_{x},{k}_{y})=\left(\begin{array}{ll}{\varepsilon }_{0}&{t}_{0}+{t}_{1}\cos {k}_{x}+{t}_{1}\cos {k}_{y}+{\gamma }_{0}\\ {t}_{0}+{t}_{1}\cos {k}_{x}+{t}_{1}\cos {k}_{y}-{\gamma }_{0}&{\varepsilon }_{0}\end{array}\right).$$
(4)

Without loss of generality, assuming t0/t1 and γ0/t1 are positive, we classified the parameter space into four phases by the distinct forms of ER, and the detailed range is illustrated in Table 1. As shown in Fig. 1c-f, phase I and phase II both possess a single ER locating at \(\cos {k}_{x}+\cos {k}_{y}=-({t}_{0}-{\gamma }_{0})/{t}_{1}\) with Ψ± = (1, 0)T, but encircle (π, π) and (0, 0) respectively. Phase III and phase IV both possess two ERs, locating at \(\cos {k}_{x}+\cos {k}_{y}=-({t}_{0}\pm {\gamma }_{0})/{t}_{1}\) with Ψ± = (0, 1)T and (1, 0)T, where the former encircle (0, 0) and (π, π), while the latter encircle (π, π) and (π, π).

Table 1 Illustration to the phase diagram of the tight-binding model. The parameter space (t0, t1, γ0) is classified into phase I-IV according to the distinct locations and centers of the exceptional ring (ER) in the momentum space (kx, ky). Phase I and phase II both possess a single exceptional ring, but encircle (π, π) and (0, 0) respectively. Phase III and phase IV both possess two exceptional rings, where the former encircle (π, π) and (0, 0), while the latter encircle (π, π) and (π, π).
Full size table

Gauge-dependent non-Hermitian topology

As we know, the behavior of real systems is often sensitive to the boundary conditions, and the open boundary condition sometimes introduces the localized modes at the boundary or the corner. The intersection of non-Hermitian physics and topology also brings out new phases. For simplicity, we imposed OBC along x direction and PBC along y direction in the lattice model, and the system can be understood as the effective one-dimensional chain parametrized by the transverse momentum ky (see Supplementary Note 4.1). Two kinds of OBC are proposed for comparison. OBC1 requires that the hopping terms between the first and the last cells are removed from the periodic lattice, as shown in Fig. 2a. For OBC2 shown in Fig. 2b, the difference from OBC1 is the selection of the primitive cell, which can be regarded as the gauge transformation that \(H^{\prime} ({k}_{x},{k}_{y})={S}^{-1}H({k}_{x},{k}_{y})S\) with \(S={\rm{diag}}({{\rm{e}}}^{{\rm{i}}{k}_{x}},1)\), which possesses the same symmetry and spectrum as H(kx, ky) under PBC, but leads to the distinct difference in topological behaviors.

Fig. 2: Schematic views of the two-dimensional tight-binding model under open boundary condition (OBC) along x direction.
figure 2

The gray and white circles represent the two sites A and B, and the yellow blocks indicate the selection of the primitive cell. The non-reciprocal hopping terms with parameters t0 ± γ0 are denoted by orange and green lines with arrows, while the reciprocal hopping terms with parameter t1/2 are denoted by gray lines. a Lattice model under OBC1. b Lattice model under OBC2.

Full size image

The numerical results for OBC1 and OBC2 spectra are shown in Fig. S3 in Supplementary Note 4.1 and Fig. 3a, d respectively, which reveal that the former is trivial, while the latter generates topological boundary modes at the on-site energy ε0, which is the so-called topological non-triviality. For example, using the parameters belonging to phase I, the OBC2 spectrum is shown in Fig. 3a, where the bulk modes are denoted by gray lines, and the topological boundary modes denoted by orange lines can exist for any ky ∈ (0, 2π). Correspondingly, the normalized amplitude of the localized wave function is shown in Fig. 3b.

Fig. 3: Topological behaviors of the effective one-dimensional tight-binding model under open boundary condition.
figure 3

a–c Show the results for phase I with hopping parameters t0/t1 = 1.85, γ0/t1 = 0.25, and (d-f) show the results for phase IV with t0/t1 = 0.75, γ0/t1 = 0.5. a, d The absolute values of the energy spectra ∣E∣ for ky ∈ (0, 2π) with on-site energy ε0 = 0, where gray and orange lines denote bulk modes and topological boundary modes, respectively. b, e The absolute values of the normalized amplitude of the localized topological boundary modes with N = 60 unit cells (2N sites) along x direction. c, f ∣a1∣, ∣a2∣, ∣b1∣, ∣b2∣ curves are colored by red, light red, dark green and light green, respectively, where \({a}_{1,2}=-[({t}_{0}+{\gamma }_{0})/{t}_{1}+\cos {k}_{y}]\mp \sqrt{{[({t}_{0}+{\gamma }_{0})/{t}_{1}+\cos {k}_{y}]}^{2}-1}\) and \({b}_{1,2}=-[({t}_{0}-{\gamma }_{0})/{t}_{1}+\cos {k}_{y}]\mp \sqrt{{[({t}_{0}-{\gamma }_{0})/{t}_{1}+\cos {k}_{y}]}^{2}-1}\), and the colored regions marked by the non-zero winding numbers W(R) satisfy the condition of topological boundary modes.

Full size image

To investigate the underlying mechanism of the existence or non-existence of topological boundary modes, we followed a convenient criterion applied for one-dimensional systems35. Generally, by polynomial factorization and rescaling the overall constants to unity without changing the topology, the Hamiltonian can be rewritten as,

$$H(z)=\left(\begin{array}{ll}0&a(z)\\ b(z)&0\end{array}\right)=\left(\begin{array}{ll}0&{z}^{-{q}_{a}}{{{\Pi }}}_{i}^{{p}_{a}}(z-{a}_{i})\\ {z}^{-{q}_{b}}{{{\Pi }}}_{i}^{{p}_{b}}(z-{b}_{i})&0\end{array}\right),$$
(5)

where the on-site energy is set to zero, and \(z={{\rm{e}}}^{{\rm{i}}{k}_{x}}\), \({k}_{x}\in {\mathbb{C}}\). qa, qb count the numbers of poles locating at z = 0, and \(\{{a}_{1},...,{a}_{{p}_{a}}\}\),\(\{{b}_{1},...,{b}_{{p}_{b}}\}\) are the complex roots of a(z) = 0, b(z) = 0 respectively. The topological boundary modes exist if and only if \(\exists \,R\in {{\mathbb{R}}}_{+},{W}_{a}(R){W}_{b}(R)<0\)35, where the winding number Wg(=a/b)(R) is defined as \(\frac{1}{2\pi {\rm{i}}}{\oint }_{| z| = R}d({\rm{log}}\,{g}_{( = a/b)}(z))\), which counts the number of zeros minus the number of poles encircled by the contour ∣z∣ = R. Through the calculation on winding numbers (see Supplementary Note 4.2), the criterion of the topological non-triviality can be reformulated as the fundamental principles that,

$$ ({\rm{i}})\quad{\rm{for}}\ {{\rm{OBC}}}_{1},\max \{| {a}_{1}| ,| {a}_{2}| \}<\min \{| {b}_{1}| ,| {b}_{2}| \}{\rm{or}}\max \{| {b}_{1}| ,| {b}_{2}| \}<\min \{| {a}_{1}| ,| {a}_{2}| \},\\ ({\rm{ii}})\quad\!\!{\rm{for}}\ {{\rm{OBC}}}_{2},\min \{| {b}_{1}| ,| {b}_{2}| \}<\max \{| {a}_{1}| ,| {a}_{2}| \},$$
(6)

where {a1, a2, b1, b2} are the solutions to \({\rm{Det}}\ H(z)=0\) for both OBC1 and OBC2. For example, for the case belonging to phase I, {∣a1∣, ∣a2∣, ∣b1∣, ∣b2∣} curves are shown in Fig. 3c, which demonstrates that, criterion (i) is impossible to be satisfied, verifying the non-existence of topological boundary modes for OBC1. However, criterion (ii) can be satisfied for OBC2, where the colored regions satisfy the condition that Wa(R) and Wb(R) have opposite signs, confirming the existence of topological boundary modes. The winding number W(R) is defined as [Wa(R) − Wb(R)]/2, and the zero value of this topological invariant represents the non-existence of topological boundary modes. The case for phase IV is shown in Fig. 3d–f, where the topological boundary modes can appear only when \(\cos {k}_{y}<1-({t}_{0}+{\gamma }_{0})/{t}_{1}\), which also can be verified by the criterion(ii) in Eq. (6).

We also explored the distribution properties of the topological eigenstates, in accordance with the biorthogonal bulk-boundary correspondence theory13,42,43,44 (see Supplementary Note 5). For example, as shown in Fig. 3b, when ∣a2∣ < 1, ∣b2∣ < 1, two topological eigenstates are localized at both ends along x direction with penetration length \(-1/{\mathrm{ln}}\,| {b}_{2}|\) (n = 1, on A sites) and \(-1/{\mathrm{ln}}\,| {a}_{2}|\) (n = N, on B sites). In addition, when ∣a2∣ < 1, ∣b2∣ = 1, two topological modes are identical to each other and both localized at n = N along x direction, on B sites, with penetration length \(-1/{\mathrm{ln}}\,| {a}_{2}|\). Furthermore, the relevant biorthogonal polarization was calculated to predict the appearance of topological modes, consistent with the results derived from winding numbers.

Both OBC1 and OBC2 systems exhibit the conventional bulk-boundary correspondence and non-existence of skin effect, where the bulk modes under OBC are consistent with those under PBC. It should be noted that, symmetry plays a significant role in our non-reciprocal hopping model. Restricted by the pseudo-Hermiticity, the bulk Hamiltonian is generally insensitive to the boundary conditions, because the wave numbers are real even in the generalized Brillouin zone38, thus the bulk modes are delocalized. To further investigate the connection between the non-existence of the non-Hermitian skin effect and the restoration of the bulk-boundary correspondence, we followed the transfer-matrix method10, and found that \(| \det T| =1\) for our model (see Supplementary Note 6).

Topolectrical circuit lattice

To clarify the previous results and explore the crucial role of pseudo-Hermitian symmetry in a practical system, we designed a 2D topolectrical circuit to map the tight-binding model. As shown in Fig. 4a, following the method described by Yu et al.20, the A/B site in the tight-binding model corresponds to the A/B junction in the circuit lattice, and the reciprocal hopping term between sites corresponds to the capacitor which connects the junctions, while the non-reciprocal interaction is realized by the operational amplifier which operates as a voltage follower. Furthermore, the 2D circuit lattice contains 80 sub-circuits, and each sub-circuit contains 20 unit cells arranged along y direction. The connection between the two sub-circuits is illustrated in Fig. 4b. Followed by the Kirchhoff’s Laws described in Methods, the effective Hamiltonian He for the circuit lattice is given by

$${H}_{e}({k}_{x},{k}_{y})=\left(\begin{array}{ll}{C}_{A}+{C}_{\gamma }+{C}_{m}+4{C}_{t}&-2{C}_{t}(\cos {k}_{x}+\cos {k}_{y})-{C}_{m}-{C}_{\gamma }\\ -2{C}_{t}(\cos {k}_{x}+\cos {k}_{y})-{C}_{m}&{C}_{B}+{C}_{m}+4{C}_{t}\end{array}\right),$$
(7)

where Cm = − (t0 − γ0), Ct = − t1/2 and Cγ = − 2γ0 and CA + Cγ = CB, by comparing with the model Hamiltonian. The resonant frequency ω corresponds to the eigenvalue E with the relation of \(\omega =1/\sqrt{EL}\), where L represents the inductor value. Therefore, various phases can be realized in topolectrical circuits through tuning the values of capacitors. The voltage signals V(r, t) of the 2N2(N = 40) junctions can be extracted after the transient analysis of the circuit simulation, and then through Fourier transformation, the amplitude of eigenstates V(f) in the frequency domain can be calculated.

Fig. 4: Schematic illustration of the two-dimensional topolectrical circuit.
figure 4

a Two unit cells in the circuit lattice. The reciprocal hopping terms are realized by capacitors Cm, and the non-reciprocal hopping terms are realized by the operational amplifiers and capacitors Cγ, where current flow can exist between A sites and the output of the amplifier, but cannot exist between B sites and the input of the amplifier. The LC-circuits which connect the A/B sites and the ground provide the on-site frequency response. b The 40 × 40 lattice contains 80 sub-circuits, and each sub-circuit contains 20 unit cells, arranged along y direction. The schematic view shows the connection between two sub-circuits along x direction, where An, Bn denote the sites of the nth unit cell inside the sub-circuit, and the connection between the unit cells is the same as (a).

Full size image

We carried out the simulation to realize the frequency response of phase I and phase IV for both PBC and OBC2, because (t0 − γ0)/t1 > 0 should be satisfied to avoid negative values of capacitors. As shown in Fig. 5a, for phase I under PBC, the simulated frequency response colored by gray is consistent with the ideal spectra, and the single ER which locates at \(\cos {k}_{x}+\cos {k}_{y}=-{C}_{m}/(2{C}_{t})=-1.6\), is shown in Fig. 5b. The results of the OBC system are shown in Fig. 5c, d, which reveals that, when stimulated by the on-site frequency, both of the bulk modes and the topological boundary modes exist, and the combined modes are localized at the left side of the circuit lattice, if the source is only placed at the left boundary to avoid signal divergence. Similarly, as shown in Fig. 5e-h, the ERs of phase IV locate at \(\cos {k}_{x}+\cos {k}_{y}=-{C}_{m}/(2{C}_{t})=-0.5\) and \(\cos {k}_{x}+\cos {k}_{y}=-({C}_{m}+{C}_{\gamma })/(2{C}_{t})=-1\), and the combined modes stimulated by the on-site frequency are localized at the left side as well. Owing to the pseudo-Hermitian symmetry, in spite of the negative imaginary part of the frequency, the system is still stable in time domain, which can be used as reference for further experimental maneuverability. As mentioned above, the eigenstates \({\Psi }_{+}={({V}_{A}({\boldsymbol{k}}),{V}_{B}({\boldsymbol{k}}))}^{{\rm{T}}}\) is always paired with \({\Psi }_{-}={(-{V}_{A}({\boldsymbol{k}}),{V}_{B}({\boldsymbol{k}}))}^{{\rm{T}}}\) or \({({V}_{A}({\boldsymbol{k}}),-{V}_{B}({\boldsymbol{k}}))}^{{\rm{T}}}\) under PBC, thus the voltage signal is approximately equal to \(| {\Psi }_{+}| {{\rm{e}}}^{-{\rm{Im}}[\omega ]t}{{\rm{e}}}^{{\rm{i}}{\rm{Re}}[\omega ]t}\). Therefore, the amplitude of the voltage cannot diverge seriously within several time periods.

Fig. 5: Simulation results of the topolectrical circuit.
figure 5

a–d Show the results for phase I with electronic components L = 5.6 μH, CA = 100 pF, CB = 150 pF, Cm = 160 pF, Ct = Cγ = 50 pF, and (e–h) show the results for phase IV with components L = 5.6 μH, CA = 210 pF, CB = 260 pF, Cm = Ct = Cγ = 50 pF. a, e Frequency response of the topolectrical circuit lattice under periodical boundary condition, where the ideal model results and simulation results are colored by light red and gray respectively. b, f Exceptional rings stimulated by the on-site frequency \({f}_{0}=1/(2\pi \sqrt{({C}_{b}+{C}_{m}+4{C}_{t})L})\). c, g Frequency response of the topolectrical circuit under open boundary condition. d, h The amplitude of the localized topological boundary modes stimulated by the on-site frequency.

Full size image

Conclusions

In conclusion, we have proposed the general form of the two-dimensional non-reciprocal hopping model protected by time-reversal symmetry and pseudo-Hermitian symmetry, which exhibits exceptional elliptical rings or exceptional hyperbolic lines under PBC. The simplified form is mainly discussed, and the parameters space is classified into phases I-IV, according to the distinct forms of exceptional rings. Through the suitable selection of the primitive cell, the topological boundary modes can appear for all four phases, which is verified by the non-zero winding numbers, and the penetration lengths of the topological boundary modes are analyzed through the biorthogonal bulk-boundary correspondence method. In addition, in the presence of pseudo-Hermitian symmetry, our non-Hermitian model behaves like the Hermitian system under OBC, where the bulk-boundary correspondence exists and the non-Hermitian skin effect vanishes, verified by \(| \det T| =1\). Finally, we designed the proposed phase I and phase IV in the topolectrical circuits, and the simulation results not only correspond to those in the model, but also demonstrate the crucial role of pseudo-Hermitian symmetry in a practical system. In a broader view, our findings can be compared to other platforms such as photonics, acoustics, mechanics or meta-surface, for the purpose on the control of frequency response and localization properties.

Methods

Derivation of the effective Hamiltonian for circuit lattice

As shown in Fig. 4a, the non-reciprocal interaction is realized by the operational amplifier which operates as a voltage follower. Ideally, when working at the linear region, the operational amplifier can amplifies the difference of voltage between the two inputs, and the output voltage is given by Vout = β(V+ − V−), where β is the open-loop gain, and V± is the voltage of the non-inverting/inverting input. Therefore, if the inverting input is connected to the output and the non-inverting input is connected to junction B, which means V− = Vout, V+ = VB, thus \({V}_{out}=\frac{\beta }{\beta +1}{V}_{B}\). Since β is generally large enough for amplifiers, the voltage of the output of amplifier equals to VB and no current flows through the two inputs.

Based on Kirchhoff’s Law that, the sum of current into a junction equals the sum of current out of the junction, the currents through junction A and B can be written as

$$ {I}_{A}=\; {\rm{i}}\omega {C}_{A}(0-{V}_{A})+\frac{1}{{\rm{i}}\omega L}(0-{V}_{A})+{\rm{i}}\omega {C}_{m}({V}_{B}-{V}_{A})+{\rm{i}}\omega {C}_{t}({V}_{B}{{\rm{e}}}^{{\rm{i}}{k}_{x}}-{V}_{A})+{\rm{i}}\omega {C}_{t}({V}_{B}{{\rm{e}}}^{-{\rm{i}}{k}_{x}}-{V}_{A})\\ +{\rm{i}}\omega {C}_{t}({V}_{B}{{\rm{e}}}^{{\rm{i}}{k}_{y}}-{V}_{A})+{\rm{i}}\omega {C}_{t}({V}_{B}{{\rm{e}}}^{-{\rm{i}}{k}_{y}}-{V}_{A})+{\rm{i}}\omega {C}_{\gamma }({V}_{B}-{V}_{A})=0,\\ {I}_{B}=\; {\rm{i}}\omega {C}_{B}(0-{V}_{B})+\frac{1}{{\rm{i}}\omega L}(0-{V}_{B})+{\rm{i}}\omega {C}_{m}({V}_{A}-{V}_{B})+{\rm{i}}\omega {C}_{t}({V}_{A}{{\rm{e}}}^{{\rm{i}}{k}_{x}}-{V}_{B})+{\rm{i}}\omega {C}_{t}({V}_{A}{{\rm{e}}}^{-{\rm{i}}{k}_{x}}-{V}_{B})\\ +{\rm{i}}\omega {C}_{t}({V}_{A}{{\rm{e}}}^{{\rm{i}}{k}_{y}}-{V}_{B})+{\rm{i}}\omega {C}_{t}({V}_{A}{{\rm{e}}}^{-{\rm{i}}{k}_{y}}-{V}_{B})=0.$$
(8)

Rewriting the equation above into a matrix form, the effective Schrödinger’s equation for the periodic circuit lattice is given by,

$${H}_{e}\left(\begin{array}{l}{V}_{A}\\ {V}_{B}\end{array}\right)=\frac{1}{{\omega }^{2}L}\left(\begin{array}{l}{V}_{A}\\ {V}_{B}\end{array}\right),$$
(9)

where the voltage VA/VB at A/B junctions corresponds to the wave function ΨA/ΨB, and the resonant frequency ω corresponds to the eigenvalue E with the relation of \(\omega =1/\sqrt{EL}\). The effective Hamiltonian He for the circuit lattice is given by Eq. (7).

Simulation details

Transient analysis and Fourier transformation were carried out to simulate the frequency response of the designed topoelectrical circuit. First, the amplifiers, capacitors and inductors were selected as ideal elements, and the values of the components are chosen to limit that the resonant frequency ranges from 105 to 106 Hz, for further practical consideration. Secondly, the source of the lattice is set as pulse-excitation with 6 μs width, 0.1 μs rising edge and 0.2 μs falling edge. For OBC, the source was placed at the left of the circuit lattice, while for PBC, the source can be placed at any position of the lattice. Third, to satisfy the Nyquist sampling theorem, the total time of the transient analysis is set as 12 μs for both PBC and OBC with time step 10 ns, and the frequency step was set as 10 kHz when operating the Fourier transformation.