introduction

Quantum entanglement is an extremely important concept in research, such as quantum information and quantum magnetism1. Low-dimensional quantum spin systems are attracting attention because they are expected to have a strong entanglement. A quantum entanglement analysis for quantum spin models has recently attracted attention because it can characterize various phases2,3,4,5,6,7,8,9,10, even in states without a break in the translational symmetry or long-range dipole orders, such as the Haldane state in integer spin chains11 and the Tomonaga–Luttinger liquid (TLL) state in half-integer spin chains. According to conformal field theory, the central charge c characterizing the excitation properties can be obtained by calculating the entanglement entropy2,3,4,5,6. In a TLL state, there is a gapless excitation with a non-zero integer value of c, whereas in a Haldane state, there is a gapped excitation with c = 0. Moreover, the Haldane state can be characterized by the degeneracy of the entanglement spectrum7,8,9,10. For example, the spin-1 chain exhibits a doubly degenerate entanglement spectrum7.

In two-dimensional frustrated quantum spin systems, quantum spin liquid states, such as the resonating valence bond (RVB) introduced by Anderson, are expected to emerge12,13. The RVB state is a resonant state of singlet dimers covering the whole lattice. It is believed that one of the possible models for exhibiting RVB states is the spin-\(\frac{1}{2}\) antiferromagnetic Heisenberg model on the kagome lattice14. However, the ground state has been predicted to be a Z2 RVB spin liquid with topological order14,15,16,17, U(1) spin liquid18,19,20,21, and valence bond crystal (VBC)22,23,24,25,26, although the exact ground state is unknown owing to the difficulty in solving two-dimensional frustrated systems. In the presence of a magnetic field, magnetization plateaus were predicted at M/Msat = 0, 1/9, 1/3, 5/9, and 7/9, where M is the magnetization and Msat is the saturation magnetization16,27,28,29. These magnetization plateaus are realized by the effect of the strong geometric frustration peculiar to the kagome lattice.

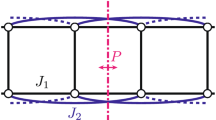
Kagome strip chains (KSCs), which are one-dimensional kagome lattices, have been recently studied, because the presence of exotic quantum states is expected in the kagome lattice30,31,32,33,34,35,36,37. In the KSC, as shown in Fig. 1, it was found that the magnetization plateaus emerge at M/Msat = 0, 1/5, 3/10, 1/3, 2/5, 7/15, 3/5, and 4/535. Among them, four types of plateaus were found at M/Msat = 1/5. The number of different types in each plateau was the largest at M/Msat = 1/5. Therefore, we can expect the presence of quantum phases generated by a strong geometrical frustration in this 1/5 plateau. Furthermore, when the model compound for the KSC is synthesized in the near future, the 1/5 plateau can be easily accessed with a small magnetic field.

Fig. 1: Structure of a kagome-strip chain.
figure 1

The black solid, red dashed, and blue broken lines denote the exchange interactions JX, J1, and J2, respectively. The green circles denote the sites with spin. The numbers below the vertical dotted lines represent the distance of the sites along the x-axis from the left edge. We set JX = 1.

Full size image

In this study, we investigate the 1/5 plateaus of the KSC using the density matrix renormalization group (DMRG) method. We developed a magnetic phase diagram of the 1/5 plateau and, to the best of our knowledge, found two new plateau phases that have yet to be identified in the previous studies35. As our main result, although one of the two phases exhibits a gapless spin-liquid behavior with c = 1, the entanglement spectrum of the phase is doubly degenerate. This means that this plateau phase has the properties of both a half-integer spin chain and a spin-1 chain. This feature is known to be realized in the gapless symmetry-protected topological (SPT) phase, which has been studied in recent years38,39. Furthermore, we calculate the dynamical spin structure factor (DSSF) in this phase using the dynamic DMRG (DDMRG)40 (see Methods section). The DSSF of the Sz (magnetic field) direction exhibits gapless and dispersion-less low-energy excitations. To describe these properties during the phase, we propose a resonating dimer–monomer liquid (RDML) state, which is a mixed state of singlet dimers and up-spin monomers.

Results

Model

The unit cell of the KSC consists of one site located in the center and four sites located in the four corners. The Hamiltonian for the spin-\(\frac{1}{2}\) KSC in a magnetic field is defined as

$$H=\mathop{\sum}\limits_{\langle i,j\rangle }{J}_{i,j}{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}-h\mathop{\sum}\limits_{i}{S}_{i}^{z},$$
(1)

where Si is the spin-\(\frac{1}{2}\) operator, \({S}_{i}^{z}\) is the z component of Si, 〈i, j〉 runs over the nearest-neighbor spin pairs. The first and second terms in Eq. (1) represent the Heisenberg interaction and Zeeman interaction with the magnetic field h along the z direction, respectively. Ji,j in the first term corresponds to one of JX, J1, or J2 in Fig. 1. JX in Fig. 1 represents the antiferromagnetic exchange interaction between the central site and one of the other sites in the unit cell. J1 is the exchange interaction between the nearest-neighbor sites along the upper and lower edges in the unite cell, while J2 is the nearest-neighbor interaction along the upper and lower edges connecting neighboring unit cells. In the following, we set JX = 1 as the energy unit.

Phase diagram of the kagome strip chain

We first determined the phase diagram of the KSC at M/Msat = 1/5 using the DMRG method. We obtained six 1/5 plateau phases using N = 120–1000 clusters under the open boundary condition (OBC), as shown in Fig. 2, where N denotes the number of sites. We determined the phase boundaries for each magnetization plateau from the magnetization curve and their magnetic structures, as shown in Fig. 3. The regions of phases I–VI are denoted by different colors. The white region had no magnetization plateau. Phases II and III were found in the present study, whereas the other phases had already been found in a previous study35.

Fig. 2: Phase diagram of the kagome strip chain at M/Msat = 1/5.
figure 2

M is the magnetization and Msat is the saturation magnetization. Here, J1 and J2 are the exchange interactions shown in Fig. 1. The colored regions denote the 1/5 plateau phases, which are distinguished by Roman numerals and colors.

Full size image
Fig. 3: Magnetic structures of each phase.
figure 3

The nearest-neighbor spin-spin correlation \(\langle {{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\rangle -\langle {S}_{i}^{z}\rangle \langle {S}_{j}^{z}\rangle\) and the local magnetization \(\langle {S}_{i}^{z}\rangle\) around the center of the chain with N = 200 under the open boundary condition for the six phases, where Si is the spin-\(\frac{1}{2}\) operator, \({S}_{i}^{z}\) is the z component of Si, and N is the number of sites. Black solid (purple dashed) lines connecting two nearest-neighbor sites denote negative (positive) values of the spin–spin correlation, and their thickness represents the magnitude of the correlation. The blue (red) circles on each site denote the positive (negative) value of \(\langle {S}_{i}^{z}\rangle\), and their diameter represents its magnitude. Roman numerals denote the 1/5 plateau phases and correspond to those in Fig. 2. In VI, the value of \(\langle {S}_{i}^{z}\rangle\) at the center is 0.4193, and that of \(\langle {{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\rangle -\langle {S}_{i}^{z}\rangle \langle {S}_{j}^{z}\rangle\) of the thickest line is − 0.6513.

Full size image

Figure 3 shows the nearest-neighbor spin-spin correlation \(\langle {{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\rangle -\langle {S}_{i}^{z}\rangle \langle {S}_{j}^{z}\rangle\) and local magnetization \(\langle {S}_{i}^{z}\rangle\) for the six phases. The lines connecting two nearest-neighbor sites denote the sign and magnitude of the spin-spin correlation by color and thickness, respectively. The circle in each site represents \(\langle {S}_{i}^{z}\rangle\). The stability of phases I, IV, V, and VI can be explained by the energy gain owing to a local strong spin correlation, as evidenced by the thick lines in Fig. 3. By contrast, phases II and III do not have such a distinguished thick line. In phase II, the periodic magnetic structure of the spin–spin correlation and local magnetization are not observed, whereas the mirror and inversion symmetries at the center of the chain, which should exist under the OBC, are unbroken (see Supplementary Note 1). In phase III, the spin-spin correlation and local magnetization have a periodic structure, and there is no symmetry breaking.

Magnetization process and magnetization plateau

Figure 4a, b show magnetization curves at J1 = 1.0 and J2 = 0.7 (phase II), and J1 = 0.9 and J2 = 0.3 (phase III), respectively. The 1/5 plateaus are clearly visible under both conditions. These magnetization curves show little variation with size N and the boundary conditions. However, in Fig. 4a (phase II), a plateau deviating from 1/5 in only one step, that is, M/Msat = 1/5 + 2/N, appears under the OBC. We confirmed that this deviation appears in the other sets of J1 and J2 in phase II, implying the presence of edge excitations that appear in the Haldane chain. For example, in the spin-1 Haldane chain under the OBC, the magnetization plateau does not appear at M = 0 but at M = 1. This is because two spins at both ends of the chain cannot form a valence bond, and thus both spins have almost spin-1/2 degrees of freedom, forming an M = 1 state under a magnetic field41. We also confirm the excitation owing to the edge spins in phase II (see Supplementary Note 1). In the following, we regard the 1/5 plateau in phase II under the OBC as the state with M/Msat = 1/5 + 2/N. Phases I, IV, V, and VI were examined in a previous study ??. Therefore, we investigate phases II and III in the following.

Fig. 4: Magnetization curves in phases II and III as a function of the magnetic field.
figure 4

The black, red, and blue solid lines show the results of the periodic boundary condition for N = 60, periodic boundary condition for N = 120, and open boundary condition for N = 300, respectively, at zero temperature, where N is the number of sites. In addition, M is the magnetization, Msat is the saturation magnetization, and h is the magnitude of the magnetic field. a J1 = 1.0 and J2 = 0.7 (phase II). b J1 = 0.9 and J2 = 0.3 (phase III). J1 and J2 are the exchange interactions shown in Fig. 1.

Full size image

Evidence of spin liquid in phase II form the central charge

Figure 5 shows the entanglement entropy for L = 200(N = 5 × L) under the OBC as a function of \({\mathrm{ln}}\,[L/\pi \sin (\pi j/L)]\) with a variable j denoting the position of the 5-site unit. This plot comes from the following relation between the central charge c and the position-dependent entanglement entropy, EE(j):

$$EE(j)=\frac{c}{{b}_{{\rm{c}}}}{\mathrm{ln}}\,\left[\frac{L}{\pi }\sin \left(\frac{\pi j}{L}\right)\right]+{a}_{{\rm{c}}},$$
(2)

where ac is a nonuniversal constant, and bc = 6 (3) for the OBC (PBC)3,4,5,6. The value of c becomes finite when the spin-spin correlation exhibits a power-law decay, and gives c = 1 in the TLL. By contrast, when the spin-spin correlation decays exponentially, e.g., in the Haldane phase, c = 0. The value of c in Fig. 5 was obtained by fitting the entanglement entropy data using straight lines. Because c for phase II is nearly unity, as in the TLL, phase II is expected to be a gapless spin liquid. Because plateau phases should have an energy gap, there should be a gapless excitation only in the subspace where the total Sz does not change. This feature has also been observed in the 1/3 magnetization plateau in frustrated three-leg spin tubes42,43,44. We also confirm that the spin-spin correlations of the Sz and Sx components exhibit a power decay corresponding to the gapless excitation and exponential decay corresponding to the energy gap, respectively (see Supplementary Note 2).

Fig. 5: Entanglement entropy of the kagome strip chain.
figure 5

The cluster used in the calculations is the open boundary condition for L = 200(N = 5 × 200), where L is the number of five-site units in the kagome strip chain. The results of the calculation of the entanglement entropy with respect to \({\mathrm{ln}}\,[L/\pi \sin (\pi j/L)]\) at J1 = 1.0 and J2 = 0.7 (Phase II), and J1 = 0.9 and J2 = 0.3 (Phase III), are represented by black squares and red circles, respectively, where j denotes the position of the 5-site unit. Here, J1 and J2 are the exchange interactions shown in Fig. 1. The value of the central charge c was obtained by fitting the entanglement entropy data using straight lines. The fitting lines are shown as dashed lines.

Full size image

In phase III, c is nearly zero. This indicates that there is an energy gap in this phase. Moreover, we confirm that the ground state has no degeneracy, and there is no symmetry breaking, as shown in Fig. 3. We note that when the ground state has no degeneracy and no symmetry breaking, the Oshikawa–Yamanaka–Affleck (OYA) criterion45 which is given by pS(1 − M/Msat) = n must be satisfied, where p is the ground-state period, S is the spin magnitude, and n is an integer. In phase III, the OYA criterion is satisfied because p = 5, S = 1/2, M/Msat = 1/5 gives integer n = 2.

Continuous excitation in dynamical spin structure factor

To investigate phase II in more detail, we calculate the DSSF, Sαβ(q, ω), which is defined by

$${S}_{\alpha \beta }(q,\omega)=-\frac{1}{\pi }{\rm{Im}}\left\langle 0\right|{\tilde{S}}_{-q}^{\beta }\frac{1}{\omega -H+{E}_{0}+i\eta }{\tilde{S}}_{q}^{\alpha }\left|0\right\rangle ,$$
(3)

where q denotes the momentum of the lattice geometry shown in Fig. 1, \(\left|0\right\rangle\) is the ground state with energy E0, and η is the broadening factor. In addition, \({\tilde{S}}_{q}^{\alpha (\beta)}={S}_{q}^{\alpha (\beta)}-\left\langle 0\right|{S}_{q}^{\alpha (\beta)}\left|0\right\rangle\), where \({S}_{q}^{\alpha (\beta)}={N}^{-1/2}{\sum }_{i}{e}^{iq{x}_{i}}{S}_{i}^{\alpha (\beta)}\), xi is the position of the spin i, and α(β) = + , − , z.

Figure 6 shows Szz(q, ω) corresponding to the Sz component and [S+−(q, ω) + S−+(q, ω)]/2 corresponding to the Sx and Sy components for L = 12 (N = 5 × 12) with η = 0.05 under the PBC. Because the position xi is defined in Fig. 1, the range of 0 ≤ q/π ≤ 4 corresponds to half of the extended Brillouin zone. As shown in Fig. 6a, a gapless excitation in the Sz component emerges at approximately q/π = 2. This excitation is consistent with the expected result from the fact that c = 1. We confirm that the value of q showing the lowest-energy excitation is size-dependent. As the size increases, the q value tends to move toward 2π (see Supplementary Note 3). Thus, we expect that in the thermodynamic limit, a gapless excitation emerges at q/π = 2. In addition, low-energy excitations at ω ≲ 0.2 show a less dispersive feature. This feature will be discussed later.

Fig. 6: Dynamical spin structure factor of phase II.
figure 6

a Szz(q, ω) and b [S+−(q, ω) + S−+(q, ω)]/2, obtained from the dynamic density matrix renormalization group for the kagome strip chain under the periodic boundary condition for L = 12 (N = 5 × 12) at J1 = 1.0 and J2 = 0.7, where L is the number of the 5-site units, and J1 and J2 are the exchange interactions shown in Fig. 1. In addition, Szz(q, ω) corresponds to the Sz component of the dynamical spin structure factor, and [S+−(q, ω) + S−+(q, ω)]/2 correspond to the Sx and Sy components.

Full size image

As shown in Fig. 6b, [S+−(q, ω) + S−+(q, ω)]/2, corresponding to the excitations of the S+ and S− components, has a gap. Here, the external magnetic field h is set to 0.63, which is the value at the center of the 1/5 magnetization plateau. The minimum excitation gap is found to exist at approximately q/π = 2 and q/π = 3. Continuous excitations exist up to the high-energy region at more than ω = 1.5 at q/π = 2.

Entanglement spectrum with double degeneracy in phase II

Finally, we calculated the entanglement spectrum to investigate each phase in more detail. The ground state can be Schmidt decomposed as follows:

$$\left|0\right\rangle =\mathop{\sum}\limits_{\alpha }{\lambda }_{\alpha }\left|{{{\Phi }}}_{\alpha }^{L}\right\rangle \left|{{{\Phi }}}_{\alpha }^{R}\right\rangle ,$$
(4)

where \(\left|{{{\Phi }}}_{\alpha }^{L}\right\rangle\) and \(\left|{{{\Phi }}}_{\alpha }^{R}\right\rangle\) are orthonormal basis vectors of the left and right part of the chain, respectively7. Here, \({\lambda }_{\alpha }^{2}\) are the eigenvalues of the reduced density matrix. The entanglement spectrum is defined as \(-2{\mathrm{ln}}\,({\lambda }_{\alpha })\). Figure 7 shows the results of the entanglement spectrum as a function of J2 at J1 = 0.9. Phases I, III, and V are trivial phases owing to the mixture of singly and doubly degenerate states of the entanglement spectrum7. By contrast, in phase II, all the entanglement spectra are doubly degenerate. Furthermore, in phase II, edge excitation occurs, as discussed in Discussion section. The doubly degenerated entanglement spectrum and edge excitation are identical to the features of the spin-1 Haldane chain. Therefore, we speculate that phase II is a nontrivial topological phase7. However, we have not yet been able to identify the symmetry protecting the degeneracy in phase II, which remains a future study. We also confirm that the double degeneracy is independent of L, J1, and J2. Degeneracy is obtained even for L = 2 (the shortest chain).

Fig. 7: Entanglement spectrum of the kagome strip chain with respect to J2 at J1 = 0.9.
figure 7

Here, J1 and J2 are the exchange interactions shown in Fig. 1. The cluster used in the calculations is the open boundary condition for L = 80(N = 5 × 80), where L is the number of five-site units in the kagome strip chain. In addition, \({\lambda }_{\alpha }^{2}\) are the eigenvalues of the reduced density matrix, and α is an index of the eigenvalues. The Roman numerals correspond to the phases shown in Fig. 2. The vertical dotted lines represent the phase boundaries determined by the entanglement spectrum and the magnetic structures. The horizontal bars indicate the values of λα, and the filled circles indicate the degeneracy of λα.

Full size image

Discussion

To the best of our knowledge, phases II and III are newly identified magnetization plateau phases in the present study. Phase III was concluded to be a trivial phase based on (i) c = 0, (ii) no degeneracy in the ground state, and (iii) a trivial distribution of the entanglement spectrum. By contrast, phase II is a phase that has the characteristics of both a gapless spin liquid and spin-1 Haldane state because of c = 1 and the double degeneracy of the entanglement spectrum. These characteristics are the same as those of the gapless SPT phase38,39.

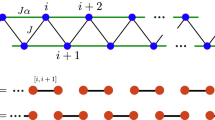
Why does phase II have these characteristics? We anticipate that a mixed state of singlet dimers and up-spin monomers, which reveals a liquid behavior similar to the RVB, is the ground state of phase II. We refer to this state as RDML. The RDML state in the KSC under the OBC is introduced as \({|\psi \rangle }_{{\rm{RDML}}}={\sum }_{i}{a}_{i}{|{\phi }_{i}\rangle }_{{\rm{DM}}}\), where ai is a constant and \({|{\phi }_{i}\rangle }_{{\rm{DM}}}\) is one of the dimer–monomer states, which has only one monomer in all 5-site units except at both ends, and there is no nearest-neighboring monomer, as shown in Fig. 8. In other words, all states of \(\{{\left|{\phi }_{i}\right\rangle }_{{\rm{DM}}}\}\) have one dimer (not two dimers) in all 5-site units. In addition, the four spins at both ends are up-spin monomers, reflecting the results of the numerical calculation (see Supplementary Note 1). The monomers at both ends induce edge excitations, which lead to an extra 2/N in M/Msat = 1/5 + 2/N. The typical \({\left|{\phi }_{i}\right\rangle }_{{\rm{DM}}}\) for L = 8 is shown in Fig. 8a, b. The RDML state defined in this study does not require \({|{a}_{i}|}^{2}={|{a}_{j}|}^{2}\)(i ≠ j). This definition allows for excitation from an RDML state to other RDML states. This is important for understanding the gapless and dispersion-less excitations of Szz(q, ω). The entanglement spectrum in these dimer–monomer states shows double degeneracy because every state contains a singlet dimer at the center of the chain. The singlet dimer state is represented by \(\frac{1}{\sqrt{2}}(\left|\,\uparrow \right\rangle \left|\,\downarrow \right\rangle -\left|\,\downarrow \right\rangle \left|\,\uparrow \right\rangle)\), where the first and second terms have the same absolute value. Therefore, when the singlet dimer is located at the center, the entanglement spectrum must be doubly degenerate. For this reason, we can obtain the double degeneracy even for L = 2, where the RDML consists of two dimer–monomer states, \({|{\phi }_{i = 1,2}\rangle }_{{\rm{DM}}}\) with the central singlet bond, as shown in Fig. 8c, d, respectively.

Fig. 8: Schematic diagrams of the dimer–monomer states.
figure 8

Two dimer–monomer states for (a and b) L = 8 and (c and d) L = 2 under the open boundary condition at M/Msat = 1/5 + 2/N, where L is the number of the 5-site unit, M is the magnetization, and Msat is the saturation magnetization. The green circles denote the sites with spin. The monomers are depicted as blue arrows, whereas the dimers are represented as red ellipses containing two sites. Note that all 5-site units except at both ends in a and b have only one monomer, and there is no nearest-neighboring monomer. The monomers at both ends correspond to the edge excitations.

Full size image

One may construct RDML states orthogonal to the RDML ground state by changing the distribution of {ai}. The constructed RDML state is expected to be in an excited state with infinitesimal or small excitation energy. This corresponds to local excitations, which should form a nearly dispersion-less structure in Szz(q, ω). The DMRG result shown in Fig. 6 confirms this property. As the size increases, the dispersion-less excitations become more pronounced at approximately q/π = 2 (see Supplementary Note 3). We note that such a dimensionless spectral distribution depends on the values of {ai} for both the ground and excited states. Similarly, the nonuniformity of the weight of Szz(q, ω) at approximately q/π = 2 in Fig. 6a is presumably due to the distribution of {ai}. Assuming the presence of the RDML state, we can explain the gapless excitation, double degeneracy of the entanglement spectrum, and dispersion-less low-energy excitations in Szz(q, ω). Therefore, we believe that phase II is the RDML state.

In summary, we obtained the phase diagram of the 1/5 plateaus of the KSC using the DMRG method. To the best of our knowledge, we discovered two new plateau phases (II and III). As the most surprising result, phase II exhibits a gapless spin liquid with c = 1 as in the half-integer spin chain and the double degeneracy of the entanglement spectrum as in the spin-1 chain. These features are the same as those of the gapless SPT phases found in previous studies38,39. We also calculated the DSSF in phase II using the DDMRG. We found that the DSSF of Szz(q, ω) exhibits a gapless excitation corresponding to c = 1 and dispersion-less low-energy excitations corresponding to local excitations. Finally, we proposed an RDML state that can explain the gapless excitation, double degeneracy of the entanglement spectrum, and dispersion-less low-energy excitations in Szz(q, ω) in phase II. Based on this proposal, newly derived questions include what symmetry protects the degeneracy during phase II and whether the RDML corresponds to a gapless SPT order.

The KSC compounds with five exchange interactions have been previously reported46. Therefore, it is possible that compounds with our model will be synthesized in the future. Because M/Msat = 1/5 is a relatively low magnetization, the 1/5 plateau may be observed experimentally. As such, we anticipate that our study will promote future experimental studies on the KSC.

Methods

We conducted DMRG calculations at zero temperature up to a system size N = 1000( = 5 × 200) for various values of J1 and J2. For the system, we construct a snakelike one-dimensional chain. The number of states m kept in the DMRG calculation is 400 − 2500, and truncation errors are less than 5 × 10−7. For the calculation of the dynamical spin structure factors, we use DDMRG for N = 60( = 5 × 12) and N = 80( = 5 × 16) under a periodic boundary condition (PBC). In our DDMRG, we use three kinds of target states: for Szz(q, ω), (i) \(\left|0\right\rangle\), (ii) \({\tilde{S}}_{q}^{z}\left|0\right\rangle\), and (iii) \({(\omega -H+{E}_{0}+i\eta)}^{-1}{\tilde{S}}_{q}^{z}\left|0\right\rangle\). Target state (iii) is evaluated using a kernel-polynomial expansion method40, where the Lorentzian broadening η is replaced by a Gaussian broadening with a width of 0.05. We divide the energy interval [0, 1.6] by 80 mesh points and target all of the points at once with m = 1000.