Abstract
Willis metamaterial enables exotic manipulations of acoustic waves with a precise combination of bulk modulus, mass density, and Willis parameters. While the realization of unrestricted and completely decoupled constitutive parameters would extend the horizon of future applications, the restriction of passivity and reciprocity dictate a hard bound in the values of achievable polarizabilities and correlations between them. Here, we break the bound of passivity and reciprocity by instituting a basis and independent kernel for each constitutive polarization in a virtualized metamaterial platform, active metamaterials realizing artificial polarization with the digital convolution. We demonstrate decoupled control of all four constitutive parameters in a nonreciprocal regime, at the same time achieving values of polarizabilities beyond the passivity limit. Broadband, flat-response nonreciprocal Willis coupling is also demonstrated with analytically designed causal frequency dispersion. Our approach will be useful for nonreciprocal wave manipulation and communication for broadband operation.
Similar content being viewed by others
Introduction
Metamaterials enable novel applications by providing unconventional wave properties in many wave systems1,2,3. In acoustic systems, unusual wave parameters such as extremely high4, negative5,6, or zero bulk moduli and mass densities7,8 have now also become a reality, enabling exotic applications such as superfocusing9,10, extraordinary diffraction11, and acoustic cloaking12,13,14. Recently, with the experimental realization of the Willis coupling7,15,16,17,18,19,20,21 as an acoustic duality of bianisotropy in electromagnetic waves22, the scope of acoustic metamaterials, also known as acoustic Willis metamaterials in extended perspective, has been greatly extended by allowing coupling between pressure and velocity fields. Designer Willis parameter combined with a precisely tuned bulk modulus and mass density, acoustic metamaterials now enable applications that were impossible before, such as the separate control of reflected and transmitted waves7, diffraction-free metasurfaces23, bianisotropic nihility24, and metagratings25,26,27.
Despite the great successes achieved thus far, the full potential of Willis metamaterials has not been fully explored. While the unrestricted and decoupled control of all four constitutive parameters would be ideal, yet the passivity and reciprocity in relation to the metamaterial structure command stringent bound in their values and correlations. In order to realize acoustic properties that go beyond conventional metamaterials, it has been proposed that electroacoustic metamaterials utilizing transducer arrays achieve control of wave parameters such as mass density28,29,30, bulk modulus30,31,32, and acoustic Willis coupling parameters18,19,33,34,35 and also enable the manipulation of acoustic waves34,35,36,37. Although it is clear that active components could provide total power larger than the input, and while single-polarization control of nonreciprocal and broadband active Willis coupling has been demonstrated in acoustic18,35 and elastic waves19, the breaking of the passive Willis bound and nonreciprocal control of all four constitutive parameters has not been realized as it requires precise control of balance on realizing stable resonance.
In this work, we break the bound of passivity and the conditions for nonreciprocity, extending the boundary of Willis metamaterial to the causality limit. We analyze the passivity condition and its implications to the correlation between four constitutive parameters and then institute the condition of overcoming these limitations based on the recently developed concept of virtualized meta-atoms31. By employing a representation basis for each polarization and then applying independent scattering kernel functions, we demonstrate the breaking of passive bounds of all four polarizabilities and correlations between them to achieve a full nonreciprocity. As an example of the wide-open flexibility in the manipulation of polarizabilities, we further realize Willis metamaterial with broadband and flat bianisotropy, in both the purely reciprocal and purely nonreciprocal regimes, from the dispersion curve analytically constructed via the inverse design method.
Results
Polarization process based on parity symmetry
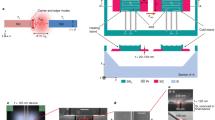
To study the condition of passivity and its implications to the correlation between four constitutive parameters, here we define a scattering matrix S having parity symmetry17 in the one-dimensional system, as depicted in Fig. 1, for incident (a) and scattered (b) waves propagating in the forward (+) and backward (–) directions, which are decomposed into components of even (e) and odd (o) parities: ae = (a+ + a–)/2, ao = (a+ – a–)/2, be = (b+ + b–)/2, and bo = (b+ – b–)/2. The couplings between the incident fields and scattered fields are then written as (be bo)T = S (ae ao)T, where the superscript T is transpose operator with the scattering matrix S defined as
where r and t are the reflection and transmission coefficients, respectively. Then the relation between the scattering matrix S and the normalized polarizability α becomes:
where k0 is the free space wavenumber (see Supplementary Note S1 for the derivation of and detailed expressions for each element). In this representation, the diagonal terms relating even-incident to even-scattering components (see) and odd-incident to odd-scattering components (soo) correspond to the inverse bulk modulus and mass density, respectively, while the off-diagonal components coupling even to odd components (soe) and odd to even components (seo) are the acoustic bianisotropy or Willis coupling parameters.
The definition of the scattering matrix S in a one-dimensional system. The incident (a) and resultant scattered fields (b) propagating in the forward (+) and backward (–) directions are decomposed into even (e) and odd (o) components where k is the wavenumber. The even-to-even and odd-to-odd scattering parameters correspond to the inverse bulk modulus and density, respectively, while the even-to-odd and odd-to-even scattering parameters are the Willis parameters.
Willis coupling beyond the passivity bound
Following the derivation in Li et al.25 for two- and three-dimensional systems, the bound and correlation for Willis parameters and other polarizabilities in the one-dimensional passive system is dictated by the following two inequalities (see Supplementary Note S2 for the derivation):
Thus, the maximum bound of the Willis coupling is given by |αvp | (|αpv | ) ≤ k0–1, where the equality is satisfied only when αpp (αvv) = ik0–1. If the systems are strictly reciprocal, i.e., t+ = t–, then the inequalities in Eq. (3) are reduced to a single inequality equation of |r+ – r–| ≤ 2, where the maximum Willis coupling is achieved only at the stringent condition of t+ = t– = 0 and r+ = –r– = eiφ, where φ is the arbitrary real number. It is noted that the passivity condition not only restricts the maximum value of Willis couplings |αvp | and |αpv | , but also bounds the achievable diagonal polarizabilities αpp by |1 + ik0αpp | ≤ 1 at αvp = 0, and αvv by |1 + ik0αvv | ≤ 1 at αpv = 0.
To break the correlation in Eq. (3) and to realize all the polarization responses independently without bound, it is needed to unharness the condition of t+ = t– and |t+(–)|2 + |r+(–)|2 ≤ 1, in our case employing a platform of a virtualized meta-atom - which can feed energy to the system and directly mold scattering parameters with designer convolution functions31. As depicted in Fig. 2, the microprocessor returns output values to two speakers (Si) from the detected signals of two microphones (Mj) by means of the programmed convolution kernels (Ỹij). I.e., the output voltages of the sources are calculated in the time domain as follows:
where * is the convolution operator, and the subscripts i, j = 1 or 2 are the labels of the speakers and microphones.
A virtualized metamaterial consisting of two microphones and two speakers connected to a microprocessor embedded in the cover of an acoustic waveguide. The bottom-right inset shows a photograph of a transducer module of a virtualized meta-atom. The top inset shows an analytical representation of the virtualized metamaterial atom: two microphones (Mj) are convolved with a 2 × 2 matrix (Yij) returning signals to fire at the two speakers (Si) as secondary radiation. The distances between the two speakers and microphones are equally set to Δ = 50 mm. The scattering property of the meta-atom is tested by incident waves coming from the forward and backward directions to identify all 4 scattering parameters (r+, t+, r–, and t–).
In the frequency domain, the entire operation is summarized as Si(ω) = Yij(ω)Mj(ω) where Yij(ω) = ω2Ỹij(ω). To achieve a connection between the speaker output Si and the microphone-detected signal Mj, similar to the polarization process in Eq. (1), we decompose the convolution kernel Yij by introducing a basis of convolution matrices:
which satisfy Y = Yeeeee + Yeoeeo + Yoeeoe + Yooeoo. The relation between speaker outputs and microphone signals can then be rewritten in terms of the symmetric and antisymmetric components of the speakers and microphones as follows:
It is important to note that this representation in terms of a constitutive parameter basis eij and coefficients Yij, instead of usual S-parameters18, enables independent access toward each of the four polarizability parameters, including the two Willis parameters. In our meta-atom configuration shown in Fig. 2, with excitation (i.e., Y = ∑Yij eij) in the weak excitation limit (Yij ≪ 1), the polarizability parameters can then be written as follows (see Supplementary Note S3):
where Δ is the distance between the two speakers (and microphones). Therefore, decoupled control or balancing among all acoustic wave parameters can be realized with analytically constructed kernels Yij of the desired design. It is noted that the unabridged Eq. (S23) is analogous to the effective medium theory expression38 for composite scatterers, however critically, except the independently addressable kernels Yoe and Yeo in our realization.
Figure 3 shows an experimental demonstration of the selective excitation of each polarizability parameter in the virtual Willis metamaterial. We set the program to have one of the basis convolution matrices eee, eeo, eoe, and eoo given in Eq. (5) with the Lorentzian-form coefficient Ỹ0(ω). For time-domain microprocessor signal processing, Ỹ0(ω) can then be implemented as the following impulse response function:
where u(t) is the Heaviside step function, a is the total scaling factor, ω0 is the resonance frequency, θ is the phase, and γ is the resonance bandwidth. Figure 3a, b shows the Lorentzian polarizations experimentally realized with even-to-even eee and odd-to-odd eoo excitations, which are responsible for inverse bulk modulus and mass density, respectively, and Fig. 3c, d shows the implementation of bianisotropy achieved with odd-to-even eeo and even-to-odd eoe convolutions. Each polarization component is exclusively excited, with the other components suppressed, in excellent agreement with the precise analytical results in Eq. (S23). Since this approach enables simultaneous independent control of the four wave parameters, by balancing the even-to-odd and odd-to-even couplings, we can also easily realize the purely reciprocal and nonreciprocal Willis parameters κ = i(αpv – αvp)/2 and χ = (αpv + αvp)/2: from the symmetric convolution kernels Y = Y0(eeo + eoe) for the reciprocal case (Fig. 3e) and the antisymmetric Y = Y0(eeo – eoe) in the nonreciprocal case (Fig. 3f). Our results are not subject to the strict restriction imposed by the geometry of the scatterers in physical metamaterials, in contrast with previous approaches, in which the resonance strengths and bandwidths of individual polarization components are unlikely to be independently configurable. It is further noted that because the virtualized Willis metamaterial can also handle complex polarizabilities, it is possible to achieve controllable gain and loss of the system as well as complex bianisotropy, enabling phenomena such as imaginary reciprocal and nonreciprocal coefficients, which are impossible with conventional bianisotropic media22.
a–d Virtualized Willis metamaterial for the four basis convolution matrices eee (a), eoo (b), eeo (c), and eoe (d) with the same Lorentzian convolution kernel Y0, where the model parameters are set to a = 2π × 15, θ = –π/2, γ = 2π × 15 Hz, and ω0 = 2π × 1.0 kHz. The polarizabilities αpp, αvv, αpv, and αvp are depicted in black, green, blue and red, respectively, with solid/empty symbols representing the real/imaginary parts of the experimental results. The corresponding theoretical models are plotted with solid/dashed lines for the real/imaginary parts. e, f Purely reciprocal and purely nonreciprocal Willis couplings κ = i(αpv – αvp)/2 and χ = (αpv + αvp)/2, realized with a balanced eoe and eeo. The purely reciprocal Willis coupling satisfying αvp = –αpv is demonstrated by their summation, i.e., Y = Y0(eeo + eoe) (e), and the purely nonreciprocal term satisfying αvp = αpv is demonstrated by subtracting the two basis convolution matrices, Y = Y0(eeo – eoe) (f).
Figure 4 shows the magnitudes of the Willis couplings |αpv | (Fig. 4a) and |αvp | (Fig. 4b) for Lorentzian convolution kernels with two different scaling factors a = 2π × 15 (dashed-lines) and 2π × 30 (solid-lines), respectively, each for below and above the passivity bound at different resonance center frequencies, in agreement with analytical models in Eq. (7). In contrast to the maximum bianisotropy |αvp | (or |αpv | ) = k0–1 of a passive metamaterial (black dashed line), the newly established maximum bianisotropy for the virtualized Willis metamaterial (magenta dotted line) is modified to |αvp | (or |αpv | ) = 2k0–1 | sin(k0Δ)Y0 | with |Y0 | = aγ−1/2 at the resonance frequency, revealing the set of parameters for controlling the Willis coupling strength (Supplementary Note S2). The breaking of passive bound for αpp and αvv is also discussed in the Supplementary Note S5. It is worth mentioning that in addition to the control parameter a which represents the power drawn by the active devices, the layout of the scatterers, represented by Δ can also be used to control the strength of the polarizability. However, it is noted that for smaller Δ, polarizabilities become weaker except αpp, because the radiation and the detection of dipole mode scale to sin(k0Δ/2) as in Eq. (7). Therefore, the minimum size of Δ and meta-atoms footprint is bound by the targeted magnitude of polarizability, which is set by the dynamic range and sensitivity of active components. In our implementation, a small Δ ~ λ/7 was used in the regime of metamaterials.
Willis coupling beyond the passivity bound achieved by controlling the scaling factors. a The magnitude of αpv for the odd-to-even convolution kernel eeo. The Lorentzian responses at three center frequencies, f0 = 900 Hz (red), 1000 Hz (green) and 1100 Hz (blue), are demonstrated with two different scaling factors, a = 2π × 15 (empty symbols) and 2π × 30 (filled symbols). The analytical results for each scaling factor are also plotted as solid and dashed lines, and the magenta dotted lines denote the theoretical values of the Lorentzian peaks at the resonance frequencies. The black dashed line represents the passivity limit of Willis coupling, i.e., |αpv | = k0–1. b Same as a except that |αvp | for the even-to-odd convolution kernel eoe is demonstrated.
Inverse design of the broadband Willis response
Recalling that there is no reason for the frequency response of Y to be restricted to a Lorentzian in our implementation as long as the system satisfies the causality and stability conditions (see Supplementary Note S4 for the stability analysis), here, we address a metamaterial realization with an arbitrary target response function F0(ω) based on the notion of inverse design. To realize αpv(ω) (or αvp(ω)) = F0(ω), we utilize the relation in Eq. (7) and obtain the convolution function Yeo(ω) = F0(ω)k0 sin(k0Δ)–1/2 (or Yoe(ω) = –F0(ω)k0sin(k0Δ)–1/2) for the target frequency response F0. By applying inverse Fourier transformation to Yeo(ω) (or Yoe(ω)), we can then numerically obtain the required time-domain convolution function y(t). As metamaterials restrict k0Δ to be small, the resultant time-domain function of this inverse design process will be similar to the inverse Fourier transform of the original target frequency response F0(ω). For example, we consider an intriguing target frequency dispersion with a flat broadband response between ω1 and ω2, specifically,
which satisfies the Kramers-Kronig relation, along with its inverse Fourier transform,
When ω2 is set to be much larger than ω1, the above function F0(ω) with θ = 0 (θ = –π/2) provides a flat real (imaginary) spectrum over a broad frequency range while suppressing the imaginary (real) part, while peaks appear in the vicinity of ω1 and ω2. This F0(ω) in combination with convolution kernel as used in Fig. 3e, f could then be used to design broadband Willis metamaterials achieving real- or imaginary- κ and χ.
It is worth to mention that, to achieve flat responses, we remove the software-driven derivative in Eq. (4), so the convolution response having the first derivative compensates ω–1 dependency of Willis coupling polarizabilities αpv and αvp in Eq. (7). Figure 5 shows the experimental realization of the purely reciprocal Willis parameter κ and the purely nonreciprocal parameter χ, achieving a flat broadband spectrum over (ω1, ω2) = (800 Hz, 1200 Hz) for θ = 0 (Fig. 5b, c) and θ = –π/2 (Fig. 5a, d), with a = 0.225.
a, b Demonstration of broadband frequency dispersion in Willis couplings. Analytically designed target dispersions are calculated with Eq. (9), which provide broadband flat real values. By balancing αpv and αvp, (a) broadband reciprocal Willis coupling parameters κ = i(αpv – αvp)/2 and (b) broadband nonreciprocal Willis coupling parameters χ = (αpv + αvp)/2 are achieved. The polarizabilities κ and χ are depicted in magenta and cyan, respectively, with solid/empty symbols representing the real/imaginary parts of the experimental results. The corresponding analytic models are plotted with solid/dashed lines for the real/imaginary parts. c, d, Same as a and b respectively, except that broadband flat imaginary polarizabilities are demonstrated.
Here we emphasize that while Fig. 5a, b each correspond to conventional Willis couplings for omega media and moving media, which have real components of κ and χ, respectively, the Willis couplings shown in Fig. 5c, d newly achieve phase-rotated imaginary κ and χ values, providing an additional degree of freedom in terms of energy, i.e., gain and loss in the Willis coupling. While even more general frequency responses can be constructed beyond the Lorentzian resonance and flat dispersion demonstrated here, we note that it is necessary to keep some reservations due to the causality restriction. For example, the time-domain convolution function from the inverse Fourier transform of the target frequency response could contain non-causal components, i.e., y(t) ≠ 0 for t < 0 (see Supplementary Note S6 for the flat broadband dispersion of the inverse bulk modulus and mass density) which would require modification of the virtual metamaterial configuration, such as placing the microphones far ahead the speakers.
Discussion
In summary, we demonstrate active Willis meta-atom offering decoupled constitutive parameters beyond the bound of passivity and reciprocity. The conditions for maximum bound and reciprocity in the passivity regime are revisited, and then, the new bound of the constitutive parameters and the reciprocity with the introduction of an active metamaterial are analyzed. By employing a virtualized metamaterial platform that enables the flexible design of scattering properties utilizing constitutive parameter basis representation and software programmed convolution functions, all of the four polarizability parameters are demonstrated independently, which has been impossible for previous electroacoustic metamaterials19,28,29,30,31,32,33,34,35. This capability will open the door to a wider range of applications in nonreciprocal wave manipulation, under the notion of the metasurface. For example, a one-dimensional array of our meta-atoms operated for t+ = t––1 = s and r+ = r– = 0, which is realized with nonreciprocal bianisotropy αvp = αpv = (s – s–1)/2ik0 and αpp = αvv = (s + s–1 – 2)/2ik0 supports amplification of any incident fields by s times without scattering or phase perturbation. Extension to the two-dimensional application is also possible by placing meta-atom array at the boundary, instead of using complex potential landscape in the whole interior region39 (see Supplementary Note S7 for the independent control of t+ and t–). Exploiting the fully independent excitation of each parameter as well as precise balancing between them, the operations of purely reciprocal and nonreciprocal Willis couplings are realized. We also demonstrate the breaking of the Willis bound in the passivity limit for the first time while isolating the control parameters involved with the newly established Willis bound in the active regime, such as the amplitude, bandwidth, and frequency of the active Lorentzian resonator that feeds in external power for the scattered fields. Extreme Willis coupling could also enable compact design. For example, Li et al.24 showed the zero-index enhanced nonreciprocal metasurfaces in the moving media yet assuming a very large Mach number of ~ 0.1. It is noted that our platform supports unprecedented nonreciprocity of Mach number of 0.4 (corresponding to experimentally achieved nonreciprocal polarizability of χ ~ 0.03 in Fig. 3f) in addition to the tunability of other acoustic parameters. As well, the number of reciprocal bianisotropic atoms used for extreme impedance matching7 could be reduced to 1/6 with the use of our design at κ ~ 0.04 in Fig. 3e. Finally, we demonstrate the inverse design of flat-amplitude Willis coupling over a broad frequency range, for the reciprocal and nonreciprocal cases as well as the newly revealed case of phase-rotated, nonconserved bianisotropy. Demonstrating full control and top-down tailoring of dispersion, reciprocity, bianisotropy, bulk modulus and mass density within the same platform, our work will enable diverse applications of Willis metamaterials beyond the passivity limit.
Methods
Experimental setup
For the measurement, we used the 4-point measurement method with a National Instruments DAQ device and LabVIEW. Two microphones, each on the front and back, are placed in an impedance tube and 20 cm and 15 cm away from the specimen. The scattering properties of the meta-atom were tested by means of incident waves coming from the forward and backward directions to identify all four scattering parameters (r+, t+, r–, and t–). In the experimental setup, we flipped the orientation of the meta-atom, while the waves were always incident from the same end of the impedance tube.
Fabrication of the meta-atom
The virtualized meta-atom consists of two MEMS microphones (INMP401) and speakers (SMT-1028-t-2-r) laterally located on each edge of the acrylic frame, which are connected to an external single-board computer (Raspberry Pi 4B + ) with amplifiers and analog-to-digital/digital-to-analog converters (see Fig. 2). For digital processing, the input signals sampled by the microphones are digitally processed by the microprocessor and then fed to the speakers in real time with a sampling frequency of fs = 7.5 kHz and a number of samples equal to N = 400. The convolution is calculated as \(S_i^V\left[ n \right] = \mathop {\sum}\nolimits_j {\mathop {\sum}\nolimits_{k = 0}^N {Y_{ij}\left[ k \right]( {M_j\left[ {n - k} \right] - M_j\left[ {n - k - 1} \right]} )} }\), where the index n = t/Ts is the discrete time with sampling period Ts = fs–1. The speakers and microphones, which communicate with the microprocessor through the SPI (Serial Peripheral Interface), are mounted in an acrylic frame (width = 3.0 cm, length = 6.5 cm). This transducer module is, in turn, mounted on the acoustic waveguide (width = 3.0 cm, height = 3.0 cm).
Data availability
The data that support the plots in this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Smith, D. R., Padilla, W. J., Vier, D., Nemat-Nasser, S. C. & Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 84, 4184 (2000).
Cummer, S. A., Christensen, J. & Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 1, 16001 (2016).
Zheludev, N. I. & Kivshar, Y. S. From metamaterials to metadevices. Nat. Mater. 11, 917–924 (2012).
Liang, Z. & Li, J. Extreme acoustic metamaterial by coiling up space. Phys. Rev. Lett. 108, 114301 (2012).
Li, J. & Chan, C. T. Double-negative acoustic metamaterial. Phys. Rev. E 70, 055602 (2004).
Lee, S. H., Park, C. M., Seo, Y. M., Wang, Z. G. & Kim, C. K. Composite acoustic medium with simultaneously negative density and modulus. Phys. Rev. Lett. 104, 054301 (2010).
Koo, S., Cho, C., Jeong, J.-H. & Park, N. Acoustic omni meta-atom for decoupled access to all octants of a wave parameter space. Nat. Commun. 7, 1–7 (2016).
Brunet, T. et al. Soft 3D acoustic metamaterial with negative index. Nat. Mater. 14, 384–388 (2015).
Zhu, J. et al. A holey-structured metamaterial for acoustic deep-subwavelength imaging. Nat. Phys. 7, 52–55 (2011).
Zhu, X., Liang, B., Kan, W., Zou, X. & Cheng, J. Acoustic cloaking by a superlens with single-negative materials. Phys. Rev. Lett. 106, 014301 (2011).
Lu, M.-H. et al. Extraordinary acoustic transmission through a 1D grating with very narrow apertures. Phys. Rev. Lett. 99, 174301 (2007).
Cummer, S. A. & Schurig, D. One path to acoustic cloaking. N. J. Phys. 9, 45 (2007).
Chen, H. & Chan, C. Acoustic cloaking in three dimensions using acoustic metamaterials. Appl. Phys. Lett. 91, 183518 (2007).
Chen, H. & Chan, C. T. Acoustic cloaking and transformation acoustics. J. Phys. D: Appl. Phys. 43, 113001 (2010).
Muhlestein, M. B., Sieck, C. F., Wilson, P. S. & Haberman, M. R. Experimental evidence of Willis coupling in a one-dimensional effective material element. Nat. Commun. 8, 1–9 (2017).
Melnikov, A. et al. Acoustic meta-atom with experimentally verified maximum Willis coupling. Nat. Commun. 10, 1–7 (2019).
Liu, Y. et al. Willis metamaterial on a structured beam. Phys. Rev. X 9, 011040 (2019).
Zhai, Y., Kwon, H.-S. & Popa, B.-I. Active Willis metamaterials for ultracompact nonreciprocal linear acoustic devices. Phys. Rev. B 99, 220301 (2019).
Chen, Y., Li, X., Hu, G., Haberman, M. R. & Huang, G. An active mechanical Willis meta-layer with asymmetric polarizabilities. Nat. Commun. 11, 1–8 (2020).
Merkel, A., Romero-García, V., Groby, J.-P., Li, J. & Christensen, J. Unidirectional zero sonic reflection in passive PT-symmetric Willis media. Phys. Rev. B 98, 201102 (2018).
Sieck, C. F., Alù, A. & Haberman, M. R. Origins of Willis coupling and acoustic bianisotropy in acoustic metamaterials through source-driven homogenization. Phys. Rev. B 96, 104303 (2017).
Sihvola, A., Viitanen, A., Lindell, I. & Tretyakov, S. Electromagnetic Waves in Chiral and Bi-Isotropic Media (Artech House Antenna Library). Norwood, MA, USA: Artech House (1994).
Li, J., Shen, C., Díaz-Rubio, A., Tretyakov, S. A. & Cummer, S. A. Systematic design and experimental demonstration of bianisotropic metasurfaces for scattering-free manipulation of acoustic wavefronts. Nat. Commun. 9, 1–9 (2018).
Quan, L., Sounas, D. L. & Alù, A. Nonreciprocal Willis coupling in zero-index moving media. Phys. Rev. Lett. 123, 064301 (2019).
Quan, L., Ra’di, Y., Sounas, D. L. & Alù, A. Maximum Willis coupling in acoustic scatterers. Phys. Rev. Lett. 120, 254301 (2018).
Chiang, Y. K. et al. Reconfigurable acoustic metagrating for high-efficiency anomalous reflection. Phys. Rev. Appl. 13, 064067 (2020).
Craig, S. R., Su, X., Norris, A. & Shi, C. Experimental realization of acoustic bianisotropic gratings. Phys. Rev. Appl. 11, 061002 (2019).
Baz, A. The structure of an active acoustic metamaterial with tunable effective density. N. J. Phys. 11, 123010 (2009).
Baz, A. M. An active acoustic metamaterial with tunable effective density. J. Vib. Acoust. 132, 041011 (2010).
Chen, Y., Hu, G. & Huang, G. A hybrid elastic metamaterial with negative mass density and tunable bending stiffness. J. Mech. Phys. Solids 105, 179–198 (2017).
Cho, C., Wen, X., Park, N. & Li, J. Digitally virtualized atoms for acoustic metamaterials. Nat. Commun. 11, 1–8 (2020).
Yi, K., Ouisse, M., Sadoulet-Reboul, E. & Matten, G. Active metamaterials with broadband controllable stiffness for tunable band gaps and non-reciprocal wave propagation. Smart Mater. Struct. 28, 065025 (2019).
Chen, Y., Li, X., Scheibner, C., Vitelli, V. & Huang, G. Self-sensing metamaterials with odd micropolarity. arXiv preprint arXiv:2009.07329 (2020).
Chen, Y., Li, X., Nassar, H., Hu, G. & Huang, G. A programmable metasurface for real time control of broadband elastic rays. Smart Mater. Struct. 27, 115011 (2018).
Popa, B.-I., Zhai, Y. & Kwon, H.-S. Broadband sound barriers with bianisotropic metasurfaces. Nat. Commun. 9, 1–7 (2018).
Fleury, R., Sounas, D. & Alu, A. An invisible acoustic sensor based on parity-time symmetry. Nat. Commun. 6, 1–7 (2015).
Zhu, R. et al. Experimental study of an adaptive elastic metamaterial controlled by electric circuits. Appl. Phys. Lett. 108, 011905 (2016).
Alu, A. First-principles homogenization theory for periodic metamaterials. Phys. Rev. B 84, 075153 (2011).
Yu, S., Piao, X. & Park, N. Bohmian photonics for independent control of the phase and amplitude of waves. Phys. Rev. Lett. 120, 193902 (2018).
Acknowledgements
J.L. acknowledges funding from the Research Grants Council under Grant no. 16303019. N.P. was supported by the NRF of Korea through the Global Frontier Program (2014M3A6B3063708).
Author information
Authors and Affiliations
Contributions
J.L. conceived the idea of the virtualization of a Willis metamaterial. C.C. and J.L. established the maximum Willis coupling in a one-dimensional system. C.C. and N.P. established the inverse design of broadband Willis coupling. C.C. and X.W. established the setup of the atom and the control program and performed the measurements. All authors contributed to the data analysis and the writing of the manuscript. J.L. and N.P. managed the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cho, C., Wen, X., Park, N. et al. Acoustic Willis meta-atom beyond the bounds of passivity and reciprocity. Commun Phys 4, 82 (2021). https://doi.org/10.1038/s42005-021-00584-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00584-6
This article is cited by
-
Pine-like elastic metamaterials for urban seismic Rayleigh wave attenuation
Urban Lifeline (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.