Learning the best nanoscale heat engines through evolving network topology

Abstract

The quest to identify the best heat engine has been at the center of science and technology. Considerable studies have so far revealed the potentials of nanoscale thermal machines to yield an enhanced thermodynamic efficiency in noninteracting regimes. However, the full benefit of many-body interactions is yet to be investigated; identifying the optimal interaction is a hard problem due to combinatorial explosion of the search space, which makes brute-force searches infeasible. We tackle this problem with developing a framework for reinforcement learning of network topology in interacting thermal systems. We find that the maximum possible values of the figure of merit and the power factor can be significantly enhanced by electron-electron interactions under nondegenerate single-electron levels with which, in the absence of interactions, the thermoelectric performance is quite low in general. This allows for an alternative strategy to design the best heat engines by optimizing interactions instead of single-electron levels. The versatility of the developed framework allows one to identify full potential of a broad range of nanoscale systems in terms of multiple objectives.

Introduction

In 1824, Sadi Carnot found¹ that the efficiency of heat engines operating between a hot reservoir at temperature T_h and a cold one at T_c is universally bounded from above by the value

$${\eta }_{{\rm{C}}}=1-\frac{{T}_{{\rm{c}}}}{{T}_{{\rm{h}}}},$$

(1)

which is now known as the Carnot efficiency. This limit can be reached for ideal reversible machines operating at quasistatic conditions, leading to infinite operation time and vanishing output power. In contrast, any useful devices must supply nonvanishing power that necessarily associates with nonzero entropy productions and efficiency below η_C. Thus, it is of both fundamental and practical importance to consider what is the best heat engine with finite power. In this direction, a seminal work was done by Curzon and Ahlborn, who have considered² a thermal machine operating at the maximum power as the optimal engine.

Since efficiency and power are two conflicting objectives, one cannot in general find a heat engine that optimizes both of them simultaneously. This class of problems is known as the multiobjective optimization problem for which the solution is given by the quantitative identification of trade-off between multiple objectives³. More specifically, here we propose to characterize the best heat engines by a set of machines for which efficiency and power cannot be further improved without compromising the other. In the language of the multiobjective optimization theory, such type of set is known as the Pareto front³. From this viewpoint, the engines considered by Carnot¹ and Curzon–Ahlborn² are two specific examples of the Pareto front, i.e., a general set of the multiobjective-optimal heat engines.

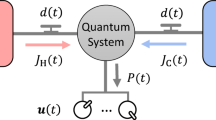
A promising candidate for realizing efficient heat engines is nanostructured thermoelectric^4,5,6, which converts heat flows into electrical power (see Fig. 1a). It has attracted considerable interest as promoted by the prospect of an enhanced efficiency due to quantum confinement effects and significant reduction of the phonon thermal conductivity. In the linear-response regime, its thermodynamic properties are fully characterized by the figure of merit ZT and the power factor Q, which are related to the maximum possible values of efficiency and power, respectively. Thus, we can reduce a problem of seeking the best heat engines to the search of the Pareto front on the objective space spanned by ZT and Q (see Fig. 1b). In noninteracting systems, brute-force optimizations of transport functions have allowed one to identify the best thermal machine achieving the highest ZT⁷ and, more generally, the optimal power-efficiency trade-off^8,9. However, the challenging goal of identifying the best interacting heat engine is still unexplored.

Fig. 1: Graphical representation of interacting nanothermoelectric and characterization of the best heat engines.

a Nanoscale heat engine is characterized by a network, in which each node represents a single-particle level labeled by an integer like m, n. Each edge connecting two nodes indicates the presence of interaction between the corresponding single-particle levels (in, e.g., quantum dots). The width of the edge between node m and node n is labeled by w_mn, and represents the interaction strength. The system is connected with hot (h) and cold (c) reservoirs at temperatures T_h,c and electrochemical potentials μ_h,c. Each node exchanges electrons with the reservoirs and can be occupied by at most a single electron. b Set of the best heat engines is characterized by the best trade-off (known as the Pareto front) between their power P and efficiency η (thick solid curve in the main panel). The inset illustrates the concept of dominance in terms of power factor Q and figure of merit ZT; machines M_1,2 dominate M₃, while there are no dominance relations between M₁ and M₂. The Pareto front ${\mathcal{C}}$ in the inset is defined by the Pareto-optimal machines (such as M₁ and M₂) that are not dominated by any other ones. The dashed loops in the main panel indicate the power-efficiency curves with varying chemical potentials at fixed Q and ZT (cf. Eq. (4)), which correspond to machines M_1,2,3 indicated in the inset. The envelope of all the possible loops provides the Pareto front on the P–η plane in the main panel. The efficiency and power are normalized by the Carnot efficiency η_C and the maximum power ${P}_{\max }$, respectively.

In the noninteracting case, it is well known that the optimal engine in terms of both power and efficiency can be realized when all the single-electron energies are degenerate⁷. Yet, its thermodynamic performance can significantly be degraded compared to this optimal case if such a perfect degeneracy is not attained. Thus, a search for better nanothermoelectrics has so far been explored mainly in the context of optimizing single-electron energies in a noninteracting setup. Here, we propose yet another way toward achieving the best heat engines, namely, by optimizing electron interactions instead of single-electron energies. This strategy can potentially work even under nondegenerate single-electron levels.

Indeed, to realize the promise of on-chip power production, it is indispensable to assemble a large number of nanomachines, where fluctuations in single-electron energies are often inevitable and many-body interaction among the constituents is ubiquitous due to, e.g., long-range nature of the Coulomb interaction. One of our goals in the present work is to attempt to address such a major challenge in nanoscale heat engines, that is, an individual thermal machine can only supply low power output. More specifically, this challenge motivates us to reveal full potential of many-body interaction on thermodynamic performance of nanoscale engines and to ask two questions as follows:

• (A) Can one identify the best possible interacting thermal machines?

• (B) Does the interaction enhance efficiency and power and, if yes, to what extent?

Here, we answer these questions in the affirmative by developing a framework for reinforcement learning of network topology in interacting thermal systems. The key idea is to map the many-body interaction among microscopic constituents onto the network (see Fig. 1a); each node represents a single-electron level that exchanges electrons with reservoirs and each edge between two nodes indicates the presence/absence of interaction between the corresponding levels. We then train the topology of this network via varying interaction parameters for the purpose of identifying a set of the best heat engines. Since the present optimization problem is computationally hard due to combinatorial explosion of the search space, we employ the differential evolution, that is, one of the most competitive training algorithms in high-dimensional nonconvex search space^10,11.

Building on this framework, we reveal a physical mechanism by which each element of the best heat engines can significantly improve the thermodynamic properties in comparison with the noninteracting counterparts. From a broad perspective of physics, the identified mechanism of enhancing thermodynamic efficiency and power can be applied to an ensemble of various nanoscale machines, such as molecular motors, colloidal particles, and biophysical networks as well as thermoelectric materials. Moreover, the reinforcement learning framework developed here will allow one to determine the best trade-off relations in those nanoscale systems through the global multiobjective optimization.

Below we first introduce a standard model to describe transport phenomena of typical nanothermoelectric systems, and present a reinforcement learning framework for identifying a set of the best interacting nanothermoelectric systems in terms of thermodynamic efficiency and power. We then provide the main results of the present paper, namely, a variety of realizations of the best interacting heat engines that are identified by the proposed framework. We also reveal the mechanisms of how interacting machines can improve their thermodynamic efficiency and power compared to their noninteracting counterparts. Building on these findings, we propose a designing principle to realize the highest-power interacting engines. We discuss that the power factor diverging with the number of single-particle levels can allow one to attain the asymptotic Carnot efficiency at subextensive, yet stable and finite power. Finally, we discuss possible experimental realizations in quantum dot arrays, and suggest several interesting future directions.

Results

Interacting systems linked with network topology

We here consider nanothermoelectric systems as a most prototypical and representative class of nanoscale heat engines, and introduce a model to describe transport phenomena therein. Specifically, we consider a fermionic system described by the many-body Hamiltonian

$$H=\mathop{\sum}\limits _{l}({\epsilon }_{l}-{v}_{g}){n}_{l}+\frac{1}{2}\mathop{\sum}\limits _{l\ne m}{w}_{lm}{n}_{l}{n}_{m},$$

(2)

where ϵ_l denotes single-electron energy of mode l = 1, 2, …, N_f, v_g is the ground voltage, n_l = 0, 1 represents the occupation of zero or one electron, and w_lm ≥ 0 are generic two-body interaction parameters. The system is in contact with hot (h) and cold (c) common reservoirs at temperatures T_h,c and electrochemical potentials μ_h,c (see Fig. 1a). We are interested in a general situation associated with nondegenerate single-electron levels {ϵ_l}.

We describe the dynamics based on the classical master equation¹². This description can be justified when the tunneling rates to reservoirs are sufficiently small such that (i) the bath correlation time is shorter than the relaxation timescale due to the system-bath coupling, and thus the Born–Markov approximation is valid and (ii) the sequential limit is achieved, i.e., transport occurs due to single-electron tunnelings to reservoirs and the generation of quantum coherence can be neglected (see “Methods”). We note that it is essential to employ the so-called global approach¹³ to the master equation as performed here, which requires the explicit inclusion of interaction terms in the system Hamiltonian H. The reason is that we are interested in the correlated regime with the interaction strength being comparable to the level spacing of single-electron energies¹³. The tunneling rates to reservoirs are assumed to be energy independent and denoted by γ_h,c > 0; for the sake of simplicity, we set them to be the same value γ ≡ γ_h = γ_c in this paper. Denoting the particle current and the heat flow out of each reservoir as Jⁱ and ${J}_{q}^{i}$ with i = h, c, the power and the efficiency are given by P = − ∑_iμ_iJⁱ and $\eta =P/{J}_{q}^{{\rm{h}}}$, respectively.

Our aim is to establish which of electronic systems modeled by Eq. (2) can fundamentally achieve the best power-efficiency trade-off. To this end, we take into account all the possible (repulsive) interactions w, while the phonon contribution to heat flow is not included as it is external to the electronic system⁴. The present model can thus be graphically represented as a network as shown in Fig. 1a. Here, each node indicates a single-particle level (in, e.g., quantum dots) that exchanges electrons with reservoirs. An edge between two nodes represents the presence of interaction between the corresponding single-particle levels, and its width indicates the strength of the interaction. From this perspective, the problem of identifying the best heat engines via optimizing (i.e., training) parameters w can be considered, as reinforcement learning of underlying topology and weight values of the interaction network.

Power-efficiency trade-off and Pareto-optimal machines

We next introduce a framework to identify a set of the best heat engines in terms of thermodynamic power and efficiency. To proceed further, hereafter we focus on the linear-response regime, δT = T_h − T_c ≪ T_h and ∣δμ∣ = ∣μ_h − μ_c∣ ≪ k_BT_h, and denote T = T_h ≃ T_c. The thermoelectric properties are then characterized by the figure of merit ZT and the power factor Q that are defined by

$${{ZT}}=\frac{\sigma {S}^{2}T}{\kappa }=\frac{QT}{\kappa }.$$

(3)

Here, σ is the electrical conductance, S is the Seebeck coefficient, and κ is the thermal conductance; their values can be associated with the Onsager coefficients (see “Methods”). More explicitly, the power-efficiency trade-off can be fully characterized by ZT and Q via the linear-response formula¹⁴

$$\frac{\eta (P)}{{\eta }_{{\rm{C}}}}=\frac{P/(Q\delta {T}^{2}/4)}{2\left[1+2/ZT\mp \sqrt{1-P/(Q\delta {T}^{2}/4)}\right]},$$

(4)

which have two branches as they correspond to changing δμ from zero to SδT at which P = 0 again; the stopping value SδT corresponds to the point at which the sign of the electron flow reverses. It follows from Eq. (4) that ZT and Q characterize the maximum possible values of the efficiency $\eta /{\eta }_{{\rm{C}}}\le (\sqrt{{ZT}+1}-1)/(\sqrt{{ZT}+1}+1)$ and the power P ≤ QδT²/4, respectively.

The problem of finding the best heat engines now reduces to the multiobjective optimization of ZT and Q. To this end, let ${{\rm{M}}}_{{\mathcal{W}}}$ symbolically represent a thermoelectric machine characterized by a set of 1 + N_f(N_f − 1)/2 variables ${\mathcal{W}}=\{{v}_{g},w\}$, which includes the ground voltage and interaction parameters while a set of generic, nondegenerate single-electron energies is fixed through the optimization process. We call that a machine ${{\rm{M}}}_{{\mathcal{W}}}$ dominates³ ${{\rm{M}}}_{{\mathcal{W}}^{\prime} }$ (denoted as ${{\rm{M}}}_{{\mathcal{W}}}\succ {{\rm{M}}}_{{\mathcal{W}}^{\prime} }$) if ${{\rm{M}}}_{{\mathcal{W}}}$ is no worse than ${{\rm{M}}}_{{\mathcal{W}}^{\prime} }$ in both ZT and Q, and ${{\rm{M}}}_{{\mathcal{W}}}$ is strictly better than ${{\rm{M}}}_{{\mathcal{W}}^{\prime} }$ in at least one of them. A machine ${{\rm{M}}}_{{{\mathcal{W}}}^{* }}$ is Pareto-optimal if no other machines dominate it. Then, the Pareto front³ ${\mathcal{C}}$ is the curve defined by a set of $(Q({{\mathcal{W}}}^{* }),ZT({{\mathcal{W}}}^{* }))$ for all the possible Pareto-optimal machines. We illustrate these concepts in the inset of Fig. 1b, where the machines satisfy M_1,2 ≻ M₃, while there are no dominance relations between M₁ and M₂.

We emphasize that optimizing ZT alone is insufficient as ZT has no information about the maximum possible power, which is crucial for realizing any useful devices. We instead characterize the best thermal machines in terms of the Pareto front ${\mathcal{C}}$ on the Q-ZT plane, which allows us to identify the full set of the optimal engines at finite power. The corresponding Pareto front on the power-efficiency plane can be also given as the envelope of the image space of ${\mathcal{C}}$ through the mapping (Eq. (4); (cf. the main plane in Fig. 1b and also the figures in “Methods”).

We are now left with the task of finding the best nanoscale engines by using machine learning to train the network parameters ${\mathcal{W}}$. However, even after the above simplifications, the problem still remains challenging as the transport coefficients σ, S, and κ are adversely interdependent, while brute-force approaches become quickly infeasible. The latter is due to the exponential growth $\sim {({L}_{{\rm{dis}}})}^{{N}_{f}^{2}/2}$ of the search space with the system size N_f, where L_dis is the number of bins for discretizing a continuous parameter (see “Methods”). Moreover, the greedy (gradient-based) algorithms overwhelmingly fail even for few-level systems because of the proliferation of local optima (see the figures in “Methods”). To overcome the challenges, we employ a global search approach based on the differential evolution¹⁰, which is one of the most powerful gradient-free algorithms inspired by a process whereby biological organisms adapt and survive. The key advantage is its autonomous adaption of the balance between exploitation and exploration, which can significantly expedite an efficient search over a high-dimensional nonconvex landscape¹¹ (see “Methods” for further details).

Learning the power-efficiency trade-off in nanoscale engines

A reinforcement learning framework formulated in the previous section allows us to identify a set of the best heat engines in terms of fundamental thermodynamic properties. In the linear-response regime, which is of interest in this paper, such a set is characterized by the optimal trade-off relation between the power factor Q and the figure of merit ZT. Applying the linear-response formula (Eq. (4)), one can then readily determine the corresponding trade-off relation between thermodynamic power P and efficiency η. The heat engines lying on this tradeoff curve defines the Pareto-optimal solutions, giving a variety of the best nanoscale engines. Below, we present the solutions identified by the present machine learning framework and clarify their physical properties in detail.

Figure 2f shows the Pareto front on the Q-ZT plane, which is identified by the above learning protocol. With many-body interaction and generic (nondegenerate) single-electron levels, the values of Q and ZT can be enhanced by orders of magnitudes in comparison with those in the noninteracting case. As a consequence, interaction can significantly improve power-efficiency trade-off in heat-to-work conversion (see Fig. 2e). We emphasize that the noninteracting results are obtained under the multilevel setting with the same set of single-electron energies as considered in the interacting case. The substantial enhancements originate from the ability of interaction to activate many paths of state transitions, as well as attain the approximate tight-coupling condition J ∝ J_q. The former leads to a much higher Q than that in the noninteracting case, while the latter can feature a significantly large ZT^15,16.

Fig. 2: Learning network topologies of the best nanoscale heat engines.

a–d Topologies of the interaction networks (insets) and the state-transfer networks (main panels) for the Pareto-optimal heat engines indicated by labels (a–d) in e, f. They attain a the highest ZT, b the suboptimal ZT and Q, c the highest Q, and d the highest Q in the noninteracting case. The red edges in the state-transfer networks indicate the activated transfer edges along which the probability flow is significant. In c, the highest power is achieved by the sparse interaction network, where degenerate weakly interacting holes result in the maximal activation of transfer edges. In a and b, the strong and dense interactions isolate several states from the other ones and solely activate transfer edges within those isolated manifolds. The thickness of links in the insets represents the strength of interaction. e, f The obtained best trade-offs between e power P and efficiency η, and f power factor Q and figure of merit ZT. The blue (red) shaded region is allowed for interacting (noninteracting) heat engines and its upper boundary indicated by solid curves represents the Pareto front, i.e., the set of the optimal machines for which two objectives cannot be further improved without compromising the other. The dashed curves correspond to the power-efficiency curves for each Pareto-optimal machine. The black dashed curve in e indicates the scaling $1-\eta /{\eta }_{{\rm{C}}}\propto \sqrt{P}$ at low power in the noninteracting case (see the figures in “Methods”). We set N_f = 5, ϵ_l = lΔ with Δ/k_BT = 3, γ_h = γ_c ≡ γ and plot Q in the unit of Q₀ = k_Bγ/T. The efficiency and power factor are normalized by η_C and Q₀.

To further elucidate this physical mechanism, we visualize typical realizations of the Pareto-optimal heat engines in Fig. 2a–d. Here, the pentagon-shaped, inset networks show the identified optimal interactions, where nodes (edges) represent N_f single-electron levels (interactions between them). The networks in the main panels of Fig. 2a–d visualize the whole state-transfer networks with nodes (edges) being ${2}^{{N}_{f}}$ many-body states (transitions between them).

The inset network in Fig. 2c demonstrates that the highest power has been achieved by a surprisingly sparse interaction. More specifically, the sparse topology in the interaction network indicates that the number of other sites interacting with each site is significantly smaller than the maximally allowed value N_f(N_f − 1)/2. As shown in the state-transfer network (the main panel of Fig. 2c), probability flows concentrate on the transfer edges among the fully occupied state, single- and two-hole states as highlighted by red color. This activation of many transfer paths originates from the degeneracies of single-hole states and the suppression of inevitable hole–hole interactions, both of which are achieved by the observed sparse interaction; we will revisit this important point in later discussions. In this way, the power is maximized by activating transfer edges as many as possible.

As making the interaction network stronger and denser, the Pareto-optimal machines can improve ZT (i.e., efficiency) at the expense of compromising Q (i.e., power). This can be inferred from the state-transfer networks in Fig. 2a, b, where the strong and dense repulsive interaction isolates a particular energy manifold from the other many-body states, realizing the approximate tight-coupling condition J ∝ J_q within that manifold. This emergent unicyclic structure in the probability flow allows for high ZT; yet, it comes at the price of sacrificing Q due to the reduced number of activated transitions.

The divergence of ZT at Q/Q₀ ≃ 0.21 (cf. Fig. 2f) originates from an almost perfect unicyclic structure^15,16. Here, the dense interaction isolates two many-body states from the other ones such that only the probability flow between these two levels is significant (cf. the main panel in Fig. 2a). This ensures the tight-coupling condition with great accuracy and thus leads to the divergent ZT. As concrete realizations of the Pareto-optimal heat engines in Fig. 2a–c, we illustrate possible real-space configurations in quantum dot arrays in the figures in “Methods”. We remark that the all-to-all mean-field coupling (i.e., w_lm = w_MF for all l ≠ m), which has been mainly discussed in the previous literature^{12,17,18,19,20,21,22,23}, does not give the Pareto-optimal solutions here. In general, we find that this type of uniform, maximally dense interaction is largely suboptimal.

Figure 2d demonstrates that the noninteracting machine with multiple and nondegenerate single-electron levels activates only a few edges, resulting in low power output due to the bipolar effect, i.e., a nonzero heat conduction at the zero particle current. In Fig. 2e, it is worthwhile to mention that the obtained Pareto front in the noninteracting (resp. interacting) case is consistent with the scaling at low power, 1 − η/η_C ∝ P^a with a = 1/2 (resp. a = 1; see the figures in “Methods”). We note that a similar feature has previously been discussed based on the Landauer–Büttiker theory^8,9 and the molecular simulations^24,25. In this respect, the scaling laws at the low power output hold true independently of a specific choice of the underlying theoretical formalisms, indicating their universality in a broad range of physical systems. We recall that the noninteracting results in Fig. 2d are obtained by using exactly the same set of nondegenerate and multiple single-electron levels as used in the interacting case. Physically, the inclusion of such fluctuations in electron levels is of fundamental importance in a broad range of physical systems; for instance, single-electron energies in solid-state devices are highly nondegenerate, and dot energies in quantum dot arrays are subject to inevitable size fluctuations.

To further elucidate the interplay between many-body interactions and fluctuations in single-electron levels, in Fig. 3a, we show the optimal power-efficiency trade-off under random single-electron energies sampled from the Gaussian distribution with the width δϵ. When the energy width δϵ is substantially smaller than the temperature scale k_BT, the optimal engines achieve almost the same performance in both interacting and noninteracting cases. However, in the noninteracting machines, the power-efficiency bound substantially degrades as the fluctuation δϵ is increased because only a smaller portion of single-electron levels close to the (optimized) ground voltage can contribute to the transport dynamics. Meanwhile, in the interacting case, one can harness many-body interactions to nearly attain the optimal power-efficiency bound, and the result is almost insensitive to a specific choice of single-electron levels (compare the blue solid curves in Figs. 2 and 3a). One of the main advantages in the interacting machines is this robustness against the fluctuations in single-electron levels owing to the flexibility of the optimal interaction network for realizing high power and efficiency.

Fig. 3: Comparisons between noninteracting and interacting optimal heat engines.

a Power-efficiency bound under randomly generated single-electron energies. The inset illustrates the fact that single-electron energies are randomly sampled from the Gaussian probability distribution with the width δϵ. The main panel shows the efficiency-power bounds obtained at different widths δϵ, and with or without interactions. The noninteracting bounds substantially degrade as the width δϵ is increased. The interacting bound is almost insensitive to a specific choice of δϵ, and we plot the result for δϵ/k_BT = 15 as a blue solid curve. The dashed error bars indicate the standard deviations of the numerical results. We set N_f = 5, γ_h = γ_c ≡ γ, and plot the power in terms of Q₀δT²/4 with Q₀ = k_Bγ/T. Here, N_f is the number of single-electron levels, γ_h,c are hopping rates to the hot and cold reservoirs, respectively. b Finite-size scaling of the maximum possible power. The blue dashed curve shows an extrapolation of the highest-power factors at different sizes N_f using the form ${Q}_{\max }/{Q}_{0}=\mathop{\sum }\nolimits_{i = 1}^{4}{a}_{i}{N}_{f}^{i-3}$, with fitting parameters a_1,2,3,4. It asymptotically achieves the fundamental bound (cf. Eq. (5)) indicated by the green solid curve. The inset plots the associated figure of merit ${ZT}{| }_{Q = {Q}_{\max }}$ of the highest-power machine against N_f, where the blue dashed line shows the fitted scaling ${ZT}{| }_{Q = {Q}_{\max }}\propto {N}_{f}^{1.31}$. The noninteracting results obtained under the same setting of generic (nondegenerate) single-electron levels fitted from N_f-independent extrapolations are shown by the red dashed lines. The dots represent the data points at each value of N_f. We set ϵ_l = lΔ with Δ/k_BT = 3 and γ_h = γ_c ≡ γ.

Based on these observations, we now conjecture that the Pareto-optimal interacting machine at the highest power can be generally achieved by satisfying the following conditions: (i) single-hole excitation energies e_l = ϵ_l + ∑_m ≠ lw_lm are degenerate, i.e., ∣e_l − e_l + 1∣ ≪ k_BT for l = 1, 2, …, N_f − 1, (ii) at most N_f − 1 variables of ${\{{w}_{lm}\}}_{l \,{> }\,m}$ can be nonzero, and (iii) the ground voltage is set to be v_g = e_h + αk_BT, where e_h is the degenerate single-hole energy and α ≃ 2.40. Physically, the first condition ensures that all the transfer edges between the fully occupied state and single-hole states are activated. The second one makes interactions among hole excitations as sparse as possible, leading to the maximal activation of transfer edges between single-hole states and double-hole states. The final one optimizes the ground voltage in such a way that the power is maximized^26,27,28. We confirm the conjecture up to a system with ${2}^{{N}_{f}}=512$ states as demonstrated in Fig. 4a–d, where the concrete examples of the highest-power machines are also indicated. Figure 4e, f demonstrates that the maximum possible values of efficiency and power increase with the number of levels N_f. To further investigate the size dependence, in Fig. 3b, we perform the finite-size scaling of the maximum possible power factor ${Q}_{\max }$ and the associated figure of merit ${ZT}{| }_{Q = {Q}_{\max }}$. It is clear that both quantities grow with system size N_f. In particular, in the thermodynamic limit ${Q}_{\max }$ diverges in proportion to N_f, and the power per level asymptotically attains the fundamental bound set by an ideal unicyclic system²⁷

$$\frac{{Q}_{\max }}{{N}_{f}}\to \xi \frac{{k}_{{\rm{B}}}}{T}\frac{{\gamma }_{{\rm{h}}}{\gamma }_{{\rm{c}}}}{{\gamma }_{{\rm{h}}}+{\gamma }_{{\rm{c}}}}\ \ \ \ ({N}_{f}\to \infty ),$$

(5)

where ξ ≃ 0.439. For the noninteracting case with nondegenerate single-electron levels, both Q and ZT do not grow with N_f and remain to be small finite values even if the number of available energy levels diverges.

Fig. 4: Size dependence of the highest-power nanoscale heat engine.

a–d Topologies of the interaction networks (insets) and the state-transfer networks (main panels) for the highest-power heat engines with a ${2}^{{N}_{f}}=64$, b 128, c 256, and d 512 states. The red edges in the state-transfer networks indicate the activated transfer edges associated with significant probability flows. The interaction networks are optimized such that single-hole excitation energies are degenerate and its topology is sparse as much as possible. The former leads to the activation of all the transfer edges between the fully occupied state and single-hole states (see also magnified insets in c and d). The latter eliminates unfavorable interactions among hole excitations, leading to the maximal activation of transfer edges between single-hole states and double-hole states. Here, the white and black nodes represent the empty and occupied levels, respectively, and the thickness of links indicates the strength of interaction. e The best trade-offs between power P and efficiency η for the highest-power heat engines at different system sizes N_f. f The corresponding Pareto fronts in terms of power factor Q and figure of merit ZT. In e, f, the allowed regions (color shaded with the upper bounds indicated by the solid curves) expand with increasing N_f. The dashed curves represent the efficiency-power curves for the maximum-power machines. The data of the noninteracting case for N_f = 9 with the same set of (nondegenerate) single-electron levels as used in the interacting case are given in e, f. We set ϵ_l = lΔ with Δ/k_BT = 3, γ_h = γ_c ≡ γ, and plot Q in the unit of Q₀ = k_Bγ/T. The efficiency and power factor are normalized by η_C and Q₀.

In general, to enhance the power factor per level Q/N_f, one has to activate a larger portion of the transfer edges in the state-transfer network. The convergence to the unicyclic limit in Eq. (5) can be understood from a simple scaling argument on the activation of the state-transfer network as follows. On one hand, the condition (i) for the highest-power machines above allows one to activate all the transfer edges between the fully occupied state and single-hole states (Fig. 5a), leading to the linear scaling of the power factor ${Q}_{\max }\propto {N}_{f}$. On the other hand, at the next level of transitions between single- and double-hole states, only a part of the transfer edges can be activated due to the inevitable hole–hole interaction causing the energy mismatch (Fig. 5b). The discrepancy between ${Q}_{\max }/{N}_{f}$ and Q_uni originates from this imperfect activation of the transfer edges in the state-transfer network. Yet, because of the condition (ii), one can estimate the fraction f_1 − 2 of the activated transfer edges between single- and double-hole sectors as f_1 − 2 = 1 − 2/N_f, which still converges to the ideal value f_1 − 2 → 1 in the thermodynamic limit. It is this convergence that lies at the heart of the asymptotic realization of the unicyclic limit as indicated in Eq. (5) and Fig. 3b (see “Methods” for further discussions). Given that not only the power, but also the efficiency scales with system size (cf. Fig. 4e, f), we expect the present analysis to be generalized to Pareto-optimal machines other than the highest-power machine discussed here. We remark that the above arguments are based on a setup of the single-electron energies with a finite spacing, which is a common setting in studies of nanothermoelectrics; for example, energy levels in quantum well structures of multilevel dots can be described in this way²¹. These scalings can in general be different if one chooses an alternative set of single-electron energies.

Fig. 5: Transport processes relevant to the highest-power machines.

a Transport process between two reservoirs associated with a single-hole excitation. This type of processes lead to the activation of all the transfer edges in the state-transfer networks between the fully occupied state (i.e., the no-hole state) and the single-hole states. The blue and red reservoirs represent the cold and hot ones, respectively. b Transport processes between two reservoirs associated with two-hole excitations, which correspond to activated and inactivated state transitions, respectively. In the latter, the inactivation of the transitions originates from the energy mismatch in two-hole states due to the inevitable hole–hole interaction between two holes. Here, the white and black nodes represent the empty and occupied electron levels, respectively. The wavy lines indicate the interaction and the arrows represent the exchanges of electrons with reservoirs. Only a part of the transfer edges between single-hole states and double-hole states can be activated, where red (blue) edges correspond to activated (inactivated) edges. The fraction of the activated edges in the highest-power machines can asymptotically approach to the unity in the thermodynamic limit (see the figures in “Methods”).

The asymptotic Carnot efficiency at nonzero power

It has previously been argued that a Carnot engine at nonzero power accompanies divergent fluctuation of power in steady-state regimes^29,30 or under cyclic protocols at the criticality^31,32. Previous studies^31,32 have discussed the possibility of attaining the Carnot efficiency at the power output with superextensive scaling. In contrast, it is still worthwhile to note that the diverging power factor ${Q}_{\max }\propto {N}_{f}$ of the highest-power machines discussed in the previous section suggests a pathway to asymptotically realize the Carnot efficiency at (subextensive, yet) nonzero and stable power even under generic single-electron levels.

To this end, we note that the maximum-power machine found in the previous section can be used as a faithful engine as long as the mean power satisfies $P\propto {N}_{f}^{\zeta }$ with 1/2 < ζ < 1 because its fluctuation scales with a weaker exponent as $\delta P\propto \sqrt{\sigma }\propto \sqrt{{N}_{f}}$. The latter follows from the expression of the power P = Jδμ, the fluctuation-dissipation theorem δJ² = 2k_BTσ, and the fact that σ is the extensive quantity that linearly scales with N_f in the highest-power machines (see “Methods”); we note that the chemical potential difference δμ does not scale with N_f at the leading order.

As inferred from Eq. (4), the diverging Q and ZT of the highest-power engines then enable the asymptotic Carnot efficiency η(P) → η_C in the limit of N_f → ∞ with sustaining subextensive, but still stable power P ≫ δP. The price one must pay is precise control of the chemical potentials according to $\delta \mu =S\delta T(1-{N}_{f}^{\zeta -1})$, where we note that S is the intensive quantity $S\propto {N}_{f}^{0}$. Then, the scaling $P\propto {N}_{f}^{\zeta }$ follows from that of the power factor ${Q}_{\max }\propto {N}_{f}$ and the following linear-response formula

$$\frac{P}{Q}=4\frac{\delta \mu }{S\delta T}\left(1-\frac{\delta \mu }{S\delta T}\right)\propto {N}_{f}^{\zeta -1}.$$

(6)

The inset in Fig. 3b numerically indicates the scaling of the figure of merit ${ZT}=QT/\kappa \propto {N}_{f}^{1.31}$, leading to the vanishingly small thermal conductivity $\kappa \propto {N}_{f}^{-0.31}$. This disappearance of κ is indeed consistent with the asymptotic tight-coupling condition associated with the convergence to the unicyclic limit, which we have discussed in Eq. (5). Our consideration does not contradict with a known trade-off^33,34, such as P ≤ M(1 − η/η_C), since a constant M is diverging in the present case.

Several remarks are in order. Firstly, we remark that the above mechanism can in principle be applied to the noninteracting case if single-electron levels are perfectly degenerate⁷. Specifically, suppose that a system possesses N_f electron levels connected with the common two reservoirs, and it can operate as a heat engine owing to electrical current flowing between them. Then, the power factor Q of the corresponding heat engine can linearly scale with N_f provided that all the single-electron energies are degenerate in such a way that all the single-electron levels can equally contribute to the transport dynamics. In contrast, one of main contributions in the present work is to show the universality of this mechanism in a broad range of interacting systems beyond the restrictive noninteracting case. More specifically, we reveal the potential of harnessing many-body interactions to realize the asymptotic Carnot efficiency at nonzero power even under generic single-electron levels {ϵ_l}. Indeed, for any set of {ϵ_l}, we show that there exist an excessive number of the highest-power interacting machines satisfying the conditions (i)–(iii) above as appropriate for a variety of physical systems. In this respect, our finding mitigates the severe restriction in the noninteracting case, thus demonstrating great promise for utilizing many-body interactions to enhance thermodynamic performance.

Secondly, we note that our main conclusion, i.e., thermodynamic efficiency and power can in general be better in the presence of interaction, is qualitatively valid independent of a specific choice of single-electron levels (cf. Fig. 3a). That said, some quantitative feature, such as the scaling of the highest power with respect to system size, can still depend on those specifics. For instance, if one randomly samples single-electron energies from a fixed distribution, the power factor can scale linearly with system size ${Q}_{\max }=c{N}_{f}$ even in the absence of interaction. Especially, this implies that the above mechanism of attaining the asymptotic Carnot efficiency at subextensive power can be realized in the noninteracting case, if the figure of merit diverges sufficiently faster in the sense that ${ZT}/{N}_{f}^{1-\zeta }\to \infty$. The latter condition can in principle be met, e.g., when the fluctuation of single-electron energies is vanishingly small compared to the temperature. Nevertheless, in a general case of the nonzero fluctuation, the coefficient c in the power factor is still smaller than the optimal value in Eq. (5) (i.e., the optimal power is higher in interacting cases than the noninteracting counterpart), and the scaling of ZT with respect to system size is rather modest.

Possible experimental implementations

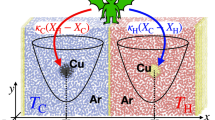
Our findings can be of experimental relevance to nanoscale heat engines described by the classical master equation. As a concrete realization, one may use semiconductor quantum dots embedded into an insulator weakly connected with metallic electrodes. An amorphous insulator (such as SiO₂) can be used for this purpose since it has low phonon conductivity and its high-potential barrier can block interdot electron hopping³⁵. Interaction strengths should be controlled by varying the dot distances. For typical experimental conditions, the temperature is 1–30 meV, quantum dots with nanometer size have interaction that is the order of 10–100 meV, and tunneling rates are ~10 GHz, which are well within the sequential regime. We note that a typical width δϵ of the single-electron levels due to size fluctuations is an order of 100 meV (ref. ⁵), corresponding to δϵ ~ 4k_BT at a room temperature for which the interaction enhancement is expected to be significant (cf. Fig. 3a). In practice, however, fluctuations may also exist in interaction parameters depending on controllability of dot configurations, which can in general degrade thermodynamic properties.

To implement the heat engine supplying the maximum power, we propose two specific examples of quantum dot arrays with nearest-neighbor interactions, as illustrated in Fig. 6. This type of systems might be engineered by applying manipulation capabilities of nanoporous molecular structures³⁶ or nanoparticles³⁷. The configurations in Fig. 6 can attain the conditions (i)–(iii) discussed above, and thus realize the highest-power heat engines (see “Methods”). More generally, a guiding principle of realizing the highest-power machine is to make interactions among low (high) single-electron levels strong (weak) to compensate energy differences and make hole excitations degenerate as much as possible. While it may in practice be challenging to achieve the ideal limit N_f → ∞, the proposed configurations can still attain high efficiency even at modest system sizes. For instance, assuming N_f = 20 and the scaling of power $P\propto {N}_{f}^{0.6}$, one can achieve the efficiency η/η_C ≃ 0.90 with controlling the chemical potential δμ at the level of ~8% accuracy of the stopping value SδT. We remark that a specific choice of dot configurations does not alter the results discussed here, as long as the corresponding interaction network among electron levels satisfies the conditions (i)–(iii) proposed above. For instance, while we envision that a two-level dot can be used to realize the interaction network in Fig. 6b, it can in principle be realized also by using only single-level dots.

Fig. 6: Designing the highest-power nanoscale heat engines with quantum dot arrays.

Illustrations of specific array configurations that can achieve the maximum-power heat engines. The single-electron energies are assumed to be equally spaced, i.e., ϵ_l = lΔ with Δ being energy spacing. a Each quantum dot (gray circles) has a single level and exchanges electrons (green arrows) with reservoirs at temperatures T_h,c (where h stands for hot, the red reservoir, and c stands for cold, the blue reservoir). Quantum dots are linearly aligned from the center in order of increasing energies ϵ_l with l = 1, 2, …, . Distances are controlled in such a way that nearest-neighbor interactions represented by u (wavy lines) progressively weaken with the distance from the center. The corresponding network topology of the interaction is also shown. b The leftmost dot has two levels, while the other dots have a single level and are linearly aligned in order of increasing energies. Distances are controlled in such a way that the interdot (nearest-neighbor) interaction between two leftmost dots is weak, while the other interactions progressively weaken as distance from the left. The corresponding network topology of the interaction is also shown.

Discussion

We formulated a machine learning framework to identify a set of the best nanoscale systems in terms of multiple objectives, and applied it to identify the best interacting nanothermoelectric systems. We found a class of the Pareto-optimal engines whose thermoelectric figure of merit and power factor can in principle be enhanced by orders of magnitudes in comparison with the noninteracting counterparts (see Fig. 2). We revealed the physical mechanisms underlying in a variety of the best heat engines and, in particular, proposed a designing principle to attain the asymptotic Carnot efficiency at subextensive, yet still finite and stable power. A possible experimental realization in quantum dot arrays is also proposed (cf. Fig. 6).

The identified physical mechanism to improve thermodynamic properties can be applied to other types of interacting thermal machines obeying the standard (classical) master equation¹⁶, as employed here. Such universality indicates the broad implications of our results; for instance, the developed framework for reinforcing network topology on discrete physical states can be applied to the multiobjective optimization problem in assembled biomolecules³⁸, chemical reactions³⁹, and photovoltaic devices⁴⁰. One can then maximize desired objective functions, e.g., mobility, reaction yield, and rectifications, while keeping a high thermodynamic efficiency.

We here put our work in broader contexts. Firstly, the mechanism of enhancing thermodynamic properties mentioned above is reminiscent of what has been discussed in the case of noninteracting systems⁷. There, the optimal heat engine can be realized when all the single-electron energies take the same value, i.e., the density of states becomes the delta function. The main contribution of the present work, however, is to point out the ubiquity of this mechanism in interacting systems under generic nondegenerate single-electron levels, in contrast to the perfectly degenerate levels required in noninteracting systems. Importantly, we propose concrete conditions for interaction to attain the enhancement as detailed below, and find that there exist an excessive number of interaction parameters to satisfy those conditions. Secondly, thermodynamic efficiency and power of nanoscale interacting systems have previously been discussed in refs. ^{12,17,18,19,20,21,22,23}. While these studies have focused on the case of all-to-all homogeneous two-body couplings, our study permits all the possible two-body interactions in the optimization process. Interestingly, the present machine learning framework reveals that the all-to-all homogeneous couplings are suboptimal in terms of both thermodynamic efficiency and power in general.

It still remains as an intriguing open question to include further complexities, such as nonlinear effects, time-reversal symmetry breaking, and quantum coherence^41,42,43,44 into the present analysis, and address whether they can be advantageous or detrimental in terms of thermodynamic efficiency and power. Genuine quantum many-body effects, e.g., the Kondo physics⁴⁵, require an explicit account of the entanglement between a system and reservoirs. Combining the present framework with efficient solvers of quantum many-body problems might thus bring insights into quantum thermodynamics. Also, it merits further study to explore possible nonreciprocity under asymmetric coupling strengths γ_h ≠ γ_c to different reservoirs. Finally, it is intriguing to analyze interacting nanothermoelectrics from a perspective of the scattering formalism.

Methods

Stochastic thermodynamics of nanothermoelectric heat engines

Here, we provide details about the master equation framework to describe the dynamics of nanothermoelectric heat engines discussed in the main text. We consider a many-body system governed by an interacting Hamiltonian

$$H=\sum _{l}({\epsilon }_{l}-{v}_{g}){n}_{l}+\frac{1}{2}\sum _{l\ne m}{w}_{lm}{n}_{l}{n}_{m},$$

(7)

where ϵ_l is single-particle energy of mode l = 1, 2, …, N_f, v_g is the ground voltage, and w_lm ≥ 0 denotes a two-body interaction between electrons occupying single-particle levels l and m. Corresponding to different sets of the occupation numbers n_l = 0, 1 (i.e., Fock states), there are ${2}^{{N}_{f}}$ states which we label by a, b, …. The system is connected to hot (h) and cold (c) reservoirs. We consider the dynamics that can be described by the master equation^12,14,16

$$\frac{{\mathrm{d}}{p}_{a}}{{\mathrm{d}}t} =\mathop{\sum}\limits _{b}{W}_{ab}{p}_{b},\ \ {W}_{ab}={{{\Gamma }}}_{ab}-{\delta }_{ab}\mathop{\sum}\limits _{d}{{{\Gamma }}}_{db},\\ {{\Gamma }} ={{{\Gamma }}}^{{\rm{h}}}+{{{\Gamma }}}^{{\rm{c}}},$$

(8)

where p_a denotes the probability distribution in the energy eigenbasis (i.e., the Fock basis), and W_ab is the ${2}^{{N}_{f}}\times {2}^{{N}_{f}}$ transition matrix. The elements of tunneling matrices Γ^h,c associated with two reservoirs are given by

$${{{\Gamma }}}_{ab}^{i} ={\gamma }_{i}f(\delta {s}_{ab}^{i}),\ \ f(x)=\frac{1}{1+{e}^{x}},\\ \delta {s}_{ab}^{i} =\frac{{E}_{a}-{E}_{b}}{{k}_{{\rm{B}}}{T}_{i}}+({N}_{a}-{N}_{b})\left(-\frac{{\mu }_{i}}{{k}_{{\rm{B}}}{T}_{i}}\right),$$

(9)

where f(x) is the Fermi distribution, $\delta {s}_{ab}^{i}$ describes the entropy production associated with the transition from state b to a via reservoir i = h, c, E_a is a many-body eigenenergy of the Hamiltonian (Eq. (7)) with respect to state a, N_a is the corresponding particle number, and μ_i and T_i are the chemical potential and temperature of reservoir i = h, c, respectively. We here assume that the tunneling rates are independent of energies, i.e., ${\gamma }_{{\rm{h}},{\rm{c}}}^{a}={\gamma }_{{\rm{h}},{\rm{c}}}$ for all a. In particular, we set γ ≡ γ_h = γ_c > 0 in all the results presented in the main text. For the sake of simplicity, we do not include transitions between eigenstates with the same particle number; such a transition can be relevant when the electron–phonon interaction becomes important^46,47. This assumption together with the fact that transport occurs due to single-electron tunnelings to reservoirs can uniquely fix the connectivity of the transition matrix W. We note that the master equation has a unique steady-state solution Wp^ss = 0, since the transfer matrix satisfies the ergodicity¹⁵.

The description based on the master Eq. (8) can be justified when (I) the Born–Markov approximation is valid and (II) the sequential limit is attained. The former condition can be satisfied when the system-bath coupling is sufficiently weak such that the backaction from the system on the bath can be ignored. More specifically, denoting the bath correlation time and the relaxation time due to the system-bath couplings as τ_bath and τ_rel, respectively, the condition (I) requires

$${\tau }_{{\rm{bath}}}\ll {\tau }_{{\rm{rel}}} \sim \frac{\delta }{{\gamma }^{2}},$$

(10)

where δ is a typical level spacing in the system Hamiltonian. The second condition (II) can be attained if γ is much smaller than the level spacing such that no quantum coherence is generated during the dynamics:

$$\gamma \ll \delta .$$

(11)

We note that the condition (Eq. (11)) automatically ensures the secular condition 1/δ ≪ τ_rel, that is, another requirement necessary to justify the use of the master equation in the Gorini–Kossakowski–Sudarshan–Lindblad form in general. In the present work, we always consider a temperature regime, in which the energy scale of the parameters in the system Hamiltonian (Eq. (7)) is an order of k_BT. Thus, typical level spacing between Fock states can be estimated as

$$\delta \sim {{\Delta }},{v}_{\mathrm{g}},w \sim O({k}_{{\rm{B}}}T),$$

(12)

where Δ characterizes the level spacing between single-electron energies. Thus, the condition (II) can be basically attained if

$$\gamma \ll {{\Delta }},{v}_{\mathrm{g}},w \sim O({k}_{{\rm{B}}}T).$$

(13)

For a sufficiently short τ_bath, this condition can also ensure the condition (I).

Two remarks are in order. First, it is essential to employ the so-called global approach^13,48,49 to the master equation (i.e., the explicit inclusion of the interaction term in the system Hamiltonian) in the present work because interaction parameters w can be an order of the detuning of single-electron energies. It is worthwhile to note that the crucial importance of using the global approach has recently been pointed out in a number of works especially in the context of its consistency with thermodynamics^13,48,49. Second, while our estimation on the level spacing δ above holds true for most of the Fock states, it might break down if a part of Fock states exhibit the degeneracy as found in, e.g., the case of the highest-power machines. Yet, the master equation description can be still justified because this degeneracy condition requires δ ≪ k_BT while, owing to the energy-scale separation γ ≪ k_BT, one can find sufficiently small γ such that

$$\gamma \ll \delta \ll {k}_{{\rm{B}}}T,$$

(14)

which recovers the condition (II).

To calculate the transport coefficients, we focus on the regime δT = T_h − T_c ≪ T_h and ∣δμ∣ = ∣μ_h − μ_c∣ ≪ k_BT_h, and denote T = T_h ≃ T_c. We set μ_c ≃ μ_h = 0 without loss of generality. The figure of merit ZT and the power factor Q are then given by the Onsager coefficients as

$${ZT} =\frac{\sigma {S}^{2}T}{\kappa }=\frac{{L}_{12}{L}_{21}}{\det ({\bf{L}})},\ \ Q=\sigma {S}^{2}=\frac{{L}_{12}^{2}}{{T}^{3}{L}_{11}},\\ \left(\begin{array}{l}{J}^{{\rm{h}}}\\ {J}_{q}^{{\rm{h}}}\end{array}\right) ={\bf{L}}\left(\begin{array}{l}\delta \mu /T\\ \delta T/{T}^{2}\end{array}\right),$$

(15)

where σ is the conductance, S is the Seebeck coefficient, κ is the thermal conductance, and L is the Onsager matrix. The charge and heat currents into the system from the hot reservoir are denoted by J^h and ${J}_{q}^{{\rm{h}}}$, respectively. The present system can operate as a heat engine when we set δμ < 0 if S > 0, while δμ > 0 if S < 0. We numerically obtain the Onsager coefficients (and thus ZT and Q accordingly) from Eq. (15) by calculating the steady currents ${({J}^{{\rm{ss}}},{J}_{q}^{{\rm{ss}}})}^{{\rm{T}}}$ for two different steady-state solutions corresponding to δT = 0, δμ ≠ 0 and δT ≠ 0, δμ = 0. The nonzero values of δT and δμ are kept sufficiently small in such a way that the linear-response theory is valid.

In the main text, we find that the power factor and the figure of merit of the highest-power machines scale as (see Fig. 3b in the main text):

$$Q=\sigma {S}^{2}\propto {N}_{f},\ \ \ \ \ {ZT}=\frac{\sigma {S}^{2}T}{\kappa }\propto {N}_{f}^{1.31}.$$

(16)

From these scalings together with the fact that the electrical conductance (the Seebeck coefficient) is the extensive (intensive) quantity, we obtain the scalings of transport coefficients as

$$\sigma \propto {N}_{f},\ \ \ S\propto {N}_{f}^{0},\ \ \ \kappa \propto {N}_{f}^{-0.31}.$$

(17)

The vanishingly small thermal conductance κ indicates the asymptotic realization of the tight-coupling condition J ∝ J_q as inferred by its definition

$$\kappa \equiv {\left(\frac{{J}_{q}}{\delta T}\right)}_{J = 0}.$$

(18)

We note that the disappearance of κ is indeed consistent with the asymptotic convergence of the power factor to the unicyclic value as indicated by Eq. (5) in the main text, since the unicyclic machine can automatically attain the tight-coupling condition.

Size scaling of the highest-power machines

We provide a simple size-scaling argument of the fraction of the activated transfer edges in the state-transfer network of the highest-power machines, which is briefly mentioned in the main text. The residual discrepancy between the power factor per level ${Q}_{\max }/{N}_{f}$ and the unicyclic value Q_uni (cf. Fig. 3b in the main text) originates from the imperfect activation of the transfer edges in the state-transfer network. To be concrete, we consider the highest-power machine shown in Fig. 6a in the main text, while the argument presented here remains valid for general types of the highest-power machines satisfying the conditions (i)–(iii) provided in the main text.

Firstly, in the sector between the fully occupied state and single-hole states, the condition (i) in the main text ensures the activation of all the transfer edges. Secondly, however, the inevitable hole–hole interaction leads to the imperfect activation in the next sector between single- and double-hole states. Among the total number N_f(N_f − 1) of transfer edges in this sector, a transition cannot be activated if it involves a double-hole state whose holes position at neighboring sites, and thus interact with each other. One can count the number of such double-hole states as N_f − 1 because of the nearest-neighbor-type interaction realized in the highest-power machine of interest here. This fact results in 2(N_f − 1) inactivated transfer edges. Thus, one can estimate the fraction f_1 − 2 of the activated transfer edges between single- and double-hole states as

$${f}_{1-2}=1-\frac{2}{{N}_{f}}.$$

(19)

This scaling exactly agrees with the numerical values extracted from the state-transfer networks of the highest-power machines shown in Fig. 4a–d in the main text (see Fig. 7). Importantly, in the thermodynamic limit N_f → ∞, this fraction converges to unity f_1 − 2 → 1 as realized in the unicyclic machine. The scaling argument presented here can be readily generalized to the activation fractions f_2 − 3, f_3 − 4, … in the other sectors, such as the sector between double-hole states and three-hole states, the one between three-hole states and four-hole states, and so on. In particular, they can also be shown to converge to unity in the thermodynamic limit. It is this asymptotically perfect activation of the transfer edges in the highest-power interacting machines that results in the convergence of the power factor per level to the unicyclic value, as indicated in Eq. (5) in the main text.

Fig. 7: Size scaling of the activated transfer edges in the highest-power machines.

The fraction f_1 − 2 of the activated transfer edges between single-hole states and double-hole states is plotted against the inverse of system size 1/N_f. Blue dots correspond to numerical values of f_1 − 2 extracted from the state-transfer network shown in Fig. 4a–d. Green dashed line indicates the analytical scaling f_1 − 2 = 1 − N_f/2.

Analysis of noninteracting machines

To obtain the results for the noninteracting case discussed in the main text, we consider the transport problem involving N_f multiple and nondegenerate single-electron levels. We emphasize that all the comparisons between the noninteracting results and the interacting ones presented in the main text are performed based on the same setting. In particular, we use exactly the same set of generic (nondegenerate) single-electron energies for both cases. Physically, such fluctuating single-electron energies are ubiquitous in a broad range of physical systems, such as solid-state devices and quantum dot arrays.

When there exists only one single-electron level N_f = 1, the optimal power factor corresponds to the ideal unicyclic value

$${Q}_{{\rm{uni}}}=\xi \frac{{k}_{{\rm{B}}}}{T}\frac{{\gamma }_{{\rm{h}}}{\gamma }_{{\rm{c}}}}{{\gamma }_{{\rm{h}}}+{\gamma }_{{\rm{c}}}},$$

(20)

where ξ ≃ 0.439. In the multilevel case, except the special situation that all the single-electron levels are perfectly degenerate, the power factor per level Q/N_f in noninteracting machines severely degrades from this ideal unicyclic limit Q_uni in general.

To determine the power-efficiency bound in a general case of multiple and nondegenerate single-electron levels, we firstly identify a set of the Pareto-optimal values of (Q, ZT) by performing the multiobjective optimization with using the ground voltage v_g as a variational parameter (see Fig. 8). For each pair of (Q, ZT), we next draw the lasso-type power-efficiency curve based on the linear-response formula (4). This procedure leads to a generation of a large number of the power-efficiency loops, as shown in the red curves (see Fig. 8). Finally, the power-efficiency bound is determined by numerically determining the envelope curve of these loops. At low power output, the resulting bound is consistent with the square-root scaling $\propto \sqrt{P}$, as shown by the black dotted curve (see Fig. 8). The power-efficiency bounds of the interacting cases shown in the main text are also obtained by following the similar procedures outlined above, while the scaling at the low power output is consistent with the linear one ∝ P in the interacting cases.

Fig. 8: Determination of the power-efficiency bound in the noninteracting machines.

a The Pareto-optimal values of (Q, ZT) pairs are determined from the multiobjective optimization. b For each pair of the optimal solutions of (Q, ZT) plotted in a, the lasso-type power-efficiency curve (red dotted curve) is drawn as indicated by the black dotted arrow. c Magnified plot of the power-efficiency bound at the low power output. Black dotted line indicates the envelope curve of the power-efficiency loops (red dotted curves), which agrees with the square-root scaling $\propto \sqrt{P}$. We use the multilevel setting with the number of single-electron levels N_f = 9 and generic (nondegenerate) single-electron levels. We set ϵ_l = lΔ with Δ/k_BT = 3, γ_h = γ_c ≡ γ, and plot Q in the unit of Q₀ = k_Bγ/T. The efficiency and power factor are normalized by η_C and Q₀.

Global optimization for the best heat engines

We here describe in detail the global optimization algorithm introduced in the main text, which is used to identify the best nanoscale heat engines. We start from finding the engine that achieves the maximum possible power factor. This has been done by using the differential evolution^10,11 to optimize the objective function Q with respect to the parameters ${\mathcal{W}}=\left\{{v}_{\mathrm{g}},{\{{w}_{lm}\}}_{l \,{> }\,m}\right\}$.

Specifically, we first randomly generate a population of N_pd-dimensional real-valued vectors $\{{{\mathcal{W}}}_{t = 0}^{i}\}$ with i = 1, 2, …, N_p. Here, d = 1 + N_f(N_f − 1)/2 is the number of variables in the present problem. At each iteration step t, we create a mutant vector ${{\mathcal{V}}}_{t}^{i}\in {{\Bbb{R}}}^{d}$ with i = 1, 2, …, N_p by

$${{\mathcal{V}}}_{t}^{i}={{\mathcal{W}}}_{t}^{k}+F({{\mathcal{W}}}_{t}^{l}-{{\mathcal{W}}}_{t}^{m})$$

(21)

where k, l, m ≠ i are mutually exclusive integers randomly chosen from [1, N_p], ${{\mathcal{W}}}_{t}^{k}$ is a vector sampled from the population at step t, and F > 0 is the scaling factor. We next prepare an offspring vector ${{\mathcal{X}}}_{t}^{i}\in {{\Bbb{R}}}^{d}$ by randomly choosing an integer k from [1, d] and then applying the following rule to each element of ${{\mathcal{X}}}_{t}^{i}$:

$${({{\mathcal{X}}}_{t}^{i})}_{j}=\left\{\begin{array}{ll}{({{\mathcal{V}}}_{t}^{i})}_{j}&{\rm{if}}\ j=k\ {\rm{or}}\ {{\rm{rand}}}_{i,j}[0,1]\le {C}_{r}\\ {({{\mathcal{W}}}_{t}^{i})}_{j}&{\rm{otherwise}}\end{array}\right.$$

(22)

where rand_i,j[0,1] denotes a randomly generated number from [0,1] for each pair of (i, j) and C_r > 0 is the crossover factor. We then update all the vectors $\{{{\mathcal{W}}}_{t}^{i}\}$ in the population according to the rule

$${{\mathcal{W}}}_{t+1}^{i}=\left\{\begin{array}{ll}{{\mathcal{X}}}_{t}^{i}&{\rm{if}}\ Q({{\mathcal{X}}}_{t}^{i})\ge Q({{\mathcal{W}}}_{t}^{i})\\ {{\mathcal{W}}}_{t}^{i}&{\rm{otherwise}}\end{array}\right.$$

(23)

To improve the convergence, we restrict the search space by setting the lower and upper bounds on the parameters as $0 \, \le \, {w}_{lm} \, \le \, {w}_{\max }$ and $-{v}_{\max } \, \le \, {v}_{g} \,\le \,{v}_{\max }$; we set ${w}_{\max }={v}_{\max }=50{k}_{{\rm{B}}}T$ for all the results provided in the main text. The population number N_p is set to be N_p = 2d. We find it useful to implement the heuristics proposed in ref. ⁵⁰, where the scaling factor and the crossover factor (F, C_r) are chosen uniformly at random from three choices (1, 0.1), (1, 0.9) and (0.8, 0.2) at each iteration. The choice of (1, 0.9) leads to large perturbations on the donor vectors and thus expedites the exploration of the search space, while the other two choices expedite the exploitation of the search space. In this way, we can find the optimal parameters ${{\mathcal{W}}}_{Q}^{* }$ for the highest-power heat engine, which provides an unambiguous element of the Pareto-optimal solutions³. It thus allows us to determine the Pareto front on the Q-ZT plane by starting the search of the front with setting ${{\mathcal{W}}}_{Q}^{* }$ to be the initial point.

Nonconvex landscape and the failure of the local algorithms

The search of the Pareto front has been performed based on the standard alternate search algorithm⁵¹. Specifically, at the initialization stage, the algorithm randomly samples the values of both Q and ZT around a given input of the parameters for the initial thermal machine. In practice, to improve the optimization performance, it is advantageous to use an unambiguous element of the Pareto-optimal solutions as the initial search point. We found that the machine with the parameters ${{\mathcal{W}}}_{Q}^{* }$ achieving the highest Q, which is identified after the first step of the optimization process outlined above, is the most legitimate choice in this respect. In contrast, if one starts the search of the Pareto front from random initial values, the performance of the optimization can be degraded.

After generating the samples, the algorithm next defines the feasible parameter region for searching the Pareto-optimal solutions. Specifically, the algorithm creates a list of previously evaluated nondominated points in the samples, which are the points with (at least) one of Q and ZT being strictly better than that of the other evaluated points. At each iteration, the algorithm uses this list of the nondominated points and the corresponding neighbors as the feasible parameter region to choose the next evaluation point. If the newly evaluated point dominates some of the previous nondominated points, i.e., if both of Q and ZT of the newly evaluated point are no worse than some of the previous nondominated points and at least one of them is strictly better, the algorithm accepts the newly evaluated point as a new member of the list for the feasible parameter region, while eliminates the dominated previous points from the list. Thus, the multiobjective algorithm is based on this alternate search of the feasible parameter region and the higher values of the objective functions Q and ZT. In particular, one may summarize the iterative update outlined above as follows:

$${{\mathcal{W}}}_{t+1}^{i}\ \ =\ \ \left\{\begin{array}{ll}{{\mathcal{X}}}_{t}^{i}&{\rm{if}}\ (Q({{\mathcal{X}}}_{t}^{i}),{ZT}({{\mathcal{X}}}_{t}^{i}))\succ \left(Q({{\mathcal{W}}}_{t}^{i},{ZT}({{\mathcal{W}}}_{t}^{i}))\right.\\ {{\mathcal{W}}}_{t}^{i}&{\rm{otherwise}}\end{array}\right.$$

(24)

where we recall that the symbol ≻ indicates that (Q, ZT) values for the newly evaluated machine ${{\mathcal{W}}}_{t+1}^{i}$ dominates a previous member ${{\mathcal{X}}}_{t}^{i}$ in the list, i.e., both of Q and ZT for ${{\mathcal{W}}}_{t+1}^{i}$ are no worse than those for ${{\mathcal{X}}}_{t}^{i}$, while at least one of them for ${{\mathcal{W}}}_{t+1}^{i}$ is strictly better than the corresponding value for ${{\mathcal{X}}}_{t}^{i}$. Importantly, it has been theoretically proved that this algorithm is guaranteed to converge to points close to the correct Pareto-optimal solutions after performing a sufficiently large number of iterations⁵¹.

Finally, to obtain the Pareto front on the power-efficiency plane, we generate a large number of loops according to the linear-response formula (Eq. (4)) with substituting the values of (Q^*, ZT^*) for the Pareto-optimal solutions into it. The envelope curve of these loops provide the Pareto front on the P–η plane (see, for example, Fig. 2e in the main text and also Fig. 8).

Full training for the interacting case with the largest system size has been done by running the algorithm within ~3 days on a single 24-core CPU machine. Most of the time is spent on the diagonalization of the transition matrix to evaluate the fitness values of machines in a large population at each iteration. Thus, the exponential computational cost for the matrix diagonalization currently limits the available number of single-particle levels N_f. A reduction of computational times could be made possible by applying the efficient solvers of many-body problems^52,53 or by parallelizing the code over large-core CPU + GPU machines.

When the optimization landscape is smooth and local traps therein are negligible, the greedy algorithms should be the primary choice since they can usually reach to the global optimum with faster convergence rate than that for the global (derivative-free) algorithms. We here briefly mention the difficulties of applying such greedy (gradient-based) optimization algorithms to identify the best interacting nanoscale heat engines. To demonstrate this, we show typical training processes in optimizing the minus of the power factor, −Q, see Fig. 9. The result is presented for a small system size with ${2}^{{N}_{f}}=16$ states. We here apply three standard local optimization algorithms: the sequential quadratic programming (green)⁵⁴, the quasi-Newton method (black)⁵⁵, and the interior-point algorithm (red)⁵⁶. As inferred from the figure, all of three greedy algorithms overwhelmingly fail to identify the global-optimum solution and are easily trapped by the local optima. For instance, through the training processes shown, the value of the suboptimal power factor reached by the greedy algorithms is almost the same as in that of the best power factor achieved by the noninteracting engine (see, e.g., Fig. 2f in the main text). This observation can be understood from the fact that the suboptimal engines are able to activate only a very few number (one or two) of transfer edges in the state-transfer network (cf. Fig. 2a, d in the main text), resulting in low (yet locally optimal) values of the power factor.

Fig. 9: Visualization of the nonconvex landscape and the failure of the greedy algorithms.

a The optimization surface of (minus) the power factor −Q around the global-optimum solution ${{\mathcal{W}}}_{Q}^{* }$ positioned at the center. We here project the high-dimensional optimization landscape onto the two-dimensional surface based on the approach used in ref. ⁵⁷. b The convergence behavior of the optimization of the objective function −Q for the sequential quadratic programming (SQP; green), the quasi-Newton method (black), the interior-point algorithm (red), and the differential evolution (blue). The parameters are N_f = 4, ϵ_l = lΔ with Δ/k_BT = 3, γ_h = γ_c ≡ γ, and we plot the power factor in the unit of k_Bγ/T. Here, N_f is the number of single-electron levels, Δ is the energy spacing, and γ_h,c represent the hopping rates to the hot and cold reservoirs.

Numerical evidence of the failure of the greedy algorithms indicates the presence of a large number of proliferated local optima in the nonconvex landscape of the search space. To demonstrate this more explicitly, we visualize the optimization landscape based on the approach previously applied to the problem of optimizing the deep neural network⁵⁷. Specifically, we randomly choose vectors $\phi ,\psi \in {{\Bbb{R}}}^{d}$ with d = 1 + N_f(N_f − 1)/2 and project the landscape onto the two-dimensional surface via introducing the objective

$$L(\alpha ,\beta )=Q({{\mathcal{W}}}_{Q}^{* }+\alpha \phi +\beta \psi ),$$

(25)

where ${{\mathcal{W}}}_{Q}^{* }$ is the global-optimum solution and α, β are real parameters. Figure 9a shows a typical example of the obtained two-dimensional projected optimization landscape. It exhibits the dramatic nonconvexities and, in many regions, the surface gradients do not point toward the global optimum positioned at the center. Thus, most trials of the greedy algorithms to find the global optimum converge to local traps in the landscape. It is this complex nature of the optimization landscape that leads to the failure of the greedy (gradient-based) algorithms as demonstrated in Fig. 9b. In contrast, the differential evolution (detailed in the previous section) is known as one of the most powerful approaches to find the global solution in the high-dimensional nonconvex landscape¹¹, and has indeed been able to find the globally optimal power factor (see the blue line in Fig. 9b).

We finally mention the difficulty of applying the brute-force search to the present problem. Since the brute-force approach requires the search over all the possible patterns of the interaction network, one has to discretize the range of each continuous parameter in ${\mathcal{W}}$ with a total amount L_dis of bins. Thus, the resulting number of the required trials becomes exponentially large, i.e., it scales as $\propto {({L}_{{\rm{dis}}})}^{d}$ with d = N_f(N_f − 1)/2 + 1. Since the computational cost for each trial also grows exponentially with N_f due to the need of diagonalizing the transition matrix W, the brute-force search leads to the double-exponential growth of the numerical cost as increasing the system size. We note that the resulting solutions may still not reach the global optimum since the search is (by nature) nonexhaustive due to the discretization of the continuous parameters.

Details of the parameters for the asymptotic Carnot engines at nonzero power

We here mention the concrete examples of the interaction parameters appropriate for realizing the highest-power heat engines discussed in the main text. They can asymptotically achieve the Carnot efficiency at nonzero and stable power in the thermodynamic limit N_f → ∞, owing to the diverging power factor Q. Firstly, as the parameters appropriate for the one-dimensional chain configuration with single-particle energies ϵ_l = lΔ (cf. Fig. 5a in the main text), one may use

$${w}_{12}=2\left[\frac{{N}_{f}+1}{4}\right]{{\Delta }},$$

(26)

$${w}_{l,l+2}=\left(\left\lceil\frac{{N}_{f}-1}{2}\right\rceil-\left[\frac{l}{2}\right]\right){{\Delta }}\ \ \ {\rm{for}}\ \ \ l=1,2,5,6,\ldots ,$$

(27)

$${w}_{l,l+2}={w}_{12}-2\left\lceil\frac{l}{4}\right\rceil{{\Delta }}\ \ \ {\rm{for}}\ \ \ l=3,4,7,8,\ldots ,$$

(28)

and set the other interaction parameters to be zero. Here, [⋅] is the Gauss symbol and ⌈⋅⌉ is the ceiling function. Secondly, as the parameters appropriate for the semi-infinite chain configuration (cf. Fig. 6b in the main text), one may use

$${w}_{23}=\frac{\lceil3{N}_{f}/2\rceil-6}{2}{{\Delta }},\ \ {w}_{12}\ -\ {{\Delta }}\ =\ {w}_{13}=\frac{[{N}_{f}/2]{{\Delta }}}{2},$$

(29)

$${w}_{14}=(\lceil{N}_{f}/2\rceil-2){{\Delta }},$$

(30)

$${w}_{l,l+1}=\left[\frac{{N}_{f}-l}{2}\right]{{\Delta }}\ \ \ {\rm{for}}\ \ \ l=4,5,\ldots .$$

(31)

One can check that these two sets of the parameters satisfy the optimality conditions for the maximum-power engines (proposed in the main text), which include (i) single-hole excitation energies are degenerate and (ii) the number of nonzero parameters in ${\{{w}_{lm}\}}_{l \,{> }\,m}$ is minimal. Figure 10 illustrates further concrete examples of realizations of the Pareto-optimal machines in interacting regimes.

Fig. 10: Graphical representations of the optimal configurations.

Panels a–c correspond to concrete examples of realizations of the Pareto-optimal interacting machines identified in Fig. 2a–c, where ϵ_l is a (nondegenerate) single-electron energy of lth level considered in Fig. 2. A wave line between quantum dots indicates the presence of interaction between them. The width of the wave line shows the interaction strength.