Abstract
In photoacoustic (PA) imaging, time domain reconstruction techniques are the current gold standard for image formation. While these techniques provide high-resolution spatial maps of optical absorption, they neglect the structural information encoded in the frequency domain of the broadband PA signals. In this work, we introduce a frequency domain technique for PA image formation, termed F-Mode. By leveraging information contained in the frequency content of PA signals, F-Mode can be used to generate images with scale-specific contrast. To demonstrate the robustness of our technique, we apply F-Mode to datasets acquired using both PA tomography and PA microscopy systems, utilizing linear array and single-element transducers with central frequencies ranging from 40–400 MHz. Here we show that the technique can be used to: differentiate between vessels and microspheres of different size in phantoms, enhance visualization of organelles in cultured cells, and selectively display single blood vessels in vivo in zebrafish larvae.
Similar content being viewed by others
Introduction
Since its discovery by Alexander Graham Bell late in the nineteenth century1, the photoacoustic (PA) effect has found many applications in fields ranging from spectroscopy2, to non-destructive testing3, and most recently, biomedicine4,5,6,7. The endogenous absorption of abundant biomolecules—including hemoglobin, melanin, and DNA—has enabled label-free imaging of complex biological structures ranging from nanometers to centimeters in scale. At opposite ends of this spectrum are the techniques of photoacoustic microscopy (PAM), which offers sub-cellular resolution that facilitates imaging of individual organelles including cell nuclei, melanosomes, and mitochondria8,9,10; and photoacoustic tomography (PAT), which is capable of non-invasive in vivo imaging of mouse organs11,12, as well as human breast13,14 and skin cancers15.
The emission of a PA wave from an object occurs subsequent to optical excitation and non-radiative relaxation. After emission, PA waves are analogous to the mechanical waves employed in ultrasound (US) imaging. As such, there are numerous similarities between the two imaging techniques; including the use of ultrasonic transducers for the conversion of mechanical waves to electrical signals (henceforth referred to as radiofrequency-lines, or RF-Lines), and the algorithms used for image reconstruction. In addition to conventional US image reconstruction techniques (for example: B-Mode and M-Mode), the maximum amplitude projection (MAP) technique is widely used in PA imaging, especially in PAM. As the name implies, in MAP, the maximum value of the envelope of the RF-Line acquired at each spatial location is projected onto a two-dimensional (2D) space for image formation. This technique produces striking spatial maps of chromophore distribution, but due to the nature of MAP, contains no information in the axial direction.
The aforementioned image reconstruction techniques are implemented in the time domain, and are heavily dependent upon the characteristics of the system and transducer used for acoustic detection. Convolution of the emitted PA wave with the transducer impulse response causes distortion of the temporal profile in the resultant RF-Line due to the finite transducer bandwidth. This decreases the sensitivity to slight variations in absorber size and shape, and presents a challenge when attempting to differentiate structures with comparable morphology. However, these variations in morphology, which would otherwise be undetectable in the time domain, are readily detected using spectral features in the frequency domain representation of the recorded PA signals16,17. It has been demonstrated that this frequency encoded information readily lends itself to quantitative analysis techniques10,18. In particular, analysis of the power spectrum of acquired RF data at ultra-high frequencies (>100 MHz) has enabled studies of the size and shape of both inorganic19,20,21 and biological18,22,23 samples. Quantitative frequency domain analysis of PA signals acquired at lower ultrasonic frequencies (<100 MHz) has been used for monitoring tumor response to cancer therapy24 and assessing red blood cell aggregation25. Aside from quantitative PA signal analysis, techniques that leverage changes to the frequency content of emitted PA signals can be used as in Doppler to enable measurement of transverse blood flow velocity in the microvasculature of the mouse ear26, and in second harmonic PA imaging to enhance image resolution via tissue-specific nonlinear changes in thermal diffusivity27.
We hypothesized that these unique spectral signatures could be further leveraged for frequency-based image reconstruction, analogous to the parametric images used for defect detection in scanning acoustic microscopy28. By appropriately subdividing the power spectra of the RF data into bands, spectral features within the divisions can be isolated and used as a mechanism for generating image contrast. Displaying the contents of one such band at each location in the scan dataset results in images that are highly sensitive to small deviations in object size and shape. Furthermore, due to the inherently broadband nature of photoacoustic signals, rich contrast can be achieved over many length scales. Adopting the nomenclature from traditional US techniques, we have termed these images ʻfrequency-modeʼ or F-Mode images. The segmentation and enhancement of features of different scale for disease diagnosis and treatment planning is of great importance in medical imaging. In particular, emphasis has been placed on the development of techniques for selective enhancement of blood vessels of various scale29,30,31, with clinical applications in ophthalmology and neurosurgery32. While selective enhancement of vessels has been investigated extensively for imaging modalities such as Magnetic Resonance Imaging (MRI) and angiography29,33, only a few segmentation techniques for vessel enhancement in PA images have been proposed34,35,36. Here we introduce the F-Mode technique and use it to selectively visualize structures of different scale in image datasets acquired using both PAT and PAM imaging systems. We show the robustness of F-Mode over a wide range of transducer configurations and central frequencies, ranging from pre-clinical linear array transducers (40 MHz) to ultra-high-frequency single-element transducers (400 MHz). We then demonstrate the ability of the technique to selectively isolate structures spanning orders of magnitude difference in scale, including: macrovasculature mimicking vessels in a phantom, individual organelles in cultured biological cells, and perfused blood vessels in a live zebrafish larva.
Results
Description of the F-Mode technique
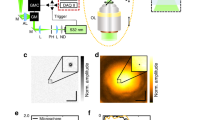
In this section we detail the steps required for the generation of F-Mode images. For the case of systems which utilize single-element transducers (such as those commonly employed in PAM), the F-Mode technique outlined in this section can be applied directly to the raw data acquired by the system. For setups which utilize multi-element array transducers, such as those commonly used in PAT, the raw data must first be reconstructed into a three-dimensional (3D) dataset via beamforming (e.g., using a delay-and-sum beamforming algorithm) and then the F-Mode technique can be applied to the reconstructed data. A diagrammatic overview of the technique is provided in Fig. 1. First, each RF-line of length l in a three-dimensional PA dataset of size l × m × n is converted to its frequency domain representation via the fast Fourier transform (FFT). The number of points, \(K \in {\Bbb N}\), in the FFT is set to be:
where fs is the system sampling frequency, and Δf is the desired resolution of the resultant frequency domain spectrum. The corresponding power spectra are then computed and partitioned into Q discrete frequency bands with length equal to an integer multiple of Δf. The total power in each band is then calculated via summation, and stored in a vector of length Q.
An overview of the F-Mode technique. Photoacoustic (PA) waves are generated from two spherical structures due to laser absorption and subsequent non-radiative relaxation. The PA response waveform is dependent upon both the size and shape of the absorbing structure. Here, the blue waveform is from the large sphere and the red waveform is from the small sphere. Recorded time domain RF-signals can be used directly to create a maximum amplitude projection (MAP) image; however, if the strength of the PA response from both objects is similar, the objects in the resultant image will have similar intensity. In the F-Mode technique, the power spectrum of each RF signal is computed and divided into discrete frequency bands of uniform spectral width. The effect of structure size and shape is more prominent in the frequency domain representation of the PA wave, which leads to unique features in the power spectra. The power within each band is added at each spatial coordinate and stored in an array, preserving spatial organization. Each row in the array can then be used to form an independent F-Mode image. Depending on the spectral features in the selected frequency band, objects of certain size will exhibit enhanced contrast in some bands, while being nearly indistinguishable from the background in others
Applying this algorithm to each RF-line in the dataset results in a new array of size Q × m × n, which can be thought of as a stack of Q distinct F-Mode images, each of size m × n. The intensity of a given pixel in an F-Mode image is determined by the relative magnitude of its summed power in relation to all other pixels within the same band. For this reason, each F-Mode image has a unique dynamic range, with signal to noise ratio (SNR) robust to large changes in transducer sensitivity. In each F-Mode image, pixels from an object which exhibit minima in a selected frequency band may be indistinguishable from the background, effectively concealing the object while greatly enhancing the visibility of the objects that remain. However, due to the oscillating power spectra (Fig. 1), these same pixels may contain the highest summed power in a different frequency band, and hence will be the brightest pixels in the corresponding F-Mode image. The contrast of a pixel within a given object is thus constantly changing with respect to pixels from other objects. Animations created from the entire F-Mode image stack provide visual displays of the local power as a function of frequency (Supplementary Movie 1) and can be used to display the size-specific contrast dynamically.
F-Mode imaging in photoacoustic tomography
To demonstrate proof-of-concept for our F-Mode technique, we imaged a gelatin phantom containing cylindrical, ink-filled vessels with a commercial PAT system equipped with a 40 MHz central frequency linear array transducer. Vessel diameters of approximately 150, 200, and 250 µm were chosen to mimic the sizes of subcutaneous small arteries in humans37. Assessment of sub-millimeter changes in vessel diameter is an important indicator of diseases including hypertension, which is associated with a reduction in lumen diameter; in some cases on the order of 100 µm37.
The MAP image from the time domain RF data is shown in Fig. 2a, and depicts the 250, 200, and 150 µm vessels from top to bottom, respectively. Despite the fact that the lateral resolution of the commercial system is 120 µm38, it is difficult to ascertain relative vessel size from the MAP image alone. A B-Mode image of the phantom is shown in Fig. 2b, with the 250 µm vessel situated on the left side of the image. B-Mode sacrifices information in the scanning direction to provide an indication of relative vessel diameter in the axial direction. However, accompanying this is a misrepresentation of the vessel cross-sectional area due to beamforming artifacts introduced as a result of the poor lateral resolution beyond the transducer’s acoustic focus, and the limited-view geometry of the linear array transducer39,40. Thus, while both MAP and B-Mode techniques are capable of resolving complementary structural aspects of the vessels, neither provides satisfactory indication of all information concurrently.
Demonstration of F-Mode on a gelatin vessel phantom imaged with a 40 MHz linear array transducer. a Maximum amplitude projection (MAP) image. The vessels have diameters of 250, 200, and 150 µm, from top to bottom, respectively. The vertical and horizontal scale bars are both 2 mm. b A photoacoustic B-Mode image showing a cross-sectional view of the vessels through the center of a. The 250 µm vessel is to the leftmost side of the image, and the 150 µm vessel is to the rightmost side. c The averaged F-Mode power spectra from a region of interest within each vessel. There is a clear distinction between the vessel power spectra due to the change in vessel diameter. Each shape overlaid on the power spectra corresponds to a frequency band which was used to generate an F-Mode image. d–i F-Mode images depicting different permutations of the vessels. Images d–f show individual vessels, while images g–i show two vessels and exclude the third. The vertical and horizontal scale bars in a are applicable to all F-Mode images
A representative power spectrum from each vessel is shown in Fig. 2c. Comparing the three graphs, the location and number of spectral features (i.e., the spacing between adjacent minima) increases with decreasing vessel diameter. This finding is consistent with theoretical solutions of the PA wave equation for cylindrical absorbers19. The frequency bands used to generate the F-Mode images shown in Fig. 2d–i are denoted by symbols in Fig. 2c. An F-Mode animation demonstrating the dynamic transition in image appearance between frequency bands is provided in Supplementary Movie 2.
If each vessel is regarded as being in either a ‘visible’ or ‘non-visible’ state, there are eight possible combinations of vessels which can be depicted in an F-Mode image. Here we ignore the cases in which all vessels are visible (as in the MAP image) and all vessels are non-visible (no detected PA signal). The remaining images demonstrate the capability of F-Mode to specifically target vessels of different size, or combinations thereof. In Fig. 2d–f only one of the three vessels is in the visible state. This occurs when a frequency band contains a local maximum for one vessel and local minima for the other two. In Fig. 2g–i, two of the vessels are visible, while the spectral power of the third is comparable to the background and thus too low for its visualization. In all F-Mode images it was observed that as the frequency increased, the apparent width of the vessels decreased. This was expected, as in an acoustic resolution PAT system such as the VevoLAZR, the frequency response of the transducer determines the spatial resolution of the images, with finer resolution occurring at higher acoustic frequencies41.
The results of this section demonstrate the capacity of the F-Mode technique for generating images which contain information both in the plane orthogonal to the transducer central axis (as in MAP) and in the axial direction (as in B-Mode). As the diameter of vessels in the body can vary significantly with vessel subtype (e.g., arteries, arterioles, and capillaries), we envision that the diameter specific selective isolation demonstrated here could be useful when visualizing PA data acquired from complex biological systems containing vessels with characteristically different sizes, such as the chaotic vasculature of tumors42, or the plexus of vessels in the mouse brain43.
F-Mode imaging in photoacoustic microscopy
As in PAT, the axial resolution of PAM is determined solely by the properties of the acoustic transducer used for signal acquisition, and becomes finer with increasing transducer bandwidth44. For this reason, transducers with high central frequency and large bandwidths are highly desirable and are employed in PAM experiments which require sub-cellular resolution10. Furthermore, since the number of observable spectral features increases directly with increased transducer bandwidth, the broadband RF data acquired by ultra-high-frequency PAM systems readily lends itself to F-Mode analysis.
To demonstrate the robustness of our F-Mode technique with respect to both transducer configuration and frequency response, we scanned two samples with a modular PA microscope. Our PAM system allows the user to easily alternate between different transducers (frequency range 80–1200 MHz), optical objectives (from 4–40x), and laser sources (covering the UV–VIS–IR range). Additional system details can be found in ref. 22.
F-Mode imaging of polystyrene microspheres
We first tested our F-Mode technique by acquiring a scan of an agarose phantom containing two populations of black polystyrene microspheres (diameters of 6 and 10 µm) as shown in Fig. 3a. For this experiment, the modular PAM setup was comprised of a 400 MHz transducer, 10x optical objective, and a 532 nm Nd:YAG laser. A MAP image formed from the acquired RF data is shown in Fig. 3b. Representative power spectra from a 6 and 10 µm sphere are shown in Fig. 3c. At approximately 326 MHz, the summed power is equal for both spheres, with the 6 µm sphere dominating at lower frequencies and the 10 µm sphere dominating at higher frequencies. F-Mode images were formed using the spectral bands which demonstrated the relative greatest contrast for each sphere. The identified bands are indicated with vertical lines in Fig. 3c. The corresponding F-Mode images are shown in Fig. 3d, e.
Scale-specific visualization of polystyrene beads using F-Mode. a Optical micrograph of an agarose phantom containing black polystyrene beads with diameters of 6 and 10 µm. The scale bar is 10 µm. b Maximum amplitude projection (MAP) image of the beads acquired with a 400 MHz single-element transducer. c Averaged photoacoustic power spectrum of a 10 µm (blue) and 6 µm (orange) bead. The vertical dashed lines correspond to the frequency bands which were used to generate F-Mode images d and e. d, e F-Mode image formed using the 257 and 445 MHz frequency bands, respectively. In d, only the 6 µm beads are visible, while only the 10 µm beads can be seen in e. The scale bar in b is applicable to both F-Mode images
In Fig. 3d only the 6 µm spheres were visible, while in Fig. 3e this trend is reversed, with only the 10 µm spheres being visible. In addition, the 10 µm spheres in Fig. 3e appear to have a distinct patterning which was observed to change as a function of spectral band (Supplementary Movie 3). By synchronizing the playback of F-Mode movies of individual spheres of different diameter as a function of ka (where k is the wavenumber corresponding to the acoustic frequency of the band, and a is the radius of the microsphere) it can be shown that the patterning exhibited by the spheres is identical for both bead sizes (Supplementary Movie 4). Unlike the other samples examined in this study, the microspheres are solid and thus support transverse acoustic waves which can be accounted for when considering homogeneous illumination of the micropshere45. It is our hypothesis that the tight optical focusing of the objective results in an inhomogeneous heating profile in the microsphere, causing it to deviate from the monopole expansion predicted by theory, and support the propagation of surface waves. Specifically, we believe that the spatial patterns observed in F-Mode arise due to resonant modes excited on the surface of the spheres, as has been demonstrated for the case of US backscatter46,47. Preliminary investigations on individual beads (data not shown) for the same system setup with broad optical illumination support these assertions, and elucidation of the physics underlying these observations will be the focus of future work. To our knowledge this is the first time that a relationship between acoustic wavenumber and PA image appearance has been observed for solid microspheres, and opens up avenues for investigating fundamental behavior of surface waves and resonances with PAM.
In vitro imaging of unstained CAKI-2 cells
Biological cells grown in culture are widely used in the study of drug efficacy, genome modification, and development of theranostic agents48. Adherent cells tend to have a ʽfried-eggʼ appearance; with an increased thickness near the nucleus that tapers toward the cell periphery49,50. Traditional optical microscopy is the gold standard for 2D cell imaging; however, without the use of specialized techniques like confocal microscopy51, Raman Imaging52, or scanning acoustic microscopy53, no indication of cell thickness is typically obtained.
Here we demonstrate the sensitivity of F-Mode to micron-size structures and changes in the topology of cultured cells. The modular PA microscope, equipped with a 200 MHz transducer and a 266 nm Nd:YAG laser, was used to scan a population of unstained CAKI-2 renal carcinoma cells. In the deep-UV optical regime (<300 nm), the endogenous absorption of cells increases drastically due to the high extinction coefficient of amino acids (primarily tryptophan, tyrosine, phenylalanine) and nucleic acids54. This has previously enabled high resolution label-free imaging of single cells in both deep-UV microscopy55,56, and deep-UV PAM57 studies. A representative brightfield image of an unstained CAKI-2 cell is shown in Fig. 4a. The frequency response of our 200 MHz transducer is shown in Fig. 4b, and a PA MAP image of the CAKI-2 cell from Fig. 4a is shown in Fig. 4c. The cell appears homogenous in the MAP image except for the non-absorbing vesicles and the strongly absorbing nucleoli (denoted by arrows 1 and 2 in Fig. 4a, respectively). The MAP image representation agrees well with results obtained in deep-UV microscopy studies by Cheung et al.55,56. The authors observed uniform absorption throughout a majority of the cell at 260 nm due to uniform protein concentration in the cell cytoplasm and nucleus. The increased PA signal observed in the nucleoli in Fig. 4c is consistent with previous microspectroscopy studies reporting increased absorption in the nucleoli compared to the remainder of the nucleus58, and can be attributed to an increase in both the nucleic acid and protein content55,56.
Application of F-Mode to enhance visualization of structure in cultured biological cells. a Optical micrograph of CAKI-2 renal carcinoma cells grown on a UV fused silica substrate. Arrows indicate features which are accentuated in F-Mode images. b Frequency response of the 200 MHz transducer used to scan the sample. The vertical dashed lines with markers correspond to bands used to create F-Mode images. The difference in transducer sensitivity between the central frequency and each band exceeds 20 dB. c Label-free maximum amplitude projection image of the cells acquired with a 266 nm Nd:YAG laser. The strongest signal is from the cell nucleoli, with relatively homogeneous intensity throughout the remainder of the cell. The scale bar is 10 µm. d–f F-Mode images generated using the 90.5, 390.5, and 490.5 MHz frequency bands, respectively. In d, the cell appears uniform with prominent dark vesicles. In e, the periphery of both cells is accentuated, with a dark region in the center of the cells. Finally, in f only the nucleoli are apparent. The scale bar in c can be applied to all F-Mode images
The vertical dashed lines shown in Fig. 4b indicate the bands used for F-Mode image generation. It should be noted that for each selected frequency band, the sensitivity of the transducer was more than 20 dB lower than the sensitivity at the transducer’s central frequency. Despite this, high SNR was observed in all F-Mode images (Fig. 4d–f). Compared to the MAP image, the F-Mode image from the frequency band centered at 90.5 MHz has a uniform distribution of intensities within the cell; the weakly absorbing vacuoles (denoted by the arrow) providing the dominant source of PA contrast in the cell interior. In comparison, the F-Mode image generated from the band centered at 390.5 MHz (Fig. 4e) portrays a dark central region with a bright outer rim and good visualization of the nucleoli (arrows 2 and 3). We hypothesize that this contrast is due to increased thickness at the cell interior, where the nucleus and a majority of the other organelles are located49. Such topography would result in a significant difference in the summed spectral power in the central region of the cell, relative to the thin cell periphery and nucleoli. Finally, in the F-Mode image generated from the 490.5 MHz band, only the two nucleoli of the central cell are depicted (Fig. 4f). The prominence of the nucleoli in this band is most likely due to a combination of two factors: the strong PA signal generated by the nucleoli, and the increased spectral power density for micron-sized structures such as nucleoli at high frequencies10, which maximizes the F-Mode contrast relative to the rest of the cell.
The results of this section demonstrate the feasibility of translating the F-Mode technique to biological samples, enabling enhanced visualization of individual organelles. Furthermore, to our knowledge, this is the first time individual nucleoli have been clearly visualized with label-free PAM. In the future, we hope to use this technique to investigate the sequestering and aggregation of contrast agents, e.g., nanoparticles and porphyrin liposomes, within cultured cells.
In vivo imaging of zebrafish larvae
To demonstrate the feasibility of translating the F-Mode technique to in vivo models, we imaged the vasculature of a 5 day-post fertilization (dpf) zebrafish larvae. Owing to their low cost, ease of care, and large colony size, zebrafish are rapidly gaining popularity as biological models for drug discovery59 and the study of disease modeling60. Furthermore, early in their developmental stages wild type zebrafish larvae have optical properties which are conducive to photoacoustic imaging61,62. In wild type zebrafish larvae, the dominant PA chromophores in the visible regime are melanin and hemoglobin. Isolation of PA signals from perfused vasculature can be achieved with the use of pigmentation blockers (e.g., 1-phenyl 2-thiourea (PTU))63, or by using mutant zebrafish lines (e.g., the casper fish) which express no pigmentation64,65.
We used the modular PAM system equipped with an 80 MHz transducer and 532 nm laser to image the trunk of a live mutant casper zebrafish larvae. The approximate scan region is denoted by a dashed box in Fig. 5a, with a cartoon of the vasculature in the region shown in Fig. 5b. A MAP image of the vessels denoted with a dashed box in Fig. 5b is shown in Fig. 5c. As has been shown in previous PA studies, there is excellent visualization of the vasculature at this illumination wavelength due to the endogenous absorption of hemoglobin within the fish erythrocytes61,62. The three main classifications of trunk vessel at 5 dpf are readily identified; namely the dorsal aorta (DA), posterior cardinal vein (PCV), and intersegmental vessels (ISV)66. In the standard MAP image, the ISV has a more granular appearance than the other vessels due to the intermittent flow of single erythrocytes through the vessel. In contrast, the flow within the DA and PCV is more uniform, leading to fewer fluctuations in the PA signal intensity during data acquisition and a more homogeneous intensity in the resultant image. In the MAP image, all three vessels appear with a similar intensity, and selective isolation of individual vessels is not possible. The F-Mode technique was capable of accentuating various combinations of vessels. Restricting analysis to the band centered at 12.5 MHz produces an image depicting only the PCV at the ventral side of the fish (Fig. 5d). The frequency band centered at 31.5 MHz shows both the DA and PCV (Fig. 5e); however, the ISV is not discernable. Finally, the 97.5 MHz frequency band delineates the entire ISV, including its origin point on the PCV, which is indicated with an arrowhead (Fig. 5f).
Application of F-Mode for scale-specific visualization of vessels in live larval zebrafish. a Cartoon depiction of a zebrafish larva. b Depiction of the vasculature in the region denoted by the dashed box in a. DLAV = dorsal longitudinal anastomotic vessel, ISV = intersegmental vessel, DA = dorsal aorta, PCV = posterior cardinal vein. c Label-free in vivo maximum amplitude projection image of the trunk vasculature denoted by the dashed box in b. The PCV and DA run horizontally, while the ISVs run diagonally between PCV and DA. d–f F-Mode images generated from the indicated frequency bands. In d only the PCV can be seen, while in e both the PCV and DA are visible. The ISV becomes the dominant structure in f. The scale bar in c is 20 µm and can be applied to all F-Mode images
The success of these preliminary in vivo studies points toward future application in larger animal models, and could ultimately be used in conjunction with deeply penetrating PAT to probe for vessels which have atypical lumen diameters, for example, those which contain atherosclerotic plaques67. The method could also be adapted to newly developed PA methods, such as microtomy-assisted photoacoustic microscopy (mPAM)68, to provide scale-specific contrast in 3D imaging of large tissue specimens.
Discussion
The F-Mode technique proposed in this study utilizes unique features in the frequency domain of PA RF-signals as a novel source of image contrast. Images generated with the technique surpass the capabilities of standard MAP reconstruction when differentiating between objects of different scale within phantoms (Figs. 2 and 3). When used in conjunction with label-free PAM, F-Mode provides a dynamic way to selectively enhance the visualization of organelles in single cells (Fig. 4) and vessels of different sizes in small in vivo animal models (Fig. 5). In the future, we plan to apply F-Mode analysis to PA datasets acquired with functional PA to further enhance the selectivity of visualizing arteries and veins in situ43. Furthermore, due to the similarity between the two modalities, we plan to apply F-Mode analysis to datasets acquired with ultra-high-frequency US techniques, such as those used for single-cell imaging49,69, to provide a dynamic source of contrast for samples with little deviation in local mechanical properties.
The F-Mode technique is still being refined and there is potential for further optimization of the algorithm. A current challenge is appropriate selection of the size of the frequency band size used for F-Mode analysis. If the band size is too narrow, the F-Mode technique becomes increasingly sensitive to noise and small fluctuations in absorber size (i.e., on the order of a few percent). While in some cases such sensitivity may be desired, in others it could pose a challenge. For example, the characteristic size (and hence, the location of the spectral features) of some blood vessels can vary spatially due to changes in lumen diameter along the vessel length. This could potentially cause different segments of the vessel to be accentuated in different F-Mode images if the band size is too narrow. Increasing the width of the frequency band can compensate for these slight variations in size. In general, we have found that selecting a band size between two and ten times the spectral resolution of the FFT yields satisfactory results when implementing the F-Mode algorithm for both PAT and PAM systems. On the other hand, if the band size is made too large then several minima will be captured in the same band and the features in the power spectrum will be smoothed. This smoothing effect begins to occur when the size of the band is approximately half the spacing between two adjacent minima. Assuming a speed of sound of 1500 m s−1, this would correspond to a band size of approximately 3.75 MHz for a cylindrical vessel with a radius of 100 μm, and a band size of 37.5 MHz for a vessel with radius of 10 μm. The size of the F-Mode frequency band used in this work was fixed based on the central frequency of the imaging system’s transducer. This tactic is effective when the scale of the structure being probed is known a priori; however, this information may not always be readily available, especially in in vivo implementations. In such cases, the FFT of a representative RF-line from the object can be computed and used as an aid to select a band of appropriate size. Going forward, we will integrate this process into the algorithm workflow so that the selection of optimal band size becomes fully automated.
As with all other PA techniques, F-Mode faces challenges in multi-spectral PA imaging due to the dependence of the optical absorption coefficient on the illumination wavelength. For optically thick samples (μaa > 1), the assumption of uniform optical energy deposition is not valid, and the resultant PA power spectra will deviate from those predicted by theory. However, we believe that F-Mode can be applied in multi-spectral PA imaging when the sample is optically thin (μaa < 1) at all illumination wavelengths employed. At normal biological concentrations (150 g L−1), the optical absorption coefficient of whole oxygenated blood at the 710 nm illumination wavelength used in the PAT system in this work is 1.7 cm−170. At these wavelengths, blood vessels with characteristic length of up to 6 mm can be considered optically thin, and quantitative F-Mode imaging should be possible. In the visible region (e.g., at 532 nm) oxygenated blood has a μa of approximately 225 cm−170, and the upper limit for vessel diameters which can be considered optically thin is approximately 90 μm. Such vessel sizes are of great interest for PAM imaging of microvasculature, such as that found in the mouse ear4 or in zebrafish larvae65.
For objects with the same shape and acoustic properties, the location of, and distance between, adjacent spectral minima is directly related to the size of the object and can be significantly different even when the time domain PA signals are almost identical (Supplementary Fig. 1). This imposes a limit on the minimum object size for which oscillations in the F-Mode intensity can be detected. For example, the locations of the minima in the power spectrum for a spherical droplet are given by the zeros of the spherical Bessel function \(j_1\left( {\frac{{2\pi a}}{{v_{\mathrm{s}}}}f} \right)\)20,22. The first minimum occurs when the argument is approximately equal to 4.49. Thus, for a transducer with an upper bandwidth limit fmax, the smallest radius, a, of a spherical droplet (such as a mammalian cell in suspension), which would yield a spectral minimum in the transducer bandwidth is given by \(a = \frac{{4.49v_{\mathrm{s}}}}{{2\pi f_{{\mathrm{max}}}}}\), where vs is the speed of sound of the droplet. For the 400 MHz transducer used in this work, this corresponds to a droplet with radius a ≈ 2 μm, assuming a speed of sound of 1500 m s−1. Objects smaller than this limit will not exhibit a dynamic change in contrast; however, they can still serve as useful standards for comparing the fluctuations observed in other objects present in the image.
Our F-Mode technique is applicable to data acquired from a wide range of PA imaging systems, operating at transducer frequencies ranging from the tens to hundreds of megahertz. As no modification to existing PA hardware is required for F-Mode analysis, it can easily be implemented in tandem with other PA reconstruction techniques to provide additional structural information with minimal additional post-processing. We believe that due to its versatility, ease of implementation, and sensitivity to objects of different scale, F-Mode has the potential to develop into a valuable tool with a wide range of applications in the field of biomedical imaging.
Methods
Photoacoustic tomography system
The commercially available VevoLAZR (Fujifilm-VisualSonics, Toronto, Canada) was used for all PAT measurements. The system was equipped with the LZ550 probe which has central frequency and −6 dB bandwidth of 40 and 15 MHz, respectively. A pulsed OPO laser with a Nd:YAG pump and 20 Hz pulse repetition frequency (PRF) was tuned to a wavelength of 710 nm and used to illuminate the sample. Signal acquisition was performed at a sampling frequency of 1064 MHz, and RF data was averaged four times to increase SNR. The raw recorded PA data was beamformed offline in MATLAB using a standard delay and sum algorithm. All measurements were performed at room temperature, with deionized water to provide acoustic coupling.
Photoacoustic microscopy system
A modified SASAM scanning acoustic microscope (Kibero, Saarbruken, Germany) was used for all PAM measurements. The SASAM is customizable, and allows major system components (e.g., transducer, focusing objective, laser source) to be interchanged. In these experiments, two lasers were used: a 532 nm Nd:YAG laser (Teem Photonics, Meylan, France), operating at a PRF of 4 kHz with a pulse width of 330 ps; and a UV Nd:YAG laser (Bright Solutions, Pavia, Italy) with wavelength of 266 nm, PRF of 10 kHz, and pulse width of 500 ps.
When the 532 nm laser was used, the laser was attenuated using a variable neutral density filter (Thorlabs, New Jersey, USA) and coupled into an optical fiber (Coastal Connections, California, USA). The fiber output was collimated using a fiber coupler (Schafter + Kirchhoff, Hamburg, Germany), directed off a dichroic mirror (Chroma Technology, Vermont, USA), and focused through a 10x optical objective (Olympus, Tokyo, Japan) onto the sample. For the 266 nm illumination pathway, the laser was first directed through a beam expander to increase the beam width. This laser emits both 266 and 532 nm beams collinearly, thus the 266 nm wavelength was isolated using a 4th harmonic Nd:YAG laser line mirror (Thorlabs, New Jersey, USA). The UV beam was directed into a dichroic mirror (Chroma Technology, Vermont, USA) and focused onto the sample using a 10x UV objective (Thorlabs, New Jersey, USA).
One of three different single-element transducers (Kibero, Saarbruken, Germany) was used to record the PA waves: an 80 MHz transducer with −6 dB bandwidth of 90 MHz, a 200 MHz transducer with −6 dB bandwidth of 120 MHz, or a 400 MHz transducer with −6 dB bandwidth of 180 MHz. All recorded PA signals were digitized at a rate of 8 GS s−1 with a 10-bit digitizer (Aquiris, USA). Signal averaging for the 80, 200, and 400 MHz transducer was performed at 400, 200, and 100 times, respectively. Unless otherwise stated, all PAM experiments were performed at 37 °C, with acoustic coupling provided by 1x PBS.
The F-Mode algorithm
Acquired RF data was imported into MATLAB for processing. The RF datasets were transformed into their frequency domain representations by applying the MATLAB 1D fast Fourier transform (FFT) to each individual RF-line. The RF-Lines were zero padded to a length of \(K = \frac{{f_{\mathrm{s}}}}{{1{\mathrm{E}}5}}\), where fs is the sampling frequency of the system used for signal acquisition, to ensure that the spacing between points in the transformed spectrum was equal to 100 kHz. To satisfy Parseval’s theorem, the frequency spectra were then scaled by a factor of \(\frac{1}{{f_{\mathrm{s}}}}\). The signal power spectrum was then estimated by taking the squared magnitude of the scaled frequency spectrum. An F-Mode matrix was generated by partitioning each power spectrum into discrete spectral bands and computing the total power in each band at each scan position. The value, F, of the pixel at location (x, y) for the F-Mode image corresponding to band i is calculated as:
where P(x,y) is the power spectrum of the RF-line at location (x, y), Π(z) is the rect function, and \(f_{\mathrm{c}} = \frac{{\left( {2i - 1} \right)N}}{2}\), where N, the width of the band, is an integer multiple of Δf. Due to the large difference in transducer bandwidths, a spectral band size of 0.2 MHz was used for the PAT acquired data, and a band size of 1 MHz was used for the PAM data.
Preparation and imaging of vessel phantom
For the VevoLAZR experiment, a gelatin phantom composed of 10% (w/v) porcine skin gelatin was prepared. Briefly, the gelatin powder was slowly added to degassed water which had been heated to 35 °C. The mixture was magnetically stirred until it reached 65 °C and the gelatin was entirely dissolved. The molten gelatin mixture was then poured into a custom-made mold containing three taught fishing lines with diameters of 250, 200, and 150 µm, respectively, and was kept at 4 °C for 24 h. Prior to imaging, the fishing lines were gently removed and the cavities filled with a 70% (v/v) ethanol in water mixture containing Sudan Black B (Sigma-Aldrich Canada, Oakville, Canada).
The vessel phantom was scanned with a 40 MHz central frequency linear array transducer (LZ550) probe. The imaging plane was oriented orthogonally to the long axis of the vessels. The resultant PA data was beamformed using MATLAB, and the F-Mode algorithm was applied. A representative F-Mode spectrum from each vessel was used to identify the spectral bands which exhibited the greatest contrast between the vessels.
Preparation and imaging of bead phantom
A glass-bottom petri dish (MatTek, Massachusetts, USA) was filled with 300 µL of molten 0.5% (w/v) low melting point agarose (Sigma Aldrich, USA) dissolved in PBS. The agarose was allowed to solidify in the dish for 30 min at room temperature. In the meantime, 1 mL of molten agarose was pipetted into an aliquot along with 2 µL of PBS solution containing black polystyrene microspheres with 6 µm diameter (Polysciences, USA), and 2 µL of another PBS solution containing black polystyrene microspheres with 10 µm diameter (Polysciences, USA). The aliquot was vortexed, and then 40 µL of the bead laden agarose was pipetted on top of the solidified agarose layer in the petri dish. The dual layer phantom was allowed to cool for 20 min at 4 °C. The sample was raster scanned with the SASAM using the 400 MHz transducer and the 532 nm laser. For display purposes, the spectra shown in Fig. 3c were smoothed using a lowpass filter to remove high-frequency oscillations due to the system response.
Culturing and imaging of CAKI-2 cells
The cover slip of a glass-bottom petri dish (MatTek, Massachusetts, USA) was removed and a UV-Grade fused silica cover slip (Esco Optics, New Jersey, USA) was epoxied in its place. The epoxied cover slip was coated with Poly-D-Lysine prior to cell plating to promote cellular adhesion. Briefly, 1 mL of Poly-D-Lysine was pipetted onto the cover slip surface. After 5 min, excess Poly-D-Lysine was rinsed off using deionized water and the dish was allowed to dry for 2 h. CAKI-2 cells were then plated, covered with 2 mL of McCoy’s 5A media, and were allowed to adhere to the substrate overnight. Prior to scanning, the cell media was aspirated and the dish was flooded with 2 mL of ice cold methanol for 3 min. The sample was finally rinsed twice with 2 mL of Milli-Q water immediately before imaging. The cells were scanned in the SASAM with the 200 MHz transducer and 266 nm laser in a raster pattern, with a fast and slow step size of 1 µm. For display purposes, the transducer response of the 200 MHz transducer was smoothed using a lowpass filter to remove high-frequency oscillations due to the system response. Both the MAP and F-Mode images created from the resultant dataset were smoothed using a 2D 2-point averaging filter, and interpolated using 2D 1-point linear interpolation.
Preparation and imaging of zebrafish larvae
Five day-post-fertilization mutant casper zebrafish larvae were anesthetized using a 0.003% (w/v) solution of tricane (Sigma, Cat. #A5040) and pipetted into a solution of molten 1.5% (w/v) low melting point agarose in PBS at 40 °C. A glass-bottom petri dish coated with a flat layer of 1.5% (w/v) agarose was prepared as in the previous section. A drop of the molten agarose was pipetted onto the dish along with the anesthetized larva. A pipette tip was used to position the specimen in the still molten agarose so that the sagittal plane of the fish was visible under optical microscopy. Once the larva was correctly positioned, the agarose was allowed to solidify for 30 min at room temperature. The dish was then filled with approximately 4 mL of egg water, and scanned using the 80 MHz transducer and the 532 nm laser focused through a 4x optical objective. Raster scans were performed with a step size of 2 µm in both the fast and slow scan directions. Both the MAP and F-Mode images created from the resultant dataset were smoothed using a 2D 2-point averaging filter, and interpolated using 2D 1-point linear interpolation. Zebrafish studies were performed under animal protocol ACC660 of St. Michael’s Hospital.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Bell, A. G. On the production and reproduction of sound by light. Am. J. Sci. 20, 305–324 (1880).
Rosencwaig, A. Photoacoustic spectroscopy of solids. Opt. Commun. 7, 305–308 (1973).
Tam, A. C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 58, 381–431 (1986).
Wang, L. V. & Hu, S. Photoacoustic tomography: In vivo imaging from organelles to organs. Science 335, 1458–1462 (2012).
Wang, L. V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics 3, 503–509 (2009).
Beard, P. Biomedical photoacoustic imaging. Interface Focus 1, 602–631 (2011).
Mallidi, S., Luke, G. P. & Emelianov, S. Photoacoustic imaging in cancer detection, diagnosis, and treatment guidance. Trends Biotechnol. 29, 213–221 (2011).
Danielli, A. et al. Label-free photoacoustic nanoscopy. J. Biomed. Opt. 19, 860061 (2014).
Zhang, C., Zhang, Y. S., Yao, D. -K., Xia, Y. & Wang, L. V. Label-free photoacoustic microscopy of cytochromes. J. Biomed. Opt. 18, 205041 (2013).
Strohm, E. M., Moore, M. J. & Kolios, M. C. Single cell photoacoustic microscopy: A review. IEEE J. Sel. Top. Quantum Electron. 22, 137–151 (2016).
Li, L., Zhu, L., Shen, Y. & Wang, L. V. Multiview Hilbert transformation in full-ring transducer array-based photoacoustic computed tomography. J. Biomed. Opt. 22, 076017 (2017).
Brecht, H. -P. et al. Whole-body three-dimensional optoacoustic tomography system for small animals. J. Biomed. Opt. 14, 064007 (2009).
Ermilov, S. A. et al. Laser optoacoustic imaging system for detection of breast cancer. J. Biomed. Opt. 14, 024007 (2009).
Dean-Ben, X. L., Fehm, T. F., Gostic, M. & Razansky, D. Volumetric hand-held optoacoustic angiography as a tool for real-time screening of dense breast. J. Biophotonics 9, 253–259 (2016).
Attia, A. B. E. et al. Noninvasive real-time characterization of non-melanoma skin cancers with handheld optoacoustic probes. Photoacoustics 7, 20–26 (2017).
Diebold, G. J., Khan, M. I. & Park, S. M. Photoacoustic ‘signatures’ of particulate matter: optical production of acoustic monopole radiation. Science 250, 101–104 (1990).
Diebold, G. J., Sun, T. & Khan, M. I. Photoacoustic monopole radiation in one, two, and three dimensions. Phys. Rev. Lett. 67, 3384–3387 (1991).
Strohm, E. M., Berndl, E. S. L. & Kolios, M. C. Probing red blood cell morphology using high-frequency photoacoustics. Biophys. J. 105, 59–67 (2013).
Khan, M. I., Sun, T. & Diebold, G. J. Photoacoustic waves generated by absorption of laser radiation in optically thin cylinders. J. Acoust. Soc. Am. 94, 931–940 (1993).
Diebold, G. J. & Westervelt, P. J. The photoacoustic effect generated by a spherical droplet in a fluid. J. Acoust. Soc. Am. 84, 2245–2251 (1988).
Strohm, E. M., Gorelikov, I., Matsuura, N. & Kolios, M. C. Acoustic and photoacoustic characterization of micron-sized perfluorocarbon emulsions. J. Biomed. Opt. 17, 0960161 (2012).
Moore, M. J., Strohm, E. M. & Kolios, M. C. Assessment of the nucleus-to-cytoplasmic ratio in MCF-7 cells using ultra-high frequency ultrasound and photoacoustics. Int. J. Thermophys. 37, 1–10 (2016).
Strohm, E. M. & Kolios, M. C. Classification of blood cells and tumor cells using label-free ultrasound and photoacoustics. Cytom. Part A 87A, 741–749 (2015).
Hysi, E. et al. Photoacoustic signal characterization of cancer treatment response: Correlation with changes in tumor oxygenation. Photoacoustics 5, 25–35 (2017).
Hysi, E., Saha, R. K. & Kolios, M. C. Photoacoustic ultrasound spectroscopy for assessing red blood cell aggregation and oxygenation. J. Biomed. Opt. 17, 1250061 (2012).
Qiao, W., Chen, Z., Zhou, W. & Xing, D. All-optical photoacoustic Doppler transverse blood flow imaging. Opt. Lett. 43, 2442–2445 (2018).
Zhang, Z., Shi, Y., Yang, S. & Xing, D. Subdiffraction-limited second harmonic photoacoustic microscopy based on nonlinear thermal diffusion. Opt. Lett. 43, 2336–2339 (2018).
Tismer, S., Brand, S., Klengel, S., Petzold, M. & Czurratis, P. Acoustic imaging of bump defects in flip-chip devices using split spectrum analysis. IEEE Int. Ultrason. Symp. IUS 950–953 (2013).
Frangi, A. F., Niessen, W. J., Vincken, K. L. & Viergever, M. A. Multiscale vessel enhancement filtering. Proc. Med. Image Comput. Comput.-Assist. Interv. 1496, 130–137 (1998).
Sato, Y. et al. Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. Med. Image Anal. 2, 143–168 (1998).
Krissian, K., Malandain, G., Ayache, N., Vaillant, R. & Trousset, Y. Model-based detection of tubular structures in 3D images. Comput. Vis. Image Underst. 80, 130–171 (2000).
Moccia, S., De Momi, E., El Hadji, S. & Mattos, L. S. Blood vessel segmentation algorithms—Review of methods, datasets and evaluation metrics. Comput. Methods Prog. Biomed. 158, 71–91 (2018).
Kirbas, C. & Quek, F. A review of vessel extraction techniques and algorithms. ACM Comput. Surv. 36, 81–121 (2004).
Li, Q. et al. Vascular tree extraction for photoacoustic microscopy and imaging of cat primary visual cortex. J. Biophotonics 10, 780–791 (2017).
Raumonen, P. & Tarvainen, T. Segmentation of vessel structures from photoacoustic images with reliability assessment. Biomed. Opt. Express 9, 2887–2904 (2018).
Haq, I. U., Nagoaka, R., Makino, T., Tabata, T. & Saijo, Y. 3D Gabor wavelet based vessel filtering of photoacoustic images. Proc. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 3883–3886 (2016).
Heagerty, A. M., Aalkjaer, C., Bund, S. J., Korsgaard, N. & Mulvany, M. J. Small artery structure in hypertension. Dual processes of remodeling and growth. Hypertension 21, 391–397 (1993).
Needles, A. et al. Development and initial application of a fully integrated photoacoustic micro-ultrasound system. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60, 888–897 (2013).
Xu, Y., Wang, L. V., Ambartsoumian, G. & Kuchment, P. Reconstructions in limited-view thermoacoustic tomography. Med. Phys. 31, 724–733 (2004).
Preisser, S. et al. Vessel orientation-dependent sensitivity of optoacoustic imaging using a linear array transducer. J. Biomed. Opt. 18, 26011 (2013).
Xu, M. & Wang, L. V. Analytic explanation of spatial resolution related to bandwidth and detector aperture size in thermoacoustic or photoacoustic reconstruction. Phys. Rev. E 67, 0566051 (2003).
Jain, R. K. Normalization of tumor vasculature: An emerging concept in antiangiogenic therapy. Sci. (80−). 307, 58–62 (2005).
Yao, J. et al. High-speed label-free functional photoacoustic microscopy of mouse brain in action. Nat. Methods 12, 407–410 (2015).
Zhang, C., Maslov, K., Yao, J. & Wang, L. V. In vivo photoacoustic microscopy with 7.6-μm axial resolution using a commercial 125-MHz ultrasonic transducer. J. Biomed. Opt. 17, 116016 (2012).
Khan, M. I. & Diebold, G. J. The photoacoustic effect generated by an isotropic solid sphere. Ultrasonics 33, 265–269 (1995).
Falou, O., Jafari Sojahrood, A., Kumaradas, J. C. & Kolios, M. C. Surface modes and acoustic scattering of microspheres and ultrasound contrast agents. J. Acoust. Soc. Am. 132, 1820–1829 (2012).
Baddour, R. E., Sherar, M. D., Hunt, J. W., Czarnota, G. J. & Kolios, M. C. High-frequency ultrasound scattering from microspheres and single cells. J. Acoust. Soc. Am. 117, 934–943 (2005).
Wang, Y. et al. Biodegradable polymeric nanoparticles containing gold nanoparticles and Paclitaxel for cancer imaging and drug delivery using photoacoustic methods. Biomed. Opt. Express 7, 4125–4138 (2016).
Bereiter-Hahn, J., Karl, I., Lüers, H. & Vöth, M. Mechanical basis of cell shape: investigations with the scanning acoustic microscope. Biochem. Cell Biol. 73, 337–348 (1995).
Bereiter-Hahn, J. Probing Biological Cells and Tissues with Acoustic Microscopy in Advances in Acoustic Microscopy. Vol. 1. (ed. Briggs, A.) 79–110 (Plenum Press, 1995).
Stephens, D. J. Light microscopy techniques for live cell imaging. Sci. (80−.). 300, 82–86 (2003).
Kallepitis, C. et al. Quantitative volumetric Raman imaging of three dimensional cell cultures. Nat. Commun. 8, 14843 (2017).
Pasternak, M. M., Strohm, E. M., Berndl, E. S. L. & Kolios, M. C. Properties of cells through life and death - an acoustic microscopy investigation. Cell Cycle 14, 2891–2898 (2015).
Caspersson, T. Chapter IV: Cytochemical analysis of the tumour tissue. Acta Radiol. 23, 32–75 (1942).
Cheung, M. C. et al. Intracellular protein and nucleic acid measured in eight cell types using deep-ultraviolet mass mapping. Cytom. Part A 83A, 540–551 (2013).
Cheung, M. C., Evans, J. G., Mckenna, B. & Ehrlich, D. J. Deep ultraviolet mapping of intracellular protein and nucleic acid in femtograms per pixel. Cytom. Part A 79A, 920–932 (2011).
Yao, D.-K., Maslov, K., Shung, K. K., Zhou, Q. & Wang, L. V. In vivo label-free photoacoustic microscopy of cell nuclei by excitation of DNA and RNA. Opt. Lett. 35, 4139–4141 (2010).
Hatfield, J. M. R., Schulze, L. & Ernst, D. Measurement of the ultraviolet absorption in specific parts of both living and fixed mammalian cells, using a specially designed microspectrophotometer. Exp. Cell Res. 59, 484–486 (1970).
Zon, L. I. & Peterson, R. T. In vivo drug discovery in the zebrafish. Nat. Rev. Drug Discov. 4, 35–44 (2005).
Lieschke, G. J. & Currie, P. D. Animal models of human disease: zebrafish swim into view. Nat. Rev. Genet. 8, 353–367 (2007).
Chen, Q., Jin, T., Qi, W., Mo, X. & Xi, L. Label-free photoacoustic imaging of the cardio-cerebrovascular development in the embryonic zebrafish. Biomed. Opt. Express 8, 2359 (2017).
Ma, R., Distel, M., Deán-Ben, X. L., Ntziachristos, V. & Razansky, D. Non-invasive whole-body imaging of adult zebrafish with optoacoustic tomography. Phys. Med. Biol. 57, 7227–7237 (2012).
Karlsson, J., von Hofsten, J. & Olsson, P. E. Generating transparent zebrafish: a refined method to improve detection of gene expression during embryonic development. Mar. Biotechnol. (NY). 3, 522–527 (2001).
White, R. M. et al. Transparent adult zebrafish as a tool for in vivo transplantation analysis. Cell Stem Cell 2, 183–189 (2008).
Moore, M. J. et al. Simultaneous ultra-high frequency photoacoustic microscopy and photoacoustic radiometry of zebrafish larvae in vivo. Photoacoustics 12, 14–21 (2018).
Isogai, S., Horiguchi, M. & Weinstein, B. M. The vascular anatomy of the developing zebrafish: An atlas of embryonic and early larval development. Dev. Biol. 230, 278–301 (2001).
Ross, R. Atherosclerosis–An inflammatory disease. N. Engl. J. Med. 340, 115–126 (1999).
Wong, T. T. W. et al. Label-free automated three-dimensional imaging of whole organs by microtomy-assisted photoacoustic microscopy. Nat. Commun. 8, 1–8 (2017).
Strohm, E. M., Moore, M. J. & Kolios, M. C. High resolution ultrasound and photoacoustic imaging of single cells. Photoacoustics 4, 36–42 (2016).
Bosschaart, N., Edelman, G. J., Aalders, M. C. G., van Leeuwen, T. G. & Faber, D. J. A literature review and novel theoretical approach on the optical properties of whole blood. Lasers Med. Sci. 29, 453–479 (2014).
Acknowledgements
We would like to thank Koroboshka Brand-Arzamendi for the larval zebrafish cartoon. This research was supported in part by: the Natural Sciences and Engineering Research Council of Canada, the Canadian Cancer Society, the Canadian Foundation for Innovation, the Ontario Ministry for Research and Innovation, and the Terry Fox Foundation Funding agencies.
Author information
Authors and Affiliations
Contributions
M.J.M. and M.C.K. developed the theory for the F-Mode technique and designed the experiments. M.J.M. performed all measurements with the PAM system and generated all F-Mode images. E.H. and M.F. developed the vessel phantoms and performed all measurements and beamforming of the data for the PAT experiments. S.E., Y.L., and X.Y. cultured and provided zebrafish samples for the PAM experiments. All parties were involved with the production of the finalized manuscript.
Corresponding author
Ethics declarations
Competing interests
M.C.K. has a financial interest in WaveCheck Inc., and Echofos Medical Inc., which, however, did not support this work. M.J.M. has a financial interest in Echofos Medical. The remaining authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moore, M.J., Hysi, E., Fadhel, M.N. et al. Photoacoustic F-Mode imaging for scale specific contrast in biological systems. Commun Phys 2, 30 (2019). https://doi.org/10.1038/s42005-019-0131-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0131-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.