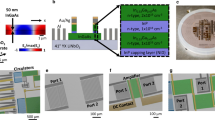
Abstract
Acoustic waves are versatile on-chip information carriers that can be used in applications such as microwave filters and transducers. Nonreciprocal devices, in which the transmission of waves is non-symmetric between two ports, are desirable for the manipulation and routing of phonons, but building acoustic non-reciprocal devices is difficult because acoustic systems typically have a linear response. Here, we report non-reciprocal transmission of microwave surface acoustic waves using a nonlinear parity–time symmetric system based on two coupled acoustic resonators in a lithium niobate platform. Owing to the strong piezoelectricity of lithium niobate, we can tune the gain, loss and nonlinearity of the system using electric circuitry. Our approach can achieve 10 dB of non-reciprocal transmission for surface acoustic waves at a frequency of 200 MHz, and we use it to demonstrate a one-way circulation of acoustic waves in cascading non-reciprocal devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Chu, Y. et al. Quantum acoustics with superconducting qubits. Science 358, 199–202 (2017).
Satzinger, K. J. et al. Quantum control of surface acoustic-wave phonons. Nature 563, 661–665 (2018).
Whiteley, S. J. et al. Spin–phonon interactions in silicon carbide addressed by Gaussian acoustics. Nat. Phys. 15, 490–495 (2019).
Maity, S. et al. Coherent acoustic control of a single silicon vacancy spin in diamond. Nat. Commun. 11, 193 (2020).
Arrangoiz-Arriola, P. et al. Resolving the energy levels of a nanomechanical oscillator. Nature 571, 537–540 (2019).
Otterstrom, N. T., Behunin, R. O., Kittlaus, E. A., Wang, Z. & Rakich, P. T. A silicon Brillouin laser. Science 360, 1113–1116 (2018).
Campbell, C. Surface Acoustic Wave Devices and their Signal Processing Applications (Academic Press, 1989).
Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R. & Alù, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519 (2014).
Liang, B., Guo, X. S., Tu, J., Zhang, D. & Cheng, J. C. An acoustic rectifier. Nat. Mater. 9, 989–992 (2010).
Liang, B., Yuan, B. & Cheng, J. C. Acoustic diode: rectification of acoustic energy flux in one-dimensional systems. Phys. Rev. Lett. 103, 104301 (2009).
Li, Y. et al. Tunable asymmetric transmission via lossy acoustic metasurfaces. Phys. Rev. Lett. 119, 035501 (2017).
Popa, B. I. & Cummer, S. A. Non-reciprocal and highly nonlinear active acoustic metamaterials. Nat. Commun. 5, 3398 (2014).
Walker, E. et al. Nonreciprocal linear transmission of sound in a viscous environment with broken P symmetry. Phys. Rev. Lett. 120, 204501 (2018).
Devaux, T., Cebrecos, A., Richoux, O., Pagneux, V. & Tournat, V. Acoustic radiation pressure for nonreciprocal transmission and switch effects. Nat. Commun. 10, 3292 (2019).
Sasaki, R., Nii, Y., Iguchi, Y. & Onose, Y. Nonreciprocal propagation of surface acoustic wave in Ni/LiNbO3. Phys. Rev. B 95, 020407 (2017).
Nomura, T. et al. Phonon magnetochiral effect. Phys. Rev. Lett. 122, 145901 (2019).
Xu, H., Jiang, L., Clerk, A. A. & Harris, J. G. E. Nonreciprocal control and cooling of phonon modes in an optomechanical system. Nature 568, 65–69 (2019).
Bender, C. M. & Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 80, 5243–5246 (1998).
El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. Nat. Phys. 14, 11–19 (2018).
Konotop, V. V., Yang, J. & Zezyulin, D. A. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 88, 035002 (2016).
Li, Y. et al. Anti-parity–time symmetry in diffusive systems. Science 364, 170–173 (2019).
Feng, L., El-Ganainy, R. & Ge, L. Non-Hermitian photonics based on parity–time symmetry. Nat. Photon. 11, 752–762 (2017).
Peng, B. et al. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 10, 394–398 (2014).
Feng, L. et al. Experimental demonstration of a unidirectional reflectionless parity–time metamaterial at optical frequencies. Nat. Mater. 12, 108–113 (2013).
Chang, L. et al. Parity–time symmetry and variable optical isolation in active–passive-coupled microresonators. Nat. Photon. 8, 524–529 (2014).
Feng, L., Wong, Z. J., Ma, R.-M., Wang, Y. & Zhang, X. Single-mode laser by parity–time symmetry breaking. Science 346, 972–975 (2014).
Klauck, F. et al. Observation of PT-symmetric quantum interference. Nat. Photon. 13, 883–887 (2019).
Zhen, B. et al. Spawning rings of exceptional points out of Dirac cones. Nature 525, 354–358 (2015).
Özdemir, Ş. K., Rotter, S., Nori, F. & Yang, L. Parity–time symmetry and exceptional points in photonics. Nat. Mater. 18, 783–798 (2019).
Fleury, R., Sounas, D. & Alu, A. An invisible acoustic sensor based on parity–time symmetry. Nat. Commun. 6, 5905 (2015).
Shi, C. et al. Accessing the exceptional points of parity–time symmetric acoustics. Nat. Commun. 7, 11110 (2016).
Auregan, Y. & Pagneux, V. PT-symmetric scattering in flow duct acoustics. Phys. Rev. Lett. 118, 174301 (2017).
Zhu, X., Ramezani, H., Shi, C., Zhu, J. & Zhang, X. PT-symmetric acoustics. Phys. Rev. X 4, 031042 (2014).
Zhang, J. et al. Giant nonlinearity via breaking parity–time symmetry: a route to low-threshold phonon diodes. Phys. Rev. B 92, 115407 (2015).
Xu, X.-W., Liu, Y.-x, Sun, C.-P. & Li, Y. Mechanical PT symmetry in coupled optomechanical systems. Phys. Rev. A 92, 013852 (2015).
Bender, C. M., Berntson, B. K., Parker, D. & Samuel, E. Observation of PT phase transition in a simple mechanical system. Am. J. Phys. 81, 173–179 (2013).
Assawaworrarit, S., Yu, X. & Fan, S. Robust wireless power transfer using a nonlinear parity–time-symmetric circuit. Nature 546, 387–390 (2017).
Morgan, D. & Paige, E. G. S. Surface Acoustic Wave Filters with Applications to Electronic Communications and Signal Processing (Academic Press, 2007).
Shao, L. et al. Phononic band structure engineering for high-Q gigahertz surface acoustic wave resonators on lithium niobate. Phys. Rev. Appl. 12, 014022 (2019).
Jiang, X. et al. On-chip optical nonreciprocity using an active microcavity. Sci. Rep. 6, 38972 (2016).
Wen, J. et al. Modeling of on-chip optical nonreciprocity with an active microcavity. Photonics 2, 498–508 (2015).
Shi, Y., Yu, Z. & Fan, S. Limitations of nonlinear optical isolators due to dynamic reciprocity. Nat. Photon. 9, 388–392 (2015).
Acknowledgements
We thank S. Bogdanovic, M. Yu, M. Zhang, C. Chia, B. Machielse and Y.-F. Xiao for fruitful discussions. This work is supported by the STC Center for Integrated Quantum Materials, NSF grant no. DMR-1231319, NSF CQIS grant no. ECCS-1810233, ONR MURI grant no. N00014-15-1-2761 and AFOSR MURI grant no. FA9550-14-1-0389. N.S. acknowledges support by the Natural Sciences and Engineering Research Council of Canada (NSERC), the AQT Intelligent Quantum Networks and Technologies (INQNET) research programme and the DOE/HEP QuantISED programme grant and QCCFP (Quantum Communication Channels for Fundamental Physics) award no. DE-SC0019219. W.M. acknowledges support from the undergraduate overseas internship programme of Nankai University supported by the National Science Fund for Talent Training in the Basic Sciences, grant no. J1103208. This work was performed in part at the Center for Nanoscale Systems (CNS), Harvard University.
Author information
Authors and Affiliations
Contributions
L.S. conceptualized, designed, fabricated and measured the devices. W.M. and Y.H. analysed the system theoretically, with discussion from other authors. W.M. and L.S. performed numerical simulations. All authors analysed and interpreted the results. L.S. and W.M. prepared the manuscript with contributions from all authors. M.L. and L.Y. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
M.L. is involved in developing lithium niobate technologies at HyperLight Corporation. The other authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Photo of the printed circuit board (PCB) used for non-reciprocal SAW device measurements.
This PCB supports simultaneous measurements of two devices. Signal from Port 1 to Port 2 is defined as the forward direction.
Extended Data Fig. 2 Measured non-reciprocity of the broken-PT-symmetric SAW resonators versus various input powers.
The non-reciprocity is defined in Equ. (1).
Supplementary information
Supplementary Information
Supplementary Notes 1–5 and Figs. 1–12.
Source data
Source Data Fig. 1
Source data of the plots.
Source Data Fig. 2
Source data of the plots.
Source Data Fig. 3
Source data of the plots.
Source Data Fig. 4
Source data of the plots.
Source Data Extended Data Fig. 2
Source data of the plots.
Rights and permissions
About this article
Cite this article
Shao, L., Mao, W., Maity, S. et al. Non-reciprocal transmission of microwave acoustic waves in nonlinear parity–time symmetric resonators. Nat Electron 3, 267–272 (2020). https://doi.org/10.1038/s41928-020-0414-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-020-0414-z
This article is cited by
-
Activating non-Hermitian skin modes by parity-time symmetry breaking
Communications Physics (2024)
-
Linear and phase controllable terahertz frequency conversion via ultrafast breaking the bond of a meta-molecule
Nature Communications (2024)
-
Non-reciprocal acoustoelectric microwave amplifiers with net gain and low noise in continuous operation
Nature Electronics (2023)
-
Observation of non-reciprocal harmonic conversion in real sounds
Communications Physics (2023)
-
Photonic van der Waals integration from 2D materials to 3D nanomembranes
Nature Reviews Materials (2023)