Abstract
Heatwaves can have devastating impact on society and reliable early warnings at several weeks lead time are needed. Previous studies showed that north-Pacific sea surface temperatures (SST) can provide long-lead predictability for eastern US temperature, mediated by an atmospheric Rossby wave. The exact mechanisms, however, are not well understood. Here we analyze two different Rossby waves associated with temperature variability in western and eastern US, respectively. Causal discovery analyses reveal that both waves are characterized by positive ocean-atmosphere feedbacks at daily timescales. Only for the eastern US, a long-lead causal link from SSTs to the Rossby wave exists, which generates summer temperature predictability. We show that this SST forcing mechanism originates from the evolution of the winter-to-spring Pacific Decadal Oscillation (PDO). During pronounced winter-to-spring PDO phases (either positive or negative) eastern US summer temperature forecast skill more than doubles, providing a temporary window of enhanced long-lead predictability.
Similar content being viewed by others
Introduction
Quasi-stationary or recurrent Rossby waves in boreal summer play an important role in the development of high impact heat waves1,2. Such Rossby waves create persistent clear-sky high pressure systems, which, in combination with soil desiccation and land-atmosphere feedbacks, can lead to extreme heatwaves such as seen in Russia 20103,4 and the United States 20125. These Rossby waves (RW) can arise due to internal atmospheric variability, with a preferred phase6 that largely depends on orography7, land-ocean boundaries8 and atmospheric waveguidability8,9,10. Vorticity anomalies induced by e.g., tropical convection or mid-latitude sea surface temperature (SST) anomalies can also force quasi-stationary Rossby waves7,11,12,13.
Understanding the role of mid-latitude ocean-atmosphere interactions in generating and maintaining Rossby waves is needed to improve subseasonal-to-seasonal (S2S) predictions14,15,16 and climate change projections17,18,19. Currently, these interactions are not well understood. We know that, especially on intra-seasonal timescales, mid-latitude SST anomalies are predominantly forced by atmospheric variability20,21, yet the ocean can also influence the atmosphere22,23. The initial atmospheric response to diabatic heating at the ocean surface is baroclinic, with a low-level trough and high-level ridge slightly downstream of a mid-latitude warm SST anomaly7. Subsequently, the baroclinic response is modified to a local or slightly downwind-shifted warm ridge (barotropic) response via a transient eddy feedback13,24. In the upper atmosphere, the warm ridge is associated with a negative vorticity anomaly. The atmosphere responds to this negative vorticity anomaly by moving air equatorward, mainly at the downstream edge of the warm ridge. This adjustment can lead to a downstream Rossby wave response consisting of alternating highs and lows25.
The atmospheric response to SST anomalies is thus complicated due to the transient eddy feedback, which strongly depends on the strength of the background flow, and therefore also on season and location of the anomaly22. A stronger atmospheric response is expected when the SST anomaly is close to the storm tracks and when the storm tracks are strong (e.g., in winter)26. This sensitivity of the atmospheric response to the storm track’s characteristics is also linked to the waveguidability of the jet stream26. Vorticity disturbances in the storm track near the core of the jet will be refracted to the core9,27, thereby generating a more zonally elongated Rossby wave response. A higher waveguidability is found for a strong and/or more narrow jet stream, leading to a stronger atmospheric wave-response28. The jet and storm track are tightly coupled29, and it is thus likely that both strongly affect the atmospheric response to an SST induced vorticity anomaly.
The atmospheric response also depends on the persistence of an imposed mid-latitude SST anomaly. While the timescale of the baroclinic adjustment is only a few days, to reach the equilibrium barotropic adjustment takes approx. 1 to 2 months13,30. The SST persistence is governed by the oceanic Rossby wave response to atmospheric forcing31, yet it is also affected by the thermal inertia of the ocean mixed layer and the turbulent heat fluxes32. The mixed layer is shallower during summer, and therefore SST anomalies are less persistent (dissipating within a couple of months) compared to winter (>1 year)33,34. Vice versa, the shallower mixed layer also means that the persistence of summer SST is more sensitive to atmospheric forcing34. All these factors illustrate the complexity of the coupled ocean-atmosphere Rossby wave interactions, with (1) a seasonally varying ocean-atmosphere coupling strength, (2) a seasonally varying persistence of SST, (3) the slow atmospheric baroclinic-to-barotropic adjustment to an SST anomaly, and (4) the dependence on the location of the SST anomaly (and background atmospheric state).
Here, we focus on United States (US) temperature variability and its relationship with atmospheric Rossby waves, and how these Rossby waves interact with north-Pacific SST anomalies. Previous work showed that extra-tropical Pacific SSTs, associated with a Rossby wave, provide long-lead predictability for eastern US hot temperatures15. Follow-up work showed that using only SST precursors to predict high temperature events renders predictive skill up to 50 days lead-time, while adding local soil moisture only slightly improves skill at shorter lead-times (up to 30 days lead-time)16. Thus, we focus here on interactions between SST and Rossby Waves (SST-RW), and how those interactions affect the long-lead SST signal for eastern US temperature. It was hypothesized that, in summer, amplifying two-way feedbacks between the Rossby wave and the underlying SST pattern can generate long-lead predictability15. The SST pattern would initially arise as response to a strong atmospheric Rossby wave, and subsequently amplify via positive ocean-atmosphere feedbacks. An alternative hypothesis is that the long-lead SST signal predominantly originates from the Pacific Decadal Oscillation (PDO), since the robust SST precursor pattern as found in16, projects strongly onto the PDO pattern. This suggests that the low-frequency PDO dynamics leads to a continuous and persistent boundary condition for the atmosphere16. Both processes might also simultaneously contribute to the long-lead signal between SST and eastern US temperature.
To test these hypotheses, we use a causal discovery technique to quantify the SST-RW coupling strength of the Rossby wave associated with eastern US temperature variability. As a comparison, we perform the same analyses for the western US and show that this region is modulated by a different Rossby wave pattern with different dynamical characteristics. Importantly, we show that only for the eastern RW, a long-lead SST signal exists, and thus long-lead predictability is possible. If the long-lead signal for the eastern RW originates from a positive SST-RW feedback, we expect to find a stronger SST-RW coupling on (sub)-synoptic timescales (1–10 days) compared to the western RW. On the other hand, if the ocean is forcing the atmosphere by acting as a boundary forcing, we expect to find a pronounced upward ocean-to-atmosphere link for the eastern RW.
To measure the coupling strength, lagged univariate correlation analyses are inadequate since the autocorrelation of both the Rossby wave and especially the SST variability will spuriously inflate the correlation coefficient35. Therefore, we will use a causal discovery algorithm which has been specifically developed to deal with strongly autocorrelated climate data36.
Results
Quantifying ocean-atmosphere coupling of Rossby Waves
Figure 1a, b shows that western (Tw) and eastern (TE) US summer temperatures strongly correlate with two distinct Rossby wave patterns, here called the western (RWW) and eastern RW (RWE) pattern. These are phase-shifted by about half a wavelength with respect to each other. Tw and TE are the area-weighted 15-day mean anomaly temperature timeseries of the western and eastern US spatial cluster, respectively. The western and eastern US temperature clusters are based on gridcells that tend to show simultaneous occurrences of warm temperature periods15,16 (“Method”).
Correlation map between geopotential height at 500 hPa (z500) and TW (panel a) and TE (panel b). Panel (c), (d), (e) and (f) are similar to the upper panels, but versus SSTA, showing instantaneous and lag 2 correlation values. Based on 15-day mean data. For the significance (αFDR = 0.05), we correct for the False Discovery Rate using the Benjamini/Hochberg correction. Gridcells are highlighted by black contour lines if they are significant at least 60 out of 70 data subsets (“Method”). The white contour line indicates the western US cluster (panel a) and eastern US cluster (panel b). The green rectangles in (a) and (b) indicates the region that is used to calculate the spatial covariance, see “Method”.
The western RW pattern is more zonally elongated and resembles a dominant Northern Hemispheric mode of variability. The eastern RW consists of an arcing pattern over the Pacific and North America. This wave-pattern is reminiscent of the winter Pacific North American (PNA) pattern in its negative phase37 and the ENSO-forced atmospheric bridge response38. Interestingly, it does not resemble the summer PNA pattern, and it does not appear to be related to a circumglobal mode of variability. See Supplementary Note 1 for a more detailed discussion and evidence. Hence, while the RWW clearly relates to an atmospheric mode of variability, the RWE does not appear to match any summer mode of variability.
Figure 1e, f show there is a strong instantaneous and lagged SST correlation with eastern US temperature (TE). For the west (Tw), no long-lead signal SST signal is detected (Fig. 1d), only an instantaneous one (Fig. 1c). To investigate the role of ocean-atmosphere feedbacks, we quantify the coupling strength between SST and the western and eastern Rossby waves, respectively, using the Peter and Clark - Momentary Conditional Information (PCMCI) algorithm. To visualize the causal dependencies found by PCMCI, we plot Causal Effect Networks (CEN), which are directed network graphs.
By calculating the spatial covariance of the RW patterns within the green rectangles (shown in Fig. 1a, b), we quantify timeseries that capture the RW variability for both the western and eastern RW, referred to as \({{{\mathrm{RW}}}}_t^W\) and \({{{\mathrm{RW}}}}_t^E\) (“Method”). Figure 2a, g show the SST correlation with the \({{{\mathrm{RW}}}}_t^W\) and \({{{\mathrm{RW}}}}_t^E\) timeseries, respectively. By calculating the spatial covariance within the green rectangle of these SST correlation patterns, we capture the SST variability (\({{{\mathrm{SST}}}}_t^W\) and \({{{\mathrm{SST}}}}_t^E\)) associated with the two Rossby waves (“Method”). We use the PCMCI algorithm that consists of two-steps: (1) an adaptation of the PC39 (Peter and Clark) algorithm and (2) the Momentary Conditional Information metric40. If one is interested to test the causal relationship between the timeseries xt-1 and yt, first, the PC-step estimates the lagged parents of both timeseries (xt-1 and yt) by iteratively performing conditional independence tests. The MCI-step tests if xt-1 and yt are conditionally independent, given the influence of the lagged parents of both xt-1 and yt. To measure conditional independence, we use partial correlation analyses, e.g., parcorr(xt-1,yt|Z), in which Z is a single or set of timeseries to condition on. For more information, see “Method”. To measure the SST-RW feedback on (sub)-synoptic timescales we perform the PCMCI analysis on 1, 5, 10 and 15 day means. To measure the effect of lower-frequency variability, we aggregate to 30, 45, 60 day mean timescales. For conciseness, we present the CEN’s for 1, 5, 10, 30 and 60 day means, as for the other timescales (15 and 45 day mean) we only found instantaneous links (not informing us about the directionality of the forcing). Note that we focus on summer (June, July, August), yet when using 60-day means, we extend into May, June, July, and August to increase sample-size (2 datapoints per year instead of 1).
Panel (a, g): lag 0 correlation maps of SST versus the western (eastern) RW timeseries. Panels (b–f) and (h–l): CENs between the respective SST pattern timeseries and the RW pattern timeseries for different temporal aggregations [1, 5, 10, 30, and 60]. The Link strength (link color) shows the MCI value (mean over significant links), which is the correlation strength, after removing the information of the parents of both variables. The Auto-strength (node color) shows the autocorrelation after regressing out the influence of its parents. The link labels indicate at which lags [in days] there was a causal link. CEN link is only plotted if they are significant at least 60 out of 70 perturbation experiments, similar for the indication of significance in panel a and g by black contour lines.
Since a CEN depicts causal links as a yes/no answer, we implement a sensitivity analysis to ensure we present robust links only. We do this by repeating the PCMCI analysis 70 times on slightly different subsets of data (“Method”). For the CENs, a link is only shown if it is significant (αFDR = 0.05) in 60 out of 70 perturbation experiments. The spread in the link strength that results from the sensitivity experiments also represents the uncertainty due to sampling. Given this spread, a double-sided t test is used to measure if the western SST-RW link strengths (n = 70 perturbations) are significantly different (α = 0.05) from the eastern SST-RW coupling (n = 70 perturbations), indicated with a * in Table 1.
The CENs for the west and east both show a positive two-way coupling between SST and the Rossby waves on daily timescales, but there are important differences (Fig. 2). The causal influence of the atmosphere on the ocean is more pronounced for the western US Rossby wave as compared to the eastern one. On the daily and 5-day timescale, the downward causal link for the west (RWW→SSTW) is stronger by about a factor 2 compared to the east (Table 1). Similarly, the instantaneous RW-SST link on these timescales is also stronger for the western RW (again by about a factor 2). On longer timescales than 5-day means, no robust directed links for the western RW are found (only instantaneous links).
On timescales longer than 5-day means, the influence of the ocean to the atmosphere is consistently stronger for the eastern Rossby wave compared to the western one. Using 60-day aggregated data, the 60-day lagged causal link SSTE→RWE is stronger by roughly a factor 10 (Table 1). This 60-day aggregated \({{{\mathrm{SST}}}}_{t - 1}^E \to {{{\mathrm{RW}}}}_t^E\) link is very robust and found to be causal by PCMCI in all the 70 perturbation experiments.
Figure 2 also shows that the \({{{\mathrm{SST}}}}_t^E\) timeseries has a higher persistence compared to \({{{\mathrm{SST}}}}_t^W\), as indicated by the higher auto-strength values (color of SST nodes). The auto-strength value is similar to the conventional autocorrelation, but accounts for factors that might artificially inflate it. For Fig. 2f, l, the auto-strength is calculated by the partial correlation of SSTt versus SSTt-1, conditioned on SSTt-2 (parcorr(SSTt-1, SSTt|SSTt-2)).
Note that for the eastern RW, for timescales longer than daily, there are no causal links from the atmosphere to the ocean. More precisely, the \(parcorr\left( {{{{\mathrm{RW}}}}_{t - 1}^E \to {{{\mathrm{SST}}}}_t^E|{{{\mathrm{SST}}}}_{t - 1}^E} \right)\) link is non-significant. From this, it can be deduced that the higher persistence of \({{{\mathrm{SST}}}}_t^E\) in the first place results from the past SST state (\({{{\mathrm{SST}}}}_{t - 1}^E\)) with only a minor influence of antecedent atmospheric forcing (\({{{\mathrm{RW}}}}_{t - 1}^E\)).
To get a better understanding on the interaction between RWE and SST prior to the summer, we calculate the ocean-atmosphere coupling between SST and the eastern RW for winter and spring (see Supplementary Note 1). The ensure that we focus on the same RW pattern, we project the summer eastern RW pattern (as defined Fig. 1b) onto the winter and spring z500 field. Supplementary Fig. 8 verifies how the Rossby wave timeseries correlates with z500 variability. For JJA we retrieve a pattern very similar to what is shown in Fig. 1b, confirming that our \({{{\mathrm{RW}}}}_t^E\) index is a good proxy for the eastern Rossby wave. In winter and spring, the \({{{\mathrm{RW}}}}_t^E\) index projects strongly on the same eastern Rossby wave and additionally correlates with the tropical belt and is again similar to the Pacific-North-American pattern and the ENSO-forced teleconnection called the atmospheric bridge, which starts above the ENSO region and arcs over the Pacific-North American domain41. In Supplementary Fig. 9 the correlation maps in winter (panel a) and spring (panel g) between SST and the \({{{\mathrm{RW}}}}_t^E\) index show a clear resemblance to main features of the PDO pattern in its negative phase. The CENs in panels b–f show that during winter, we find a strong downward forcing (atmosphere-to-ocean). For spring, in addition to a strong downward forcing, we also observe two-way coupling on the 5-day mean timescale (panels h–l). In the next section, we use partial correlation to further investigate the importance of different processes in winter and spring for the upward (ocean-to-atmosphere) forcing that we find in summer (Fig. 2l).
Explaining the long-lead causal link
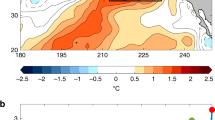
Here we show that the long-lead upward ocean-forcing that drives the eastern US Rossby wave in summer (as identified above), is closely related to low-frequency PDO variability. From here on, we work with 2-month mean data (instead of 60-day means) to ease interpretation. On the 2-month mean timescale, eastern RW correlation pattern is clearly in phase with the PDO pattern, while the western RW is not. This can be seen in Fig. 3 which shows the PDO (1st EOF loading) pattern together with the instantaneous and lag-1 (corresponding to a 2-months lag) correlations maps between SSTs and the western and eastern RW, respectively.
Panel (a) and (c) show the western RW, panel (b) and (d) show the eastern RW. The Rossby wave patterns are still the as depicted in Fig. 1, yet the data is now aggregated to 2-month means. For the significance (αFDR = 0.05), we correct for the False Discovery Rate using the Benjamini/Hochberg correction. Gridcells are highlighted by the thin black contour lines if they are significant at least 5 out of 10 training subsets. The thick contour lines indicate the negative PDO pattern (1st EOF loading pattern) ranging from −0.7 (black dashed) to 0 (green solid) to 0.7 (black solid).
In Fig. 4, we investigate how the intra-seasonal evolution of the eastern Rossby wave, ENSO and PDO (at lag 2) affect the SSTA signal at lag 1. We do so by creating lag-1 correlation maps that are conditioned on different actors at lag 2. Figure 4a shows the SST-RWE correlation pattern at lag 1 (2 months). The correlation values and their significance are reduced when conditioning on RWE at lag 2 (Fig. 4b), implying that the Rossby wave activity at lag 2 plays some role in forcing the SST signal at lag 1. We calculate the low-frequency (winter-to-spring mean) \(\overline {{{{\mathrm{ENSO}}}}_{t - 2}}\)and \(\overline {{{{\mathrm{PDO}}}}_{t - 2}}\) timeseries as described in “Method”. When conditioning on \(\overline {{{{\mathrm{ENSO}}}}_{t - 2}}\), the SST signal does not weaken indicating that the mean ENSO state has little or no effect (Fig. 4c). Figure 4d shows the SSTt-1 influence on \({{{\mathrm{RW}}}}_t^E\)is most effectively weakened when conditioning on the winter-to-spring PDO variability (\(\overline {{{{\mathrm{PDO}}}}_{t - 2}}\)). Thus, most of the information originates from winter-to-spring PDO variability. These results show that the lagged SST signal - relevant for forcing the May–August eastern RW (\({{{\mathrm{RW}}}}_t^E\)) - is influenced in the first place by the winter-to-spring PDO state. An additional (but smaller) influence is provided by the prior atmospheric wave forcing. That they both show an influence is in line with strong co-variability between the PDO and RWE in spring (Supplementary Fig. 10).
Panel (a) shows the correlation map between SSTt-1 and \({\rm{RW}}_t^E\), whereas panel (b), (c) and (d) show the partial correlation maps that are removing the effect of (b) the \({\rm{RW}}_{t - 2}^E\) timeseries, the 6-month rolling mean (c) ENSO and (d) PDO timeseries. The rolling mean is defined at (and prior to) lag 2. Gridcells are highlighted by contour lines if they are significant (αFDR = 0.05) at least 5 out of 10 training subsets.
Temperature predictability
A robust lagged Pacific SST signal can only be found for temperature in the eastern US cluster, but not for the west (Fig. 5). This is in line with the lack of any long-lead causal links to the western RW (Fig. 2) or any significant lagged SST correlation for western US temperature variability (Fig. 1d). For the eastern US, the lagged SST signal is clearly strongest for July–August (Fig. 5). The correlating regions (Fig. 5, July–August mean) are clustered into the mid- and eastern Pacific region (Fig. 6), these two regions are used as a mask to calculate 1-dimensional spatial mean timeseries (“Method”). These timeseries will be used for predictions in “Results”. This method is referred as the response-guided dimensionality reduction (DR), i.e., the dimensionality reduction is based on precursor regions that correlate with the target variable16,42.
a Response guided dimensionality reduction (RGDR) and (b) (climate index) PDO timeseries. For the RGDR method, the same lag 1 (May–June SST) correlation analysis is done as shown for the TE July–August temperature in Fig. 5. For the EOF analysis, all months (Jan–Dec) are used.
We make out-of-sample Ridge Regression forecasts for July–August mean TE using two different precursor sets, i.e., (a) precursors found by the response-guided DR and (b) the PDO climate index timeseries (Fig. 6). The test data is obtained by splitting the data into training and test years using a 10-fold stratified cross-validation (see “Method”). Both DR methods are done on only training data and extrapolated to the test set to make out-of-sample predictions. We use the correlation coefficient and the Mean Absolute Error Skill Score (MAE-SS) for the verification. The latter is defined as \({{{\mathrm{MAE - SS}}}} = 1 - \frac{{{{{\mathrm{MAE}}}}_{forecast}}}{{{{{\mathrm{MAE}}}}_{clim}}}\), where MAEdim is the error when always predicting the climatological mean of the TE anomalies (≈0).
The response-guided DR leads to better forecast skill compared to using the PDO as a predictor (Table 2 and “Discussion” for more details). We construct Ridge Regressions using lag 1, lag 1 and 2, and lag 1, 2 and 3 (Table 2). We observe that using lag 1 and 2 (May–June and March–April) and the Response-guided DR provides the best predictive skill for July–August temperatures in eastern US (out-of-sample correlation value of 0.62). Hence, although there is a clear link to PDO variability, using a more tailored method to extract the signal renders a clear boost in skill (see “Discussion”).
Window of opportunity by winter-to-spring PDO state
July–August mean eastern US temperature are substantially more predictable when the forecasted summer is preceded by a strong (instead of a weak) winter-to-spring PDO state (Fig. 7). We demonstrate this by comparing the skill during the 50% of years with strongest winter-to-spring PDO states (either positive or negative) with the skill of the 50% with weak PDO states. The winter-to-spring PDO state is defined by the DJFMAM mean PDO. During strong positive or negative PDO states, there is a 54% reduction in the MAE compared to years with weak PDO states (Fig. 7, left column). When comparing the forecast skill to the climatological benchmark (MAE-SS), we observe that most skill is present in these strong PDO state years (Fig. 7, right column). This result is robust when using different train-test splits. If we make a stricter selection of anomalous winter-to-spring PDO states (top 30%), the skill further increases with MAE-SS values ranging between 0.48 and 0.57 and correlation values ranging between 0.85 and 0.89 (Supplementary Table 1). During weak PDO state years, the model hardly outperforms a climatological mean temperature forecast.
The strong PDO sub-set contains 21 (50%) years with the most anomalous DJFMAM mean PDO states. The weak PDO sub-set contains the other 21 years. The whiskers indicate the 95% confidence intervals, data outside the confidence interval are shown as outliers, red line shows the median, black line shows the quartiles, and the green triangle shows the mean.
Similarly, using partial correlation to remove the \(\overline {{{{\mathrm{PDO}}}}_{t - 2}}\) from the lag 1 SST timeseries and the \(\overline {{{{\mathrm{PDO}}}}_{t - 3}}\) from the lag 2 SST timeseries causes the forecast skill to vanish (mean MAE-SS\(= 0.03_{ - 0.23}^{0.20}\), with the lower and upper subscript denoting the C.I. at α = 0.05). Once more this indicates that the low-frequency antecedent PDO evolution is the background mechanism that is vital for predictability and that it can be used to identify a window of opportunity at the time of the forecast.
Discussion
We show that two different Rossby waves are important drivers of temperature variability in western and eastern US, respectively (Fig. 1a, b). While both Rossby waves correlate equally strong with surface temperatures over the US on synoptic timescales (15-day means), a long-lead signal between temperature and SST is only present for the eastern US (Fig. 1c–f). As hypothesized in the introduction, the CEN analyses confirms that the associated summer eastern RW is forced by the low-frequency north-Pacific SST variability (Fig. 2).
We show that low-frequency PDO variability is a crucial aspect for this long-lead signal, and thus for predictability (“Results”). In our view, the mid- and eastern Pacific timeseries are the direct causal precursors, while the antecedent low-frequency PDO dynamics are vital to develop the persistent and high amplitude signal that is needed to force a persistent RW response in summer. This is in line with modeling experiments which show that a persistent [order of 2 months] SST forcing is needed for a barotropic (RW-like) response to develop and that a stronger boundary forcing (higher amplitude SSTA) results in a stronger atmospheric response13. To first order, the PDO pattern arises from extra-tropical atmospheric forcing and the corresponding oceanic Rossby wave response43,44. This downward forcing is strongest in winter31, as is also observed in our winter CEN (Supplementary Note 2). Multiple processes are important for strengthening the PDO variability, such as (1) the re-emergence mechanism32, (2) the ENSO teleconnection named “the atmospheric bridge”41,45,46 and (3) active ocean-atmosphere coupling43,46 and the associated local positive feedbacks47. However, the relative importance of these processes is uncertain. Our CEN analysis quantifying the SST-RW coupling for winter and spring indeed support that processes (2) and (3) strengthen the PDO pattern (Supplementary Note 2). The CENs show that forcing in winter and spring is predominantly downward (from atmosphere to ocean). In spring, we also observe a more pronounced two-way feedback. Finally, the forcing is predominantly upward in summer. This is consistent with observational findings (their Fig. 3)21 and previous work23,48.
Since persistence is a requirement to get a clear barotropic RW response, the spatial patterns of any low-frequency mode of SST variability will provide a physical constraint on the location and phase-position of quasi-stationary Rossby waves and therefore on the downstream surface impact of the Rossby waves. Results for the western RW supports the latter hypothesis, as its wave pattern is not in phase with the PDO pattern (Fig. 3). We argue that this is the reason why the western RW is not forced by the north-Pacific SSTs at longer timescales (Fig. 2), and therefore no long-lead SST signal is found for western US temperature (Fig. 1d). In contrast, the eastern RW is in phase with the PDO pattern (Fig. 3) resulting in a long-lead SST signal that forces the atmosphere (Fig. 2). The persistent SST forcing originates from the co-evolution of winter-to-spring PDO dynamics and the associated ocean-atmosphere interactions. Hence, these are the key process behind predictability for the eastern US summer temperature.
We show that using the mid- and eastern Pacific SST timeseries yields higher forecast skill compared to using the PDO index as a predictor (“Results”), in line with previous work16. The PDO timeseries captures variability in a much larger domain over the Pacific and therefore includes disturbances that are irrelevant to the Rossby wave forcing mechanisms described in the introduction. In contrast, the mid- and eastern Pacific regions are the core PDO regions which – based on theoretical and modeling experiments – are expected to force an eastern RW-like response13,21. Moreover, while the PDO (simply explaining most variance of SSTA in the North Pacific) suggests that the mid- and eastern Pacific regions are part of the same variability, the correlation between the mid- and eastern Pacific timeseries is only −0.56. Using a separate mid- and eastern Pacific SST timeseries (extracted by the Response-Guided Dimensionality Reduction, RGDR), enables the Ridge regression to (1) learn a more detailed model and (2) use timeseries that are more directly related to the forcing of the RW. Nevertheless, the importance of the background PDO state is further illustrated by the considerable increase in forecast skill for the July–August mean temperature for years with a persistent high amplitude winter-to-spring PDO state (“Results”).
Seasonal dependence of the lagged SST signal for eastern US temperature is evident from Fig. 5. The exact reason for this specific window of predictability is not fully understood yet. It might be explained by (1) the atmosphere being less chaotic in summer which results in a higher signal-to-noise-ratio or, (2) the seasonal cycle of solar radiation resulting in a stronger impact of high-pressure systems on surface temperature during summer months or (3), potentially amplifying effects of soil-moisture deficits become important near the end of summer49. We also note that it is likely that the persistent summer eastern RW – forced by spring SSTs – leads to both higher temperatures and reduced rainfall, thereby simultaneously affecting summer soil-moisture content. Similarly, the winter-to-spring atmospheric variability that is associated with a strong winter-to-spring PDO state might already affect rainfall over eastern US in those months.
We unraveled the role of ocean-atmosphere feedbacks that are driving long-lead predictability of eastern US summer temperature based on careful analyses with causal discovery algorithms. As shown in “Results”, understanding the sources of predictability paves the way for identifying windows of enhanced S2S predictability and our approach might be successful in finding other potential windows of predictability.
Method
Data
Our analysis relies on 42 years of data (1979–2020) from the ERA-5 reanalysis50. Daily maximum 2-meter temperature (on a 0.25° x 0.25° grid) is calculated by computing the daily maximum of the “maximum 2 m temperature since previous post-processing”, with a step-size of 1 h. We use daily mean sea surface temperature (SST), geopotential height at 500 hPa (z500) and meridional wind at 300 hPa (v300), all on a 1 x 1 degree grid. Z500 Denotes the thickness of the atmospheric layer at 500 hPa, therefore, it clearly discriminates between high- and low-pressure systems, and it is directly affected by vortex stretching/compression that can arise due to diabatic anomalies51. Meridional wind (v) at 300 hPa is less affected by lower tropospheric disturbances, therefore, v300 is often used to investigate large-scale Rossby wave patterns8,52.
For the daily data, we determine the seasonal cycle by (1) applying a 25-day rolling mean, (2) calculating the multi-year mean of each day-of-year of the smoothened timeseries and (3) then construct the final seasonal cycle by fitting the first 6 annual harmonics to the calculated seasonal cycle based on the smoothened data. The 1-dimensional target timeseries for the analyses in “Results” are aggregated from pre-processed daily data to 2-month means. We also use raw monthly mean SST data as input when analyzing data on the 2-monthly timescale for computational efficiency. For the raw monthly mean SST data, we construct the seasonal cycle by calculating the multi-year mean of each month. We subtract the seasonal cycle from the daily/monthly data and remove the climate change signal by subtracting the long-term linear trend of each gridcell.
Clustering North American temperature events
We use Hierarchical agglomerative clustering to identify coherently behaving regions15 (Fig. 8). We apply the clustering on US gridcells and a part of Canada and Greenland (up to 70 °N). Regions that tend to experience temperature above the 66th percentile simultaneously are clustered together. Because the dynamics behind temperature variability might be different at high elevation, we excluded all gridcells with an altitude above 1500 m (e.g., the Rocky Mountains). We performed the clustering for a range of temporal aggregations [5, 10, 15, 30 days] and number of clusters [4, 5, 6, 7, 8, 9, 10] to test for robustness. From the results presented in the Supplementary Method 1, we choose the two robust clusters, to simplify notations we refer to this as the western and eastern US cluster. By testing the spatial decorrelation radius within each cluster (Supplementary Fig. 2), we verified that the size of the clusters is appropriate. Of these two clusters an area-weighted spatial mean temperature is calculated, rendering two 1-dimensional timeseries. The timeseries convey the western and eastern US daily maximum temperature variability, these are referred to by TW and TE, respectively.
Link between temperature, circulation, and sea surface temperature
To quantify the temperature versus z500 relationship, we aggregated to 15-day means and calculate one-point correlation maps (αFDR = 0.05) at lag 0 for both the west (TW) and eastern US (TE) temperature timeseries. We account for the False Discovery Rate using the Benjamini/Hochberg correction53,54. For Fig. 1 and Fig. 2a, g, we test for robustness of the correlation maps by re-calculating them on 70 subsets (36 years) sampled from the 42 years of data. See “Method” for more information. In the one-point correlation maps, gridcells are only presented as significant if they are found significant in 60/70 subsets of data. The RW pattern (RWpattern) is defined by the significantly correlating gridcells within the green rectangle as shown in the z500 correlation maps (Fig. 1a, b). We reduce it to a 1-dimensional timeseries by calculating the area-weighted spatial covariance, i.e.,
using only the Nsignificantly correlating grid cells. Where wi denotes the area weight at grid cell i, RWpattern denotes a vector with the correlation values of the significantly correlating grid cells, the overbar denotes the spatial mean and z(t) denotes the geopotential height field at time t. Temperature correlates strongest with local geopotential height. The higher correlation values result in a much stronger weight for the local high-pressure system compared to adjacent lows and highs of the RW pattern. To obtain a RW timeseries where the high and lows have equal weights, we set all significant positively (negatively) correlating gridcells to 1 (−1). This is done only for the RW timeseries. We tested other options, but this method led to a timeseries that was best capable to reproduce the RW pattern that the timeseries is supposed to capture (Supplementary Method 2). We use this procedure to calculate both the west (\({{{\mathrm{RW}}}}_t^W\)) and eastern US \(\left( {{{{\mathrm{RW}}}}_t^E} \right)\) RW timeseries, which we will use for the PCMCI and (partial) correlation analysis.
Causal effect network using PCMCI
To obtain the link between the RW timeseries and north-Pacific SST, we first calculate one-point correlation maps with SSTA versus both the west and eastern RW timeseries (Eq. 1). These correlation maps show the RW imprint on the SSTA. Substituting RWpattern for SSTpattern and z for SST in Eq. (1), we obtain a 1-dimensional timeseries for the SST pattern. At this point, we have the SST pattern timeseries and the RW pattern timeseries, i.e., (\({{{\mathrm{SST}}}}_t^W\) and \({{{\mathrm{RW}}}}_t^W\)) and (\({{{\mathrm{SST}}}}_t^E\) and \({{{\mathrm{RW}}}}_t^E\)).
To quantify the SST-RW coupling strength, we use the PCMCI algorithm55 in combination with conditional independence (CI) tests based on partial correlation56. For each significantly correlating link, a partial correlation analysis is performed which is conditioning on all relevant information that might statistically inflate the correlation link strength.
The relevant information is found by step (1) of the PCMCI algorithm, which attempts to find the parents \(\left( {{{\mathcal{P}}}} \right)\) of both to-be-tested variables through an iterative process of CI tests. In this case, we only have two variables (\(x_t^i\) and \(x_t^j\)). For example, the first parent subset \({{{\mathcal{P}}}}^0(x_t^i)\) consists of all possible lagged correlations (the lag is indicated by τ) with p value < 0.05. The maximum lag for lagged correlations is restricted by the parameter τmax. Next, each timeseries in subset \({{{\mathcal{P}}}}^0(x_t^i)\) is only kept if it passes all partial correlations tests (e.g., \(parcorr(x_{t - \tau }^j,x_t^i|z)\)), where z is a single variable of the subset \({{{\mathcal{P}}}}^0\) that is not \(x_{t - \tau }^j\). All variables that are conditionally dependent are stored in the second subset \({{{\mathcal{P}}}}^1(x_t^i)\). Next, all possible CI tests are performed again with the cardinality of z increased from 1 to 2. Using our settings, the cardinality may increase up to the total size (minus one) of the first parent subset \({{{\mathcal{P}}}}^0(x_t^i)\). Once the final sets of parents are estimated, i.e., \(\hat {{{\mathcal{P}}}}\left( {x_t^i} \right)\) and \(\hat {{{\mathcal{P}}}}\left( {x_t^j} \right)\), step (2) of PCMCI calculates the Momentary Conditional Information (MCI), which is using partial correlation and is defined as,
where \(\hat {{{\mathcal{P}}}}\left( {x_t^i} \right)\backslash \left\{ {x_{i - \tau }^i} \right\}\) are the estimated parents of \(x_t^i\), excluding the to-be-tested variable \(x_{i - \tau }^i\). All links are tested in both directions, as well as instantaneous, i.e., from τmin = 0 up to τmax. If the MCI is significant (αFDR = 0.05) when conditioning on all the parents and assuming the underlying assumptions are satisfied35, the link is deemed causal. When we state there is a causal link, it should be interpreted as causal within the context of the experiment, i.e., not the result of a spurious link due to the past SST evolution or RW occurrences, with the past (i.e., maximum lag considered) being limited by τmax.
Sensitivity analyses are performed by re-iterating the analysis workflow, i.e., from calculating the RW pattern and timeseries (“Method”) up to the CEN, each time using a unique set of 36 out of the 42 years of data. Since we apply PCMCI repeatedly on different subsets of data and PCMCI tests many different dependency tests within the algorithm, we correct for the False Discovery Rate (FDR) using the Benjamin/Hochberg correction. With these sensitivity analyses, we are propagating uncertainties due to leaving out data through the entire workflow. Similar types of robustness/stability tests are becoming more common in the machine learning community57,58. The results of the sensitivity analyses are also used to quantitively compare the western vs the eastern CENs in Table 1.
Partial correlation maps
We use the partial correlation conditional independence tests to construct latitude, longitude maps where we test the influence of a potential confounder of interest. We use these maps to regress out the influence of the RW at lag 2, the low-frequency ENSO and the low-frequency PDO timeseries when testing the link between SSTt-1 and \({{{\mathrm{RW}}}}_t^E\). The low-frequency variability is obtained by apply a 6-month rolling mean (indicated by \(\overline {{{{\mathrm{ENSO}}}}_t}\)and \(\overline {{{{\mathrm{PDO}}}}_t}\)). When selecting the dates at lag 2 we approx. select the winter-to-spring mean timeseries. We ensure that the rolling mean is based on data prior and including lag 2 to avoid information leakage. The ENSO is calculated using the area-weighted nino3.4 bounding box [5°N–5°S, 170–120°W]. The PDO pattern is found by calculating the first area-weighted Empirical Orthogonal Function of Pacific SSTA [115–250°E,20–70°N]. For the (partial) correlation maps in Fig. 4, we use the same cross-validation as introduced in “Method” to obtain different subsets of data. Hence, the partial correlation maps are calculated 10 times on subsets of 36 years.
Forecasting
To investigate the seasonal dependence, we use a response-guided approach16,42,59,60. This approach encompasses methods that reduce dimensionality of the precursor field based on a relationship to a target, instead of using some statistic of the precursor field (e.g., maximizing the explained variance). First, we calculate one-point correlation maps based on training data (at lag 1). Second, adjacent regions of the same correlation sign are grouped together into precursor regions. This is done using the Density-based spatial clustering of applications with noise (DBSCAN)61. Third, for each precursor region, an area-weighted and correlation-value weighted spatial mean is calculated.
The resulting 1-dimensional timeseries are standardized and then fitted on the training data using a Ridge regression. The regularization parameter α is tuned using the default Generalized Cross-Validation62. The alphas range between 0.1 and 1.5, with 25 steps spaced evenly on a log scale with base = 10. The standardizing and fitting are done on the same training data as is used to calculate the correlation maps.
We use the Pearson-r correlation coefficient and mean absolute error skill score (MAE-SS) for verifying the deterministic forecasts. The MAE gives equal weights to each observation/forecast pair, making the analysis we present in Fig. 7 a fairer comparison between the two data subsets. It is defined as, \(MAE = \frac{1}{n}\mathop {\sum }\nolimits_{i = n}^n \left| {y_{pred,t} - y_{true,t}} \right|,\) where n are the number of observation/forecast pairs, ypred,i is the predicted value at timestep t and ytrue is the observation at timestep t.
We implement a stratified 10-fold cross-validation (training sets consist of 36 or 35 yrs, test sets 4 or 5 yrs). The stratification is achieved by creating the training sets, such that these contain similar statistics in terms of the magnitude of July-August temperature values. This ensures that the training/test sets are good approximations of the climatological US temperature dynamics. Since we cannot reliably estimate the skill score based on a single test set of 4 years. We implement a double cross-validation for tuning the regularization parameter within each training sample, as done in16. This means that we fit (and tune) a statistical model on each training set and use that to forecast the test set. The verification metrics are computed on the 10 concatenated test sets.
Warm temperature periods are defined as 15-day mean temperature exceeding the 66th percentile. The white gridcells indicate (the Rocky) mountains (altitude > 1500 metre). These were left out of the analysis because temperature variability at high altitudes might have a different relationship with Rossby wave variability compared to low altitude gridcells. The purple contour lines indicate the western and eastern US spatial clusters.
Data availability
All data used in this study is publicly available. ERA-5 SST and mx2t is available at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview and geopotential height at 500 hPa (z500) and meridional wind at 300 hPa (v300) data are available at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=overview. The PNA timeseries from the Climate Prediction Center of NCEP/National Oceanic and Atmospheric Administration (NOAA) was downloaded from the KNMI Climate Explorer, https://climexp.knmi.nl/getindices.cgi?WMO=NCEPData/cpc_pna_daily&STATION=PNA&TYPE=i&id=someone@somewhere&NPERYEAR=366 on 01-09-2020.
Code availability
Python code for all output presented in this article are publicly available in the Github release: https://github.com/semvijverberg/RGCPD/releases/tag/v0.95-a.
Change history
28 March 2022
In this article the title was incorrectly given as ‘The role of the Pacific Decadal Oscillation and ocean-atmosphere interactions in driving US temperature variability’ but should have been ‘The role of the Pacific Decadal Oscillation and ocean-atmosphere interactions in driving US temperature predictability’. The original article has been corrected.
References
Wolf, G., Brayshaw, D. J., Klingaman, N. P. & Czaja, A. Quasi‐stationary waves and their impact on European weather and extreme events. Q. J. R. Meteorol. Soc. 144, 2431–2448 (2018).
Röthlisberger, M., Frossard, L., Bosart, L. F., Keyser, D. & Martius, O. Recurrent synoptic-scale Rossby wave patterns and their effect on the persistence of cold and hot spells. J. Clim. JCLI-D.- 18-0664, 1 (2019).
Lau, W. K. M. & Kim, K.-M. The 2010 Pakistan Flood and Russian heat wave: teleconnection of hydrometeorological extremes. J. Hydrometeorol. 13, 392–403 (2012).
Petoukhov, V., Rahmstorf, S., Petri, S., Schellnhuber, H. J. & Joachim, H. Quasiresonant amplification of planetary waves and recent Northern Hemisphere weather extremes. Proc. Natl Acad. Sci. 110, 5336–5341 (2013).
Wang, H., Schubert, S., Koster, R., Ham, Y. G. & Suarez, M. On the role of SST forcing in the 2011 and 2012 extreme U.S. heat and drought: a study in contrasts. J. Hydrometeorol. 15, 1255–1273 (2014).
Kornhuber, K. et al. Amplified Rossby waves enhance risk of concurrent heatwaves in major breadbasket regions. Nat. Clim. Chang. 10, 48–53 (2020).
Hoskins, B. J. & Karoly, D. J. The steady linear response of a spherical atmosphere to thermal and orographic forcing. J. Atmos. Sci. 38, 1179–1196 (1981).
Kornhuber, K. et al. Summertime planetary wave resonance in the Northern and Southern hemispheres. J. Clim. 30, 6133–6150 (2017).
Hoskins, B. J. & Ambrizzi, T. Rossby wave propagation on a realistic longitudinally varying flow. J. Atmos. Sci. 50, 1661–1671 (1993).
Branstator, G. & Teng, H. Tropospheric waveguide teleconnections and their seasonality. J. Atmos. Sci. 74, 1513–1532 (2017).
Ding, Q., Wang, B., Wallace, J. M. & Branstator, G. Tropical-extratropical teleconnections in boreal summer: Observed interannual variability. J. Clim. 24, 1878–1896 (2011).
Di Capua, G. et al. Dominant patterns of interaction between the tropics and mid-latitudes in boreal summer: causal relationships and the role of timescales. Weather Clim. Dyn. 1, 519–539 (2020).
Ferreira, D. & Frankignoul, C. The transient atmospheric response to midlatitude SST anomalies. J. Clim. 18, 1049–1067 (2005).
Switanek, M. B., Barsugli, J. J., Scheuerer, M. & Hamill, T. M. Present and past sea surface temperatures: a recipe for better seasonal climate forecasts. Weather Forecast 35, 1221–1234 (2020).
McKinnon, K. A., Rhines, A., Tingley, M. P. & Huybers, P. Long-lead predictions of eastern United States hot days from Pacific sea surface temperatures. Nat. Geosci. 9, 389–394 (2016).
Vijverberg, S., Schmeits, M., van der Wiel, K. & Coumou, D. Subseasonal statistical forecasts of Eastern U.S. hot temperature events. Mon. Weather Rev. 148, 4799–4822 (2020).
Simpson, I. R., Shaw, T. A. & Seager, R. A diagnosis of the seasonally and longitudinally varying midlatitude circulation response to global warming. J. Atmos. Sci. 71, 2489–2515 (2014).
Baker, H. S. et al. Forced summer stationary waves: the opposing effects of direct radiative forcing and sea surface warming. Clim. Dyn. 53, 4291–4309 (2019).
Raymond, C. et al. Projections and Hazards of Future Extreme Heat. In (eds W. T., Pfeffer, J. B., Smith & K. L., Ebi) The Oxford Handbook of Planning for Climate Change Hazards 6–11. (Oxford Handbooks Online) Oxford University Press. https://doi.org/10.1093/oxfordhb/9780190455811.013.59 (2019).
Frankignoul, C. & Hasselmann, K. Stochastic climate models, Part II Application to sea-surface temperature anomalies and thermocline variability. Tellus 29, 289–305 (1977).
Kushnir, Y. et al. Atmospheric GCM Response to Extratropical SST Anomalies: Synthesis and Evaluation*. J. Clim. 15, 2233–2256 (2002).
Peng, S. & Robinson, W. A. Relationships between atmospheric internal variability and the responses to an extratropical SST anomaly. J. Clim. 14, 2943–2959 (2001).
Frankignoul, C. & Sennéchael, N. Observed influence of North Pacific SST anomalies on the atmospheric circulation. J. Clim. 20, 592–606 (2007).
Liu, Z. & Wu, L. Atmospheric response to North Pacific SST: The role of ocean-atmosphere coupling. J. Clim. 17, 1859–1882 (2004).
Zhou, G., Latif, M., Greatbatch, R. J. & Park, W. State dependence of atmospheric response to extratropical North Pacific SST anomalies. J. Clim. 30, 509–525 (2017).
Zhou, G. Atmospheric response to sea surface temperature anomalies in the mid-latitude oceans: a brief review. Atmos. - Ocean 57, 319–328 (2019).
Branstator, G. Circumglobal teleconnections, the Jet Stream Waveguide, and the North Atlantic Oscillation. J. Clim. 15, 1893–1910 (2002).
Manola, I., Selten, F., De Vries, H. & Hazeleger, W. ‘Waveguidability’ of idealized jets. J. Geophys. Res. Atmos. 118, 10432–10440 (2013).
Lorenz, D. J. & Hartmann, D. L. Eddy-zonal flow feedback in the Northern Hemisphere winter. J. Clim. 16, 1212–1227 (2003).
Deser, C., Tomas, R. A. & Peng, S. The transient atmospheric circulation response to North Atlantic SST and sea ice anomalies. J. Clim. 20, 4751–4767 (2007).
Newman, M. et al. The Pacific decadal oscillation, revisited. J. Clim. 29, 4399–4427 (2016).
Deser, C., Alexander, M. A., Xie, S.-P. & Phillips, A. S. Sea Surface Temperature Variability: Patterns and Mechanisms. Ann. Rev. Mar. Sci. 2, 115–143 (2010).
Namias, J. & Born, R. M. Temporal coherence in North Pacific sea-surface temperature patterns. J. Geophys. Res. 75, 5952–5955 (1970).
Deser, C., Alexander, M. A. & Timlin, M. S. Understanding the persistence of sea surface temperature anomalies in midlatitudes. J. Clim. 16, 57–72 (2003).
Runge, J. Causal network reconstruction from time series: From theoretical assumptions to practical estimation. Chaos Interdiscip. J. Nonlinear Sci. 28, 075310 (2018).
Runge, J., Petoukhov, V. & Kurths, J. Quantifying the strength and delay of climatic interactions: the ambiguities of cross correlation and a novel measure based on graphical models. J. Clim. 27, 720–739 (2014).
Liu, Z. et al. Recent contrasting winter temperature changes over North America linked to enhanced positive Pacific‐North American pattern. Geophys. Res. Lett. 42, 7750–7757 (2015).
Lopez, H. & Kirtman, B. P. ENSO influence over the Pacific North American sector: uncertainty due to atmospheric internal variability. Clim. Dyn. 52, 6149–6172 (2019).
Sprites, P., Glymour, C. & Scheines, R. Causation, Prediction, and Search. 2nd edn in (MIT press 2001).
Runge, J., Heitzig, J., Marwan, N. & Kurths, J. Quantifying causal coupling strength: A lag-specific measure for multivariate time series related to transfer entropy. Phys. Rev. E 86, 061121 (2012).
Alexander, M. A. et al. The atmospheric bridge: The influence of ENSO teleconnections on air-sea interaction over the global oceans. J. Clim. 15, 2205–2231 (2002).
Kretschmer, M., Runge, J. & Coumou, D. Early prediction of extreme stratospheric polar vortex states based on causal precursors. Geophys. Res. Lett. 44, 8592–8600 (2017).
Zhang, L. & Delworth, T. L. Analysis of the characteristics and mechanisms of the pacific decadal oscillation in a suite of coupled models from the Geophysical Fluid Dynamics Laboratory. J. Clim. 28, 7678–7701 (2015).
Liu, Z. & Di Lorenzo, E. Mechanisms and predictability of pacific decadal variability. Curr. Clim. Chang. Rep. 4, 128–144 (2018).
Newman, M., Compo, G. P. & Alexander, M. A. ENSO-forced variability of the pacific decadal oscillation. J. Clim. 16, 3853–3857 (2003).
Lau, N. C. & Nath, M. J. Impact of ENSO on SST variability in the North Pacific and North Atlantic: Seasonal dependence and role of extratropical sea-air coupling. J. Clim. 14, 2846–2866 (2001).
Luo, H., Zheng, F., Keenlyside, N. & Zhu, J. Ocean–atmosphere coupled Pacific Decadal variability simulated by a climate model. Clim. Dyn. 54, 4759–4773 (2020).
Liu, Q., Wen, N. & Liu, Z. An observational study of the impact of the North Pacific SST on the atmosphere. Geophys. Res. Lett. 33, 1–5 (2006).
Seneviratne, S. I. et al. Earth-Science Reviews Investigating soil moisture – climate interactions in a changing climate: a review. Earth Sci. Rev. 99, 125–161 (2010).
Copernicus Climate Change Service, (C3S). ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. Copernicus Climate Change Service Climate Data Store (CDS) (2017).
Holton, J. R. An introduction to dynamic meteorology. 4rd edn in (Elsevier Academic Press 2004).
Teng, H. & Branstator, G. Amplification of Waveguide Teleconnections in the Boreal Summer. Curr. Clim. Chang. Rep. 5, 1–12 (2019).
Benjamini, Y. & Hochberg, Y. Controlling the False Discovery Rate: a practical and powerful approach to multiple. Test. J. R. Stat. Soc. Ser. B 57, 289–300 (1995).
Wilks, D. S. “The stippling shows statistically significant grid points”: How research results are routinely overstated and overinterpreted, and what to do about it. Bull. Am. Meteorol. Soc. 97, 2263–2273 (2016).
Runge, J. et al. Inferring causation from time series in Earth system sciences. Nat. Commun. 10, 1–13 (2019).
Runge, J. et al. Identifying causal gateways and mediators in complex spatio-temporal systems. Nat. Commun. 6, 8502 (2015).
Szegedy, C. et al. Intriguing properties of neural networks. 2nd Int. Conf. Learn. Represent. ICLR 2014 - Conf. Track Proc. 1–10 (2014).
Belgiu, M. & Drăgu, L. Random forest in remote sensing: a review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 114, 24–31 (2016).
Bello, G. A. et al. ECML PKDD 2015 part II. Proceedings, Part II (2015).
Di Capua, G. et al. Long-lead statistical forecasts of the indian summer monsoon rainfall based on causal precursors. Weather Forecast 34, 1377–1394 (2019).
Schubert, E., Ester, M., Xu, X., Kriegel, H. P. & Sander, J. DBSCAN revisited, revisited: why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 42, 1–21 (2017).
Varoquaux, G. et al. Scikit-learn. GetMobile Mob. Comput. Commun. 19, 29–33 (2015).
Acknowledgements
S.V. would like to thank dr. Giorgia Di Capua for the fruitful discussions on the experiment design and the anonymous reviewer who greatly helped to improve the clarity of the manuscript. The authors acknowledge funding from the Netherlands Organization for Scientific Research (NWO), project: 016.Vidi.171.011.
Author information
Authors and Affiliations
Contributions
D.C. has made substantial contributions to the interpretation of the results and revisions of the text. S.V. has designed the study, performed the analysis, and led the writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vijverberg, S., Coumou, D. The role of the Pacific Decadal Oscillation and ocean-atmosphere interactions in driving US temperature predictability. npj Clim Atmos Sci 5, 18 (2022). https://doi.org/10.1038/s41612-022-00237-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-022-00237-7