Introduction

Pacific decadal variability has been historically understood in terms of the North Pacific-focused Pacific decadal oscillation (PDO1) and by the basin-scale interdecadal Pacific oscillation (IPO2). However, neither the PDO nor the IPO explicitly isolates the South Pacific contribution. Analogous to the PDO, the South Pacific decadal oscillation (SPDO3,4) has been identified and described as the South Pacific centre of action contributing to the entire basin-wide Pacific decadal variability. Studies4,5 show that the SPDO can be viewed as a combination of different dynamical processes operating on different timescales. Those processes include the atmospheric forcing, tropical El Niño–Southern Oscillation (ENSO) teleconnections, and the internal oceanic dynamics. Importantly, the atmospheric forcing associated with the Pacific-South American pattern 1 (PSA1) has been identified as the main stochastic driver of the SPDO4 (cf. Fig. 1 (left)). ENSO has been shown to impact extratropical variability via the atmospheric bridge6 and oceanic pathways7. Recent studies point out that extratropical ocean dynamics can feed back to the tropical Pacific via a sea surface temperature (SST) quadrupole pattern8 or a South Pacific meridional mode9,10,11. Despite showing similar spatial patterns8,9, the dynamical connections between the quadrupole pattern and the meridional mode in the South Pacific remain unclear. These oceanic processes act as extratropical precursors that might potentially guide the predictability and evolution of ENSO.

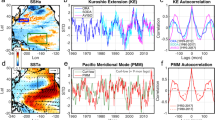
Fig. 1: Atmospheric forcing of the leading two SST modes in the South Pacific Ocean.
figure 1

The PSA1 (a) and PSA2 (b) patterns are obtained by regressing the monthly near-global Z500 anomalies (NCEP-NCAR; contour) and monthly SST anomalies (ACCESS-O; shade) onto the PSA1 and PSA2 time series, respectively. c, d The corresponding normalised PSA1 and PSA2 time series. e, f The time series of the leading two SST modes of variability in the South Pacific Ocean (ACCESS-O; black) are reconstructed (red) using an AR1 model forced by the PSA1 and PSA2 time series. The blue curve in (e) indicates the second integration forced by the SST SPDO time series. The units are in standard deviations (s.d.). The significance of the temporal correlations is estimated taking account of the effective number of degrees of freedom due to serial correlation48.

Full size image

In this study, we propose a paradigm for South Pacific climate variability whereby the atmospheric eastward-propagating PSA mode pair can excite extratropical South Pacific Ocean responses on multiple time scales ranging from seasonal to decadal. Although the South Pacific Ocean responds to fast-varying atmospheric forcing on distinct timescales, the resultant spatial SST features remain difficult to distinguish from the background state. This suggests that the characterisation and identification of predictable signals, and their sources, require careful separation of the climate signal and relevant noise processes. This remains a necessary but challenging problem.

Results and discussion

The atmospheric Pacific-South American mode

The PSA mode is represented by an eastward-propagating wave train extending from eastern Australia to Argentina, characterised in mid-tropospheric geopotential height by two invariant empirical orthogonal function (EOF) patterns with associated principal component (PC) time series (PSA1 and PSA2; see Fig. S1) whose phases are nearly in quadrature with each other and whose explained variances are of nearly equal amplitude12,13. In combination, they produce the single propagating PSA mode. The PSA mode is known to strongly influence the Antarctic cryosphere14, wind and significant wave heights across the Southern Hemisphere oceans, and the South American monsoon system including rainfall15 and weather and climate extremes over Brazil16.

The respective PSA1 pattern has been widely recognised as being highly correlated with ENSO, where previous studies argue that it results in part as an atmospheric response to ENSO15,17,18. While regression analysis shows that there is indeed a very close relationship between PSA1 and ENSO (Fig. 1a), the origin of this relationship remains an active area of research19,20. Meanwhile, the connection between the atmospheric PSA2 and tropical SST variability is less clear. Reference15 argues that PSA2 is responsible for the quasi-biennial component of ENSO (Fig. 1b). Although ENSO-PSA correlations are widely documented, the processes by which ENSO and the PSA mode are dynamically connected, and, in particular, how the PSA mode feeds back to the tropics, remain unclear.

Diverse views exist on the mechanisms that link the atmospheric PSA mode with ENSO. Some studies15,17,21,22 argue that the ENSO-PSA connection is directly linked via atmospheric Rossby wave propagation. However, other studies20,23,24 point out that synoptic-scale Rossby waves are primarily generated and trapped locally within the Southern Hemisphere subtropical and polar jet streams. Unlike the teleconnection between the Madden−Julian oscillation and North Atlantic oscillation25, there is little direct dynamical evidence in terms of Rossby wave source or wave activity flux19,20,26 to suggest that poleward propagating large-scale tropical Pacific Rossby waves, potentially initiated by ENSO variability, teleconnect the PSA to ENSO. Even if sufficient Rossby wave sources were to be generated in the equatorial Pacific, ray tracing theory and wave activity flux calculations make it readily apparent that they are blocked by a reflecting barrier associated with the presence of the subtropical jet, and low latitude wave breaking, from propagation to the midlatitudes. Instead, ref. 27 argues that the PSA mode is linked to ENSO via a direct modulation of the midlatitude jets by the thermal winds generated by tropical convection that is highly correlated with ENSO. This indirectly influences the interannual variability of coherent synoptic features forming within these midlatitude waveguides where local Rossby wave sources are prevalent.

Oceanic signal driven by the PSA mode

Analysis of South Pacific SST shows that the first two modes of SST variability, referred to as the SPDO3,4 and South Pacific SST quadrupole pattern8 (Fig. S2), are primarily driven by the variability associated with the atmospheric PSA1 and PSA2 patterns (Fig. 1e, f). Using a univariate first-order autoregressive (AR1) model28,29, we found that the integrated atmospheric PSA1 and PSA2 variability could explain a significant fraction of the variance of the first two SST modes in the South Pacific Ocean (Fig. 1e, f; R = 0.76 and 0.71, respectively; significant at >99% level; see the “Methods” section for details).

A second integration of the AR1 model (following a similar approach to refs. 4,30)—with the first integration being from the atmosphere to the surface ocean, and the second integration from the surface ocean to the subsurface ocean—reveals that the leading SST mode is further reddened by the extratropical upper ocean (Fig. 1e). The integrated SPDO signal (blue curve in Fig. 1e) resembles the time evolution of the leading vertically averaged temperature (VAT) mode through the upper 300 m of the ocean (see the “Methods” section), with a temporal correlation of R = 0.88 (statistically significant at the 99% level). To first order, we conclude that the South Pacific Ocean integrates the fast-varying atmospheric “noise” forcing to produce a “reddened” oceanic signal, with a pronounced increase in the amplitude of the spectrum at low frequencies and decreased amplitude at high frequencies, where the main potentially predictable signal is generated on the time scales of the ocean dynamics.

Oceanic noise driven by the PSA mode

The extratropical South Pacific not only responds via reddening processes to the fast-varying atmosphere but also via coherence resonances31. Specifically, the forcing due to coherent synoptic-scale disturbances in the atmosphere associated with the PSA imprints onto the surface ocean further enhancing internal SST variability at its preferred frequency. To examine this mechanism, we generalised the univariate AR1 model to a higher-dimensional multivariate field through the inclusion of SST anomalies in the tropical and South Pacific oceans using a linear inverse model32 (LIM; see “Methods” section). Previous studies have shown that the tropical and South Pacific oceans can be approximated as a stochastically forced linear system, where different dynamical processes are represented by distinct damping time scales via the decomposition of the LIM5,32,33,34,35.

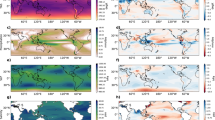
Figure 2 shows the fastest damped SST mode pair with a damping time scale of two months. This pair of complex patterns (Fig. 2a, b) constitutes a single propagating wave train with a complete cycle of 26 months. Along with the propagating features, the spatial patterns of the fastest damped modes also bear a strong resemblance to the atmospheric PSA1 and PSA2 patterns. Projecting the corresponding time series of the real and imaginary components of the fastest damped mode onto the monthly 500 hPa geopotential height (Z500) anomalies produces regression maps (Fig. 2c, d) that closely resemble the atmospheric PSA1 and PSA2 with spatial correlations of 0.74 and 0.69 (statistically significant at the 95% level), respectively, in the South Pacific region. This suggests that the high-frequency atmospheric PSA fluctuations can excite SST modes whose frequencies are subject to the atmospheric drivers. In contrast to the reddening processes that act to excite the potentially predictable low-frequency ocean signal, the pair of most damped SST modes are correlated with the atmospheric PSA forcing that acts as noise on the SST system.

Fig. 2: The fastest damped SST modes.
figure 2

The imaginary (a) and real (b) parts of the fastest damped SST modes are obtained using a reduced-order linear inverse model (see the text for details). The pair of SST modes shown has the fastest damping time scale of 2.3 months. The maps are obtained by regressing the monthly Z500 anomalies (NCEP-NCAR) onto the time series of the imaginary (c) and real (d) parts of the fastest damped modes.

Full size image

The optimal growth and extratropical precursor

Previous studies have extensively discussed the tropical and extratropical precursors of ENSO8,10,32,36,37. Despite there being little direct evidence, in terms of atmospheric dynamics, to show that the atmospheric PSA mode can directly modulate ENSO evolution in the tropics27, the indirect influence has nevertheless been widely identified in both observations11 and model simulations36,38 via the “atmosphere → extratropical ocean → tropical ocean” pathway. One way in which this indirect influence may occur is through a “seasonal footprinting” mechanism39, where the atmospheric forcing drives an extratropical anomalous SST “footprint” in the boreal spring, which persists through the boreal summer, and sustains wind stress anomalies in the tropics that are crucial to initiate ENSO events.

The LIM approach enables an objective determination of the optimal initial perturbations that maximise, for example, ENSO and SPDO growth. This provides an ideal framework through which to investigate the dynamical precursors and predictability of the peak phases of ENSO and the SPDO. Unlike lead-lag correlations that have been widely applied to identify ENSO precursors8,9,11, the LIM represents a multivariate linear stochastically forced model and provides a dynamical approximation (see “Methods” section) that satisfies conditionally causal40 relationships between the optimal precursors and their peak phases.

The interference between the non-normal damping SST modes can give rise to a transient amplification of the variance of the deterministic SST system at a preferred temporal growth scale. Such transient amplification is useful in sampling and interpreting errors in initial conditions41 and explains the actual variance growth in the system32. Transient amplification of monthly tropical and South Pacific SST anomalies allows a specific set of initial perturbations to develop into the peak phases that are found to exist at 6- to 10-month lead times5,9,32,33,42. Our LIM experimental results show that the optimal growth time of SST anomalies in the tropical and South Pacific oceans (see “Methods” section) is 9 months. These results imply the existence of linear growth events that act to maximise ENSO and SPDO development leading to enhanced predictability if the initial perturbations can be sufficiently well specified.

The spatial patterns of the initial SST perturbations in the tropical Pacific and South Pacific are shown in Fig. 3a, c, respectively. These initial patterns co-evolve over nine months into the optimal final peak phases in Fig. 3b, d, which are closely associated with ENSO and the SPDO with pattern correlations of 0.99 and 0.97 (statistically significant at the 99% level), respectively. The tropical ENSO precursor (Fig. 3a) has been discussed in the previous studies32,33,37,43 and may be associated with the recharge−discharge mechanism as first described by Jin44. The extratropical precursor (Fig. 3c) resembles a quadrupole structure similar to the second South Pacific SST mode with the pattern correlation of 0.85 (significant at the 95% level). The initial and final spatial patterns (Fig. 3c, d) were projected onto the monthly SST anomalies to reconstruct the time series. The reconstructed time series of the optimal initial perturbations and final peak phases in the South Pacific (Fig. 3e, f) are highly correlated with the second and first South Pacific SST modes with temporal correlations of 0.86 and 0.98 (statistically significant at the 99% level), respectively. This suggests that the South Pacific quadrupole SST pattern, which is primarily driven by the atmospheric PSA2, is the optimal local (linear) precursor that maximises the SPDO growth. Given the almost synchronous features between ENSO and the SPDO3,4, these results imply that the extratropical SST precursor of ENSO is also related to the quadrupole SST pattern in the South Pacific Ocean. Our results support the “seasonal footprinting” mechanism whereby the atmospheric PSA2 excites the South Pacific quadrupole SST anomalies, which then persist through the boreal summer to guide ENSO growth.

Fig. 3: The optimal evolution of the tropical and South Pacific SST.
figure 3

The optimal initial structures in the a tropical Pacific and c South Pacific are obtained using a linear inverse model (see the text for details), which linearly co-evolve over 9 months into their peak phases in the b tropical Pacific and d South Pacific. The spatial patterns shown in (a–d) are normalised according to the variance in each domain. The reconstructed time series of the e optimal initial structure and f peak phase in the South Pacific (black) are compared with the time series of the leading two South Pacific SST modes (red).

Full size image

A paradigm for South Pacific climate variability and predictability

Figure 4 summarises the atmospheric PSA mode and its South Pacific Ocean responses based on the combined results from the AR1 and LIM investigations. Our results suggest that the eastward-propagating PSA mode provides an important source of atmospheric forcing to excite the extratropical South Pacific Ocean responses operating on multiple time scales via reddening processes and coherence resonances. To first order, the close relationships between the integrated PSA1 and PSA2 patterns and the leading South Pacific SST modes support the general concept that fast atmospheric variations are a critically important excitation source of low-frequency oceanic variability. The leading integrated subsurface temperature mode, that resembles the spatial pattern of its SST counterpart, can be regarded as a cumulative response to atmospheric PSA1 forcing. That is, the inclusion of extratropical subsurface processes further reddens the SST variations thereby enhancing the most persistent and potentially predictable signal. Furthermore, the atmospheric PSA1 and PSA2 patterns can excite SST variations via coherence resonances such that the resultant fastest damping SST modes are slaves to the atmospheric forcing but synchronised to the spatiotemporal features of the real and imaginary components of the propagating PSA.

Fig. 4: Schematic of the paradigm for South Pacific Ocean variability and predictability.
figure 4

The top panels are the same as shown in Fig. 2a and b indicating the fastest damped mode pair. The middle panels are the second and third modes of the monthly Z500 anomalies (NCEP-NCAR) in the southern hemisphere. The left panels of the bottom layer are the leading EOF modes of the monthly SST anomalies and VAT anomalies in the South Pacific Ocean, respectively. The right panel of the bottom layer is the same as shown in Fig. 3c indicating the optimal precursor of the SPDO (illustrated by the green arrow). Red arrows indicate reddening processes. Blue arrows indicate coherence resonances. Grey arrows indicate the propagating features of the corresponding modes.

Full size image

The extratropical SST precursor of ENSO and SPDO growth is strongly associated with the South Pacific quadrupole SST pattern. The set of initial conditions related to this quadrupole pattern can optimally determine how the SST anomalies will evolve along its deterministic (linear) trajectory and lead to the SPDO and ENSO peaks over the following nine months, and from which the linear predictability intrinsic to the SST system can be inferred. While the influence of the atmospheric PSA mode on tropical SST variability is less apparent than the influence of the tropical SST variability on the PSA mode8,20,27, our results indicate that the South Pacific quadrupole SST pattern acts as an oceanic bridge that links the atmospheric PSA forcing to ENSO dynamics centred in the tropics, and represents the most probable pathway for midlatitude atmospheric variability to influence tropical SST via an indirect “seasonal footprinting” mechanism. Although the actual observed nonlinear dynamics are more complicated than the tangent linear dynamics that form the basis of the LIM propagator, the proposed paradigm provides a mechanistic framework to understand the dynamics and predictability of South Pacific climate variability and to interpret extratropical atmospheric drivers and the oceanic responses on multiple time scales.

Methods

The reanalysis data used here were monthly detrended anomalies of the 500 hPa geopotential heights (Z500) from the National Centres for Environmental Prediction/National Centre for Atmospheric Research (NCEP-NCAR)45. The monthly detrended SST anomalies were generated using an atmosphere-forced ocean model, the Australian Community Climate and Earth-System Simulator-Ocean (ACCESS-O). The ACCESS-O is forced by observed atmospheric fields from the Coordinated Ocean–Ice Reference Experiments (CORE; 1948–2007)46. The model configuration is described in ref. 47. The original 360 × 300 tripolar ACCESS-O model grid has been remapped to a regular 2.5° × 2.5° grid. The reanalysis data and model simulations were linearly detrended at each grid point, with monthly anomalies calculated by removing the climatological monthly mean.

The atmospheric PSA1 and PSA2 patterns were defined by computing the second and third empirical orthogonal functions/principal components (EOFs/PCs) of the monthly Z500 anomalies in the Southern Hemisphere, respectively, which explain 11.2 and 8.3% of the total variance. The leading two South Pacific SST modes, which are referred to as the South Pacific decadal oscillation (SPDO) and the South Pacific quadrupole SST pattern, were obtained by computing the first and second EOFs/PCs of the monthly SST anomalies in the South Pacific Ocean domain from (20°S−70°S; 120°E−60°W), and explain 19.0 and 9.6% of the total variance. The subsurface temperature variability was characterised by spatiotemporal variations of vertically averaged temperatures (VAT) through the upper 300 m of the ocean, which includes the mixed layer and thermocline across most regions. The subsurface SPDO is derived from the first EOF/PC of the VAT in the South Pacific Ocean (20°S−70°S; 120°E−60°W) and explains 19.8% of the total variance. Statistical significance tests of the correlation coefficients calculated in this study took account of the effective number of degrees of freedom due to serial correlation in the time series, following the method of ref. 48.

The oceanic reddening response to atmospheric PSA forcing was quantified using a doubly integrated first-order autoregressive (AR1) model. A univariate AR1 model can be written as

$$\frac{{{{{{\mathrm{d}}}}}}x}{{{{{{\mathrm{d}}}}}}t}=lx+\xi ,$$
(1)

where \(x\) is a time series and \(-1/l\) is associated with the damping time scale. This univariate AR1 process only has one degree of freedom and is unable to oscillate when the damping coefficient \(l\) is positive49. Predictability of the time series \(x\) is largely limited by the damping scale \(-1/l\). \(\xi\) in Eq. (1) represents a high-frequency noise forcing term.

The optimal damping time scales are 6 months and 5 months, respectively, when the time series of the PSA1 and PSA2 patterns were specified as the atmospheric forcing of the first two South Pacific SST modes in the first AR1 integration from the atmosphere to the surface ocean. In the second integration from the surface ocean to the subsurface ocean, the optimal damping time scale is 15 months when the time series of the SST SPDO was specified as the forcing of the leading South Pacific VAT mode.

The pair of fastest damped noise mode and optimal initial perturbations were estimated using a generalised AR1 model, here referred to as the linear inverse model (LIM)32, or alternatively termed principal oscillation pattern (POP) analysis49. The LIM can be written in the form of a linear stochastic differential equation:

$$\frac{{{{{{\rm{d}}}}}}{{{{{\bf{X}}}}}}}{{{{{{{\mathrm{d}}}}}}t}}={{{{{\bf{L}}}}}}{{{{{\bf{X}}}}}}+{{{{{\boldsymbol{\xi }}}}}}$$
(2)

where the evolution of the state vector \({{{{{\bf{X}}}}}}\) can be expressed as the sum of the deterministic dynamics, \({{{{{\bf{LX}}}}}}\), that constitute “slow” processes and the stochastic forcing term, \({{{{{\boldsymbol{\xi }}}}}}\), that constitutes “fast” processes. In this study, we defined the model state vector \({{{{{\bf{X}}}}}}\) as

$${{{{{\bf{X}}}}}}=\left[\begin{array}{c}{{{{{\bf{S}}}}}}{{{{{\bf{S}}}}}}{{{{{{\bf{T}}}}}}}_{{{{{{\bf{T}}}}}}{{{{{\bf{P}}}}}}}\\ {{{{{\bf{S}}}}}}{{{{{\bf{S}}}}}}{{{{{{\bf{T}}}}}}}_{{{{{{\bf{S}}}}}}{{{{{\bf{P}}}}}}}\end{array}\right],$$
(3)

where we considered monthly SST anomalies from the tropical Pacific (i.e., \({{{{{{\bf{SST}}}}}}}_{{{{{{\bf{TP}}}}}}}\) in the region 20°S−20°N, 120°E−60°W) and South Pacific Ocean (i.e., \({{{{{{\bf{SST}}}}}}}_{{{{{{\bf{SP}}}}}}}\) in the region 22.5°S−70°S, 120°E−60°W). We retained the leading 4 tropical Pacific and 6 South Pacific SST EOFs/PCs in the LIM to reduce the spatial degrees of freedom and ensure linearity and stability of the SST system. The robustness of the LIM has been demonstrated in the refs. 5,50, showing that the choices of using the leading 10−16 EOFs/PCs to construct the state vector \({{{{{\bf{X}}}}}}\) and the different combinations of the leading EOFs/PCs used from the different regions give similar results.

The dynamical operator \({{{{{\bf{L}}}}}}\) in Eq. (2) encapsulates the evolution of the state vector \({{{{{\bf{X}}}}}}\) and can be estimated from

$${{{{{\bf{L}}}}}}={\tau }_{0}^{-1}\,{{{{\mathrm{ln}}}}}\,[{{{{{\bf{C}}}}}}({\tau }_{0}){{{{{\bf{C}}}}}}{(0)}^{-1}],$$
(4)

where \({{{{{\bf{C}}}}}}\left({\tau }_{0}\right)\) and \({{{{{\bf{C}}}}}}\left(0\right)\) are the time-lagged and zero-lagged (cross-)covariance matrices of the state vector \({{{{{\bf{X}}}}}}\). That is, \({{{{{\bf{C}}}}}}{{{{{\boldsymbol{(}}}}}}{\tau }_{0}{{{{{\boldsymbol{)}}}}}}=\left\langle {{{{{\bf{X}}}}}}{{{{{\boldsymbol{(}}}}}}t+{\tau }_{0}{{{{{\boldsymbol{)}}}}}}{{{{{{\bf{X}}}}}}}^{{{{{{\bf{T}}}}}}}{{{{{\boldsymbol{(}}}}}}t{{{{{\boldsymbol{)}}}}}}\right\rangle\) and \({{{{{\bf{C}}}}}}{{{{{\boldsymbol{(}}}}}}0{{{{{\boldsymbol{)}}}}}}{{{{{\boldsymbol{=}}}}}}\left\langle {{{{{\bf{X}}}}}}{{{{{\boldsymbol{(}}}}}}t{{{{{\boldsymbol{)}}}}}}{{{{{{\bf{X}}}}}}}^{{{{{{\bf{T}}}}}}}{{{{{\boldsymbol{(}}}}}}t{{{{{\boldsymbol{)}}}}}}\right\rangle\), where the angle brackets here denote an ensemble average or a time average over all t for variables with stationary statistics. Here, \({\tau }_{0}=1{{{{{\rm{month}}}}}}\) was used to ensure the stability of the LIM. Previous studies5,50 examined the sensitivity of using different choices of \({\tau }_{0}\) to estimate the dynamical operator \({{{{{\bf{L}}}}}}\), finding that the LIM is insensitive to \({\tau }_{0}\) ranging from 1 month to 6 months.

For a system described by Eq. (2), the most probable evolution at time t + τ can be determined by

$${{{{{\bf{X}}}}}}(t+\tau )={{{{{\bf{G}}}}}}(\tau ){{{{{\bf{X}}}}}}(t)={{{{{{\mathrm{e}}}}}}}^{{{{{{\bf{L}}}}}}\tau }{{{{{\bf{X}}}}}}(t),$$
(5)

given a state vector \({{{{{\bf{X}}}}}}\left(t\right)\).

The damping modes can then be diagnosed by applying eigen-decomposition to the dynamical operator \({{{{{\bf{L}}}}}}\) (i.e., \({{{{{\bf{Lp}}}}}}=\lambda {{{{{\bf{p}}}}}}\)). Since the \({{{{{\bf{L}}}}}}\) matrix is not symmetric, some or all of its eigenvalues \(\lambda\) and eigenvectors \({{{{{\bf{p}}}}}}\) are complex. The damping time scales −1/σ and/or the oscillatory periods 2π/ω of the damping modes can be directly estimated from the corresponding eigenvalues \(\lambda =\sigma +{{{{{\mathrm{i}}}}}}\omega\), where \(\sigma\) and \(\omega\) are the real and imaginary parts of \(\lambda\), respectively. In this study, the pair of complex damping modes that have the fastest damping time scale has been discussed.

The transient growth over any time interval \(\tau\) can be written as the norm of the final state \({{{{{\bf{X}}}}}}\left(t\right)\) divided by the norm of the initial state \({{{{{\bf{X}}}}}}\left(0\right)\):

$${\gamma }^{2}=\frac{\|{{{{{\bf{X}}}}}}{(t)}\|^{2}}{\,{\|{{{{\bf{X}}}}}}{(0)}\|^{2}}=\frac{{{{{{{\bf{X}}}}}}}^{{{{{{\rm{T}}}}}}}(t){{{{{\bf{X}}}}}}(t)}{{{{{{{\bf{X}}}}}}}^{{{{{{\rm{T}}}}}}}(0){{{{{\bf{X}}}}}}(0)}=\frac{{{{{{{\bf{X}}}}}}}^{{{{{{\rm{T}}}}}}}(0){{{{{{\bf{G}}}}}}}^{{{{{{\rm{T}}}}}}}(\tau ){{{{{\bf{G}}}}}}(\tau ){{{{{\bf{X}}}}}}(0)}{{{{{{{\bf{X}}}}}}}^{{{{{{\rm{T}}}}}}}(0){{{{{\bf{X}}}}}}(0)}.$$
(6)

The optimal growth that maximises the amplification of the variance can be estimated as the leading eigenvalue\(\,{\gamma }_{1}^{2}\) of \({{{{{{\bf{G}}}}}}}^{{{{{{\rm{T}}}}}}}\left(\tau \right){{{{{\bf{G}}}}}}\left(\tau \right)\). The leading eigenvalues at different time intervals (i.e., \({\gamma }_{1}^{2}(\tau )\)) then form a trajectory that indicates the modal interferences and variance changes of the system in the absence of stochastic forcing. Since the dynamical operator of the LIM is nonnormal (i.e., \({{{{{{\bf{L}}}}}}}^{{{{{{\bf{T}}}}}}}{{{{{\bf{L}}}}}}\, \ne\, {{{{{\bf{L}}}}}}{{{{{{\bf{L}}}}}}}^{{{{{{\bf{T}}}}}}}\)), it allows the resultant damping modes to interact with each other and contribute to the transient amplification of the variance without the presence of stochastic forcing. This provides a perspective to, for example, interpret errors in the initial conditions and understand the error growth of the system. In the present LIM, the largest transient amplification of the SST variance was found at 9 months.

The optimal precursor indicates the initial condition that maximises the growth of the state vector over a specified time interval τ (τ = 9 months in this case). The optimal precursor is derived as the corresponding leading eigenvector of \({{{{{{\bf{G}}}}}}}^{{{{{{\rm{T}}}}}}}\left(\tau \right){{{{{\bf{G}}}}}}\left(\tau \right)\) when τ = 9 months is specified.