Investigation of N$_3$C$_5$ and B$_3$C$_5$ bilayers as anode materials for Li-ion batteries by first-principles calculations

Abstract

The best choice today for a realistic method of increasing the energy density of a metal-ion battery is to find novel, effective electrode materials. In this paper, we present a theoretical investigation of the properties of hitherto unreported two-dimensional B$_3$C$_5$ and N$_3$C$_5$ bilayer systems as potential anode materials for lithium-ion batteries. The simulation results show that N$_3$C$_5$ bilayer is not suitable for anode material due to its thermal instability. On the other hand B$_3$C$_5$ is stable, has good electrical conductivity, and is intrinsically metallic before and after lithium intercalation. The low diffusion barrier (0.27 eV) of Li atoms shows a good charge and discharge rate for B$_3$C$_5$ bilayer. Moreover, the high theoretical specific capacity (579.57 mAh/g) connected with moderate volume expansion effect during charge/discharge processes indicates that B$_3$C$_5$ is a promising anode material for Li-ion batteries.

Introduction

Studies into alternative energy sources, particularly renewable energy, are being driven by the modern world’s rising energy consumption, concerns about the fossil fuel dilemma, and the need for environmental protection¹. The method of storing the generated energy is also a huge challenge. Currently, lithium-ion batteries (LIBs) are the preferred energy storage technology for various applications, including portable electronics, electric vehicles, and grid energy storage^2,3. The materials in use as electrodes have a significant impact on the properties of LIBs. In industrial LIBs, graphite is the anode material that is most frequently used^4,5. According to estimates, graphite has a theoretical capacity of 372 mAh/g⁶. Unfortunately, the main drawbacks of the graphite electrode, which restrict its use and advancement, are structural deformation, initial loss of capacity, and electrical disconnect⁷. As one of the alternatives to the commonly used graphite as an anode material, titanium dioxide (TiO$_2$) has been looked into. The attractive properties of TiO$_2$, which include low cost, high chemical stability, low volume expansion during charging/discharging, eco-friendliness, high energy density, and ease of availability, have made it one of the promising anode materials for LIBs^8,9. Unfortunately, in comparison with commercially used graphite anode materials, TiO$_2$ has a relatively low theoretical capacity of around 335 mAh/g¹⁰.

The continuous demand for higher energy density, improved cycling stability, and longer battery life drives extensive research on developing advanced materials for LIB electrodes. In this context, two-dimensional (2D) materials have emerged as promising candidates for enhancing the performance of LIB anodes.

The unique properties of 2D materials, such as large surface area, atomically thin structure, and tunable electronic properties, make them attractive for energy storage applications^{11,12,13,14,15,16}. The atomically thin nature of 2D materials allows for efficient lithium ion diffusion and accommodation during charge and discharge processes, leading to improved capacity and cycling stability. Additionally, the large surface area of 2D materials facilitates increased electrochemically active sites, enhancing the overall electrochemical performance of the anode¹⁷. Several types of 2D materials have been recently investigated as potential anode materials for LIBs. These include transition metal dichalcogenides (TMDs) such as MoS$_2$, graphene, MXenes, and various other 2D carbides, nitrides, and oxides. Each of these materials possesses unique properties that can influence their electrochemical behavior, capacity, and cycling stability^18,19,20.

In the present study, we propose that graphene bilayers substitutionally doped with B and N atoms, specifically the B$_3$C$_5$ and N$_3$C$_5$ systems, are promising as potential anode materials for LIBs. Li-ion battery swelling during the intercalation of Li into the electrodes is a major cause of battery electrode degradation and can contribute significantly to cell failure. The swelling effect can only be investigated by studying the bilayer or bulk systems, therefore, herein we take into account bilayer systems. This investigation is based on DFT computations. It has been observed that both hitherto unreported B$_3$C$_5$ and N$_3$C$_5$ exhibit metallic properties with significant conductance after the adsorption of metal ions. Additionally, these systems demonstrate a remarkable specific Li capacity, which is significantly greater than that of pure graphene. Moreover, B$_3$C$_5$ and N$_3$C$_5$ display a low diffusion barrier and moderate volume expansion effect during charge/discharge processes. These attributes suggest that the investigated B$_3$C$_5$ and N$_3$C$_5$ systems could be ideal electrode materials for Li-ion batteries. Our comprehensive analysis aims to illuminate the potential of 2D materials as anode components for LIBs, providing insights into their distinctive properties and their contribution to the overall performance of lithium-ion batteries. The outcomes of this study have the potential to guide the design and development of advanced 2D anode materials, enhancing their electrochemical characteristics and elevating their energy storage capabilities.

Computational methods

The first-principles calculations in this study were performed using the Quantum ESPRESSO package^21,22, employing projector augmented wave (PAW) potentials within density-functional theory (DFT). The exchange-correlation energy of the electrons was treated within the generalized gradient approximation (GGA) functional of Perdew–Burke–Erzenhoff (PBE). The charge density and kinetic energy cut-off values were set to 500 Ry and 50 Ry, respectively. To minimize interactions between neighboring slabs, a vacuum of 20 Å was included. Van der Waals (VdW) interactions between the layers were accounted for using Grimme’s DFT-D correction²³. The geometrical structure is optimized by using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) quasi-Newton algorithm²⁴ with the convergence criterion of $10^{-5}$ eV for energy. The forces on all atoms are less than 0.001 eV/Å. Structural optimization and band structure computations were performed using a Monkhorst pack k-point grid of $36 \times 36 \times 1$. The diffusion barrier is calculated by the climbing image nudged elastic band (Cl-NEB) method²⁵. The thermal stability of the B$_3$C$_5$ and N$_3$C$_5$ bilayer systems was examined through ab initio molecular dynamics (AIMD) simulations at 300 K using the CP2K software²⁶ with a constant volume and temperature ensemble (NVT ensemble) and a time step of 1 fs and 10000 ionic steps.

The intercalation energy of Li between B$_3$C$_5$ and N$_3$C$_5$ bilayers was computed as below:

$$\begin{aligned} E_{\textrm{int}}=({E_{\textrm{Li}_n{\textrm{X}_3C_5}}} - E_{\textrm{X}_3C_5} - nE_{\textrm{Li}})/n, \end{aligned}$$

(1)

where $E_{\textrm{X}_3C_5}$ is the total energy of pristine ${\textrm{X}_3C_5}$ bilayer (X = B or N), $E_{\textrm{Li}}$ is the energy of a single Li atom (in bulk bcc phase), ${E_{\textrm{Li}_n{\textrm{X}_3C_5}}}$ means the total energy of Li-intercalated ${\textrm{X}_3C_5}$ bilayer and n is the number of intercalated lithium atoms. From this definition, the more negative the value of $E_{\textrm{int}}$, the more it illustrates the exothermic nature of the reaction, indicating a higher likelihood of the reaction occurring. Conversely, a positive value of $E_{\textrm{int}}$ indicates an endothermic reaction, suggesting that the reaction is less likely to occur.

Theoretical Li capacity can be estimated as below:

$$\begin{aligned} C=\frac{nzF}{\textrm{M}_{X_3C_5}}, \end{aligned}$$

(2)

where n is the number of intercalated Li atoms ($n=16$), z is the valence number ($z=1$ for Li), F is the Faraday constant (26801 mAh/mol), and $\textrm{M}_{X_3C_5}$ is the molar mass of B$_3$C$_5$ or N$_3$C$_5$ bilayer.

Results and discussion

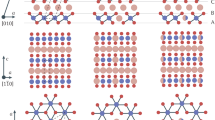
A fully-relaxed structure of pristine B$_3$C$_5$ and N$_3$C$_5$ bilayer systems that have a hexagonal resemblance to graphene, but with a rippled surface, can be observed in Fig. 1a, b, respectively. Lattice constants a and b are both 5.22 Å for B$_3$C$_5$ and 4.81 Å for N$_3$C$_5$. The C–C and C–B bond lengths are 1.443 Å and 1.541 Å (1.592 Å) in the case of B$_3$C$_5$ and the C–C and C–N bond lengths are 1.387 Å and 1.388 Å (1.481 Å) in the case of N$_3$C$_5$.

Figure 1

Atomic structure (top and side views) of pristine $2\times 2$ supercell of (a) B$_3$C$_5$ and (b) N$_3$C$_5$ bilayer.

To check the energetical stability of our bilayer structures, we evaluate the cohesive energies:

$$\begin{aligned} E_{\textrm{coh}} = \frac{6E_{\textrm{X}} + 10E_{\textrm{C}} - E_{\textrm{X}_3C_5}}{16}, \end{aligned}$$

(3)

where $E_{\textrm{X}}$ is the energy of an isolated B or N atom, $E_{\textrm{C}}$ means the energy of an isolated C atom, and $E_{\textrm{X}_3C_5}$ represents the total energy of X$_3$C$_5$ bilayer. The calculated cohesive energies of B$_3$C$_5$ and N$_3$C$_5$ bilayers are 7.76 eV/atom and 8.26 eV/atom, respectively. The higher cohesive energy indicates a more stable structure, indicating that the N$_3$C$_5$ monolayer has a more stable structure. The values of B$_3$C$_5$ and N$_3$C$_5$ monolayers are higher than those of phosphorene (3.48 eV/atom), silicene (3.71 eV/atom), SnC (5.5 eV/atom), GeP$_3$ (3.34 eV/atom), P$_3$C (4.18 eV/atom), MoS$_2$ (4.98 eV/atom) and Mo$_2$C (6.31 eV/atom) and close to Ti$_3$BN monolayer (7.46 eV/atom) and graphene (7.95 eV/atom)^{27,28,29,30,31,32,33}.

To investigate the dynamical stability of studied structures, phonon calculations were performed along $\Gamma$–M–K–$\Gamma$ symmetry points. As we can see in Fig. 2, no imaginary frequencies are observed in the entire Brillouin zone, confirming the dynamical stability of both investigated systems, which is an important result, especially from the energy storage point of view.

Figure 2

Calculated phonon spectra of (a) B$_3$C$_5$ bilayer and (b) N$_3$C$_5$ bilayer.

We also used AIMD simulations to investigate the thermal stability of the B$_3$C$_5$ and N$_3$C$_5$ bilayers. Our structures retain their integrity after being heated to 300 K (see insert of Fig. 3). Simultaneously, the energy fluctuation is quite small, with a variation of around 0.003 Ry, indicating that both systems are thermally stable.

Figure 3

Fluctuation graphs of the total energy of $2\times 2$ (a) B$_3$C$_5$ and (b) N$_3$C$_5$ bilayers supercells as a function of time at 300 K. The embedded figures show the corresponding top views of the initial configurations and configurations after 10 ps of simulation.

The intercalation energy ($E_{\textrm{int}}$) of B$_3$C$_5$ and N$_3$C$_5$ bilayers was estimated using Eq. (4). To denote the concentration of Li per unit bilayer cell, we use the notation of Li$_{\textrm{n}}$(X$_3$C$_5$)$_2$. The calculated $E_{\textrm{int}}$ of the single lithium atom (1:17 ratio) equals $-3.96$ eV and $-1.75$ eV for B$_3$C$_5$ and N$_3$C$_5$ bilayers, respectively. With further increase of Li number, the intercalation energy almost linearly decreases in the case of B$_3$C$_5$ and nonlinearly changes in the case of N$_3$C$_5$, as shown in Table 1. The obtained results showed that from the energy storage point of view, the B$_3$C$_5$ has better properties than the N$_3$C$_5$ due to the enhancement of intercalation energy. In the case of N$_3$C$_5$, the most energetically favorable is Li$_3$(N$_3$C$_5$)$_2$ configuration with the intercalation energy of $-2.46$ eV. The bilayer B$_3$C$_5$ exhibits an intercalation energy of $-4.43$ eV in the fully lithiated case, Li$_4$(X$_3$C$_5$)$_2$, illustrating that it is most promising and worth considering for the study of new anode materials for LIBs.

The formation energy relative to stable reference materials is crucial for assessing the stability of various phases at 0 K. The formation energy of structure with intermediate lithium content can be delineated as follows³⁴:

$$\begin{aligned} E_{\textrm{f}}=\frac{{E_{\textrm{Li}_n{\textrm{X}_3C_5}}} - E_{\textrm{X}_3C_5} - nE_{\textrm{Li}}}{n+1}, \end{aligned}$$

(4)

The convex hulls obtained from the formation energies are presented in Fig. 4. The minimum value of $E_{\textrm{f}}$ corresponds to the most thermodynamically stable adsorption concentrations. The corresponding structures are illustrated in Fig. 4 insets.

Figure 4

Formation energy convex hull of Li$_n$(B$_3$C$_5$)$_2$ and Li$_n$(N$_3$C$_5$)$_2$ systems.

It’s worth noting that a geometry optimization was conducted for different intercalation sites. The most energetically favorable position is found to be the hole position, where atoms from the initial bridge and top positions migrate during the optimization process. This indicates that the hole position is indeed the most energetically favorable configuration. Crystal structures of all Li-intercalated stages for Li$_n$(B$_3$C$_5$)$_2$ and Li$_n$(N$_3$C$_5$)$_2$ are included in Supplementary Information.

Table 1 Intercalation energy per lithium atoms (in eV) for the Li-intercalation between B$_3$C$_5$ and N$_3$C$_5$ bilayers as a function of Li atoms concentration in the unit cell.

Figure 5

Atomic structure (top and side views) of Li-intercalated $2\times 2$ supercell of (a) B$_3$C$_5$ and (b) N$_3$C$_5$ bilayer.

After full lithiation (Li atoms intercalation between monolayers at all hole positions, Li$_4$(B$_3$C$_5$)$_2$), the monolayers in pristine B$_3$C$_5$ bilayer transforms from the initial structure with a rippled surface into a graphene-like plane structure, as shown in Fig. 5a. In the case of N$_3$C$_5$ bilayer (Li$_3$(N$_3$C$_5$)$_2$), the Li-intercalation contributes to the increase of rippling of the surface and changes ideal AA stacking where atoms of both layers have identical lateral coordinates into degenerate AA stacking where the one layer is slightly shifted relative to the other one (see Fig. 5b). Moreover, in both systems, the Li-intercalation increases the interlayer distance from 2.53 Å to 3.63 Å for B$_3$C$_5$ and from 2.78 Å to 4.69 Å in the case of N$_3$C$_5$. The practical application of new 2D anode materials is strongly impeded by large volume expansion during lithiation/delithiation processes which can result in loss of electrical contact with the conductive additive or the current collector and even peeling off from the current collector³⁵. The results obtained for B$_3$C$_5$ and N$_3$C$_5$ clearly show a low volume expansion of about $43-69$%, compared to 2D Si/C composite (54%), commercial Si (183%) and pure Si nanosheets (95%)^36,37.

Figure 6

Fluctuation graphs of the total energy of $2\times 2$ (a) Li$_4$(B$_3$C$_5$)$_2$ and (b) Li$_3$(N$_3$C$_5$)$_2$ supercells as a function of time at 300 K. The embedded figures show the corresponding top views of the initial configurations and configurations after 10 ps of simulation.

Structural stability during the charging and discharging process at finite temperatures is an important factor in the performance of LIBs. An AIMD simulation is used to investigate the thermal stability of the Li$_4$(B$_3$C$_5$)$_2$ and Li$_3$(N$_3$C$_5$)$_2$ structures. Figure 6 show the calculated total energy of the fully lithiated bilayers during the AIMD simulation time of 10 ps at 300 K. As expected, the total energy of Li$_4$(B$_3$C$_5$)$_2$ does not change much during the AIMD steps. Such a slight change in energy indicates good thermal stability of a fully Li-intercalated B$_3$C$_5$ bilayer. In the case of Li$_3$(N$_3$C$_5$)$_2$ we observed structural deformation and energy drift, indicating that N$_3$C$_5$ bilayer is thermally unstable. Due to the above, we eliminated it from further analysis and we focused our attention only on the B$_3$C$_5$ bilayer.

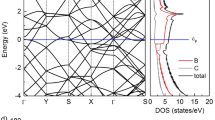
Figure 7 represents the electronic band structure of pristine B$_3$C$_5$ and alterations in its electronic structure after Li intercalation. Both materials show a metallic character as indicated by the electronic states crossing the Fermi level. The metallic properties of the B$_3$C$_5$ bilayer offer an intrinsic profit in high electrical conductivity and a satisfying electrochemical property for better battery cycling.

Figure 7

The electronic band structure along the $\Gamma$–K–M–$\Gamma$ high-symmetry line, together with the total and partial density of states for (a) pristine B$_3$C$_5$ bilayer and (b) Li-intercalated B$_3$C$_5$ bilayer.

Figure 8

The comparison diffusion barriers in different paths of Li atom between two B$_3$C$_5$ layers.

To determine the diffusion and mobility features, we calculated the energy barrier for Li-ion diffusion with three main diffusion pathways as shown in Fig. 8. Path 1 is shown by the red color. The Li atom diffuses in the interlayer space from the hole of the B$_2$C$_4$ ring to the hole of the B$_2$C$_4$ ring through the C–B bridge. Path 2 is shown by the green color. The Li atom diffuses from the B$_2$C$_4$ ring position to the B$_3$C$_3$ ring also through the C–B bridge. In the case of path 3, which is shown by the black color, the Li atom migrates between two adjacent B$_2$C$_4$ rings through the C–C bridge. Data illustrating the diffusion stages of Li atom between two B$_3$C$_5$ layers are included in Supplementary Information.

The calculations reveal that the diffusion energy barriers corresponding to path 1, path 2 and path 3 are 1.16 eV, 1.22 eV and 0.27 eV, respectively. The diffusion energy barrier through the C–C bridge is lower than the C–B bridge, indicating that Li atoms are more inclined to spread in an anisotropic way across the C–C bridge. We also note that the lowest diffusion barrier obtained for the Li atom is superior to the graphene bilayer (0.34 eV)³⁸, therefore, B$_3$C$_5$ shows great potential to serve as a LIB electrode.

The maximum theoretical storage capacity (C) is an important parameter to evaluate the performance of the LIB. It depends on the concentration of the Li ions intercalated between B$_3$C$_5$ layers and can be calculated using Eq. (2). The capacity of a fully lithiated B$_3$C$_5$ bilayer is as high as 579.57 mAh/g for LIBs (1159.15 mAh/g if we take into calculations only one layer of B$_3$C$_5$). The obtained result is much larger compared to the storage capacities of commercially used graphite (372 mAh/g)⁶ or TiO$_2$ (335 mAh/g)¹⁰ and other typical 2D anode materials for LIBs like VS$_2$ (466 mAh/g)³⁹, Zr$_2$B$_2$ (526 mAh/g)⁴⁰, NbSe$_2$ (203 mAh/g)⁴¹, Nb$_2$C (542 mAh/g)⁴², TaC$_2$ (523 mAh/g)⁴³ or W$_2$C (259 mAh/g)⁴⁴.

Open circuit voltage (OCV) is another crucial parameter to characterize the performance of metal-ion batteries which can be calculated using the following equation:

$$\begin{aligned} V\approx \frac{{-E_{\textrm{Li}_{x_2}X_3C_5}}+{E_{\textrm{Li}_{x_1}X_3C_5}}+(\mathrm {x_2-x_1})E_{\textrm{Li}}}{z(\mathrm {x_2-x_1}) {e}}, \end{aligned}$$

(5)

where, $E_{\textrm{Li}_{x_2}B_3C_5}$ and $E_{\textrm{Li}_{x_1}B_3C_5}$ are the total energies of Li-intercalated B$_3$C$_5$ supercell with the Li concentration of $\mathrm x_2$ and $\mathrm x_1$, respectively. The symbol e denotes the fundamental charge. The calculated average OCV of Li-intercalated B$_3$C$_5$ bilayer is 2.47 V, which is comparable to those of the commercial anode materials such as TiO$_2$ with an open circuit voltage of 1.5–1.8 V⁴⁵ and lower than OCV obtained for 2D phosphorene (2.9 V)⁴⁶ or black arsenic (4.31 V)⁴⁷.

Conclusions

Lithium-ion batteries have brought about a significant transformation in the realm of energy storage, playing an indispensable role in both portable electronic devices and electric vehicles. To cater to the ever-growing demand for high-performance batteries, the quest for advanced anode materials with augmented capacity, improved lithium ion mobility, and minimal swelling effects has taken on paramount importance. This study delves into a theoretical exploration of the characteristics exhibited by novel two-dimensional B$_3$C$_5$ and N$_3$C$_5$ bilayer systems, considering their potential as anode materials for lithium-ion batteries (LIBs). The ab initio molecular dynamics (AIMD) simulations conducted at a temperature of 300 K reveal that pristine B$_3$C$_5$ and N$_3$C$_5$ bilayer systems exhibit very good stability. However, upon the introduction of lithium atoms, the N$_3$C$_5$ bilayer loses stability, prompting its exclusion from further analysis. Furthermore, the first-principles calculations demonstrate that the B$_3$C$_5$ bilayer boasts outstanding electronic conductivity, a notably lower Li diffusion barrier (0.27 V meV), and an impressive theoretical storage capacity (579.57 mAh/g). These exceptional properties strongly indicate its suitability for use as an anode material.