Abstract
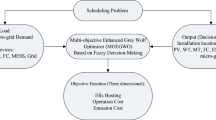
The integration of renewable energy resources into the smart grids improves the system resilience, provide sustainable demand-generation balance, and produces clean electricity with minimal leakage currents. However, the renewable sources are intermittent in nature. Therefore, it is necessary to develop scheduling strategy to optimise hybrid PV-wind-controllable distributed generator based Microgrids in grid-connected and stand-alone modes of operation. In this manuscript, a priority-based cost optimization function is developed to show the relative significance of one cost component over another for the optimal operation of the Microgrid. The uncertainties associated with various intermittent parameters in Microgrid have also been introduced in the proposed scheduling methodology. The objective function includes the operating cost of CDGs, the emission cost associated with CDGs, the battery cost, the cost of grid energy exchange, and the cost associated with load shedding. A penalty function is also incorporated in the cost function for violations of any constraints. Multiple scenarios are generated using Monte Carlo simulation to model uncertain parameters of Microgrid (MG). These scenarios consist of the worst as well as the best possible cases, reflecting the microgrid’s real-time operation. Furthermore, these scenarios are reduced by using a k-means clustering algorithm. The reduced procedures for uncertain parameters will be used to obtain the minimum cost of MG with the help of an optimisation algorithm. In this work, a meta-heuristic approach, grey wolf optimisation (GWO), is used to minimize the developed cost optimisation function of MG. The standard LV Microgrid CIGRE test network is used to validate the proposed methodology. Results are obtained for different cases by considering different priorities to the sub-objectives using GWO algorithm. The obtained results are compared with the results of Jaya and PSO (particle swarm optimization) algorithms to validate the efficacy of the GWO method for the proposed optimization problem.
Similar content being viewed by others
Introduction
Microgrid (MG) is a scaled-down version of the conventional grid. It is self-sufficient and can supply the local demands of a particular geographic area. The active components of the MG are renewable energy sources like wind turbines (WT), photovoltaic (PV), micro-hydro generators, biomasses, fuel cells, etc. The other associated components of MG are energy storage units, combined heat and power (CHP) units, thermal and electric loads, etc.1.
For ensuring supply reliability, fuel savings, lesser emissions, voltage security, full exploitation of renewable potential, and coordinated output of multiple DGs, there is a need for energy management and optimal dispatch of microgrids. Two different approaches that have widely been used in the literature for the optimal operation of MG are (a) deterministic approaches and (b) heuristic optimization approaches2,3,4,5,6,7,8.
Deterministic algorithms like linear programming, mixed-integer linear programming, and dynamic programming have been used in articles9,10,11,12,13,14,15 for unit commitment and economic load dispatch (ELD) of microgrids with or without the energy storage system. Various objectives, i.e. cost minimization, reliability maximization, emission reduction, power loss minimization, voltage security, and utilization of bio-waste in microgrids, are developed with multiple constraints in these papers. However, deterministic methods have some drawbacks: (a) they take more time with the complexity of the problem; (b) they become intractable with the increase in the number of parameters; (c) they have a high dependency on the initial solutions; (d) these methods are gradient-dependent, etc. Using meta-heuristic algorithms has resolved the issues related to deterministic methods. Some of the meta-heuristic algorithms, like a genetic algorithm (GA), modified genetic algorithm, particle swarm optimization (PSO), modified particle-swarm optimization (MPSO), grey-wolf optimization (GWO), artificial fish algorithms, african vultures optimization algorithms (AVOA) etc. were used in the literature16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32 to solve the optimization problems of MG. A GA has been used in the papers16 and17 for the energy trading strategy of the MG considering uncertain quantities.
In Ref.16, the energy trading strategy was developed for optimal scheduling of conventional generators, energy storage systems, and grid power exchanges. In Ref.17, the objective is cost minimization, including the installation cost of battery storage, solar modules, and the operational cost of diesel generators. The goal is subjected to equality constraints like active and reactive power balance and inequality constraints to ensure stability. A modified genetic algorithm has been used in article18 to share the power generation among the various DERs optimally. The results show that the modified GA gives better results than the GA.
PSO-based optimization algorithms have been developed in article19,21,22,33 for the ELD problems with multiple thermal units, energy storage devices, etc. Some of these works include the impact of large-scale EV integration along with the numerous constraints and load uncertainty. These studies show that the results obtained by the PSO algorithm are much better than those obtained by the GA. However, in article24,25,26,34 researchers have analyzed the performance of variants of PSO named “improved, coordinated aggregation-based particle swarm optimization (ICA-PSO)” algorithm and “PSO with BA parameter inspired acceleration coefficients (MHPSO-BAAC)” to solve the ELD problem with valve point loading for all combinations of RES-based power plants. These algorithms proved that the PSO variants performed better than basic PSO.
In papers27,35, another meta-heuristic-based Grey Wolf Optimization algorithm has been developed to solve the economic operation of the microgrid system, the sizing optimization of BESS, etc. The results obtained by GWO have been compared with the results of other meta-heuristic algorithms like GA, PSO, ABC, etc. to show the effectiveness of GWO. A fuzzy PID control based modified slime mould algorithm (MSMA) is developed for optimal battery management system in article30. In this article, the tuning of fuzzy PID controller is performed to accommodate the uncertainties of the automatic voltage variation and power management. An African vultures optimization algorithm (AVOA) has been developed in article31 for the optimization of a novel two-degree of freedom PID (2DOFPID) controller to emulate the virtual inertia and damping into the Microgrid. The performance of the proposed controller has been compared with the other conventional controller to show its effectiveness. The developed methodlogy31 has also been validated on OPAL-RT real time environmental simulator. A slime mold meta-heuristic optimization algorithm for the operation management of Microgrids considering Demand Response Program (DRP) is presented in article32. The obtained results show that the developed slime mold optimization algorithm performs better than PSO and Genetic Algorithms.
From the above-discussed literature, the key limitations of the work have been identified and presented as follows: (i) Few studies consider the deterministic approach, and others use the stochastic process; however, computational tractability is an issue. (ii) The scheduling under uncertainty is addressed by a reduced number . of scenarios of load, PV, wind, etc., which makes the system unrealistic. (iii). Only a few pieces of literature have discussed the priority factor-based cost components and the static penalty associated with constraints and limit violations; it needs further investigation.
The main contribution of this work is listed below:
-
To tackle the volatile and intermittent nature of PV, wind, and load, maximum scenarios are considered to represent the real system.
-
Economic scheduling in both grid-connected and islanded modes uses the concept of load and power curtailment with the help of the GWO algorithm, considering the entire day of system data.
-
A combination of the stochastic nature of resources, unpredictable loads, and the heuristic approach to solving the problem.
-
An optimal scheduling methodology for MG considering uncertain parameters is proposed along with the existence of an energy storage system.
The remaining paper is organised as follows: In Sect. "Optimal operation of microgrid", the optimal operation of MG is discussed. Section "Results and discussion" describes the results and discussion of the proposed methodology, whereas Sect. "Conclusion" gives the conclusion part of the work.
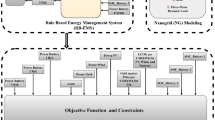
Optimal operation of microgrid
The microgrid can be operated in two modes, grid-connected or stand-alone. The fundamental steps of the proposed optimal scheduling strategy of the microgrid in both modes are given:
-
1.
Component modeling
-
2.
Scenario generation and reduction of uncertain parameters
-
3.
Problem formulation
-
4.
Implementation of optimization techniques
Component modelling
The basic structure of a grid-connected microgrid is shown in Fig. 1, which considers controllable generations, PV generations, wind generations, and energy storage systems.
PV system
Sun is the ultimate source of solar energy. The solar irradiance received from the sun can be converted into DC power with the help of solar cells (basic semiconductors), which is further converted into AC power with the help of inverters. The output power (\(P_{pv}\)) of the PV module depends upon the effective global irradiance, the area of the module, the energy conversion efficiency of the solar module, and the temperature. It is given as,
where \(G_{eff}\) is the effective global irradiance \(\eta _{g} \) is the conversion efficiency of the generator, \(A_g\) is the active surface area of the module, \( T_c\) is the temperature. Generally, the hourly irradiance is modeled by using the Beta distribution function36 and is given as,
The value of the parameters a and b is calculated with the help of mean value u and standard deviation n as,
Wind system
The kinetic energy of wind can be converted into electricity with the help of the wind turbine, however the speed of the wind is intermittent. Therefore, the wind velocity (u) is modeled by using the Weibull probability distribution function and is given as36,
The output power \(P_{W}(u)\) of the wind turbine can be modeled in terms of the wind velocity (u) as,
where \(P_{W}^{rated}\) (MW) is the rated power output of the wind turbine, u (m/s) is the maximum wind speed up to which generation is possible, \(u_{in}\) (m/s) is the cut in speed at which wind turbine generates, \(u_{r}\) (m/s) is the average wind speed.
Controllable distributed generator (CDG)
It is one of the important components of the microgrid to supply the base demand and increase the system’s reliability.
The cost associated with conventional generators is the fuel cost and is modeled as,
where \(P_i\) is the output power, a, b, and c are the fuel consumption curve parameters for any CDG whose units are \(\$ /Kw^2h\), \(\$ /Kwh\) and \(\$\) respectively.
Another significant cost associated with CDGs is the emission cost. It is the penalty for polluting the environment and can be calculated using37.
Where \(K_i\) is the penalty term for pollution, whose unit is \(\$/Kg\). \(m_i, n_i\) and \(o_i\) are the emission coefficients, whose units are \(Kg/Kw^2h\), Kg/Kwh and Kg respectively.
Battery energy storage system
It is a device used to store energy. It takes energy from various sources, uses it when required by the loads, and helps balance generation and loads. The battery’s power output can be positive or negative depending on the discharging or charging mode.
This is determined by calculating the net energy and state of charge of the battery38.
When the load is greater than a generation, the battery will get discharged,
similarly, when we have sufficient generation, and the battery is not fully charged, it will be charging,
Scenario generation and reduction of uncertain parameters
There is uncertainty associated with renewable generation because of the intermittent nature of wind and solar irradiance. It can be forecasted based on the previous data, but there are some errors. These errors can be modeled using MCS39.
Scenario generation
To generate the scenarios, there is a need for the forecasted value and error associated with the various stochastic quantities like wind speed (to calculate the wind power) and global irradiance (to calculate PV output) over the entire scheduling horizon36.
Then, for each hour, the value of the stochastic quantity is equal to the sum of the forecasted value for that hour, and the error is generated randomly with the help of historical data40,41. The same procedure is followed for the load scenario generation as it also keeps changing from time to time and is uncertain.
Scenario reduction
Since there are many scenarios for this proposed optimization problem, a proper reduction method must be used to decrease the number of generated techniques so that the solution will become tractable. Clustering is a classic machine learning and computational geometry issue. In this work, we have used the K-mean clustering algorithm. The k-means method is one of the popular clustering methods (unsupervised) where the aim is to reduce the distance between the points of the same cluster42.
Problem formulation
The main objective of microgrid operators is to minimize the overall operating cost of the microgrid by the maximum utilization of renewable energy. The operating cost function of the microgrid is as follows,
where
In Eq. (11), \(\pi _s\) is the probability of each scenario, and \(\sum _{s\in S} \pi _s=1\), where S is the total number of scenarios. The \(\alpha ,\beta ,\gamma ,\delta \), and \(\zeta \) are the priority factors that are changed for different cases to get the optimal solution. \(J_1, J_2, J_3, J_4\), and \(J_5\) are the costs associated with CDGs, emission costs, the cost associated with power exchange between microgrid and utility, battery costs, and the value of load loss, respectively. \(\sum _{j=1}^{l+m} \lambda _j \times g_j\) represents the penalty term, where \(\lambda _j\) is the penalty factor of the \(j^{th}\) constraint and \(g_j\) represents the \(j^{th}\) constraint function that is being violated. l and m are the equality and inequality constraints, respectively. \(C_i^{CDG}\) is the operating cost, and \(P_{i,t,s}^{CDG}\) is the power output at time t for scenario s of the \(i^{th}\) conventional generator, whose units are \(\$/KWh\) and Kw, respectively. \(C_{i,t,s}^{SU}\) and \(C_{i,t,s}^{SD}\) are the start-up and shut-down costs. \(m_i, n_i\), and \(o_i\) are the emission cost coefficients of the CDGs. \( \rho _{t,s}^{RT,Buy}\) and \(\rho _{t,s}^{RT,Sell}\) are the buying and selling prices of electricity with the utility grid, respectively. \(P_{t,s}^{RT,Buy}\) and \(P_{t,s}^{RT,Sell}\) are the amounts of energy bought and sold to the utility grid, respectively. \(P_{t,s}^{Char}\) and \(P_{t,s}^{Dischar}\) are the charging and discharging energies of the battery. \(\rho _{t,s}^{Char}\) and \(\rho _{t,s}^{Dischar}\) are the charging and discharging costs associated with the battery.
The objective function given in (11) is subjected to multiple constraints, among which the power balance is the most important and is given by (17).
where \(P_{grid}=P_{Buy}-P_{Sell}\).
Other inequality constraints subjected to the (11) are as follows,
\(P_{CDG}\) is output of CDG and \(P_{CDG,Min}\) and \(P_{CDG,Max}\) are the minimum and maximum limits of the power output of CDG. \(P_{PV}\) is the output of the PV panel, and it has a minimum limit of \( P_{PV,Min}\) and a maximum limit of \(P_{PV,Max}\). \( P_{W} \) is the wind output with \(P_{W,Min}\) and \(P_{W,Max}\) as the minimum and maximum limit, respectively. State of charge (SOC) is the indicator of battery energy, and it should also be in between minimum \(SOC_{Min}\) and maximum limit \(SOC_{Max}\).
Optimization technique: Grey Wolf optimization GWO
GWO is a population-based metaheuristic algorithm proposed by Mirjaliali et al. in 2014. The social hierarchy and hunting mechanism of grey wolves inspire this algorithm. They belong to the Canidae family, and their scientific name is Canis lupus. Grey wolves are social animals and live together in a group called packs. Each pack consists of 6-12 wolves divided into four categories \(\alpha _G\), \(\beta _G\), \(\delta _G\), and \(\omega _G\). The first level leads the pack to decisions such as hunting, sleeping location, etc. They need not be the strongest, but they are best at pack management. The second member of the hierarchy is \(\beta _G\). These are the supporting wolves that aid the leader in decision-making. Play the role of discipliner and advisor for the pack. It provides feedback to the alpha and guarantees that all other wolves obey the command. In the absence of \(\alpha _G\), they will be leading the team. Sentinels, scouts, hunters, and caretakers form the next hierarchy. Scouts monitor the territory’s boundary and warn the pack in case of danger. Sentinels guarantee safety for the other members of the pack. Hunters and caretakers hunt prey and take care of the pack’s ill and wounded members. Rest all are the \(\delta _G\), wolves.
The hunting mechanism of wolves is as follows:
-
Encircling prey: During the hunt, grey wolves encircle prey, whose position is (\(\textbf{X}_{ p}\))
-
Hunting: \(\textbf{A}_{ k}\) and \(\textbf{C}_{k}\) are coefficient vectors, here encircling and hunting is done through \(\textbf{D}_{k}\) & \(\textbf{X}_{new}\), respectively along with new population are computed where, \(\textbf{rd}\) is a random number between 0 and 1, and \(\textbf{a}_{gwo}\) changes linearly from 2 to 0 with each iteration. The entire process is described below
$$\begin{aligned} \textbf{A}_{ k}= & {} 2\cdot \textbf{a}_{gwo}\cdot \textbf{rd}-\textbf{a}_{gwo}, \end{aligned}$$(22)$$\begin{aligned} \textbf{C}_{ k}= & {} 2\cdot \textbf{rd}, \end{aligned}$$(23)$$\begin{aligned} \textbf{D}_{ k}= & {} \Vert \textbf{C}_{ k}\cdot \textbf{X}_{ p}- \textbf{X}_{k}\Vert, \end{aligned}$$(24)$$\begin{aligned} \mathbf {X'}_{ k}= & {} \textbf{X}_{ k}-\textbf{A}_{ k}\cdot \textbf{D}_{ k}, \end{aligned}$$(25)$$\begin{aligned} \textbf{X}_{new}= & {} \frac{\sum _{k=1}^{3}\mathbf {X'}_{ k}}{3}, \end{aligned}$$(26) -
Attacking the prey: Once the prey stops moving, wolves attack the prey.
-
Exploration: Grey wolves mainly seek according to the alpha, beta, and delta positions. They disperse from each other to hunt for prey and converge to attack prey. We use random values larger than 1 or less than -1 to mathematically describe divergence to force the search agent to diverge from the prey.
Another feature of GWO that encourages exploration is \(\textbf{C}\). This vector has random values in the range [0, 2], allowing GWO to behave more randomly during optimization, promoting exploration and avoiding local optima.
Implementation steps of algorithm: Implementation of GWO algorithm for the objective function formulated in (11), is illustrated as follows:
-
Choose initial parameters and set priority factor \(\gamma = 0\) for isolated mode.
-
Choose other priority factors \((\alpha _G, \beta _G, \gamma _G\) and \(\delta _G)\) for Grid-connected mode.
-
Subject to inequality constraints in (18)–(21), minimize the objective function given in (11) using GWO algorithm as described in Algorithm 1.
-
Repeat the process for the calculation of \(J_1\), \(J_2\), \(J_3\) and \(J_4\) using (12) - (16).
-
Stop the procedure once termination criterion meets.
The flowchart for the proposed algorithm is shown in Fig. 2.
Results and discussion
To validate the proposed methodology, a standard LV Microgrid CIGRE test network is considered. The various data of LV MG CIGRE test system for wind turbine, photovoltaic, battery energy storage system, controllable load etc. are collected from43. The GWO algorithm, as discussed in Sect. Optimization technique: Grey Wolf optimization GWO, is implemented in MATLAB software to get the optimal solution of the developed optimization problem, along with the Jaya and PSO algorithms. Each search agent in the optimisation approach has number of variables that keep changing every hour. Cost analysis is carried out to demonstrate the efficiency of GWO and Jaya. At first, the total 2000 scenarios for loads, PV output, and wind output were generated to get all the uncertainties associated with them, as discussed in the Sect. Scenario generation and reduction of uncertain parameters.
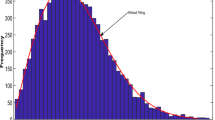
Figure 8 shows all the strategies generated for load using the MCS for the entire day. The blue line curve shows the upper limit curve of the load profile, the green line shows the lower limit of the load curve, and the red dotted curve is the forecasted load curve. Figure 3 is all the scenario sets for the wind power output with a deviation of 15%. The blue curve is the upper limit of the wind curve for 24 hours; the green colour shows the lower acceptable limit curve for wind scenarios; and the red curve shows the predicted values of the wind but is highly uncertain compared to the load and PV scenarios. Figure 4 shows the multiple techniques for solar output generated with the help of MCS using the base value forecasted (red curve) and the error produced using their probability distribution function. The blue and green lines in the set of scenarios show the upper and lower limits of the solar output with the maximum deviations.
It is reduced into smaller samples using the K-mean clustering algorithms to reduce the computational time and complexity. Figure 5 is the graph obtained after applying the k-mean algorithm to the load scenario graph. The set of two thousand load curves is reduced to the group of ten load curves represented by S1, S2, S3, S4, S5, S6, S7, S8, S9, and S10, respectively. In Figs. 6 and 7, the total 2000 of wind power output and solar power output curves are also reduced to a set of 10 curves represented as S1 to S10 with the help of K-mean clustering, respectively. Data sets of PV, wind, and load are obtained with their associated probabilities for each of the ten scenarios.
Grid connected mode
The grid can be considered the virtual generator. A microgrid can buy power when there is a deficit and supply power when it has excess renewable generation.
In Table 1, different priority factor terms like \( \alpha \), \(\beta \), \(\gamma \), \(\delta \), and \(\zeta \) show the relative significance of each cost component in the overall objective function. Based on these priority factors, five cases have been considered.
-
Case1: The value of \(\alpha \) is taken as .75, it shows the relative significance of fuel cost \(J_1\), the value of \(\beta \) is .04, it is the weight factor for the emission cost \(J_2\), and the values of \(\gamma \) and \(\delta \) are 0.1 and 0.1, respectively, and these show the weight factor of the cost associated with energy exchanged with grid \((J_3)\) and battery cost \((J_4)\), respectively.
-
Case2: The value of \(\alpha \) is taken as .6, which is associated with fuel cost \(J_1\); the value of \(\beta \) is 0.1; it is the weight factor for the emission cost \(J_2\); and the values of \(\gamma \) and \(\delta \) are 0.2 and 0.1, respectively, and these show the weight factors of \(J_3\) and \(J_4\), respectively.
-
Case3: The value of \(\alpha \) is reduced to .5, the value of \(\beta \) is .1, and the values of \(\gamma \) and \(\delta \) are 0.25 and 0.15, respectively.
-
Case4: The value of \(\alpha \) is .5, the value of \(\beta \) is .15, and the values of \(\gamma \) and \(\delta \) are 0.2 and 0.15, respectively.
-
Case5: For this case, the values of \(\alpha \), \(\beta \), \(\gamma \), and \(\delta \) are assumed to be 1.
In each case, 10 scenarios are taken, with (PV1W1L1) or S1 of PV from Fig. 8, S1 of wind from Fig. 7, S1 of load from Fig. 6 being the first scenario or the first data set, PV2W2L2 (S2 of PV, S2 of wind, S2 of load) being the second scenario (second data set), and so on. For these data sets, optimisation is carried out using the GWO and Jaya algorithms. For each scenario, there is an optimal value, but we are focusing on stochastic optimisation, so to consider the uncertain nature, we need to take the average optimal values of all the scenarios.
From Table 3, GWO gives better results than Jaya for all the cases. The lowest cost for case 4 in the GWO algorithm value is \(4004\$\). The standard deviation is less when using GWO and quite high when using Jaya.
The main cost is the operating cost of CDGs, followed by the grid exchange cost, battery cost, and emission cost. The same can be observed from Table 2, when the priority of all the cost terms is equal, the cost is maximum, as in case 5 of all the optimisation methods, but if it is allotted properly, the overall cost reduces. From Table 3, GWO is giving better results than the Jaya algorithm for my problem. Although the difference between the optimal cost obtained from GWO and Jaya is not high for one day, it will significantly affect the cost for longer. Figure 9 shows the load curve, total of CDGs power, wind power output, solar output, exchange with the grid, battery power output, and dump energy (PL-PG) by using the GWO algorithm. Similarly, Fig. 10 shows the load curve, the total of CDGs power, wind power output, solar output, exchange with the grid, battery power output, and the dump using the Jaya algorithm.
Isolated mode
In this mode, there is no grid to act like a virtual generator, so we will go for load curtailment when we don’t have sufficient generation. This load curtailment is associated with some revenue loss for the operator, which we call VOLL (value of loss load), which is higher than the price of electricity offered to the customer. In isolated mode, the third term of the objective function (exchange with the grid) is not there, and the Lshed term comes into the picture.
-
Case1: The value of \(\alpha \) is taken as .75, it shows the relative significance of fuel cost \(J_1\), the value of \(\beta \) is .04, it is the weight factor for the emission cost \(J_2\), and the values of \(\zeta \) and \(\delta \) are 0.1 and 0.1, respectively, and these show the weight factor of the cost associated with load shedding \(J_5\) and battery cost \((J_4)\), respectively.
-
Case2: The value of \(\alpha \) is taken as .6, which is associated with fuel cost \(J_1\); the value of \(\beta \) is .1; it is the weight factor for the emission cost \(J_2\); and the values of \(\zeta \) and \(\delta \) are 0.2 and 0.1, respectively, and these show the weight factors of \(J_5\) and \(J_4\), respectively.
-
Case3: The value of \(\alpha \) is reduced to .5, the value of \(\beta \) is .1, and the values of \(\zeta \) and \(\delta \) are 0.25 and 0.15, respectively.
-
Case4: The value of \(\alpha \) is .5, the value of \(\beta \) is .15, and the values of \(\zeta \) and \(\delta \) are 0.2 and 0.15, respectively.
-
Case5: For this case, the values of \(\alpha \), \(\beta \), \(\zeta \), and \(\delta \) are assumed to be 1.
Table 5 observed that the overall cost has increased in isolated mode on the operator side sometimes when GWO optimization is used and for all instances where the Jaya algorithm is used. This is because of load curtailment to balance demand and supply and improve reliability. Load curtailment is associated with incentives given to the customer because of overall cost increases. For the GWO algorithm, the best optimal cost is 3754$ for case 4, and the worst case is 9106$, whereas for Jaya, the best case is case 3 with 4222$ dollars, and the worst case is case 5 with 11608$. The detailed description of different cost components obtained in isolated mode is in Table 4 for PSO, GWO, and Jaya.
Conclusion
This paper proposes a day-ahead stochastic scheduling problem for the MG with uncertainty. The main aim is to minimise the overall cost of the microgrid, and a scenario-based method is modelled for the uncertain nature of RESs (PV and wind) and load. The economic load dispatch problem has been solved using two popular metaheuristic algorithms, the Grey-Wolf algorithm and Jaya. Jaya and PSO performed equally well compared to GWO. The proposed strategy’s effectiveness in economics and reliability is investigated on a standard benchmark LV microgrid CIGRE test network. Economic load dispatch was performed for both the grid-connected and the islanded microgrid. During isolated mode, the cost was maximised by the Jaya algorithm and a little less by GWO. In grid-connected mode, GWO has obtained the best optimal solution.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Wang, S., Ge, L., Wang, K. & Cai, S. Energy management and economic operation optimization of microgrid under uncertainty. Energy Manag. Distrib. Gen. Syst.https://doi.org/10.5772/63802 (2016).
Al-Ismail, F. S. DC microgrid planning, operation, and control: A comprehensive review. IEEE Access 9, 36154–36172. https://doi.org/10.1109/access.2021.3062840 (2021).
Gorripotu, T. S. et al. Tlbo algorithm optimized fractional-order PID controller for AGC of interconnected power system. In Soft Computing in Data Analytics (eds Nayak, J. et al.) 847–855 (Springer Singapore, 2019).
Ammar, H. H., Azar, A. T., Shalaby, R. & Mahmoud, M. I. Metaheuristic optimization of fractional order incremental conductance (fo-inc) maximum power point tracking (mppt). Complexity 2019, 1–13 (2019).
Meghni, B., Dib, D., Azar, A. T. & Saadoun, A. Effective supervisory controller to extend optimal energy management in hybrid wind turbine under energy and reliability constraints. Int. J. Dyn. Control 6, 369–383 (2018).
Meghni, B., Dib, D., Azar, A. T., Ghoudelbourk, S. & Saadoun, A. Robust adaptive supervisory fractional order controller for optimal energy management in wind turbine with battery storage. In Fractional Order Control and Synchronization of Chaotic Systems Vol. 688 (eds Azar, A. T. et al.) 165–202 (Springer International Publishing, 2017).
Yadav, U. K., Meena, V., Gupta, A. & Singh, V. Jaya assisted approximation of sylvester based higher-order mimo power system model. In 2022 IEEE Global Conference on Computing, Power and Communication Technologies (GlobConPT), 1–5 (IEEE, 2022).
Behera, S. A systematic review of energy management system based on various adaptive controllers with optimization algorithm on a smart microgrid. Int. Trans. Electr. Energy Syst. (Wiley)https://doi.org/10.1002/2050-7038.13132 (2021).
Khodayar, M. E., Barati, M. & Shahidehpour, M. Integration of high reliability distribution system in microgrid operation. IEEE Trans. Smart Grid 3, 1997–2006. https://doi.org/10.1109/tsg.2012.2213348 (2012).
Zhang, X., Sharma, R. & He, Y. Optimal energy management of a rural microgrid system using multi-objective optimization. In 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), https://doi.org/10.1109/isgt.2012.6175655 (IEEE, 2012).
Riffonneau, Y., Bacha, S., Barruel, F. & Ploix, S. Optimal power flow management for grid connected PV systems with batteries. IEEE Trans. Sustain. Energy 2, 309–320. https://doi.org/10.1109/tste.2011.2114901 (2011).
Singh, S., Singh, M. & Kaushik, S. C. Optimal power scheduling of renewable energy systems in microgrids using distributed energy storage system. IET Renew. Power Gen. 10, 1328–1339. https://doi.org/10.1049/iet-rpg.2015.0552 (2016).
Xiaoping, L., Ming, D., Jianghong, H., Pingping, H. & Yali, P. Dynamic economic dispatch for microgrids including battery energy storage. In The 2nd International Symposium on Power Electronics for Distributed Generation Systems, https://doi.org/10.1109/pedg.2010.5545768 (IEEE, 2010).
Sobu, A. & Wu, G. Dynamic optimal schedule management method for microgrid system considering forecast errors of renewable power generations. In 2012 IEEE International Conference on Power System Technology (POWERCON), https://doi.org/10.1109/powercon.2012.6401287 (IEEE, 2012).
Hill, J. & Nwankpa, C. System constraints effects on optimal dispatch schedule for battery storage systems. In 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), https://doi.org/10.1109/isgt.2012.6175634 (IEEE, 2012).
Changsong, C., Shanxu, D., Tao, C., Bangyin, L. & Jinjun, Y. Energy trading model for optimal microgrid scheduling based on genetic algorithm. In 2009 IEEE 6th International Power Electronics and Motion Control Conference, https://doi.org/10.1109/ipemc.2009.5157753 (IEEE, 2009).
Suresh, V. & Janik, P. Optimal power flow in microgrids using genetic algorithm. In 2019 2nd International Conference on Power and Embedded Drive Control (ICPEDC), https://doi.org/10.1109/icpedc47771.2019.9036669 (IEEE, 2019).
Askarzadeh, A. A memory-based genetic algorithm for optimization of power generation in a microgrid. IEEE Trans. Sustain. Energy 9, 1081–1089. https://doi.org/10.1109/tste.2017.2765483 (2018).
Raghavan, A., Maan, P. & Shenoy, A. K. B. Optimization of day-ahead energy storage system scheduling in microgrid using genetic algorithm and particle swarm optimization. IEEE Access 8, 173068–173078. https://doi.org/10.1109/access.2020.3025673 (2020).
Meena, V., Jangid, H. & Singh, V. Gwo based reduced-order modeling of doha water treatment plant. In 2021 International Conference on Control, Automation, Power and Signal Processing (CAPS), 1–5 (IEEE, 2021).
Jiang, H., Ning, S. & Ge, Q. Multi-objective optimal dispatching of microgrid with large-scale electric vehicles. IEEE Access 7, 145880–145888. https://doi.org/10.1109/access.2019.2945597 (2019).
Gholami, K. & Dehnavi, E. A modified particle swarm optimization algorithm for scheduling renewable generation in a micro-grid under load uncertainty. Appl. Soft Comput. 78, 496–514. https://doi.org/10.1016/j.asoc.2019.02.042 (2019).
Meena, V. et al. Location and size selection using hybrid Jaya-Luus-Jaakola algorithm for decentralized generations in distribution system considering demand-side management. IET Renew. Power Gen. 17, 1535–1544 (2023).
Ellahi, M., Abbas, G., Satrya, G. B., Usman, M. R. & Gu, J. A modified hybrid particle swarm optimization with bat algorithm parameter inspired acceleration coefficients for solving eco-friendly and economic dispatch problems. IEEE Access 9, 82169–82187. https://doi.org/10.1109/access.2021.3085819 (2021).
Vlachogiannis, J. & Lee, K. Economic load dispatch—a comparative study on heuristic optimization techniques with an improved coordinated aggregation-based PSO. IEEE Trans. Power Syst. 24, 991–1001. https://doi.org/10.1109/tpwrs.2009.2016524 (2009).
Ellahi, M. & Abbas, G. A hybrid metaheuristic approach for the solution of renewables-incorporated economic dispatch problems. IEEE Access 8, 127608–127621. https://doi.org/10.1109/access.2020.3008570 (2020).
Sukumar, S., Marsadek, M., Ramasamy, A. & Mokhlis, H. Grey wolf optimizer based battery energy storage system sizing for economic operation of microgrid. In 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I &.CPS Europe), https://doi.org/10.1109/eeeic.2018.8494501 (IEEE, 2018).
Rajan, C. S. & Ebenezer, M. Grey wolf optimizer algorithm for performance improvement and cost optimization in microgrids. In 2022 6th International Conference on Green Energy and Applications (ICGEA), https://doi.org/10.1109/icgea54406.2022.9791902 (IEEE, 2022).
Kumar, K. P., Saravanan, B., Swarup, K. S. & Day ahead scheduling of generation and storage sources in a microgrid using artificial fish swarm algorithm. In 21st Century Energy Needs - Materials Systems and Applications (ICTFCEN) 2016, https://doi.org/10.1109/ictfcen.2016.8052753 (IEEE, 2016).
Behera, S. Modelling and simulations of modified slime mould algorithm based on fuzzy pid to design an optimal battery management system in microgrid. Clean. Energy Syst. 3, 100029. https://doi.org/10.1016/j.prime.2023.100108 (2022).
Swain N, S. N. & Behera, S. Stabilized frequency response of a microgrid using a two-degree-of-freedom controller with African vultures optimization algorithm. ISA Trans. (Elsevier) 140, 412–425. https://doi.org/10.1016/j.isatra.2023.05.009 (2023).
Behera, S. Maiden application of the slime mold algorithm for optimal operation of energy management on a microgrid considering demand response program. SN Comput. Sci. (Springer) 4, 491. https://doi.org/10.1007/s42979-023-02011-9 (2023).
Yousif, M. et al. An optimal dispatch strategy for distributed microgrids using PSO. CSEE J. Power Energy Syst.https://doi.org/10.17775/cseejpes.2018.01070 (2019).
Meena, V. & Singh, V. Design of fopid controller for riverol-pilipovik water treatment plant exploiting jaya algorithm. In 2023 International Conference on Computer, Electronics & Electrical Engineering & their Applications (IC2E3), 1–5 (IEEE, 2023).
Meena, V., Yadav, U., Gupta, A. & Singh, V. Reduced-order model based design of pid control for zeta converter using gwo algorithm. In 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), 1–5 (IEEE, 2022).
Vahedipour-Dahraie, M. et al. Flexible stochastic scheduling of microgrids with islanding operation complemented by optimal offering strategies. CSEE J. Power Energy Syst.https://doi.org/10.17775/cseejpes.2019.02560 (2020).
Alvarez, E., Lopez, A. C., Gomez-Aleixandre, J. & de Abajo, N. On-line minimization of running costs, greenhouse gas emissions and the impact of distributed generation using microgrids on the electrical system. In 2009 IEEE PES/IAS Conference on Sustainable Alternative Energy (SAE), https://doi.org/10.1109/sae.2009.5534847 (IEEE, 2009).
Kuntal, P., Mathur, A. & Alam, M. N. Optimal power scheduling of hybrid power system. In 2021 IEEE 2nd International Conference on Smart Technologies for Power, Energy and Control (STPEC), https://doi.org/10.1109/stpec52385.2021.9718620 (IEEE, 2021).
Gazijahani, F. S., Hosseinzadeh, H., Abadi, A. A. & Salehi, J. Optimal day ahead power scheduling of microgrids considering demand and generation uncertainties. In 2017 Iranian Conference on Electrical Engineering (ICEE), https://doi.org/10.1109/iraniancee.2017.7985174 (IEEE, 2017).
Nguyen, D. T. & Le, L. B. Optimal bidding strategy for microgrids considering renewable energy and building thermal dynamics. IEEE Trans. Smart Grid 5, 1608–1620. https://doi.org/10.1109/tsg.2014.2313612 (2014).
Toubeau, J.-F., Bottieau, J., Vallee, F. & Greve, Z. D. Deep learning-based multivariate probabilistic forecasting for short-term scheduling in power markets. IEEE Trans. Power Syst. 34, 1203–1215. https://doi.org/10.1109/tpwrs.2018.2870041 (2019).
Agarwal, S., Yadav, S. & Singh, K. Notice of violation of IEEE publication principles - k-means versus k-means ++ clustering technique. In 2012 Students Conference on Engineering and Systems, https://doi.org/10.1109/sces.2012.6199061 (IEEE, 2012).
Kotsampopoulos, P. et al. A benchmark system for hardware-in-the-loop testing of distributed energy resources. IEEE Power Energy Technol. Syst. J. 5, 94–103. https://doi.org/10.1109/JPETS.2018.2861559 (2018).
Acknowledgements
The authors would like to acknowledge the support of the Norwegian University of Science and Technology for paying the Article Processing Charges (APC) of this publication. This research is supported by Automated Systems and Soft Computing Lab (ASSCL), Prince Sultan University, Riyadh, Saudi Arabia. The authors would like to thank Prince Sultan University, Riyadh, Saudi Arabia for their support.
Funding
Open access funding provided by Norwegian University of Science and Technology. This research was funded by the Norwegian University of Science and Technology.
Author information
Authors and Affiliations
Contributions
Conceptualization, A.M., R.K., V.P.M., V.P.S.; Methodology, A.M., R.K., V.P.M., V.P.S., A.T.A., I.A.H.; Software, A.M., R.K., V.P.M., V.P.S.; Validation, A.T.A., I.A.H.; Formal analysis, A.M., R.K., V.P.M., V.P.S., A.T.A., I.A.H.; Investigation, A.T.A., I.A.H.; Resources, A.M., R.K., V.P.M., V.P.S., A.T.A., I.A.H.; Data curation, A.M., R.K., V.P.M., V.P.S., A.T.A., I.A.H.; Writing—original draft, A.M., R.K., V.P.M., V.P.S.; Writing—review & editing, A.M., R.K., V.P.M., V.P.S., A.T.A., I.A.H.; Visualization, A.M., R.K., V.P.M., V.P.S., A.T.A., I.A.H.; Supervision, V.P.M. and A.T.A.; Funding acquisition, I.A.H. All authors have read and agreed to the published version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mathur, A., Kumari, R., Meena, V.P. et al. Data-driven optimization for microgrid control under distributed energy resource variability. Sci Rep 14, 10806 (2024). https://doi.org/10.1038/s41598-024-58767-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-58767-4
Keywords
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.