A novel group decision making method based on CoCoSo and interval-valued Q-rung orthopair fuzzy sets

Abstract

Interval-valued q-rung orthopair fuzzy set (IVq-ROFS) is a powerful tool for dealing with uncertainty. In this paper, we first propose a new method for aggregating multiple IVq-ROFSs, which is easier to understand and implement in the multi-attribute group decision making process compared to current aggregation operators. Secondly, this paper introduces a new fuzzy entropy with parameters based on IVq-ROFS, which is highly flexible due to its adjustable parameters. Based on this, the IVq-ROFS-based attribute weight calculation method is proposed to obtain the objective weights of the attributes, which is more reasonable and objective than the existing methods. Then, for the dimensional differences between the three compromise scores in the original Combined Compromise Solution (CoCoSo) method, the enhanced compromise scores are proposed. These scores are obtained by normalizing the three dependent compromise scores, ensuring that they fall within the same range. Finally, a novel CoCoSo mothed on IVq-ROFS using the proposed fuzzy entropy and enhanced compromise scores is presented. The proposed method is highly adaptable and scalable, not limited to IVq-ROFS. The excellent performance and robustness of the proposed method are verified in sepsis diagnosis applications.

Introduction

The fuzziness and imprecision of the data in many real-world problems make it extremely difficult to make effective data-driven decisions^1,2,3. Numerous mathematical models have been developed in recent decades to deal with uncertainties. Zadeh⁴ proposed the concept of fuzzy sets as a generalization of crisp sets. Takeuti⁵ extended the traditional fuzzy set theory and introduced the concept of intuitionistic fuzzy sets (IFS). IFSs introduced the non-membership degree (NMD) as the supplement to the membership degree (MD), which has been extensively applied in many fields, including decision making^6,7, cluster analysis^8,9, medical diagnosis^10,11, and pattern recognition^12,13. Turksen¹⁴ proposed the concept of interval-valued fuzzy set. Atanassov¹⁵ further extended IFSs and proposed the concept of interval valued intuitionistic fuzzy set (IVIFS) to make the consideration more comprehensive in practical applications. IVIFSs use subintervals in the interval [0,1] to describe the MD and NMD, making them more flexible and practical than IFSs when dealing with ambiguous or uncertain data. Yager¹⁶ proposed Pythagorean fuzzy set (PFS), which extended the concept of IFS and provided new research ideas and methods for solving uncertainty problems. This theory is more widely used in the field of MADM¹⁷. Compared with IFS, PFS have the sum of squares of MD and NMD, which are less than or equal to 1, allowing decision makers to give a wider range of values. Later, Zhang¹⁸ further extended PFS and proposed the concept of Interval-valued Pythagorean Fuzzy Set (IVPFS). Furthermore, in order to cover more data, fermatean fuzzy sets^19,20 and interval-valued fermatean fuzzy sets²¹ were presented. Integration of IFS, PFS and fermatean fuzzy sets described above, q-rung orthopair fuzzy^22,23,24,25 set was proposed. When the q-ROFS will degenerate to IFS, PFS, FFS. Similarly, interval valued q-rung orthopair fuzzy set (IVq-ROFS)²² was proposed, and when the IVq-ROFS will degenerate to IVIFS, IVPFS, IVFFS. Compared with IVIFS, IVPFS, IVFFS, and IVq-ROFS have more data that can be covered than IVIFS, IVPFS, and IVFFS. Based on the above models, there are many extension models such as picture fuzzy set^26,27 , complex fuzzy set, fuzzy soft set²⁸ and their extensions^{29,30,31,32,33,34,35,36,37}. The current research on IVq-ROFS mainly focuses on the aggregation operators^38,39,40, information measures^41,42,43, extended IVq-ROFS^44,45,46, MADM methods^47,48,49.

Experts and scholars have studied IVq-ROFS and its applications in MADM from different perspectives and proposed many valuable decision-making methods. The q-connection number was shown in^50,51, and a new MAGDM method was proposed based on the q-connection number and IVq-ROFS. A scientific risk evaluation method based on IVq-ROFS capable of solving these deficiencies in the existing method was given in⁵¹. Seker et al.⁵² proposed a COPRAS method for IVq-ROFS. Yang et al.⁵³ focused on the preference relations of IVq-ROFS and presented a related GDM method. Gurmani et al.⁵⁴ created a new approach to determining expert weights using distance and similarity measures for IVq-ROFS.

However, there are some research gaps below. From a theoretical point of view, firstly, for MAGDM for IVq-ROFS, it is necessary to aggregate information from many different experts. However, the existing multi-source information aggregation method in⁵⁵, which used the Archimedean Muirhead mean operators to aggregate fuzzy data, is not easy to understand and implement. Secondly, the existing method in^52,55,56,57 related to attribute weight determination has a certain degree of subjectivity. Therefore, presenting a weight calculation method with complete objectivity is essential. Thirdly, for the original CoCoSo method⁵⁸ proposed by Yazidani et al., which combined three comprised scores to calculate the final rating, there is an unavoidable problem that the value domains of the three dependent compromise scores are different, which directly affects the final score calculation. It is necessary to convert three dependent compromise scores to a unified scale for the CoCoSo method. From a practical point of view, in diagnosing disease, the diagnostic process in clinical care cannot rely solely on test data, as there is often excessive variability in patients' signs and symptoms and a lack of specificity. If a patient with suspected or confirmed infection presents with a worsening condition and is at risk of organ dysfunction, early recognition and prompt treatment as appropriate is critical to improving outcomes. By the time the diagnosis becomes apparent, and multiple physiologic parameters are abnormal, the risk of death is very high. Therefore, multi-expert collective decision making is crucial in clinical diagnosis because MAGDM can gather the decision-making ideas of multiple experts and finally unify them to complete the initial diagnosis of the disease at an early stage when the patient has fewer signs and data abnormalities. The rate of misdiagnosis of the conventional clinical diagnosis may be higher, doctors are in a state of uncertainty about the diagnosis of sepsis, the interval- value q-rung fuzzy MAGDM can be a good solution of this problem.

The main contributions of this paper are as follows:

• (1) A novel multi-source aggregation method of aggregating multiple IVq-ROFSs from various specialists is introduced. Compared to the traditional method, it is easier to understand and implement.

• (2) A novel fuzzy entropy with parameter derived from IVq-ROFS, which is more flexible and versatile compared to conventional fuzzy entropy. Additionally, the IVq-ROFS-based attribute weight calculation method is proposed, utilizing this fuzzy entropy as a basis.

• (3) This work aims to enhance the dimensional distinctions among the three compromise scores of the original CoCoSo approach.

• (4) There is a limited number of fuzzy MAGDM methods available for sepsis diagnosis. Therefore, we want to validate the accuracy and applicability of our proposed method using a case study on sepsis diagnosis.

The structure of this paper is as follows: “Preliminaries” section describes the related concepts of IVq-ROFS and the original CoCoSo method. In “A novel CoCoSo group decision making method on IVq-ROFSs” section defines the multi-source information aggregation method, presents the new fuzzy entropy based on IVq-ROFS and the proposed CoCoSo group decision method. In “Case Study: Sepsis diagnosis” section describes the application of our method in Sepsis dignose case. In “Sensitivity analysis and comparative analysis” section, we make sensitivity analysis and the comparative analysis with other methods to verify feasibility of our method. And then the merits of our method are discussed. In “Conclusion” section we conclude this paper.

Preliminaries

This section introduces the definitions associated with interval-valued q-rung orthopair fuzzy sets. It then describes the fundamental principles of fuzzy entropy for existing interval-valued fuzzy sets. Finally, the algorithmic flow of the original CoCoSo technique is presented.

Interval-valued fuzzy set

Definition 1

¹⁴ Interval-valued fuzzy set (IVFS): Let the universe X be a non-empty set, then the IVFS on X can be expressed as:

$$A=\left\{\left(x,\left[{\mu }_{A}^{-}\left(x\right),{\mu }_{A}^{+}\left(x\right)\right]|x\in X\right)\right\},$$

where ${\mu }_{A}^{-}\left(x\right)$ is the lower bound of MD, ${\mu }_{A}^{+}\left(x\right)$ is the upper bound of MD.

Interval-valued intuitionistic fuzzy set

Definition 2

¹⁵ Interval-valued intuitionistic fuzzy set(IVIFS):Let the universe X be a non-empty set, then the IVIFS on X can be expressed as:

$${A}^{I*}=\left\{\langle x,{\mu }_{{A}^{I*}}\left(x\right),{\nu }_{{A}^{I*}}\left(x\right)\rangle |x\in X\right\},$$

where ${\mu }_{{A}^{I*}}\left(x\right)\in \left({\mu }_{{A}^{I*}}^{-},{\mu }_{{A}^{I*}}^{+}\right)$, ${\nu }_{{A}^{I*}}\left(x\right)\in \left({\nu }_{{A}^{I*}}^{-},{\nu }_{{A}^{I*}}^{+}\right)$ and $0\le {\mu }_{{A}^{I*}}^{-}\le {\mu }_{{A}^{I*}}^{+}\le 1$, $0\le {\nu }_{{A}^{I*}}^{-}\le {\nu }_{{A}^{I*}}^{+}\le 1$. ${\mu }_{{A}^{I*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ and ${\nu }_{{A}^{I*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ for all $x\in X$ meet ${\mu }_{{A}^{I*}}^{+}+{\nu }_{{A}^{I*}}^{+}\le 1$. ${\mu }_{{A}^{I*}}\left(x\right)$ and ${\nu }_{{A}^{I*}}\left(x\right)$ denote the MD and NMD of elements in $X$ belonging to ${A}^{I*}$ ,respectively.

Interval-valued pythagorean fuzzy set

Definition 3

¹⁸ Interval-valued Pythagorean fuzzy set (IVPFS):Let the universe X be a non-empty set, then the IVPFS on X can be expressed as:

$${A}^{P*}=\left\{\langle x,{\mu }_{{A}^{P*}}\left(x\right),{\nu }_{{A}^{P*}}\left(x\right)\rangle |x\in X\right\},$$

where ${\mu }_{{A}^{P*}}\left(x\right)\in \left({\mu }_{{A}^{P*}}^{-},{\mu }_{{A}^{P*}}^{+}\right)$, ${\nu }_{{A}^{P*}}\left(x\right)\in \left({\nu }_{{A}^{P*}}^{-},{\nu }_{{A}^{P*}}^{+}\right)$ and $0\le {\mu }_{{A}^{P*}}^{-}\le {\mu }_{{A}^{P*}}^{+}\le 1$, $0\le {\nu }_{{A}^{P*}}^{-}\le {\nu }_{{A}^{P*}}^{+}\le 1$. ${\mu }_{{A}^{P*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ and ${\nu }_{{A}^{P*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ for all $x\in X$ meet ${\left({\mu }_{{A}^{P*}}^{+}\right)}^{2}+{\left({\nu }_{{A}^{P*}}^{+}\right)}^{2}\le 1$. ${\mu }_{{A}^{P*}}\left(x\right)$ and ${\nu }_{{A}^{P*}}\left(x\right)$ denote the MD and NMD of elements in $X$ belonging to ${A}^{P*}$, respectively.

Interval-valued Fermatean fuzzy set

Definition 4

²¹ Interval-valued Fermatean fuzzy set (IVFFS): Let the universe X be a non-empty set, then the IVFFS on X can be expressed as:

$${A}^{F*}=\left\{\langle x,{\mu }_{{A}^{F*}}\left(x\right),{\nu }_{{A}^{F*}}\left(x\right)\rangle |x\in X\right\},$$

where ${\mu }_{{A}^{F*}}\left(x\right)\in \left({\mu }_{{A}^{F*}}^{-},{\mu }_{{A}^{F*}}^{+}\right)$, ${\nu }_{{A}^{F*}}\left(x\right)\in \left({\nu }_{{A}^{F*}}^{-},{\nu }_{{A}^{F*}}^{+}\right)$ and $0\le {\mu }_{{A}^{F*}}^{-}\le {\mu }_{{A}^{F*}}^{+}\le 1$, $0\le {\nu }_{{A}^{F*}}^{-}\le {\nu }_{{A}^{F*}}^{+}\le 1$. ${\mu }_{{A}^{F*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ and ${\nu }_{{A}^{F*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ for all $x\in X$ meet ${\left({\mu }_{{A}^{F*}}^{+}\right)}^{3}+{\left({\nu }_{{A}^{F*}}^{+}\right)}^{3}\le 1$. ${\mu }_{{A}^{F*}}\left(x\right)$ and ${\nu }_{{A}^{F*}}\left(x\right)$ denote the MD and NMD of elements in $X$ belonging to ${A}^{F*}$, respectively.

Interval-valued q-rung orthopair fuzzy set

Definition 5

²² Interval-valued q-rung orthopair fuzzy set (IVq-ROFS): Let the universe X be a non-empty set, then the IVq-ROFS on X can be expressed as:

$$ \begin{array}{*{20}c} {A^{Q*} = \left\{ {x,\mu_{{A^{Q*} }} \left( x \right),\nu_{{A^{Q*} }} \left( x \right)|x \in X} \right\},} \\ \end{array} $$

(1)

where ${\mu }_{{A}^{Q*}}\left(x\right)\in \left({\mu }_{{A}^{Q*}}^{-},{\mu }_{{A}^{Q*}}^{+}\right)$, ${\nu }_{{A}^{Q*}}\left(x\right)\in \left({\nu }_{{A}^{Q*}}^{-},{\nu }_{{A}^{Q*}}^{+}\right)$ and $0\le {\mu }_{{A}^{Q*}}^{-}\le {\mu }_{{A}^{Q*}}^{+}\le 1$, $0\le {\nu }_{{A}^{Q*}}^{-}\le {\nu }_{{A}^{Q*}}^{+}\le 1$. ${\mu }_{{A}^{Q*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ and ${\nu }_{{A}^{Q*}}\left(x\right):X\to \left[\mathrm{0,1}\right]$ for all $x\in X$ meet ${\left({\mu }_{{A}^{Q*}}^{+}\right)}^{q}+{\left({\nu }_{{A}^{Q*}}^{+}\right)}^{q}\le 1$. ${\mu }_{{A}^{Q*}}\left(x\right)$ and ${\nu }_{{A}^{Q*}}\left(x\right)$ denote the MD and NMD of elements in $X$ belonging to ${A}^{Q*},$ respectively. The values of MD and NMD of IVq-ROFS are as shown in Fig. 1.

Figure 1

The values of MD and NMD of IVq-ROFS.

For each IVq-ROFS on ${X}^{Q*}$, the hesitancy degree in²⁰ ${\pi }_{{A}^{Q*}}\left(x\right)\in \left({\pi }_{Q*}^{-},{\pi }_{Q*}^{+}\right)$ is given, where

$$\begin{array}{c}\left\{\begin{array}{l}{\pi }_{Q*}^{-}=\sqrt[q]{1-{\left({\mu }_{{A}^{Q*}}^{+}\right)}^{q}-{\left({\nu }_{{A}^{Q*}}^{+}\right)}^{q}}\\ {\pi }_{Q*}^{+}=\sqrt[q]{1-{\left({\mu }_{{A}^{Q*}}^{-}\right)}^{q}-{\left({\nu }_{{A}^{Q*}}^{-}\right)}^{q}}\\ \left({\pi }_{Q*}^{-},{\pi }_{Q*}^{+}\right)\in \left(\mathrm{0,1}\right)\end{array}\right.\end{array}$$

(2)

For IVq-ROFS the following basic operations are established.

$$\begin{aligned}{A}_{1}^{Q*} ={A}_{2}^{Q*} & \Leftrightarrow \left[{\mu }_{{A}_{1}^{Q*}}\left(x\right),{\nu }_{{A}_{1}^{Q*}}\left(x\right)\right]=\left[{\mu }_{{A}_{2}^{Q*}}\left(x\right),{\nu }_{{A}_{2}^{Q*}}\left(x\right)\right]\\ & \Leftrightarrow {\mu }_{{A}_{1}^{Q*}}^{-}={\mu }_{{A}_{2}^{Q*}}^{-},{\mu }_{{A}_{1}^{Q*}}^{+}={\mu }_{{A}_{2}^{Q*}}^{+},{\nu }_{{A}_{1}^{Q*}}^{-}={\nu }_{{A}_{2}^{Q*}}^{-},{\nu }_{{A}_{1}^{Q*}}^{+}={\nu }_{{A}_{2}^{Q*}}^{+}\end{aligned}$$

(3)

$$\begin{aligned}{A}_{1}^{Q*}\subseteq {A}_{2}^{Q*} & \Leftrightarrow \left[{\mu }_{{A}_{1}^{Q*}}^{-},{\mu }_{{A}_{1}^{Q*}}^{+}\right]\le \left[{\mu }_{{A}_{2}^{Q*}}^{-},{\mu }_{{A}_{2}^{Q*}}^{+}\right],\left[{\nu }_{{A}_{1}^{Q*}}^{-},{\nu }_{{A}_{1}^{Q*}}^{+}\right]\ge \left[{\nu }_{{A}_{2}^{Q*}}^{-},{\nu }_{{A}_{2}^{Q*}}^{+}\right]\\ & \Leftrightarrow {\mu }_{{A}_{1}^{Q*}}^{-}\le {\mu }_{{A}_{2}^{Q*}}^{-},{\mu }_{{A}_{1}^{Q*}}^{+}\le {\mu }_{{A}_{2}^{Q*}}^{+},{\nu }_{{A}_{1}^{Q*}}^{-}\ge {\nu }_{{A}_{2}^{Q*}}^{-},{\nu }_{{A}_{1}^{Q*}}^{+}\ge {\nu }_{{A}_{2}^{Q*}}^{+}\end{aligned}$$

(4)

$$\begin{aligned}{A}_{1}^{Q*}\preccurlyeq {A}_{2}^{Q*} & \Leftrightarrow \left[{\mu }_{{A}_{1}^{Q*}}^{-},{\mu }_{{A}_{1}^{Q*}}^{+}\right]\preccurlyeq \left[{\mu }_{{A}_{2}^{Q*}}^{-},{\mu }_{{A}_{2}^{Q*}}^{+}\right],\left[{\nu }_{{A}_{1}^{Q*}}^{-},{\nu }_{{A}_{1}^{Q*}}^{+}\right]\succcurlyeq \left[{\nu }_{{A}_{2}^{Q*}}^{-},{\nu }_{{A}_{2}^{Q*}}^{+}\right]\\ & \Leftrightarrow {\mu }_{{A}_{1}^{Q*}}^{-}\le {\mu }_{{A}_{2}^{Q*}}^{-},{\mu }_{{A}_{1}^{Q*}}^{+}\ge {\mu }_{{A}_{2}^{Q*}}^{+},{\nu }_{{A}_{1}^{Q*}}^{-}\ge {\nu }_{{A}_{2}^{Q*}}^{-},{\nu }_{{A}_{1}^{Q*}}^{+}\le {\nu }_{{A}_{2}^{Q*}}^{+}\end{aligned}$$

(5)

Fuzzy entropy

Fuzzy entropy is a measure used to scale the uncertainty of fuzzy elements which is come from statistics. The common fuzzy entropies are mainly as follows:

Definition 6

⁵⁹ Intuitionistic fuzzy entropy: A real-valued function $E\left({A}^{I}\right):IF\left(X\right)\to \left[\mathrm{0,1}\right]$ is named as an entropy on IFS, if E satisfies all the following properties:

(I1):

$0\le E\left({A}^{I}\right)\le 1$;

(I2):

$E\left({A}^{I}\right)=0$ if ${A}^{I}$ is a crisp set;

(I3):

$E\left({A}^{I}\right)=1$ if ${\mu }_{{A}^{I}}\left(x\right)={\nu }_{{A}^{I}}\left(x\right)={\pi }_{{A}^{I}}\left(x\right)=\frac{1}{3}$;

(I4):

$E\left({A}^{I}\right)\le E\left({B}^{I}\right)$ if $A$ is crisper than $B$, which is defined as:

$${\mu }_{A}\left(x\right)\le {\mu }_{B}\left(x\right)\mathrm{ and }{\nu }_{A}\left(x\right)\le {\nu }_{B}\left(x\right)\mathrm{ for }max\{{\upmu }_{B},{\upnu }_{B}\}\le \frac{1}{3};$$

$${\mu }_{A}\left(x\right)\ge {\mu }_{B}\left(x\right)\mathrm{ and }{\nu }_{A}\left(x\right)\ge {\nu }_{B}\left(x\right)\mathrm{ for }min\{{\upmu }_{B},{\upnu }_{B}\}\ge \frac{1}{3};$$

Definition 7

⁶⁰ Interval-valued intuitionistic fuzzy entropy: A real-valued function $E({A}^{I*})$: $IVIF\left(X\right)\to [\mathrm{0,1}]$ is named as an entropy on IVIFS, if $E({A}^{I*})$ satisfies all the following properties:

(I^*1):

$0\le E({A}^{I*})\le 1.$

• (i) $E\left({A}^{I*}\right)=0$ if ${A}^{I*}$ is a crisp set.

• (ii) $E({A}^{I*})$ iff ${\mu }_{{A}^{I*}}\left({x}_{i}\right)={\upnu }_{{A}^{I*}}\left({x}_{i}\right)$.

(I^*2):

$E\left({A}^{I*}\right)=E({\left({A}^{I*}\right)}^{C}).$

(I^*3):

$E\left({A}^{I*}\right)\le E\left({B}^{I*}\right)$ if A is crisper than B, which is defined as:

$$ \mu_{{A^{I*} }} \left( {x_{i} } \right) \le \mu_{{B^{I*} }} \left( {x_{i} } \right), \;\upnu _{{A^{I*} }} \left( {x_{i} } \right) \ge\upnu _{{B^{I*} }} \left( {x_{i} } \right) \;{\text{for}}\;\mu_{{B^{I*} }} \left( {x_{i} } \right) \le\upnu _{{B^{I*} }} \left( {x_{i} } \right); $$

$$ \mu_{{A^{I*} }} \left( {x_{i} } \right) \ge \mu_{{B^{I*} }} \left( {x_{i} } \right), \upnu _{{A^{I*} }} \left( {x_{i} } \right) \le\upnu _{{B^{I*} }} \left( {x_{i} } \right)\;{\text{for}}\;\mu_{{B^{I*} }} \left( {x_{i} } \right) \ge\upnu _{{B^{I*} }} \left( {x_{i} } \right); $$

$$ \mu_{{A^{I*} }} \left( {x_{i} } \right){ \preccurlyeq }\mu_{{B^{I*} }} \left( {x_{i} } \right),{{ \nu }}_{{A^{I*} }} \left( {x_{i} } \right){ \succcurlyeq }{\upnu }_{{B^{I*} }} \left( {x_{i} } \right)\;{\text{for}}\;\mu_{{B^{I*} }} \left( {x_{i} } \right){ \preccurlyeq }{\upnu }_{{B^{I*} }} \left( {x_{i} } \right); $$

$$ \mu_{{A^{I*} }} \left( {x_{i} } \right){ \succcurlyeq }\mu_{{B^{I*} }} \left( {x_{i} } \right),\upnu _{{A^{I*} }} \left( {x_{i} } \right){ \preccurlyeq \nu }_{{B^{I*} }} \left( {x_{i} } \right)\;{\text{for}}\;\mu_{{B^{I*} }} \left( {x_{i} } \right){ \succcurlyeq \nu }_{{B^{I*} }} \left( {x_{i} } \right). $$

The combined compromise solution (CoCoSo) method

Yazdani et al.⁵⁸ proposed an eclectic MADM, which is an efficient way to deal with complex decision question by using conflict analysis. CoCoSo method is implemented by the following steps for decision making after determining the alternatives and evaluation criteria:

Step 1 The original decision matrix is normalized by Eq. (6):

$$ \left\{ {\begin{array}{*{20}l} {\overline{x}_{ij} = \frac{{x_{ij} - min\;x_{ij} }}{\tau }, \quad for\;benefit\;criteria;} \hfill \\ {\overline{x}_{ij} = \frac{{max\;x_{ij} - x_{ij} }}{\tau },\quad for\;cost\;criteria,} \hfill \\ \end{array} } \right. $$

(6)

where $\tau =\mathit{max}\,{x}_{ij}-\mathit{min}\,{x}_{ij}$.

Step 2 Calculate the weighted sum and weighted product for each alternative based on the attribute weights by Eqs. (7–8):

$$ S_{\omega i} = \mathop \sum \limits_{j = 1}^{n} \omega_{j} \overline{x}_{ij} $$

(7)

$$ \begin{array}{*{20}c} {M_{\omega i} = \mathop \prod \limits_{j = 1}^{n} \left( {\overline{x}_{ij} } \right)^{{\omega_{j} }} } \\ \end{array} $$

(8)

Step 3 Generate three dependent compromise scores for each alternative using the three dependent aggregation operators from different perspectives by using Eq. (9):

$$ \left\{ {\begin{array}{*{20}l} {S_{i}^{1} = \frac{{S_{\omega i} + M_{\omega i} }}{{\mathop \sum \nolimits_{i = 1}^{m} \left( {S_{\omega i} + M_{\omega i} } \right)}};} \hfill \\ {S_{i}^{2} = \frac{{S_{\omega i} }}{{min\,S_{\omega i} }} + \frac{{M_{\omega i} }}{{min\,M_{\omega i} }};} \hfill \\ {S_{i}^{3} = \frac{{\varepsilon S_{\omega i} + \left( {1 - \varepsilon } \right)M_{\omega i} }}{{\varepsilon max_{i} S_{\omega i} + \left( {1 - \varepsilon } \right)max_{i} M_{\omega i} }}, \quad 0 \le \varepsilon \le 1} \hfill \\ \end{array} } \right. $$

(9)

Step 4 Calculate the three dependent compromise scores using the mixed integration operator as shown as Eq. (10):

$$\begin{array}{c}{S}_{i}=\frac{1}{3}\left({S}_{i}^{1}+{S}_{i}^{2}+{S}_{i}^{3}\right)+{\left({S}_{i}^{1}{S}_{i}^{2}{S}_{i}^{3}\right)}^\frac{1}{3}\end{array}$$

(10)

A novel CoCoSo group decision making method on IVq-ROFSs

In this section, a new MAGDM method is proposed. Firstly, a new multi-source aggregation method is given for multiple IVq-ROFSs. And then a new fuzzy entropy with parameter and related weight calculation method is introduced. Finally, the new CoCoSo method on IVq-ROFS utilizing the proposed fuzzy entropy and the enhanced compromise scores is presented.

Multi-source aggregation method on IVq-ROFSs

The information aggregation method is the first step of fuzzy MAGDM method, this paper defines a multi-source aggregation method of IVq-ROFSs inspired by Petry’s method⁶¹. Distinguishing from the complex aggregation operators proposed in other studies^62,63,64 for the MAGDM problem, a framework for multi-source aggregation methods and two simpler approaches that satisfied the framework are presented in this section.

Definition 8

Let the universe $X$ be a non-empty set, then Multi-source Aggregation Interval-valued q-rung orthopair fuzzy set (MsAIVq-ROFS) is defined as follows:

$$ \begin{array}{*{20}c} {A_{agg}^{Q*} = \left\{ {x,\mu_{{A_{agg}^{Q*} }} \left( x \right),\nu_{{A_{agg}^{Q*} }} \left( x \right)|x \in X} \right\},} \\ \end{array} $$

(11)

where ${\mu }_{{A}_{agg}^{Q*}}=AGG\left({\mu }_{{A}_{1}^{Q*}},{\mu }_{{A}_{2}^{Q*}},\cdots ,{\mu }_{{A}_{n}^{Q*}}\right)$ and ${\nu }_{{A}_{agg}^{Q*}}=AGG\left({\nu }_{{A}_{1}^{Q*}},{\nu }_{{A}_{2}^{Q*}},\cdots ,{\nu }_{{A}_{n}^{Q*}}\right)$. $AGG\left({x}_{1},{x}_{2},\cdots ,{x}_{n}\right)$ is the aggregation function of the MD and NMD to be defined for the IVq-ROFS, expanding the function we can obtain:

$${\mu }_{{A}_{agg}^{Q*}}=AGG\left({\mu }_{{A}_{1}^{Q*}},{\mu }_{{A}_{2}^{Q*}},\cdots ,{\mu }_{{A}_{n}^{Q*}}\right)=\left[AGG\left({\mu }_{{A}_{1}^{Q*}}^{-},{\mu }_{{A}_{2}^{Q*}}^{-},\cdots ,{\mu }_{{A}_{n}^{Q*}}^{-}\right),AGG\left({\mu }_{{A}_{1}^{Q*}}^{+},{\mu }_{{A}_{2}^{Q*}}^{+},\cdots ,{\mu }_{{A}_{n}^{Q*}}^{+}\right)\right],$$

$${\nu }_{{A}_{agg}^{Q*}}=AGG\left({\nu }_{{A}_{1}^{Q*}},{\nu }_{{A}_{2}^{Q*}},\cdots ,{\nu }_{{A}_{n}^{Q*}}\right)=\left[AGG\left({\nu }_{{A}_{1}^{Q*}}^{-},{\nu }_{{A}_{2}^{Q*}}^{-},\cdots ,{\nu }_{{A}_{n}^{Q*}}^{-}\right),AGG\left({\nu }_{{A}_{1}^{Q*}}^{+},{\nu }_{{A}_{2}^{Q*}}^{+},\cdots ,{\nu }_{{A}_{n}^{Q*}}^{+}\right)\right] ,$$

and ${\mu }_{{A}_{n}^{Q*}}^{+}$,${\mu }_{{A}_{n}^{Q*}}^{-}$,${\nu }_{{A}_{n}^{Q*}}^{+}$,${\nu }_{{A}_{n}^{Q*}}^{-}$ are the upper and lower bounds of the MD and NMD of IVq-ROFS. Next, considering the different requirements needed by different decision makers in a complex decision environment, this paper proposes two aggregation functions for IVq-ROFSs.

Definition 9

For n IVq-ROFSs of the same universe $X$, the compromised MsAIVq-ROFS is as follows:

$$\begin{array}{c}{A}_{pos}^{Q*}=\left\{\langle x,{\mu }_{{A}_{pos}^{Q*}}\left(x\right),{\nu }_{{A}_{pos}^{Q*}}\left(x\right)\rangle |x\in X\right\}\end{array}$$

(12)

$$\begin{array}{c}{\mu }_{{A}_{pos}^{Q*}}=\left[\frac{\sum_{i=1}^{n}{\mu }_{{A}_{i}^{Q*}}^{-}}{n},\frac{\sum_{i=1}^{n}{\mu }_{{A}_{i}^{Q*}}^{+}}{n}\right],{\nu }_{{A}_{pos}^{Q*}}=\left[\frac{\sum_{i=1}^{n}{\nu }_{{A}_{i}^{Q*}}^{-}}{n},\frac{\sum_{i=1}^{n}{\nu }_{{A}_{i}^{Q*}}^{+}}{n}\right]\end{array}$$

(13)

${S}_{{\mu }_{{A}_{i}^{Q*}}^{+}}$, ${S}_{{\mu }_{{A}_{i}^{Q*}}^{-}}$, ${S}_{{\nu }_{{A}_{i}^{Q*}}^{+}}$, ${S}_{{\nu }_{{A}_{i}^{Q*}}^{-}}$ are the sets of upper and lower bounds of the MD and NMD to be aggregated. ${\mu }_{{A}_{i}^{Q*}}^{+}\in {S}_{{\mu }_{{A}_{i}^{Q*}}^{+}}$, ${\mu }_{{A}_{i}^{Q*}}^{-}\in {S}_{{\mu }_{{A}_{i}^{Q*}}^{-}}$, ${\nu }_{{A}_{i}^{Q*}}^{+}\in {S}_{{\nu }_{{A}_{i}^{Q*}}^{+}}$, ${\nu }_{{A}_{i}^{Q*}}^{-}\in {S}_{{\nu }_{{A}_{i}^{Q*}}^{-}}$.

Definition 10

For n IVq-ROFSs of the same object set X, the inclusive MsAIVq-ROFS is as follows:

$$\begin{array}{c}{A}_{neg}^{Q*}=\left\{\langle x,{\mu }_{{A}_{neg}^{Q*}}\left(x\right),{\nu }_{{A}_{neg}^{Q*}}\left(x\right)\rangle |x\in X\right\}\end{array}$$

(14)

$$\begin{array}{c}{\mu }_{{A}_{neg}^{Q*}}=\left[min\left({\mu }_{{A}_{s}^{Q*}}^{-}\right),max\left({\mu }_{{A}_{s}^{Q*}}^{+}\right)\right],{\nu }_{{A}_{neg}^{Q*}}=\left[min\left({\nu }_{{A}_{s}^{Q*}}^{-}\right),max\left({\nu }_{{A}_{s}^{Q*}}^{+}\right)\right].\end{array}$$

(15)

These two approaches to aggregation of information sources are illustrated below by a supplier selection problem.

Example 1

Let the existing supplier object set be $O=\left\{{O}_{1},{O}_{2},{O}_{3},{O}_{4},{O}_{5},{O}_{6}\right\}$, data information sources $S=\left\{{S}_{1},{S}_{2}\right\}$, attribute set $A=\left\{{a}_{1},{a}_{2},{a}_{3},{a}_{4},{a}_{5}\right\}$. Here ${a}_{1}$ is delivery capability, ${a}_{2}$ is product price, ${a}_{3}$ is technical support, ${a}_{4}$ is service level, ${a}_{5}$ is inventory level. The original IVq-ROFSs given by the two information sources are Tables 1 and 2 respectively.

Table 1 The original data set given by ${S}_{1}$.

Table 2 The original data set given by ${S}_{2}$.

The compromised MsAIVq-ROFS and inclusive MsAIVq-ROFS on the Tables 1 and 2 are obtained using the formulas of Definition 9 and Definition 10 as Tables 3 and 4 shown.

Table 3 Compromised MsAIVq-ROFS.

Table 4 Inclusive MsAIVq-ROFS.

Among them, inclusive MsAIVq-ROFS may have a certain problem that the sum of the squares of the upper limit of MD and the upper limit of NMD of the elements to be aggregated may be greater than 1. Therefore, we need to restrict the merge aggregation by setting the upper limit of NMD degree to $\left\lfloor {\sqrt[q]{{1 - \left( {\mu_{{A^{{Q^{*} }} }}^{ - } } \right)^{q} }}} \right\rfloor$ when the sum of the squares of the upper limit of MD and the upper limit of NMD of the aggregated elements is greater than 1, so as to solve this problem.

From the comparison of information before and after aggregation, it can be seen that the aggregated MsAIVq-ROFS has the characteristics of two data information sources at the same time, and two methods bring radical and conservative strategies to the subsequent decision-making ideas. And compared with complex aggregation operators in recent researches⁵⁵, these two methods are more concise and more accessible to calculate.

In summary, the two aggregation methods for IVq-ROFSs proposed in this paper perform different operations on the upper and lower values of the interval values, respectively, and obtain two types of IVq-ROFSs decision datasets that can provide different decision-making opinions. The compromised method calculates the mean value of the upper and lower values of multiple IVq-ROFSs to reduce the range of intervals that can be calculated and contain the original data set’s characteristic information to achieve a more decision-making idea. The inclusive method calculates the maximum value of the upper and lower values of multiple IVq-ROFSs to ensure that all the original data set information can be includedto achieve a more accurate decision-making idea. Both approaches will work for different scenarios.

A new fuzzy entropy with parameter and related weight calculation method on IVq-ROFS

Objective attribute weight calculation is the second step of fuzzy MAGDM, given the “Fuzzy entropy” section conditions, a new fuzzy entropy with parameters for IVq-ROFS is proposed here:

Definition 11

Interval-valued q-rung orthopair fuzzy entropy: A real-valued function E: $IVq-ROF\left(X\right)\to [\mathrm{0,1}]$ is named as an entropy on IVq-ROFS, if E satisfies all the following properties:

(Q1):

$0\le E({A}^{Q*})\le 1$.

• (i) $E\left({A}^{Q*}\right)=0$ if ${A}^{Q*}$ is a crisp set.

• (ii) $E\left({A}^{Q*}\right)=1$ iff ${\mu }_{{A}^{Q*}}\left({x}_{i}\right)={\upnu }_{{A}^{Q*}}\left({x}_{i}\right)=[\sqrt[q]{k},\sqrt[q]{k}]$.

(Q2):

$E\left({A}^{Q*}\right)=E({\left({A}^{Q*}\right)}^{C})$.

(Q3):

$E\left({A}^{Q*}\right)\le E\left({B}^{Q*}\right)$ if ${A}^{Q*}$ is crisper than ${B}^{Q*}$,which is defined as:

$${\mu }_{{B}^{Q*}}\left({x}_{i}\right)\ge {\mu }_{{A}^{Q*}}\left({x}_{i}\right)\ge [\sqrt[q]{k},\sqrt[q]{k}]\quad\text{and}\quad{\upnu }_{{B}^{Q*}}\left({x}_{i}\right)\ge {\upnu }_{{A}^{Q*}}\left({x}_{i}\right)\ge [\sqrt[q]{k},\sqrt[q]{k}]$$

where $k\in [\mathrm{0,1}]$. The parameter k is a balance parameter to improve the flexibility of the fuzzy entropy.

Definition 12

Let the theoretical domain X be a nonempty set X and ${A}^{Q*}=\{<{x}_{i},{\mu }_{{A}^{Q*}}\left({x}_{i}\right),{\nu }_{{A}^{Q*}}\left({x}_{i}\right)>|{x}_{i}\in X\}$ be an IVq-ROFS, the new entropy formula of IVq-ROFS is as follow:

$$\begin{array}{c}E\left({A}^{Q*}\right)=\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-{\mu }_{{A}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow }\right]+\left[1-{\mu }_{{A}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow }\right]}{2},\end{array}$$

(16)

where ${\mu }_{{A}^{Q*}}^{\searrow }={\text{min}}\left(\left|{{\mu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,\left|{{\mu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|\right),$ ${\upnu }_{{A}^{Q*}}^{\searrow }={\text{min}}\left(\left|{{\upnu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,\left|{{\upnu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|\right),$ ${\mu }_{{A}^{Q*}}^{\nearrow }={\text{max}}\left(\left|{{\mu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,\left|{{\mu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|\right),$ ${\upnu }_{{A}^{Q*}}^{\nearrow }={\text{max}}(\left|{{\upnu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,|{{\upnu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}|)$.

Proof

(Q1)(i):

If ${A}^{Q*}$ is a crisp set, then we have ${\mu }_{{A}^{Q*}}=[\mathrm{0,0}]$ and ${\upnu }_{{A}^{Q*}}=[\mathrm{1,1}]$ or ${\mu }_{{A}^{Q*}}=[\mathrm{1,1}]$ and ${\upnu }_{{A}^{Q*}}=[\mathrm{0,0}]$

When ${\mu }_{{A}^{Q*}}=[\mathrm{0,0}]$ and ${\upnu }_{{A}^{Q*}}=[\mathrm{1,1}]$, $E\left({A}^{Q*}\right)=\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-k-(1-k)\right]+\left[1-k-(1-k)\right]}{2}=0.$ When ${\mu }_{{A}^{Q*}}=[\mathrm{1,1}]$ and ${\upnu }_{{A}^{Q*}}=[\mathrm{0,0}]$,$E\left({A}^{Q*}\right)=\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-k-(1-k)\right]+\left[1-k-(1-k)\right]}{2}=0.$

(Q1)(ii):

Firstly, sufficiency is proofed as follows: when $E\left({A}^{Q*}\right)=\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-{\mu }_{{A}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow }\right]+\left[1-{\mu }_{{A}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow }\right]}{2}=1$, so we have ${\mu }_{{A}^{Q*}}^{\searrow }={\upnu }_{{A}^{Q*}}^{\searrow }={\mu }_{{A}^{Q*}}^{\nearrow }={\upnu }_{{A}^{Q*}}^{\nearrow }=0$. It means that, ${\text{min}}\left(\left|{{\mu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,\left|{{\mu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|\right)$ $={\text{min}}\left(\left|{{\upnu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,\left|{{\upnu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|\right)$ $={\text{max}}\left(\left|{{\mu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,\left|{{\mu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|\right)$ $={\text{max}}\left(\left|{{\upnu }_{{A}^{Q*}}^{-}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|,\left|{{\upnu }_{{A}^{Q*}}^{+}}^{q}\left({{\text{x}}}_{i}\right)-{\text{k}}\right|\right)=0.$ So we have ${\mu }_{{A}^{Q*}}\left({x}_{i}\right)={\upnu }_{{A}^{Q*}}\left({x}_{i}\right)=[\sqrt[q]{k},\sqrt[q]{k}]$.Secondly, necessity is proofed as follows: when ${\mu }_{{A}^{Q*}}\left({x}_{i}\right)={\upnu }_{{A}^{Q*}}\left({x}_{i}\right)=[\sqrt[q]{k},\sqrt[q]{k}]$, then we have ${\mu }_{{A}^{Q*}}^{\searrow }={\upnu }_{{A}^{Q*}}^{\searrow }={\mu }_{{A}^{Q*}}^{\nearrow }={\upnu }_{{A}^{Q*}}^{\nearrow }=0$. So we have $E\left({A}^{Q*}\right)=\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-{\mu }_{{A}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow }\right]+\left[1-{\mu }_{{A}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow }\right]}{2}=1.$

(Q2):

$E\left({A}^{Q*}\right)=\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-{\mu }_{{A}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow }\right]+\left[1-{\mu }_{{A}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow }\right]}{2}=\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-{\upnu }_{{A}^{Q*}}^{\searrow }-{\mu }_{{A}^{Q*}}^{\searrow }\right]+\left[1-{\upnu }_{{A}^{Q*}}^{\nearrow }-{\mu }_{{A}^{Q*}}^{\nearrow }\right]}{2}=E({\left({A}^{Q*}\right)}^{C})$

(Q3):

$E\left({A}^{Q*}\right)-E\left({B}^{Q*}\right)=$ $\frac{1}{n}\sum_{i=1}^{n}\frac{\left[1-{\mu }_{{A}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow }\right]+\left[1-{\mu }_{{A}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow }\right]-\left[1-{\mu }_{{B}^{Q*}}^{\searrow }-{\upnu }_{{B}^{Q*}}^{\searrow }\right]+\left[1-{\mu }_{{B}^{Q*}}^{\nearrow }-{\upnu }_{{B}^{Q*}}^{\nearrow }\right]}{2}=$ $\frac{1}{n}\sum_{i=1}^{n}\frac{\left[{(\mu }_{{B}^{Q*}}^{\searrow }-{\mu }_{{A}^{Q*}}^{\searrow })+({\upnu }_{{B}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow })\right]+\left[\left({\mu }_{{B}^{Q*}}^{\nearrow }-{\mu }_{{A}^{Q*}}^{\nearrow }\right)+({\upnu }_{{B}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow })\right]}{2}$. According to this equation, we know that the value of $E\left({A}^{Q*}\right)-E\left({B}^{Q*}\right)$ depends on $\left[{(\mu }_{{B}^{Q*}}^{\searrow }-{\mu }_{{A}^{Q*}}^{\searrow })+({\upnu }_{{B}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow })\right]+\left[\left({\mu }_{{B}^{Q*}}^{\nearrow }-{\mu }_{{A}^{Q*}}^{\nearrow }\right)+({\upnu }_{{B}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow })\right]$. When ${\mu }_{{B}^{Q*}}\left({x}_{i}\right)\ge {\mu }_{{A}^{Q*}}\left({x}_{i}\right)\ge [\sqrt[q]{k},\sqrt[q]{k}]$ and ${\upnu }_{{B}^{Q*}}\left({x}_{i}\right)\ge {\upnu }_{{A}^{Q*}}\left({x}_{i}\right)\ge [\sqrt[q]{k},\sqrt[q]{k}]$, then $\left[{(\mu }_{{B}^{Q*}}^{\searrow }-{\mu }_{{A}^{Q*}}^{\searrow })+({\upnu }_{{B}^{Q*}}^{\searrow }-{\upnu }_{{A}^{Q*}}^{\searrow })\right]+\left[\left({\mu }_{{B}^{Q*}}^{\nearrow }-{\mu }_{{A}^{Q*}}^{\nearrow }\right)+({\upnu }_{{B}^{Q*}}^{\nearrow }-{\upnu }_{{A}^{Q*}}^{\nearrow })\right]\ge 0$. It means that $E\left({A}^{Q*}\right)-E\left({B}^{Q*}\right)\ge 0$.

It can be seen that the proposed new fuzzy entropy satisfies the condition that can represent the fuzziness of any IVq-ROFSs.

The traditional entropy weight calculation method generally uses Shannon entropy to calculate entropy values, a quantitative measure of information. However, fuzzy entropy is used for weight calculation instead of Shannon entropy to fit the fuzzy idea. Fuzzy entropy is based on fuzzy theory and expresses the quantitative fuzzy degree of a certain fuzzy element. Based on the fuzzy entropy formula proposed above and the traditional entropy weight method, an IVq-ROFS-based attribute weight calculation method is proposed.

IVq-ROFS-based attribute weight calculation method is introduced as follow:

Calculation of the corresponding attribute based on Eq. (16) is given by:

$$\begin{array}{c}{\omega }_{j}=\frac{1-{E}_{j}^{({A}^{Q*})}}{n-\sum_{i=1}^{n}{E}_{i}^{({A}^{Q*})}}\end{array}$$

(17)

Further normalization is performed to obtain the final normalized attribute weights:

$$\begin{array}{c}{\overline{\omega }}_{j}=\frac{{\omega }_{j}}{\sum_{i=1}^{j}{\omega }_{i}}\end{array}$$

(18)

A new CoCoSo method based on IVq-ROFS

The core of the fuzzy MAGDM method is the ranking calculation of alternatives, and the CoCoSo method is optimized by the multi-source aggregation method and IVq-ROFS-based attribute weight calculation method proposed in “Multi-source Aggregation method on IVq-ROFSs” and “A new fuzzy entropy with parameter and related weight calculation method on IVq-ROFS” sections. The original CoCoSo method has some defects. We find that because there is no normalization in the calculation of the eclectic score ${S}_{i}^{2}$, so that ${S}_{i}^{2}\ge 2$, at the same time for the same set of data $0\le {S}_{i}^{1}\le 1$, $0\le {S}_{i}^{3}\le 1$, so in the final the ranking of alternatives will lead to the ranking results dominated by ${S}_{i}^{2}$. To apply the new CoCoSo method to the IVq-ROFS environment, we calculate the fuzzy entropy value of each fuzzy element and use the entropy value as the basic element of the decision matrix for subsequent decisions. Based on the IVq-ROFS-fuzzy entropy weight method and the improvement of the hybrid score operator of three dependent such scores, we propose a new CoCoSo method in this section.

Step 1 Standardization. The decision matrix is constructed using the new fuzzy entropy Eq. (16) for each attribute, while making $k=\frac{1}{3}$ in Eq. (16), using normalized fuzzy entropy values for benefit attributes and normalized fuzzy entropy complements for cost attributes, the standardization process is as follows.

$$ \left\{ {\begin{array}{*{20}l} {r_{ij} = E^{{k = \frac{1}{3}}} \left( {A^{Q*} } \right),\quad for \;benefit\;criteria;} \hfill \\ {r_{ij} = 1 - E^{{k = \frac{1}{3}}} \left( {A^{Q*} } \right),\quad for\;cost\;criteria,} \hfill \\ \end{array} } \right. $$

(19)

$$\begin{array}{c}{\overline{r} }_{ij}=\frac{{r}_{ij}}{\sum_{i=1}^{n}{r}_{ij}}\end{array}$$

(20)

Step 2 Calculate the attribute weights. Use the Eq. (16) to calculate the weight of the sum of the original attribute fuzzy values for each attribute. The attribute fuzzy entropy is normalized by Eq. (21).

$$\begin{array}{c}{E}_{j}^{\left({A}^{Q*}\right)}=\frac{{E}_{j}^{\left({A}^{Q*}\right)}}{\sum_{i=1}^{n}{E}_{j}^{\left({A}^{Q*}\right)}}\end{array}$$

(21)

From the above equation, the normalized fuzzy entropy of each attribute is obtained, and the attribute weights are calculated using Eqs. (22, 18).

$$\begin{array}{c}{\omega }_{j}=\frac{1-{\overline{E} }_{j}^{\left({A}^{Q*}\right)}}{n-\sum_{i=1}^{n}{\overline{E} }_{i}^{\left({A}^{Q*}\right)}}\end{array}$$

(22)

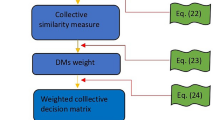
Step 3 Calculate the arithmetic weighted sum and arithmetic weighted product as shown as Eqs. (23, 24) for each alternative.

$$\begin{array}{c}{\overline{S} }_{\omega i}=\sum_{j=1}^{n}{\omega }_{i}{\overline{E} }_{j}^{\left({A}^{Q*}\right)}\end{array}$$

(23)

$$\begin{array}{c}{\overline{M} }_{\omega i}=\prod_{j=1}^{n}{\left({\overline{E} }_{j}^{\left({A}^{Q*}\right)}\right)}^{{\omega }_{i}}\end{array}$$

(24)

Step 4 Generate three dependent compromise scores as shown as Eq. (25) for each alternative.

$$ \left\{ {\begin{array}{*{20}l} {\overline{S}_{i}^{1} = \frac{{\overline{S}_{\omega i} + \overline{M}_{\omega i} }}{{\mathop \sum \nolimits_{i = 1}^{m} \left( {\overline{S}_{\omega i} + \overline{M}_{\omega i} } \right)}};} \hfill \\ {\overline{S}_{i}^{2} = \frac{{\overline{S}_{\omega i} }}{{min \overline{S}_{\omega i} }} + \frac{{\overline{M}_{\omega i} }}{{min \overline{M}_{\omega i} }};} \hfill \\ {\overline{S}_{i}^{3} = \frac{{\varepsilon \overline{S}_{\omega i} + \left( {1 - \varepsilon } \right)\overline{M}_{\omega i} }}{{\varepsilon max_{i} \overline{S}_{\omega i} + \left( {1 - \varepsilon } \right)max_{i} \overline{M}_{\omega i} }},\quad 0 \le \varepsilon \le 1} \hfill \\ \end{array} } \right. $$

(25)

where $\varepsilon$ is an equilibrium parameter in the compromise scores to enhance the universality of the proposed method.

Step 5 Based on the above three dependent compromise scores, the final score of each alternative is calculated using the improved compromise score function as shown as Eq. (26).

$$\begin{array}{c}{S}_{i}=\frac{1}{3}\left({S}_{i}^{1}+{S}_{i}^{2}+{S}_{i}^{3}\right)+{\left({S}_{i}^{1}{S}_{i}^{2}{S}_{i}^{3}\right)}^\frac{1}{3}\end{array}$$

(26)

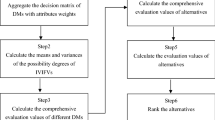
The results of the alternative ranking are in descending order according to the final performance index, which can get more accurate ranking results. The process of proposed method is shown as Fig. 2.

Figure 2

The process of proposed method.

Case Study: Sepsis diagnosis

In this section, the applicability of the proposed improved CoCoSo method will be demonstrated in terms of Sepsis diagnosis.

The description of Sepsis diagnosis

Sepsis^65,66 is a vicious condition with a high morbidity and mortality rate. Early recognition and treatment of sepsis is the key to reducing sepsis mortality, which has been high in morbidity and mortality over the past decades. Early and accurate morbidity prediction can lead to more aggressive and effective treatment of sepsis, thereby reducing the incidence of multiorgan dysfunction and significantly reducing mortality. Early recognition can be complex due to the complexity of the disease in the clinical setting. Typically, sepsis can be judged based on attributes^{67,68,69,70,71} such as temperature, pulse, pain level, SaO2, blood pressure, level of consciousness, capillary refill time, urine output, and degree of ScvO2/base deficiency, as shown in Table 5. The pain level and level of consciousness are subjective attributes, for initial diagnosis in case of suspected infection. To ensure data integrity while considering expert ability, we will use sepsis feature datasets from experts P₁ and P₂.

Table 5 Description of attributes.

The decision process of Sepsis diagnosis

The effectiveness of the method proposed in this paper for early sepsis diagnosis is demonstrated below. Simulation dataset is used for the research data in this paper. These datasets are shown in Tables 6 and 7.

Table 6 Sepsis characteristics on IVq-ROFS X₁ by Expert P₁.

Table 7 Sepsis characteristics on IVq-ROFS X₂ by Expert P₂.

Equations (13) and (15) are used for X₁, X₂ to obtain Tables 8, 9.

Table 8 Compromised MsAIVq-ROFS X₃ based on IVq-ROFS X₁, X₂.

Table 9 Inclusive MsAIVq-ROFS X₄ based on IVq-ROFSs X₁, X₂.

The processing steps of proposed improved CoCoSo method are as follows:

Step 1 Firstly, IVq-ROFSs X₁ and X₂ obtained from P₁ and P₂ for one patient are aggregated as X₃ and X₄ which are obtained by the two proposed aggregation methods, as shown in Tables 8 and 9, respectively.

Step 2 From Table 5, we know that C₁, C₄, C₆, C₇, C₈ are benefit criteria, C₂, C₃, C₅, C₉ are cost criteria. So according to Eqs. (19) and (20), the aggregated set of patient attributes is normalized. Here we take X₃ obtained by inclusive MsAIVq-ROFS as an example, we can get the normalized decision matrix as Table 10.

Table 10 The normalized decision matrix based on inclusive MsAIVq-ROFS.

Step 3 Calculate the objective weights of the attributes by using the Eqs. (21–22), and the corresponding weights of each attribute are shown as the following Table 11.

Table 11 Objective weighting of attributes.

Step 4 According to the compromise calculation steps of the IVq-ROFS-CoCoSo method, the ranking algorithm of the alternatives is carried out sequentially, and the arithmetic weighted sum and arithmetic weighted product of each alternative are first calculated by the Eqs. (23, 24) as shown as Table 12.

Table 12 Arithmetic weighted sum and arithmetic weighted product of each alternative.

Next, the values of the three types of compromise functions are calculated for each alternative by the Eq. (25) as shown as Table 13, where $\varepsilon =0.5$.

Table 13 The values of the three types of compromise functions.

Finally, the alternatives are ranked by the improved score function Eq. (26). The result is as shown as Table 14.

Table 14 Score values and sort results based on compromised MsAIVq-ROFS.

Similar to the above process, the final scores of the inclusive MsAIVq-ROFS based on X_1, X₂ and the ranking results of the alternatives are shown in Table 15.

Table 15 Score values and sort results based on inclusive MsAIVq-ROFS.

From the ranking results obtained by the proposed method for the compromised MsAIVq-ROFS and the inclusive MsAIVq-ROFS based on two identical IVq-ROFSs, it can be seen that the two different multi-source aggregation strategies can give the decision maker an optimistic or pessimistic opinion on the decision.

Sensitivity analysis and comparative analysis

In this section, we first make sensitivity analysis. Then we made the comparative analysis with other methods to verify the feasibility of our method. Finally, we describe the merits of our method.

Sensitivity analysis

This section focuses on the sensitivity analysis of the two parameters of the proposed method. The first parameter is the k in the IVq-ROFS-based attribute weight calculation method Eq. (21), and the second parameter is the equilibrium parameter $\varepsilon$ in the Eq. (25). So, based on the inclusive MsAIVq-ROFS in the previous section data, the sensitivity analysis is performed for the two parameters set in increments of 0.1 from 0. The results obtained from the analysis are shown below in Fig. 3.

Figure 3

Sensitivity analysis for parameter changes.

The figure shows that for different values of k, the balance parameter does not affect the ranking for any value. However, different values of k will have a particular impact on the difficulty of ranking the alternatives. It can be clearly seen in the above figure that when k = 1, the gap between the scores of A₁, A₂ and A₃ and between the scores of A₄ and A₅ is not clear. For other values of k, alternatives can be ranked more clearly.

Comparison analysis with Other MAGDM

Based on Table 8 in “The decision process of Sepsis diagnosis” section, we rank the alternatives using the traditional CoCoSo method⁵⁸, the extended WASPAS method proposed by⁵⁶, the improved PDM method proposed in⁵⁷, and the COPRAS method proposed in⁵². After using the weights obtained from the weighting method proposed in this paper, the process of the rest of the steps is basically the same, and the final ranking of the alternatives is calculated. The calculations results are shown as Table 16 and Fig. 4 below.

Table 16 Results analysis with other methods.

Figure 4

Results analysis with other methods.

From the Table 16 and Fig. 4, it can be seen that this paper's method can obtain consistent optimal solutions with other methods in the same data set, and the ranking of alternatives are almost the same, which indicates the correctness of this paper's method.

Advantages analysis

In this section, we compare the proposed method with the existing methods to discuss the advantages of our method.

• (1) Aggregation method

In this paper, we propose two new multi-source aggregation methods in a more straightforward form as a pre-data processing method for MAGDM. The method in⁵⁶ used the additive mean of fuzzy numbers to aggregate fuzzy data, and in⁵⁵ the Archimedean Muirhead mean operators were used to aggregate fuzzy data. In other studies, the complex aggregation operators^62,63,64 were applied, which are complicated to implement and not easy to understand. Compared with them, the proposed aggregation method is easier to understand and implement, and the proposed aggregation method can be extended into most of MAGDM.

• (2) Weight Calculation method.

A novel fuzzy entropy with a parameter based on IVq-ROFS, which is more flexible and versatile due to the settable parameter, is proposed. The entropy weight method is a known proven weight calculation method with excellent performance, and fuzzy entropy with a parameter is combined with the traditional entropy weight method, and can be applied to IVq-ROFS. Scholars have yet to apply the entropy weight method to IVq-ROFS in previous studies, and this paper fills the gap in this area. Compared with the method in^55,56,58, the more objective attribute weights will be obtained in the method proposed.

• (3) Enhanced compromise score in CoCoSo method.

In the original CoCoSo method, there is an unavoidable problem, as shown in Eq. (9) and (10), in which $0\le {S}_{i}^{1}\le 1$, $0\le {S}_{i}^{3}\le 1$, ${S}_{i}^{2}\ge 2$, the value domains of the three dependent compromise scores are different, directly affecting the final score calculation. It is necessary to convert three dependent compromise scores to a unified scale for the CoCoSo method. So this paper uses the logarithmic function to limit the value domain of ${S}_{i}^{2}$ to $[\mathrm{0,1}]$ which can eliminate dimensional differences among three dependent compromise scores of the existing CoCoSo methods.

• (4) Higher versatility and scalability.

The proposed approach has excellent versatility and scalability, which is not only limited to the IVq-ROFS, but also applies to IVIFS, IVPFS and IVFFS.

We summarize the merits of our method in Table 17.

Table 17 The comparison of existing methods and the proposed method.

Conclusion

In this study, a novel MAGDM method based on IVq-ROFS is proposed. Firstly, a new multi-source IVq-ROFS aggregation method is proposed, which is simpler and easier to implement than the existing complex aggregation methods. Secondly, a parametric fuzzy entropy based on IVq-ROFS, which is more flexible and universal than the traditional fuzzy entropy, is introduced. Based on the fuzzy entropy, we propose a fuzzy entropy weighting method to determine the objective weights of attributes. After that, we improve the defects of the original CoCoSo method by restricting the three compromise scores to the same range. It solves the problem of dimensional differences in the original one. Finally, a novel improved CoCoSo method based on IVq-ROFS is proposed. It is created based on these theoretical innovations and applied to sepsis case analysis.

Among the main implications of this study for sepsis diagnosis are: first, because early sepsis is difficult to be diagnosed exactly by doctors, this problem can be solved by using fuzzy theory. Secondly, CoCoSo, as a multi-attribute decision model, can synthesize the diagnoses of multiple experts to reduce the problem of misdiagnosis in the early stage of sepsis. Finally, doctors nowadays use precise instruments for medical diagnosis, however, the early symptoms of sepsis make doctors uncertain even with precise instruments, CoCoSo in a fuzzy environment allows multiple doctors to consider the summed assessment of multiple experts from a fuzzy point of view in the early stages of sepsis, which helps to minimize the risk of disease for the patient.

Some outstanding issues require additional investigation in future research. The MAGDM method in this study is proposed based on IVq-ROFS and does not consider hesitant fuzzy information and complex fuzzy information. In later work, more diverse fuzzy information will be considered. The application of the study focuses on sepsis diagnosis, and future work will try to apply it to psychological diagnosis or supply chain location.