Economical-environmental-technical optimal power flow solutions using a novel self-adaptive wild geese algorithm with stochastic wind and solar power

Abstract

This study introduces an enhanced self-adaptive wild goose algorithm (SAWGA) for solving economical-environmental-technical optimal power flow (OPF) problems in traditional and modern energy systems. Leveraging adaptive search strategies and robust diversity capabilities, SAWGA distinguishes itself from classical WGA by incorporating four potent optimizers. The algorithm's application to optimize an OPF model on the different IEEE 30-bus and 118-bus electrical networks, featuring conventional thermal power units alongside solar photovoltaic (PV) and wind power (WT) units, addresses the rising uncertainties in operating conditions, particularly with the integration of renewable energy sources (RESs). The inherent complexity of OPF problems in electrical networks, exacerbated by the inclusion of RESs like PV and WT units, poses significant challenges. Traditional optimization algorithms struggle due to the problem's high complexity, susceptibility to local optima, and numerous continuous and discrete decision parameters. The study's simulation results underscore the efficacy of SAWGA in achieving optimal solutions for OPF, notably reducing overall fuel consumption costs in a faster and more efficient convergence. Noteworthy attributes of SAWGA include its remarkable capabilities in optimizing various objective functions, effective management of OPF challenges, and consistent outperformance compared to traditional WGA and other modern algorithms. The method exhibits a robust ability to achieve global or nearly global optimal settings for decision parameters, emphasizing its superiority in total cost reduction and rapid convergence.

Introduction

Motivation and incitement

The safe, secure, and inexpensive functioning of the electrical network is referred to as the optimum power flow (OPF), and this is made possible by properly configuring the system's control variables. According to the mathematical formulation, OPF is a static, nonlinear, large-scale, restricted issue with many discrete and continuous decision parameters. OPF is a vital instrument for electrical networks' cheaper and safer functioning^1,2. OPF is used in the power system to achieve various goals, including lowering overall generating costs of thermal units (Ths), improving voltage stability, minimizing network losses, cutting CO2 emissions, and preserving the best settings for control variables^3,4. This method is often restricted by a number of requirements that must be met, including the different technical limitations, transmission line capacity, bus voltage, ability of the power generator, and several physical limitations⁵.

Power plants using fossil fuels are the focus of the traditional OPF issue. Renewable energy sources (RESs) have proliferated over the last 20 years due to factors like rising demand, the urgent need to decrease the emissions of greenhouse gases, favorable pricing for RESs, and triggering and deregulation of the electrical energy market⁶. The most significant alternatives to fossil fuels for power production seem to be wind and solar energy^7,8. The use of improved wind power generating units (WTs) and solar photovoltaic power units (PVs), which lower the cost of system installations, has permitted the rapidly expanding RESs use⁹. Additionally, it might be claimed that solar photovoltaic and wind turbine generating systems are tried-and-true technology^10,11.

Based on economic indicators like the cost of fuel used to produce electrical energy in energy production systems, quality indicators of produced electrical energy, and system and transmission network losses, the performance of the electrical network operation may be significantly impacted by the locations, quantity, with technological features of RESs^12,13. Due to its intermittent power-generating characteristics, adding several RESs into an electrical network increases the difficulty of OPF^10,14. Recent research has focused on finding a strong, fast, and simple optimization algorithm, considering renewable energies in the electrical networks, multi-objective OPF (MOOPF) problems, and considering various objective functions to the OPF problems¹⁵.

Literature review

In recent literature, numerous methods of incorporating RESs into OPF and different solution methodologies for the OPF issue have been proposed. Most scholars explored bio-inspired optimization met heuristics for OPF settings in recent studies. To tackle OPF in the electrical networks with RESs, Ullah et al. developed a combination of gravitational search algorithm (GSA) and an improved particle swarm optimization (PSO)¹⁶, the coronavirus herd immunity optimizer (CHIO)¹⁷ for the technical-environmental-economical dispatch problem in the two standards IEEE electrical networks. The five goals of this investigation were total fuel expenses, active losses, pollution level, stability, and variation of the network’s voltage. Using the analytical hierarchy process and a weighted collect method, the multi-objective OPF was reduced to a normalized one-objective OPF. The outcomes showed that CHIO outperforms the other EETD problem-solving methodologies. Elattar concentrated on applying modified moth swarm optimization (MMSO) to mathematically model the OPF with a hybrid power and heat system through stochastic WT, and the resulting methodology was applied to the IEEE 30-bus electrical network with different test settings. In contrast to previous algorithms, RESs into OPF and the proposed technique to address it generated successful optimal solutions¹⁸. The OPF issue was modeled by a modified colliding bodies optimization (ICBO)¹⁹, and applications were made using 16 case studies on three IEEE standard electrical networks to evaluate the effectiveness and resilience of ICBO. A new, improved chaotic PSO for solving MOOPF in a test system with RESs suggested in²⁰, that this PSO, compared to recent algorithms, generated superior optimal solutions²⁰. In²¹, the dynamic OPF (DOPF) has been optimized by a new enhanced honey bee mating algorithm while taking into account the valve-point effects (VPEs) in the 14, 30, and 118-bus standard electrical networks. Salkuti used a new glowworm swarm algorithm (GSA) that was successfully executed to resolve an MOOPF in the IEEE systems incorporating a WT under various operating circumstances²². A more effective improved manta ray foraging algorithm (IMOMRFO)²³, twenty-four benchmark tasks of varying sorts and degrees of difficulty were used to examine the effectiveness of the created approach and compare it to competing methods. The analysis's findings demonstrated that IMOMRFO produced competitive results on several MOOPFs and identified the optimum results in the recent studies for MOOPFs that arise in practice²³. Using thermal with RESs, Kathiravan et al. studied OPF using a flower pollination algorithm (FPA). In various test situations, FPA has been examined on Indian utility 30-bus and IEEE 30-bus electrical networks²⁴. The suggested solution strategy for the OPF issues has been applied to the new IEEE 30-bus electrical network using a hybrid PSO-GWO algorithm, which combines PSO with grey wolf optimization (GWO)²⁵. The hybrid PSO-GWO method performed well in comparison to other algorithms, according to simulation findings, and showed that it may be a good option for solving OPF issues²⁵. With adjustable WT and PV energy systems, Duman et al. solved the OPF issue using the differential evolutionary (DE) PSO (DEPSO). For testing the method under various goal functions, IEEE 30-, 57-, and 118-bus electrical networks have been studied²⁶. In²⁷, a new hybrid firefly-bat algorithm (HFBA-COFS) directed to handle the strictly-constrained MOOPF, which the proposed method increased the original system's capacity for population diversity and global exploration of the three different IEEE test systems to demonstrate the significant benefits of the HFBA-COFS method, the HFBA-COFS algorithm was capable of producing high-quality optimal solutions, which is crucial for realizing the secure and efficient operation of massive electrical networks. In a different research, they suggested using FACTS devices to address the OPF issue. They used a modified chaotic PSOGSA to account for the uncertainty of wind energy systems²⁸. A unique adaptive Gaussian teaching–learning-based optimization (TLBO) (AGTLBO) that enhanced the performance of traditional TLBO and addressed the OPF issue was proposed in²⁹. The results demonstrated that it met the heuristics described in the recent studies compared to modern optimization. The AGTLBO was more efficient and successful. TLBO augmented with Lévy mutation (LTLBO)³⁰ was examined, assessed, and compared to other approaches using the IEEE 30-bus and IEEE 57-bus electrical networks with various OPF functions. A modified population external optimization method (CMOPEO) was suggested by Chen et al. as an improved optimizer to OPF with RESs, and CMOPEO was evaluated on the IEEE 30-bus electrical network for several test scenarios³¹. The goal function of the slime mold algorithm (SMA)³² was the system's total cost, which included a penalty cost for underestimating RESs and a reserve cost for overestimation. Algeria's DZA 114-bus and IEEE 30-bus electrical networks were used to assess SMA performance. Four optimization strategies were compared to the SMA. According to the overall simulation findings, SMA outperformed the other analyzed algorithms over a variety of function landscapes. The 5-bus and new IEEE 30-bus electrical networks with and without unified power flow controller (UPFC) were used to evaluate the performance of bat optimization algorithm (BA)-based OPF as an effective and robust solution³³. The performance of the turbulent flow of a water-based optimizer (TFWO)³⁴ to OPF was demonstrated by a comparison of the statistical indices, convergence trend, and optimal solutions to modern optimizers in recent studies^35,36. The study's findings led the authors to conclude that TFWO was better and more successful in solving OPF optimization issues. Compared to other well-known algorithms, it had higher convergence rates and made significant technological and financial advancements. The suggested TFWO for the large-scale tested system decreases the range from 4.6% to 33.12%. The proposed solution technique resulted in a more competitive solution for the evaluated system with a notable improvement in the techno-economic aspects. Three separate target functions in OPF, including reducing overall operating costs, carbon pollution with tax, and power losses, were taken into consideration by the chaotic bonobo optimizer (CBO)³⁷. To demonstrate the potency and advantage of CBO to arrive at the best result, CBO was tested on two standard IEEE electrical networks. The founded optimal solutions demonstrated the effectiveness and dependability of CBO for solving OPF using stochastic RESs, a hybrid DE, symbiotic organisms search (SOS)³⁸, etc.

In the realm of optimal power flow (OPF) solutions, the landscape has witnessed a surge in innovative methodologies, each striving to address the complex challenges posed by integrating renewable energy sources (RESs) into electrical networks. The advantages and disadvantages inherent in the current state-of-the-art optimization methods employed for OPF can be summarized as follows:

Advantages of state-of-the-art methods in OPF

• 1. Versatility in Problem Solving:

  • Advantage: Many state-of-the-art algorithms demonstrate adaptability and effectiveness in addressing specific challenges, such as technical-environmental-economical dispatch problems, making them versatile solutions.

• 2. Improved Performance Metrics:

  • Advantage: Several methodologies exhibit superior performance in optimizing key metrics, including total fuel expenses, active losses, pollution levels, network stability, and voltage variations, showcasing their effectiveness in enhancing system efficiency.

• 3. Optimal Solutions for Specific Scenarios:

  • Advantage: Certain algorithms excel in solving particular OPF scenarios, such as hybrid power and heat systems with stochastic renewable sources like wind turbines (WTs), providing tailored solutions for specific applications.

Disadvantages of state-of-the-art methods in OPF

• 1. Limited Scope of Application:

  • Disadvantage: Some algorithms may have a narrow focus, limiting their applicability to specific IEEE electrical networks or certain types of OPF issues.

• 2. Reduced Versatility:

  • Disadvantage: While effective for targeted challenges, certain methodologies might lack the versatility needed to address a broad spectrum of OPF problems, potentially hindering their widespread adoption.

• 3. Limited Evaluation on Broader OPF Issues:

  • Disadvantage: Some algorithms may have limited evaluations beyond specific OPF scenarios, leaving uncertainties about their performance in addressing broader optimization challenges.

Contribution and paper organization

Building upon the current state-of-the-art, our work introduces a novel self-adaptive wild goose algorithm (SAWGA) to tackle the OPF problem in a modified IEEE 30-bus electrical network with stochastic RESs, including photovoltaic (PV) and WT units. With the suggested SAWGA method and a few additional optimization techniques, we attempted to solve OPF in a modified IEEE 30-bus and 118-bus electrical networks⁹, including stochastic RESs in this work. The suggested SAWGA algorithm aimed to enhance the power of basic WGA's exploitation and exploration to resolve various operational test cases of OPF, including stochastic RESs.

We have accomplished this by carefully choosing the control settings and algorithm coefficients. Lognormal and Weibull probability distribution functions were applied to stochastic RES irradiation conditions of the systems, respectively. The obtained optimal solutions by SAWGA's five evaluation items, which had been used for various OPF functions, were compared to those from the original WGA, thermal exchange optimization algorithm (TEO)³⁹, grasshopper optimization (GOA)⁴⁰, Harris hawks optimization (HHO)⁴¹, and honey badger algorithm (HBA)⁴², which have been recently reported.

The key contributions of our study include:

• 1. We present SAWGA, an enhanced version of the wild goose algorithm (WGA), demonstrating superior performance in real-world optimization problems, particularly in OPF scenarios with high difficulty levels and multiple locally optimal solutions.

• 2. Our proposed SAWGA method is tailored to address various OPF challenges in a modified IEEE 30-bus electrical network, accounting for the complexities introduced by stochastic RESs.

• 3. We conduct a thorough evaluation of SAWGA against benchmark algorithms, including thermal exchange optimization algorithm (TEO), grasshopper optimization (GOA), Harris hawks optimization (HHO), and honey badger algorithm (HBA), in addition to the original WGA. The evaluation encompasses multiple OPF optimization functions, considering diverse power generation operating situations and scenarios, such as voltage deviation, emission, and network losses.

Through these contributions, our study advances the field of bio-inspired optimization for OPF, offering a novel and efficient solution for practical applications in electrical networks with renewable energy integration.

The remains of this research have been structured as follows. OPF, with its optimization functions in the electrical networks with stochastic RESs, is presented in "Formulation of OPF in the electrical network with stochastic RESs" section. Models for RES generation power are shown in "Power and uncertainty models in the PVs and WTs" section. Two sub-sections of "The proposed algorithm" section each introduce the WGA algorithm and the suggested SAWGA approach. The experimental research conditions and the criteria considered are presented in "SAWGA for solving the different OPF problems with stochastic wind and solar power" section of the article. Finally, "Multi-objective SAWGA (MOSAWGA) for solving the different classical OPF problems" section provides the study's findings and recommendations for further research.

Formulation of OPF in the electrical network with stochastic RESs

Traditional OPF issue was identified as an essential and vital challenge to analyze, design, and manage the power grids and energy production and transmission networks that strive to achieve the affordable and lowest cost of energy production and transmission With the condition of complying with the various stipulations and different demands, and with inequality and equality limitations of the electrical energy production and transmission system and network^9,43. Solving this problem with various optimization functions and considering stochastic RESs such as WTs and PVs through a new modified algorithm called self-adaptive wild geese algorithm (SAWGA) has been the main goal of this research. The problem's suggested solution and its broad organization are represented below. The definition of the standard OPF issue is as follows¹⁰.

Minimalize:

$${f}_{obj}\left(x,u\right)$$

(1)

Subject to:

$$\begin{array}{c}a\left(x,u\right)=0,\\ b\left(x,u\right)\le 0,\end{array}$$

(2)

when ${f}_{obj}\left(x,u\right)$ is the OPFs’ optimization function, $u$ and $x$ show the independent and dependent decision parameters and the equality and inequality constraints have been shown through $a(x, u)$ and $b(x, u)$, respectively.

Dependent parameters

The dependent parameters in OPF have been shown in Eq. (3)¹⁰

$$x=\left[{P}_{T{h}_{1}},{V}_{L},{Q}_{Th},{Q}_{WS},{Q}_{PV}\right],$$

(3)

where ${P}_{T{h}_{1}}$ shows the slack generator's active power, ${V}_{L}=\left[{V}_{{L}_{1}},\ldots,{V}_{{L}_{NPQ}}\right]$ shows the PQ buses' voltage values, ${Q}_{Th}=\left[{Q}_{T{h}_{1}},\ldots,{Q}_{T{h}_{NTHG}}\right]$, ${Q}_{WS}=\left[{Q}_{W{S}_{1}},\ldots,{Q}_{W{S}_{NW}}\right]$, and ${Q}_{PV}=\left[{Q}_{P{V}_{1}},\ldots,{Q}_{P{V}_{NPV}}\right]$ are the reactive power of Ths, WTs, and PVs, and ${S}_{L}=\left[{S}_{{L}_{1}},\ldots,{S}_{{L}_{NTL}}\right]$ shows the network lines’ transition power; NPQ, NTHG, NW, NPV, and NTL show the numbers of the test power system's PQ buss, Ths, WTs , PVs, and network lines.

Independent decision parameters

These parameters of OPF have been shown follows¹⁰

$$u=\left[{P}_{Th},{P}_{WS},{P}_{PVS},{V}_{G}\right].$$

(4)

If ${V}_{G}=\left[{V}_{{G}_{1}},\ldots,{V}_{{G}_{NG}}\right]$ denotes the values of all generator buses’ voltage including PVs, Ths, WTs, and also, ${P}_{Th}=\left[{P}_{T{h}_{2}},\ldots,{P}_{T{h}_{NTHG}}\right]$, ${P}_{PVS}=\left[{P}_{PV{S}_{1}},\ldots,{P}_{PV{S}_{NPV}}\right]$, and ${P}_{WS}=\left[{P}_{W{S}_{1}},\ldots,{P}_{W{S}_{NW}}\right]$ denote the active power of Th, PV, WT units excluding the slack generator, respectively. The number of Th, PV, WT units is known as $NG, NPV,$ and $NW,$ respectively.

Modeling of the test electrical network

This part of the study models how Th, PV, and WT power generation units may be integrated into contemporary power systems. Table 1 lists the specifications of the studied IEEE 30-bus electrical network⁹.

Table 1 The specifications of the test electrical network.

OPF model of Ths

According to the produced output active power, Eq. (5) describes the traditional OPF function in Ths as a quadratic objective function. Also, Eq. (6) contains the OPF model for Ths that includes VPEs, where ${r}_{i}$ and ${p}_{i}$ stand for the VPEs specifications while ${o}_{i}$, ${n}_{i}$, and ${m}_{i}$ are the OPF function specifications for the ith Th generator^10,45.

$$CF\left({P}_{Th}\right)=\sum_{i=1}^{NTHG}\left({m}_{i}+{n}_{i}{\cdot {P}_{Th}}_{i}+{o}_{i}{\cdot P}_{T{h}_{i}}^{2}\right),$$

(5)

$${CF}_{1}\left({P}_{Th}\right)=\sum_{i=1}^{NTHG}\left({m}_{i}+{n}_{i}{\cdot {P}_{Th}}_{i}+{o}_{i}{\cdot P}_{T{h}_{i}}^{2}+\left|{p}_{i}\cdot {{\sin}}\left({r}_{i}\cdot \left({P}_{TH{h}_{i}}^{min}-{{P}_{Th}}_{i}\right)\right)\right|\right).$$

(6)

Pollution level model with carbon tax ${{\varvec{C}}}_{{\varvec{t}}{\varvec{a}}{\varvec{x}}}$

Mathematically, Eq. (7)^9,10 describes how to calculate the overall emission value from heat-producing units utilizing fossil fuel. Additionally, a carbon tax model was taken into account owing to the increasing threat of global warming, and the emission cost value is determined through the addition ${C}_{tax}$ to the overall emission value that has been given in Eq. (8). In this case, CE and FE stand in for the emission costs, and sum emissions, respectively^9,10.

$${F}_{E}=\sum_{i=1}^{NTHG}\left(0.01\cdot \left({\sigma }_{i}+{\beta }_{i}\cdot {{P}_{Th}}_{i}+{\tau }_{i}{\cdot P}_{T{h}_{i}}^{2}\right)+{\omega }_{i}\cdot {e}^{{\mu }_{i}\cdot {P}_{T{h}_{i}}}\right),$$

(7)

$${C}_{E}={F}_{E}{\cdot C}_{tax},$$

(8)

where ${\sigma }_{i}$, ${\tau }_{i},$ ${\omega }_{i}$, ${\beta }_{i}$, and ${\mu }_{i}$ are the emission characteristics of the ith Th generator.

Prohibited operating zones (POZs)

The following characteristics of a Th generator that uses fossil fuel and has several POZs³⁸:

$$\begin{array}{c}{P}_{T{h}_{i}}^{min}\le {P}_{T{h}_{i}}\le {P}_{T{h}_{i},1}^{L},\\ {P}_{T{h}_{i},Z-1}^{U}\le {P}_{T{h}_{i}}\le {P}_{T{h}_{i},Z}^{L}\\ {P}_{T{h}_{i},{z}_{i}}^{U}\le {P}_{T{h}_{i}}\le {P}_{T{h}_{i}}^{max},\end{array}, Z={2,3},\dots ,{z}_{i},$$

(9)

where $Z$ shows the number of POZs, ${z}_{i}$ shows the sum of POZs, ${P}_{T{h}_{i},Z}^{L},$ and ${P}_{T{h}_{i},Z-1}^{U}$ indicate the lower and upper bounds of the $(Z - 1)$ th POZ of the ith unit. Figure 1 shows the specification curves of the OPF objective function without and with VPEs (a), and with the POZs (b) of the Th generators.

Figure 1

OPF objective function curves: (a) without and with VPEs, (b) with POZs.

Direct objective function models of RESs include PVs and WTs

A linear function of planned power may be used to represent a wind energy source's direct cost model^9,10. Where $D{C}_{{WP}_{i}}$, ${wsh}_{i}$, and ${P}_{{WS}_{i}}$ stand for the ith wind power system's planned power, the direct objective function of WT, and the direct objective function specification.

$$D{C}_{{WP}_{i}}={P}_{{WS}_{i}}\cdot C{F}_{{WP}_{i}}={P}_{{WS}_{i}}\cdot {wsh}_{i}.$$

(10)

Equation (11) makes a model for the direct objective function of PV. Where $D{C}_{{PV}_{i}}$, ${pvsh}_{i}$, and ${{P}_{PVS}}_{i}$ have been recognized as the direct objective function of PV, the direct objective function specification, and the planned output power of ${PV}_{i}$ ^9,10.

$$D{C}_{{PV}_{i}}={{P}_{PVS}}_{i}\cdot C{F}_{{PV}_{i}}={{P}_{PVS}}_{i}\cdot {pvsh}_{i}.$$

(11)

Uncertainty objective function models of PVs and WTs

The uncertain objective function models of PVs and WTs are characterized as the little-known and underestimation scenarios of these studied energy sources. The uncertainty objective function models of WTs are described in Eqs. (12) and (13)^9,10.

$$O{C}_{WP,i}={C}_{Ow,i}\cdot \left({P}_{{WS}_{i}}-{P}_{wr,i}\right)={C}_{Ow,i}{\int }_{0}^{{P}_{WS,i}}\left({P}_{{WS}_{i}}-{p}_{w,i}\right){f}_{w}\left({p}_{w,i}\right)d{p}_{w,i},$$

(12)

$$U{C}_{WP,i}={C}_{Uw,i}\cdot \left({P}_{wr,i}-{P}_{{WS}_{i}}\right)={C}_{Uw,i}{\int }_{{P}_{WS,i}}^{{P}_{wr,i}}\left({p}_{w,i}-{P}_{{WS}_{i}}\right){f}_{w}\left({p}_{w,i}\right)d{p}_{w,i},$$

(13)

where $U{C}_{WP,i}$ and $O{C}_{WP,i}$ are the underestimation and overestimation objective function values, ${C}_{Ow,i}$ and ${C}_{Uw,i}$ have been defined as the uncertainty objective function specification. Also, ${P}_{{WS}_{i}}$ and ${P}_{wr,i}$ are the available and rated power of ${WT}_{i}$. A proper technique in Refs.^9,10 had been applied to achieve the comprehensive formulation of the uncertainty objective functions of a PV, with the over- and under-estimation specifications ${C}_{WP,i}$ and $U{C}_{WP,i}$, have been given in Eq. (3):

$$\begin{aligned}O{C}_{PV,i}&={C}_{Opv,i}\cdot \left({P}_{PVS,i}-{P}_{PVav,i}\right)={C}_{Opv,i}\cdot {f}_{PV}\left({P}_{PVav,i}<{P}_{PVS,i}\right)\\ &\cdot \left[{{P}_{PVS}}_{i}-E\left({P}_{PVav,i}<{P}_{PVS,i}\right)\right].\end{aligned}$$

(14)

$$\begin{aligned}U{C}_{PV,i}&={C}_{Upv,i}\cdot \left({P}_{PVav,i}-{{P}_{PVS}}_{i}\right)={C}_{Upv,i}\cdot {f}_{PV}\left({P}_{PVav,i}>{P}_{PVS,i}\right)\\ &\cdot \left[E\left({P}_{PVav,i}>{P}_{PVS,i}\right)-{P}_{PVS,i}\right],\end{aligned}$$

(15)

where ${C}_{Opv,i}$ and ${C}_{Upv,i}$ represent the uncertainty objective function specification, and ${P}_{PVav,i}$ is the available or output power in the $i$ th PV (i.e., $PVi$).

OPF optimization functions

Fuel cost optimization function considering VPEs

Equation (16) models the OPF optimization function that includes the sum of the fuel costs for Ths considering VPEs and the cost of operation and transmission of the power of the WT and PV units^9,10.

$${F}_{obj1}=C{F}_{1}\left({P}_{Th}\right)+\sum_{i=1}^{NW}\left(D{C}_{WP,i}+O{C}_{WP,i}+U{C}_{WP,i}\right)+\sum_{i=1}^{NPV}\left(D{C}_{PV,i}+O{C}_{PV,i}+U{C}_{PV,i}\right).$$

(16)

Fuel cost optimization function considering pollution level with ${{\varvec{C}}}_{{\varvec{t}}{\varvec{a}}{\varvec{x}}}$

This OPF problem has been modeled in Eq. (17).

$${F}_{obj2}={F}_{obj1}+{C}_{E}.$$

(17)

Fuel cost optimization function considering POZs

Equation (18), which is the main goal of the mathematical model of this OPF, has been suggested to be the conventional OPF objective function in Th generators considering POZs^9,10.

$${F}_{obj3}=CF\left({P}_{Th}\right)+\sum_{i=1}^{NW}\left(D{C}_{WP,i}+O{C}_{WP,i}+U{C}_{WP,i}\right)+\sum_{i=1}^{NPV}\left(D{C}_{PV,i}+O{C}_{PV,i}+U{C}_{PV,i}\right).$$

(18)

Network losses

The objective function presented in Eq. (19) may be used to explain the minimization of the network power losses^9,10.

$${F}_{obj4}={P}_{loss}=\sum_{n=1}^{NTL}{G}_{s(i,j)}(n)\cdot \left({V}_{i}^{2}+{V}_{j}^{2}-2{V}_{i}\cdot {V}_{j}{{\cos}}{\delta }_{ij}\right),$$

(19)

where ${\delta }_{ij}$ shows the difference between voltage angles in buses i and j, and ${G}_{s(i,j)}$ shows conductance in the sth network line between buses $i$ and $j$. Also, the voltage value at the ith network bus is considered by the letter ${V}_{i}$.

Voltage deviation (V.D.)

In the considered OPF objective function, the V.D. value for the developed energy networks is determined as indicated in Eq. (20)^9,10.

$${F}_{obj5}=VD=\sum_{i=1}^{NPQ}\left|{V}_{{L}_{i}}-1\right|.$$

(20)

Considered OPF's constraints

Equality OPF's constraints

The suggested OPF problem's equality restrictions may be formulated as given in Eq. (21) and Eq. (22)^9,10:

$${P}_{Gi}-{P}_{Di}-{V}_{i}\sum_{j=1}^{{N}_{bus}}{V}_{j}\cdot \left({B}_{ij}{{\sin}}\left({\delta }_{i}-{\delta }_{j}\right)+{G}_{ij}{{\cos}}\left({\delta }_{i}-{\delta }_{j}\right)\right)=0,$$

(21)

$${Q}_{Gi}+{Q}_{SHi}-{Q}_{Di}-{V}_{i}\sum_{j=1}^{{N}_{bus}}{V}_{j}\cdot \left({G}_{ij}{{\sin}}\left({\delta }_{i}-{\delta }_{j}\right)-{B}_{ij}{{\cos}}\left({\delta }_{i}-{\delta }_{j}\right)\right)=0,$$

(22)

where ${P}_{Gi}$ shows the output power of the ith unit, ${P}_{Di}$ shows the demanded power of the ith load bus, the ${Q}_{Gi}$ shows the output reactive power of the ith generator, and ${Q}_{SHi}$ shows the output reactive power of the ith parallel reactive power compensator. ${Q}_{Di}$ is the demanded reactive power of the ith load bus and ${N}_{bus}$ indicates the number of network buses. The transmission line's conductance and susceptance values are denoted by the letters ${G}_{ij}$ and ${B}_{ij}$.

Inequality OPF's constraints

• Generator limits

As indicated in Eq. (23), there are down and up restrictions on the output power levels as well as the voltage magnitudes of the Ths, WTs, and PVs^9,10.

$$\begin{array}{cc}{P}_{T{h}_{i},min}\le {P}_{T{h}_{i}}\le {P}_{T{h}_{i},max},& i={1,2},\dots ,NTHG,\\ {P}_{{WS}_{i},min}\le {P}_{{WS}_{i}}\le {P}_{{WS}_{i},max},& i={1,2},\dots ,NW,\\ {P}_{{PV}_{i},min}\le {P}_{{PV}_{i}}\le {P}_{{PV}_{i},max},& i={1,2},\dots ,NPV,\\ {Q}_{T{h}_{i},min}\le {Q}_{T{h}_{i}}\le {Q}_{T{h}_{i},max},& i={1,2},\dots ,NTHG,\\ {Q}_{{WS}_{i},min}\le {Q}_{{WS}_{i}}\le {Q}_{{WS}_{i},max},& i={1,2},\dots ,NW,\\ {Q}_{{PV}_{i},min}\le {Q}_{{PV}_{i}}\le {Q}_{{PV}_{i},max},& i={1,2},\dots ,NPV,\\ {V}_{{G}_{i},min}\le {V}_{{G}_{i}}\le {V}_{{G}_{i},max},& i={1,2},\dots ,NG .\end{array}$$

(23)

• Security constraints

Each PQ bus' voltage magnitude value must fall within certain bounds, and each transmission line's apparent power value may be constrained by its maximum capacity. Where ${S}_{{L}_{i},max}$ and ${S}_{{L}_{i}}$ indicate the maximum and apparent power levels in the $i$ th line; ${V}_{{L}_{i},min}$ and ${V}_{{L}_{i},max}$ represent the minimum and maximum voltage levels of the ith PQ bus^9,10.

$$\begin{aligned} &{S}_{{L}_{i}}\le {S}_{{L}_{i},max} {\text{for}} i={1,2},\dots ,NTL,\\ &\quad {V}_{{L}_{i},min}\le {V}_{{L}_{i}}\le {V}_{{L}_{i},max}\quad{\mathrm{for}}\; i={1,2},\dots ,NPQ.\end{aligned}$$

(24)

The SCOPFs’ objective function in the studied electrical network, including Ths, PVs, and WTs, is in Eq. (25)^46,47,48.

$$J={f}_{obj}\left(G,H\right)+{\lambda }_{VPQ}\sum_{i=1}^{NPQ}{\left({V}_{{L}_{i}}-{V}_{{L}_{i}}^{lim}\right)}^{2}+{\lambda }_{Pslack}\cdot {\left({P}_{T{h}_{1}}-{P}_{{Th}_{1}}^{lim}\right)}^{2}+{\lambda }_{QTH}\sum_{i=1}^{NTHG}{\left({Q}_{T{h}_{i}}-{Q}_{{Th}_{i}}^{lim}\right)}^{2}+{\lambda }_{QWS}\sum_{i=1}^{NW}{\left({Q}_{{WS}_{i}}-{Q}_{{WS}_{i}}^{lim}\right)}^{2}+{\lambda }_{QPV}\sum_{i=1}^{NPV}{\left({Q}_{{PV}_{i}}-{Q}_{{PV}_{i}}^{lim}\right)}^{2}+{\lambda }_{SL}\sum_{i=1}^{NTL}{\left({S}_{{L}_{i}}-{S}_{{L}_{i}}^{lim}\right)}^{2},$$

(25)

where ${\lambda }_{VPQ}$, ${\lambda }_{Pslack}$, ${\lambda }_{QTH}$, ${\lambda }_{QWS}$, ${\lambda }_{QPV}$, and ${\lambda }_{SL}$ represent the penalty factors^9,10 and “limit values’’ ${V}_{{L}_{i}}^{lim}, {P}_{{Th}_{1}, }^{lim}{Q}_{{Th}_{i}}^{lim},$ ${Q}_{{WS}_{i}}^{lim},$ ${Q}_{{PV}_{i}}^{lim},$ and ${S}_{{L}_{i}}^{lim}$ are defined in the same way as described in the following identity

$${x}^{lim}=\left\{\begin{array}{cc}x,& {x}^{min}\le x\le {x}^{max};\\ {x}^{max},& x>{x}^{max};\\ {x}^{min},& x<{x}^{min}.\end{array}\right.$$

Power and uncertainty models in the PVs and WTs

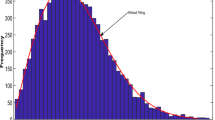
Weibull probability density function (PDF), as stated in Eq. (26), identifies the wind speed distribution, where $\psi ,$, $\xi ,$ and ${v}_{w}$ indicate the scale factor, and the shape factor, the wind speed, respectively^9,10.

$${f}_{v}\left({v}_{w}\right)=\frac{\xi }{\psi } {\left(\frac{{v}_{w}}{\psi }\right)}^{\xi -1}{e}^{-{\left(\frac{{v}_{w}}{\psi }\right)}^{\xi }}.$$

(26)

Weibull fittings’ outcomes in wind frequency distributions are shown in Fig. 2⁹. They were derived using a Monte Carlo simulation with 8000 iterations^9,10. WTs’ output power has been modeled as in Eq. (27):

$${p}_{W}\left({v}_{w}\right)=\left\{\begin{array}{cc}0,& {{v}_{w,out}<v}_{w }{<v}_{w,in};\\ \frac{{v}_{w}-{v}_{w,in}}{{v}_{w,r}-{v}_{w,in}}\cdot {p}_{wr},& {{v}_{w,in}\le v}_{w}\le {v}_{w,r};\\ {p}_{wr},& {{v}_{w,r}\le v}_{w}\le {v}_{w,out},\end{array}\right.$$

(27)

where the rated power, cut-in, cut-out, and rated wind speeds are denoted by ${p}_{wr}$, ${v}_{w,in}$, ${v}_{w,out}$, and ${v}_{w,r}$, respectively, according to wind speeds, a wind farm's electricity is divided into distinct portions, as shown in Eq. (27). The probability values are shown between Eqs. (28) to (30) in these sections^9,10.

Figure 2

Wind frequency distributions for wind speed: (a) WT₁ at bus 5, and (b) WT₂ at bus 11⁹.

$${f}_{w}\left({p}_{w}\right)\left\{{p}_{w}=0\right\}=1-{\text{exp}}\left(-{\left(\frac{{v}_{w,in}}{\psi }\right)}^{\xi }\right)+{\text{exp}}\left(-{\left(\frac{{v}_{w,out}}{\psi }\right)}^{\xi }\right) ,$$

(28)

$${f}_{w}\left({p}_{w}\right)\left\{{p}_{w}={p}_{wr}\right\}={\text{exp}}\left(-{\left(\frac{{v}_{w,r}}{\psi }\right)}^{\xi }\right)-{\text{exp}}\left(-{\left(\frac{{v}_{w,out}}{\psi }\right)}^{\xi }\right),$$

(29)

$${f}_{w}\left({p}_{w}\right)=\frac{\xi \cdot \left({v}_{w,r}-{v}_{w,in}\right)}{{\psi }^{\xi }{p}_{wr}}\cdot {\left({v}_{w,in}+\frac{{p}_{w}}{{p}_{wr}}\left({v}_{w,r}-{v}_{w,in}\right)\right)}^{\xi -1}\cdot {\text{exp}}\left(-{\left(\frac{{v}_{w,in}+\frac{{p}_{w}}{{p}_{wr}}\left({v}_{w,r}-{v}_{w,in}\right)}{\psi }\right)}^{\xi }\right).$$

(30)

Table 2 shows the PDF components of the PVs and WTs. Wind speeds for units had been selected as ${v}_{w,out}=25$ m/s, ${v}_{w,r}= 16$ m/s, and ${v}_{w,in}= 3$ m/s, respectively^9,10, and with selected rated power equal to 3 MW.

Table 2 Specifications of the WT and PV units.

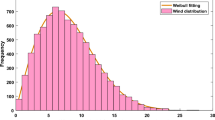
The Lognormal PDF was used to characterize the generation power of PV like a mathematical model of solar irradiation. According to Eq. (31) and Eq. (32) ^9,10, it is possible to identify the generation power and likely function of PV mathematically.

$${f}_{{G}_{pv}}\left({G}_{pv}\right)=\frac{1}{{G}_{pv} \cdot\Omega \sqrt{2\pi }} {\text{exp}}\left(\frac{-{\left({\text{ln}}{G}_{pv}-\xi \right)}^{2}}{2{\Omega }^{2}}\right)\quad{\mathrm{for}}\; {G}_{pv}>0,$$

(31)

where $\Omega$ and $\xi$ show the standard deviation and mean of the Lognormal PDF⁹, as shown in Table 2.

By an 8000-generation Monte Carlo simulation, Fig. 3 gives the frequency distribution and lognormal probability for solar irradiation⁹.

$${P}_{P{V}_{0}}=\left\{\begin{array}{cc}{P}_{PVrate}\cdot \frac{{G}_{pv}}{{G}_{pv}\cdot {R}_{C}} ,& 0<{G}_{pv}<{R}_{C};\\ {P}_{PVrate}\cdot \frac{{G}_{pv}}{{G}_{pvstd}},& {G}_{pv}\ge {R}_{C} ,\end{array}\right.$$

(32)

where ${G}_{pvstd}$, ${G}_{pv}$ and ${P}_{PVrate}$ are the standard solar irradiance level, the solar irradiance’s probability level, and the rated power of PV, respectively, that have been chosen equal to 800 W/m² and 50 MW at bus 13. ${R}_{C}$ has been set equal to 120 W/m². The generation power of PV has been shown via the histogram in Fig. 4⁹. The line shows the anticipated amount of electricity power that this PV will provide to the electrical network. It's important to keep in mind that the value of the anticipated production of solar electricity might alter.

Figure 3

The Lognormal PDF solar irradiance distribution of PV⁹.

Figure 4

Output power (MW) distribution of PV⁹.

The proposed algorithm

In this chapter, we will focus on the construction of a new SAWGA optimizer, which is based on the improvement of the previously proposed WGA algorithm.

Wild Goose algorithm (WGA)

In⁴⁹, an effective method for high-dimension complicated and difficult optimization problems was introduced. Its name is the WGA, and it is inspired by the lives of wild geese, such as their altogether regular movement, breeding, and development, as well as mortality in a group of geese. In the rest of this subsection, we recap the steps of the WGA algorithm.

An altogether regular migration

In PSO, each wild goose has been first identified as a population member; hence, the $i$ th wild goose is equivalent to the $i$ th member with the changing location ${X}_{i}$. The migration velocity ${X}_{i}$ and individual optimal solution ${P}_{i}$ are calculated. Then, all Wild Goose populations are ranked according to their intended function, from best to worst. The wild goose migration is a collective, organized, and controlled migration that relies on power and places the upfront members so that their locations will be regularized from the most optimal solution to the worst solution (from 1 to $Np$), as $f\left({ P}_{i+2}^{Iter}\right)\le f\left({ P}_{i+1}^{Iter}\right)\le f\left({ P}_{i}^{Iter}\right)\le f\left({ P}_{i-1}^{Iter}\right)$. Equations (33) and (34) describe velocity and displacement in accordance with the altogether regular motion of the geese. According to Eq. (33), each wild goose's velocity and position changes are dependent on the speed of their front and rear goose, or $\left({V}_{i+1}^{Iter}-{V}_{i-1}^{Iter}\right)$, as well as on their locations, which have been decided through the value of the optimization function of the ordered group members $f\left({X}_{i}^{Iter}\right)$. In other words, the forefront member is the most efficient member of the wild goose since they benchmark and navigate their group as a whole as well as coordinate with the whole group. So, the migration velocity equation of the ith member by⁴⁹ has the following form:

$$\begin{aligned}&{v}_{i,d}^{Iter+1}={r}_{1,d}\cdot {v}_{i,d}^{Iter}+{r}_{2,d}\cdot \left({v}_{i+1,d}^{Iter}-{v}_{i-1,d}^{Iter}\right)\\ &\quad+{r}_{3,d}\cdot \left({p}_{i,d}^{Iter}-{x}_{i-1,d}^{Iter}\right)+{r}_{4,d}\cdot \left({p}_{i+1,d}^{Iter}-{x}_{i,d}^{Iter}\right)\&\quad\ +{r}_{5,d}\cdot \left({p}_{i+2,d}^{Iter}-{x}_{i+1,d}^{Iter}\right)-{r}_{6,d}\cdot \left({p}_{i-1,d}^{Iter}-{x}_{i+2,d}^{Iter}\right).\end{aligned}$$

(33)

Birds in a flock always travel in the direction of the leader. The leader is in the best position globally, thus if the leader deviates, then all other birds will deviate as well. As a result, on the one hand, the best wild goose G serves as the group's leader-member, directing all other wild goose to their objective, and in other words, the position changes of these wild goose rely on their velocity.

Therefore, the amounts of displacement and change ${X}_{i}$ resulting from wild goose migration, i.e., ${X}_{i}^{V}$, are calculated based on the member's best local position ${P}_{i}$ and migration velocity ${V}_{i}$, as well as the member who is in front of them ${P}_{i+1}$, the group leader $G$ which has been explained in Eq. (34). The geese constantly adjust their separation from one another to maintain a safe spacing. The product of two random numbers between 0 and 1,${r}_{7,d}\cdot {r}_{8,d}$ has been utilized since the quantity is small⁴⁹:

$${x}_{i,d}^{V}={r}_{7,d}\cdot {r}_{8,d}\cdot \left({v}_{i,d}^{Iter+1}+\left({p}_{i+1,d}^{Iter}+{g}_{d}^{Iter}-2{p}_{i,d}^{Iter}\right)\right)+{p}_{i,d}^{Iter}.$$

(34)

Search for food

The ith wild goose (or any other goose) moves toward its upfront wild goose ${P}_{i+1}^{Iter}$, and the upfront goose's walking and seeking for food has been modelled as its scheme. The $i$ th member imitates the $(i+1)$ th member and attempts to achieve that ${P}_{i+1}^{Iter}-{X}_{i}^{Iter}$. The wild geese's ${X}_{i}^{W}$ equation for foraging while on the move is as follows⁴⁹

$${x}_{i,d}^{W}={p}_{i,d}^{Iter}+{r}_{9,d}\cdot {r}_{10,d}\cdot \left({p}_{i+1,d}^{Iter}-{p}_{i,d}^{Iter}\right).$$

(35)

Reproduction and evolution of wild gooses

One part of wild gooses’ living similar to other alive extant has been based on the reproduction and evolution. Its modeling has been applied similarly to that of DE algorithm (Eq. (36)), where a combination (crossover operation) between migration equation ${X}_{i}^{V}$, search for food ${X}_{i}^{W}$ has been applied. In⁴⁹, $Cr$ size in the WGA algorithm has been considered equal to 0.5.

$${x}_{i,d}^{Iter+1}=\left\{\begin{array}{cc}{x}_{i,d}^{V},& {r}_{11,d}\le Cr;\\ {x}_{i,d}^{W},& \text{otherwise.}\end{array}\right.$$

(36)

Regular evolution, migration and death

The algorithm starts out in this phase with the maximum population ${Np}^{initial}$, and as it iterates, the weaker individuals in terms of Eq. (37) will be eliminated from the total members (death of the weaker individuals) and the act of optimization will continue until the final members in the final generation achieves its final size ${Np}^{final}$. Algorithm 1 illustrates the code for this simple and effective approach⁴⁹.

$$p={\text{round}}\left(N{p}^{initial}-(N{p}^{initial}-N{p}^{final})\frac{FEs}{FE{s}_{max}}\right),$$

(37)

where ${FEs}_{max}$ shows the maximum fitness evaluations and $FEs$ shows the recent fitness evaluations.

Algorithm 1

.

In addition, the optimization process of the proposed modified algorithm has been shown in Fig. 5.

Figure 5

Optimization process of the proposed modified algorithm.

Self-adaptive decision parameters in WGA: A Self-adaptive wild geese algorithm (SAWGA)

Choosing appropriate control parameter values is typically a challenge that depends on the type of issue. Multiple optimization runs are needed since the control settings are tuned by trial and error⁵⁰. We provide a self-adaptive technique for control settings in this section. Values for the parameter are extended to each member of the population. For Eqs. (34) to (36), we chose control-based random coefficients and modeled them for this investigation. We have recreated the equations once again and identified an appropriate connection for them, as indicated in Eqs. (38) to (40).

${\varvec{C}}{\varvec{r}}$ and ${\varvec{F}}$ are the control variables that will be modified through evolution. Both are used on an individual basis. Superior individuals result from these (encoded) control parameter values because they are more likely to live, procreate, and spread these superior parameter values to new individuals.

$${x}_{i,d}^{Iter+1}=\left\{\begin{array}{cc}{F}_{i}^{Iter}\cdot \left({v}_{i,d}^{Iter+1}+\left({p}_{i+1,d}^{Iter}+{g}_{d}^{Iter}-2{p}_{i,d}^{Iter}\right)\right)+{p}_{i,d}^{Iter},& C{r}_{i}^{Iter}\ge rand;\\ {p}_{i,d}^{Iter}+{F}_{i}^{Iter}\cdot \left({p}_{i+1,d}^{Iter}-{p}_{i,d}^{Iter}\right),& \begin{array}{c}\\ {\text{o}}{\text{t}}{\text{h}}{\text{e}}{\text{r}}{\text{w}}{\text{i}}{\text{s}}{\text{e}}\text{.}\end{array}\end{array}\right.$$

(38)

$${F}_{i}^{Iter+1}=\left\{\begin{array}{cc}0.1+ran{d}^{2}\cdot 0.9,& rand<0.1;\\ {F}_{i}^{Iter},& \begin{array}{c}\\ {\text{o}}{\text{t}}{\text{h}}{\text{e}}{\text{r}}{\text{w}}{\text{i}}{\text{s}}{\text{e}}\text{.}\end{array}\end{array}\right.$$

(39)

$${Cr}_{i}^{Iter+1}=\left\{\begin{array}{cc}0.4+rand\cdot 0.2,& rand<0.1;\\ {Cr}_{i}^{Iter},& {\text{otherwise}}.\end{array}\right.$$

(40)

where rand is a uniform random number from the interval [0, 1].

SAWGA for solving the different OPF problems with stochastic wind and solar power

On the IEEE 30-bus electrical network, as given in Fig. 6, the WGA, GOA, TEO, HHO, HBA, and SAWGA approaches were investigated to resolve an OPF issue, including PV and VT units. Additionally, Table 3 provides the control settings for the optimization techniques that were collected from references. The system parameters for the IEEE 30-bus electrical network have been shown in Table 4 and were derived from references^3,9,10,51.

Figure 6

The IEEE 30-bus electrical network.

Table 3 The control variables of the optimization techniques.

Table 4 The pollution level and cost factors of Th units in the IEEE 30-bus electrical network.

Table 5 displays the underestimation, overestimation, and direct cost factors for PVs and WTs. The load flow framework shown in MATPOWER^51,52 has been applied to this OPF, including Ths, PVs, and WTs. For the optimization functions of the suggested OPF, all optimization methods were performed 30 times to statistically analyze the obtained optimal solutions. The optimization functions of the suggested OPF have been optimized in accordance with the different scenarios that follow.

Table 5 The cost factors of the PVs and WTs of the electrical network.

• Case 1: OPF considering total cost in Th units considering VPEs, PVs, and WTs.

• Case 2: OPF considering total cost in Th units considering emission and carbon tax, and PVs and WTs.

• Case 3: OPF considering total cost in Th units considering POZs, PVs, and WTs.

• Case 4: OPF considering power losses of the electrical network.

• Case 5: OPF considering the voltage deviation (V.D.) of the electrical network.

Case 1: Total cost considering VPEs of Th units

OPF’s objective function, considering VPEs of Th units, as well as the cost function of the PVs and WTs, are used in Case 1 to optimize for lowering the overall cost. In this instance, produced electric power from all various kinds of generation units employed in the redesigned electrical network are optimized to reduce the basic power cost to its absolute lowest. Table 6 lists the outcomes of all factors that were ideally determined, including reactive powers, total cost, decision parameters, and other variables—values the best, worst, average, and Std. for the algorithms and the suggested SAWGA approach after 30 separate runs are shown in Table 6. The simulation findings of this case demonstrate the efficacy of SAWGA. SAWGA offers a quick convergence trend and improved results quality compared to the traditional WGA, GOA, TEO, HHO, and HBA optimization approaches for OPF. SAWGA obtained the lowest overall power cost of 782.0238 $/h among all used algorithms. The convergences of used OPF optimization approaches have been given in Fig. 7.

Table 6 The obtained optimal decision parameters for Case 1.

Figure 7

Convergences of the optimization techniques for Case 1.

Case 2: Total cost considering emission and carbon tax in Th units

By imposing a set ${C}_{tax}$ on Th units due to their CO2 emissions, the case's goal is to reduce the electricity’s total cost⁹. The mandated ${C}_{tax}$ is set at $20 per ton⁹. The simulation findings clearly support the idea that imposing the carbon fee would increase the amount of wind and solar energy that is incorporated into the electricity system. Similar to scenario 1, Fig. 8 compares the convergence of the SAWGA, WGA, GOA, TEO, HHO, and HBA algorithms, and Table 7 lists the best results for OPF as Table 6. SAWGA outperforms WGA and all other used approaches based on overall cost reduction and the convergence of the beast result since it achieves a minimum value of 810.7448 $/h.

Figure 8

Convergences of the optimization techniques for Case 2.

Table 7 The obtained optimal decision parameters for Case 2.

Case 3: OPF considering POZs in Th units

According to the OPF problem stated in Eq. (9), optimization of the overall cost while taking POZs has been explored. Like instances 1 and 2, Fig. 9 compares the convergence of the SAWGA, WGA, GOA, TEO, HHO, and HBA algorithms, and Table 8 lists the optimum attained results for the reactive powers, total cost, decision parameters, and other variables. The suggested SAWGA algorithm produced a simulation result of 781.9047 $/h, which was superior to that of the WGA and other approaches.

Figure 9

Convergences of the optimization techniques for Case 3.

Table 8 The obtained optimal decision parameters for Case 3.

Case 4: OPF considering power losses of the electrical network

In this instance, the considered algorithms suggested optimizing the power losses of the electrical network updated by utilizing PVs and WTs. The SAWGA method produced a result of 2.1037 MW for this scenario, less than the optimization results from the other methods. Also, Table 9 shows this case's findings at the simulation research's conclusion. For scenario 4, Fig. 10 compares the convergence of the SAWGA, WGA, GOA, TEO, HHO, and HBA algorithms.

Table 9 The obtained optimal decision parameters for Case 4.

Figure 10

Convergences of the optimization techniques for Case 4.

Case 5: OPF considering the voltage deviation (V.D.)

In Case 5, the goal was to optimize V.D. of the electrical network using PVs and WTs. The outcomes of the WGA, GOA, TEO, HHO, HBA, and SAWGA algorithms were, respectively, 0.37658, 0.41849, 0.39531, 0.38066, 0.38570, and 0.37576, as shown in Table 10. Table 10 makes it quite evident that the SAWGA method produced a worse outcome than the other algorithms. Figure 11 displays the convergence patterns for all optimization techniques.

Table 10 The obtained optimal decision parameters for Case 5.

Figure 11

Convergences of the optimization techniques for Case 5.

Multi-objective SAWGA (MOSAWGA) for solving the different classical OPF problems

To address the multi-objective problem (MOP), we utilize the Pareto method, elaborated upon in the subsequent section:

Pareto optimization method

In the realm of multi-objective problems (MOPs), the optimization process encompasses the simultaneous optimization of multiple independent objective functions (OFs), all while adhering to a spectrum of equality and inequality constraints. The formulation of these problems is as follows^39,40:

$${{\min}}J(x,u)={\left[{J}_{1}(x,u),{J}_{2}(x,u),\ldots,{J}_{n}(x,u)\right]}^{T}.$$

(41)

The Pareto method endeavors to identify a collection of solutions that takes into account all OFs and strikes a balance among them. The ultimate outcome of this process is identifying of Pareto optimal points—solutions that are not surpassed by any other solutions. In a broader sense, solution ${X}_{1}$ is considered to dominate solution ${X}_{2}$ if the following conditions are satisfied:

$$\begin{aligned}\forall i\in \left\{{1,2},\ldots,n\right\},{J}_{i}({X}_{1})\le {J}_{i}({X}_{2})\\ \exists h\in \left\{{1,2},\ldots,n\right\},{J}_{h}({X}_{1})<{J}_{h}({X}_{2})\end{aligned}$$

(42)

The group of solutions not dominated by other solutions is termed “dominant solutions.” To manage the size of this set, the paper employs the fuzzy grouping method.

Fuzzy grouping method

In certain MOPs, there is a need to standardize OFs to bring their values into a comparable range. Subsequently, the normalized values of OFs are merged. The fuzzy grouping method introduces a membership function (MF) for each OF, characterized by:

$${\sigma }_{{J}_{i}}(X)=\left\{\begin{array}{cc}1,& {J}_{i}\left(X\right)<{J}_{i}^{{{\min}}};\\ 0,& {J}_{i}\left(X\right)>{J}_{i}^{{{\max}}};\\ \frac{{J}_{i}^{{{\max}}}-{J}_{i}(X)}{{J}_{i}^{{{\max}}}-{J}_{i}^{{{\min}}}},& {J}_{i}^{{{\min}}}{\le J}_{i}\left(X\right)\le {J}_{i}^{{{\max}}},\end{array}\right.$$

(43)

where ${J}_{i}^{{{\min}}}$ and ${J}_{i}^{{{\max}}}$ show the minimum and maximum values of the $i$ th OF, respectively, these values are calculated by optimizing each OF as a single objective problem.

For available solutions in the stored set, the normalized value of MF is computed using (44):

$${N}_{\sigma }\left(i\right)=\frac{\sum_{h=1}^{n}{\phi }_{h}\cdot {\sigma }_{{J}_{h}}\left({X}_{i}\right)}{\sum_{i=1}^{q}\sum_{h=1}^{n}{\phi }_{h}\cdot {\sigma }_{{J}_{h}}\left({X}_{i}\right)},$$

(44)

where $q$ shows the number of non-dominated solutions and ${\phi }_{h}$ is the weighing factor pertaining to the $h$-th OF.

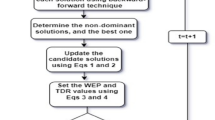
MOSAWGA to solve multi-objective OPF problems

To solve multi-objective OPF problems using MOSAWGA, the subsequent procedure is followed:

Step 1: Enter the necessary data for the algorithm and system Step 2: Embedding constraints into objective functions using the penalty functions method Step 3: Initialization of the wild goose population Step 4: Evaluate the objective function for the wild gooses Step 5: Putting non-dominated solutions in a repository Step 6: Sorting population considering the normalized values of the objective function of the previous step Step 7: Applying the altogether regular migration, search for food, and reproduction and evolution of wild gooses Step 8: Regular evolution, migration, and death Step 9: Swapping wild gooses’ positions and refreshing dominant solutions in the repository Step 10: Repeating steps 7 to 9 until finishing the total number of iterations

Numerical results and comparison

To evaluate the performance and efficacy of MOSAWGA, it is examined on the IEEE 30-bus power system, demonstrated in Fig. 12^1,2,6.

Figure 12

One-line representation of the IEEE 30-bus system.

This system has six generating units located at buses 1, 2, 5, 8, 11, and 13 and four tap-adjusting transformer units at branches 6–9, 6–10, 4–12, and 28–27. The total system power demand is 2.834 p.u. with base power equal to 100 MVA base. The lower limits of voltage magnitudes of generator buses, voltage magnitudes of load buses, VAR compensation, and transformers’ tap settings are set to 0.95, 0.95, 0.0, and 0.95 p.u., respectively. Also, their higher limits are set to 1.1, 1.05, 0.3, and 1.1 p.u., respectively.

Setting the parameters of the algorithms is the same as in the fifth section. To demonstrate the efficiency of the proposed algorithm, the following three cases were taken into account:

Case 1: Minimization of fuel cost and real power transmission losses.

Case 2: Minimization of fuel cost and voltage magnitudes’ deviance (voltage profile improvement).

Case 3: Minimization of fuel cost and emissions.

Case 1: Minimization of fuel cost and real power losses

The best fuel costs and power losses of the best compromise solution (BCS) achieved by MOSAWGA and those of other algorithms are presented in Table 11. The best fuel costs and real power losses achieved by MOSAWGA are 822.0989 $/h and 5.55 MW, respectively.

Table 11 The best results of Case 1 by different algorithms.

The final non-dominated solutions of different algorithms are demonstrated in Fig. 13 (only 20 points are presented).

Figure 13

Final non-dominated solutions obtained for Case 1.

Case 2: Minimization of fuel cost and voltage magnitudes deviation

Table 12 gives the summarized optimization results obtained by MOSAWGA, and Table 13 compares the best result of MOSAWGA with that of other metaheuristic methods mentioned in the introductory part of the article.

Table 12 Best values for decision variables and the minimum fuel costs for different cases using MOSAWGA.

Table 13 The best results of Case 2 by different algorithms.

The Pareto optimal solutions acquired by WGA-based methods are presented in Fig. 14. It is observed in the figure that MOSAWGA gives well-distributed solutions compared with other algorithms.

Figure 14

Final non-dominated solutions found for Case 2.

Case 3: Minimization of fuel cost and emissions

The best solutions found by MOSAWGA in 50 trials for Case 3 are shown in Table 12. Also, Table 14 yields a comparison of all algorithms. It is deduced by investigating these tables that MOSAWGA found a solution with fuel cost equal to 862.923 $/h and emission equal to 0.2244 ton/h, which are less than those of other algorithms. The non-dominated solutions of this case are given in Fig. 15.

Table 14 The best results of Case 3 by different algorithms.

Figure 15

Final non-dominated solutions found for Case 3.

IEEE 118 bus test network

The effectiveness of the proposed SAWGA in addressing larger power systems is assessed using the IEEE 118-bus test system^{53,54,55,56,57,58,59,60,61,62,63,64} in the field of electrical engineering. This test network features 54 generators, 2 reactors, 12 capacitors, 9 transformers, and 186 branches. A total of 129 control variables are considered, encompassing 54 generator active powers and bus voltages, 9 transformer tap settings, and 12 shunt capacitor reactive power injections. Voltage limitations for all buses are maintained between 0.94 and 1.06 p.u. The shunt capacitors offer reactive powers from 0 to 30 MVAR, and transformer tap settings are assessed within the range of 0.90–1.10 p.u.²⁶.

Case 1: The quadratic cost function for conventional generators in OPF, excluding solar and wind energy sources, can be expressed as follows:

In Table 15, the performance of the proposed SAWGA is juxtaposed with outcomes from alternative algorithms explored in the field of electrical engineering. A comprehensive literature review also includes various techniques utilized for solving large-scale OPF problems. The comparative analysis in these tables showcases the superiority of SAWGA over other optimization methodologies in achieving optimal OPF solutions. The simulation results reveal a noteworthy reduction in cost, with SAWGA achieving a minimum cost of $129,522.5891 per hour, surpassing the outcomes produced by alternative algorithms.

Table 15 Optimal results for Case 1.

Case 2: OPF incorporating a quadratic cost function for conventional generators, along with the integration of solar and wind energy sources, can be articulated as follows:

Addressing the OPF challenge involves formulating a quadratic cost function for traditional generators, accounting for their operational costs. Additionally, the inclusion of solar and wind energy sources in this scenario introduces complexities related to their intermittent nature and variable outputs. The overarching goal is to optimize the power flow in the system while considering the unique characteristics and cost implications associated with both traditional and renewable energy sources.

This system is similar to the previous case study, incorporating renewable energy sources at various buses. Wind energy sources are placed at buses 18, 32, 36, 55, 104, and 110, while solar energy generation units are located at buses 6, 15, and 34.

The optimal solution for this case, obtained through the proposed SAWGA algorithm, is presented in Table 16 with a comparative study between the results of the algorithms WGA and the solutions obtained in reference²⁶. These results demonstrate that SAWGA is a highly capable algorithm for optimizing and efficiently distributing loads in large, realistic power systems.

Table 16 Optimal results for Case 2.

Ethical approval

This article does not contain any studies with human participants or animals performed by the author.

Informed consent

Informed consent was not required as no human or animals were involved.

Declaration of Generative AI and AI-assisted technologies in the writing process

The authors declare that they did not use AI-assisted technologies to create this article.

Discussion

In the final discussion, the study has successfully implemented and assessed the enhanced Self-Adaptive Wild Goose Algorithm (SAWGA) in optimizing Economical-Environmental-Technical Optimal Power Flow (OPF) problems within traditional and modern energy systems. Leveraging adaptive search strategies and robust diversity capabilities, SAWGA, integrating four powerful optimizers, proves its efficiency. Applied to OPF models on IEEE 30-bus and 118-bus electrical networks featuring conventional thermal power units, solar photovoltaic (PV), and wind power (WT) units, SAWGA addresses the complexities introduced by renewable energy sources (RESs). The algorithm demonstrates superior performance in optimizing various objective functions, effectively managing OPF challenges, and consistently outperforming traditional WGA and other modern algorithms. Noteworthy attributes include its robust ability to achieve global or nearly global optimal settings for decision parameters, resulting in significant reductions in overall fuel consumption costs with faster and more efficient convergence. The findings highlight the substantial contributions of SAWGA in navigating the intricate landscape of OPF problems in the presence of RESs, reinforcing its role as a potent tool for the sustainable and efficient operation of power systems. On the one hand, considering the simulation times in the tables, especially based on Table 15, which represents simulation results for a large-scale energy system, it is evident that the proposed method exhibits a suitable optimization speed and time, particularly compared to the original WGA algorithm. The proposed SAWGA method significantly improves the final optimal results without introducing any specific complexity or additional simulation time compared to the original WGA algorithm.

Conclusions

In conclusion, this study introduces the self-adaptive wild geese algorithm (SAWGA) as a novel and practical approach for addressing various optimal power flow (OPF) problems. We conducted a comprehensive comparison with four modern optimization algorithms (GOA, TEO, HHO, and HBA) and the traditional WGA, as well as the optimal results in the recent papers, showcasing SAWGA's superior efficiency. Our evaluation considered different objective functions within two different IEEE 30-bus and IEEE 118-bus electrical networks, incorporating wind turbine units (WTs) and solar photovoltaic units (PVs).

SAWGA demonstrates remarkable capabilities in optimizing diverse objective functions and effectively managing OPF challenges. The algorithm consistently outperforms traditional WGA and other modern algorithms, achieving global or nearly global optimal settings for decision parameters. The comparison of optimization results emphasizes SAWGA's superiority in total cost reduction and fast convergence.

Our future work will focus on developing a stochastic multi-objective model for the OPF problem in the presence of renewable power generations. This avenue promises to further enhance the applicability and robustness of optimization algorithms in addressing evolving challenges in power system management.