Introduction

Driven by the successful advances of deep generative models in the past few years, scientific data generation has become one of the essential topics in the scientific research field. Novel computational approaches based on deep generative models have been developed to generate scientific data from experimental or simulation datasets. The deep generative models stand for deep neural networks which are designed to generate synthetic data by approximating complicated and high-dimensional data distribution1. The two representative deep generative models, variational autoencoder (VAE)2 and generative adversarial network (GAN)3, are extensively used for scientific research and data generation. For example, VAEs have been used for new physics mining at the Large Hadron Collider4 and molecular designing5, whereas GANs have been used for weather prediction6 and CT image augmentation7.

In condensed matter physics, the magnetic system is a representative system where deep learning techniques are actively applied8,9,10. This is not only because unique physical characteristics appear due to the competition of several complicated magnetic interactions, but also because several toy models based on magnetic systems (such as the Ising and Heisenberg models) are generally used to analyze the physical phenomena observed in various research fields. Among the deep learning techniques, VAE-based models have been widely adapted to various magnetic systems for investigating phase transition behaviors11,12,13,14,15, characterizing crystal structures16, interpolating and extrapolating magnetic structures17, searching for optimal magnetic structures18, estimating effective fields19, and finding the ground states20, 21.

Despite these successful applications, the sampling data for topological spin structures using VAE still has certain limitations, which originated from the representative disadvantage of VAE called the latent space smoothness22. In the usual training process of VAE, the latent space is formed to follow a simple prior distribution (e.g., Gaussian distribution). It means that complicated target data distributions may not be accurately represented by the simple continuous latent space of VAE, and it leads to difficulties in capturing intricate relationships between the data points. Also in the case of sampling data for topological spin structures, each of the spin structures is distinctly separated with high energy barriers induced by topological properties, but VAE cannot learn the details of topological difference between the spin structures. Consequently, it allows the generation of non-plausible spin structures with topological defects including nodal points18, 21. The previous studies address this issue using prior scientific knowledge of the target system, such as adding the energy of generated spin configurations to the cost function21 or polishing the generated samples to lower their energies18. However, prior knowledge is often absent for other datasets, thus additional studies are needed for generating topological data avoiding topological defects without any prior knowledge.

On the other hand, the various deep generative models based on GANs are also applied to generate scientifically plausible data in various research fields of condensed matter physics23, 24. In a usual GAN model, a discriminator network learns to distinguish between real and fake samples while a generator network is trained to produce samples that are realistic enough to deceive the discriminator network. Because of the adversarial relationship between the discriminator and generator, the GAN-based models have shown greater capabilities in photo-realistic data generation compared with the VAE25. Analogously, it is expected that the GAN-based models can produce more realistic spin structures with no or fewer nodal points. However, a problem of GAN-based models is that the diversity of generated samples is poorer than VAE-based models26. To secure both the high plausibility of GAN-based models and the high diversity of VAE-based models simultaneously, recently the hybrid models of VAE and GAN are intensively studied and applied to various research fields27,28,29.

The goal of this study is to implement a generator which can produce physically and topologically reliable magnetic structures. To achieve our goal, we build a hybrid model of two representative deep generative models, VAE and GAN, and train it with two-dimensional spin structures to exhibit its strengths as a topological structure generator. The results are compared with those of standalone VAE and GAN. The trained models are quantitatively evaluated by coverage and energy metrics that measure the diversity and fidelity of generated samples, respectively. We visualize the latent space manifolds of the trained models to analyze the underlying reasons for topological defects that appeared in generated samples. Additionally, we suggest that the discriminator-driven latent sampling (DDLS) method30,31,32 can be applied to improve the plausibility of generated samples by eliminating topological defects.

Strategy

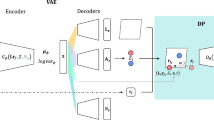
VAE-GAN hybrid model

The hybrid model combines the training workflows of VAE and GAN. For the comparative investigation, we train three models: VAE, GAN, and the hybrid model. The VAE is built with two neural networks of encoder \(E\) and generator (decoder) \(G\) as shown in Fig. 1a. The encoder converts training data \({x}_{d}\) into a latent code \({z}_{E}\), and the generator decodes \({z}_{E}\) to \(\widetilde{x}\). On the other hands, the GAN consists of generator \(G\) and discriminator \(D\) as shown in Fig. 1b. A random latent code \({z}_{p}\) is sampled from a prior distribution \({p}_{0}(z)\) and becomes a fake data \({x}_{p}\) via the generator. Then, the real data \({x}_{d}\) and fake data \({x}_{p}\) are classified by the discriminator. The hybrid model has three neural networks, encoder, generator, and discriminator. Figure 1c illustrates the overall training workflow of the hybrid model. Note that the reconstructed data \(\widetilde{x}\) is also fed into the discriminator as fake data. Therefore, unlike a standalone GAN, the number of fake samples is twice the number of real samples.

Figure 1
figure 1

(a–c) Illustration of the training workflows of (a) VAE, (b) GAN, and (c) hybrid model. The \(E\), \(G\), and \(D\) denote the encoder, generator (or decoder), and discriminator, respectively. (d) The schematic description of standard sampling in VAE, GAN, and hybrid model. (e) The schematic description of DDLS sampling. The dashed arrow indicates the gradient backpropagation and the \(\alpha\) denotes the gradient step size.

Full size image

The loss function of the hybrid model also contains both components of VAE and GAN losses. The loss function of VAE, \({\mathcal{L}}^{\mathrm{VAE}}\), is shown in Eq. (1), where \(N\) is the dimensionality of input features (\(128\times 128\times 3)\), \(\beta\) is a coefficient of the regularization term33, and \({p}_{E}\left(z|x\right)\) is the posterior distribution of the encoder. The terms \({\mathbb{E}}\) and \({D}_{\mathrm{KL}}\) denote expectation value and the Kullback–Leibler divergence, respectively.

$${\mathcal{L}}^{{{\text{VAE}}}} = \frac{1}{N}{\mathbb{E}}\left[ {\left( {x_{d} - \tilde{x}} \right)^{2} } \right] + \beta D_{KL} \left( {p_{E} \left( {z{|}x} \right)p_{0} \left( z \right)} \right).$$
(1)

The first term measures how well the VAE can reconstruct the input data and the second term enforces the trained latent space of the VAE to be close to the prior distribution, \({p}_{0}\left(z\right)\), which is the Gaussian distribution in this study.

For the GAN loss functions, we use the non-saturating losses3 as shown in Eq. (2), where \({\mathcal{L}}_{D}^{\mathrm{GAN}}\) and \({\mathcal{L}}_{G}^{\mathrm{GAN}}\) denote the loss functions for the discriminator and generator, respectively.

$$\begin{gathered} {\mathcal{L}}_{D}^{{{\text{GAN}}}} = - {\mathbb{E}}\left[ {\log \left( {D\left( {x_{d} } \right)} \right)} \right] - {\mathbb{E}}\left[ {\log \left( {1 - D\left( {x_{p} } \right)} \right)} \right], \hfill \\ {\mathcal{L}}_{G}^{{{\text{GAN}}}} = - {\mathbb{E}}\left[ {\log \left( {D\left( {x_{p} } \right)} \right)} \right]. \hfill \\ \end{gathered}$$
(2)

The discriminator learns to classify real and fake data with \({\mathcal{L}}_{D}^{\mathrm{GAN}}\), the loss function of discriminator. The first term, \(-{\mathbb{E}}\left[\mathrm{log}\left(D\left({x}_{d}\right)\right)\right]\), represents the expectation of the negative log probability that the discriminator assigns to real data, denoted by \({x}_{d}\), being real. The second term, \(-{\mathbb{E}}\left[\mathrm{log}\left(1-D\left({x}_{p}\right)\right)\right]\), represents the expectation of the negative log probability that the discriminator assigns to data produced by the generator, denoted by \({x}_{p}\), being fake. It means that the discriminator learns to classify the real and fake data. On the other hand, the loss function of generator, \(-{\mathbb{E}}\left[\mathrm{log}\left(D\left({x}_{p}\right)\right)\right]\), represents the negative log probability that the discriminator assigns to the fake data \({x}_{p}\) being real.

Finally, the entire loss functions of the hybrid model are shown in Eq. (3), where \(\gamma\) is the coefficient of the GAN loss.

$$\begin{gathered} {\mathcal{L}}_{E}^{{{\text{Hybrid}}}} = {\mathcal{L}}^{{{\text{VAE}}}} , \hfill \\ {\mathcal{L}}_{D}^{{{\text{Hybrid}}}} = - {\mathbb{E}}\left[ {\log \left( {D\left( {x_{d} } \right)} \right)} \right] - \frac{1}{2}{\mathbb{E}}\left[ {\log \left( {1 - D\left( {x_{p} } \right)} \right)} \right] - \frac{1}{2}{\mathbb{E}}\left[ {\log \left( {1 - D\left( {\tilde{x}} \right)} \right){ }} \right], \hfill \\ {\mathcal{L}}_{G}^{{{\text{Hybrid}}}} = {\mathcal{L}}^{{{\text{VAE}}}} + \gamma \left( { - \frac{1}{2}{\mathbb{E}}\left[ {\log \left( {D\left( {x_{p} } \right)} \right)} \right] - \frac{1}{2}{\mathbb{E}}\left[ {\log \left( {D\left( {\tilde{x}} \right)} \right)} \right]} \right). \hfill \\ \end{gathered}$$
(3)

These loss functions are separately used to train the encoder, discriminator, and generator. Detailed training conditions and hyperparameters are described in the Experimental Section.

Discriminator-driven latent sampling

The standard sampling method of deep generative models, including VAE and GAN, is sampling a random latent code \(z\) from a prior distribution (e.g., the standard normal distribution) and feeding it into the generator network, as shown in Fig. 1d. In GAN-based models, there is another approach to generate new samples, called discriminator-driven latent sampling (DDLS). At the end of training GAN, the adversarial game between the generator and discriminator generally does not converge to the generator’s ground truth (generating extremely realistic data and completely deceiving the discriminator), thus the discriminator still watches for the implausibility of generated data. Based on this fact, previous studies have proposed various DDLS methods such as rejecting unrealistic samples34 and polishing implausible factors of generated samples using a Monte Carlo method30,31,32 via the discriminator evaluation.

We implement a simple DDLS algorithm, as shown in Fig. 1e, and use it to improve the topological plausibility of generated samples. In the algorithm, a latent code is initially sampled from a prior distribution, and it is iteratively updated using a gradient descent method to maximize the evaluation of the trained discriminator, \(D\left(G\left(z\right)\right)\). Since the discriminator is trained to return a value of one for real data and zero for fake data, the process of maximizing the discriminator’s evaluation is expected to evolve the generated spin configuration, \(G\left(z\right)\), to become more realistic (without topological defects). The results of DDLS are presented later in the Results Section.

Dataset

We train the VAE, GAN, and hybrid models on two-dimensional metastable spin structures which have various labyrinth patterns35. The dataset is generated by a simulated annealing process implemented by the Monte Carlo method. We suppose the Heisenberg model with the Hamiltonian \(\mathcal{H}=-J{\sum }_{\langle i,j\rangle }{\overrightarrow{S}}_{i}\cdot {\overrightarrow{S}}_{j}-{\sum }_{\langle i,j\rangle }{\overrightarrow{D}}_{ij}\cdot \left({\overrightarrow{S}}_{i}\times {\overrightarrow{S}}_{j}\right)\) in a square lattice of \(128 \times 128\) grid sites with a periodic boundary condition, where \(J\), \({\overrightarrow{D}}_{ij}\), and \({\overrightarrow{S}}_{i}\) denote the exchange interaction parameter, the Dzyaloshinskii-Moriya interaction vector36, 37, and the Heisenberg spin on the \(i\)-th grid site, respectively. The parameters \(J\) and \(\left|{\overrightarrow{D}}_{ij}\right|\) are fixed at 1.0 and 0.3, respectively. In this system, the spin configurations are determined by the spontaneous symmetry-breaking process, so that we can generate countless different metastable states under the fixed condition. We generate a total of 40,000 spin configurations, which are divided into 30,000 training datasets and 10,000 test datasets.

Metrics

Our goal is to evaluate the diversity and fidelity of each data generation strategy based on the VAE, GAN, and hybrid model with and without the DDLS. Unfortunately, many representative metrics, such as the Inception Score38 or Fréchet Inception distance39, evaluate generative models without discerning between diversity and fidelity. Furthermore, these metrics are properly available only to the models trained on the ImageNet dataset40 because they need a reference model pre-trained on the same dataset to embed the generated samples into the feature space of the reference model. For these reasons, we measure the diversity using the coverage metric26 which counts the mass of real data “covered” by the model distribution implied in a generator network. To evaluate the fidelity of generated spin configurations, we simply measure the energy using the Hamiltonian \(\mathcal{H}\) because the spin configurations in our dataset are the results of the simulated annealing process so that they are energetically stabilized.

Results

Comparison between the VAE, GAN, and hybrid models

The hybrid model shown in Fig. 1a is trained with our dataset and losses discussed in the Strategy Section, and the standalone VAE and GAN are also trained under the same conditions to be compared with the hybrid model. Figure 2a–d show the comparison between the ground truth (a sample of spin configuration in our test dataset) and spin configurations generated from each of the trained models. The spin configuration generated by the trained VAE model exhibits lots of nodal points, as indicated by the red circles. In contrast, the spin configurations generated by the trained GAN and hybrid models show a smaller number of nodal points in comparison with that of the VAE model. These nodal points are implausible structures; they are the topological defects in this magnetic system, thus they do not appear in the ground truth spin configuration. In addition, these nodal points are energetically unstable; in the energy density maps, there are high-energy peaks (bright points) at the positions of the nodal points exist. It means that we can measure the plausibility or fidelity of the generated spin configurations by their energy, and the number of nodal points is strongly related to them. By these facts, one can check that the fidelity of the GAN and hybrid models surpasses that of the VAE model.

Figure 2
figure 2

(a) A sample spin configuration in our test dataset and its energy density map. (b–d) Spin configurations generated by the trained (b) VAE, (c) GAN, and (d) hybrid models, and their energy density maps. The colors and black/white contrast of the spin configurations indicate the in-plane and out-of-plane directions of local spins, respectively. Red circles highlight the positions of nodal points. (e) Coverage and energy metric values of the trained models. Each scatter point indicates the result of independent trials.

Full size image

To quantitatively investigate the coverage and energy metric values, we independently perform the training processes five times and generate 10,000 samples for each trained model as shown in Fig. 2e. Higher coverage values indicate better diversity and lower energy values indicate better plausibility; the upper left part of the graph in Fig. 2e indicates better results. As mentioned above, we confirm that both GAN and hybrid models produce lower energy samples compared with the VAE. This is consistent with the conventional understanding that usual GAN-based generative models have the advantage to generate more realistic samples than VAE-based models. On the other hand, the coverages of the VAE and hybrid models are around 0.92 and 0.90 on average, respectively, whereas the coverage of GAN is only 0.80 on average. Consequently, we confirm that the hybrid model takes advantages of both the high coverage of VAE and the high fidelity of GAN simultaneously. Another advantage of the hybrid model is that it is more stable than the standalone GAN. This can be observed from the fact that the coverage and energy metric values of the five independent trials of hybrid models show less dispersion compared to those from the standalone GANs.

Latent space analysis

To investigate the underlying characteristics of the deep generative models trained with the topological magnetic structure dataset, we analyze the latent space manifolds of the models as shown in Fig. 3. To display the high-dimensional latent space of each model, we arbitrarily select two axes, \({z}_{1}\) and \({z}_{2}\), out of a total \(n\) axes (\(n=128\), where \(n\) is the dimensionality of a latent space) and sample various latent codes by scanning a specific region of the chosen two-dimensional latent space. The other \(n-2\) components of latent codes are fixed as the random numbers sampled from the standard normal distribution which is the prior distribution of our models. It is verified that the choice of axes does not make any significant differences in the discussion of this section. The sampled latent codes are decoded into the spin configurations through the trained decoder or generators of VAE, GAN, and hybrid models for calculating the energy and discriminator logits of them. To plot the calculated values on the chosen two-dimensional latent space, we use heatmap representations as shown in Fig. 3a for the energies and (b) for the discriminator logits on the same latent space region.

Figure 3
figure 3

Latent space visualization. (a–b) Heatmaps for the representations of (a) energy values and (b) discriminator logits along two axes, \({z}_{1}\) and \({z}_{2}\), within a range from − 2 to 2. The brighter(darker) color in (a) and (b) indicates the higher(lower) energy values and the real-like(fake-like) samples in the perspective of the discriminators, respectively, for each trained model (no discriminator in VAE). (c) Spin configurations decoded from the latent codes on the \(k\), \(l\), and \(m\) positions in (a). Red circles are highlighting the changing structures.

Full size image

The most interesting feature in Fig. 3a is that, compared with the blurred energy heatmap of the VAE, the energy heatmaps of the GAN and hybrid models include several narrow lines and flat regions surrounded by the lines. This interesting feature is also shown in the heatmaps for the discriminator logits of the GAN and hybrid models in Fig. 3b. Considering that the spin configurations in our dataset are distinctly separated by topological properties with high energy barriers, the latent spaces partitioned into several flat regions by the narrow lines may imply that the GAN and hybrid models properly learn the topological properties in our dataset. Specifically, the narrow lines are supposed to be indicating the specific regions in the latent spaces which can be decoded into high energy states with emerging implausible topological defects, implying the boundaries between the energetically stabilized but topologically different spin configurations.

Figure 3c directly supports that the narrow lines are closely related to the emergence of implausible topological defects. For each of the VAE, GAN, and hybrid models, three spin configurations are decoded from the latent codes at three different latent positions, \(k\), \(l\), and \(m\) marked in Fig. 3a. Within each latent space, \(k\) and \(m\) represent two separate flat regions and \(l\) is on the boundary line between them. As indicated by the red circles shown in Fig. 3c, the spin configurations from \(k\) and \(m\) exhibit topologically distinct local spin structures, while the spin configuration from \(l\) includes a nodal point.

Consequently, we confirm that the latent spaces formed by the training with our topological data are composed of multiple latent domains (flat regions) and latent domain walls (boundaries between the latent domains), which are strongly related to the topological properties implied in the dataset. In addition, it is also confirmed that the latent domains and latent domain walls are clearly distinguished in the latent spaces of the GAN and hybrid models, whereas the latent space of VAE is blurred overall than the other models.

Data generation using DDLS

As discussed in the previous section, the GAN and hybrid models considered in this study have an advantage in generating plausible data by narrowing down the latent regions which can be decoded into implausible data. However, there is still a possibility that a latent code is sampled from the narrow regions. To generate new samples without implausible defects, we apply the DDLS algorithm shown in Fig. 1e using the generator and discriminator in a trained hybrid model.

Figures 4a and b show the results of the DDLS algorithm. As the DDLS progresses, the initial spin configuration becomes energetically stabilized by removing several nodal points; for example, the nodal points within the local spin structures highlighted by the red box in the initial spin configuration are removed after the first few iterations. After 100 iteration steps, the initial spin configuration evolves into a new spin configuration without any implausible topological defects.

Figure 4
figure 4

Data generation process using the DDLS algorithm. (a) Changes in spin configuration during the iterative process of the DDLS algorithm. The red square in the initial spin configuration highlights a nodal point region. (b) Magnified view of the highlighted region in (a). (c) Grad-CAM of each spin configuration. The red color indicates an important area for the discriminator to predict the spin configuration as fake.

Full size image

To offer an insight into how the DDLS algorithm can eliminate the nodal points in the initial spin configurations, we plot a gradient-based class activation map (Grad-CAM)41 as shown in Fig. 4c to demonstrate the role of the discriminator in the DDLS algorithm. The Grad-CAM is an explanation method for convolutional neural network classifiers including the discriminators in the GAN and hybrid models. It shows the specific regions in the input data that significantly influence the decision of classifiers. Obviously, the Grad-CAM result on the initial spin configuration highlights the position of nodal points, indicating the nodal points are crucial factors for the discriminator to determine the spin configuration as a fake data. As the nodal points gradually disappear during the DDLS progresses, the level of highlighting is reduced. This means that it becomes more challenging for the discriminator to determine the spin configuration as a fake data.

Consequently, it is confirmed that the crucial factor for the discriminator to classify a spin configuration as a real or fake data is the existence of nodal points, which are the implausible topological defects in our target system. Using the discriminator, we can utilize the DDLS algorithm to generate topologically plausible data by removing implausible defects as shown in Fig. 4.

Applications of the hybrid Model

The trained hybrid model is not only capable of generating plausible data but is also applicable for various other purposes. In this section, we demonstrate two application examples. The first example is searching for the optimal solutions for various objectives, including maximizing out-of-plane magnetization \({M}_{z}\), minimizing \({M}_{z}\), and minimizing energy \(\epsilon\) of a spin configuration. Utilizing the well-trained generator in our hybrid model, various optimization algorithms can be implemented within the latent space18. Specifically, we can search for the optimal solutions according to defined objectives by obtaining the corresponding latent codes. We employ a genetic algorithm, a conventional optimization algorithm inspired by the biological evolution processes42. The second example is investigating intermediate states between the optimal spin configurations. It also can be performed in the latent space of the hybrid model by interpolating between the latent codes corresponding to the optimal solutions.

Figure 5a schematically illustrates the locations of optimized latent codes and the interpolation lines, where the I, II, and III represent the latent codes obtained by maximizing \({M}_{z}\), minimizing \({M}_{z}\), and minimizing \(\epsilon\), respectively. The results of optimizing \({M}_{z}\) (either by maximizing or minimizing) are skyrmion lattices, highlighted within the red squares on the left and right sides of Fig. 5b. Minimizing \(\epsilon\) results in well-aligned stripe structures, highlighted within the red squares on the right sides of Fig. 5c, d. The \({M}_{z}\) values of the optimal solutions are 0.211 and − 0.204, respectively, which represent extreme values compared to the \({M}_{z}\) distribution of the training dataset, which has mean of 0.000 with a standard deviation of ± 0.016 (see Fig. 5e). The optimized \(\epsilon\) value is − 0.0442, which is significantly lower than that of the training dataset: \(\epsilon\) has a mean of − 0.0423 with a standard deviation of ± 0.0002 (see Fig. 5f). These optimal solutions, the skyrmion lattices and well-aligned stripe structure, are physically reliable. In a magnetic system, the \({M}_{z}\) can be controlled by applying an out-of-plain external field. Numerous studies reported that the labyrinth structures become skyrmion structures when the external field is applied43, 44. The well-aligned stripe structures are also observed as the ground state of the system in previous studies35, 45.

Figure 5
figure 5

Application of the trained hybrid model. (a) A schematic illustration of interpolation in the latent space. Three dots, I, II, and III, represent the optimized latent codes obtained by maximizing \({M}_{z}\), minimizing \({M}_{z}\), and minimizing \(\epsilon\), respectively. (b–d) Spin configurations obtained by the linear interpolation between (b) I and II, (c) I and III, and (d) II and III. The red squares indicate each optimal spin configuration. (e) The \({M}_{z}\) distribution of test dataset. The \({M}_{z}\) values of the optimal solutions I and II are indicated by arrows. (f) The \(\epsilon\) distribution of test dataset and the \(\epsilon\) value of the optimal solution III.

Full size image

The optimization process using our trained model is completed in a short period of time (In our study, it takes approximately 20 min), whereas it is impossible to achieve the goal in a reasonable time frame with conventional micromagnetic simulations. Notably, the ground state of the system, characterized by a well-aligned stripe structure, remains elusive to conventional micromagnetic simulations due to the existence of numerous metastable states. The computational efficiency of optimization using our hybrid model is attributed to the dimensionality reduction achieved through the trained generative model. While the original system has dimensions of 128 × 128 × 3, the latent space of our model is 128-dimensional, which substantially narrows the target space where we search for optimal solutions. In the realm of optimization, higher dimensions dramatically increase the complexity of the problem and constrain the efficiency of algorithms applied. Our hybrid model effectively reduces this dimensionality, which facilitates the successful application of the genetic algorithm within the dimensionally reduced latent space of the model. We believe this optimization strategy can be applied to a wide range of systems and objectives, such as designing molecules or materials. The approach is also adaptable to other conventional optimization algorithms, including gradient-based methods and Monte Carlo methods.

It is important to highlight that, as we mentioned above, the optimized solutions generated by the hybrid model are absent from the training dataset. At a same time, they are physically reliable, not displaying any node points. This indicates that the hybrid model is capable of generating new, physically reliable samples, extending beyond the training dataset. We confirm that the hybrid model can generate a wide variety of samples (high diversity) with high fidelity.

The central areas in Fig. 5b–d illustrate the results of linear interpolation within the latent space: from the latent code I to II (b), from I to III (c), and from II to III (d). The interpolated structures transition smoothly from one optimal state to another, exhibiting few node points and maintaining physically appropriate configurations under varying out-of-plane magnetization \({M}_{z}\) and energy \(\epsilon\). The reliability of these interpolated structures can be ascribed to the adversarial training, contrasting with the increased number of node points observed in interpolations performed within the latent space of a standalone VAE model. We confirm that our hybrid model possesses advantages, including the capability to generate a diverse of new, physically reliable samples and the potential for application across various domains.

Conclusion

We investigate the performance of a VAE-GAN hybrid model as a generator for the data with topological properties. We generate a dataset composed of various spin configurations which are simulated on a two-dimensional magnetic system and use it to train a simple VAE-GAN hybrid model. The performance of the trained hybrid model is evaluated in the aspects of diversity and fidelity, and it is compared with those of standalone VAE and GAN models. It is confirmed that the hybrid model exhibits high diversity and high fidelity simultaneously by incorporating the strengths of both standalone VAE and GAN models. Through the latent space visualization, we find that the latent space built by each model is partitioned into the numerous latent domains by latent domain walls which are closely related to the topological properties implied in our dataset. We show that, even if a topologically implausible structure appears on a generated sample, the DDLS algorithm can improve the plausibility of the sample by removing the appearing topological defects. Finally, we demonstrate two application examples of the trained hybrid model, which are searching for the optimal solutions for various objectives and investigating intermediate states between them. We believe that the hybrid model has great potential as a generator for topological data, offering numerous versatile applications.

Experimental section

Neural network structures

For the neural networks, the pre-activation residual building blocks (ResBlocks)46, 47 with batch-normalization and Leaky-ReLU activation function are used, as shown in Fig. 6a. Figure 6b–d shows the generator, discriminator, and encoder architectures. Periodic padding is applied before all convolutions because of the periodic boundary condition of the dataset. The spectral normalization48 is applied for the discriminator layers, thus the batch normalization layers were removed from the discriminator network. To force the generator output pixels to be the Heisenberg spins (normalized pixels), the pixels were normalized at the end of the generator. The Up sampling of \(2\times 2\) is applied for upsizing in the generator, whereas the downsizing in the discriminator and encoder is implemented by a convolutional layer with a stride size of 2 and kernel size of \(4\times 4\).

Figure 6
figure 6

Neural networks used in this study. (a) A schematic illustration of the pre-activation residual block. For the discriminator, the batch normalization layers are removed. (b–d) The network architecture of the (b) generator, (c) discriminator, and (d) encoder. The BN and LReLU denote batch normalization and Leaky-ReLU activation, respectively.

Full size image

Hyperparameters

The \(\beta\), coefficient of the regularization loss term in the VAE loss, is chosen by \(0.001\). The \(\gamma\), coefficient of the GAN loss component in the generator of the hybrid model, is chosen by 0.001. For training, we use Adam optimizers49 with the learning rate, \({\beta }_{1}\), and \({\beta }_{2}\) of 0.0002, 0.0, and 0.9, respectively. The training dataset contains 30,000 samples. The batch size is 50 and the number of total training steps is 6000 (100 epochs).