Introduction

The basic and main component in a hydrostatic drive system is the positive displacement pump. It is the component in the system where the greatest pressure increase occurs1,2,3,4,5. The second important component in the system is the rotary hydraulic motor. It is the displacement machine and the executive in the drive system. Its role is to convert hydraulic power into mechanical power. Today, there are many design variations of different types of hydraulic displacement machines on the world market—from piston machines to gear machines. They are used in the drive systems of various machines and even in laboratory test benches6. Work on the further development of the design of these machines and the improvement of their main operating parameters are still being carried out6,7,8,9,10,11. There are also attempts to describe the influence of various factors on the phenomena occurring in these machines12,13,14,15. Tests are also being conducted to verify the operation of these machines under various environmental conditions, such as thermal shocks16,17,18.

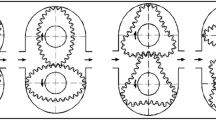
Over the past 30 years, intensive design and development work has been carried out on innovative designs of gear displacement machines. These are machines whose working mechanism consists of non-circular toothed elements. This mechanism is commonly referred to as a satellite mechanism. Examples of satellite mechanisms as used in positive displacement machines are shown in Fig. 1.

Figure 1
figure 1

Examples of satellite mechanisms: type 4 × 5 (left) and type 4 × 6 (right)19,20,21.

Full size image

The inner element of the satellite mechanism, mounted on a shaft, is called the rotor (or planet). The outer element is the curvature. The circular gear elements are the satellites. The photos above show only two types of mechanisms, namely the 4 × 5 and 4 × 6 types. The numbers in the type designation of the mechanism indicate the number of humps on the rotor and the number of humps on the curvature.

The following types of satellite mechanisms are known in the literature:

The methodology for designing these mechanisms can also be found in the above indicated literature, especially in Ref.19. Due to the fact that this literature is directly accessible (online), this methodology will not be summarized here. As already shown above, the satellite mechanism is a specific gear mechanism. The literature on gears and spur gears, regarding their design methods, kinematics and characteristics is also very extensive and widely available, for example in Refs.54,55,56,57,58. Literature on gearbox elements failures and their diagnosis are also available, for example in Refs.59,60,61. However, it is no less concerned with gears mounted on axles or shafts. That is, as in typical gears. The methodology for calculation the stresses in the teeth is also known for these gears and described in literature, for example in Refs.57,62. As can be seen in Fig. 1, the satellites in a satellite mechanism, are not fixed to an axle/shaft. The methodology for designing such mechanisms is already known19,39. On the other hand, there is a lack of sound knowledge on the method for calculation of the strength in the teeth of such mechanisms. Yes, methods for calculation the strength of teeth are known in the literature, but for gears with non-circular gears mounted on shafts. In Ref.63, for example, it was found that non-circular gear teeth are as strong in bending as circular gear teeth and for design purposes, classical spur gear theory can be used to predict static bending stresses. The analysis was carried out using a finite-element stress analysis. In Ref.64 an algorithm for mesh generation or the discretisation of gear tooth profiles of non-circular gear elements for static stress evaluation with FEM (Finite Element Method) was described. In Ref.65 the deformation of the teeth of a non-circular elliptical gear was analysed. It was found that the actual load on the teeth is variable and the deformation of cooperating pairs of teeth is also variable. This results from the smooth change in the gear ratio, which affects the change in the force acting on the individual teeth. Also in Refs.66,67 the mathematical formulae for analysis of the forces in planetary mechanism with eliptical gears were described. The planetary gear mechanism was also considered in Ref.67. In this publication the problem arising from the treatment of the pitch point force is described. In addition, the forces occurring in the gear and the efficiency of the gear are described, which is the main focus of the article.

The currently manufactured satellite mechanisms (especially 4 × 6) were designed to be made by chiselling38,49,68,69. In these mechanisms, the shape of the rotor consists of circular arcs with different radii and tangents to each other39. In this way, mechanisms with a tooth module of 1.5 mm were produced. Over time, manufacturers of satellite motors copied the shape of mechanisms made in this way and scaled them to other sizes, especially smaller sizes, with a smaller module of teeth. This allowed manufacturers to start production of other sizes of satellite motors70,71, with smaller working mechanisms using the wire electrical discharge machining (the so-called WEDM method).

Object of research, research problem and the goal of analysis

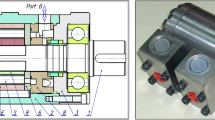
Unusual wear of the rotor’s teeth was noticed during laboratory testing of a prototype of hydraulic motor (Fig. 2) equipped with a 4 × 6 satellite mechanism. The specific wear occurs at the convexity (at the hump) of the rotor. However, no such wear was observed on the curvature teeth (Fig. 3).

Figure 2
figure 2

Prototype of the satellite motor: R rotor, S satellite, C curvatute, 1—shaft, 2,3 and 4—body, 5 and 6—manifolds, 7 and 8—commutation plate.

Full size image
Figure 3
figure 3

Specific wear of the teeth on the rotor hump (left)19,30,37. No apparent wear on the curvature teeth (right). Unknown operating time of the mechanism.

Full size image

Therefore, an attempt must be made to explain what influences such tooth wear. It is probably caused by exceeding the permissible pressures in the contact of the teeth of the interacting elements of the working mechanism. Therefore, it is advisable to analyze the loads acting on the teeth, which are influenced by the pressure difference acting on the satellite (resulting from the motor load and mechanical and pressure losses in the motor) and rotational speed of the rotor (motor shaft), resulting in inertial forces acting on the satellite. The number of contacts between the teeth of the rotor and the satellite and the number of contacts between the teeth of the curvature and the satellite also depends on the speed of rotation of the motor shaft. It is also advisable calculation the stresses in the contact of the teeth of the interacting elements and calculation of the permissible stresses in the contact of the teeth.

In order to calculate the loads acting on the teeth of the mechanism components, it is necessary to determine:

  1. (1)

    the basic geometrical relationships in the satellite mechanism;

  2. (2)

    the number of contacts of the satellite’s teeth with those of the rotor and the curvature during the rotation of the rotor;

  3. (3)

    the acceleration of the satellite as a function of the angle of rotation of the shaft (of the rotor);

  4. (4)

    pressures in the working chambers adjacent to the satellite.

Thus, as can be seen, the above-mentioned publication examples relate to various gears, the common feature of which is that the gears are mounted on an axle/shaft. Therefore, this article proposes an approximate method for calculating the stresses in the tooth contact of the satellite mechanism components. This makes it possible to estimate the value of these stresses and draw conclusions about the permissible motor load and speed. Currently, satellite engine manufacturers specify different motor speed ranges depending on the size of the engine. For example, in Refs.70,71 a speed range of 400 rpm to 2200 rpm is given. On the other hand, the nominal operating pressure for most satellite motors is given as 22 MPa and for some sizes as high as 25 MPa70,71. Therefore, the stress analyzes in the tooth contact are performed for a pressure difference in the working chambers of the motor of 25 MPa. For comparison purposes, stress values are also given for a small pressure difference, i.e. 5 MPa.

Basic geometric relationships in the satellite mechanism

The methodology for designing satellite mechanisms is described in detail in Refs.19,39,47 and in Refs.49,50. These publications show that for any function fR(x) describing the rotor pitch line, it is possible to determine the coordinates of the curvature pitch line. The method for determining the curvature pitch line was described in detail in the publication19. The shape of the curvature pitch line and its mathematical notation depend on the number nE of curvature humps. Regardless of the assumed number of curvature humps, the point E where the satellite touches the curvature lies on the line k passing through the rotor’s center of rotation and through the point F where the satellite touches the rotor19 (Fig. 4).

Figure 4
figure 4

Satellite mechanism, its contact points and basic angles.

Full size image

The coordinates of the point E are following:

$${\mathrm{x}}_{\mathrm{E}}={\mathrm{x}}_{\mathrm{F}}\cdot \left(\frac{{\mathrm{x}}_{\mathrm{F}}\cdot {\mathrm{x}}_{\mathrm{S}}+{\mathrm{y}}_{\mathrm{F}}\cdot {\mathrm{y}}_{\mathrm{S}}}{{{\mathrm{x}}_{\mathrm{F}}}^{2}+{{\mathrm{y}}_{\mathrm{F}}}^{2}}+\sqrt{{\left(\frac{{\mathrm{y}}_{\mathrm{F}}\cdot {\mathrm{y}}_{\mathrm{S}}+{\mathrm{x}}_{\mathrm{F}}\cdot {\mathrm{x}}_{\mathrm{S}}}{{{\mathrm{x}}_{\mathrm{F}}}^{2}+{{\mathrm{y}}_{\mathrm{F}}}^{2}}\right)}^{2}-\frac{\left({{\mathrm{x}}_{\mathrm{S}}}^{2}+{{\mathrm{x}}_{\mathrm{F}}}^{2}-{{\mathrm{r}}_{\mathrm{S}}}^{2}\right)}{{{\mathrm{x}}_{\mathrm{F}}}^{2}+{{\mathrm{y}}_{\mathrm{F}}}^{2}}}\right),$$
(1)
$${\mathrm{y}}_{\mathrm{E}}=\frac{{\mathrm{y}}_{\mathrm{F}}}{{\mathrm{x}}_{\mathrm{F}}}\cdot {\mathrm{x}}_{\mathrm{E}}.$$
(2)

Other basic relationships in the satellite mechanism are following:

  1. (a)

    the central angle βR covering one half of the cycle of the rotor pitch curve (corresponding to the length LRc) is19:

    $${\upbeta }_{\mathrm{R}}=\frac{\uppi }{{\mathrm{n}}_{\mathrm{R}}},$$
    (3)

    where nR is the number of rotor humps;

  2. (b)

    the central angle βE covering one half of the cycle of the curvature pitch curve (corresponding to the length LEc) is19:

    $${\upbeta }_{\mathrm{E}}=\frac{\uppi }{{\mathrm{n}}_{\mathrm{E}}},$$
    (4)

    where nE is the number of curvature humps;

  3. (c)

    the angular position αS of the satellite centre S corresponding to the angle αR of the rotor rotation19:

    $${\mathrm{\alpha }}_{\mathrm{S}}=\frac{{\mathrm{n}}_{\mathrm{R}}}{{\mathrm{n}}_{\mathrm{E}}+{\mathrm{n}}_{\mathrm{R}}}\cdot {\mathrm{\alpha }}_{\mathrm{R}}.$$
    (5)

During the rotation of the rotor by the angle αR, the satellite rolls around the rotor along the length LF of the pitch line of the rotor (Fig. 5). So, the satellite rotates through the angle:

$${\updelta }_{\mathrm{S}}=\frac{{\mathrm{L}}_{\mathrm{F}}}{{\mathrm{r}}_{\mathrm{S}}},$$
(6)

where

$${\mathrm{L}}_{\mathrm{F}}={\int }_{{\mathrm{x}}_{\mathrm{F}1}}^{{\mathrm{x}}_{\mathrm{F}}}\sqrt{1+{\left(\frac{{\mathrm{df}}_{\mathrm{R}}(\mathrm{x})}{\mathrm{dx}}\right)}^{2}}\mathrm{dx},$$
(7)
$${\mathrm{r}}_{\mathrm{S}}=0.5\cdot \mathrm{m}\cdot {z}_{S},$$
(8)

and zs is the number of teeth on the satellite.

Figure 5
figure 5

Lengths LE and LF and angle δS of satellite rotation.

Full size image

The above relationship shows that in order to calculate the length LF one must know the coordinates (xF1, yF1) and (xF, yF) of the points F1 and F. The coordinates of the point F1 are obvious and are: xF1 = 0 and yF1 = fR(0) (Fig. 5). However, to determine the coordinates (xF, yF) of the point F, it is necessary to know the coordinates (xS, yS) of the centre S of the satellite. The coordinates of the points F and S can be determined using the following system of equations:

$${\mathrm{y}}_{\mathrm{F}}={\mathrm{f}}_{\mathrm{R}}\left({\mathrm{x}}_{\mathrm{F}}\right),$$
(9)
$${\mathrm{y}}_{\mathrm{S}}=\mathrm{cot}{\mathrm{\alpha }}_{\mathrm{S}}\cdot {\mathrm{x}}_{\mathrm{S}},$$
(10)
$${\left({\mathrm{x}}_{\mathrm{F}}-{\mathrm{x}}_{\mathrm{S}}\right)}^{2}+{\left({\mathrm{y}}_{\mathrm{F}}-{\mathrm{y}}_{\mathrm{S}}\right)}^{2}={{\mathrm{r}}_{\mathrm{S}}}^{2},$$
(11)
$$\frac{{\mathrm{x}}_{\mathrm{S}}-{\mathrm{x}}_{\mathrm{F}}}{{\mathrm{y}}_{\mathrm{S}}-{\mathrm{y}}_{\mathrm{F }}}=\frac{\mathrm{d}}{\mathrm{dx}}{\mathrm{f}}_{\mathrm{R}}\left({\mathrm{x}}_{\mathrm{F}}\right).$$
(12)

The coordinates of the point F and centre S of the satellite are thus as follows:

$${\mathrm{x}}_{\mathrm{S}}=\sqrt{{{\mathrm{x}}_{\mathrm{F}}}^{2}+{\left({\mathrm{y}}_{\mathrm{F}}-{\mathrm{y}}_{\mathrm{S}}\right)}^{2}-{{\mathrm{r}}_{\mathrm{S}}}^{2}},$$
(13)
$${\mathrm{y}}_{\mathrm{S}}=\mathrm{cot}{\mathrm{\alpha }}_{\mathrm{S}}\cdot {\mathrm{x}}_{\mathrm{S}},$$
(14)
$${\mathrm{x}}_{\mathrm{F}}={\mathrm{f}}_{\mathrm{R}}^{-1}\left({\mathrm{y}}_{\mathrm{F}}\right),$$
(15)
$${\mathrm{y}}_{\mathrm{F}}={\mathrm{y}}_{\mathrm{S}}-\frac{{\mathrm{r}}_{\mathrm{S}}}{\sqrt{1+{\left(\frac{\mathrm{d}}{\mathrm{dx}}{\mathrm{f}}_{\mathrm{R}}\left({\mathrm{x}}_{\mathrm{F}}\right)\right)}^{2}}}\cdot \frac{\mathrm{d}}{\mathrm{dx}}{\mathrm{f}}_{\mathrm{R}}\left({\mathrm{x}}_{\mathrm{F}}\right).$$
(16)

The length LF corresponds to the length LE of the curvature pitch line (Fig. 5).

The number of contacts of the teeth of the satellite with the teeth of the rotor and the curvature during the rotation of the rotor

During the rotation of the rotor:

  1. (a)

    each tooth of the rotor contacts the tooth of the next satellite (point F1 in Fig. 6) at each angle:

    $${\mathrm{\alpha }}_{\mathrm{RTS}}=2\uppi \cdot \frac{1}{{\mathrm{n}}_{\mathrm{E}}} \left[{\text{rad}}\right]={360}^{^\circ }\cdot \frac{1}{{\mathrm{n}}_{\mathrm{E}}} \left[{\text{deg}}\right],$$
    (17)
  2. (b)

    each tooth of the curvature contacts the tooth of the next satellite (point E1 in Fig. 6) at each angle:

    $${\mathrm{\alpha }}_{\mathrm{ETS}}=2\uppi \cdot \frac{1}{{\mathrm{n}}_{\mathrm{R}}} \left[{\text{rad}}\right]={360}^{^\circ }\cdot \frac{1}{{\mathrm{n}}_{\mathrm{R}}} \left[{\text{deg}}\right].$$
    (18)
Figure 6
figure 6

The contact point F1 of the tooth of the rotor with the tooth of the next satellite after the rotation of the rotor with the angle αRTS and contact point E1 of the tooth of the curvature with the tooth of the next satellite after rotation of the rotor with the angle αETS.

Full size image

Thus, during one full revolution of the rotor, the number of contacts of each tooth of the rotor with the tooth of the satellites is:

$${\mathrm{i}}_{\mathrm{RTS}}=2\uppi \cdot \frac{1}{{\mathrm{\alpha }}_{\mathrm{RTS}}}={\mathrm{n}}_{\mathrm{E}},$$
(19)

while the number of contacts of each tooth of the curvature with the tooth of the satellites is:

$${\mathrm{i}}_{\mathrm{ETS}}=2\uppi \cdot \frac{1}{{\mathrm{\alpha }}_{\mathrm{ETS}}}={\mathrm{n}}_{\mathrm{R}}.$$
(20)

From the above formulas, it can be concluded that the following relationship exists between iRTS and iETS:

$${\mathrm{i}}_{\mathrm{RTS}}=\frac{{\mathrm{n}}_{\mathrm{E}}}{{\mathrm{n}}_{\mathrm{R}}}\cdot {\mathrm{i}}_{\mathrm{ETS}}.$$
(21)

After determining the coordinates (xE, yE) of points E on the curvature corresponding to the elementary angle δαR of the rotor rotation, the length LE can be calculated as the sum of the elementary sections of the curvature pitch line. The method of determining the length LE is described in detail in the publication1. Using the lengths LF and LE the corresponding number of teeth can be calculated.

If the rotor rotates by the angle αR, then:

  1. (a)

    the number zRF of rotor teeth that were in contact with satellite teeth (the number is zSF) is:

    $${\mathrm{z}}_{\mathrm{RF}}={\mathrm{z}}_{\mathrm{SF}}=\frac{{\mathrm{L}}_{\mathrm{F}}}{\uppi \cdot \mathrm{m}},$$
    (22)
  2. (b)

    the number zCE of curvature teeth that were in contact with satellite teeth (the number is zSE) is:

    $${\mathrm{z}}_{\mathrm{CE}}={\mathrm{z}}_{\mathrm{SE}}=\frac{{\mathrm{L}}_{\mathrm{E}}}{\uppi \cdot \mathrm{m}}.$$
    (23)

If αR = 360° then LF is the length of the pitch line of the rotor, i.e.:

$${\mathrm{L}}_{\mathrm{F}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{^\circ }\right)}=\uppi \cdot \mathrm{m}\cdot {\mathrm{z}}_{\mathrm{R}},$$
(24)

where zR is the number of teeth of the rotor. Then from Eqs. (6) and (8) the angle of satellite rotation is:

$${\updelta }_{\mathrm{S}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{^\circ }\right)}=2\cdot\uppi \cdot {\mathrm{i}}_{\mathrm{SR}} \left[{\text{rad}}\right]=360\cdot {\mathrm{i}}_{\mathrm{SR}} \left[{\text{deg}}\right],$$
(25)

where

$${\mathrm{i}}_{\mathrm{SR}}=\frac{{\mathrm{z}}_{\mathrm{R}}}{{\mathrm{z}}_{\mathrm{S}}},$$
(26)

is the number of revolutions of the satellite around its own axis and at the same time the number of contacts of each tooth of the satellite with the teeth of the rotor.

Equation (5) shows that the angular position of the satellite at one full revolution of the rotor is as follows:

$${\mathrm{\alpha }}_{\mathrm{S}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{^\circ }\right)}=2\uppi \cdot \frac{{\mathrm{n}}_{\mathrm{R}}}{{\mathrm{n}}_{\mathrm{E}}+{\mathrm{n}}_{\mathrm{R}}} \left[{\text{rad}}\right]=360\cdot \frac{{\mathrm{n}}_{\mathrm{R}}}{{\mathrm{n}}_{\mathrm{E}}+{\mathrm{n}}_{\mathrm{R}}} \left[{\text{deg}}\right].$$
(27)

For this position of the satellite, there are points E and F. The coordinates of these points can be calculated using the formulas (1), (2) and (13) ÷ (16). Thus, if αR = 360°, then the length of the pitch line of curvature is:

$${\mathrm{L}}_{\mathrm{E}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{^\circ }\right)}=\uppi \cdot \mathrm{m}\cdot {\mathrm{z}}_{\mathrm{E}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{^\circ }\right)},$$
(28)

where zE is the number of teeth of the curvature, that were in contact with the teeth of the satellite during its roll along the curvature, i.e. zE(αR = 360°) = zS(αR = 360°). Thus, the number of revolutions of the satellite along the pitch line of the curvature is:

$${\mathrm{i}}_{\mathrm{SE}}=\frac{{\mathrm{z}}_{\mathrm{E}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{^\circ }\right)}}{{\mathrm{z}}_{\mathrm{S}}} ,$$
(29)

and at the same time the number of contacts of each tooth of the satellite with the teeth of the curvature.

The total number of contacts of the teeth of the satellite with the teeth of the rotor and the curvature during one revolution of the rotor is:

$${\mathrm{i}}_{\mathrm{S}}={\mathrm{i}}_{\mathrm{SR}}+{\mathrm{i}}_{\mathrm{SE}}=\frac{{\mathrm{z}}_{\mathrm{R}}+{\mathrm{z}}_{\mathrm{E}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{^\circ }\right)}}{{\mathrm{z}}_{\mathrm{S}}}.$$
(30)

If the satellite rolls along the entire length of the curvature pitch line, i.e. αS = 360°, then the rotor makes the following number of revolutions:

$${\mathrm{i}}_{\mathrm{RE}}=360\cdot \frac{1}{{\mathrm{\alpha }}_{\mathrm{S}\left({\mathrm{\alpha }}_{\mathrm{R}}={360}^{\mathrm{o}}\right)}}=\frac{{\mathrm{n}}_{\mathrm{E}}}{{\mathrm{n}}_{\mathrm{R}}}+1.$$
(31)

Loads on the teeth of the interacting elements of the satellite mechanism

In working hydraulic motor, the satellite mechanism is loaded by active and passive forces. The active forces result directly from the motor load with torque M. The effect of the motor load (torque M) is the pressure difference ∆pi in the working chambers of the motor. This pressure difference generates forces that load the interacting teeth of the elements of the working mechanism. The passive forces are the effects of the rotational speed of the motor shaft. Thus, they are the inertial forces of the satellites. These forces also have a direct influence on the load of the teeth. To determine these forces, it is necessary to calculate the total acceleration of the satellite as a function of the angle of rotation of the rotor (the shaft).

Accelerations of the satellite

In the satellite mechanism, the satellite moves in a flat motion. So there is a linear and an angular acceleration of the satellite. The angle γS is necessary to determine the angular acceleration of the satellite (Fig. 7). This angle is different for a mechanism with a rotating rotor than for a mechanism with a rotating curvature. Therefore, this angle is referred to as γS* for a mechanism with a rotating rotor. The points S and F also become the points S* and F*.

Figure 7
figure 7

Transform the points E, F, S and the angle γS in a mechanism with a rotating curvature into the points E*, F*, S* and the angle γS* in a mechanism with a rotating rotor.

Full size image

The values of the angle γS* can be calculated from the relation:

$${\upgamma }_{\mathrm{S}}^{*}={\updelta }_{\mathrm{S}}-\mathrm{atan}\left(\frac{{\mathrm{x}}_{\mathrm{S}}^{*}-{\mathrm{x}}_{\mathrm{F}}^{*}}{{\mathrm{y}}_{\mathrm{S}}^{*}-{\mathrm{y}}_{\mathrm{F}}^{*}}\right),$$
(32)

where xS*, yS*, xF*, xF* are the coordinates of the points S* and F*.

The linear acceleration of the satellite is:

$${\mathrm{a}}_{\mathrm{S}}=\frac{{\mathrm{d}}^{2}{\mathrm{L}}_{\mathrm{S}}^{*}}{{\mathrm{dt}}^{2}},$$
(33)

where LS* is the distance between the centre S* of the satellite and the axis of rotation of the rotor, i.e.:

$${\mathrm{L}}_{\mathrm{S}}^{*}=\sqrt{{\left({\mathrm{x}}_{\mathrm{S}}^{*}\right)}^{2}+{\left({\mathrm{y}}_{\mathrm{S}}^{*}\right)}^{2}} ,$$
(34)

and the angular acceleration of the satellite is:

$${\upvarepsilon }_{\mathrm{S}}=\frac{{\mathrm{d}}^{2}{\upgamma }_{\mathrm{S}}^{*}}{{\mathrm{dt}}^{2}}.$$
(35)

If the angular velocity ωR of the motor shaft (and therefore of the rotor) is constant (ωR = const.), then:

$${\mathrm{a}}_{\mathrm{S}}={\upomega }_{\mathrm{R}}\cdot \frac{{\mathrm{d}}^{2}{\mathrm{L}}_{\mathrm{S}}^{*}}{\mathrm{d}{\mathrm{\alpha }}_{\mathrm{R}}^{2}} ,$$
(36)
$${\upvarepsilon }_{\mathrm{S}}={\upomega }_{\mathrm{R}}\cdot \frac{{\mathrm{d}}^{2}{\upgamma }_{\mathrm{S}}}{\mathrm{d}{\mathrm{\alpha }}_{\mathrm{R}}^{2}}.$$
(37)

The centrifugal force acting on the satellite

The centrifugal force FcS acts on the satellite (Fig. 8). If the angular velocity ωR of the motor shaft (rotor) is constant (ωR = const.), then:

Figure 8
figure 8

Forces acting on the satellite due to its plane motion.

Full size image
$${\mathrm{F}}_{\mathrm{cS}}={\mathrm{m}}_{\mathrm{S}}\cdot {\upomega }_{\mathrm{R}}^{2}\cdot {\left(\frac{\mathrm{d}{\mathrm{\alpha }}_{\mathrm{S}}}{\mathrm{d}{\mathrm{\alpha }}_{\mathrm{R}}}\right)}^{2}\cdot {\mathrm{L}}_{\mathrm{S}}^{*}.$$
(38)

The effect of this force are the following forces in the contact points E* and F* (Fig. 8):

$${\mathrm{F}}_{\mathrm{cF}}={\mathrm{F}}_{\mathrm{cS}}\cdot \frac{{\mathrm{r}}_{\mathrm{S}}}{\sqrt{{\left({\mathrm{x}}_{\mathrm{E}}^{*}-{\mathrm{x}}_{\mathrm{F}}^{*}\right)}^{2}+{\left({\mathrm{y}}_{\mathrm{E}}^{*}-{\mathrm{y}}_{\mathrm{F}}^{*}\right)}^{2}}}\cdot \frac{\mathrm{sin}{\upkappa }_{3}}{\mathrm{sin}{\upkappa }_{1}} ,$$
(39)
$${\mathrm{F}}_{\mathrm{cE}1}={\mathrm{F}}_{\mathrm{cS}}\cdot \mathrm{sin}{\upkappa }_{3}+{\mathrm{F}}_{\mathrm{cF}}\cdot \mathrm{sin}\left({\upkappa }_{1}+{\upkappa }_{2}\right),$$
(40)
$${\mathrm{F}}_{\mathrm{cE}2}={\mathrm{F}}_{\mathrm{cS}}\cdot \mathrm{cos}{\upkappa }_{3}-{\mathrm{F}}_{\mathrm{cF}}\cdot \mathrm{cos}\left({\upkappa }_{1}+{\upkappa }_{2}\right),$$
(41)

where

$${\upkappa }_{1}=\mathrm{arctan}\left(\frac{{\mathrm{x}}_{\mathrm{S}}^{*}-{\mathrm{x}}_{\mathrm{F}}^{*}}{{\mathrm{y}}_{\mathrm{S}}^{*}-{\mathrm{y}}_{\mathrm{F}}^{*}}\right)-{\mathrm{\alpha }}_{\mathrm{E}},$$
(42)
$${\upkappa }_{2}=\mathrm{arctan}\left(\frac{{\mathrm{x}}_{\mathrm{S}}^{*}-{\mathrm{x}}_{\mathrm{E}}^{*}}{{\mathrm{y}}_{\mathrm{E}}^{*}-{\mathrm{y}}_{\mathrm{S}}^{*}}\right)+{\mathrm{\alpha }}_{\mathrm{E}},$$
(43)
$${\upkappa }_{3}=\mathrm{arctan}\left(\frac{{\mathrm{x}}_{\mathrm{S}}^{*}-{\mathrm{x}}_{\mathrm{E}}^{*}}{{\mathrm{y}}_{\mathrm{E}}^{*}-{\mathrm{y}}_{\mathrm{S}}^{*}}\right)+{\mathrm{\alpha }}_{\mathrm{S}}.$$
(44)

However, the coordinates of the points S*, F* and E* can be calculated from the following relations (Fig. 7):

$${\mathrm{x}}_{\mathrm{S}}^{*}=-\sqrt{{\mathrm{x}}_{\mathrm{S}}^{2}+{\mathrm{y}}_{\mathrm{S}}^{2}}\cdot \mathrm{sin}\left(\mathrm{arcsin}\left(\frac{{\mathrm{x}}_{\mathrm{S}}}{\sqrt{{\mathrm{x}}_{\mathrm{S}}^{2}+{\mathrm{y}}_{\mathrm{S}}^{2}}}\right)-{\mathrm{\alpha }}_{\mathrm{R}}\right),$$
(45)
$${\mathrm{y}}_{\mathrm{S}}^{*}=\sqrt{{\mathrm{x}}_{\mathrm{S}}^{2}+{\mathrm{y}}_{\mathrm{S}}^{2}}\cdot \mathrm{cos}\left(\mathrm{arcsin}\left(\frac{{\mathrm{x}}_{\mathrm{S}}}{\sqrt{{\mathrm{x}}_{\mathrm{S}}^{2}+{\mathrm{y}}_{\mathrm{S}}^{2}}}\right)-{\mathrm{\alpha }}_{\mathrm{R}}\right),$$
(46)
$${\mathrm{x}}_{\mathrm{F}}^{*}=-\sqrt{{\mathrm{x}}_{\mathrm{F}}^{2}+{\mathrm{y}}_{\mathrm{F}}^{2}}\cdot \mathrm{sin}\left(\mathrm{arcsin}\left(\frac{{\mathrm{x}}_{\mathrm{F}}}{\sqrt{{\mathrm{x}}_{\mathrm{F}}^{2}+{\mathrm{y}}_{\mathrm{F}}^{2}}}\right)-{\mathrm{\alpha }}_{\mathrm{R}}\right),$$
(47)
$${\mathrm{y}}_{\mathrm{F}}^{*}=\sqrt{{\mathrm{x}}_{\mathrm{F}}^{2}+{\mathrm{y}}_{\mathrm{F}}^{2}}\cdot \mathrm{cos}\left(\mathrm{arcsin}\left(\frac{{\mathrm{x}}_{\mathrm{F}}}{\sqrt{{\mathrm{x}}_{\mathrm{F}}^{2}+{\mathrm{y}}_{\mathrm{F}}^{2}}}\right)-{\mathrm{\alpha }}_{\mathrm{R}}\right),$$
(48)
$${\mathrm{x}}_{\mathrm{E}}^{*}={\mathrm{x}}_{\mathrm{F}}^{*}\cdot \left(\frac{{\mathrm{x}}_{\mathrm{F}}^{*}\cdot {\mathrm{x}}_{\mathrm{S}}^{*}+{\mathrm{y}}_{\mathrm{F}}^{*}\cdot {\mathrm{y}}_{\mathrm{S}}^{*}}{{\mathrm{x}}_{\mathrm{F}}^{2}+{\mathrm{y}}_{\mathrm{F}}^{2}}+\sqrt{{\left(\frac{{\mathrm{x}}_{\mathrm{F}}^{*}\cdot {\mathrm{x}}_{\mathrm{S}}^{*}+{\mathrm{y}}_{\mathrm{F}}^{*}\cdot {\mathrm{y}}_{\mathrm{S}}^{*}}{{\mathrm{x}}_{\mathrm{F}}^{2}+{\mathrm{y}}_{\mathrm{F}}^{2}}\right)}^{2}-\frac{{\mathrm{x}}_{\mathrm{S}}^{*2}+{\mathrm{y}}_{\mathrm{S}}^{*2}-{\mathrm{r}}_{\mathrm{S}}^{2}}{{\mathrm{x}}_{\mathrm{F}}^{2}+{\mathrm{y}}_{\mathrm{F}}^{2}}}\right),$$
(49)
$${\mathrm{y}}_{\mathrm{E}}^{*}=\frac{{\mathrm{y}}_{\mathrm{F}}^{*}}{{\mathrm{x}}_{\mathrm{F}}^{*}}\cdot {\mathrm{x}}_{\mathrm{E}}^{*}.$$
(50)

Forces resulting from the angular and linear accelerations of the satellite

The effect of the angular acceleration εS and the linear acceleration αS of the satellite is the force FaS and the moment of force MεS, i.e.:

$${\mathrm{F}}_{\mathrm{aS}}={\mathrm{m}}_{\mathrm{S}}\cdot {\mathrm{a}}_{\mathrm{S}},$$
(51)
$${\mathrm{M}}_{\mathrm{\varepsilon S}}=\frac{1}{2}\cdot {\mathrm{m}}_{\mathrm{S}}\cdot {\mathrm{r}}_{\mathrm{S}}^{2}\cdot {\upvarepsilon }_{\mathrm{S}},$$
(52)

where mS is the mass of the satellite. The moment MεS can be replaced by the couple of forces FεS (Fig. 8):

$${\mathrm{F}}_{\mathrm{\varepsilon S}}=\left({\mathrm{F}}_{\mathrm{\varepsilon SE}}={\mathrm{F}}_{\mathrm{\varepsilon SF}}\right)=\frac{1}{4}\cdot {\mathrm{m}}_{\mathrm{S}}\cdot {\mathrm{r}}_{\mathrm{S}}\cdot {\upvarepsilon }_{\mathrm{S}}.$$
(53)

The effect of the force FεS are the following forces in the contact points E* and F*:

$${\mathrm{F}}_{\mathrm{aF}}=\frac{{\mathrm{F}}_{\mathrm{aSx}}\cdot \left({\mathrm{y}}_{\mathrm{E}}^{*}-{\mathrm{y}}_{\mathrm{S}}^{*}\right)+{\mathrm{F}}_{\mathrm{aSy}}\cdot \left({\mathrm{x}}_{\mathrm{S}}^{*}-{\mathrm{x}}_{\mathrm{E}}^{*}\right)}{\sqrt{{\left({\mathrm{x}}_{\mathrm{E}}^{*}-{\mathrm{x}}_{\mathrm{F}}^{*}\right)}^{2}+{\left({\mathrm{y}}_{\mathrm{E}}^{*}-{\mathrm{y}}_{\mathrm{F}}^{*}\right)}^{2}}}\cdot \frac{1}{\mathrm{cos}{\upkappa }_{1}},$$
(54)
$${\mathrm{F}}_{\mathrm{aE}1}={\mathrm{F}}_{\mathrm{aF}}\cdot \left(\mathrm{sin}{\upkappa }_{5}\cdot \mathrm{sin}{\upkappa }_{4}+\mathrm{cos}{\upkappa }_{5}\cdot \mathrm{cos}{\upkappa }_{4}\right)+{\mathrm{F}}_{\mathrm{aSx}}\cdot \mathrm{cos}{\upkappa }_{4}+{\mathrm{F}}_{\mathrm{aSy}}\cdot \mathrm{sin}{\upkappa }_{4},$$
(55)
$${\mathrm{F}}_{\mathrm{aE}2}={\mathrm{F}}_{\mathrm{aF}}\cdot \left(\mathrm{sin}{\upkappa }_{5}\cdot \mathrm{cos}{\upkappa }_{4}+\mathrm{cos}{\upkappa }_{5}\cdot \mathrm{sin}{\upkappa }_{4}\right)-{\mathrm{F}}_{\mathrm{aSx}}\cdot \mathrm{sin}{\upkappa }_{4}+{\mathrm{F}}_{\mathrm{aSy}}\cdot \mathrm{cos}{\upkappa }_{4},$$
(56)

where FaSx and FaSy—components of the force FaS responsible for the acceleration aS (formula (33)), k4 and k5—angles (Fig. 8):

$${\upkappa }_{4}=\mathrm{arctan}\left(\frac{{\mathrm{x}}_{\mathrm{S}}^{*}-{\mathrm{x}}_{\mathrm{E}}^{*}}{{\mathrm{y}}_{\mathrm{E}}^{*}-{\mathrm{y}}_{\mathrm{S}}^{*}}\right),$$
(57)
$${\upkappa }_{5}=\mathrm{arctan}\left(\frac{{\mathrm{x}}_{\mathrm{S}}^{*}-{\mathrm{x}}_{\mathrm{F}}^{*}}{{\mathrm{y}}_{\mathrm{S}}^{*}-{\mathrm{y}}_{\mathrm{F}}^{*}}\right).$$
(58)

The influence of the pressure difference in the working chambers on the load on the interacting teeth

In the satellite mechanism between the filling working chamber (high-pressure chamber HPC) and the emptying working chamber (low-pressure chamber LPC) exist pressure difference:

$$\Delta {\mathrm{p}}_{\mathrm{i}}={\mathrm{p}}_{\mathrm{H}}-{\mathrm{p}}_{\mathrm{L}},$$
(59)

where pH—high-pressure (in the filling working chamber), pL—low-pressure (in the emptying working chamber).

It should be noted that during the rotation of the rotor, the working chamber C passes from the high-pressure chamber HPC to the chamber with the maximum volume VC-max and then to the low-pressure chamber LPC. Experimental studies have shown that in the VC-max chamber there is a mean pressure pM equal to (37) and (39):

$${\mathrm{p}}_{\mathrm{M}}=\frac{{\mathrm{p}}_{\mathrm{H}}+{\mathrm{p}}_{\mathrm{L}}}{2}.$$
(60)

Thus, the value of the force F∆p and its direction of action change abruptly (Fig. 9). In the satellite mechanism, the change of the volume of the working chamber C from VC-max to VC-min and vice versa take place at each angle of rotation of the rotor equal to:

Figure 9
figure 9

Forces originating from the pressure difference ∆pi and acting on the satellite: (a) initial state (αR = 0°); (b) example of the position of the working mechanism elements corresponding to two adjacent working chambers being in the same phase (emptying); (c) the position of the elements of the working mechanism corresponding to the chamber with the maximum volume VC-max; (d,e) the position of the elements of the working mechanism corresponding to the chamber with the minimum volume VC-min.

Full size image
$${{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)}=180\cdot \left(\frac{1}{{\mathrm{n}}_{\mathrm{E}}}+\frac{1}{{\mathrm{n}}_{\mathrm{R}}}\right).$$
(61)

The effect of the pressure difference ∆pi is the pressure difference ∆pS acting on the satellite. Thus, for:

  1. (a)

    \({\mathrm{\alpha }}_{\mathrm{R}}\in \langle \left.0;\frac{180}{{\mathrm{n}}_{\mathrm{E}}}\right)\) and \({\mathrm{\alpha }}_{\mathrm{R}}\in \left(\frac{180}{{\mathrm{n}}_{\mathrm{R}}};\frac{180}{{\mathrm{n}}_{\mathrm{E}}}+{{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)}\right)\) is ∆pS = ∆pi and respectively:

    $${\mathrm{F}}_{\Delta \mathrm{p}}={\Delta \mathrm{p}}_{\mathrm{i}}\cdot \mathrm{H}\cdot \sqrt{{\left({\mathrm{x}}_{\mathrm{E}}^{*}-{\mathrm{x}}_{\mathrm{F}}^{*}\right)}^{2}+{\left({\mathrm{y}}_{\mathrm{E}}^{*}-{\mathrm{y}}_{\mathrm{F}}^{*}\right)}^{2}},$$
    (62)

    where H is the height of the satellite mechanism;

  2. (b)

    \({\mathrm{\alpha }}_{\mathrm{R}}\in \left(\frac{180}{{\mathrm{n}}_{\mathrm{E}}};\frac{180}{{\mathrm{n}}_{\mathrm{R}}}\right)\) and \({\mathrm{\alpha }}_{\mathrm{R}}\in \left(\frac{180}{{\mathrm{n}}_{\mathrm{E}}}+{{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)};\frac{180}{{\mathrm{n}}_{\mathrm{R}}}+{{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)}\right)\) two adjacent chambers are in the same phase, i.e. in the emptying phase or in the filling phase (Fig. 9c)). Therefore ∆pS = 0 and F∆p = 0, FpE = 0, FpF = 0 (see below);

  3. (c)

    \({\mathrm{\alpha }}_{\mathrm{R}}=\frac{180}{{\mathrm{n}}_{\mathrm{E}}}\) and \({\mathrm{\alpha }}_{\mathrm{R}}=\frac{180}{{\mathrm{n}}_{\mathrm{E}}}+{{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)}\) and for \({\mathrm{\alpha }}_{\mathrm{R}}=\frac{180}{{\mathrm{n}}_{\mathrm{R}}}\):

    $$\Delta {\mathrm{p}}_{\mathrm{S}}=\frac{{\mathrm{p}}_{\mathrm{H}}-{\mathrm{p}}_{\mathrm{L}}}{2},$$
    (63)

    and the F∆p = should be calculated according to the formula (62) with the ∆pS instead of ∆pi.

The circumferential forces FpE and FpF, occurring at points E* and F* were assumed to be reactions to the force F∆p (Fig. 9). The values of these forces can be calculated using the following relationship:

$${\mathrm{F}}_{\mathrm{pE}}={\mathrm{F}}_{\mathrm{pF}}=\frac{{\mathrm{F}}_{\Delta \mathrm{p}}}{2}\cdot \frac{\mathrm{cos}{\mathrm{\alpha }}_{\mathrm{p}}}{\mathrm{cos}\left({\upkappa }_{2}-{\mathrm{\alpha }}_{\mathrm{p}}\right)},$$
(64)

where αp is the pressure angle.

Total values of forces loading the interacting teeth of the mechanism elements

The total values of the circumferential forces FpE and FpF acting at points E* and F* are as follows:

  1. (a)

    in the range of the rotor rotation angle \({\mathrm{\alpha }}_{\mathrm{R}}\in \langle \left.0;\frac{180}{{\mathrm{n}}_{\mathrm{E}}}\right)\):

    • at point E*:

      $${\mathrm{F}}_{\mathrm{E}-\mathrm{p}}={{\mathrm{F}}_{\mathrm{pE}}-\mathrm{F}}_{\mathrm{aE}1}-{\mathrm{F}}_{\mathrm{cE}1}-{\mathrm{F}}_{\mathrm{\varepsilon SE}},$$
      (65)

    • at point F*:

      $${\mathrm{F}}_{\mathrm{F}-\mathrm{p}}={{\mathrm{F}}_{\mathrm{pF}}-\mathrm{F}}_{\mathrm{aF}}-{\mathrm{F}}_{\mathrm{cF}}+{\mathrm{F}}_{\mathrm{\varepsilon SF}},$$
      (66)
  2. (b)

    in the range of the rotor rotation angle \({\mathrm{\alpha }}_{\mathrm{R}}\in \langle \frac{180}{{\mathrm{n}}_{\mathrm{E}}};\frac{180}{{\mathrm{n}}_{\mathrm{R}}}\rangle \) and \({\mathrm{\alpha }}_{\mathrm{R}}\in \langle \frac{180}{{\mathrm{n}}_{\mathrm{E}}}+{{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)};\frac{180}{{\mathrm{n}}_{\mathrm{R}}}+{{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)}\rangle \):

    • at point E*:

      $${\mathrm{F}}_{\mathrm{E}-\mathrm{p}}={\mathrm{F}}_{\mathrm{aE}1}+{\mathrm{F}}_{\mathrm{cE}1}+{\mathrm{F}}_{\mathrm{\varepsilon SF}},$$
      (67)

    • at point F*:

      $${\mathrm{F}}_{\mathrm{F}-\mathrm{p}}={\mathrm{F}}_{\mathrm{aF}}{+\mathrm{F}}_{\mathrm{cF}}-{\mathrm{F}}_{\mathrm{\varepsilon SF}},$$
      (68)
  3. (c)

    for \({\mathrm{\alpha }}_{\mathrm{R}}\in \left(\frac{180}{{\mathrm{n}}_{\mathrm{R}}};\frac{180}{{\mathrm{n}}_{\mathrm{E}}}+{{\mathrm{\alpha }}_{\mathrm{R}}}^{\left(\mathrm{C}\right)}\right)\):

    • at point E*:

      $${\mathrm{F}}_{\mathrm{E}-\mathrm{p}}={{\mathrm{F}}_{\mathrm{pE}}+\mathrm{F}}_{\mathrm{aE}1}+{\mathrm{F}}_{\mathrm{cE}1}+{\mathrm{F}}_{\mathrm{\varepsilon SE}},$$
      (69)

    • at point F*:

      $${\mathrm{F}}_{\mathrm{F}-\mathrm{p}}={{\mathrm{F}}_{\mathrm{pF}}+\mathrm{F}}_{\mathrm{aF}}+{\mathrm{F}}_{\mathrm{cF}}-{\mathrm{F}}_{\mathrm{\varepsilon SF}}.$$
      (70)

Problems of contact stress of the interacting teeth

The method of calculating the permissible normal stresses σN in the contact of the interacting teeth of two steel gears is generally known and can be found, for example, in Ref.57. At the present stage of consideration, it is proposed to adopt the well-known model of permissible stresses (for gears) for the satellite mechanism. Because the radii of the pitch line of the rotor and the curvature are variable, it is proposed to take their smallest values for the strength calculations (i.e. rQ and rC2 according to Fig. 10). Thus, for the teeth of the interacting elements, the contact ratio ε (according to Ref.57) is propose to calculate according to the following relation:

$$\upvarepsilon =\frac{\sqrt{{{\mathrm{r}}_{\mathrm{aS}}}^{2}-{{\mathrm{r}}_{\mathrm{bS}}}^{2}}+\sqrt{{{\mathrm{r}}_{\mathrm{a}}}^{2}-{{\mathrm{r}}_{\mathrm{b}}}^{2}}-{\mathrm{a}}_{\mathrm{w}}\cdot \mathrm{sin}{\mathrm{\alpha }}_{\mathrm{w}}}{{\mathrm{p}}_{\mathrm{bS}}},$$
(71)

where raS—the tip radius of the satellite teeth, rbS—the base radius of the satellite, pbS—the base pitch of the satellite teeth, ra and rb—the tip radius and the base radius of the circle of radius rQ or rC2, aw—the true distance between the centre of the satellite and the circle of radius rQ or the circle of radius rC2, αw—the pitch pressure angle.

For the gear elements of the satellite mechanism which are made of the same material, it is proposed to calculate the normal stress at the contact surface of the teeth according to the following formula:

$${\upsigma }_{\mathrm{N}}=\sqrt{\frac{4-\upvarepsilon }{6\uppi }\cdot \left(1+\frac{\mathrm{z}}{{\mathrm{z}}_{\mathrm{S}}}\right)\cdot \frac{\mathrm{F}}{\mathrm{H}\cdot {\mathrm{r}}_{\mathrm{S}}}\cdot \frac{\mathrm{E}}{1-{\upnu }^{2}}\cdot \frac{\mathrm{K}}{\mathrm{sin}{\mathrm{\alpha }}_{\mathrm{w}}\cdot \mathrm{cos}{\mathrm{\alpha }}_{\mathrm{p}}}} \le {\upsigma }_{\mathrm{per}},$$
(72)

where F—the circumferential force at the point of contact of the teeth of the mating elements, H—the length of the tooth line (the height of the satellite mechanism), E—the Young’s modulus of the gear material, ν—the Poisson’s ratio of the gear material, z—the theoretical number of teeth of the gear engaging the satellite, i.e. zR or zE (Fig. 10), K—the coefficient defined as57,62:

$$\mathrm{K}={\mathrm{K}}_{\mathrm{A}}\cdot {\mathrm{K}}_{\mathrm{v}}\cdot {\mathrm{K}}_{\mathrm{H}},$$
(73)

where KA—the overload factor, KH—the coefficient of uneven load distribution along the length of the tooth, Kv—the coefficient of dynamic force, σper—permissible stress.

According to Refs.57,62, the value of permissible stress in gears is calculated as follows:

$${\upsigma }_{\mathrm{per}}=\frac{{\upsigma }_{\mathrm{Hlim}}}{{\mathrm{S}}_{\mathrm{H}}}\cdot \mathrm{Z},$$
(74)

where

$$\mathrm{Z}={\mathrm{Z}}_{\mathrm{NT}}\cdot {\mathrm{Z}}_{\mathrm{L}}\cdot {\mathrm{Z}}_{\mathrm{R}}\cdot {\mathrm{Z}}_{\mathrm{v}}\cdot {\mathrm{Z}}_{\mathrm{W}}\cdot {\mathrm{Z}}_{\mathrm{X}},$$
(75)

where σHlim—the contact fatigue strength of gears materials, ZNT—the coefficient of durability at contact load, ZL—the coefficient of oil viscosity, ZR—the factor of surface condition (roughness), Zv—the speed factor, ZW—the coefficient of surface squeeze (deformation), ZX—the size factor at contact loading, SH—the safety factor at contact loading.

In the literature (e.g.57,62) methods for estimating the values of the above coefficients of K and Z can be found, but for typical gears, i.e. for circular interacting toothed elements. The ranges of values of these coefficients and the safety factor are given in Table 1.

Figure 10
figure 10

Tip clearance TC and circumferential backlash CB in satellite–rotor pair.

Full size image
Table 1 The values of the coefficients type K and Z for nitrided elements57.
Full size table

In the satellite mechanism, the satellite is not fixed on any axis. In this way, the satellite can change its position relative to the rotor and the curvature in terms of inter-tooth clearance and tip clearance. In extreme cases (with a suitable value of the tooth clearance), the tip clearance can be cancelled. Thus, the distance between the centre of the satellite and the centre of a circle of radius rQ or rC2 can vary. In extreme cases, as a result of the centrifugal forces acting on the satellite, the circumferential backlash (and even the tip clearance) in the satellite-curvature pair may be erased and the circumferential backlash and the tip clearance in the satellite-rotor pair may increase (Fig. 11).

Figure 11
figure 11

Geometry of the rotor of the tested satellite mechanism; rC1 and rC2—radii of the equivalent circles of curvature (for calculating the number of the contact ratio ε).

Full size image

Thus, it can be assumed (especially in working gear) that the distance between the center of the satellite and:

  1. (a)

    the centre of the circle of the rotor of radius rQ is:

    $${\mathrm{a}}_{\mathrm{wQ}}={\mathrm{r}}_{\mathrm{S}}+{\mathrm{r}}_{\mathrm{Q}}-{\mathrm{h}}_{\mathrm{a}}+{\mathrm{h}}_{\mathrm{f}},$$
    (76)

    where ha and hf are the height of the tooth head and the tooth foot, respectively;

  2. (b)

    the centre of the circle of the rotor of radius rP is:

    $${\mathrm{a}}_{\mathrm{wP}}={\mathrm{r}}_{\mathrm{S}}+{\mathrm{r}}_{\mathrm{P}}-{\mathrm{h}}_{\mathrm{a}}+{\mathrm{h}}_{\mathrm{f}},$$
    (77)
  3. (c)

    the centre of the circle of the curvature of radius rC1 is:

    $${\mathrm{a}}_{\mathrm{wC}1}={\mathrm{r}}_{\mathrm{S}}+{\mathrm{r}}_{\mathrm{C}1}+{\mathrm{h}}_{\mathrm{a}}-{\mathrm{h}}_{\mathrm{f}},$$
    (78)
  4. (d)

    the centre of the circle of the curvature of radius rC2 is:

    $${\mathrm{a}}_{\mathrm{wC}2}={\mathrm{r}}_{\mathrm{S}}+{\mathrm{r}}_{\mathrm{C}2}+{\mathrm{h}}_{\mathrm{a}}-{\mathrm{h}}_{\mathrm{f}}.$$
    (79)

The pitch pressure angle for such wheels is:

$${\mathrm{\alpha }}_{\mathrm{wQ}}=\mathrm{arccos}\left(\frac{{\mathrm{r}}_{\mathrm{S}}+{\mathrm{r}}_{\mathrm{Q}}}{{\mathrm{a}}_{\mathrm{wQ}}}\cdot \mathrm{cos}{\mathrm{\alpha }}_{\mathrm{p}}\right).$$
(80)

Because hf > ha, there are worse conditions for interaction between the teeth of the satellite and the teeth of the rotor.

Worse conditions of cooperation include, among others, the appearance of an additional impact force Fim of the tooth of the satellite against the tooth of the planet. This force is the effect of the circumferential backlash CB (Fig. 11) and is created when the pressure in the working chambers adjacent to the satellite changes abruptly. So this process takes place for \({\alpha }_{R}=\frac{180}{{n}_{E}}\), \({\alpha }_{R}=\frac{180}{{n}_{E}}+{{\alpha }_{R}}^{\left(C\right)}\), \({\alpha }_{R}=\frac{180}{{n}_{R}}\), \({\alpha }_{R}=\frac{180}{{n}_{R}}+{{\alpha }_{R}}^{\left(C\right)}\) e.t.c. (Fig. 9), where \({{\alpha }_{R}}^{\left(C\right)}\) is given by Eq. (62). The value of the impact force Fim of the satellite tooth on the rotor tooth can be calculated according to the formula:

$${F}_{im}=4\cdot \frac{1}{t}\cdot \sqrt{CB\cdot {r}_{S}\cdot H\cdot {m}_{S}\cdot {\Delta p}_{S}},$$
(81)

where t—the duration of the impact, H—the height of the satellite, mS—the mass of the satellite.

Parameters of the tested satellite mechanism

The satellite mechanism type 4 × 6 (Fig. 3) with a tooth module 0.6 mm was used in a hydraulic motor (Fig. 2). As already mentioned in “Introduction” section, this mechanism is a scaled copy of the mechanism with module 1.5 mm. The mechanism with modulus 1.5 mm was designed to be manufactured by classical machining methods (chiselling and milling) and using special instruments47,50. The pitch line of the rotor consists of circles with radii rP and rQ connected at point T (point T is the point of contact of these circles). The pitch line of the curvature is approximated by fragments of circles with radii rC1 and rC247 (Fig. 10). The satellite mechanism with a module of 0.6 mm was manaufactured using the wire electrical discharge machining (WEDM) process. Technical data of the satellite mechanism are presented in Table 2. While Table 3 shows the values of the distance between the axes, the values of the rolling pressure angle and the values of the contact ratio, assuming that in the working mechanism there is a change in the distance between the axis of the satellite and the axes of the humps of the rotor and the humps of the curvature.

Table 2 Parameters of the tested satellite mechanism.
Full size table
Table 3 Distances between the axes, angles of pressure and contact ratio, assuming the elimination of the tip clearances of the teeth of the satellite and curvature in the working mechanism.
Full size table

The mechanism was made of NIMAX steel72. The parameters of this steel are given in Table 4.

Table 4 Basic parametres of the NIMAX steel72.
Full size table

For nitrided NIMAX steel, it can be assumed that σHlim ≈ 1250 MPa57.

The coordinates (x,y) of the pitch line of the rotor can be calculated using formula (Fig. 12):

  1. (1)

    from point F1 to point T:

    $$\mathrm{x}=\frac{\mathrm{cot}{\mathrm{\alpha }}_{\mathrm{R}}\cdot {\mathrm{y}}_{\mathrm{p}}-\sqrt{\mathrm{cot}{\mathrm{\alpha }}_{\mathrm{R}}\cdot {\mathrm{y}}_{\mathrm{p}}\cdot \left(\mathrm{cot}{\mathrm{\alpha }}_{\mathrm{R}}\cdot {\mathrm{y}}_{\mathrm{p}}+2\cdot \left({{\mathrm{y}}_{\mathrm{P}}}^{2}-{{\mathrm{r}}_{\mathrm{P}}}^{2}\right)\right)}}{{\mathrm{cot}}^{2}{\mathrm{\alpha }}_{\mathrm{R}}+1},$$
    (82)
    $$\mathrm{y}=\mathrm{cot}{\mathrm{\alpha }}_{\mathrm{R}}\cdot {\mathrm{x}}_{\mathrm{R}}.$$
    (83)
  2. (2)

    from point T to point F2:

    $$x=\frac{{x}_{Q}+{\cot}{\upalpha }_{R}\cdot {y}_{Q}+\sqrt{{\left(\mathit{cot}{\alpha }_{R}\cdot {y}_{Q}+{x}_{Q}\right)}^{2}-\left({\mathit{cot}}^{2}{\alpha }_{R}+1\right)\cdot \left({x}_{Q}+{y}_{Q}-{r}_{Q}\right)}}{{\mathit{cot}}^{2}{\alpha }_{R}+1}.$$
    (84)
Figure 12
figure 12

Angles in the tested mechanism and point T.

Full size image

The y-coordinate is calculated according to formula (83).

The relationship between the coordinates of points S and F is as follows. If the point F of contact of the satellite pitch line with the rotor pitch line is between points F1 and T, then (Fig. 12):

$${\mathrm{x}}_{\mathrm{F}}=\frac{1}{{\mathrm{r}}_{\mathrm{P}}-{\mathrm{r}}_{\mathrm{s}}}\cdot \left({\mathrm{r}}_{\mathrm{P}}\cdot {\mathrm{x}}_{\mathrm{s}}-{\mathrm{r}}_{\mathrm{s}}\cdot {\mathrm{x}}_{\mathrm{p}}\right),$$
(85)
$${\mathrm{y}}_{\mathrm{F}}=\frac{1}{{\mathrm{r}}_{\mathrm{P}}-{\mathrm{r}}_{\mathrm{s}}}\cdot \left({\mathrm{r}}_{\mathrm{P}}\cdot {\mathrm{y}}_{\mathrm{s}}-{\mathrm{r}}_{\mathrm{s}}\cdot {\mathrm{y}}_{\mathrm{p}}\right),$$
(86)
$${\mathrm{x}}_{\mathrm{s}}=\frac{{\mathrm{x}}_{\mathrm{p}}+{\mathrm{a}}_{\mathrm{s}}\cdot {\mathrm{y}}_{\mathrm{p}}}{{{\mathrm{a}}_{\mathrm{s}}}^{2}+1}-\sqrt{{\left(\frac{{\mathrm{x}}_{\mathrm{p}}+{\mathrm{a}}_{\mathrm{s}}\cdot {\mathrm{y}}_{\mathrm{p}}}{{{\mathrm{a}}_{\mathrm{s}}}^{2}+1}\right)}^{2}-\frac{{{\mathrm{x}}_{\mathrm{p}}}^{2}+{{\mathrm{y}}_{\mathrm{p}}}^{2}-{\left({\mathrm{r}}_{\mathrm{p}}-{\mathrm{r}}_{\mathrm{s}}\right)}^{2}}{{{\mathrm{a}}_{\mathrm{s}}}^{2}+1}},$$
(87)
$${\mathrm{y}}_{\mathrm{s}}={\mathrm{a}}_{\mathrm{s}}\cdot {\mathrm{x}}_{\mathrm{s}},$$
(88)

where

$${\mathrm{a}}_{\mathrm{s}}=\mathrm{cot}\left({\mathrm{\alpha }}_{\mathrm{R}}-{\mathrm{\alpha }}_{\mathrm{s}}\right).$$
(89)

If point F is between points T and F2, then the relationship between the coordinates of points S and F is as follows (Fig. 12):

$${\mathrm{x}}_{\mathrm{F}}=\frac{1}{{\mathrm{r}}_{\mathrm{Q}}+{\mathrm{r}}_{\mathrm{s}}}\cdot \left({\mathrm{r}}_{\mathrm{Q}}\cdot {\mathrm{x}}_{\mathrm{s}}+{\mathrm{r}}_{\mathrm{s}}\cdot {\mathrm{x}}_{\mathrm{Q}}\right),$$
(90)
$${\mathrm{y}}_{\mathrm{F}}=\frac{1}{{\mathrm{r}}_{\mathrm{Q}}+{\mathrm{r}}_{\mathrm{s}}}\cdot \left({\mathrm{r}}_{\mathrm{Q}}\cdot {\mathrm{y}}_{\mathrm{s}}+{\mathrm{r}}_{\mathrm{s}}\cdot {\mathrm{y}}_{\mathrm{Q}}\right),$$
(91)
$${\mathrm{x}}_{\mathrm{S}}=\frac{{\mathrm{x}}_{\mathrm{Q}}+{\mathrm{a}}_{\mathrm{s}}\cdot {\mathrm{y}}_{\mathrm{Q}}}{{{\mathrm{a}}_{\mathrm{s}}}^{2}+1}+\sqrt{{\left(\frac{{\mathrm{x}}_{\mathrm{Q}}+{\mathrm{a}}_{\mathrm{s}}\cdot {\mathrm{y}}_{\mathrm{Q}}}{{{\mathrm{a}}_{\mathrm{s}}}^{2}+1}\right)}^{2}-\frac{{{\mathrm{x}}_{\mathrm{Q}}}^{2}+{{\mathrm{y}}_{\mathrm{Q}}}^{2}-{\left({\mathrm{r}}_{\mathrm{Q}}+{\mathrm{r}}_{\mathrm{s}}\right)}^{2}}{{{\mathrm{a}}_{\mathrm{s}}}^{2}+1}.}$$
(92)

The values of yS and aS should be calculated according to formulae (88) and (89) respectively.

If the point F coincides with the point T (i.e. xF = xT i yF = yT) then the coordinates of the satellite centre are as follows:

$${\mathrm{x}}_{\mathrm{S}}=\left(1-\frac{{r}_{s}}{{r}_{P}}\right)\cdot {x}_{T}+\frac{{r}_{s}}{{r}_{P}}\cdot {x}_{p},$$
(93)
$${\mathrm{y}}_{\mathrm{S}}=\left(1-\frac{{r}_{s}}{{r}_{P}}\right)\cdot {y}_{T}+\frac{{r}_{s}}{{r}_{P}}\cdot {y}_{p},$$
(94)

and the curvature must make a rotation through an angle:

$${\mathrm{\alpha }}_{\mathrm{T}}=\left(1+\frac{{\mathrm{n}}_{\mathrm{R}}}{{\mathrm{n}}_{\mathrm{E}}}\right)\cdot \mathrm{arctan}\left(\frac{{\mathrm{x}}_{\mathrm{S}}}{{\mathrm{y}}_{\mathrm{S}}}\right).$$
(95)

For the considered mechanism, this is the angle αT = 33.80°.

The rotation angles of the satellite and the number of teeth contacts in the mechanism

For one full revolution of the rotor, i.e. for αR = 360°:

  1. (a)

    the angle of rotation of the satellite about its axis is δS(αR = 360°) = 1584°;

  2. (b)

    the satellite moves relative to the curvature by an angle αS = 144°;

  3. (c)

    the angle αS = 144° corresponds to the length LE = 49.73 mm of the curvature pitch line;

  4. (d)

    the number of contacts of each tooth of the satellite with:

    • the teeth of the rotor (and hence the number of revolutions of the satellite about its own axis) is iSR = 4.4;

    • the teeth of the curvature (and hence the number of revolutions of the satellite about its own axis) is iSE = 2.6;

  5. (e)

    the total number of contacts of the teeth of the satellite with the teeth of the rotor and the curvature is iS = 7;

  6. (f)

    the number of contacts of each rotor tooth with the satellite tooth is iRTS = 6;

  7. (g)

    the number of contacts of each curvature tooth with the satellite tooth is iETS = 4.

However, for the satellite to make one complete revolution in relation to the curvature, i.e. αS = 360°, the shaft (rotor) must make iRE = 2.5 revolutions.

In the motor working at n = 1500 rpm, in 1 min:

  1. (a)

    the number of contacts of each tooth of the satellite with the teeth of the rotor:

    $${\mathrm{i}}_{\mathrm{SR}(\mathrm{n})}=\mathrm{n}\cdot {\mathrm{i}}_{\mathrm{SR}}=6600,$$
    (96)
  2. (b)

    the number of contacts of each tooth of the satellite with the teeth of the curvature:

    $${\mathrm{i}}_{\mathrm{SE}(\mathrm{n})}=\mathrm{n}\cdot {\mathrm{i}}_{\mathrm{SE}}=3900,$$
    (97)
  3. (c)

    the number of contacts of the teeth of the satellite with the teeth of the rotor and the curvature:

    $${\mathrm{i}}_{\mathrm{S}(\mathrm{n})}=\mathrm{n}\cdot {\mathrm{i}}_{\mathrm{S}}=\mathrm{10,500},$$
    (98)
  4. (d)

    the number of contacts of each tooth of the rotor with the tooth of the satellites:

    $${\mathrm{i}}_{\mathrm{RTS}(\mathrm{n})}=\mathrm{n}\cdot {\mathrm{i}}_{\mathrm{RTS}}=9600,$$
    (99)
  5. (e)

    the number of contacts of each curvature tooth with the tooth of the satellites:

    $${\mathrm{i}}_{\mathrm{ETS}(\mathrm{n})}=\mathrm{n}\cdot {\mathrm{i}}_{\mathrm{ETS}}=6000.$$
    (100)

Accelerations of the satellite

The characteristics of the angular velocity ωS and the angular acceleration εS of the satellite in the considered satellite mechanism are presented in Fig. 13, while in Fig. 14 the characteristics of the linear accelerations of the satellite are presented.

Figure 13
figure 13

Characteristics of the angular velocity ωS and angular acceleration εS of the satellite as a function of the angle of rotation of the shaft (rotor) αR.

Full size image
Figure 14
figure 14

Characteristics of the linear velocity vS and linear acceleration of the satellite as a function of the angle of rotation of the shaft (rotor) αR.

Full size image

Tooth loads—forces at points E* and F*

The values of the forces acting at points E* and F* (loading of the teeth) and resulting from the accelerations of the satellite, are shown in Figs. 15 and 16.

Figure 15
figure 15

Characteristics of the forces FεSE and FεSF.

Full size image
Figure 16
figure 16

Characteristics of the forces FaS, FaE1 and FaF.

Full size image

The characteristics of the centrifugal force FcS acting on the satellite and the values of the forces FcE1 and FcF corresponding to this force at points E* and F* of the satellite mechanism under consideration are shown in Fig. 17. And Fig. 17 shows the characteristics of the force F∆p at points E* and F*, calculated according to formula (64).

Figure 17
figure 17

Characteristics of the centrifugal force FcS and the forces FcE1 and FcF at points E* and F*.

Full size image

The characteristics of the total forces FE-p and FF-p loading the teeth of the interacting elements of the satellite mechanism at points E* and F* are shown in Fig. 18.

Figure 18
figure 18

Characteristics of the circumferential forces FE-p and FF-p at the points E* and F*.

Full size image

Normal stress on the contact surface of the teeth and permissible stress

The satellite mechanism is not a typical toothed gear mechanism. The satellite is not mounted on a bearing shaft and the rotor and curvature are elements with non-circular gear rims. Therefore, at the present stage of research, it is not possible to give the exact values of the coefficients K and Z from the formulae (73) and (75). It was therefore assumed that the pressures in the contact of mating teeth are calculated for:

  1. (a)

    Two values of the coefficient K, i.e. for K = 1 (mechanism elements do not rotate and the teeth of the mechanism elements are loaded only with the force resulting from the pressure difference in the working chambers) and for the approximate value of K = 3.

  2. (b)

    Two extreme values of the coefficient Z, i.e. for Z = 0.96 and Z = 1.8.

The calculations of the contact stresses at points E and F were carried out for two cases, namely for:

  1. (a)

    Perfect cooperation of the satellite with the rotor and the curvature (i.e. without changing the axis distance).

  2. (b)

    For the case of elimination of the tip clearance of the cooperating teeth of the satellite with the curvature.

A summary of the results for the above cases for different rotation angles αR of the rotor can be found in Tables 5 and 6 respectively. Whereas the values of permissible stresses are presented in Table 7.

Table 5 Values of normal stress σN (in MPa) at the points E* and F* (Fig. 9).
Full size table
Table 6 Values of normal stress σN (in MPa) at the points E* and F* (Fig. 9)—assuming the clearance of the mating teeth of the satellite and curvature (in the working mechanism) is deleted.
Full size table
Table 7 Permissible stress σHlim (in MPa).
Full size table

If the phenomenon of the impact of the satellite tooth on the rotor tooth is taken into account, the value of the pressure force of the satellite tooth on the rotor tooth will increase by Fim and the value of stresses σN at the point of contact of these teeth will increase. The values of the Fim force are presented in Table 8, and the stress values in Table 9.

Table 8 Impact force Fim values (in N) of the satellite tooth against the rotor tooth.
Full size table
Table 9 Values of normal stress σN (in MPa) at the point F* (in MPa) assuming the impact of the satellite tooth against the rotor tooth (for t = 0.001 s).
Full size table

Conclusions

The results of the analyses have shown that in the satellite mechanism:

  1. (a)

    The number of contacts of each rotor tooth with a satellite tooth is 1.5 times larger (iRTS = 6 and iETS = 4) than the number of contacts of each curvature tooth with the satellites tooth.

  2. (b)

    The accelerations of the satellite and the corresponding forces loading the teeth are a non-linear function of the rotation angle of the rotor (Figs. 13, 16).

  3. (c)

    The highest values of the forces acting on the teeth of the satellite mechanism result from the pressure difference ∆pS acting on the satellite. The highest value of these forces occurs for αR = 105°, i.e. when the working chamber C reaches the minimum volume VC-min (Fig. 9e). The value of the forces FpE and FpF for αR = 105° and for the pressure difference ∆pS in two adjacent working chambers of 25 MPa is 1714 N (Fig. 19).

  4. (d)

    The values of FpE and FpF within the angle of rotation of the shaft \({\mathrm{\alpha }}_{\mathrm{R}}\in \left(\frac{180}{{\mathrm{n}}_{\mathrm{E}}}={30}^{^\circ };\frac{180}{{\mathrm{n}}_{\mathrm{R}}}={45}^{^\circ }\right)\) are 0N (Fig. 19). Within this angular range, the working chambers adjacent to the satellite are in the same phase (emptying—Fig. 9c).

  5. (e)

    The forces FeSE, FeSF, FaE1 and FaF loading the teeth resulting from satellite accelerations and forces FcE1 and FcF due to the centrifugal force Fc have very low values of less than 1 N (Figs. 15, 16, 17). The highest values of these forces occur for the rotor rotation angle αT = 33.80° (point T is the contact point of the satellite with the rotor—Fig. 12). After passing the point T, the values of the forces FeSE, FeSF, FaE1 and FaF decrease rapidly due to changes in the geometric parameters of the rotor. The rapid changes in these forces do not have a significant effect on the value of the stress at the contact point of the interacting teeth due to their very small values.

  6. (f)

    The forces FeSE, FeSF, FaE1, FaF and forces FcE1 and FcF can be omitted from the consideration of stresses in the teeth contact due to their low values compared to the forces FpE and FpF.

  7. (g)

    There is a shift of the satellite towards the curvature within the limits of the tip clearances and circumferential backlash of the mating teeth;

  8. (h)

    At the moment when there is a step change in pressure in the working chambers (for the presented mechanism αR = 30°, 45°, 105°, 120° etc. (Fig. 9)) the tooth of the satellite hits the tooth of the rotor with the force Fim, the value of which depends especially on the value of clearance CB and may exceed the force FpF resulting directly from the pressure difference ∆pS (Table 8).

  9. (i)

    In ideal satellite mechanism (without clearances) the stresses in the contact of the interacting teeth do not exceed the value of allowable stresses at ∆pS = 25 MPa only in the most optimistic calculation variant (for K = 1, SH = 1 and Z = 1.8).

  10. (j)

    In a real satellite mechanism, in which the impact force Fim of the satellite tooth against the planet tooth occurs, the stresses in the contact of the cooperating satellite teeth with the rotor teeth are about 4% higher (for ∆pS = 25 MPa) than the stresses in the contact of the cooperating satellite teeth with the curvature teeth (see the results in Tables 6, 9).

Figure 19
figure 19

Characteristics of the force F∆p and the forces FpE and FpF at the points E* and F*.

Full size image

In addition, based on the results of the analyzes carried out, it can be concluded that the following factors are the reason for the rapid wear of the rotor teeth (Fig. 3):

  1. (a)

    The tip clearances and circumferential backlash of the cooperating teeth, as a result of which an undesirable impact force Fim of the satellite tooth against the rotor tooth is created.

  2. (b)

    During the operation of the satellite mechanism, the clearance probably increases (as a result of wear), which increases the impact force Fim.

  3. (c)

    To large working pressure of the satellite motor (the working pressure of 25 MPa is too large for satellite mechanism).

  4. (d)

    High rotational speed of the rotor. As shown in “The rotation angles of the satellite and the number of teeth contacts in the mechanism” section, at the rotation speed of the motor shaft n = 1500 rpm, the number of contacts of each rotor tooth with the tooth of the satellites during one minute is as much as 9600. In 1 h there are 576,000 contacts and in 10 h at least 5.76 million contacts. Considering the dynamic changes in the load on the teeth, it can be assumed that the satellite mechanism will be destroyed in a relatively short operating time.

Comparing the calculation results, given in Tables 5 and 7, it can be presumed that the wear of the rotor teeth will be significantly reduced when:

  1. (a)

    The satellite mechanism will be precisely made, i.e. with minimal tip clearances and with minimal circumferential backlash (CB < 0.08 × module).

  2. (b)

    The motor will be operated with such a torque load that the pressure difference ∆pi in the working chambers does not exceed 5 MPa.

In summary, satellite positive displacement machines (pumps, motors) should operate at low speed and at most an average working pressure. For example, if the permissible speed of the hydraulic motor shaft is 100 rpm, the number of contacts of each rotor tooth with the satellite tooth will be only 38,400 within 1 h.