Introduction

The kagome network, an edge-sharing triangular net, has first gained a significant research interest in the context of spin liquid phases1,2,3. An S = 1/2 ion placed on this 3-connected grid, with nearest-neighbor interactions present only, is an archetype of a geometrically frustrated magnetic system4,5.

Magnetic frustration is not, however, the only exotic physical behavior that is displayed by the kagome net. A 3-orbital tight binding model of the band structure of an isolated kagome consists of a pair of Dirac bands crossing at the K point of the Brillouin zone (BZ) and a flat band (see Fig. 1a,b). The density of states (DOS) for such a system consists of 3 van Hove singularities: one for the flat band and two associated with the Dirac band saddle point at M. The flat band results from the localization due to a destructive interference of electron wavefunction on the kagome lattice6. The presence of the flat band marks the instability of the system towards crystal lattice distortion or magnetism7,8. In real crystalline solid-state systems the flat band gains some dispersion due to next-nearest neighbor (NNN) interactions between the kagome atoms (either direct or via other atomic layers), but the DOS still displays a peak9,10,11, which is often associated with the occurrence of ferromagnetism or superconducting transition.

Figure 1
figure 1

(a) 3-orbital tight-binding band structure of a kagome network with nearest-neighbor interactions only, showing a pair of Dirac bands crossing (DP) at the K point of the Brillouin zone. Locations of BZ points are shown schematically in (b). Crystal structure of ROs2 (c,d) shown as a stacking of Os1 breathing kagome layers separated by triangular planes of R and Os2. Note that purple and gray triangles highlighted in panel (c) are not equal in size, thus the symmetry of the 2D kagome network is reduced from p6m to p3m1.

Full size image

The hexagonal MgZn2-type structure, belonging to a large group of Laves intermetallic phases, can be seen as a stacking of kagome planes (2 per unit cell) separated by two triangular network12 (see Fig. 1c,d). In hexagonal Laves ROs2 (R = Sc, Y, Lu) the osmium Os1 atoms in the 6 h Wyckoff position form a trigonally-distorted (breathing) kagome net in the ab plane, where two hexagons and two triangles meet at each net vertex. Two kagome layers per unit cell with z = 0.25 and 0.75 are stacked along the c direction, while shifted against each other and connected by Os2 atoms at the 2a site (see Fig. 1d). The close-packed R-Os2 layer is capped above and below by the kagome nets.

Recently, we succeeded in synthesizing three ROs2 (R = Sc, Y, Lu) hexagonal Laves compounds which were briefly reported in Ref.13 to be superconductors. Though the latter report was published almost 60 years ago, to the best of our knowledge, no detailed studies have been performed as yet, aimed at determining the superconducting and normal-state parameters of these compounds. In this manuscript we report the synthesis of polycrystalline samples of ROs2 (R = Sc, Y, Lu) and experimental characterization of their electronic properties by means of dc magnetization, electrical resistivity, and heat capacity measurements. The experimental data are supplemented by the results of electronic band structure calculations. Density functional theory (DFT) calculations reveal fairly complicated band structure of ROs2 due to multiple interacting d orbitals of Os and R metal. However, the overall shape of the kagome-derived bands is preserved, and the Fermi level is found within the region of high DOS that stems from the kagome flat bands that are broadened by interaction between the layers. ROs2 can be thus considered as the kagome metal superconductors.

Experimental section

Polycrystalline compounds ScOs2, YOs2 and LuOs2 were prepared by using the standard arc-melting method. High-purity elements, i.e., (> 99.9 wt%, Onyxmet, Poland) were weighed in nominal stochiometric ratios and arc-melted together in an inert argon atmosphere on a water-cooled cooper hearth. A piece of zirconium was used as a getter material during the melting process. To improve chemical homogeneity, the ingots were remelted three times, flipping them over after each melting. Weight losses upon melting were negligible (< 0.5%). All samples were hard, silver in color and stable against air and moisture. Parts of each sample were wrapped in tantalum foil, sealed under vacuum in a quartz tube and annealed at 800 \(^\circ{\rm C}\) for 7 days. The annealing temperature (800 \(^\circ{\rm C}\)) for all samples was chosen based on a known Y-Os phase diagram14. No melting was observed during the heating process.

Powder X-ray diffraction (pXRD) measurements of as-cast and annealed samples were carried out at room temperature using Bruker D2 Phaser diffractometer [Cu Kα radiation (λ = 1.5406 Å)] equipped with a LynxEye-XE detector. Full LeBail analysis of the obtained XRD patterns was performed using the Bruker DIFFRAC.SUITE TOPAS software. The magnetization measurements were performed using a Quantum Design Evercool II Physical Property Measurement System (PPMS) with a Vibrating Sample Magnetometer (VSM) function. Both zero-field-cooled (ZFC) and field-cooled (FC) data were collected from 1.7 to 7 K under an applied field of 10 Oe. The magnetization was also measured at various temperatures in the superconducting state (T < Tc) as a function of the applied field. Magnetic measurements were performed on samples of arbitrary shape with a mass of about 15 mg. All thermodynamic and transport measurements were also performed in a PPMS system. Specific-heat measurements were carried out in zero field and field up to 3 T, using the two-τ time-relaxation method. Each sample was cut to a suitable size and mounted with the Apiezon N grease onto the α-Al2O3 measurement platform to ensure good thermal contact. Temperature- and magnetic-field-dependent electrical transport measurements were tested using a standard four-probe technique, in which Pt wires (\(\varnothing =50\, \upmu\mathrm{m}\)) were attached to the surface of polished samples by spot welding.

Electronic band structure and density of states calculations were performed by means of the density functional theory with the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE GGA)15 of the exchange–correlation potential utilizing the ELK 5.2.14 all-electron full-potential linearized augmented plane wave + local orbitals (FP-LAPW + lo) code16. Crystal structures were taken from the Materials Project database17 (MP id: mp-567612, mp-570670, mp-567590 for Sc-, Y-, and Lu-bearing compound, respectively) and were used without further relaxation. Calculations were conducted in the full- (with spin–orbit coupling) and scalar-relativistic (neglecting the SOC) on an 8 × 8 × 6 Monkhorst–Pack k-point mesh.

Tight binding models of kagome networks were created and solved using the Pybinding package18.

Results

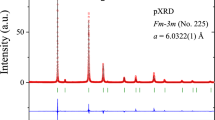
The room-temperature pXRD patterns of ScOs2, YOs2 and LuOs2 materials are presented in Fig. S1 in Supplementary Materials (SM). All compounds are reported to crystallize in a hexagonal centrosymmetric MgZn2-type structure (P63/mmc, No. 194)13. The pXRD confirmed a good quality of all samples with a small amount of impurity phases (Os; P63/mmc, No. 194). Annealing at 800 \(^\circ{\rm C}\) does not effect on the XRD patterns, indicating that all compounds melt congruently. In a more detailed analysis of the data, the P63/mmc phase was refined with the LeBail method. The LeBail fit to the powder diffraction pattern is represented by a black solid line (Fig. S1). The refined lattice parameters are a = b = 5.1791(1) Å and c = 8.4841(2) Å for ScOs2, a = b = 5.2571(3) Å and c = 8.6613(2) Å for LuOs2 and a = b = 5.3067(6) Å and c = 8.7904(1) Å for YOs2. All values are in very good agreement with the data reported previously13. Figure S2 in SM presents a schematic view of the hexagonal structure of ROs2. The 4f (1/3, 2/3, z) site is occupied by R atoms and the 2a (0,0,0) and 6h (x, 2x, 1/4) sites are occupied by Os atoms.

Figure 2 shows the unit cell volume (V) versus the atomic radius ratio of the rare earth metal to osmium metal (rR/rOs). The value of radii ratio is an important parameter governing the formation of the Laves phase structure, which ideally is 1.22519,20. The ratio of the known Laves phases often deviates from this ideal value (ranges from 1.05 to 1.70). The rR/rOs ratio was calculated based on atomic radii values given by S.M. McLennan21. The unit cell volumes for the hexagonal structure of ROs2 (R = lanthanides from La to Yb) were taken from the ICSD database. As expected, the unit cell volume increases with an increase in the radius of the rare earth metal i.e., the smallest value is noted for ScOs2 and the largest for LaOs2. It is worthwhile to mention that for ROs2 compounds one can observe polymorphic transition point (PTP), where the crystal structure changes22,23. Typically, by conventional arc melting techniques, the C15 (cubic) phase is formed with the light R's (La-Pr) and the C14 (hexagonal) phase with the heavier R's (Pr-Lu). However, it has been observed that for LaOs2, CeOs2, and PrOs2 annealing under high pressure leads to the transformation of the cubic (MgCu2-type) to the hexagonal (MgZn2-type) crystal structure24,25. Moreover, M.S. Torikachvili reported26 that the transformation of CeOs2 can be accomplished at ambient pressure by annealing at temperatures between 500 and 950 °C.

Figure 2
figure 2

The unit cell volume vs the atomic radius ratio of the rare earth metal to osmium metal, rR/rOs. LaOs2, CeOs2, and PrOs2 form in the hexagonal phase under high pressure.

Full size image

The superconducting properties of all compounds were first characterized by the measurement of temperature-dependent magnetization under zero-field-cooled and field-cooled conditions. Panels (a–c) of Fig. 3 present the volume magnetic susceptibility (defined as χ = M/H where M is the magnetization and H is the applied magnetic field) measured under an applied field of 10 Oe. The bifurcation of the ZFC and FC magnetic susceptibilities indicates the transition into the superconducting state. It can be seen that for the ZFC and FC signals, the transition is slightly broadened for all samples and reaches saturation at lower temperature. When corrected for the demagnetization effect, N = 0.33 for ScOs2 and LuOs2, and N = 0.73 for YOs2 (estimated from the M(H) data, discussed in SM), χZFC approaches a value of − 1 at the lowest temperatures, indicating volume superconductivity. It should be noted that since the measured samples were in the form of individual chunks whose shape was not well defined, it is difficult to estimate the theoretically expected values of the N-factor. However, for the YOs2 sample, the rather large value of N and the absence of χZFC(T) saturation at the lowest temperatures may indicate that the superconducting Meissner fraction is not 100%. The diamagnetic signal of the FC measurement is weaker, likely caused by the flux line pinning, typically seen for polycrystalline samples of superconductors. The divergence of ZFC and FC signals is more pronounced for ScOs2 probably due to smaller grains and greater number of grain boundaries. The critical temperature was estimated as an intersection point between the extrapolated lines corresponding to the normal and superconducting state magnetic susceptibilities27. The Tc value is 5.54 K for ScOs2, 4.31 K for YOs2 and 3.45 K for LuOs2. It is worthwhile to mention that the values of critical temperature for compounds with Y and Lu agree well with the previous report13, while for ScOs2 the superconducting transition is observed at higher temperature than reported by V.B. Compton and B.T. Matthias (4.6 K13) or J.E. Hirsch (2 K28). The conservatively determined values thus obtained are larger than these reported for the cubic Laves phases with Ir e.g., ScIr2 (2.07 K29, 1.03 K30), YIr2 (2.18 K29), and LuIr2 (2.47 K29).

Figure 3
figure 3

Zero-field-cooled (open circles) and field-cooled (full circles) temperature-dependent magnetic susceptibility data (H = 10 Oe) for ScOs2 (a), YOs2 (b), and LuOs2 (c). Temperature variation of the lower critical field for ScOs2 (d), YOs2 (e), and LuOs2 (f).

Full size image

The field-dependent magnetization at different temperatures (T < Tc) was measured to determine both the demagnetization factor, N, and estimate the value of the lower critical field, Hc1(0). M(H) measured at selected temperatures for all compounds are depicted in Fig. S3 in SM. For all investigated samples the magnetization exhibits behavior observed for the conventional type-II superconductors31,32,33. The demagnetization factor was found assuming that the initial linear response to the field for an isotherm taken at T = 1.7 K is ideally diamagnetic. For an analysis of the lower critical field (\({H}_{c1}^{*}\)) the point corresponding to the first deviation from a linear response was estimated at each temperature. To precisely calculate this point, we followed the methodology described elsewhere34,35,36,37. In panels (d–f) of Fig. 3 the values of \({H}_{c1}^{*}\) are plotted as a function of temperature for all compounds. An additional point for H = 0 Oe is a zero-field transition temperature taken from the electrical resistivity measurement. The experimental \({H}_{c1}^{*}\left(T\right)\) data points were analyzed using the equation38:

$${H}_{c1}^{*}\left(T\right)= {H}_{c1}^{*}\left(0\right)\left[1-{\left(\frac{T}{{T}_{c}}\right)}^{2}\right]$$
(1)

where Tc is the superconducting critical temperature and \({H}_{c1}^{*}(0)\) is the lower critical field at 0 K. The solid red line through the data points shows a good agreement of the Ginzburg–Landau (GL) theory. Considering the demagnetization factor, the lower critical field, Hc1(0) = Hc1*(0)/(1 − N), at 0 K is calculated to be 187 Oe for ScOs2, 83 Oe for YOs2, and 48 Oe for LuOs2. It should be noted that since the demagnetization factor N for YOs2 is likely overestimated, the value of Hc1(0) for this compound is likely smaller.

The results of low-temperature heat capacity (Cp) measurements are summarized in Fig. 4. Panels (a–c) present the zero-field data plotted as Cp/T versus temperature. The bulk nature of the superconductivity for all samples is confirmed by the pronounced heat-capacity jump on cooling through Tc. To determine the critical temperature, we employed idealized equal entropy construction, which reflects the expected entropy balance between the normal state and the superconducting state at the superconducting phase transition. The Tc’s equal 5.36 K, 4.55 K and 3.47 K for ScOs2, YOs2 and LuOs2, respectively, and agree with the magnetization data presented above.

Figure 4
figure 4

Temperature dependence of the zero-field specific heat in the vicinity of the superconducting phase transition for ScOs2 (a), YOs2 (b), and LuOs2 (c). Cp/T vs T2 measured in a magnetic field: ScOs2 (d), YOs2 (e), and LuOs2 (f).

Full size image

Panels (d–f) of Fig. 4 depict the heat capacity data plotted as Cp/T versus T2 under the magnetic field. In the normal state, the experimental data were fitted using the standard Debye expression Cp/T = γ + βT2, where βT3 and γT are the phonon and electronic contribution to the specific heat, respectively. From the fit shown by the red solid line we obtained γ = 12.7(2) mJ mol−1 K−2, β = 0.18(2) mJ mol−1 K−4 for ScOs2, γ = 11.1(1) mJ mol−1 K−2, β = 0.24(1) mJ mol−1 K−4 for YOs2, and γ = 14.5(2) mJ mol−1 K−2, β = 0.29(2) mJ mol−1 K−4 for LuOs2. Using the Sommerfeld coefficient, the normalized specific heat jump, \(\Delta\)C/γTc, turned out to be 1.51, 1.22 and 1.41 for ScOs2, YOs2 and LuOs2, respectively. For all compounds, the estimated values are close to the BCS limit (1.43), suggesting a weakly-coupled superconductivity. In a simple Debye model, the β coefficient is related to the Debye temperature ΘD through ΘD \(= {\left(\frac{12{\pi }^{4}}{5\beta }nR\right)}^{1/3}\), where R = 8.31 J mol−1 K−1 and n = 3. The resulting values of ΘD are 319(4) K for ScOs2, 291(5) K for YOs2, and 270(6) K for LuOs2. Figure 5 shows obtained values of Tc, ΘD, and γ versus atomic mass of the rare earth atom for investigated compounds.

Figure 5
figure 5

The critical temperature, the Debye temperature, and the Sommerfeld coefficient versus atomic mass of the rare earth atom in ROs2 compounds (R = Sc, Y and Lu).

Full size image

The highest Tc is noticed for ScOs2 and may be related to the strengthening of the electron–phonon interaction. The highest and the lowest value of ΘD is observed for ScOs2 and LuOs2, respectively, which can be qualitatively explained as the effect of the larger atomic weight of Lu comparing to Sc. The Sommerfeld coefficient, related to the density of states at the Fermi level, is slightly different for all compounds, with the largest value for LuOs2.

Having the estimated Debye temperature ΘD, and assuming that the Coulomb pseudopotential parameter µ* = 0.1336,37,39,40,41, we calculated the electron–phonon constant λe-p used the inverted McMillan’s formula39:

$${\lambda }_{e-p}= \frac{1.04 +{\mu }^{*}\mathrm{ln}\left(\frac{{\Theta }_{D}}{1.45{T}_{c}}\right)}{\left(1-0.62 {\mu }^{*}\right)\mathrm{ln}\left(\frac{{\Theta }_{D}}{1.45{T}_{c}}\right)- 1.04}$$
(2)

With these considerations, \({\lambda }_{e-p}\) is calculated to be 0.64, 0.63, and 0.59 for ScOs2, YOs2 and LuOs2, respectively. Determined values indicate weakly coupled superconductivity in all investigated compounds.

In addition, having the Sommerfeld coefficient and the electron–phonon coupling constant, the density of states at the Fermi energy N(EF) can be estimated:

$$N\left({E}_{F}\right)= \frac{3\gamma }{{\pi }^{2}{k}_{B}^{2}\left(1+{\lambda }_{e-p}\right)}$$
(3)

where kB is the Boltzmann constant. N(EF) = 3.30 (ScOs2), 2.90 (YOs2) and 3.86 (LuOs2) states eV−1 per formula unit (f.u.).

The results of electrical resistivity measurements for all samples are summarized in Fig. 6a–c. Resistivity shows metallic behavior for all studied compounds with a residual resistivity ratio (RRR = ρ(300)/ρ(7)) of 5.7 for ScOs2, 7.1 for YOs2, and 6.4 for LuOs2, which is either attributable to the sample’s polycrystalline nature and grain boundaries or intrinsic. One can observe that the resistivity drops abruptly to zero, confirming that a superconducting transition occurs in all investigated compounds, which was also confirmed by a large diamagnetic signal and a significant specific heat jump at Tc. To obtain the upper critical field (see insets of Fig. 6a–c), Hc2(T), we measured the resistivity at various magnetic fields (μ0H = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.75, 1, 1.25, 1.5, 1.75, and 2 T for ScOs2; μ0H = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.75, 1, 1.25, 1.5, and 1.75 T for YOs2, and μ0H = 0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.4, 0.6, 0.8, and 1 T for LuOs2). As expected, with increasing magnetic field, the superconducting transition shifts to lower temperature. For ScOs2, a two-step transition is seen when the magnetic field is applied. The origin of this behavior is unknown, although, it might originate from the surface or filamentary superconductivity, with a higher critical field. For all investigated compounds, the upper critical field (μ0Hc2(0)) is determined by the temperature when the resistivity drops to 50% of the normal-state value and is plotted as a function of temperature in the Fig. 6d. According to the Ginzburg–Landau (GL) theory, the μ0Hc2 value at 0 K can be estimated using the expression42,43,44:

$${\mu }_{0}{H}_{c2}\left(T\right)={{\mu }_{0}H}_{c2}\left(0\right)\frac{\left(1-{t}^{2}\right)}{\left(1+{t}^{2}\right)}$$
(4)

where t = T/Tc and Tc is a fitting parameter (transition temperature at zero magnetic field). The fitting line from the GL relation fairly well describes the experimental data for all compounds and one can obtain the values of μ0Hc2(0): 2.58(1) T for ScOs2, 2.23(2) T for YOs2, and 1.64(5) T for LuOs2. The paramagnetic limiting field (μ0HP) is given by μ0HP = \({\Delta }_{0}/\sqrt{2}{\mu }_{B}\) (\({\Delta }_{0}\) is the zero-temperature superconducting gap, and \({\mu }_{\mathrm{B}}\) is the Bohr magneton), which can be expressed as μ0HP = 1.86 Tc, yielding μ0HP ~ 9.9, 8.5, and 6.5 T for ScOs2, YOs2 and LuOs2, respectively. In all cases the experimental values of µ0Hc2(0) are much smaller than the Pauli limiting field, suggesting that all compounds are the conventional type-II superconductors. Table S1 (SM) gathers μ0Hc2(0) values obtained from GL and WHH models.

Figure 6
figure 6

The electrical resistivity versus temperature measured in zero applied magnetic field for ScOs2 (a), YOs2 (b), and LuOs2 (c). Insets show the superconducting transition under various magnetic fields. (d) The temperature dependence of the upper critical field of all compounds, determined from electrical resistivity measurements.

Full size image

Consequently, the coherence length, ξGL, can be estimated using the Ginzburg–Landau formula \(H_{{c2}} = \Phi _{0} /2\pi \xi _{{GL}}^{2}\), where Ф0 = hc/2e is the quantum flux. Having μ0Hc2(0) values, the GL coherence length ξGL is 113 Å for ScOs2, 121 Å for YOs2, and 141 Å for LuOs2. The superconducting penetration depth λGL(0) can then be obtained from Hc1(0) and ξGL(0) using the relation: \({H}_{c1}= \frac{{\Phi}_{0}}{4\pi {\lambda }_{GL}^{2}}\mathrm{ln}\frac{{\lambda }_{GL}}{{\xi }_{GL}}.\) The value is found to be λGL(0) = 1513 Å for Sc variant, λGL(0) = 2440 Å for Y variant, and λGL(0) = 3270 Å for Lu variant. The obtained values are comparable with these reported for the cubic Laves phases e.g., BaIr2 (1520 Å45), SrIr2 (2370 Å36) or SrRh2 (2291 Å36). Furthermore, the GL parameter \({\upkappa }_{GL}\)= λGL/ξGL equals 13, 20, and 23 for ScOs2, YOs2 and LuOs2, respectively, which are clearly larger than 1/\(\sqrt{2}\), implying that all investigated Laves compounds are the type-II superconductors. Finally, the thermodynamic critical field can be obtained from κGL, Hc1, and Hc2 using the formula: \({H}_{c1}{H}_{c2}={H}_{c}^{2}\mathrm{ln}{\upkappa}_{GL}\), yielding µ0Hc = 136 mT for ScOs2, 78 mT for YOs2, and 50 mT for LuOs2. The superconducting and normal state parameters of all compounds are gathered in Table 1.

Table 1 Superconducting and normal state parameters of ROs2 (R = Sc, Y, Lu).
Full size table

To further understand the electronic structure of ScOs2, YOs2 and LuOs2 we performed electronic DOS and band-structure calculations (see Fig. 7). DFT calculations show that the DOS in the vicinity of the Fermi level in all three cases is dominated by Os 5d states, with electropositive elements (Sc, Y, Lu) acting mostly as electron donors. Inclusion of the spin–orbit coupling does not significantly affect the DOS(EF).

Figure 7
figure 7

Band structure and electronic density of states for ScOs2 (a,b), YOs2 (c,d), and LuOs2 (e,f). In all three compounds the DOS(EF) is dominated by the contribution of Os 5d states. Besides the splitting of the completely occupied 4f band in LuOs2 (peak ca. − 4 to − 6 eV below the EF), the difference between fully- (FR; blue line in panels b,d,f) and scalar-relativistic (SR; gray line) is rather small.

Full size image

The broad peak-like feature of DOS within 1 eV around the Fermi level stems from several weakly dispersive Os d-dominated bands, followed by a number of highly dispersive bands between ca. 0 and − 6 eV (Fig. 8a,b). This is highly reminiscent of a generic tight-binding kagome band structure, as shown in Fig. 8c,d. Kagome-like bands bear a strong contribution of Os1 d states, while the Os2 d mostly contributes to a set of weakly dispersive bands around − 2 to − 3 eV below the EF.

Figure 8
figure 8

Band structure of ScOs2 with Os1 d (a) and Os2 d (b) contribution highlighted (proportional to the color intensity). Os1 dominates the kagome-like bands between 0 and − 6 eV, while Os2 contributed mostly to a number of weakly dispersive bands between − 2 and − 3 eV. Panel (d) shows the tight binding band structure of a kagome system within 3 approximations: in the simplest case (thick gray lines) only nearest-neighbor interactions are considered and all the nearest neighbor tight binding hopping integrals are set to be equal (t1, t2 = − 1), resulting in a perfect p6m kagome. When the hexagonal symmetry is broken in breathing kagome (brown line; t1 = − 1, t2 = 0.9), the Dirac point at K is gapped, but the flat band remains intact. Inclusion of next-nearest neighbor interaction (orange line, t1 = − 1, t2 = 0.9, t3 = 0.1) results in the flat band attaining some dispersion. The three tight-binding models are schematically drawn in panel (c).

Full size image

Obviously, the band structure is much more complicated than e.g. in AV3Sb5 kagome superconductors46 or in CoSn10. This is due to: (1) the presence of two Os layers (kagome + trigonal) that are within the interacting range, resulting in significant hybridization of kagome bands, (2) fairly large unit cell consisting of 2 individual kagome planes, (3) trigonal distortion (breathing kagome), lifting the degeneracy at the K point and resulting in a gap between the Dirac bands.

Nevertheless, the set of weakly dispersive bands forming the DOS around the Fermi level can be traced back to the kagome flat band that is “bent” by interactions (Fig. 8c).

Summary

In summary, a detailed investigation of superconducting and normal state properties of ROs2 (R = Sc, Y, Lu) hexagonal Laves compounds is presented. Magnetic susceptibility, electrical resistivity, and specific heat capacity measurements showed that ROs2 (R = Sc, Y, Lu) are type-II superconductors with transition temperatures of Tc = 5.36, 4.55, and 3.47 K, respectively. For ScOs2 the superconducting transition is observed at a higher temperature than reported previously, but the lack of details in the previous reports does not allow us to speculate about why the Tc is different from ours. The normalized specific heat jumps, ΔC/γTc, is calculated to be 1.51, 1.22, and 1.41 for ScOs2, YOs2, and LuOs2, evidencing the bulk nature of the superconductivity in these materials. Our band structure calculations showed that the dominating contribution to DOS(EF) came from 5d states of Os atoms. The overall domination of Osmium 5d states suggests that ROs2 compounds are Os 5d-band metals and that 5d electrons play the dominant role in superconductivity.

In addition to the superconducting properties, the studied compounds also exhibit a unique lattice structure. The Os atoms in these compounds form a trigonal breathing kagome lattice, a distorted variant of the hexagonal kagome. The band structure of the ROs2, although complicated, can be traced back to a generic kagome band model, modified by the breathing distortion and interlayer interactions.